A new class of Appell-type Changhee-Euler polynomials and related properties

1.   Introduction

Leptospirosis is an acute systemic infectious disease caused by various pathogenic leptospira, which belongs to natural foci disease. It is epidemic almost all over the world, especially severe in Southeast Asia. Most provinces, cities, and autonomous regions in China have the existence and epidemic of this disease. Rodents and pigs are the two major sources of infection, while other livestock such as cattle, pigs, and pets like cats, dogs, and mice may also transmit leptospirosis. Typically, pathogenic leptospira can survive longer in a warm and humid environment. People may contract the disease through ingestion of contaminated food or water, or when the bacteria enter the body through scratches on the skin or mucous membranes [1].

The application of mathematical models in leptospirosis research has also become increasingly widespread. Through numerical simulations and data analysis, we can delve deeper into the transmission mechanisms and dynamic characteristics of the disease, providing more precise and effective means for disease prevention and control. Regarding the research on mathematical models of leptospirosis, please refer to the literature [2,3,4,5,6]. These models analyze the factors that influence the transmission dynamics of leptospirosis, pointing out that disease transmission is not only related to the interaction between rodents and humans [4], but also to their contact with free bacteria in the environment [6]. They also demonstrate that adopting appropriate intervention mechanisms, such as reducing the transmission rate, increasing the recovery rate, reducing rodent populations, and reducing bacterial contamination in water sources, can greatly assist in reducing the spread of the disease in the population.

In the real world, infectious disease models are inevitably affected by environmental noise, and deterministic models alone cannot accurately reflect the dynamic behavior of the system when describing disease transmission processes. In recent years, most scholars have explored stochastic infectious disease models that consider environmental perturbations [7,8,9,10,11,12]. The research results indicate that random perturbations have a certain impact on the spread of diseases.

Therefore, it is highly necessary to further establish and study leptospirosis models that consider vector-environment interactions and random disturbances.

To establish the model, we make the following assumptions.

(ⅰ) Susceptible individuals who come into contact with infected vectors or free bacteria in the environment can become infected individuals, and susceptible vectors that come into contact with infected individuals or free bacteria in the environment can also become infected vectors.

(ⅱ) Infected individuals and vectors both release free bacteria into the environment.

(ⅲ) The host population $S_h(t), I_h(t), S_h(t)$, vector population $S_v(t), I_v(t)$, and the concentration of bacteria in the environment are all influenced by Gaussian white noise.

(ⅳ) The recruitment rate $\Lambda$ and the birth rate $\Pi$ of the vectors are constants. Every parameter within the system is a nonnegative real number.

Base on the above assumptions, we establish and study a stochastic model of leptospirosis with host-vector-environment interactions:

where the host population, which represents the human population, is divided into three categories at time $t$: susceptible individuals $S_h(t)$, infected individuals $I_h(t)$, and recovered individuals $R_h(t)$. The vector population is divided into susceptible vectors $S_v(t)$ and infected vectors $I_v(t)$ at time $t$. Additionally, $B(t)$ represents the free-floating bacterial population in the environment. The meanings of the parameters are as follows. $\beta_1$ and $\beta_2$ represent the infection rates of diseased vectors transmitting the disease to humans and of infected humans transmitting the disease to vectors, respectively. $\beta_3$ and $\beta_4$ represent the rates at which susceptible humans and susceptible vectors become infected through contact with bacteria in the environment. $\mu_h$ and $\mu_v$ are natural mortality rate for the human population and the vector population, and $\gamma_h$ represents the disease-induced mortality rate among humans. $\delta_h$ represents the recovery rate for infected humans, while $\lambda_h$ represents the rate at which recovered humans revert back to the susceptible state. $\alpha_1$ and $\alpha_2$ represent the rates at which infected humans and infected vectors release bacteria into the environment, respectively. $K$ serves as a half-saturation infection parameter, and $k$ is the decay rate of bacteria in the environment. $B_i(t)\, \, (i = 1, 2, 3, 4, 5, 6)$ are standard Brownian motions. Parameters $\sigma_i\, \, (i = 1, 2, \cdots, 6)$ are the intensities of noise, representing variability and stochastic effects: $\sigma_1$ represents the variability in the susceptible individuals $S_h(t)$, which arise from fluctuating contact rates or changes in population behavior that affect exposure to the virus environment and infected vectors; $\sigma_2$ reflects the random fluctuations in the number of the infected population $I_h(t)$ due to variations in the disease's infectiousness, or response to treatment; $\sigma_3$ represents stochastic factors affecting the recovered population $R_h(t)$, such as loss of immunity or the impact of interventions; $\sigma_4$ represents the variability in the susceptible vectors $S_v(t)$, which arise from fluctuating contact rates or changes in population behavior that affect exposure to the Leptospira virus environment and infected individuals; $\sigma_5$ reflects the random fluctuations in the number of the infected vectors $I_v(t)$ due to variations in the disease¡¯s infectiousness; $\sigma_6$ represents the random variation intensity of Leptospira virus $B(t)$ released into the environment by infected humans or disease vectors.

We assume the initial conditions are

The aim of this paper is to build a stochastic model of leptospirosis that incorporates both vector-borne and environmental transmission to more comprehensively describe the disease's transmission characteristics. Furthermore, by combining this model with actual reported data on leptospirosis in China in recent years, we aim to estimate important parameters of the model using statistical methods and predict the future trends of leptospirosis in China.

2.   The long-term behavior of the solution

To demonstrate that our proposed model is meaningful, we prove that there exists a unique global positive solution of the system (1.1).

Theorem 2.1. For any initial value $(S_h(0), I_h(0), R_h(0), S_v(0), I_v(0), B(0))\in\mathbb{R}^6_+$, the system (1.1) has a unique positive solution $(S_h(t), I_h(t), R_h(t), S_v(t), I_v(t), B(t))$, and the solution will remain in $\mathbb{R}^6_+$ with probability 1, i.e., $(S_h(t), I_h(t), R_h(t), S_v(t), I_v(t), B(t))\in\mathbb{R}^6_+$ for all $t > 0$ almost surly (a.s.).

Proof. Obviously, the system (1.1) has locally Lipschitz continuous coefficients, for any initial value $(S_h(0), I_h(0), R_h(0), S_v(0), I_v(0), B(0))\in\mathbb{R}^6_+$, and the system (1.1) exists a unique maximal local solution $(S_h(t), I_h(t), R_h(t), S_v(t), I_v(t), B(t))$, $t\in[0, \tau_e)$, where $\tau_{e}$ is the explosion time. To verify that this solution of the system (1.1) is global, we just have to prove that $\tau_{e} = \infty$ a.s. For this, assume $k_0\geq1$ is large enough such that $(S_h(0), I_h(0), R_h(0), S_v(0), I_v(0), B(0))$ all fall within the interval $[1/{k_0}, k_0]$. For each integer $k\geq k_0$, define the stopping time as:

where $\inf\varnothing=\infty$ ($\varnothing$ denotes the empty set). Clearly, when $k\rightarrow \infty$, $\tau_k$ are increasing. Let $\tau_\infty=\lim\limits_{k\rightarrow \infty}\tau_k$, then $\tau_\infty\leq\tau_e$ a.s. If $\tau_\infty=\infty$ a.s. holds, then $\tau_e=\infty$ a.s., which means that $(S_h(t), I_h(t), R_h(t), S_v(t), I_v(t), B(t))\in\mathbb{R}^6_+$ a.s. for $t\geq0$. Therefore, it suffices to prove that $\tau_\infty=\infty$ a.s.

Next, we assume that there exist constants $T > 0$ and $\varepsilon\in(0, 1)$, such that $P\{\tau_\infty\leq T\} > \varepsilon$, then, there exists an integer $k_1\geq k_0$, such that for any $k\geq k_1$,

Define the function $Q: \mathbb{R}^6_+\rightarrow \mathbb{R}_+$ as follows:

where $a_1, b_1$ are positive constants to be determined later. Obviously, the function $u-1-\rm {ln}u$ is non-negative for all $u > 0$.

Applying Itô's formula, we obtain

where

Choose $a_1= {\frac{\mu_v M_1}{\beta_1}}, b_1= {\frac{\mu_h M_1}{\beta_2}}$, such that ${\frac{a_1 \beta_1}{M_1}-\mu_v=0}, {\frac{b_1 \beta_2}{M_1}-\mu_h=0}$, and

where $K > 0$ is a constant. The remainder of the proof follows the similar approach given in [13]. □

Now, the sufficient conditions for the elimination of $I_h, I_v$ are presented. Denote $\langle f\rangle = \frac{1}{t}\displaystyle{\int}_0^t f(s)ds$, and the parameter as follows:

To facilitate the proof of the theorem, we first give a related lemma.

Lemma 2.1. [14,15,16] For any initial value $(S_h(0), I_h(0), R_h(0), S_v(0), I_v(0), B(0))$$\in\mathbb{R}^6_+$, the solution $(S_h(t), I_h(t), R_h(t), S_v(t), I_v(t), B(t))$$\in\mathbb{R}^6_+$ of model (1.1) possesses the following properties:

Proof of Lemma 2.1 can be similarly obtained by following the proof of Lemma 2.2 in reference [14]. The details are omitted here.

Theorem 2.2. Assume $(S_h(t), I_h(t), R_h(t), S_v(t), I_v(t), B(t))\in\mathbb{R}^6_+$ is the solution of model (1.1) that satisfies the initial condition $(S_h(0), I_h(0), R_h(0), S_v(0), I_v(0), B(0))\in\mathbb{R}^6_+$. If $\mathcal{R}_m < 1$, then $(I_h(t), I_v(t), B(t))$ converges to $(0, 0, 0)$ exponentially with probability one (a.s.), indicating the elimination of the disease, and furthermore,

Proof. Let $P(t) = I_h(t)+I_v(t)$. Applying Itô's formula, we have

Integrating both sides of (2.2) from $0$ to $t$ and dividing by $t$, we obtain

Notice

and

Integrating both sides of (2.4) and (2.5) from $0$ to $t$ and dividing by $t$, then, taking the upper limit, we obtain

Thus

Taking the upper limit of both sides of (2.3), and according to Lemma 2.1, we can obtain the desired result

Then

Hence

For the sixth equation in (1.1), by integrating both sides from $0$ to $t$, dividing by $t$, and then taking the upper limit, we can derive that $\lim\limits_{t\rightarrow \infty}B(t)=0$.

Similarly, applying the same method to the third equation in (1.1), we can obtain $\lim\limits_{t\rightarrow \infty}R_h(t) = 0$.

Since

based on the conclusions obtained above, we can derive that $\lim\limits_{t\rightarrow \infty}S_h(t)=\frac{\Lambda}{\mu_h}$. Similarly, we can obtain that $\lim\limits_{t\rightarrow \infty}S_v(t)=\frac{\Pi}{\mu_v}$. □

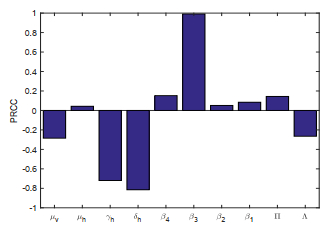
To better analyze the impact of different parameters on the spread of infectious diseases on the surface, we will proceed with a further parameter sensitivity analysis. We conduct 1000 samplings of the parameters using the Latin Hypercube Sampling (LHS) method [17]. By calculating the Partial Rank Correlation Coefficient (PRCC), we will be able to screen out the parameters that have a significant impact on the population size. This will help us identify more accurate measures to control the epidemic.

Observing Figure 1, it is evident that the parameters with significant impacts on disease transmission are $\beta_3, \delta_h, \gamma_h, \mu_v$. Here, $\beta_3$ is positively correlated with $\mathcal{R}_m$, while $\delta_h, \gamma_h, \mu_v$ are negatively correlated with $\mathcal{R}_m$. In other words, the smaller the contact rate of humans with free bacteria in the environment, the higher the human mortality rate due to the disease and the natural mortality rate of the vector population; and the faster the recovery rate from the disease, the smaller the basic reproduction number will be, making it easier to eliminate the disease. In fact, as the contact rate of humans with free bacteria in the environment declines, so does the likelihood of contracting the virus. Similarly, when the mortality rate stemming from the illness is high, infected individuals may perish during the infection period, thereby diminishing their capacity to spread the disease to others, resulting in a lower average transmission rate per infected individual. Furthermore, a high natural mortality rate among vectors lessens their chances of transmitting the disease to humans and curtails the release of virus particles into the environment. Lastly, an increase in the recovery rate of infected individuals reduces their chances of transmitting the disease to vectors. All these scenarios contribute significantly to a decrease in the $R_m$ value.

Next, we perform numerical simulations on the system (1.1) by using the high-order $Milstein$ method mentioned in [18,19], which is based on the concept of Itô's formula and stochastic Taylor expansion. The $Milstein$ method improves the accuracy of the estimates by introducing higher-order infinitesimals. Compared to the $Euler$-$Maruyama$ method, the Milstein method is more precise. However, the $Milstein$ method requires the stochastic process to be twice differentiable, which can make its implementation more complex. It is primarily suitable for stochastic differential equations with continuous sample paths. For stochastic differential equations with discontinuous sample paths or jump processes, other types of numerical methods may be required.

Assuming an initial condition of $(S_h(0), I_h(0), R_h(0), S_v(0), I_v(0), B(0)) = (400,100,150,500$, $120,$ $1000)$, the specific parameter values are as follows: $\Lambda = 35\; day^{-1},$ $\Pi = 30\; day^{-1}$, $\beta_1 = 0.004\; day ^{-1},$ $\beta_2 = 0.001\; day ^{-1}$, $\beta_3 = 0.003\; day ^{-1},$ $\beta_4 = 0.002\; day^{-1}$, $\lambda_h = 0.1\; day^{-1},$ $\delta_h = 0.6\; day^{-1}$, $\mu_h = 0.01\; day^{-1},$ $\mu_v = 0.1\; day^{-1}$, $K = 10\; cells \cdot ml ^{-1},$ $k = 0.5\; day ^{-1}$, $\alpha_1 = 0.08\; cells \cdot ml ^{-1}\cdot day ^{-1}$, $\alpha_2 = 0.09\; cells \cdot ml ^{-1}\cdot day ^{-1}$ and $\gamma_h = 0.7\; day^{-1}$.

Figures 2 and 3 demonstrate the specific time-varying situation of the number of infected individuals or infected vectors when these four parameters $\beta_3, \delta_h, \gamma_h, \mu_v$ change, while other parameters remain unchanged, respectively. From these two figures, it can be observed that despite changes in the parameters, both the infected population and the infected vectors ultimately go extinct, but the time of extinction differs. Specifically, as $\beta_3$ decreases, the extinction time of $I_h$ shortens. Similarly, when $\delta_h$ and $\gamma_h$ increase, the extinction time of $I_h$ decreases. Additionally, as $\mu_v$ increases, the extinction time of $I_v$ also shortens.

3.   Predicting the trend of leptospirosis in China

In this section, we utilize the reported leptospirosis case data in China from 2003 to 2021 to predict the future epidemic situation of the disease. The data comes from China's statistical Yearbook [20], as shown in Figure 4. The population recruitment rate of $\Lambda = 7.74\times10^6$ is estimated based on China's population statistics from 2003 to 2021, the natural death rate of humans is $\mu_h = 0.0064$, and the number of newly reported leptospirosis cases in 2003 was 1728 [20]. Assuming that the recruitment rate of vectors carrying leptospira is $\Pi = 1.0812\times10^5$, these vectors are susceptible to external factors that can lead to death, with a natural death rate of $\mu_v = 0.8125$ [21]. The specific values of the parameters are listed in Table 1.

Let the cumulative number of leptospirosis cases in the human population be defined as $D_h(t)$, and

To predict the disease, it is necessary to first estimate the two important parameters that affect the spread of the disease, namely, $\beta_1, \beta_3$. We utilize the numerical solution $D_h(t)$ from model (3.1) to fit the data. Let $\Theta(\beta_1, \beta_3)$ represent the vector of parameters to be estimated, and $D_h(t, \Theta)$ represent the numerical solution of model (3.1) corresponding to the parameters $\Theta$. The vector $Y(Y_k, k = 1, 2, 3, ..., 19)$ represents the 19 statistical data points, and $t_k$ is the corresponding time for each data point. Take the initial value of the variable as $(S_h(0), I_h(0), R_h(0), S_v(0), I_v(0), B(0), D_h(0)) = (7.74\times10^6, 1728,307, 1.0812\times10^5, 1.867\times10^3, 1.42\times10^2, 1728)$, and the initial value of the parameter $(\beta_1, \beta_3) = (3.2326\times10^{-3}, 1.2\times10^{-4})$. Random disturbance intensities are taken as $\sigma_1 = \sigma_2 = \sigma_3 = \sigma_4 = \sigma_5 = \sigma_6 = 0.1$. We estimate the parameters using two methods below: one is the least squares method, and the other is the Markov Chain Monte Carlo (MCMC) method.

1) The least squares method (LSM). The goal is to find the optimal values of $\Theta(\beta_1, \beta_3)$ that minimize the least squares criterion:

To achieve this, we utilize the fmincon command in the mathematical software MATLAB for numerical optimization. Based on the biological background, we set the ranges of $\Theta$ to be $((0, 0), \, [0.5, 0.5])$, which serve as the constraint conditions. Using the optimization algorithm, we obtain the estimated values of the parameters. Then, we run the program 100 times and calculate the average of the output parameters $\beta_1 = 0.0032308, \beta_3 = 0.00011993$, which serve as the required parameter estimates. Figure 5(a), (b) present numerical simulations of the cumulative number of leptospirosis cases in 100 sample paths and their mean output path, respectively.

2) Markov Chain Monte Carlo-Metropolis Hastings method (MCMC-MH). Now, we estimate the parameters using the MCMC parameter estimation method combined with MH sampling. Let $\Theta(\beta_1, \beta_3)$ be the proposed parameter and $\Theta'(\beta_1, \beta_3)$ be the current parameter. The proposed parameter follows $\Theta = \Theta' + \varepsilon$, where $\varepsilon$ is the step size of random walk that follows a uniform distribution. According to Bayesian statistical inference, the posterior distribution is given by:

where the likelihood function is $L(Y|\Theta) = - \sum\limits_{k = 1}^{19}|D_h(t_k, \Theta)-Y_k|^2$, and $P(\Theta)$ is the non-informative prior distribution, assumed to be a constant $C$. The acceptance probability is defined as: $\alpha(\Theta, \Theta') = \min\{1, \exp(L(Y|\Theta)- L(Y|\Theta'))\}$. The ranges of $\Theta$ are also $((0, 0),$ $[0.5, 0.5])$. After performing 5000 iterations of MCMC calculations, with a burn-in period of 1000 iterations, we computed the average of the last 4000 iterations to obtain the estimated values of the parameters as $\beta_1 = 0.0050193, \beta_3 = 0.000096193$. The 95 percent confidence interval for $\beta_1$ and $\beta_3$ is $(1.432\times10^{-3}-9.941\times10^{-3})$, ($1.5036\times10^{-5}-2.2604\times10^{-4}$), respectively. By substituting the estimated parameters into the model (3.1), we can obtain any 100 paths of $D_h(t)$. Figure 6(a), (b) present numerical simulations of the cumulative number of leptospirosis cases in 100 sample paths and their mean output path, respectively. Figure 6(c), (d) show the posterior distribution plots and trace plots for $\beta_1,$ $\beta_3$, respectively.

It can be seen from Figures 5 and 6 that both simulation results of the model (3.1) by two methods match the cumulative data of leptospirosis cases in China from 2003 to 2021. Next, we calculate the error value between the average curve and the real data, and compare the results from both two methods. It can be seen from Table 2 that the parameter values estimated by the two methods are very close, but the estimation error by the MCMC-MH method is smaller than LSM. Finally, using the parameters estimated by the MCMC-MH method, we calculate the basic reproduction number for the transmission of leptospirosis in China, $R_m\approx0.00075197 < 1$, and predict that leptospirosis will be eliminated in China in 26 years (see Figure 7).

4.   Conclusions

This article establishes a stochastic leptospirosis model with both vector and environmental transmission. Through mathematical analysis of the model, a threshold for disease elimination is derived. Then, using the partial rank correlation coefficient, an impact analysis was conducted on the model parameters to identify the key parameters that have a significant influence on disease elimination. Furthermore, a sensitivity analysis of these parameters was carried out through numerical simulations, which further revealed the mechanisms of their role in the disease transmission process. This analytical approach provides a powerful tool for gaining a deeper understanding of how model parameters affect disease transmission. In the end, using data from China's leptospirosis case reports from 2003 to 2021, two parameter estimation methods, LSM and MCMC-MH, are applied to estimate the crucial parameters of the model. The simulation results of the number of infections in model (1.1) using parameters obtained from two parameter estimation methods align well with the cumulative data of leptospirosis cases in China from 2003 to 2021. It is predicted that under the current control measures, leptospirosis in China will be completely eliminated after 26 years.

Common leptospirosis models [3,5,22] tend to only consider the interaction between hosts and vectors, overlooking the influence of environmental factors. In this paper, by incorporating environmental transmission factors into the model design and considering environmental disturbance, we construct a more comprehensive and realistic stochastic infectious disease model, providing a new perspective for a more accurate understanding of the transmission mechanisms of leptospirosis. Specifically, the parameter estimation method used in this article, which combines MH sampling with MCMC, has served as a good demonstration for parameter estimation in stochastic differential systems with numerous parameters. This approach of combining actual data with parameter estimation not only enhances the accuracy and reliability of the model, but also provides strong support for predicting the future trends of leptospirosis in China. The stochastic model of leptospirosis and its related analysis methods established in this article have important theoretical and practical significance for understanding the transmission patterns of other similar vector-borne diseases and predicting future epidemic trends.

However, it must be said that when we make predictions, we only estimate two important parameters, and some parameters are based on subjective assumptions fitted to the data, which may reduce the accuracy of the prediction. In addition, the model does not fully consider the impact of human behavior, socioeconomic factors, and climate change on disease transmission. The neglect of these factors may limit the accuracy and applicability of the model. In the future, we will incorporate human behavior, socioeconomic factors, and climate change into our model, and strive to utilize actual data to estimate more parameters in order to improve the accuracy and applicability of the model. This will help us gain a deeper understanding of the dynamics of disease transmission and design effective interventions to protect public health.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is sponsored by Nanhu Scholars Program for Young Scholars of XYNU.

Conflict of interest

The authors declare there is no conflicts of interest.