Antipredator behavior of a nonsmooth ecological model with a state threshold control strategy

1.   Introduction

Pest control plays a pivotal role in agriculture. Infestations of pests in crops can result in yield losses, reduced quality, and even total crop failure. Therefore, the implementation of effective pest control measures is essential for maintaining agricultural stability and promoting sustainable development. However, traditional pest control methods often heavily rely on chemical pesticides, which, while partially addressing pest issues, also present a range of new challenges. The excessive use of chemical pesticides may trigger issues such as soil degradation, environmental pollution, and disruption of ecosystems. To address these concerns, the Integrated Pest Management (IPM) strategy has emerged as a solution ^[1,2,3,4]. IPM combines various methods, including chemical control (such as pesticide spraying), biological control (introduction of natural predators), and physical control ^[5,6,7], in an organic and holistic approach to achieve efficient, cost-effective, and environmentally friendly pest management.

The primary objective of the IPM strategy is not the complete eradication of pests, but rather the control of their populations to acceptable levels for both crops and the environment, achieved through a combination of control measures ^[8,9,10]. This objective is rooted in practical considerations, as the complete elimination of pests is unattainable and contradicts the principles of sustainable agricultural development. Therefore, a key aspect of IPM is the utilization of strategies to manage pest populations within tolerable limits once they reach economic thresholds. The implementation of these control measures depends on the pest population density and can be described using state-dependent impulsive differential equations ^[11,12,13]. IPM strategies emphasize the reduction of chemical pesticide usage, advocating for precise application, reduced dosage, and decreased frequency, while also prioritizing the use of biological and physical control methods. By adopting these strategies comprehensively, IPM aims to achieve effective pest management while minimizing adverse impacts on the environment and non-target organisms. In doing so, it promotes agricultural stability and sustainable development ^{[14,15,16,17]}.

Furthermore, anti-predator strategies are widespread within natural prey and predator ecosystems. These tactics, employed by prey populations, serve as a vital defense mechanism against predators, playing a pivotal role in ecosystem dynamics. These defensive behaviors encompass techniques such as camouflage, concealment, toxin production, the development of protective spines, and the emission of warning signals ^[18,19,20]. In the realm of pest control, the anti-predator behaviors exhibited by insects exert a substantial influence on pest management. Many pest populations exhibit evasion, destruction of predator eggs, predation or consumption of juvenile predators, and defensive strategies to avoid natural predators. In references ^[21,22], researchers investigated the univoltine spotted lanternfly (Lycorma delicatula), which possesses features such as concealed forewings, defensive chemicals, and various behavioral defenses including rapid jumping, sudden display of conspicuous hindwings and abdomen (a startle/deimatic display), and feigning death. References ^[23,24,25] investigated how the Frankliniella occidentalis (Pergande) (Thysanoptera: Thripidae) reduces the impact of phytoseiid mites by preying on their eggs. The presence of anti-predator behaviors in pest populations significantly impacts the effectiveness of pest control measures and poses considerable challenges. Despite the hurdles posed by insects' anti-predator behaviors, a comprehensive approach that combines diverse control methods, along with continuous research and innovation, empowers us to effectively address these challenges. This approach leads to successful pest management and fosters sustainable agricultural development.

Anti-predator behaviors in the natural world take on diverse forms, making predator-prey relationships highly complex and presenting significant challenges for the analysis of pest-predator ecosystems. This article is grounded in the concept of pulse control and integrates a holistic approach to pest management. Thus, we aim to establish a pulse control model for pest-predator systems that accounts for anti-predator behaviors in which the Holling type IV functional response was also ^{[26,27,28,29]}. By exploring this model, the objective is to pinpoint optimal control strategies and offer an effective method for pest management.

The organization of our paper is structured as follows: In the upcoming section, we will introduce an innovative ecological state-dependent impulsive model incorporating antipredator behavior. Section 3 provides the dynamics of the corresponding ODE model and the definition of Poincaré maps. In Section 4, we present the sufficient conditions for the order-k periodic solution when the system lacks internal equilibria, and simultaneously derive the corresponding sufficient conditions when the system possesses internal equilibrium points in Section 5. Bifurcation analysis is conducted through a numerical method in this section. The final section offers some biological conclusions.

2.   Model formulation

In 1930, Volterra and Lotka analyzed the predation-prey relationship between predatory fish and edible fish, proposing the renowned Lotka-Volterra model. In recent years, numerous scholars have expanded upon the Lotka-Volterra model to develop a series of mathematical models for studying the dynamic behaviors and control strategies of pest-predator systems. Expanding upon the classical Lotka-Volterra model and considering the presence of anti-predator behavior, we have established the following pest-predator model with the Holling IV response function:

Here, $x(t)$ represents the pest density and $y(t)$ represents the natural-enemy density, $\delta$ is the death rate of natural enemies, $\mu$ is the prey-to-predator conversion rate, $\beta$ denotes the predation rate, and $\eta$ represents the anti-predation coefficient.

One strategy employed in IPM involves releasing natural enemies for a defined duration, followed by the application of chemical pesticides. The primary goal of IPM is to keep pest density below the Economic Injury Level (EIL), rather than striving for complete eradication. The relevant tactics are put into action when the host density exceeds the specified ET threshold. Consequently, in combination with model (2.1), we can construct the following ecological model with threshold control strategy and antipredator behavior

where $x(t^+)$ and $y(t^+)$ represent the number of pests and natural enemies, respectively, after the control strategy is applied at time $t$, we have the following definitions: $ET$ denotes the Economic Threshold, and $p\in [0, 1)$ represents the pest mortality rate due to pesticide spraying and other control methods, and $\tau$ represents the number of natural enemies released at time $t$.

3.   Poincare map

The qualitative analysis of model (2.1) is essential for comprehending the dynamic characteristics of model (2.2). Therefore, our primary emphasis will be on analyzing the dynamic behavior of Eq (2.1). The two isolines of model (2.1) are

The first and second derivatives of the function $f(x)$ with respect to $x$ are as follows

It follows from $f''(x) > 0$ that $f'(x)$ is a strictly monotonically increasing function as $x\in[0, +\infty)$, we consider the following two cases:

Case 1: $(\mu-a\eta)\leq 0$. In this case, $f'(x) > 0$ and $f(x) > f(0) = a\delta > 0$, which implies that $dy/dt < 0$ for all $x > 0$, so we can derive that $\lim_{t\to+\infty}y(t) = 0$ for any positive initial value $(x_0, y_0)$, this also indicates that natural enemy will eventually go extinct. Furthermore, by applying stability theory, model (2.1) has a stable boundary node $(K, 0)$ and an unstable saddle $(0, 0)$.

Case 2: $(\mu-a\eta) > 0$. Since $f'(x)$ is monotonically increasing as $x\in[0, +\infty)$ and $f'(0) = -(\mu-a\eta) < 0$, then $f'(x) = 0$ exists a positive root denoted by $x_g$, and

Hence, $f(x)$ is a strict decrease within $(0, x_g)$ and a strict increase within $(x_g, +\infty)$. In this case, we consider the following three subcases:

$({\bf C_1})$ The equation $f(x) = 0$ exists no positive roots, indicating that model (2.1) has no internal equilibria, in this case, which aligns with Case 1.

${\bf(C_2)}$ The equation $f(x) = 0$ exists a single positive root $x = x_g$, indicating that model (2.1) has an internal equilibrium $E_g = (x_g, y_g)$. We have

and

where $N = \sqrt {\delta^2+3\eta \big(\mu -a\eta\big)}$.

$({\bf C_3})$ The equation $f(x) = 0$ exists two positive roots denoted by $x_1$ and $x_2$, indicating that model (2.1) has two internal equilibria $E_1 = (x_1, y_1)$ and $E_2 = (x_2, y_2)$. We can use the root-finding formula ^[30] to solve the cubic equation $f(x) = 0$ and obtain two positive roots

where $A = \delta^2+3\eta (\mu-a\eta)$, $\theta = \arccos T$, $T = \frac{2A\delta-3\eta B}{2\sqrt{A^3}}$, $B = -\delta (\mu-a\eta)-9\eta a\delta$, $T\in(-1, 1)$. Then we substitute $x_i$ into $y$ and derive

Next, let's study the local stability of equilibria $E_g = (x_g, y_g)$ for model (2.1), we first calculate the Jacobian matrix of model (2.1) as

and

It follows from $f(x_g) = 0$ that $a = \frac{\eta x_g^3+\delta x_g^2-\mu x_g}{-\delta -\eta x_g}$, then

Consider the function $g(x) = \mu \delta-2\eta^2 x_g^3-4\delta \eta x_g^2-2\delta^2x_g,$ calculating the derivative of this function, we get

which indicates that $g(x)$ is monotonically decreasing. Since $f'(x_g) = 3\eta x_g^2+2\delta x_g-\big(\mu-a\eta\big) = 0$ and $f(x_g) = \eta x_g^3+\delta x_g^2-\big(\mu-a\eta\big)x_g+a\delta = 0$, we get

Thus $\left|J(x_2, y_2)\right| = 0,$ which means that $E_2$ is a degenerate equilibrium.

Furthermore, we investigate the local stability of the equilibrium $E_2 = (x_2, y_2)$, where $f'(x_g) = 3\eta x_g^2+2\delta x_g-(\mu-a\eta) = 0$ and $f(x_g) = \eta x_g^3+\delta x_g^2-\big(\mu-a\eta\big)x_g+a\delta < 0$. Then we have

and $x_g < x_2,$ this implies $g(x_2) < g(x_g) < 0.$ Thus $\left|J(x_2, y_2)\right| < 0,$ that is, $E_2$ is a saddle.

Analogously, since $f'(x_1) < 0$ and $g(x_1) = \mu \delta -2\eta^2 x_1^3-4\delta \eta x_1^2-2\delta^2x_1 > 0$, we get $\left|J(x_1, y_1)\right| > 0$ and $\text tr J(x_1, y_1) = -\frac{rx_1}{K} < 0.$ Thus, the positive equilibrium $E_1$ is stable. Meanwhile, by calculating the discriminant of the characteristic equation

$E_1$ is a node as $\sigma > 0$; otherwise, it is a focus.

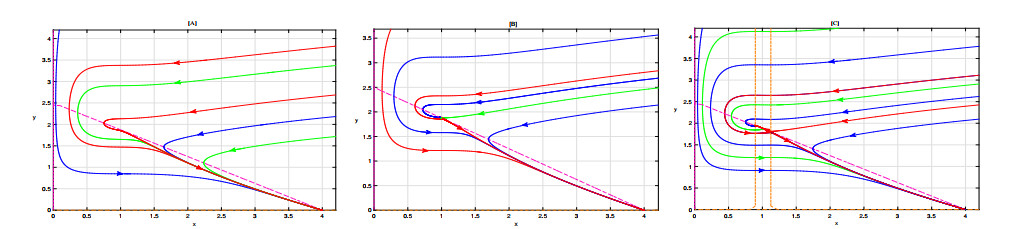
In order to better understand the dynamic behavior of model (2.1), numerical simulations were carried out for the model (2.1), as demonstrated in Figure 1. When $\mu = 0.625$, the two equilibria coincide into one equilibrium $E_g,$ as shown in Figure 1[B]. As $\mu$ decreases to $0.62$, model (2.1) exists no internal equilibrium, as shown in Figure 1[A]. When $mu$ increases to $0.63$, there are two internal equilibria, and $E_1$ is a node and $E_2$ is a saddle, as shown in Figure 1[C]. As $\mu$ continues to increase, $E_1$ changes from node to focus.

Now, we can discuss the pulse set, phase set, and Poincaré mapping of model (2.2) without internal equilibria.

For Case 1 and Case 2 ($C_1$), two lines in $R_+^2 = \big\{(x, y)|x\geq 0, y\geq 0\big\}$ are related to the pulse set and phase set:

Considering $0 < ET < K$, we can deduce that the intersection of $L_1$ and $L_4$, denoted as $Q_{ET} = (ET, y_{ET})$, and

Similarly, the intersection of $L_1$ and $L_3$ is denoted as $Q_{pET} = \Big((1-p)ET, y_{pET}\Big)$, and

Define $\Omega = \big\{(x, y)|x > 0, y > 0, x < ET \big\}\subset R_+^2,$ model (2.1) exists no internal equilibria, it has a stable boundary node $(K, 0)$ and a saddle $(0, 0)$, this implies that all initial solutions within $\Omega$ will eventually converge to $L_4$ in a finite time. Consequently, we define the pulse set $\mathcal{M}$ of model (2.2) as

and a continuous function

then the phase set $\mathcal{N}$ can be defined as

where $Y_D = [\tau, y_{ET}+\tau]$ and $(x_0^+, y_0^+)\in \mathcal{N}_0$. Obviously, any initial solution that begins at $(x_0^+, y_0^+)$ will satisfy $y_k^+ \leq y_{ET} + \tau$, where $y_0^+ > y_{ET} + \tau$.

For Case 2 $(C_2)$ and $(C_3)$, the corresponding pulse and phase sets of model (2.2) are more complex than those of Case 1 and Case 2 $(C_1)$, and we will provide a detailed explanation in Section 5.

To define the Poincaré mapping for Case 1 and Case 2 $(C_1)$, we must take into account two distinct transversals: $S_{ET}$, which pertains to the Poincaré mapping on the pulse set, and $S_{pET}$, corresponding to the Poincaré mapping on the phase set. More precisely, the definitions of these transversals are

Assume $P_k^+ = \Big((1-p)ET, y_k^+\Big)$ lies on $S_{pET}$, the solution

from $P_k^+$ will arrive $S_{ET}$ in finite time $t_1$, i.e., $x\Big(t_1, t_0, (1-p)ET, y_k^+\Big) = ET$, and we have $y_{k+1} = y\Big(t_1, t_0, (1-p)ET, y_k^+\Big)\doteq \mathcal{P}_M(y_k^+)$. After a pulse, the system will jump from $P_{k+1} = (ET, y_{k+1})$ to $P_{k+1}^+ = \Big((1-p)ET, y_{k+1}^+\Big)$, here $y_{k+1}^+ = y_{k+1}+\tau$. Thus the Poincaré mapping $P_M$ can be defined as

Similarly, assume $P_k = \left(ET, y_k\right)$ lies on $S_{ET}$, post-pulse $P_k^+ = \Big((1-p)ET, y_k+\tau\Big)$ lies on $S_{pET}$, the solution from $P_k^+$ will arrive $P_{k+1}$ in finite time $t_1$, where $P_{k+1} = (ET, y_{K+1})$ lies on $S_{ET}$. Indicating that $y_{k+1}$ is determined by $y_k$, thus Poincaré mapping $P_M$ can be defined as

For this, let

In phase space, we obtain the scalar differential equation

where $g(x, y)$ is continuously differentiable, and $\Omega_1 = \left\{(x, y)\big|x > 0, 0 < y < \frac{r}{\beta}\left(1-\frac{x}{k}\right)\right\}.$ As $\mathcal{S} < y_{pET}$, we have $x_0^+ = (1-p)ET, y_0^+\doteq \mathcal{S}, \mathcal{S}\in\mathcal{N}$, so $(x_0^+, y_0^+)\in \Omega_1,$ it gives that

It follows from equation (3.2) that

thus, the Poincaré map $P_M$ in the $\Omega_1$ is

Theorem 1. For case 1 and case 2 $(C_1)$, the Poincaré mapping $P_M$ of model (2.2) satisfies:

(i) The domain is $[0, +\infty)$, and the range is $\Big[\tau, P_M(y_{pET})\Big) = \Big[\tau, y\Big((1-p)ET, y_{pET}\Big)+\tau\Big]$ of $P_M$. Moreover, $P_M$ is monotonically increasing on $[0, y_{pET}]$ and monotonically decreasing on $[y_{pET}, +\infty)$;

(ii) $P_M$ is continuously differentiable;

(iii) $P_M$ is concave on $[0, y_{pET})$;

(iv) $P_M$ has a unique fixed point $y^*$, if $\tau > 0$, then $y^*\in (0, y_{pET})$ when $P_M(y_{pET}) < y_{pET}$, and $y^*\in (y_{pET}, +\infty)$ when $P_M(y_{pET}) > y_{pET}$.

Proof. (i) Based on model (2.1), the domain is $[0, +\infty)$, and the range is $\Big[\tau, P_M(y_{pET})\Big)$ as there exists no pulse effect. For $\forall y_{k_1}^+, y_{k_2}^+\in [0, y_{pET}]$ and $y_{k_1}^+ < y_{k_2}^+$, we have $y_{k_1+1} = y\Big((1-p)ET, y_{k_1}^+\Big) < y\Big((1-p)ET, y_{k_2}^+\Big) = y_{k_2+1}.$ That is, $P_M(y_{k_1}^+) < P_M(y_{k_2}^+),$ so $P_M$ is monotonically increasing on $[0, y_{pET}].$

For $\forall y_{k_i}^+\in [y_{pET}, +\infty), i = 1, 2$ and $y_{k_1}^+ < y_{k_2}^+$, the orbital $\Psi\Big(t, t_0, \big(1-p\big)ET, y_{k_i}^+\Big)$ will first meet $L_3$ and then intersect with $L_4.$ Here we denote the intersection points of $\Psi\Big(t, t_0, \big(1-p\big)ET, y_{k_i}^+\Big)$ and $L_4$ as $\overline{y}_{k_1}^+ = \Big(\big(1-p\big)ET, y_{k_1}^+\Big)$ and $\overline{y}_{k_2}^+ = \Big(\big(1-p\big)ET, y_{k_2}^+\Big)$. Noting that $\overline{y}_{k_1}^+ = \Big(\big(1-p\big)ET, y_{k_1}^+\Big) > \overline{y}_{k_2}^+ = \Big(\big(1-p\big)ET, y_{k_2}^+\Big)$, and $\overline{y}_{k_1}^+, \overline{y}_{k_2}^+\in [0, y_{pET}]$, then $P_M(y_{k_1}^+) = P_M(\overline{y}_{k_1}^+) > P_M(\overline{y}_{k_2}^+) = P_M(y_{k_2}^+)$. So $P_M$ is monotonically decreasing on $[y_{pET}, +\infty).$ (ii) In fact, $P(x, y)$ and $Q(x, y)$ in model (2.1) are continuously differentiable for $x, y > 0$, which satisfies the continuity and differentiability of the solution with respect to the initial values. Therefore, by applying the Cauchy-Lipschitz theorem, $P_M$ is continuously differentiable.

(iii) It follows from model (3.2) that

and we have $\left[\frac{\mu x}{a+x^2}-\delta-\eta x\right] < 0$ and $\left[rx\left(1-\frac{x}{K}\right)-\beta xy\right] > 0$ as $x < ET$ and $y < y_{pET}$, that is, $\frac{\partial g}{\partial y} < 0$ and $\frac{\partial^2 g}{\partial y^2} < 0$ when $y < y_{pET}$.

From Cauchy-Lipschitz theorem for scalar equation, we can derive that

and

thus $P_M$ is concave when $y < y_{pET}.$ (iv) $P_M$ is continuous and monotonically decreasing on $[y_{pET}, +\infty)$ and $P_M(0) = \tau\ge0$, so there exists $\tilde{y}\in[y_{pET}, +\infty)$ such that $P_M(\tilde{y}) < \tilde{y}$. Therefore, $P_M$ exists a fixed point $y^*$ on $[0, +\infty)$.

If $\tau > 0$ and $P_M(y_{pET}) < y_{pET}$, it follows from $P_M$ is monotonically decreasing on $[y_{pET}, +\infty)$ that $P_M(y_k^+) < P_M(y_{pET}) < y_{pET}$ for $y_k^+\in[y_{pET}, +\infty)$, i.e., $P_M$ does not have any fixed point on $[y_{pET}, +\infty)$, since $P_M$ is concave on $(0, y_{pET})$, so $P_M$ has a unique fixed point on $[y_{pET}, +\infty)$.

If $\tau > 0$ and $P_M(y_{pET}) > y_{pET}$, $P_M$ is concave with $P_M(0) > 0$, there exists no fixed point on $(0, y_{pET})$. Based on the monotonicity of $P_M$ over the interval, it is known that the fixed point of $P_M$ is unique on $[y_{pET}, +\infty)$. The proof is complete. □

4.   Global dynamics analysis of model (2.2) without internal equilibrium

4.1.   Existence and stability of order-1 periodic solution

For Case 1 and Case 2 ($C_1$), the chemical control is employed, i.e., $\tau = 0$, in this situation, and the density of pests will decrease. This could potentially lead to extinction of natural enemies; thus, we have the following subsystem

solving the above equation yields

with $x(0^+) = (1-p)ET$. If the solution $x(t)$ reaches $L_4$ at time $T$, then

i.e.,

Therefore, model (4.1) has a periodic solution

with a period $T$.

Theorem 2. For Case 1 and Case 2 ($C_1$), if $\tau = 0$, the boundary order-1 periodic solution $\Big(x^T(t), 0\Big)$ of model (2.2) is globally asymptotically stable.

Proof. We first prove the local stability of the solution $\Big(x^T(t), 0\Big)$. Denote $\phi(x, y) = x-ET, \quad \alpha(x, y) = -px$ and $\beta(x, y) = \tau$, it gives

and it can be obtained

where

Therefore, we can derive that

Considering $\mu_2$ as a function of $p\in[0, 1]$, and taking the derivative of $\mu_2$ with respect to $p$ yields

where $M = (1-p)ET$. Then $\frac{d\mu_2(p)}{dp} = 0$ is equivalent to

Since there is no internal equilibrium (i.e., $(\mu < a\eta)$ or $f(x_g) > 0$), we have $F_1(M) > 0$, which implies that $\frac{d\mu_2(p)}{dp} < 0$ (i.e., $\mu_2$ is strictly monotonically decreasing). Hence, $|\mu_2| < 1$ for $p\in(0, 1]$, the solution $\Big(x^T(t), 0\Big)$ is local stability.

Next, we prove the global attraction of $\Big(x^T(t), 0\Big)$. When $k\geq 0$ and $ET < K$, the impulse point sequence $y_k^+$ from phase set $\mathcal{N}$ satisfies $y_k^+\in [0, y_{pET})$, and we have $\frac{dy}{dt} < 0$ for any $x\leq ET$, $y_K^+$ is strictly monotone decreasing sequence, and $\lim\limits_{k\to\infty}y_k^+ = y^* = 0$. Otherwise, if $x\leq ET$, it would contradict the condition that $\frac{dy}{dt} < 0$. Therefore, $\Big(x^T(t), 0\Big)$ is globally asymptotically stable. The proof is complete. □

Furthermore, we have verified the above conclusion in Theorem 2 through numerical means. If $\tau = 0$, Case 1 and Case 2 $(C_1)$ hold true, the solution $\Big(x^T(t), 0\Big)$ is stable. Specifically, the natural enemy gradually reduces and eventually goes extinct, and the pest population oscillates periodically with a relatively high frequence, as shown in Figure 2[A]. If $\tau = 0.01$, then pests and natural enemies can coexist, there exists an internal order-1 periodic solution, as shown in Figure 2[B].

4.2.   Existence and stability of order-k periodic solution

When we implement both chemical and biological control strategies simultaneously (i.e., $p, \tau\neq 0$), the dynamic behavior of model (2.2) becomes highly complex. We consider the following three cases: (i) $P_M(y_{pET}) < y_{pET}$; (ii) $P_M(y_{pET}) = y_{pET}$; (iii) $P_M(y_{pET}) > y_{pET}$.

For Case 1 and Case 2 $(C_1)$, when $ET < K$, there exists an infinite sequence $y_n^+ = P_M^n(y_0^+)$ with $y_0^+\in[0, +\infty)$.

Theorem 3. If $P_M(y_{pET}) < y_{pET}$, then $P_M$ has an unique fixed point $y^*$ that is globally asymptotically stable.

Proof. From Theorem 1, it gives that $P_M(y^*) = y^*$ for $P_M(y_{pET}) < y_{pET}$ and $y^*\in(0, y_{pET})$.

For $\forall y_0^+\in[0, y^*),$ since $P_M$ is concave and monotonically increasing on $[0, y_{pET})$, we have $y^* = P_M(y^*) > P_M(y_0^+) > y_0^+$. Thus $P_M^n(y_0^+)$ is monotonically increasing and $\lim\limits_{n\to+\infty}P_M^n(y_0^+) = y^*$.

For $\forall y_0^+\in(y^*, +\infty)$, there are two subcases: (a) For all $n$, $P_M^n(y_0^+) > y^*$. Obviously, $y^* = P_M(y^*) < P_M(y_0^+) < y_0^+$, this indicates that $P_M^n(y_0^+)$ is monotonically decreasing, so we have $\lim\limits_{n\to+\infty}P_M^n(y_0^+) = y^*$; (b) There exists an integer $n_1$ such that $P_M^n(y_0^+) < y^*$ for $n > n_1$. Analogously, we can obtain that the sequence $P_M^{n_1+j}(y_0^+)$ is monotonically increasing, thus $\lim\limits_{j\to+\infty}P_M^{n_1+j}(y_0^+) = y^*$. The proof is complete. □

Theorem 4. If $P_M(y_{pET}) = y_{pET}$, then $P_M$ has a unique fixed point $y^*$ that is globally asymptotically stable.

The proof is similar to that of Theorem 3, therefore, the proof process is omitted.

Theorem 5. If $P_M(y_{pET}) > y_{pET}$ and $P_M^2(y_{pET})\geq y_{pET}$, then $P_M$ has a stable fixed point or stable two-point ring, that is model (2.2) has a stable order-1 or order-2 periodic solution.

Proof. For $\Big((1-p)ET, y_0^+\Big)\in \mathcal{N}$, when $y_0^+\in[0, y_{pET}]$, $P_M$ exists no fixed point and increases monotonically on $[0, y_{pET})$. There is an integer $n$ such that $y_{n-1}^+ < y_{pET}\leq y_n^+$ and $y_n^+ = P_M(y_{n-1}^+)\leq P_M(y_{pET}),$ so $y_n^+\in\big[y_{pET}, P_M(y_{pET})\big]$. When $y_0^+\in (y_{pET}, +\infty),$ the Poincaré mapping $P_M$ decreases monotonically on $(y_{pET}, +\infty)$, and we can obtain $y_1^+ = P_M(y_0^+)\leq P_M(y_{pET})$ and $y_n^+\in[y_{pET}, P_M(y_{pET})]$ as $n > 1$, i.e., there exists an integer $n$ such that $P_M^n(y_0^+)\in\big[y_{pET}, P_M(y_{pET})\big]$. Moreover

thus $P_M^2$ is monotonically increasing.

For any $y_0^+\in\Big[y_{pET}, P_M(y_{pET})\Big]$, assuming $y_1^+ = P_M(y_0^+)\neq y_0^+$ and $y_2^+ = P_M^2(y_0^+)\neq y_0^+$, which means that the solution of model (2.2) from $\Big(\big(1-p\big)ET, y_0^+\Big)$ is not a order-1 (or order-2) periodic. Based on reference^[31], we consider the following four cases:

(i) $P_M(y_{pET})\geq y_1^+ > y_0^+ > y_2^+\geq y_{pET}$. In this case, we have $y_3^+ = P_M(y_2^+) > P_M(y_0^+) = y_1^+$ and $y_4^+ = P_M(y_3^+) < P_M(y_1^+) = y_2^+$, further leading to $y_3^+ > y_1^+ > y_0^+ > y_2^+ > y_4^+$ and

(ii) $P_M(y_{pET})\geq y_1^+ > y_2^+ > y_0^+\geq y_{pET}$. In this case, it gives that $P_M(y_1^+) = y_2^+ < y_3^+ = P_M(y_2^+) < P_M(y_0^+) = y_1^+$ and $P_M(y_2^+) = y_3^+ > y_4^+ = P_M(y_3^+) > P_M(y_1^+) = y_2^+$, we can obtain that $y_1^+ > y_3^+ > y_4^+ > y_2^+ > y_0^+$ and

(iii) $y_{pET}\leq y_1^+ < y_0^+ < y_2^+\leq P_M(y_{pET})$. Similar to (i), we have

(iv) $y_{pET}\leq y_1^+ < y_2^ + < y_0^+\leq P_M(y_{pET})$. Similar to (ii), we have

For Cases (ii) and (iv), there exists a unique $y^*\in\Big[y_{pET}, P_M(y_{pET})\Big]$ such that $\lim\limits_{n\to\infty}y_{2n+1} = \lim\limits_{n\to\infty}y_{2n} = y^*$. Alternatively, there may exist $y_1^*, y_2^*\in\Big[y_{pET}, P_M(y_{pET})\Big]$ with $y_1^*\neq y_2^*$ such that $\lim\limits_{n\to\infty}y_{2n+1} = y_1^*$ and $\lim\limits_{n\to\infty}y_{2n} = y_2^*$. For Cases (i) and (iii), only the latter is true. The proof is complete. □

Theorem 6. If $P_M(y_{pET}) > y_{pET}$ and $P_M^2(y^+) > y^+\Big(y^+\in[y_{pET}, y^*)\Big)$, then the order-1 periodic solution of model (2.2) is globally stable.

Proof. We will prove Theorem 6 by considering three cases: (a) $y^+\in[y_{pET}, y^*)$; (b) $y^+\in[y^*, +\infty)$ and (c) $y^+\in[0, y_{pET})$.

For Case (a), note that $P_M(y_{pET})\geq P_M(y^+) > y^*$ and $P_M^2(y^+) > y^+$ for all $y^+$, we have $y^+ < P_M^2(y^+) < y^*$, and then it gives that $P_M(y_{pET})\geq P_M(y^+) > P_M^3(y^+) > y^*$ and $y^+ < P_M^2(y^+) < P_M^4(y^+) < y^*$. By mathematical induction we have $P_M^{2j}(y^+)$ is monotonically increasing, and $\lim\limits_{j\to\infty} P_M^{2j}(y^+) = y^*$ for any $j\geq1$ and $P_M^{2j-1}(y^+)$ monotonically decreasing, and $\lim\limits_{j\to\infty} P_M^{2j-1}(y^+) = y^*$ for any $j\geq1$.

For Case (b), if $P_M^j(y^+) > y^*$ for all $j$, it follows from $P_M(y^+) < y^+$ that $P_M^j(y^+)$ is monotonically decreasing and $\lim\limits_{j\to\infty} P_M^{j}(y^+) = y^*$. Otherwise, there exists a positive integer $m$ such that $P_M^m(y^+)\in[y_{pET}, y^*)$.

For Case (c), $P_M$ is monotonically increasing, there exists a positive integer $m$ such that $P_M^m(y^+)\in[y_{pET}, y^*)$ or $P_M^m(y^+) > y^*$, then the conclusion can be drawn from Cases (a) and (b). □

Theorem 7. If $P_M(y_{pET}) > y_{pET}$ and $P_M^2(y_{pET}) < y_c^+ = \min\big\{y^+ : P_M(y^+) = y_{pET}\big\}$, then model (2.2) has a non-trivial order-3 periodic solution.

Proof. From Theorem 2, the unique fixed point $y^*$ of the $P_M$ satisfies $y^*\in\Big(y_{pET}, P_M(y_{pET})\Big).$ Denote $Z(y) = P_M^3-y\in C[0, +\infty)$, we get

and

Therefore, there exists $\tilde{y}^*\in(0, y_c^+)$ such that $P_M^3(\tilde{y}^*) = \tilde{y}^*$. As $y_c^+ < y_{pET} < y^*$ and $y^*$ is unique, we conclude that model (2.2) has a non-trivial periodic solution of order-3 with the initial value $\Big(\big(1-p\big)ET, \tilde{y}^*\Big)$. The proof is complete. □

Theorem 7 provides only sufficient conditions for the existence of a non-trivial order-3 periodic solution in model (2.2). For order $k$ $(k\geq3)$ periodic solution, it is generally challenging to determine precise conditions for the existence of a system's solution through general theorems or formulas. Therefore, in these instances, reliance on numerical simulations is necessary for bifurcation analysis.

As shown in Figure 3[A] and Figure 3[B], we have investigated the bifurcation diagrams of model (2.2) through numerical methods, which demonstrate the complex dynamical behavior of model (2.2). As the bifurcation parameters $p$ and $\tau$ change respectively, model (2.2) exhibits a series of bifurcation phenomena such as period doubling, chaos, periodic window, period halving and so on. The emergence of these phenomena is due to model (2.2) transitions from an order-1 periodic solution to an order-k periodic solution, and then reverts to an order-1 periodic solution.

5.   Global dynamics analysis of model (2.2) with internal equilibrium

For Cases $(C_2)$ and $(C_3)$, model (2.2) exhibits either one or two equilibria. In such cases, the Poincaré map lacks a well-defined nature, and both its domain and range become notably intricate. Consequently, we will delve into a detailed examination of the pulse set and phase set associated with the Poincaré mapping.

5.1.   Determination of pulse sets and phase sets

For Case $(C_3)$, model (2.2) has two internal equilibria.

(i) As $\sigma < 0$, $E_1$ is a stable focus.

When $x_1 < K\leq x_2$, there exists only an internal equilibrium $E_1$, any solution to model (2.2) that begins at $\Big(\big(1-p\big)ET, y_0^+\Big)$ passes through an infinite number of pulses when $ET < x_1$, and model (2.2) has a trajectory $\Gamma_1$ tangent to $L_3$, we denote the tangent point as $Q_{pET}\Big(\big(1-p\big)ET, y_{pET}\Big)$. The orbital trajectory $\Gamma_1$ intersects the line $L_4$ at $Q(ET, y_Q)$. Thus, the pulse set and phase set can be defined respectively as

here $Y_{D_1} = [\tau, y_Q+\tau]$. There is a trajectory $\Gamma_1$ tangent to $L_4$ at $Q_{ET}$ and intersecting $L_2$ at $P(x_3,y_3)$ as $x_1\leq ET$. $\Gamma_2$ is tangent to $L_3$ at this point, as shown in Figure 4[A].

If $(1-p)ET < x_3$, the pulse set is $\mathcal{M}_1$ and the phase set is $\mathcal{N}_1$. If $(1-p)ET\geq x_3$, $\Gamma_2$ intersects with $L_3$ at $P_1\Big(\big(1-p\big)ET, y_{Q_1}\Big)$ and $P_2\Big(\big(1-p\big)ET, y_{Q_2}\Big)$ respectively, so the pulse set is $\mathcal{M}$, and the phase set is

where $Y_{D_2} = \big\{[0, y_{Q_1}]\bigcup[y_{Q_2}, +\infty)\big\}\bigcap D$. Any solution that initiates from $(x^+, y^+) \in \mathcal{N}$ does not exhibit pulsing behavior when $y_{Q_1} < y^+ < y_{Q_2}$.

When $K > x_2,$ we consider the following two cases based on the different positions of the threshold $ET$ and the equilibria $E_1, E_2$.

For Case $I_1$, if $(1-p)ET < x_3$, then the pulse and phase sets are $\mathcal{M}_1$ and $\mathcal{N}_1$, respectively. If $(1-p)ET\geq x_3$, then the pulse set is $\mathcal{M}$, and the phase set is $\mathcal{N}_2$.

For Case $I_2$, the unstable manifold $L_{U_1}$ approaching $(K, 0)$ intersects $L_4$ at $U(ET, y_{U_1})$, if $(1-p)ET\leq x_2$, then the unstable manifold $L_{U_2}$ tending to $E_2$ intersects $L_3$ at two points: lower point is $U_{min}\Big(\big(1-p\big)ET, y_{U_{min}}\Big)$ and the higher one is $U_{max}\Big(\big(1-p\big)ET, y_{U_{max}}\Big)$, as shown in Figure 4[B], so the pulse and phase sets can be defined respectively as

where $y_{D_3} = \big\{[0, y_{U_{min}})\bigcup(y_{U_{max}}, +\infty)\big\}\bigcap D$.

If $(1-p)ET > x_2$, the solutions that initiate from $Q_{pET}$ intersect $L_4$ at $Q_{ET}$, and any solutions that begin with $\Big(\big(1-p\big)ET, y^+\Big)$ intersect $L_4$ as well. Therefore, the pulse set is $\mathcal{M}_1$, and the phase set is $\mathcal{N}_1$.

(ii) When $\sigma > 0,$ $E_1$ is a stable node.

For $x_1 < K\leq x_2$, when $ET < x_1$ the pulse and phase sets are $\mathcal{M}_1$ and $\mathcal{N}_1$. When $ET > x_1$, based on $(1-p)ET\geq 0$, the orbit originating from the phase set may converge towards a stable node $E_1$ of the system along the direction of the asymptotes. During this period, it is not possible to ascertain whether the system will reach the pulse set. Consequently, the domain of the pulse set and the phase set cannot be determined.

When $K > x_2,$ we consider the following two cases:

For Case $II_1$, based on $(1-p)ET < x_1$, the pulse set is $\mathcal{M}_1$ and the phase set is $\mathcal{N}_1$.

For Case $II_2$, similar to Case $I_1$, the unstable manifold $L_{U_1}$ approaching $(K, 0)$ intersects $L_4$ at $U(ET, y_{U_1})$, if $(1-p)ET\leq x_2$, then the unstable manifold $L_{U_2}$ tending to $E_2$ intersects $L_3$ at two points: lower point is $U_{min}\Big(\big(1-p\big)ET, y_{U_{min}}\Big)$ and the higher one is $U_{max}\Big(\big(1-p\big)ET, y_{U_{max}}\Big)$, as shown in Figure 4[C], so the pulse and phase sets can be defined respectively as $\mathcal{M}_2$ and $\mathcal{N}_3,$

If $(1-p)ET > x_2$, the solutions that initiate from $Q_{pET}$ intersect $L_4$ at $Q_{ET}$, and any solutions that begin with $\Big(\big(1-p\big)ET, y^+\Big)$ intersect $L_4$ as well. Therefore, the pulse set is $\mathcal{M}_1$, and the phase set is $\mathcal{N}_1$.

For Case $(C_2)$, model (2.2) has one internal equilibrium $E_g$, we consider the following two cases:

When $ET\leq x_g$, the pulse set is $\mathcal{M}_1$, phase set is $\mathcal{N}_1$. When $ET > x_g$, similar to Case $I_1$, the unstable manifold $L_{U_1}$ approaching $(K, 0)$ intersects $L_4$ at $U(ET, y_{U_1})$.

If $(1-p)ET\leq x_g$, then the unstable manifold $L_{U_2}$ tending to $E_g$ intersects $L_3$ at $U_{min}\Big(\big(1-p\big)ET, y_{U_{min}}\Big)$ and $U_{max}\Big(\big(1-p\big)ET, y_{U_{max}}\Big)$, as shown in Figure 4[D], so the pulse and phase sets are $\mathcal{M}_2$ and $\mathcal{N}_3$.

If $(1-p)ET > x_g$, the solutions starting from $Q_{pET}$ intersect $L_4$ at $Q_{ET}$, and any solutions starting from $\Big(\big(1-p\big)ET, y^+\Big)$ also intersect $L_4$. Therefore, the pulse set is $\mathcal{M}_1$, and the phase set is $\mathcal{N}_1$.

5.2.   Stability switching of the boundary order-1 periodic solution $(x^T(t), 0)$ of model (2.2)

For Cases $(C_2)$ and $(C_3)$, as $p$ is defined in (4.2) and $\mu_2 > 1$, the $\Big(x^T(t), 0\Big)$ may exhibit instability. For this, we assume that the model (2.1) has at least one internal equilibrium.

Theorem 8. For Case $(C_3)$, if $\mu_2 > 1, \tau = 0$ and Poincaré mapping $P_M$ is well defined, then the solution $\Big(x^T(t), 0\Big)$ of model (2.2) is unstable. Moreover, there exists an internal order-1 periodic solution.

Proof. As $\mu_2 > 1$, the solution $\Big(x^T(t), 0\Big)$ is unstable. To prove model (2.2) has an internal order-1 periodic solution, we need to show that $P'_M(0) > 1$. Since

so $P'(0) = P'_M(0) = \mu_2 > 1$, it follows from Theorem 1 that $P_M$ is defined, then $P_M$ and the identical mapping have a point of intersection. Hence, model (2.2) exists an internal order-1 periodic solution. The proof is complete. □

For Case $(C_3)$, if $ET > x_2$, there are two roots from Eq (4.2)

When $\mu_2(p_1) > 1$, there are two threshold values, $p_3$ and $p_4$, such that for $p\in(0, p_3)\cup(p_4, 1)$, $\mu_2(p) < 1$ holds, while for $p\in(p_3, p_4)$, $\mu_2(p) > 1$ holds. This implies that is stable when the mortality rate of the insecticide is either low or high. However, when the mortality rate of the insecticide is maintained at a moderate level, $\Big(x^T(t), 0\Big)$ becomes unstable, allowing the coexistence of pests and natural enemies, $\Big(x^T(t), 0\Big)$ is stable as $p = 0.2$, as shown in Figure 5[A]. While $\Big(x^T(t), 0\Big)$ becomes unstable as $p = 0.7$, see Figure 5[B]. Further, $\Big(x^T(t), 0\Big)$ becomes stable again when $p = 0.88$, as shown in Figure 5[C]. Considering from the perspective of pest control, even if the insecticide has no effect on the pest, the lower or higher insecticide will outbreak the pest population and accelerate the extinction of the natural enemy population.

If $x_2 > ET > x_1$, only $p_1$ is defined. Since $\mu_2(p_1) > 1$, there exists a threshold $p_5$ such that $\mu_2(p_5) = 1$, which implies $\Big(x^T(t), 0\Big)$ is stable when $p\in(p_5, 1)$, while it is unstable when $p\in(0, p_5)$, as shown in Figure 6. Specifically, Figure 6[A] shows the $\Big(x^T(t), 0\Big)$ is stable when $p = 0.7$, while as $p$ decreases to $0.35$, $\Big(x^T(t), 0\Big)$ is unstable, and it tends to a stable internal periodic solution, see Figure 6[B]. Considering from the perspective of pest control, ensuring high insecticide concentration and a certain determined threshold is key to pest control in pest control strategies.

The implementation of the pest control strategy is closely related to the existence of the internal equilibrium point of the model (2). Therefore, when the model has two internal equilibrium points, the relationship between the internal equilibrium point and the threshold ET also needs to be considered when implementing the pest control strategy. However, when the model does not have an internal equilibrium point, using only chemical control can not achieve the effect of pest control.

In order to investigate the impact of pest anti-predator behavior on pest control, we conducted numerical analysis by adjusting the anti-predator coefficient $\eta$ according to Figure 5, as shown in Figure 7. When the anti-predator coefficient changed from $\eta = 0.1$ to $\eta = 0.09$, the originally stable boundary order-1 periodic solution $\Big(x^T(t), 0\Big)$ (Figure 5[A, C]) became unstable, as illustrated in Figure 7[A, B]. In such cases, stabilizing the solution $\Big(x^T(t), 0\Big)$ can be achieved by reducing p to $p = 0.24$ or increasing it to $p = 0.88$, as show in Figure 7[C, D]. From the perspective of pest control, as the anti-predator coefficient increases, the difficulty of pest control rises, demanding a higher precision in controlling the concentration of insecticides during spraying. In other words, effective pest control requires maintaining pest concentrations within a narrower range, posing challenges to pest management.

Notation 8. For Case $(C_2)$ of model (2.2), if equation (4.2) exists only one root, then we have $F_1(M)\geq0$, that is, $\mu_2\leq1$. This indicates that there exists no stability switching for the order-1 periodic solution.

In Figure 8[A], the bifurcation analysis with respect to $p$, shows the existence of higher-order periodic solution of model (2.2), the occurrence of phenomena such as period doubling, period halving, and chaos validates the existence of order-k periodic solutions of model (2.2). Specifically, when $\tau = 0.51$, there is a coexistence of order-1 and order-3 periodic solutions, as shown in Figure 8[B].

6.   Conclusions

Anti-predator behavior is commonly observed in the natural world. Nevertheless, prior studies frequently neglected the detrimental impacts of anti-predator behavior on natural enemies. In this article, we employ a control strategy involving insecticide spraying and the introduction of natural enemies when the pest population reaches the ET to formulate an ecological model encompassing pest-predator interactions with anti-predator behavior. The model is analyzed under two conditions: One without internal equilibrium points and one with internal equilibrium points, investigating the intricate dynamics of the system.

In the absence of internal equilibrium points and $\tau = 0$, the globally stable state is represented by the boundary order-1 periodic solution. However, when $\tau > 0$, this periodic solution may become unstable. In cases where the boundary order-1 periodic solution is unstable, the model (2.2) demonstrates an internal order-1 periodic solution, illustrated in Figure 2. When the model (2.2) includes at least one internal equilibrium point, its dynamic behavior becomes exceedingly complex, presenting significant challenges for pest control. For instance, with a large Economic Threshold ($ET > x_2$), effective pest control requires maintaining pesticide lethality within a specific range ($p\in(p_3, p_4)$). Deviating from this range, either by using lower or higher lethality, may lead to an increase in pest population density, potentially triggering outbreaks. Concurrently, the number of natural enemies might decline or even lead to extinction, as depicted in Figure 5. The occurrence of this phenomenon is because when the mortality rate of insecticides is low, the pest population rapidly increases, leading to the extinction of predator populations due to the pests' anti-predator behavior. On the other hand, when the mortality rate of insecticides is high, predator populations also become extinct due to the significant death of pests (insufficient prey). Additionally, with the increase in the anti-predator coefficient, it is necessary to control the mortality rate of insecticides within a narrower range to effectively manage pests. However, when $x_2 > ET > x_1$, ensuring pesticide density is higher than $p_5$ becomes necessary to control pest population density. This allows for the coexistence of pests and natural enemies, as demonstrated in Figure 6.

The definition and characteristics of the Poincaré map depend on the presence of internal equilibrium points in the model (2.2). When there are no internal equilibrium points in the model (2.2), the dynamical behavior is entirely determined by the properties of the Poincaré map. However, if there is at least one internal equilibrium point in the model (2.2), the domain and range of the Poincaré map may undergo significant changes, leading to complexities in the pulse set and phase set. For instance, changes in the stability and type of the internal equilibrium point $E_i$, as well as the positions of $L_3$ and $L_4$, can influence alterations in the pulse set and phase set. In the presence of nodes in the model (2.2), the vector field becomes highly complex. In such cases, it becomes challenging to ascertain whether trajectories starting from the phase set can reach the pulse set, making the determination of the Poincaré map impossible. This presents a significant research challenge.

One fundamental assumption in this paper is that when the pest population density reaches the economic threshold, actions such as pesticide spraying and predator release are completed instantaneously—a condition idealized for the analysis. However, for a more realistic modeling approach that considers factors like pesticide persistence and delay, we propose incorporating the intermittency of pesticide use. More specifically, we suggest employing the Integrated Pest Management (IPM) strategy continuously over a duration until the pest population density decreases below the economic injury level, at which point the IPM strategy is discontinued. This aspect will be a focus of our future work.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

We would like to thank the editor and the anonymous referees for their valuable comments and suggestions that greatly improved the presentation of this work. This work is supported by National Natural Science Foundation of China (Nos. 12261104, 11361104), and the Youth Talent Program of Xingdian Talent Support Plan (No. XDYC-QNRC-2022-0708), the Yunnan Provincial Basic Research Program Project (No. 202301AT070016).

Conflict of interest

The authors declare that they have no competing interests.