A state-dependent impulsive system with ratio-dependent action threshold for investigating SIR model

1.   Introduction

Infectious diseases have consistently posed a significant challenge to public health globally. Historically, pandemics such as the plague, black death, and the 1918 Spanish influenza have led to the loss of millions, even tens of millions, deeply affecting the political, social, and economic structures of societies. Today, despite major advancements in medical and healthcare sciences, outbreaks like SARS, H1N1, Ebola, and COVID-19 continue to threaten global health.

In the fight against infectious diseases, mathematical modeling has become an indispensable tool, offering insights into the study, understanding, and management of disease spread ^{[1,2,3,4,5,6,7,8,9,10]}. By establishing appropriate mathematical models, we can analyze the effectiveness of control measures quantitatively or qualitatively. Among these models, the state-dependent pulse model is particularly noteworthy for its ability to effectively describe infectious disease control ^[11,12]. The model operates under the assumption that no control measures are implemented when the number of susceptible populations is within a certain range. However, comprehensive measures, including immunization of susceptible populations and treatment of infected individuals, are implemented when the size of the susceptible population reaches or exceeds the control threshold. Subsequently, scholars have developed numerous state-dependent pulse models tailored to different types of infectious disease characteristics, delving into the impact of state-dependent pulse control strategies on dynamic behaviors, such as disease elimination and epidemics.

Nevertheless, many existing mathematical models of infectious diseases assume continuous interventions like vaccination, drug treatment, or isolation. These models frequently overlook real-world challenges, including resource constraints, high costs, and the impracticality of sustained interventions. Addressing these issues, pulse control strategies, involving periodic interventions like vaccination or patient isolation, have garnered significant attention in the field of mathematical modeling. Pulse control proves particularly beneficial in resource-limited scenarios and is extensively researched for its potential in infectious disease control ^{[13,14,15,16,17,18,19,20]}. Furthermore, state-dependent feedback control, as represented by pulse semi-dynamic systems, finds application across various fields and sciences, such as fisheries harvesting ^[21,22,23], integrated pest management ^[24,25,26], and interactions among biological populations ^[27,28,29].

In the realm of infectious disease modeling, the selection of the ratio-dependent action threshold method is driven by a meticulous consideration of the limitations inherent in traditional control strategies and the imperative need for a more realistic representation of disease dynamics. The foundational premise of triggering interventions based on a fixed population density threshold, a cornerstone of state-dependent feedback control, tends to oversimplify the intricate dynamics of real-world scenarios. This conventional approach may overlook crucial factors, such as situations where the transmission rate remains high despite a low population density or vice versa. In both scenarios, a high population density may not necessarily warrant immediate control intervention if the transmission rate remains low. To address this limitation, the adoption of a more effective control strategy becomes imperative. This strategy considers both population density and its rate of change, leading to the formulation of a nonlinear threshold control policy known as the "ratio-dependent action threshold". In this approach, the decision to implement control measures hinges on the ratio of population density to its rate of change, providing a more adaptive and realistic representation of infectious disease scenarios.

The significance of the ratio-dependent action threshold method lies in its capacity to capture the nuanced dynamics of infectious diseases. Recent research has delved into nonlinear threshold strategies, revealing diverse and dynamic behaviors in various contexts ^{[30,31,32,33,34,35,36]}. This method not only challenges prevailing assumptions in pulse control models, where the rate of change is assumed to directly correlate with population density following the introduction of control measures but also offers a more accurate representation by acknowledging inherent constraints in this relationship. Furthermore, the adoption of a saturated form that includes a nonlinear function enhances the realism of infectious disease models. This nuanced approach considers the complexities of disease dynamics, contributing to a more comprehensive understanding of infectious diseases and facilitating the development of intervention strategies aligned with the dynamic nature of disease transmission. In summary, the ratio-dependent action threshold method is chosen for its ability to address real-world complexities, offering a more accurate and adaptive representation of infectious disease dynamics in modeling and control strategies.

Our efforts aim to integrate a nonlinear threshold strategy within an infectious disease transmission model with a saturated incidence rate. In Section 2, we introduce an SIR state-dependent pulse model with a saturated incidence rate and adopt a rate-related nonlinear action threshold. Section 3 delves into constructing the corresponding Poincaré map by defining the pulse set and phase set range and discussing the essential attributes of the Poincaré map. In Section 4, conditions for the existence and stability of 1st order periodic solutions are established. Section 5 analyzes the bifurcation of the discrete mapping's one-parameter family concerning a critical parameter near the trivial fixed point when the model possesses a local disease equilibrium. Sensitivity analysis of the model is conducted in Section 6, where variations in parameters lead to complex dynamics. The analysis of the intricate interplay remains a challenging and underexplored frontier in this domain. Finally, a comprehensive conclusion and detailed discussions wrap up our study.

2.   Model

In our current study, we have chosen an SIR model with a saturated incidence rate, and extended the model presented in ^[37] by considering the density of susceptible individuals and their rate of change as action thresholds. The model is given by the following equation:

Here, $S(t)$ and $I(t)$ denote the numbers of susceptible and infected individuals, respectively. $\Lambda$ is the birth rate, $\delta$ is the mortality rate, $\gamma$ indicates the rate of recovery, $\beta$ is the rate at which transmission occurs, and $\alpha$ is the half-saturation constant. Additionally, we define $q$ as $q = \gamma+\delta$. The parameters $u_{1}$, $v_{1}$, and $ET$ are all positive constants, and to simplify the model, we set $u_{1}+v_{1} = 1$. When the population density of susceptible individuals reaches the action threshold given by

control measures will be implemented to update the numbers of susceptible individuals and infected individuals as follows: $(1-\eta_{1})S(t)$ and $(1-\eta_{2})I(t)$. In this context, $\eta_{1}$ and $\eta_{2}$ represent the maximum vaccination rate and maximum treatment rate, respectively. The parameters $u_{1}$, $v_{1}$, $ET$, $\eta_{1}$, and $\eta_{2}$ are pivotal factors within the control of decision-makers, intricately associated with infectious disease control measures. The values of these parameters can be effectively determined through practical applications in the field of infectious disease control.

The dynamic analysis of the non-pulsed model in ^[37] has been extremely valuable for our research. We define the non-pulsed model as $M_{0}$, and, based on ^[37], it is evident that $M_{0}$ possesses a disease-free equilibrium point, denoted as $E_{0}(K, 0)$, where $E_{0}$ is stable when $R_{0} < 1$, and it becomes unstable when $R_{0} > 1$, where

Furthermore, $M_{0}$ has an endemic equilibrium point denoted as $E^{*}(S^{*}, I^{*})$ for $R_{0} > 1$, where

In cases where $\Delta\geq0$, $E^{}(S^{}, I^{*})$ is a stable node, while for $\Delta < 0$, it behaves as a stable focus, where

It follows from

that we have

and we can define the impulsive curve as

Since

we can define the corresponding phase space as

According to $\dfrac{dS}{dt} = 0$, we can denote the vertical isocline as

There is an intersection point between $L_{1}$ and $L_{M}$ for

where

and the intersection point denote as

where

and

If $K > \dfrac{ET}{u_{1}}$, then there is a unique intersection $P_{ET}$ where all coordinates are positive. However, when $u_{1} = 0$, the inequality $L_{M}(S) < L_{1}(S)$ always holds, indicating that lines $L_{M}$ and $L_{1}$ do not intersect.

3.   Poincaré map for $R_{0} < 1$

The trajectory starting from any point $P_{k}^{+} = (S_{k}^{+}, I_{k}^{+})$ on $L_{N}$ will definitely reach $L_{M}$ after finite time $t$, and its intersection with $L_{M}$ is

and it will pulse to point $P_{k+1}^{+}\subset L_{N}$. Therefore, we can denote

with

and we define the Poincaré map $P_{M}$ as

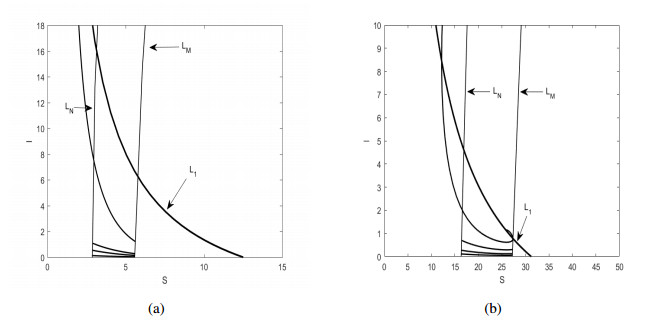
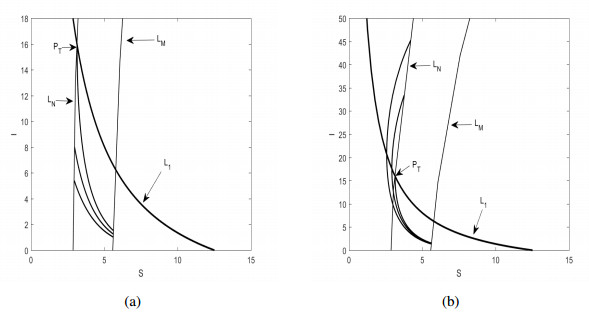
There exists a point on $L_{N}$, denoted as $P_{T} = (S_{T}, I_{T})$. The trajectory starting from $P_{T}$ reaches $L_{M}$ at point $P_{T1} = (S_{T1}, I_{T1})$ (see Figure 1). Therefore, we define the impulsive set and phase set as

We denote continuous functions $Q_{1}(S(t), I(t))$ and $Q_{2}(S(t), I(t))$ as

so we consider the following scalar differential equation:

$G(S, I)$ is a continuously differentiable function. Now we denote $S_{0}^{+} = S_{c}$, $I_{0}^{+} = Y$ with $(S_{0}^{+}, I_{0}^{+})\in N$. Then, we have

and

where the value of $S$ is between the $L_{M}$ and the $L_{N}$.

Therefore, the Poincaré map $P_{M}$ has the following form

Theorem 1. For model (1) with $R_{0}\leq1$, the Poincaré map $P_{M}$ exhibits the subsequent characteristics:

(i) $P_{M}$ has a domain spanning $[0, +\infty)$ and encompasses a range of $[0, P_{M}(I_{T})]$.

(ii) Within the interval $[0, I_{T}]$, $P_{M}$ exhibits an upward trend, but shows a decline for $(I_{T}, +\infty)$. It remains continuous and exhibits a concave nature over $[0, I_{T}]$.

(iii) The singular stable fixed point for $P_{M}$ is at $I = 0$. Hence, model (1) possesses a stable disease-free periodic solution (DFPS).

Proof. It follows from the first function of system (2) that we have

where $A = \Lambda - \delta S$, $B = 1 + \alpha S$, $C = \beta S$, and

Given that $S < K$ and $R_{0}\leq1$, it follows that $A > 0$ and $C-qB < 0$, and for $I < I_{T}$, $D > 0$, whereas for $I > I_{T}$, $D < 0$. From these observations, it is clear that both

hold true for every $I < I_{T}$.

From the principles of the Cauchy-Lipschitz theorem applied to the scalar differential equation, we can deduce that

and

Moreover, according to

we have

and

Given that $(1-\eta_{2}) > 0$, for $Y\in(0, I(T)]$, it is evident that

This suggests that $P_{M}(Y)$ is both continuously differentiable and concave within the interval $(0, I_{T}]$. Additionally, $P_{M}(Y)$ consistently rises within $(0, I_{T}]$ and falls in the range $(I_{T}, +\infty)$.

Therefore, when $R_{0}\leq1$, and taking into account that $\dfrac{ET}{u_{1}} < K$, it follows that for every $Y$ in the sets $(0, I_{T}]$ and $(I_{T}, K)$, the inequality $Y\geq I(S, Y) > P_{M}(Y)$ holds true. This implies that the Poincaré map $P_{M}$ exhibits a singular fixed point which is globally stable. As a result, model (1) maintains a distinct DFPS that demonstrates global stability. □

4.   The existence and stability of boundary order-1 periodic solution

If we define the function

solving $L_{M} = 0$ yields the intersection points of $L_{M}$ with the x-axis, which is equivalent to solving $f(S) = 0$. When $I = 0$, the model can be simplified as follows:

Furthermore, it follows from $f(S) = 0$ that we have

so model (3) is equivalent to

Denoting the initial value $S_{Z}^{+} = (1-\eta_{1})S_{Z}$, we have the following results:

Theorem 2. If $R_{0}\leq1$, then system (1) has a globally stable boundary order-1 limit cycle $(S^{T}(t), 0)$ with period $T$, where

and

Proof. Based on the premise that the solution $S(t)$ of the system moves from the initial value $S_{0}$ to $S_{Z}$ within a finite time $T$, by solving the system with initial value $S_{0} = S_{Z}^{+}$, we can conclude that the periodic solution

and

Furthermore, it follows from in [38, Lemma A.1] that we have

where

By simple calculations, we have

and

which yields

Moreover, we can obtain

where

and

Therefore,

so we can know that $\mu_{2} < 1$ for $R_{0} < 1$, which means that the boundary order-1 limit cycle $(S^{T}(t), 0)$ is orbitally asymptotically stable.

Once it is established that the boundary order-1 limit cycle $(S^{T}(t), 0)$ is globally attractive, it is tantamount to demonstrating its global stability. Thus, we make the assumption that the pulse point sequence $I_{k}^{+}$ for $k\geq0$ lies entirely on the line $L_{N}$ and $I_{k}^{+}\in[0, (1-\eta_{2})I_{T1}]$. Given that $R_{0}\leq1$, we can deduce that $\dfrac{dI}{dt} < 0$ for $S < K$. Consequently, we can ascertain that $I_{k}^{+}$ forms a strictly decreasing sequence, with

Additionally, the monotonicity of $I(t)$, as depicted in Figure 2a, dictates that $I_{0} = 0$. As a result, the boundary order-1 limit cycle $(S^{T}(t), 0)$ for model (1) is globally attractive. This completes the proof of Theorem 2. □

5.   Bifurcations for $R_{0} > 1$

5.1.   Transcritical bifurcations for $ET$

According to

taking the derivative of $\mu_{2}$ with respect to $ET$ as

where

taking the derivative of $g(S)$ with respect to $S$ yields

where

By simple calculations, we know that $g_{2}(S)$ has a minimum value $(-\alpha\delta(S^{*})^{2}+(\alpha\Lambda-\delta)S^{*}+\Lambda)$ for $S = S^{*}$, and if

then

and then $g^{'}(S) > 0$.

Based on the above discussion, if

then

and

If

then

and

Moreover, it is clear that

as $S_{Z}$ approaches $S^{*}$, and

as $S_{Z}$ approaches $K$. According to the monotonicity of $\int_{S_{Z}^{+}}^{S_{Z}}g(S)dS$, it can be inferred that there is an

such that $\mu_{2} = 1$.

It is clear that

and it follows from the definition of $P_{M}$ that we have

According to the monotonicity of $g(S)$, it can be known that

To simplify symbols, now we denote

By simple calculations, we have

For convenience, we derive the derivative of $E_{1}(x)$ with respect to $x$ as

Therefore, through inequality A, we can obtain

According to the monotonicity of $E_{1}(x)$, we know that the function $E_{2}(x)$ is monotonically decreasing for $x\in[S_{Z}^{+}, S^{*}]$ and monotonically increasing for $x\in[S^{*}, S_{Z}]$. Thus, if $ET = ET^{*}$, then

which indicates that $E_{2}(S^{*}) < E_{2}(x)\leq1$ for all $x\in[S_{Z}^{+}, S_{Z}]$. Moreover, we have

and thus, $E_{4}(x) > 0$ is monotonically increasing on $[S_{Z}^{+}, S_{Z}]$. Furthermore, we have

By simple calculations, we have

which means that

The above calculations demonstrate that the conditions of in [38, Lemma A.2] are satisfied. Therefore, we have the following conclusion:

Theorem 3. Given that $S^{*} < S_{Z} < K$ and $R_{0} > 1$, $P_{M}(Y, ET)$ undergoes a transcritical bifurcation at $ET = ET^{*}$. This indicates the emergence of an unstable positive fixed point for $P_{M}(Y, ET)$ as $ET$ transitions across $ET^{*}$ from the right to the left side. Consequently, we posit that for some sufficiently small value $\epsilon > 0$, system (1) exhibits an unstable positive periodic solution when $ET$ lies in the interval $(ET^{*}-\epsilon, ET^{*})$.

The emergence of a positive fixed point as elucidated in Theorem 3 indicates an unstable positive periodic solution for system (1). This suggests a concurrent local stability of the internal equilibrium $(S^{*}, I^{*})$ and the DFPS in system (1), leading to what we refer to as a bistable impulsive system, as shown Figure 2b. A more precise description is provided below.

Theorem 4. Given conditions $S^{*} < S_{Z} < K$, $R_{0} > 1$, and $ET \in (ET^* - \epsilon, ET^*)$, where $\epsilon > 0$ is sufficiently small, it can be concluded that system (1) exhibits bistability.

5.2.   Transcritical bifurcations for $\eta_{1}$

Here we take $\eta_{1}$ as the key factor for bifurcation. Thus, we have

By simple calculation, we have

and solving

yields a unique root $S_{Z}^{+} = S^{*}$, i.e.,

where

From the given information, for $\eta_{1}$ in the range $(0, \overline{\eta}_{1})$, it is evident that

Conversely, for $\eta_{1}$ in the interval $(\overline{\eta}_{1}, 1)$, we observe that

According to the monotonicity of $\dfrac{d\mu_{2}(\eta_{1})}{d\eta_{1}}$, it is clear that the value of $\mu_{2}(0)$ is less than that of $\mu_{2}(\overline{\eta}_{1})$, denoting that $\mu_{2}(\eta_{1})$ shows an increasing trend in the interval $[0, \overline{\eta}_{1}]$ and a decreasing trend when $\eta_{1}$ lies between $(\overline{\eta}_{1}, 1)$. Moreover, guided by the trend in the rate of change, if $\mu_{2}(\overline{\eta}_{1}) > 1$, a particular value $\eta_{1}^{*}$ exists in the interval $(0, \overline{\eta}_{1})$ for which $\mu_{2}(\eta_{1}^{*}) = 1$. Similarly, if $\mu_{2}(1) < 1$, there exists a singular value $\eta_{1}^{**}$ in the range $(\overline{\eta}_{1}, 1)$ such that $\mu_{2}(\eta_{1}^{**}) = 1$. If $\eta_{1} = \overline{\eta}_{1}$, it follows from

and

that we have

If

then

and then $\mu_{2}(\overline{\eta}_{1}) > 1$.

If $\eta_{1} = 1$, then $S_{Z}^{+} = 0$. It follows from

and

that we have

If

then

and then $\mu_{2}(1) < 1$.

Therefore, from the above discussion, we can derive the following results according to in [38, Lemma A.2].

Theorem 5. Given the conditions $S^{*} < S_{Z} < K$ and $\mu_{2}(\overline{\eta}_{1}) > 1 > \mu_{2}(1)$, there exist transcritical bifurcation points denoted by $\eta_{1} = \eta_{1}^{*}$ and $\eta_{1} = \eta_{1}^{**}$ for $P_{M}(Y, \eta_{1})$. This indicates that, as the parameter $\eta_{1}$ surpasses $\eta_{1}^{*}$ in the decreasing direction, or goes beyond $\eta_{1}^{**}$ in the increasing direction, $P_{M}(Y, \eta_{1})$ establishes an unstable positive equilibrium point. Under the presumption of a sufficiently diminutive value $\epsilon > 0$, system (1) demonstrates an unstable positive periodic solution when $\eta_{1}$ is situated in either the interval $(\eta_{1}^{*}-\epsilon, \eta_{1}^{*})$ or $(\eta_{1}^{**}, \eta_{1}^{**}+\epsilon)$.

Proof. It is obvious that

It follows from the proof of Theorem 1 that we have

Thus,

and we have

which means that

and

Through the similarity method in the proof process of Theorem 3, we have

Consequently, under the conditions $S^{*} < S_{Z} < K$, $\mu_{2}(\overline{\eta}_{1}) > 1$, and $1 > \mu_{2}(1)$, $P_{M}(Y, \eta_{1})$ results in an unstable fixed point when $\eta_{1}$ transitions past $\eta_{1}^{*}$ in a right-to-left direction or $\eta_{1}^{**}$ in a left-to-right direction. Moreover, given $\eta_{1}\in(\eta_{1}^{*}-\epsilon, \eta_{1}^{*})$ or $\eta_{1}\in(\eta_{1}^{**}, \eta_{1}^{**}+\epsilon)$, where $\epsilon > 0$ is sufficiently small, system (1) has an unstable positive periodic solution. This concludes our demonstration. □

6.   Numerical simulation and analysis

We observe the extent to which the model is affected by varying the weighted coefficients, $u_{1}$ and $v_{1}$, of the action threshold. When we set $u_{1}$ and $v_{1}$, as shown in Figure 3a, $L_{M}$ and $L_{N}$ become two lines perpendicular to the x-axis. At this point, the model is simplified to a pulse system with the threshold based solely on the density of susceptible individuals. Such systems have been extensively studied and widely applied in infectious diseases and population dynamics.

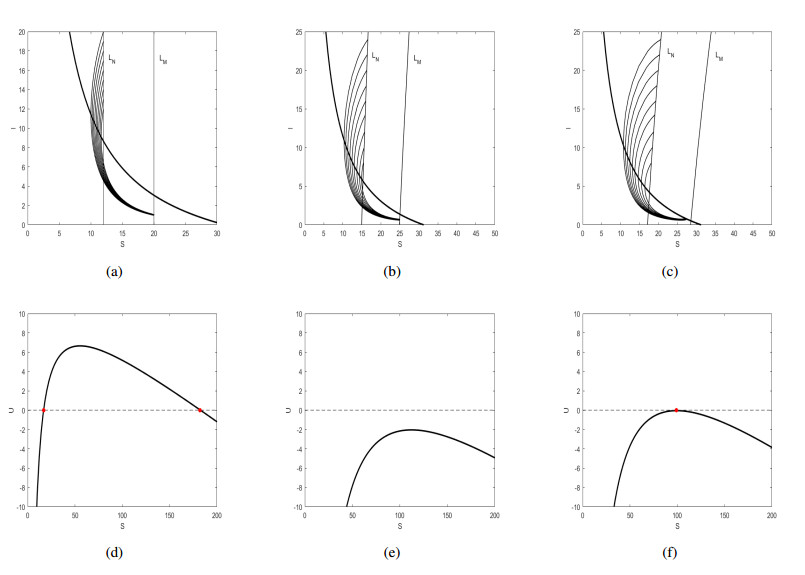
However, when the rate of change is introduced into the action threshold, $L_{M}$ and $L_{N}$ become two curves, and the curvature of these curves varies with changes in $u_{1}$ and $v_{1}$, Figure 3b, c highlights the influence of the rate of change of susceptible individuals in the implementation of a comprehensive control strategy. Properly choosing the coefficients can lead to the virus becoming extinct after a finite number of control measures.

When $v_1$ is non-zero, $L_{M}$ and $L_{N}$ represent two curves, and there is a possibility of intersection between them. We define $U = L_{M}-L_{N}$. By varying the value of $ET$, we can observe whether there are intersections between the pulse set and phase set. Figure 3d–f shows that as $ET$ increases, the number of intersections decreases from 2 to 0. The presence of intersections poses challenges in the analysis of Poincaré maps, leading to highly complex dynamics. This complexity is a primary focus of our ongoing research.

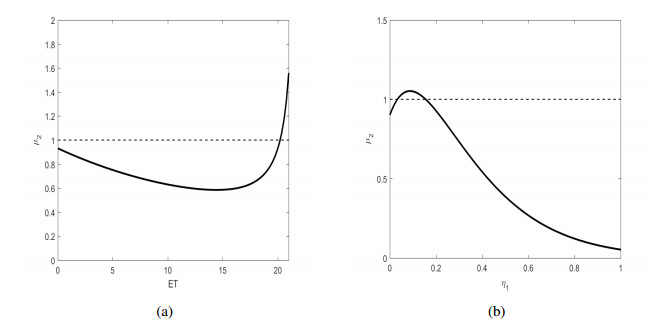
In previous sections, we explored the possibility of bifurcations with respect to individual parameters, as depicted in Figure 4. To examine the sensitivity of the model, we further investigated the impact of different weighted coefficients for the action threshold as influencing factors on bifurcations.

In Figure 5a, b, as the parameter $v_{1}$ increases, the trajectories of $\mu_{2}$ concerning $ET$ intersect with the line $\mu_{2} = 1$ at two distinct points. Specifically, with $v_{1}$ rising from 0.5 to 0.65, two intersections with the line $\mu_{2} = 1$ are highlighted. However, Figure 5c, d depict that, as $v_{1}$ decreases, the peak values of $\mu_{2}$'s trajectories in relation to $\eta_{1}$ diminish, eventually dropping below 1. Collectively, these patterns suggest that considering the rate of change in the action threshold is a more comprehensive approach for managing infectious diseases, emphasizing the importance of monitoring not just the current thresholds, but their evolution over time.

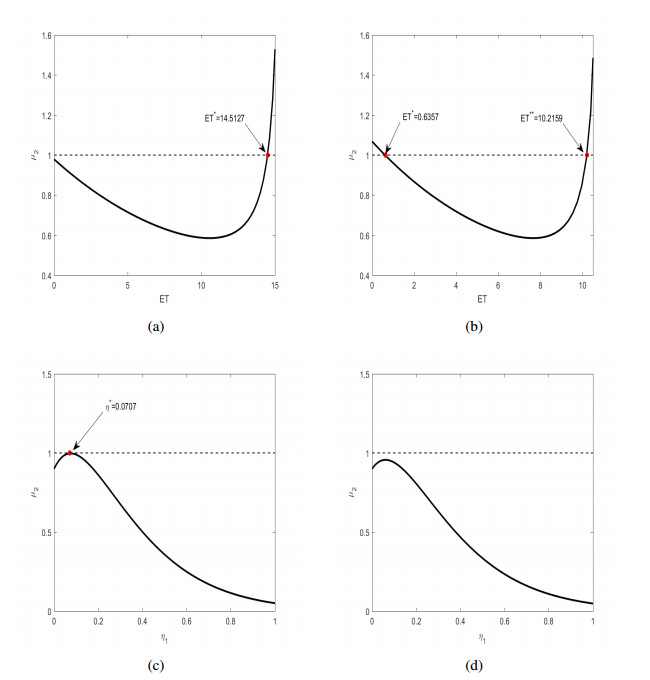
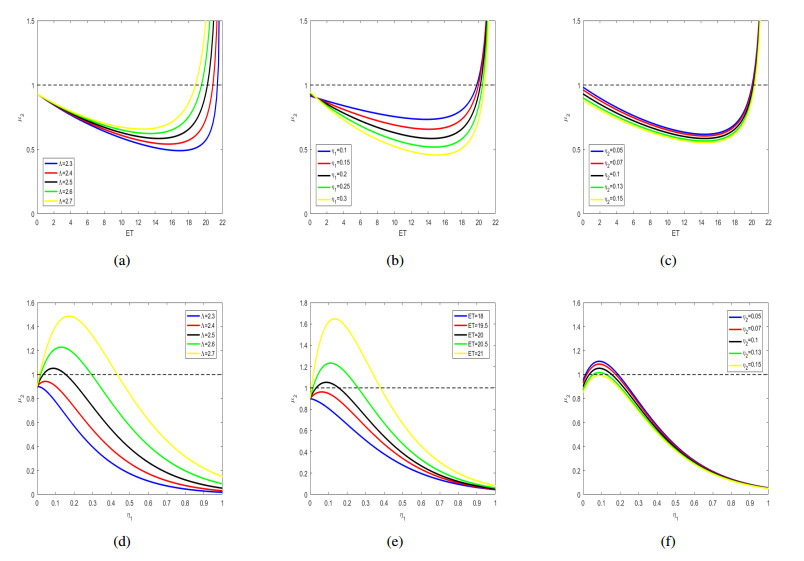
In Figure 6a–c, the float multiplier $\mu_2$ response to the action threshold $ET$ is closely related to multiple parameters. First, with an increase in the birth rate, $\Lambda$, the initial value of $\mu_2$ in the low $ET$ region rises, suggesting that a higher threshold might be needed to maintain stability of $\mu_2$ at a higher birth rate. Further considering the maximum vaccination rate $\eta_1$, its increase results in a slight rise in the initial point of $\mu_2$ at low $ET$, indicating an enhanced sensitivity of $\mu_2$ to the threshold under high vaccination scenarios. Additionally, for the maximum treatment rate $\eta_2$, similar $\mu_2$ trajectories are given at low $ET$ values, but with a higher value of $\eta_2$, the decline trend of $\mu_2$ is more rapid. This reveals that, in a high treatment rate environment, $\mu_2$ responds more quickly to threshold changes. In summary, these analyses present how the relationship between $\mu_2$ and $ET$ is influenced by the three parameters $\Lambda$, $\eta_1$, and $\eta_2$.

On the other hand, in Figure 6d–f, the relationship between $\mu_2$ and the maximum vaccination rate $\eta_1$ is significantly affected by different parameters. For instance, when the birth rate $\Lambda$ rises from 2.3 to 2.7, the peak value of $\mu_2$ consistently increases and shifts to the right. For scenarios where $\eta_1$ is close to 1, all $\mu_2$ trajectories are approximately 0. When the focus is on the maximum treatment rate $\eta_2$, even though peak positions of the trajectories are similar, with the growth of $\eta_2$, the peak gradually decreases; especially in parts where $\eta_1$ is larger, the decline of $\mu_2$ is more pronounced. For the threshold $ET$, as it increases from 18 to 21, the maximum value of $\mu_2$ seems to decrease, and its peak position shifts to the right. This aligns with the observation of $\mu_2$ trajectories approaching 0 when $\eta_1$ is near 1. These shifts provide a comprehensive view of how the system adjusts based on different parameter values.

7.   Conclusions and discussion

In conclusion, state-dependent impulsive semi-dynamic systems represent a category of highly discontinuous and non-smooth systems. These systems have been applied in various fields, including integrated pest management, viral dynamical systems, and diabetes treatment ^{[26,39,40,41]}. In recent years, significant progress has been made in the research of such systems, encompassing analytical techniques, qualitative analyses, and practical applications ^[30,42]. Notably, the Poincaré map serves as a mathematical tool promoting comprehensive exploration of impulsive systems with nonlinear impulsive functions, enabling the study of the existence and global stability of k-order periodic solutions.

In our research, we examined a state-dependent impulsive model, which incorporates a saturation incidence rate and describes the interaction between susceptibles and infectives. A highlight is that the action threshold in our model is determined by the density of susceptibles and its rate of change. This differentiates our work from previous literature ^[37,38], which primarily operated under the assumption of a fixed action threshold. Our innovation lies in introducing an action threshold determined by the density of the affected susceptibles and its rate of change, thereby translating the impulse set and phase set into more intricate nonlinear curves.

By analyzing the various positional relationships between system trajectories and equilibrium points, we derived the respective impulse and phase sets, as depicted in Figure 1. Utilizing these conditions, we constructed the Poincaré map and studied the conditions for the emergence of a first-order periodic solution within the system framework. Furthermore, we undertook a thorough examination of the stability of these first-order periodic solutions. Our theoretical findings were corroborated by numerical simulations, confirming the existence of the first-order periodic solution. Additionally, based on the results of the single parameter's influence on $\mu_{2}$, we conducted a sensitivity analysis by fixing other parameters and selecting one parameter as a benchmark to observe the trajectory changes of $\mu_{2}$, as shown in Figure 4. Under certain conditions, the threshold parameter $ET$ or vaccination rate $\eta_{1}$ can induce a transcritical bifurcation, leading to unstable positive periodic solutions. Boundary periodic solutions and equilibrium points of the impulse-free system can coexist, suggesting the possibility of backward bifurcations. Importantly, when the action threshold $ET$ is weighted by the density of susceptible individuals and its rate of change, the impulse curve and phase curve become nonlinear, as shown in Figure 3. The system's impulse curve, phase curve, and the intricate and mutable positional relationships between them and two isoclines introduce complexity, making the precise definition of the boundaries of impulse and phase sets challenging. Furthermore, based on Figure 5, variations in the weighted values of the susceptible individual density and its rate of change also impact the bifurcation results of the model. According to Figure 6, $\mu_{2}$ responds to the action threshold $ET$ based on several parameters, including birth rate, maximum vaccination rate, and maximum treatment rate. Among them, the relationship between $\mu_{2}$ and vaccination rate $\eta_{1}$ is also significantly influenced by the birth rate, maximum treatment rate, and action threshold.

Finally, we emphasize the critical role of mathematical models and control strategies in the field of infectious disease control. Future research directions may delve deeper into considering the growth rate of infected individuals as a threshold for studying disease control strategies, thereby advancing the development of more complex nonlinear pulse control methods. The further application of this technology holds the potential to have a profound impact on infectious disease control and other related fields, providing valuable directions for future research and application.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No. 12261033).

Conflict of interest

The authors declare no conflicts of interest.