1.
Introduction
Genetic regulatory networks (GRNs) are network models which intend to imitate gene activity in real organisms and abstractly generalize the regulatory relationships among genes. The process of gene regulation mainly involves gene transcription and mRNA translation, and such biochemical reactions constitute slow processes; hence, the influence of time-delay factors needs to be taken into account in the dynamics of the whole GRN system. GRNs with time delays have become a hotspot issue because of their importance in practical application and theoretical research, and a great deal of very important results on the analysis and design of GRNs have been reported [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17].
In practice, in order to monitor data and provide the right amount of proper drugs as artificial input control, the exact state values of GRNs, i.e., the concentrations of mRNA and protein, must be known. However, not all states of GRNs are easily and directly detectable, and some states may not even be detectable at all. This problem can be solved by designing the state observer to estimate the states of GRNs and replace the true states with the estimated states. Liang et al. [18] designed a linear estimator to approximate the true concentrations of the mRNA and protein of uncertain time-delay Markovian jumping GRNs through available measurement outputs. By applying the Lyapunov functional method and some stochastic analysis tools, the desired state estimator was derived such that the estimation error dynamics would be globally robustly asymptotically stable at the mean square. Additionally, by applying the Lyapunov functional method and a stochastic analysis technique, a robust state estimator was devised for delayed GRNs with SUM logic and multiple sensors to ensure that the error system was asymptotically stable at the mean square [19]. By using Lyapunov functions and some stochastic analysis techniques, Liu et al. [20] addressed the state estimation problem of random GRNs with Markovian jumping parameters with random delay. Less conservative conditions were derived so that the error dynamics were globally asymptotically stable. Li et al. [21] applied Lyapunov–Krasovskii functional (LKF) method and linear matrix inequality (LMI) technology to investigate the event-triggered state estimation for a class of discrete-time stochastic GRNs with Markovian jumping parameters and time-varying delay. Tian et al. [22] designed a state observer to estimate unknown states of hybrid delay GRNs. For discrete-time delayed GRNs with stochastic process noises and bounded exogenous disturbances under the round-robin protocols, Wan et al. [23] investigated the state estimation problem. By applying a transmission order-dependent Lyapunov-like functional and the up-to-date discrete Wirtinger-based inequality together with the reciprocally convex approach, sufficient conditions were established to guarantee the exponentially ultimate boundedness of the estimation error dynamics at the mean square with a prescribed upper bound on the decay rate; consequently, the conservativeness of the obtained results was reduced. By employing the LKF method, the Wirtinger-type integral inequality, the convex approach, Green's identity, the reciprocally convex approach, and Wirtinger's inequality, Zhang et al. [24] discussed the problem of state estimation for delayed GRNs with reaction-diffusion terms by using Dirichlet boundary conditions. Reduced-order and full-order state observers were designed for delayed GRNs in [25]. By constructing an LKF that includes quadruple integrals and employing the Wirtinger-type integral inequalities, reciprocal convex technique, and convex technique to estimate its derivative, delay-dependent sufficient conditions in the form of LMIs were proposed to ensure that the resultant error system was asymptotically stable. Based on the Lyapunov functional approach, a generalized dissipativity-type state estimator for delayed GRNs that include a leakage term has been explored to determine the exact concentrations of the protein and mRNA [26]. Song et al. [27] utilized the LKF method to deal with the state observation problem for coupled reactor-diffusion GRNs with time-varying delays under Dirichlet boundary conditions.
External disturbances generally exist in GRNs and will directly or indirectly affect the dynamic performance of GRNs. In this case, the desired state observer should also guarantee that the energy-to-energy gain from external disturbances to the estimation error may be restricted to less than a prescribed level. Up to now, the H∞ state observer design for GRNs has received increasing amounts of interest. On the topic of discrete-time GRNs with exogenous disturbances, parameter uncertainties, and time delays, Wan et al. [28] studied the problem of robust non-fragile H∞ state estimation. By constructing a mode-dependent LKF, a sufficient condition for the existence of the desired estimator was derived in terms of certain LMIs. Using the LKF method, the event-triggered H∞ state estimation problem was investigated for a class of discrete-time stochastic GRNs with both Markovian jumping parameters and time-varying delays [29]. Wan et al. [9] addressed the problem of finite-time H∞ state estimation for discrete time-delayed GRNs under stochastic communication protocols. By employing the LKF approach, sufficient conditions were established under which the estimation error system was stochastically finite-time bounded and satisfied a prescribed H∞ disturbance attenuation level. Chen et al. [30] focused on the robust H∞ state estimation problem for a class of uncertain GRNs with random delays and external disturbances by using the sampled-data method. The estimation issue for switched GRNs with uncertainties driven by the time-dependent persistent dwell-time switching regulation was explored in [31]. In consideration of the network-induced packet dropout and the loss of system modal information, a mixed mode-dependent and mode-independent estimator had been constructed, and the exponential stability and the mixed H∞ and l2−l∞ performance was obtained via switching Lyapunov theory. Shen et al. [32] designed a compatible distributed estimator for Markovian jump GRNs that are subject to round-robin scheduling. By applying the Lyapunov stability theory and a modified matrix decoupling technique, sufficient conditions were derived to assure that the distributed error system was strictly γ-stochastically dissipative. Sun et al. [33] researched the problem of H∞ state estimation for reaction-diffusion GRNs under Dirichlet boundary conditions. Utilizing the Lyapunov theory, a fuzzy state estimator was devised to approximate the concentrations of proteins and mRNAs such that the states of the error system satisfying the H∞ performance index converge to zero asymptotically. By applying the Lyapunov stability theory, Jensen's inequality, and the Gronwall inequality, the finite-time robust H∞ state estimation problem for a class of GRNs that are subject to distributed time delays and polytopic parameter uncertainties was addressed in [34]. Based on the measured concentrations of mRNA and protein, a robust state estimator for the considered GRNs was designed such that the finite-time boundedness and the H∞ performance was guaranteed. Wang et al. [35] considered the finite-time H∞ state estimation problem for switched GRNs with randomly occurring uncertainties. However, the time-delay factor was not taken into account in [31,32,35], which often lead to poor performance and/or instability.
It is worth noting that the aforementioned observer (estimator) design results were obtained by applying the LKF method, which depends on the construction of appropriate LKFs and techniques to estimate the upper bound of their derivatives/differences. However, it is hard (even impossible) to find an all-purpose method to construct appropriate LKFs and estimate the upper bound of their derivatives/differences. The challenge with this method is how to balance the computational complexity and conservativeness. Moreover, most of the results on observer (estimator) design for GRNs show that the error system is asymptotically stable, but there are very few exponential stable results, and there are almost no global exponential stable results. In the realm of practical engineering, one is more concerned with system tracking performance in a finite time period, as opposed to when time goes to infinity [36], which rouses our research interest. This paper constitutes our first attempt at exploring a novel approach to the H∞ observer design for delayed GRNs, which is directly based on the solutions of the error system and ensures that the error system is globally exponentially stable at an H∞ performance level. In addition, the proposed approach is different from the LKF method, and it does not require the construction of any LKF. This is the main motivation for the current study.
In this paper, we propose a novel method for the design of an H∞ state observer for GRNs with time-varying delays and disturbances. The main contributions of this paper are summarized as follows: (i) the parameterized bounds of the error system solutions are given, and a bounded real lemma is established to guarantee that the error system is globally exponentially stable at an H∞ performance level; (ii) the obtained bounded real lemma composes several matrix inequalities, and no LKFs are required; and (iii) via a linearization procedure, the explicit forms of the H∞ state observer gains are obtained.
The remainder of the paper is organized as follows. In Section 2, the system description and some necessary definitions are given; some preliminaries are also given. In Section 3, the main results are presented, including a bounded real lemma and the observer design. In Section 4, a numerical example is provided to demonstrate the feasibility of the above approach. Finally, we conclude the paper in Section 5.
Notations: The symbol R denotes the set of all real numbers. Let Rn and Rn×m represent the sets of all column vectors with n components and n×m matrices over R, respectively. Set ⟨l⟩={1,2,…,l} for a positive integer l. Let C([a,b],Rn) be the linear space over R consisting of all continuous functions ψ:[a,b]→Rn. For X=[xij]∈Rn×m and Y=[yij]∈Rn×m, X>Y means that xij>yij for all i∈⟨n⟩ and j∈⟨m⟩. Rn×m> denotes the sets of all n×m positive matrices. Vectors and scalars are represented in a similar way. Define |X|=[|xij|], xiM=maxj∈⟨n⟩|xij|, M(1,xiM)=max{1,xiM}, and m(1,xiM)=min{1,xiM}.
2.
Problem formulation
Consider the following GRN with time-varying delays and disturbances:
where ˜mi(t) and ˜pi(t) are, respectively, the concentrations of the ith mRNA and protein; ai>0 and ci>0 denote the degradation rates of the mRNA and protein, respectively; di>0 is the translation rate from the ith mRNA to the ith protein; bij is the dimensionless transcriptional rate of transcription factor j to gene i, and it is denoted by
θij is a nonnegative and bounded constant; Φj(s) is the feedback regulation function of Hill form; σj(t) and ϵi(t) are the time-varying delays satisfying
ˉσ and ˉϵ are known positive scalars; let τ=max{ˉσ,ˉϵ}; ωρ(t) is the external disturbance that is subject to L2[0,∞); eiρ and fiρ are the external disturbance coefficients; Ji=∑j∈χiθij, and χi is the set of all nodes which repress gene i.
Usually, the feedback regulatory function has the form Φj(s)=sHj1+sHj, s∈[0,+∞), where Hj is the Hill constant. From this, it can be easily seen that Φj is a monotonically increasing function satisfying
for all ξ1,ξ2≥0 with ξ1≠ξ2.
Let (˜m∗,˜p∗) be a nonnegative equilibrium of GRN (2.1) with ωρ(t)≡0, that is,
where ˜m∗=col(˜m∗1,…,˜m∗n) and ˜p∗=col(˜p∗1,…,˜p∗n). Let ˆmi(t)=˜mi(t)−˜m∗i and ˆpi(t)=˜pi(t)−˜p∗i for any t≥−τ, and take the expression levels and the estimated signals into account. Then, the following GRN model can be obtained:
where Υj(s)=Φj(s+˜p∗)−Φj(˜p∗), ˆymς(t) and ˆypν(t) are the system measurement outputs, ˆzmζ(t) and ˆzpι(t) are the signals to be estimated, and hςξ, gνξ, πεξ, and ψιξ are known scalars.
The following observer is considered:
where Ξiς and Λiν are the observer gains to be determined and ˉzmε(t) and ˉzpι(t) are the estimations of ˆzmζ(t) and ˆzpι(t), respectively.
Let mi(t)=ˆmi(t)−ˉmi(t), pi(t)=ˆpi(t)−ˉpi(t), zmε(t)=ˆzmε(t)−ˉzmε(t), and zpι(t)=ˆzpι(t)−ˉzpι(t). Then, the following error system can be derived:
where Ψj(pj(t))=Υj(ˆpj(t))−Υj(ˉpj(t)). The following initial functions associated with the error system (2.7) are considered:
where ϕi,φi∈C([−τ,0],R).
Denote
The following global exponential stability definition of the error system (2.7) is given.
Definition 1. The error system (2.7) with ω(t)≡0 is said to be globally exponentially stable if there exist scalars Ω>1 and γ>0 such that every solution (m(t),p(t)) starting from ϕ,φ∈C([−τ,0],Rn) satisfies
where
Define the following performances for the error system (2.7):
where γ is a given scalar.
Definition 2. The error system (2.7) is said to be globally exponentially stable with H∞ performance denoted by γ if the error system (2.7) with ω(t)≡0 is globally exponentially stable and satisfies the condition that Jm(t)≤0 and Jp(t)≤0 for any nonzero ω(t) under the zero initial conditions.
The main objectives of this paper are as follows: (i) establish a bounded real lemma for the error system (2.7), i.e., give sufficient conditions under which the error system (2.7) is globally exponentially stable with an H∞ performance of γ; and (ii) propose a novel H∞ state observer design method for GRN (2.5).
3.
Main results
In this section, first, the H∞ performance analysis of the error system (2.7) is investigated and a bounded real lemma is derived. Then, based on the obtained bounded real lemma, a novel observer design method is derived such that the designed H∞ state observer can ensure that the error system (2.7) is globally exponentially stable at an H∞ performance level.
3.1. Bounded real lemma
Let
Theorem 1. If there exist a scalar 0<λ<min{mini∈⟨n⟩ai,mini∈⟨n⟩ci}, vectors κm>ϱ and κp>ϱ, and matrices Ξ and Λ such that
then the error system (2.7) is globally exponentially stable with an H∞ performance index denoted by
where
Proof. The proof is divided into the following two steps.
Step 1. First, we will show that all solutions of the error system (2.7) satisfy
where
It shows that the error system (2.7) with ω(t)≡0 is globally exponentially stable when the inequalities (3.1a) and (3.1b) hold. For arbitrary but fixed ϕ,φ∈C([−τ,0],Rn), let (m(t),p(t)) be the unique solution of the error system (2.7). For i∈⟨n⟩, the Dini upper-right derivative of eait|mi(t)| along the state trajectories of the error system (2.7) can be obtained as follows:
Integrating both sides from 0 to t, one has
Next, the parametric estimation of |pi(t)| can be derived via a similar procedure. First, the Dini upper-right derivative of ecit|pi(t)| along the state trajectories of the error system (2.7) can be calculated by solving
Then, integrating both sides from 0 to t, we get
Obviously, the inequalities (3.1a) and (3.1b) are respectively equivalent to
and
We claim that (3.5) holds for any t≥0. When t=0, it is obvious that (3.5) holds. Thus, if this claim is false, then there exists ˆt∈(0,∞) such that (3.5a) or (3.5b) does not hold. Set
Due to the continuity of the functions mi(t) and pi(t), without loss of generality, one of the following statements holds:
(S1)
and there exists η∈⟨n⟩ such that
(S2)
and there exists η∈⟨n⟩ such that
Suppose that (S1) holds. It follows from (3.7) that
We will discuss the term eaη(s−˜t)|pj(s−σj(s))| in the following two cases:
Case 1: s−σj(s)≤0.
Case 2: 0<s−σj(s)<˜t.
Then, one can obtain
For the term ∑rς=1∑nξ=1|Ξης||hςξ|∫˜t0eaη(s−˜t)|mξ(s)|ds, the following result can be obtained:
Exchanging the order of integration, one derives
Substituting (3.17) and (3.19) into (3.14), we can derive
Because
it is given that
This, together with (3.10), implies that
which contradicts (3.12).
Suppose that (S2) holds. It follows from (3.9) that
Similar to (3.17) and (3.19), the following results can be obtained:
and
Substituting (3.23) and (3.24) into (3.22), we can obtain
This, together with (3.11), implies that
which contradicts (3.13).
In summary, all solutions of the error system (2.7) satisfies (3.5). When the inequalities of (3.1) hold and ω(t)≡0, it can be obtained that |mi(t)|≤κmi‖(ϕ,φ)‖τe−λt and |pi(t)|≤κpi‖(ϕ,φ)‖τe−λt for any t≥0 and i∈⟨n⟩. According to Definition 1, the error system (2.7) is globally exponentially stable when ω(t)≡0.
Step 2. We will show that Jm(t)≤0 and Jp(t)≤0 for any nonzero ω(t) under the zero initial conditions. From (3.5), if the initial conditions are zero, one can obtain
and
then,
This, together with (3.2) and (3.3), implies that
that is, Jm(t)≤0 for any t≥0.
Similarly, the following result can be derived from (3.2) and (3.4):
that is, Jp(t)≤0 for any t≥0.
Given Definition 2, the proof is completed by combining Steps 1 and 2. □
Remark 1. A noval bounded real lemma for the error system (2.7) has been established in Theorem 1, and it is directly based on the parameterized bounds of the solutions for the considered error system. The derived bounded real lemma involves solving only several matrix inequalities, which can be easily realized by using the usual tool software.
3.2. Observer design
In this section, the observer design method will be proposed. In order to achieve this aim, the following lemma is introduced.
Lemma 1. [37] If M∈C and N∈C satisfy
then NM+ is a solution to the equation XM=N.
Theorem 2. If there exist a scalar 0<λ<min{mini∈⟨n⟩ai,mini∈⟨n⟩ci}, vectors κm>ϱ and κp>ϱ, and α,β∈Rn> such that
then the error system (2.7) is globally exponentially stable with an H∞ performance index γ given by (3.2), and where the rest of the symbols are the same as in Theorem 1. Furthermore, the observer gain matrices can be derived as
Proof. Since |H|Meκm∈Rn> and |G|Mfκp∈Rn>, we respectively have
and
Then, according to Lemma 1, one can conclude that the matrix α(|H|Meκm)+ is a solution to the matrix equation
and the matrix β(|G|Mfκp)+ is a solution to the matrix equation
From Theorem 1, one can know that the error system (2.7) is globally exponentially stable with an H∞ performance index γ given by (3.2) if the inequalities in (3.28a) and (3.28b) are feasible. Here, we finish the proof. □
Remark 2. A novel H∞ state observer design method for GRN (2.5) is proposed in Theorem 2, and it is directly based on the parameterized bounds of solutions for the error system. The obtained H∞ state observer involves solving only several matrix inequalities. For the state observer design, the convergence time is a very important performance index. The shorter the convergence time, the faster the designed observer can approach the system states. Unlike the asymptotical convergence of most existing results, the error system (2.7) is exponentially convergent, which is more suitable for practical needs. That is, the error system can converge to zero at a larger decay rate λ, and the estimated state can approach the system state trajectory faster, which means that the convergence time is shorter. Moreover, an appropriate λ may be first selected according to actual needs, and then the H∞ state observer can be derived by applying the LMI toolbox to solve the matrix inequalities.
Remark 3. When ω(t)≡0, Theorem 2 can be employed to the state observer design for GRN (2.5), which has been investigated in [22,25] with W=0. Comparing the results in [25], the total number of variables in Theorem 2 is only 4n+1, while the number in [25, Theorem 3] is 10.5n2+8.5n. In [22, Theorem 1], the system matrices H,G,Ξ, and Λ are assumed to be diagonal matrices, which can be general matrices in this paper. In addition, the error systems in [25, Theorem 3] and [22, Theorem 1] are asymptotically stable and globally asymptotically stable, respectively, whereas the one in this paper is globally exponentially stable with a convergence rate of λ, which is an advantage of the proposed method. Furthermore, there is no restriction on the derivatives of time-varying delays, which is another advantage of the proposed method. Therefore, the state observer design method in Theorem 3.2 is simpler and easier to verify than [25, Theorem 3], and it has wider applicability than [22, Theorem 1]. Moreover, by applying Theorem 2 and [25, Theorem 3] to GRN (2.5) with ω(t)≡0, the simulation results show that the state observer designed by using Theorem 2 can approach the system state faster than that designed by using [25, Theorem 3], as will be explained by Example 1 in Section 4 below.
4.
A numerical example
In this section, we will use a numerical example to demonstrate the effectiveness of the theoretical results obtained previously.
Example 1. Consider GRN (2.5) with the following parameters: n=q=3, r=k=o=δ=2, a1=4, a2=3.5, a3=4.5, b11=−0.2, b12=−0.3, b22=−0.4, b23=−0.6, b31=−0.8, b33=−0.5, b13=b21=b32=0, c1=4, c2=4.5, c3=3.7, d1=0.4, d2=0.3, d3=0.5, e11=1.2, e12=1.1, e13=1.15, e21=0.9, e22=0.8, e23=1.1, e31=1.1, e32=1.13, e33=0.9, f11=0.9, f12=1.2, f13=1.1, f21=0.8, f22=1.1, f23=1.15, f31=0.86, f32=1.1, f33=1.13, h11=0.3, h12=0.35, h13=0.3, h21=0.3, h22=0.4, h23=0.3, g11=0.29, g12=0.32, g13=0.29, g21=0.33, g22=0.31, g23=0.27, π11=0.25, π12=0.3, π13=0.35, π21=0.29, π22=0.4, π23=0.3, ψ11=0.32, ψ12=0.35, ψ13=0.25, ψ21=0.3, ψ22=0.29, ψ23=0.37, Ψj(s)=s2/(1+s2), σ1(s)=|sin(s+1)|/4, σ2(s)=0.25+cos(s+1)/4, σ3(s)=0.5+cos(2s+1)/2, ϵ1(s)=0.125+cos(s+1)/8, ϵ2(s)=|sin(2s+1)|/4, and ϵ3(s)=0.5+|sin(s+1)|/2. Then, μ1=μ2=μ3=3√3/8. The external disturbances are as follows:
By solving the inequalities in Theorem 2, we obtain the following feasible solutions:
which indicates that the error system is globally exponentially stable with an H∞ performance index γ=13.0714. Furthermore, the gain matrices of the state observers are obtained as follows:
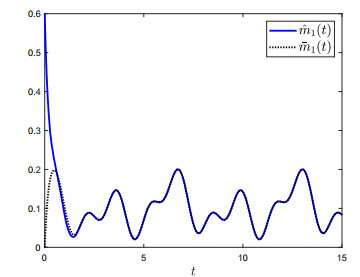
Given the initial conditions ϕ(t)=ψ(t)≡col(0.6,0.8,1.0), the state trajectories and the observation trajectories can be constructed as shown in Figures 1–6, respectively. From these figures, it is easy to find that the state observer trajectories quickly approach the system state trajectories, which indicates that the observer design approach presented in this paper is effective. Moreover, we can choose a suitable λ according to actual needs, and then the H∞ state observer can be derived by solving the inequalities of (3.28).
Under the same system parameters, the state observer can be obtained by solving [25, Theorem 3]. Given the same initial conditions, the trajectories of the error system (2.7) and (9) in [25, Theorem 3] can be constructed as shown in Figures 7–12, respectively, where m1(t),m2(t),m3(t),p1(t),p2(t), and p3(t) are the trajectories of the error system (2.7), and m∗1(t),m∗2(t),m∗3(t),p∗1(t),p∗2(t), and p∗3(t) are the trajectories of the error system (9) in [25, Theorem 3]. It can be seen from these figures that the error system (2.7) converges faster to zero. Since the system matrices H,G,Ξ, and Λ are not diagonal matrices, [22, Theorem 1] cannot be employed to design the state observer. This shows that the proposed approach in this paper is superior to the existing results in [22,25]. Moreover, the state observer derived in this paper does not require the construction of any LKF; it is also are related to the convergence rate λ.
Remark 4. To the best of the authors' knowledge, the H∞ state observer design problem for GRNs with time-varying delays has not been fully investigated in the existing literature. So, we are unable to give comparison results.
5.
Conclusions
In this paper, we have presented a direct method to design the H∞ state observer for GRNs with time-varying delays and disturbances. The parameterized bounds of solutions for the error system were first provided on the basis of the system model. Next, a bounded real lemma composed of several matrix inequalities was established such that the error system is globally exponentially stable with H∞ performance. Then, based on the obtained bounded real lemma, the H∞ state observer design method has been given. Lastly, a numerical example has been provided to illustrate the advantage of the proposed method.
Use of AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported in part by the Natural Science Foundation of Heilongjiang Province [grant number LH2022F046] and the Fundamental Research Funds for the Provincial Universities of Heilongjiang Province [grant number 2022-KYYWF-1098].
The authors would like to thank the anonymous reviewers for their very helpful comments and suggestions, which have improved the original version of the paper.
Conflict of interest
All authors declare no conflict of interest that may influence the publication of this paper.









 DownLoad:
DownLoad:














