Observer-based robust preview tracking control for a class of continuous-time Lipschitz nonlinear systems

1.   Introduction

Output tracking control, which entails designing a suitable controller to force the output vector of a control system as close as possible to follow a desired reference signal, is a crucial research frontier in control theory. Specifically, preview control can significantly improve the tracking performance of a closed-loop system using the known future information of a reference signal or disturbances. This technique has attracted considerable attention because of its superior tracking performance. In recent decades, preview control has been combined with various advanced control theories, resulting in a series of control methods, such as robust preview control ^[1,2,3], fault-tolerant preview control ^[4,5,6], adaptive preview control ^[7,8,9], information fusion preview control ^[10,11,12], and decentralized preview control ^[13,14]. For example, in ^[2], the robust preview control problem was solved for convex polyhedral uncertain discrete-time systems with a time-varying delay, and an AES that included the preview information of the reference signal was constructed using a difference operator method; thus, the preview tracking control was converted to a robust control problem. A LMI condition to ensure the asymptotic stability of the closed-loop system and the design method of the preview controller are subsequently provided based on the scaled small gain theorem. In ^[6], using the model transformation method, unknown input observer theory, robustness parameter optimisation theory and preview control technology, a fault-tolerant preview tracking control method based on simultaneous state and fault estimation was proposed for convex polyhedral LPV systems. In ^[7], by combining multimodel adaptive control with preview control, a multimodel adaptive preview controller with preview compensation was designed for a discrete-time system with unknown piecewise constant coefficients. In ^[12], an event-triggered information fusion preview control scheme was employed for the flight control problem of a two-degree-of-freedom helicopter system. Owing to its fast response, small overshoot, and high tracking precision, preview control has several practical applications, such as UAV flight control systems ^[15], vehicle active suspension control systems ^[16] and robots ^[17].

Lipschitz nonlinear systems are a class of nonlinear systems comprising a linear system and a nonlinear part satisfying global or local Lipschitz conditions. These systems have a strong engineering background and appear in many practical applications. For example, the neuron activation function in memristive neural networks ^[18] and the sinusoidal and cosinusoidal terms in dynamics of single-link flexible and rigid robot systems ^[19,20], which are globally Lipschitz. In addition, owing to limitations in measurement means or costs, the state variables of an actual system are not always directly accessible. Thus, it is necessary to estimate the unknown state of the system with the aid of state observers to achieve feedback control. Several studies have been conducted on the design of observers and observer-based controllers for Lipschitz nonlinear systems ^{[21,22,23,24]}. For example, in ^[21], a controller design scheme based on a sliding window observer was proposed for a class of discrete-time Lipschitz nonlinear systems with bounded disturbances. The basic principle was to use the input and output data of the system in the recent period of time to perform state estimation within each sliding time window and dynamically update the state estimation through recursive methods to ensure prediction accuracy. In ^[22], the separation principle was proven to be applicable to Lipschitz nonlinear systems, and an observer-based tracking control scheme was proposed. Subsequently, the results in ^[22] were extended to quasi-one-sided Lipschitz nonlinear systems in ^[23]. The problem of observer-based preview tracking control in discrete-time Lipschitz nonlinear systems was also considered in ^[24]. However, to our knowledge, studies on preview control via a state observer for continuous-time Lipschitz systems have not been reported in the literature.

In this paper, the problem of robust preview tracking control via a state observer is studied for a class of continuous-time Lipschitz nonlinear systems with external disturbances and unknown states. First, a state observer is designed to estimate the unknown state variables when the system states are not fully measurable. Second, using differentiation, the state lifting technique, and several ingenious mathematical manipulations, an AES, including the observer information, tracking error, and preview information of the reference signal, is constructed. The tracking problem is then converted to a robust $H_{\infty}$ control problem. Based on Lyapunov stability theory, a sufficient condition for asymptotic stability and robust $H_{\infty}$ performance of the closed-loop system is established in the form of an LMI. Furthermore, a robust preview tracking controller via a state observer is proposed for the original system. Finally, numerical simulations are performed. The main contributions of this paper are summarized as follows:

1) With respect to the tracking control of Lipschitz nonlinear systems, existing studies, such as ^[22,24], consider only a linear output (in the form of $y = Cx$). In contrast, both nonlinear outputs and external disturbances are considered in this paper, thereby making the system model more general and applicable.

2) Compared with the study in ^[25], the proposed control strategy is applicable in situations where the states are not fully measurable and ensures the simultaneous convergence of both the system tracking and estimation errors to zero. Thus, the proposed controller has the advantages of greater practicability and robustness in actual complex environments.

3) Compared with the observer-based tracking controller presented in ^[22], the observer-based preview controller proposed in this paper makes full use of the preview information of the reference signal, leading to better output tracking performance. Furthermore, unlike the two-step algorithm in ^[22], a one-step algorithm that allows the observer and tracking controller gains to be computed simultaneously via LMI in a straightforward manner is used in this paper. Thus, the control design complexity is considerably simplified, and the computational load is reduced.

Notation: ${\mathbb {R}}^{n}$ denotes the $n$-dimensional Euclidean space; ${\mathbb {R}}^{m \times n}$ denotes the $m \times n$ matrix space; $P$ is a square matrix, and the notation $P > 0$($P < 0$) means that $P$ is a positive (or negative) definite matrix; ${A^{\rm{T}}}$ and ${A^{- 1}}$ represent the transposed matrix and the inverse matrix of $A$, respectively. The notion "*" in a symmetric matrix represents the transpose of the element in the symmetric position, that is $\left[ {\begin{array}{*{20}{c}} X & *\\ Y&Z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} X & {{Y^{\rm{T}}}}\\ Y&Z \end{array}} \right]$. ${\rm{Sym}}\{ A\}$ denotes $A + {A^{\rm{T}}}$; $diag(\cdots)$ denotes a diagonal matrix composed of elements in the parentheses; ${L_2}[0, \infty)$ refers to the space of square integrable infinite vector sequences, and for $Z(t) \in {L_2}[0, \infty)$, its norm is given by ${\left\| {{\rm{Z}}(t)} \right\|_2} = \sqrt {\int_0^\infty {Z(t)Z(t){\rm{d}}t} }$; ${e_s}(i) = {\left({\underbrace {0, \cdots, 0, \overbrace 1^{i{\rm{th}}}, 0, \cdots 0}_{s \; {\rm{components}}}} \right)^{\rm{T}}} \in {\mathbb {R}}^s, s \ge 1$ is a vector of the canonical basis of ${\mathbb {R}}^{s}$.

2.   System formulation and basic assumptions

In this paper, we consider the following Lipschitz nonlinear system:

where $x(t) \in {\mathbb {R}}^{n}$ is the system state, $u(t) \in {\mathbb {R}}^{m}$ is the control input, $\omega(t) \in {\mathbb {R}}^{q}$ is the external disturbance, and it satisfies ${\dot {\omega} (t)} \in {L_2}[0, \infty)$, $y(t) \in {\mathbb {R}}^{p}$ is the system output. $A, B, C, D$, and $E$ are real constant matrices of appropriate dimensions. The nonlinear functions $f(x): {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{n}$ and $g(x): {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{p}$ are differentiable.

With regard to system (1), the following basic assumptions are made:

A1. The nonlinear terms $f(x)$ and $g(x)$ satisfy

where ${\underline f_{ij}}$, ${\bar f_{ij}}$$(i, j = 1, \cdots, n)$ and ${\underline g_{ij}}$, ${\bar g_{ij}}$$(i = 1, \cdots, p, j = 1, \cdots, n)$ are real constants.

Remark 1. Lipschitz nonlinear systems satisfying A1 widely exist in practical problems, such as single-link flexible joint systems ^[19,22], vehicle lateral dynamics models ^[26], nonlinear tire models ^[27], and diesel engine models ^[28]. In particular, if $f(x)$ and $g(x)$ are linear functions, ${\underline f_{ij}} = {\bar f_{ij}}, {\underline g_{ij}} = {\bar g_{ij}}$ are real constants in A1.

When A1 is satisfied, it can be proven that $f(x)$ and $g(x)$ are globally Lipschitz. Hence, they are called Lipschitz nonlinear terms, and system (1) is referred to as a Lipschitz nonlinear system.

The reference signal $r(t) \in {\mathbb {R}}^{p}$ is piecewise differentiable with finite discontinuity points in $[0, \infty)$ and satisfies the following assumption.

A2. The reference signal $r(t)$ converges to a constant vector $r$ as time tends to infinity, i.e., $\mathop {\lim }\limits_{t \to \infty } r(t) = r$. In addition, the derivative of $r(t)$ satisfies ${\dot r}(t) \in {L_2}[0, \infty)$. Moreover, the reference signal $r(t)$ is assumed to be previewable in the sense that future values $r(\tau)(t \le \tau \le t + {l_r})$ are available at each time $t$, where $l_r$ denotes the preview length of the reference signal.

Remark 2. A2 is a basic assumption in the field of preview control ^[29,30,31]. In practical problems, the information of a reference signal is usually fully or partially known, such as a vehicle's driving path and an aircraft's scheduled flight path. Previous studies, such as ^[32,33], have shown that the known information of a reference signal is used to design a feedforward compensator that significantly improves the tracking behavior of a closed-loop system.

To facilitate the subsequent analysis and proof, the following lemmas are given.

Lemma 1. (Schur complement lemma) ^[34] A symmetric matrix $S = \left[ \begin{matrix} {{S}_{11}} & {{S}_{12}} \\ S_{12}^{\rm T} & {{S}_{22}} \\ \end{matrix} \right]<0$ is equivalent to any one of the following conditions:

(ⅰ) ${{S}_{22}}<0,{{S}_{11}}-{{S}_{12}}S_{22}^{-1}S_{12}^{\rm T}<0$ ;

(ⅱ) ${{S}_{11}}<0,{{S}_{22}}-S_{12}^{\rm T}S_{11}^{-1}S_{12}^{{}}<0$ .

Lemma 2. ^[35] For matrices $T$, $H$, $V$, $W$ with appropriate dimensions and a scalar $\zeta$, the inequality

is fulfilled if the following condition holds:

3.   Main results

3.1.   AES construction

In practical applications, it is generally impossible to obtain all the states of a system via measurement. Therefore, to estimate the unknown system states, we consider the following observer dynamical system:

where $\hat x(t) \in {\mathbb R}^{n}$ is the observer state, $\hat y(t) \in {\mathbb R}^{p}$ is the output of the observer, and $L$ is the observer gain matrix to be designed.

The estimation error is defined as follows:

From systems (1) and (2), the dynamic equation of the estimation error is obtained as follows:

Taking the derivatives of both sides of the observer system (2) leads to

where $\frac{{\partial f(\hat x)}}{{\partial \hat x}}$ and $\frac{{\partial g(\hat x)}}{{\partial \hat x}}$ can be expressed as follows:

For simplicity, the following notations are used.

and

Combined with A1, we assume $\phi$, $\eta$, $\varphi$, and $\xi$ are unknown parameter vectors whose elements satisfy

Notably, the unknown parameters $\phi$ and $\varphi$ belong to the same bounded convex set:

Similarly, the unknown parameters $\eta$ and $\xi$ belong to the same bounded convex set as shown below:

The tracking error is defined as

From Eqs (1) and (8), the tracking error satisfies the following:

where

Moreover, using Eqs (3), (6), and (7) and the previously described notations, Eq (5) can be rewritten as follows:

where $C(\xi)$ is as stated in Eq (10),

Combining the first equation of system (11) and Eq (9) yields the following error system:

According to A2, the information $r(\tau)(t \le \tau \le t + {l_r})$ of the reference signal $r(t)$, which ranges from the current time $t$ to the future $l_r$ steps, is known in advance. To use such information to construct the preview compensation mechanism and retain the dynamic process of the system itself, several ingenious mathematical operations are now applied to system (15).

By defining a new state vector $\bar x(t) = \left[\begin{matrix} {{\dot {\hat x}}(t)} \\ {e(t) - \int_t^{t + {l_r}} {\dot r(s){\rm{d}}s} } \end{matrix} \right]$ and a disturbance vector $\varpi (t) = \left[\begin{matrix} {\dot \omega (t)} \\ {\dot r(t + {l_r})} \end{matrix} \right]$, Eq (15) can be expressed as

where

with

Taking the derivatives of both sides of Eq (4) leads to

where $G(\xi, \eta)$ and $C(\xi)$ are given by Eqs (14) and (10), respectively, and

Combining Eqs (16) and (17), we obtain

where ${A_{11}}(\xi, \phi, \eta)$, ${A_{12}}(\xi)$, $\bar B$ and $\bar E$ are as previously described, and

with

To evaluate the system performance, we introduce the following linear quadratic performance function

where ${Q_e} > 0, {Q_\varepsilon } > 0$, and $R > 0$ are weighting matrices that can be tuned based on the designer's experience.

In fact, if we define a performance signal as follows:

where

then, the performance index function (19) can be expressed as the square of the $L_{2}$ norm of the performance signal:

Combining Eqs (18) and (20), we obtain

Notably, system (22) is still in the form of an LPV system. In the study of preview control, it is generally referred to as an AES. By introducing state feedback control to this system, a dynamic output feedback tracking controller with a preview compensation mechanism can be established for the original system (1). At this point, the observer-based robust preview tracking control problem of system (1) is transformed into a robust $H_{\infty}$ controller design problem of system (22) under the performance index (21).

Precisely, the main problem to be addressed is stated as follows:

The controller for system (22) is designed to satisfy these two requirements:

(ⅰ) The closed-loop system of AES (22) with $\varpi (t) = 0$ is asymptotically stable.

(ⅱ) Under the zero initial condition, the closed-loop system of AES (22) has a prescribed $H_{\infty}$ disturbance attenuation level $\gamma > 0$, i.e.,

is satisfied for any nonzero $\varpi (t) \in {L_2}$.

Note that the inequality (23) is also known as the disturbance attenuation condition, which means that the effect of external disturbance $\varpi (t)$ on performance signal $z(t)$ is attenuated at least by a level $\gamma$.

We say that the closed-loop system is asymptotically stable with $H_{\infty}$ performance level $\gamma$ if the above two requirements are satisfied. The corresponding controller is said to be the robust controller with $H_{\infty}$ performance level $\gamma$.

3.2.   Observer-based robust preview controller design

For AES (22), we introduce the following state feedback controller:

where $K$ is the controller gain matrix to be determined.

With control law (24), the closed-loop system of AES (22) is expressed as follows:

Notably, the unknown parameters $\phi$ and $\varphi$ belong to the previously mentioned bounded convex set ${\varsigma _1}$, whose set of vertices is defined by

Moreover, the unknown parameters $\eta$ and $\xi$ belong to the previously stated bounded convex set ${\varsigma _2}$, whose set of vertices is defined by

For convenience, we define the following matrices:

Theorem 1. Suppose that A1 and A2 hold. Given scalars $\vartheta > 0$ and $\gamma > 0$, the closed-loop system (25) is asymptotically stable with $H_{\infty}$ performance level $\gamma$ for all admissible uncertainties $\varphi$, $\phi$, $\xi$, and $\eta$ if there exist matrices ${P_1} > 0$, ${P_2} > 0$, $X$, $U$, and $V$ such that

for $\forall \varphi \in {\upsilon _{{\varsigma _1}}}$, $\forall \phi \in {\upsilon _{{\varsigma _1}}}$, $\forall \xi \in {\upsilon _{{\varsigma _2}}}$ and $\forall \eta \in {\upsilon _{{\varsigma _2}}}$, where

Furthermore, the controller and observer gain matrices are computed as $K = XP_1^{ - 1}$ and $L = U{V^{ - 1}}$, respectively.

Proof. Consider the following positive-definite Lyapunov function candidate:

Inspired by ^[25], the asymptotic stability of the closed-loop system (25) is guaranteed under the prescribed $H_{\infty}$ performance criterion if the following inequality holds:

In fact, by denoting

we have

Using Eq (30), the left side of Eq (29) can be reformulated as follows:

where

At this point, the problem is transformed to finding a sufficient condition for $\Omega < 0$. By the Schur complement lemma, i.e., Lemma 1, the inequality $\Omega < 0$ is equivalent to

By performing the powerful congruence transformation, i.e., premultiplying and postmultiplying the matrix on the left side of Eq (32) by the invertible matrix $diag({P_1}, {P_2}, I, I)$ and its transpose, respectively, we obtain a sufficient condition for inequality (32):

Using Eq (26), ${A_{11}}(\xi, \phi, \eta)$, ${A_{12}}(\xi)$, and ${A_{21}}(\varphi, \phi, \xi, \eta)$ in Eq (33) can be rewritten as follows:

where

From Eqs (34)–(36), inequality (33) can be rewritten as follows:

where

Denote the matrix on the left side of inequality (37) as $\Phi$. Because of the presence of some nonlinear coupling terms, such as ${T_3}LC(\xi){P_2}$, the matrix inequality $\Phi < 0$ cannot be solved directly. To avoid any nonlinearities and make the proposed design scheme easier to handle numerically, the change-of-variable technique and a novel auxiliary matrix approach are used to solve this problem. With the change in variable $X = K{P_1}$, the controller gain matrix is calculated as $K = XP_1^{ - 1}$. To conveniently determine the observer gain matrix, we introduce a nonsingular matrix $V$ and define $L = U{V^{ - 1}}$. Then, the following equation holds:

From Eqs (38) and (39), the matrix $\Phi$ on the left side of Eq (37) can be re-expressed as follows:

where

with

According to Lemma 2, the matrix inequality $\Phi < 0$ is satisfied if the following condition holds:

where

The matrix inequality (40) is equivalent to condition (27) stated in Theorem 1. Hence, if condition (27) is satisfied, then condition (37), i.e., $\Phi < 0$, is satisfied. As a result, the condition $\Omega < 0$ is ensured. This completes the proof of Theorem 1. □

Remark 3. Notably, a direct result of the LMI condition (27) being satisfied in Theorem 1 is

for $\forall \xi \in {\upsilon _{{\varsigma _2}}}$. Furthermore, by applying the differential mean value theorem to $f(x(t)) - f(\hat x(t))$ and $g(x(t)) - g(\hat x(t))$ in dynamic equation (4) for estimation error, the state matrix is $A(\varphi) - LC(\xi)$. By inequality (41), the estimation error system (4) is asymptotically stable, indicating that the proposed observer system (2) achieves an asymptotic estimation of the true state of system (1). Therefore, the LMI condition stated in Theorem 1 ensures that the state estimation and output tracking errors converge to zero simultaneously as time tends to infinity.

Remark 4. To obtain a robust tracking control structure with superior performance, the disturbance attenuation level $\gamma$ should be reduced as much as possible. Thus, the controller design problem can be formulated as the following minimization problem:

Now we discuss the controller design structure of system (1).

If the LMI problem of Theorem 1 has a feasible solution, then the controller gain matrix is calculated as $K = XP_1^{ - 1}$. To clearly illustrate the structure of the proposed tracking controller, the controller gain matrix $K$ is partitioned as follows:

where ${K_1} \in {\mathbb R}^{m \times n}$ and ${K_2} \in {\mathbb R}^{m \times p}$. As a result, controller (23) can be expressed as follows:

To attain the control input $u(t)$ of system (1), we choose a constant $\ell$ satisfying $\ell \ge {l_r}$ and calculate the integral of both sides of Eq (43) over $[ - \ell, t]$:

Notably, $u(- \ell) = 0$, $e(s) = 0{\rm{ }}(- \ell \le s < 0)$, $\hat x(- \ell) = 0$, and $r(- \ell + s) = 0{\rm{ }}(0 \le s \le {l_r})$. Substituting these conditions into the above equation, the second theorem of this paper can be derived.

Theorem 2. Suppose that A1 and A2 hold. If LMI (27) in Theorem 1 has a feasible solution, then the observer-based robust preview tracking controller of system (1) is

where the estimated state $\hat x(t)$ is given by the observer system (2) with the observer gain matrix $L = U{V^{ - 1}}$ and the controller gain matrices $K_1$ and $K_2$ are determined via Eq (42).

Remark 5. The innovation of this paper is the design of an observer-based robust preview controller for Lipschitz nonlinear systems in the form of (1). As shown in Eq (44), the proposed controller consists of three parts. The first part ${K_1}\hat x(t)$ represents the observer-based state feedback control action, the second part ${K_2}\int_0^t {e(s){\rm{d}}s}$ represents the integral control action used to eliminate the steady-state error, and the third part $- {K_2}\int_t^{t + {l_r}} {r(s){\rm{d}}s}$ represents the preview compensation action composed of the known future information of the reference signal. The novel observer-based preview controller design significantly enhances robust tracking control performance.

Remark 6. Recently, the tracking control problem of continuous-time Lipschitz nonlinear systems has received considerable attention. Novel and interesting methods for solving related problems have been proposed ^[22,25]. Unlike ^[22], the previewable information of the reference signal is fully used in the controller design in this paper. As such, the proposed tracking controller includes a preview feedforward compensation mechanism, which can improve the output tracking performance of the closed-loop system. Furthermore, compared with the two-step algorithm in ^[22], the observer-based robust preview tracking controller design method in Theorem 2 is quite simple and straightforward, and the observer and tracking controller gains can be determined simultaneously through a one-step LMI algorithm. Hence, the design complexity and computational load are effectively reduced. In addition, if the full system state information cannot be measured, the preview tracking controller in ^[25] will not be applicable. In this case, the observer-based preview control method proposed in this paper offers an effective and practical solution. In this sense, our design can be considered an improvement and optimization of techniques in ^[22,25].

4.   Numerical simulation

To illustrate the effectiveness and superiority of the proposed control scheme, simulation experiments are performed using a well-known single-link flexible joint robot system and a numerical example in this section. A simulation comparison is performed among the control scheme in ^[22], the proposed scheme, and the LQR scheme based on linearization via MATLAB software.

Example 1. Consider the well-known single-link flexible joint robot system^[19,22,36]

where

The nonlinear term $f(x)$ satisfies A1 with ${\underline f_{41}} = {\bar f_{41}} = {\underline f_{42}} = {\bar f_{42}} = {\underline f_{44}} = {\bar f_{44}} = 0, {\underline f_{43}} = -3.33, {\bar f_{43}} = 3.33. {\underline f_{ij}} = {\bar f_{ij}} = 0, i = 1, 2, 3;j = 1, 2, 3, 4$. Suppose that the desired reference signal satisfies A2.

Set ${Q_e} = 8, {Q_\varepsilon } = 0.06, R = 8, \gamma = 10, \vartheta = 0.5$. From Theorem 1, by resorting to the LMI toolbox in MATLAB, the observer and tracking controller gain matrices are calculated concurrently as follows:

According to Theorem 2, a robust observer-based preview tracking controller can then be derived.

For simulation, the previewable reference signal is taken as

The initial state of the system is $x(0) = {\left[\begin{matrix} 0 & 0 & 0 & 0 \end{matrix} \right]^{\rm{T}}}$, and the initial state of the observer is set as $\hat x(0) = {\left[\begin{matrix} 0.01 & 0 & 0.01 & 0.02 \end{matrix} \right]^{\rm{T}}}$.

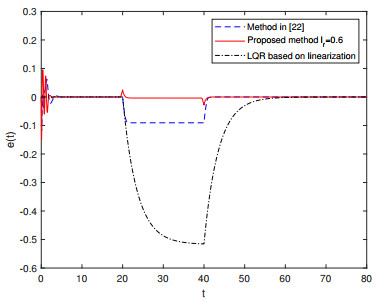
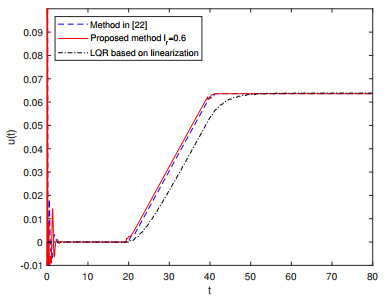
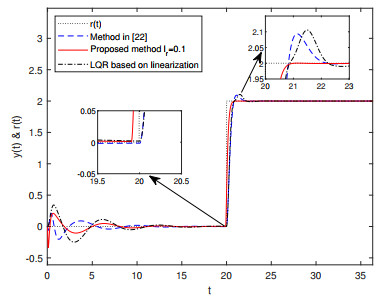
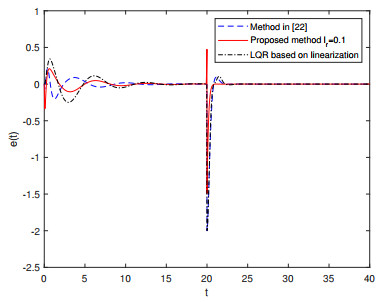
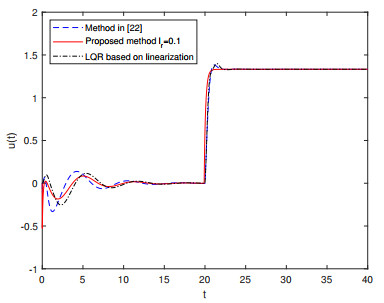
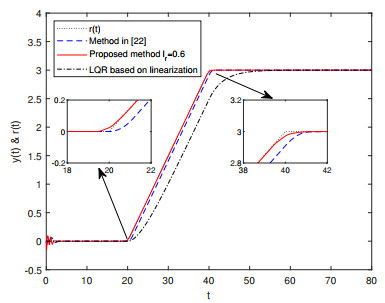
The output response curve of the closed-loop system is plotted in Figure 1, and the response curves of the tracking error and control input are shown in Figures 2 and 3, respectively. These figures reveal that the system outputs in three methods can realize asymptotic tracking of the reference signal regardless of the effects of disturbance and Lipschitz nonlinearities. Compared with the method in ^[22] and the LQR method based on linearization, the proposed control scheme forces the output signal to track the reference signal more rapidly and accurately. The excellent tracking performance mainly benefits from the feedforward compensation mechanism of the preview information of the reference signal.

To quantitatively demonstrate the superiority of the proposed method, the ISE, ITSE, IAE, and ITAE deviation integral indicators are evaluated (Table 1). Compared with the method in ^[22] and the LQR method based on linearization, the proposed method can significantly decrease the integral index values, thereby achieving excellent tracking performance.

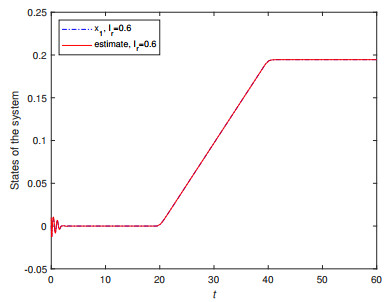
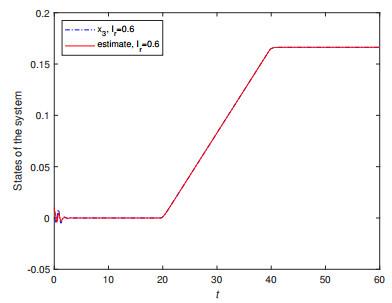
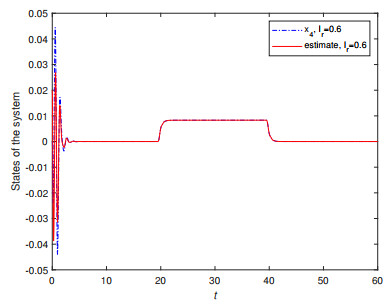
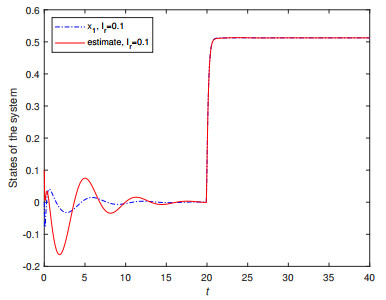
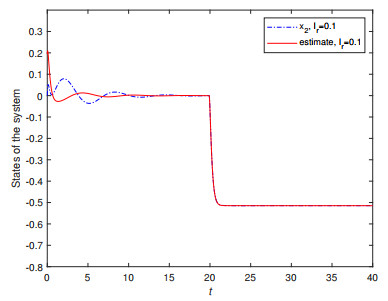
To illustrate the excellent observation effect, Figures 4–7 show the response curves of the true and estimated system states. The estimated state provided by the observer converges quickly and accurately to the true state.

Example 2. Consider a nonlinear system in the form of Eq (1) with the following system parameters:

The nonlinear terms $f(x)$ and $g(x)$ satisfy A1 with ${\underline f_{11}} = {\bar f_{11}} = {\underline f_{12}} = {\bar f_{12}} = {\underline f_{22}} = {\bar f_{22}} = 0, {\underline f_{21}} = -0.5$, ${\bar f_{21}} = 0.5. {\underline g_{11}} = {\bar g_{11}} = 0, {\underline g_{12}} = 0, {\bar g_{12}} = 0.1$. Suppose that the desired reference signal satisfies A2.

Set ${Q_e} = 1, {Q_\varepsilon} = 0.05, R = 2, \gamma = 2, \vartheta = 0.1$. By Theorem 1, using the LMI toolbox in MATLAB, the observer and tracking controller gain matrices are computed simultaneously as follows:

According to Theorem 2, a robust observer-based preview tracking controller can then be derived.

For simulation, the reference signal is taken as

The external disturbance is considered $\omega (t) = \sin (t){e^{ - 0.25t}}$, the initial system state is $x(0) = {\left[\begin{matrix} 0 & 0 \end{matrix} \right]^{\rm{T}}}$, and the initial observer state is $\hat x(0) = {\left[\begin{matrix} 0.1 & 0.2 \end{matrix} \right]^{\rm{T}}}$.

The output response curve of the closed-loop system is shown in Figure 8, and the response curves of the tracking error and control input are shown in Figures 9 and 10, respectively. By analyzing the simulation graphs, it is evident that compared with the control method in ^[22] and the LQR method based on linearization, the proposed control method reduces the effects caused by the disturbance and has a faster response speed, lower overshoot, and smaller tracking error. The significant improvement in tracking performance of the closed-loop system is mainly attributed to the feedforward compensation mechanism of the preview information of the reference signal. Numerical simulation results confirm the effectiveness and superiority of the proposed preview controller in improving the system tracking performance.

The quantitative comparison results via some direct and simple performance criteria, such as ISE, ITSE, IAE, and ITAE, are provided in Table 2. As can be seen in the table, the performance indices are decreased when using the proposed controller compared with the method in ^[22] and the LQR method based on linearization.

Figures 11 and 12 show the response curves of the true and estimated system states. The estimated state provided by the observer produces fast and accurate convergence to the actual system state. The observation performance of the constructed state observer is satisfactory.

Remark 7. The possible challenges for implementing the proposed method in practical applications include the following: (ⅰ) The actual system is complex and variable, making it difficult to mathematically model it in the form of system (1). (ⅱ) Model simplification may lead to deviations between theory and practice. (ⅲ) It is uncertain whether suitable sensors can be found to detect the preview information of the reference signal mentioned in A1 for specific tracking problems.

5.   Conclusions

In this paper, a novel observer-based robust preview tracking controller is designed for a class of continuous-time Lipschitz nonlinear systems with external disturbances and unknown states. First, a state observer is considered to reconstruct the unmeasured system state variables. Second, based on differentiation, the state lifting technique, the differential mean value theorem, and several ingenious mathematical manipulations, an AES, which includes the preview information of a reference signal, is constructed in the form of an LPV system. Thus, the tracking problem is transformed into a robust $H_\infty$ control problem. Based on the Lyapunov stability theory and the LMI approach, a state feedback controller is developed to guarantee that the closed-loop system is asymptotically stable with robust $H_\infty$ performance. Then, by regressing the controller to the original system, an observer-based robust preview tracking controller design is derived. In particular, the preview information of the reference signal is used as feedforward compensation to improve the tracking performance of the system. In addition, the observer and tracking controller gains can be computed via a one-step LMI algorithm. Numerical simulation results demonstrate that the tracking performance of the proposed controller is superior to that of existing controllers.

Author contributions

Xiao Yu: Conceptualization, Methodology, Software, Validation, Writing-original draft, Writing-review & editing; Yan Hua: Conceptualization, Methodology, Software, Validation, Writing-original draft, Writing-review & editing; Yangrong Lu: Writing-review & editing. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No. 62303280), the Shandong Provincial Natural Science Foundation of China (No. ZR2020QA036, ZR2021MF009, ZR2023MF055), the Shandong Provincial Youth Innovation and Technology Plan for Universities (No. 2021KJ067), the Hubei Provincial Natural Science Foundation of China (No. 2022CFB139) and the Doctoral Research Fund in Shandong Jianzhu University (No. X19053Z).

Conflict of interest

All authors declare no conflicts of interest in this paper.