On rough generalized Marcinkiewicz integrals along surfaces of revolution on product spaces

1.   Introduction

The establishment and analysis of differential equation models have proven to be an effective approach for understanding and predicting the dynamics of biological populations. The prey-predator relationship is one of basic relationships of species interactions in ecology, so a significant number of ordinary differential prey-predator models have been studied in recent years; refer to ^[1,2,3,4]. A key area of interest is the Leslie-Gower prey-predator model ^[5], which can be expressed in the following form:

where $x$ and $y$ denote the densities of prey and predator, respectively, and the parameters $\beta$, $\mu$ are positive constants. Korobeinikov ^[6] has proved that the unique positive singularity of (1.1) is globally asymptotically stable by constructing Lyapunov function.

The prey in system (1.1) grows at a logistic pattern, which posits that population growth will accelerate when density is low. However, in the real natural environment, due to factors such as mate limitation, homologous reproduction, cooperative defense, and environmental conditioning, it was recognized that the prey species may have a growth rate of Allee effect in recent years; see references ^{[7,8,9,10,11]}. Mathematically, the Allee effect is often expressed as the following growth model:

where $x$ is the population size and $b$ is the Allee threshold. The Allee effect is usually divided into two types: strong Allee effect when $0 < b < 1$ and weak Allee effect when $b\leq0$. The dynamic properties of strong and weak Allee effects are fundamentally distinct. In the case of strong Allee effect, if the population size falls below the Allee threshold $b$, the population will become extinct. The weak Allee effect shares similar dynamic properties with the logistic growth model, that is, the population tends to the maximum environmental carrying capacity as $t\to\infty$. Therefore, in order to avoid the extinction of populations, people are more interested in studying population models with strong Allee effects, and there have been many research achievements in recent years.

Considering the influence of strong Allee effect on prey in (1.1), Ni and Wang ^[7] established and discussed the following prey-predator system with strong Allee efect on prey

where $0 < b < 1$ is the Allee threshold. They investigated the dynamical properties of solutions and the unstable and stable manifolds of the positive singularity when the system (1.3) has only one positive singularity. Min and Wang ^[8] discussed Hopf bifurcation of (1.3) in great detail and used the center manifold and normal form theory to determine the direction of the Hopf bifurcation and the stability of the branched periodic solutions.

The functional response plays a crucial role in prey-predator models, as it describes the interaction between the prey and predator populations in nature. Functional responses are often divided into prey-dependent type, such as Holling type functional response and prey-predator-dependent, like ratio-dependent functional response and Bddington-DeAngelis functional response. The interference and cooperation between conspecific predators is a common phenomenon. For example, bats prevent other bats from feeding by emitting special interference sounds, while wild dogs cooperate to attack prey to increase their chances of success in hunting. Therefore, prey-predator-dependent functional responses are more consistent with the real situation in nature than prey-dependent functional responses. However, as far as we know, most of prey-predator-dependent functional responses assume that predators are mutually interfering with each other, such as the ratio-dependent functional response and Bddington-DeAngelis functional response. On the contrary, the cooperative hunting relationships between predators are rarely considered. In 2017, considering the cooperative hunting behavior observed among predators, Alves and Hilker ^[12] developed the following prey-predator-dependent type functional response

where $\lambda$ is the attack rate of the predator, and $a$ describes the intensity of hunting cooperation among predators. In recent years, some scholars have begun to investigate the impact of cooperative hunting on predator-prey models; see references ^{[13,14,15,16,17]}. Ye and Wu ^[13] incorporated the factor of cooperative hunting in system (1.3) and studied its dynamic properties.

As people's demand for natural resources increases, the issue of how to meet this demand without disrupting the balance of ecosystems has become an increasingly important topic. Therefore, introducing a harvesting term into prey-predator models has significant practical significance. In fact, harvesting of biological populations has been widely practiced in industries such as forestry, fishing, and wildlife resource management. The introduction of harvesting will make the dynamics of ecosystems more complex and diverse, so the impact of harvesting on ecosystems and the role of harvesting in resource management have both been studied by more and more scholars in depth. A common harvesting mechanism is constant-yield harvesting, where the harvesting rate is independent of the number of species being harvested. This type of harvesting has recently attracted the attention of scholars; see references ^{[18,19,20,21,22]}. However, it is evident that there are some drawbacks to constant yield harvesting from both a biological and economic perspective. For example, if the population being harvested is very small and below the harvest constant, constant-yield harvesting can easily lead to the extinction of the biological population. On the other hand, May et al. proposed the concept of proportional harvesting, also known as constant-effort harvesting in their paper ^[23], in which the harvesting rate is proportional to both the number of the harvested species and the human effort invested. Clearly, from an ecological perspective, the constant-effort harvesting is more realistic than constant-yield harvesting.

According to our investigation, there is no research on prey-predator models currently that considers strong Allee effects and harvesting effects in prey and cooperative hunting effects in predators. We are very interested in the dynamics of such models, therefore, this article mainly discusses the following system:

where $x$ and $y$ represent the densities of prey and predator, respectively; paremeters $a$, $\mu$, $h$ are positive constants, $0 < b < 1$; $b$ represents the threshold of strong Allee effect on the prey, and $h$ represents the harvestable yield of the prey and human effort. Obviously, the system (1.4) is defined on the set $\Omega = \{(x, y)|x > 0, y\geq0\}$ and not defined along the axis $x = 0$, especially at the point (0, 0).

From a mathematical research perspective, the analysis of system (1.4) presents considerable challenges. On the one hand, unlike the classical prey-predator systems, $(0, 0)$ is not an equilibrium of (1.4), and the system is not even defined at the axis $x = 0$. Specifically, when $0 < x < b$ and $y > 0$,

which means that $x$ may tend to zero and the term $y/x$ may be unbounded. Such a bad structure will bring a lot of difficulties in the analysis. On the other hand, the interaction of three ecological factors, namely, Allee effect, harvesting effect, and hunting cooperation, makes theoretical analysis more complex. This paper aims to explain how the three ecological factors mentioned above collectively influence the dynamic properties of species.

The layout of this paper is as follows. In Section 2, the positivity and boundedness of solutions are obtained. Specifically, we give the uniform persistence of the system under some conditions. In Section 3, we discuss the existence of nonnegative singularity of (1.4). In Section 4, we analyze the type of all singularities including primary singularities and higher-order singularities. In Section 5, the origin is proved to be an attractor and the basin of attraction is given. In Section 6, we discuss saddle node bifurcation and Hopf bifurcation that occur in system (1.4). In Section 7, we illustrate the conclusions of our theoretical analysis through some numerical simulations.

2.   Basic properties of the system (1.4)

It is evident that the system (1.4) with nonnegative initial values $(x_0, y_0)$ has a unique solution $(x(t), y(t))$ in $[0, +\infty)$ by the existence and uniqueness theorem and extension theorem of solutions for ordinary differential equations ^[24]. In this section, we will give some other basic properties about the system (1.4), such as the positivity and boundedness of solutions, the uniform persistence of the system (1.4), etc.

Proposition 2.1. If $x_0 > 0$ and $y_0 > 0$, then any solution $(x(t), y(t))$ of (1.4) is positive and bounded for $t\geq0$.

Proof. It is obvious that $x = 0$ is an invariant set from the first equation of (1.4). According to the theorem of existence and uniqueness of solutions ^[24], solutions starting from $x_0 > 0$ will not intersect with the solusion $x = 0$. Therefore, if $x_0 > 0$, then $x(t) > 0$ for all $t\geq0$. Similarly, one can also know that if $y_0 > 0$, then $y(t) > 0$ for all $t\geq0$. Accordingly, every solution of (1.4) with the initial values $x_0 > 0$ and $y_0 > 0$ is positive.

On the other hand, since $x(t)$ satisfies

it follows from the comparison principle that $x(t)\leq\max\{1, x_0\}$ for $t\geq0$. Denote $A = \max\{1, x_0\}$. From the second equation of (1.4), we have

Once again, based on the principle of comparison, it follows that $y(t)\leq\max\{A, y_0\}$ for $t\geq0$. Therefore, every solution of (1.4) with the initial values $x_0 > 0$ and $y_0 > 0$ is bounded. □

Remark 2.1. The proof of proposition $2.1$ suggests that the set $\Omega$ is an invariant set for the system (1.4).

Proposition 2.2. If $0 < x_0\leq b$ and $(x_0, y_0)\neq(b, 0)$, then $\lim\limits_{t\to\infty}(u(t), v(t)) = (0, 0)$.

Proof. If $0 < x_0 < b$ and $y_0\geq0$, then it follows (2.1) that $x(t)$ converges to $0$ as $t\to\infty$. Thus, for any $\varepsilon > 0$, there exists $T > 0$ such that $x(t) < \varepsilon$ for $t\geq T$. From the second equation of (1.4), we have

As a result, $\limsup\limits_{t\to\infty}y(t)\leq \varepsilon$. The arbitrariness of $\varepsilon$ leads to $\lim\limits_{t\to\infty}y(t) = 0$.

If $x_0 = b$ and $y_0 > 0$, from the first equation of (1.4),

According to the proof of proposition 2.1, we know that if $y_0 > 0$, then $y(t) > 0$ for all $t\geq0$. To sum up, the solution $(x(t), y(t))$ of (1.4) satisfies $x(t_0) < b$ and $y(t_0) > 0$ at some small time $t_0 > 0$. Then, utilizing results of $0 < x_0 < b$ and $y_0\geq0$, we have

In conclusion, the proof is finished. □

Remark 2.2. Proposition $2.2$ indicates that when the prey density is too low, the prey will perish and the predator also becomes extinct. This phenomenon contradicts the traditional perspective of population dynamics. In fact, this is caused by the Allee effect. From a biological perspective, congregating is conducive to the reproduction and survival of the population. Each species has its own optimal density, and too dense or too sparse will have a restraining effect on the population.

Definition 2.1. ^[25] If there are two positive numbers $\omega_1$ and $\omega_2$, such that any positive solution of the system (1.4) with nonnegative initial values $(x_0, y_0)$ satisfies the following inequalities

then the system (1.4) is said to be uniformly persistent.

Theorem 2.1. If $(1-b)^2/(4b) > 1+a+h$ and $x_0\geq x_0^*$, then the system (1.4) is uniformly persistent, where $x_0^* = \frac{1+b-\sqrt{(1+b)^2-4b(2+a+h)}}{2a}.$

Proof. Because $(1-b)^2/(4b) > 1+a+h$, there exists $\varepsilon > 0$ such that $(1-b)^2/(4b) > 1+a+h+ \varepsilon(1+2a+a \varepsilon)$. Let $(x(t), y(t))$ be the unique solution of (1.4) with nonnegative initial values $(x_0, y_0)$. From (2.1), we easily get $\limsup\limits_{t\to\infty}x(t)\leq1$. Then, for the above $\varepsilon$, there is $T > 0$ such that $x(t) < 1+ \varepsilon$ for all $t\geq T$. Replace $\varepsilon$ with $1+ \varepsilon$ in (2.2). Similarly to the proof of Proposition 2.2, since $\varepsilon$ here can be arbitrary, we have $\limsup\limits_{t\to\infty}y(t)\leq1$. Consequently,

In view of the second equation of (1.4), when $t$ is sufficiently large, we have

It is clear that $\Phi(x) = 0$ has two positive roots when $(1-b)^2/(4b) > 1+a+h$, which can be denoted as $\hat x$ and $\tilde x$, where

Furthermore, we have

which implies that $\liminf\limits_{t\to\infty}x(t)\geq\hat x$ when $x_0 > x_0^*$.

Similarly, according to the second equation of (1.4), when $t$ is sufficiently large, we have

Obviously, $\liminf\limits_{t\to\infty}y(t)\geq\hat x$. Hence, $\min\{\liminf\limits_{t\to\infty}x(t), \liminf\limits_{t\to\infty}y(t)\}\geq\hat x$. In summary, it can be concluded that system (1.4) is uniformly persistent. □

Remark 2.3. Theorem $2.1$ indicates that prey and predators will always coexist when the quantity of prey is sufficient and the human capture intensity of prey is moderate. From a biological perspective, when the quantity of prey is sufficient and the capture amount is not large, the prey can satisfy the capture of both predator and humans so that the prey and the predator can always coexist.

3.   The existences of singularities

If $(x^*, y^*)$ is the nonnegative singularities of (1.4), then $(x^*, y^*)$ satisfies the following equations:

From the second equation of (3.1), we know that $y^* = 0$ or $y^* = x^*$. Obviously, the singularities obtained when $y^* = 0$ are the boundary singularities, and the singularities obtained when $y^* = x^*$ are the positive singularities. Next, we will discuss the two cases of $y^* = 0$ and $y^* = x$, respectively.

For the case of $y^* = 0$, $x^*$ is the positive root of equation

Letting $\Delta_1 = (1+b)^2-4b(1+h)$ and $h_1 = (1-b)^2/(4b)$, we have the following results:

● If $h > h_1$, then Eq (3.2) has no roots.

● If $h = h_1$, then Eq (3.2) has unique positive root $x_1$, and $x_1 = (1+b)/2$.

● If $h < h_1$, then Eq (3.2) has two positive roots $x_2$ and $x_3$, where

For the case of $y^* = x^*$, $x^*$ is the positive root of equation

Denote $\Delta_2 = 1-4b(1+ab)(1+h)$, $h_2 = [1-4b(1+ab)]/[4b(1+ab)]$, and $a^* = (1-4b)/(4b^2)$. It easy to obtain $h_2 < h_1$ by direct calculation. Then, the situation about the roots of (3.3) is as follows:

● When $1/4\leq b < 1$ or $a\geq a^*$, $\Delta_2 < 0$, which means that the Eq (3.3) has no roots.

● When $0 < b < 1/4$ and $a < a^*$, the value of $\Delta_2$ is also related to the parameter $h$.

(1) If $h > h_2$, then $\Delta_2 < 0$, so the Eq (3.3) has no roots;

(2) If $h = h_2$, then $\Delta_2 = 0$, so the Eq (3.3) has unique positive roots $x_4$ with $x_4 = 1/[2(1+ab)]$;

(3) If $h < h_2$, then $\Delta_2 > 0$, so the Eq (3.3) has two positive roots $x_5$ and $x_6$, where

Base on the above discussion, we obtain the following theorem about the existence of nonnegative singularities.

Theorem 3.1. Assume $a, \, h, \, \mu > 0$, and $0 < b < 1$. Denote $h_1 = (1-b)^2/(4b)$, $h_2 = [1-4b(1+ab)]/[4b(1+ab)]$, and $a^* = (1-4b)/(4b^2)$. Then, the following conclusions about the existence of singularities for the system (1.4) are valid.

(1) If $h > h_1$, then the system (1.4) has no singularity;

(2) If $h = h_1$, then the system (1.4) has unique boundary singularities denoted by $E_1(x_1, 0)$;

(3) If $h < h_1$, then the system (1.4) has two boundary singularities denoted by $E_2(x_2, 0)$ and $E_3(x_3, 0)$, respectively;

(4) When $1/4\leq b < 1$ or $a\geq a^*$, the system (1.4) has no positive singularity;

(5) When $0 < b < 1/4$ and $a < a^*$. If $h > h_2$, then the system (1.4) has no positive singularity; if $h = h_2$, then the system (1.4) has a unique positive singularity denoted by $E_4(x_4, x_4)$; if $h < h_2$, then the system (1.4) has two positive singularities denoted by $E_5(x_5, x_5)$ and $E_6(x_6, x_6)$, respectively;

where $x_1$, $x_2$, $x_3$, $x_4$, $x_5$, $x_6$ are defined as in above discussions.

From Theorem (3.1), harvesting behavior, hunting cooperation, and Allee effect collectively affect the number of singularities and the system (1.4) has at most four singularities, which imply the system (1.4) is likely to exhibit rich dynamic properties.

4.   The types of singularities

Denote ${\bf x} = (x, y)$ and

For the simplicity of the notations, we denote

The direct analysis reveals what the sign of $A(x_i)$ is when $i = 1, 2, 3$, i.e.,

Because $x_i(i = 1, 2, 3)$ satisfy Eq (3.2), the Jacobian matrix of (1.4) at the boundary singularities $E_i(x_i, 0)$ is

Furthermore, the determinant and trace of the Jacobian matrix $J_{E_i}$ are, respectively,

Similarly, since $x_i(i = 4, 5, 6)$ satisfy the Eq (3.3), the Jacobian matrix of (1.4) at the positive singularities $E_i(x_i, x_i)$ is

Accordingly, the determinant and trace of the Jacobian matrix $J_{E_i}$ are, respectively,

Based on (4.3) and (4.5), it is easy to know that $E_i(i = 2, 3, 5, 6)$ are primary singularities and $E_i(i = 1, 4)$ are higher-order singularities. For the primary singularities, the traditional linearization method is used to determine their types. For higher-order singularities, we will apply the method of Theorem $1$ and Theorem $3$ of Chapter 2 in reference ^[26] to give their types.

4.1.   Primary singularities and their types

Theorem 4.1. Let $a, \, h, \, \mu > 0$, and $0 < b < 1$. If $h < h_1$, the boundary singularities $E_2(x_2, 0)$ and $E_3(x_3, 0)$ are an unstable node and a saddle, respectively. Moreover, $E_2(x_2, 0)$ is a degenerate node when $\mu = A(x_2)$, where $x_2$, $x_3$, $h_1$, and $A(x_2)$ are defined as in Theorem $3.1$ and (4.1).

Proof. (1) From (4.3) with $i = 2$ and $A(x_2) > 0$, we get the determinant and trace of $J_{E_2}$, i.e.,

Then, further calculation generates

It follows that the linearized matrix $J_{E_2}$ may have a double positive real eigenvalue or two different positive real eigenvalues, respectively, when $\mu = A(x_2)$ and $\mu\neq A(x_2)$. Thus, $E_2$ is an unstable node. Especially, when $\mu = A(x_2)$, $J_{E_2}$ is an upper triangular matrix that cannot be diagonalized, so the eigen-space corresponding to its double eigenvalue is one-dimensional, which implies $E_2$ is a degenerate node.

(2) Based on (4.3) and $A(x_3) < 0$, it is obvious that

so $E_3$ is a saddle point. □

To analyze the stability of $E_6$, we will make the following preparations. According to Theorem 3.1, the following analysis is based on the conditions $0 < b < 1/4$, $0 < a < a^*$, and $0 < h < h_2$. We care about the sign of $A(x_6)$. Let

It is evident that $\tilde{\mu}$ and $A(x_6)$ have the same sign. Direct observation shows that $\tilde{\mu}$ is strictly increasing on $h$. Moreover,

and

To determine the sign of the limit of $\tilde{\mu}$ as $h\to0$, let

Direct calculation shows that $\tilde{a} < a^*$ and the sign of $\tilde{a}$ is related to the key value $b = \sqrt{5}-2$. Specifically, if $\sqrt{5}-2\leq b < 1/4$, then $\tilde{a}\leq0$. Now, $a > \tilde{a}$, which implies $\tilde{\mu} > 0$, i.e., $A(x_6) > 0$. If $0 < b < \sqrt{5}-2$, then $\tilde{a} > 0$. Furthermore, if $a\geq\tilde{a}$, then $\tilde{\mu}\geq0$, i.e., $A(x_6)\geq0$; if $0 < a < \tilde{a}$, then $\lim\limits_{h\to0}\tilde{\mu} < 0$, and then there exists $\tilde{h}$ such that $\tilde{\mu} = 0$. Therefore, when $0 < b < \sqrt{5}-2$, $0 < a < \tilde{a}$, if $0 < h < \tilde{h}$($h = \tilde{h}$, $\tilde{h} < h < h_2$, respectively), then $\tilde{\mu} < 0$($= 0$, $> 0$, respectively), i.e., $A(x_6) < 0$($= 0$, $> 0$, respectively).

For the convenience of description, based on the above analysis, the following conditions are summarized:

$\rm{(a1)}\ 0 < b < \sqrt{5}-2$, $a\geq\tilde{a}$, and $0 < h < h_2$;

$\rm{(a2)}\ 0 < b < \sqrt{5}-2$, $0 < a < \tilde{a}$, and $0 < h < \tilde{h}$;

$\rm{(a3)}\ 0 < b < \sqrt{5}-2$, $0 < a < \tilde{a}$, and $h = \tilde{h}$;

$\rm{(a4)}\ 0 < b < \sqrt{5}-2$, $0 < a < \tilde{a}$, and $\tilde{h} < h < h_2$;

$\rm{(a5)}\ \sqrt{5}-2\leq b < 1/4$, $0 < a < a^*$, and $0 < h < h_2$.

According to the above analysis, the following lemma can be obtained.

Lemma 4.1. Let $0 < b < 1/4$, $0 < a < a^*$, $0 < h < h_2$, $\tilde{a}$, and $\tilde{h}$ be defined in the above analysis, where $x_6$, $a^*$, and $h_2$ are defined in Theorem $3.1$. Then,

(1) If one of the three conditions $(a1)$, $(a4)$, and $(a5)$ holds, then $A(x_6) > 0$;

(2) If the condition $(a2)$ holds, then $A(x_6) < 0$;

(3) If the condition $(a3)$ holds, then $A(x_6) = 0$.

Theorem 4.2. Suppose $0 < b < 1/4$, $0 < a < a^*$, $0 < h < h_2$, and $\mu > 0$. Let $a^*$, $h_2$, $A(x_6)$, $\tilde{a}$, and $\tilde{h}$ be defined as in Lemma $4.1$. Then, the following conclusions are true.

(1) The positive singularity $E_5(x_5, x_5)$ always is a saddle point.

(2) When one of the three conditions $(a1)$, $(a4)$, and $(a5)$ holds.

(2.1) If $\mu < A(x_6)$, the positive singularity $E_6(x_6, x_6)$ is an unstable node or focus;

(2.2) If $\mu > A(x_6)$, $E_6(x_6, x_6)$ is a stable node or focus;

(2.3) If $\mu = A(x_6)$, $E_6(x_6, x_6)$ is a center or fine focus.

(3) Either the condition $(a2)$ or the condition $(a3)$ holds, and $E_6(x_6, x_6)$ is a stable node or focus.

Proof. Acoording to (4.5) with $i = 5$, it is clear that ${\rm det}(J_{E_5}) < 0$, which implies that $E_5$ a saddle point. On the other hand, we can also know that ${\rm det}(J_{E_6}) > 0$ and ${\rm tr}(J_{E_6}) = A(x_6)-\mu$. Therefore, when $\mu < A(x_6)$, i.e., ${\rm tr}(J_{E_6}) > 0$, $E_6$ is an unstable node or focus; when $\mu > A(x_6)$, i.e., ${\rm tr}(J_{E_6}) < 0$, $E_6$ is a stable node or focus; when $\mu = A(x_6)$, i.e., ${\rm tr}(J_{E_6}) = 0$, $E_6$ is a center or fine focus. Combined with the conclusion of Lemma 4.1, this theorem is proved. □

4.2.   Higher-order singularities and their types

Theorem 4.3. Let $a, \, h, \, \mu > 0$, $0 < b < 1$, and $h_1$ be defined as in Theorem $3.1$. When $h = h_1$, the system (1.4) has a unique singularity $E_1(x_1, 0)$, which is a repelling saddle-node.

Proof. From (4.2) and (4.3) with $i = 1$, the eigenvalues of $J_{E_1}$ are 0 and $\mu > 0$, which means that $E_1$ is a higher-order singularity of (1.4). To study the type of $E_1$, we first transform $E_1$ to $(0, 0)$ by letting $(X, Y) = (x-(1+b)/2, y)$. Then, the system (1.4) becomes

where $P_1(X, Y)$ and $Q_1(X, Y)$ are $C^{\infty}$ functions of at least third order in terms of $(X, Y)$. Continuing with the transformation $(u, v) = (X+(1+b)/(2\mu)Y, Y)$, the system (4.7) becomes

where $P_2(u, v)$ and $Q_2(u, v)$ are $C^{\infty}$ functions of at least third order in terms of $(u, v)$. Introduce a new time variable $\tau$ by $\tau = \mu t$, and we get

where $P_3(u, v)$ and $Q_3(u, v)$ are $C^{\infty}$ functions of at least third order in terms of $(u, v)$.

Since the coefficient of $u^2$ is $-(1+b)/(2b\mu) < 0$, by Theorem $1$ of Chapter 2 in reference ^[26], the boundary singularity $E_1$ is a repelling saddle-node. □

Lemma 4.2. ^[26] The system

is equivalent to the system

after some non-singular transformations in the neighborhood of $(0, 0)$.

Theorem 4.4. Let $a, \, h, \, \mu > 0$, and $0 < b < 1$. If $h = h_2$, the system (1.4) has a unique positive singularity $E_4(x_4, x_4)$. Moreover,

$\rm{(1)}$ if $\mu < A(x_4)$, $E_4$ is a repelling saddle-node;

$\rm{(2)}$ if $\mu > A(x_4)$, $E_4$ is an attracting saddle-node;

$\rm{(3)}$ if $\mu = A(x_4)$ and $a^2b^3+(3a^2+2a)b^2+(4a^2+2a+1)b-a-1\neq0$, then $E_4$ is a cusp of co-dimension $2$;

where $h_2$ and $x_4$ are defined as in Theorem $3.1$ and $A(x_4)$ are defined in (4.1).

Proof. According to (4.4) and (4.5) with $i = 4$, both eigenvalues of $J_{E_4}$ are $\lambda_1 = 0$ and $\lambda_2 = A(x_4)-\mu$. First, transform $E_4(x_4, x_4)$ to $(0, 0)$ by making $(X, Y) = (x-x_4, y-x_4)$. Then, the system (1.4) becomes

where

and $\widetilde{P_1}(X, Y)$, $\widetilde{Q_1}(X, Y)$ are $C^{\infty}$ functions of at least third order in terms of $(X, Y)$.

$\rm (1)$ When $\mu\neq A(x_4)$, $J_{E_4}$ has only one zero eigenvalue, and we still apply Theorem $7.1$ of Chapter 2 in reference ^[26] to study the type of $E_4$. Make the following transformation:

Then, system (4.10) becomes (still denoting $\tau$ as $t$)

where

and $\widetilde{P_2}(u, v)$, $\widetilde{Q_2}(u, v)$ are $C^{\infty}$ functions of at least third order in terms of $(u, v)$.

Next, we will determine the sign of $c_{20}$. Rewrite $q_0$ as follows:

and denote its root discriminant as $\Delta_q = 4a_{10}^2a_{01}^2+4a_{01}a_{10}^3$. Direct calculations indicate that $\Delta_q < 0$; thus, it can be determined that $q_0 < 0$. By calculation, we can know that the sum of the fourth and fifth terms of polynomial $q_1$ is $0$. Further calculations yield

Therefore, it shows that $c_{20} < 0$. Combining the time variable $\tau$, it follows Theorem $1$ of Chapter 2 in reference ^[26] that $E_4$ is an attracting saddle-node if $\mu > A(x_4)$, and a repelling saddle-node if $\mu < A(x_4)$.

$\rm (2)$ When $\mu = A(x_4)$, both eigenvalues are zero. Let $(X, Y) = (a_{01}u, -a_{10}u+v)$, then system (4.10) becomes

where

and $\bar{P}_2(u, v)$, $\bar{Q}_2(u, v)$ are $C^{\infty}$ functions of at least third order in terms of $(u, v)$.

By using Lemma 4.2, it can be obtained that system (4.11) is equivalent to

in the small neighborhood of $(0, 0)$, where $\overline{Q}_3(u, v)$ is a $C^{\infty}$ function of at least third order in terms of $(u, v)$. After complex calculations, we have

where

and

Hence, if $\mu = A(x_4)$ and $a^2b^3+(3a^2+2a)b^2+(4a^2+2a+1)b-a-1\neq0$, then $E_4$ is a cusp of co-dimension $2$ by the Theorem $3$ of Chapter 2 in reference ^[26]. In addition, if $\mu = A(x_4)$ and $a^2b^3+(3a^2+2a)b^2+(4a^2+2a+1)b-a-1 = 0$, then $E_4$ is a cusp of co-dimension at least $3$. □

5.   Dynamical properties of (1.4) near the origin

Although the system (1.4) is not defined at $(0, 0)$, proposition 2.2 implies that the system may exhibit interesting dynamic behavior at $(0, 0)$. In order to facilitate the study of the dynamic properties of (1.4) at $(0, 0)$, we will use the idea of topological equivalence proposed in ^[27] to obtain a system that is topologically equivalent to system (1.4) and is defined at $(0, 0)$.

Lemma 5.1. The system (1.4) is topologically equivalent to system

which is a continuous extension of the system (1.4) and is defined at $\tilde{\Omega} = \{(x, y)\in R^2|x\geq0, y\geq0\}$.

Proof. By means of the time rescaling given by $t = x\tau$ and using the chain rule we have

In view of (1.4), the system (5.1) can be obtained. In fact, we have constructed the function $\psi:\tilde{\Omega}\times R\longrightarrow\Omega\times R$ satifying

Simple calculations can yield

Hence, $\psi$ is a diffeomorphism and preserves the orientation of time. It follows that system (5.1) is topologically equivalent to system (1.4). Furthermore, we note that system (5.1) is a fourth order polynomial differential equations system, which guarantees that it can be extended continuously to $x = 0$. □

Notice that the Jacobian matrix of system (5.1) at $(0, 0)$ is a null matrix. Thus, we will discuss the stability of (5.1) near orgin by the blow-up method in the following.

Theorem 5.1. The origin $(0, 0)$ is an attractor in system (1.4).

Proof. According to the Lemma 5.1, we can obtain the dynamical properties of the system (1.4) at $(0, 0)$ by studying the trajectory structure of (5.1) near the origin (0, 0). It was clear that the system (5.1) has an invariant line $x = 0$ and ${\rm d}y/{\rm d}\tau|_{x = 0} = -\mu y^2 < 0$. Taking the transformation

the system (5.1) becomes

When $x\neq0$, making a time transformation $u dt = d\tau$, the system (5.2) becomes

Systems (5.1) and (5.3) are topologically equivalent, which means their trajectories are the same. The system (5.3) has two boundary singularities $(0, 0)$ and $(0, 1+(1+h)/\mu)$. By direct calculation, the Jacobian matrices of (5.1) at $(0, 0)$ and $(0, 1+(1+h)/\mu)$ are, respectively,

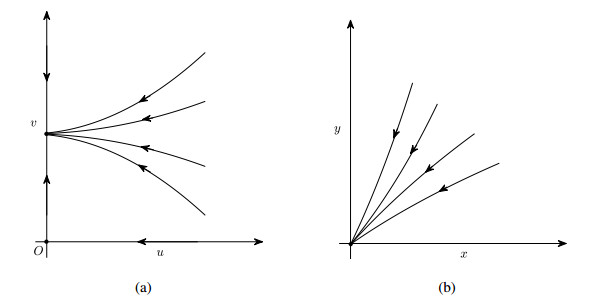
Hence, $(0, 0)$ is a saddle point and $(0, 1+(1+h)/\mu)$ a stable node (see Figure 1(a)). After a blow-down, the orgin $(0, 0)$ of (5.1) is an attractor (see Figure 1(b)). In view of Lemma (5.1), the orgin $(0, 0)$ is an attractor in the system (1.4). □

Theorem 5.2. Assume $0 < b < 1/4$, $0 < a < a^*$, $0 < h < h_2$, and $\mu > 0$. If $x_0 < \min\{y_0, x_5\}$, then $\lim\limits_{t\to\infty}(x(t), y(t)) = (0, 0)$, where $a^*$, $h_2$, and $x_5$ are defined as in Theorem 3.1.

Proof. Let $\mathscr{A} = \{(x, y)\mid 0 < x < y, x < x_5\}$ and $(x(t), y(t))$ be the unique solution of (1.4) with $(x_0, y_0)\in\mathscr{A}$. Set $w(t) = y(t)-x(t)$, and

Then, $w$ satisfies

Due to $x < x_5$, we have

It follows from the first equation of (1.4) and $x < y$ that

Therefore,

In summary, it can be seen that $\mathscr{A}$ is an invariant region.

If $(x_0, y_0)\in \mathscr{A}$, then

where $K = (1-x_0) \left(x_0/b-1 \right)-(1+ax_0)x_0-h < 0$. Thus, $\lim\limits_{t\to\infty}x(t) = 0$. Similarly to the proof of Proposition 2.2, $\lim\limits_{t\to\infty}y(t) = 0$. □

Similarly to the proof of Theorem 5.2, we can also get the following result.

Theorem 5.3. Assume $0 < b < 1/4$, $0 < a < a^*$, $h = h_2$, and $\mu > 0$. If $x_0 < \min\{y_0, x_4\}$, then $\lim\limits_{t\to\infty}(x(t), y(t)) = (0, 0)$, where $a^*$, $h_2$, and $x_4$ are defined as in Theorem 3.1.

6.   Bifurcation

Section $4$ shows that both $E_1$ and $E_4$ are higher-order singularities and $E_6$ may be non-hyperbolic, which indicates that system (1.4) may undergo saddle-node bifurcations at $E_1$ and $E_4$ and Hopf bifurcation at $E_6$. In this section, we will discuss saddle-node bifurcation and Hopf bifurcation that occur in system (1.4).

6.1.   Saddle-node bifurcation

In view of Theorem 3.1, the number of singularities of (1.4) will vary as parameter $h$ changes around at $h = h_1$ and $h = h_2$. In this subsection, based on Sotomayor's theorem in ^[28], we will prove that system (1.4) exhibits saddle-node bifurcation at $E_1$ and $E_4$.

Theorem 6.1. Assume $a, \, h, \, \mu > 0$, $0 < b < 1$, and $h_1$, $h_2$ are defined as in Theorem $3.1$.

$\rm (1)$] As the parameter $h$ passes through the threshold value $h_1$, the system (1.4) will experience a saddle-node bifurcation at $E_1$.

$\rm (2)$]If $0 < b < \frac{1}{4}$, $0 < a < a^*$, and $\mu\neq A(x_4)$, then the system (1.4) experiences a saddle-node bifurcation at $E_4$ as the parameter $h$ passes through the threshold value $h_2$.

Proof. (1) Reviewing (4.2) with $i = 1$, we get

Clearly, the two eigenvalues of $J_{E_1}$ are $0$ and $\mu$. Let $\xi$ and $\eta$ be two eigenvectors respectively corresponding to eigenvalue $0$ for the matrices $J_{E_1}$ and $J_{E_1}^T$. After simple calculations, we get

and

Let

It is easy to obtain that

Furthermore,

Clearly,

Therefore, it follows from Sotomayor's theorem that the system (1.4) undergoes a saddle-node bifurcation at $E_1$ as the parameter $h$ passes through the threshold value $h_1$.

(2) Similar to the proof of (1), it follows from (4.4) and (4.5) that

${\rm det}(J_{E_4}) = 0$, and ${\rm tr}(J_{E_4}) = A(x_4)-\mu$. When $\mu\neq A(x_4)$, $J_{E_4}$ has a simple eigenvalue $0$. Let $V$ and $W$ be two eigenvectors respectively corresponding to eigenvalue $0$ for the matrices $J_{E_4}$ and $J_{E_4}^T$. By simple calculation, we get

and

Moreover,

Therefore, it is easy to see that $V$ and $W$ satisfy the transversality conditions

Hence, in view of Sotomayor's theorem, the system (1.4) experiences a saddle-node bifurcation at $E_4$ as the parameter $h$ passes through the threshold value $h_2$. □

6.2.   Hopf bifurcation

As stated in Theorem 4.2, the stability of $E_6(x_6, x_6)$ will change as the parameter $\mu$ changes. Specially, if $\mu = A(x_6)$, then $E_6(x_6, x_6)$ is a center or fine focus under some conditions. In this subsection, we will analyze the Hopf bifurcation occurring at $E_6$ in system (1.4) by choosing $\mu$ as the bifurcation parameter.

Based on Theorem 4.2 and Lemma 4.1, when $0 < b < 1/4$, $0 < a < a^*$, and $0 < h < h_2$, if any one of the three conditions $(a1)$, $(a4)$, and $(a5)$ in Subsection $4.1$ holds, then $A(x_6) > 0$. Recalling

in (4.5), we let $\lambda = \alpha(\mu)\pm i\omega(\mu)$ be the roots of $\lambda^2- \lambda{\rm tr}(J_{E_6})+{\rm det}(J_{E_6}) = 0$, where $\alpha(\mu) = {\rm tr}(J_{E_6})/2$ and $\omega(\mu) = \sqrt{{\rm det}(J_{E_6})- \alpha^2(\mu)}$. Moreover, the Jacobian matrix $J_{E_6}$ has a pair of imaginary eigenvalues $\lambda$ when $\mu = A(x_6)$ and $\alpha'(\mu)|_{\mu = A(x_6)} = -1/2\neq0$. By the poincar$\acute{e}$-Andronov-Hopf Bifurcation theorem in ^[29], the system (1.4) undergoes a Hopf Bifurcation at $E_6$ when $\mu = A(x_6)$.

Next, we will employ the methods in the literature ^[30,31] to discuss the more detailed nature of hopf bifurcation generated in system (1.4), and we will directly adopt the notation of symbols utilized in ^[30,31].

First, we translate $E_6(x_6, x_6)$ to the origin by using the transformation $\tilde{x} = x-x_6$ and $\tilde{y} = y-x_6$. For convenience, we still denote $\tilde{x}$ and $\tilde{y}$ with $x$ and $y$, respectively. Then, the system (1.4) becomes

which is equivalent to the system

where

Set matrix

where

and

Apparently,

By the transformation

then system (6.2) becomes

where

In order to determine the stability of the periodic solution, we need to calculate the sign of the coefficient $a(A(x_6))$, which is given by

where

Summarizing the above analysis, we obtain the main result of this section:

Theorem 6.2. Let $0 < b < 1/4$, $0 < a < a^*$, $0 < h < h_2$, and $\mu > 0$. Suppose that one of the three conditions $(a1)$, $(a4)$, and $(a5)$ in Subsection 4.1 is true. Then, the system (1.4) will experience a Hopf bifurcation at $E_6$ as $\mu$ passes through $A(x_6)$. Moreover,

$\rm{(1)}$if $a(A(x_6)) < 0$, then the system (1.4) undergoes a supercritical Hopf bifurcation and a stable limit cycle appears around $E_6$;

$\rm{(2)}$if $a(A(x_6)) > 0$, then the system (1.4) undergoes a subcritical Hopf bifurcation and an unstable limit cycle appears around $E_6$.

7.   Simulation

In this section, we will utilize the Matlab software (version 2021b) for conducting numerical simulations to support our theoretical analysis results. In the system (1.4), we take $b = 0.2$, $a = 0.3$, $h = 0.1$, and $\mu = 1$ to vary Proposition 2.2. From Figure 2(a), we find that both species will go extinct when the initial value of prey is less than $b$. In fact, this phenomenon is known as the Allee effect. With $b = 0.1$, $a = 0.9$, $h = 0.1$, and $\mu = 1$, we can obtain $x_0^* = 5/9$ in Theorem 2.1 by direct calculation. In Figure 2(b), we can see that the prey and predator will coexist when the density of the prey is greater than $x_0^*$.

The boundary singularities $E_2(x_2, 0)$ is always an unstable node and $E_3(x_3, 0)$ is always a saddle in Figure 3(a). Especially, when $\mu = A(x_2)$, $E_2(x_2, 0)$ is a degenerate node in Figure 3(b). In Theorem 4.2, the singularity $E_5$ is always a saddle (see Figure 4(a)). The situation of the singularity $E_6(x_6, x_6)$ is complicated. Let $b = 0.2$, $a = 1$, $h = 0.03$, then the parameters satisfy condition (a4) in Theorem 4.2 and $A(x_6) = 0.6416$. When $\mu = 0.2 < A(x_6)$, $E_6(x_6, x_6)$ is an unstable focus (see Figure 4(b)); when $\mu = 0.6 < A(x_6)$, $E_6(x_6, x_6)$ is an unstable node (see Figure 5(a)); when $\mu = 0.7 > A(x_6)$, $E_6(x_6, x_6)$ is a focus (see Figure 5(b)); when $\mu = 10 > A(x_6)$, $E_6(x_6, x_6)$ is a stable node (see Figure 6(a)); when $\mu = A(x_6)$, $E_6(x_6, x_6)$ is a focus (see Figure 6(b)).

When $h = h_1$, the system (1.4) has a unique higher-order singularity $E_1(x_1, 0)$. It always a repelling saddle-node (see Figure 7(a)). When $h = h_2$, the system (1.4) has a unique higher-order singularity $E_4(x_4, x_4)$. If $\mu = 0.25 < A(x_4)$, $E_4$ is a repelling saddle-node (see Figure 7(b)); if $\mu = 0.5 > A(x_4)$, $E_4$ is an attracting saddle-node (see Figure 8(a)); if $\mu = A(x_4) = 17/64$, $E_4$ is a cusp of co-dimension 2 (see Figure 8(b)).

The origin $(0, 0)$ is an attractor in the system (1.4). When two distinct positive singularities coexist simultaneously, if the initial population of the prey is lower than that of the predator and $x_5$, both species will ultimately perish (see Figure 9(a)). Similarly, when there is only one positive singularity, if the initial value of the prey is less than that of the predator and $x_4$, then both species will perish (Figure 9(b)). The simulation results above are consistent with the conclusions of Theorems 5.1–5.3.

When the parameters $b = 0.2$, $a = 1$, and $\mu = 1$ are set, the system (1.4) experiences two saddle point bifurcations at $h = h1$ and $h = h_2$, respectively; see Figure 10(a). With parameters $b = 0.1$, $a = 5$, $h = 0.5$, and $\mu = 0.97$, the system (1.4) undergos a Hopf bifurcation, where a stale limit cycle emerges surrounding $E_6(x_6, x_6)$.

8.   Conclusions

In this paper, we consider several ecological factors, including the Allee effect, the impact of harvesting on prey populations, and cooperative hunting behaviors among predators, within the framework of a Leslie-Gower prey-predator model. The consideration of various ecological factors makes the model (1.4) closer to the real world, while also making the theoretical results more instructive. These biological phenomena are well presented in the new system and bring rich dynamic properties. We have conducted a fairly comprehensive qualitative analysis and bifurcation study for the system (1.4). It is worth noting that we have studied the types of higher-order singularities and found that there may be two saddle-nodes and a cusp of co-dimension $2$. The system (1.4) is not defined at $(0, 0)$. By using topological equivalent and the blow-up method, we prove that the origin is attractor, and a defined basin of attraction was given. We investigated the stability of limit cycles where Hopf bifurcation occurs by calculating the first Lyapunov coefficient.

There are four parameters in system (1.4), and as these parameters vary, the system demonstrates distinct dynamic properties. Next, we will discuss the significance of the theoretical results obtained in this article from the perspective of these four parameters and their ecological meanings.

The Allee effect parameter $b$ is presented in the new model. When the prey density is too low, the prey will perish and the predator also becomes extinct (see Figure 2(a)). This phenomenon contradicts the traditional perspective of population dynamics. From a biological perspective, congregating is conducive to the reproduction and survival of the population. For example, a box of bees can generate and maintain considerable heat, which enables all members to survive in low-temperature conditions. Conversely, if they are isolated, they risk freezing to death. Therefore, each species has its own optimal density, and too dense or too sparse will have a restraining effect on the population. This is also evident from the mathematical model (1.2) of the Allee effect, where the population density will only increase when the prey density is between $b$ and $1$. In fact, for some low-density populations, such as tigers, $b$ cannot be too large. If $b$ is significantly high, it becomes improbable for the population density to surpass this threshold, which could ultimately result in the extinction of the population. Theorem $3.1$ demonstrates that if the value of $b$ exceeds $1/4$, the population is destined to decline.

The harvesting parameter $h$ affects the number of singularities (Theorem 3.1). When $h > h_1$, the system has no any singularity; when $h > h_2$, it has no positive singularity. It reveals that excessive human production activities can lead to ecological imbalances and species extinction. In addition, when $h = h_1$ or $h_2$, the system has undergone saddle-node bifurcation (Theorem 6.1). This means that the ecosystem is likely to experience collapse when the capture rate of the prey population reaches $h_1$ and $h_2$.

Cooperative hunting $a$ also has a significant impact on singularities of the system (Theorem 3.1). When $a > a^*$, it has no positive singularity. This explains why certain invasive species can proliferate rapidly. Since native species are unfamiliar with invasive species, it enhances the efficiency of cooperative hunting by invasive species, leading to the extinction of local species.

The intrinsic growth rate $\mu$ of predator determines the stability of the singularity $E_6$ (Theorem 4.2). The positive singularity $E_6$ is stable(unstable) when $\mu > A(x_6)$($\mu < A(x_6)$), and the system (1.4) will undergo a Hopf bifurcation when $\mu = A(x_6)$ (see Figure 10(b)). Based on the above theoretical results, we can conclude that the intrinsic growth rate of predators should not be too low. If the population of predators decreases, it may have an indirect impact on the prey population, thereby disrupting the balance of the entire ecosystem.

In order to present the key values of these parameters and their possible ecological significance in the real world, we have organized them in Table 1.

Author contributions

Na Min: Conceptualization, Methodology, Software, Visualization, Formal analysis, Validation, Investigation, Writing-original draft; Hongyang Zhang: Validation, Investigation, Writing-original draft; Xiaobin Gao: Supervision, Funding acquisition; Pengyu Zeng: Software, Project administration. All the authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors would like to thank the anonymous referees for their valuable comments and sugges- tions, which led to considerable improvement of the article. This work is supported by GABRP 2023A04J1317, NSFC 11901116, NSFC 62403152, and NSFC 62403133.

Conflict of interest

The authors declare that they have no competing interests.