Bifurcations of a Leslie-Gower predator-prey model with fear, strong Allee effect and hunting cooperation

1.   Introduction

The evolution of species in an ecosystem is driven by the interactions between their individuals. The predation between organisms and their natural enemies is one of the most common interactions, which is termed as prey-predator interactions. The prey-predator system is one of the central themes in mathematical ecology ^[1].

The energy converted by predating prey is usually considered as the only way to sustain the reproduction of the predator. However, in practice, many factors can affect the survival of predators in the real world. For example, Leslie ^[2] observed that, due to the environmental capacity, the number of predators was limited to a certain range. Predators would stabilize to some extent. Unlike the growth of prey, there was a certain quantitative relationship between its environmental capacity and prey fluctuations. Therefore, in 1960, Leslie and Gower established the classic Leslie-Gower predator-prey model ^[3], which has been widely used in theoretical ecology and has attracted many authors' attentions in recent years. Since the interesting dynamics, the Leslie-Gower prey-predator model plays a special role in recent ecological researches ^[4,5,6,7,8].

Predators rely on prey for survival, so they always try to improve their predation ability to increase their population biomass. The functional response is a significant element describing the mutual coupling between species, resulting in complex dynamical properties. Therefore, many kinds of functional responses depending on prey are proposed, such as Holling-type ^[9,10,11] and square root response ^[12].

Actually, the functional response relying on both prey and predator is more realistic than that of prey-dependent interaction. Therefore, Crowley-Martin type ^[13] and Beddington-DeAngelis type functional responses ^[14] were proposed. On the other hand, the competition for resources is a crucial aspect in predators, but many predators utilize the hunting cooperation strategy to attack prey in groups, as a primary form of predation in the ecosystem. Usually, two or more individuals cooperate together toward a common goal to enhance their fitness. There are various advantages of predator hunting cooperation, including more chances of killing large prey, a higher rate of hunting success when the number of adults increases, and a reduction in carcass theft by other predators. Successful hunting cooperation leads to more food for predators and helps the survival of the predator. For example, lionesses hunt in a configuration in which some lionesses surround prey, while others keep waiting for the prey to approach them ^[15]. Other examples include dogs ^[16], wolves ^[17], and so on. Based on the cooperating strategy, Alves and Hilker ^[18] proposed a functional response of hunting cooperation, which has attracted many authors' attention ^{[19,20,21,22]}.

The Allee effect (originally called the Allee principle) was discovered by biologist Allee in an experiment on goldfish ^[23] which was used to describe the positive relation between an individual's fitness and density of the conspecific species. Traditionally, there exist the demographic Allee effect and component Allee effect. The former is used to describe a positive correlation between the population density and the average individual fitness, while the latter illustrates this correlation between population density and any measurable component of individual fitness (for more details, see ^[24,25]).

Biologists have observed that lots of biological phenomena can induce the Allee effect, such as cooperating breeding, mating difficulty, antipredator defence among the prey, social thermoregulation, foraging efficiency, and environmental conditions ^[26]. In fact, many empirical evidences of Allee effect have been perceived in populations, such as birds, insects ^[27], mammals ^[28], and marine invertebrates ^[29]. Notably, the social interaction among populations is an important characteristic for diverse populations. The collaborative activity among species can also induce the Allee effect ^[30,31]. Allee effects are often classified into strong Allee effect and weak Allee effect. Generally, if there exists a threshold level, when the species density is below it, then it will become extinct, and it is called strong Allee effect. However, the weak Allee effect means that the growth rate decreases but remains positive at low population density. As the species give rise to extinction owing to the Allee effect, it has now become the focus of refreshed interest in the study of both theoretical and empirical ecological conservation in the exploited ecosystem ^[32,33,34].

Recently, many interesting properties caused by the Allee effect were found. For example, Allee effect leads to the appearance of a new equilibrium point which changes the stability of other equilibria ^[35]. Garain et al. ^[36] showed that, due to Allee effect, the phenomenon of bubbling occurred resulting in reduction of amplitudes of cycles. The prey-predator system with Allee effect underwent a rich dynamics even leading to the extinction of species.

As mentioned before, the functional response is an essential element affecting the system dynamics, but it only depicts the effect of directly killing prey by predator. Actually, the predator can not only affect the ecology by directly consuming prey, but also indirectly inflict their behavior and physiology ^[37,38]. The fear induced by predator is almost everywhere. When prey perceive the appearance of predator by smell or sound, they will produce predation risk to avoid predators and adjust their behavior and physiological state to prevent predation, which is called anti-predation strategy. Experiments have showed that due to the cost of anti-predation activities, the elk has changed its reproductive physiology and population size ^[39], and tiger sharks in the ocean are highly sensitive to dugongs ^[40]. To reflect the fear effect, Wang ^[41] proposed a prey-predator model incorporating the fear effect on the birth rate of prey. Since then, many researches have been carried out to reveal the cost of fear effect on system dynamics. Kumar and Dubey ^[42] analyzed a prey-predator model with fear induced by predator, gestation time delay and prey refuge and found that the appearance of Hopf bifurcation is induced by the fear effect. Considering the double fear effects on the birth and death rates of prey, Das et al. ^[43] proposed a prey-predator model to investigate the cost of fear. Shao ^[44] formulated a food chain system incorporating fear and delay into the process of prey reproduction, resulting in complex phenomena like Hopf bifurcation, bistability and multi-stability. In the latest years, more and more researchers have focused on the fear effect on system dynamics and have reported many supporting results ^{[45,46,47,48]}.

The central topic of biodiversity conservation is to study the complex dynamical properties of biological models. To the best of the author's knowledge, the research of the 'Leslie-Gower' predator-prey model, which simultaneously includes fear effect, strong Allee effect, and hunting cooperation, has never been done. The purpose of this article is to study the dynamics of the above model and explore how the fear, Allee effect, and hunting cooperation affect system stability.

This article is arranged as follows. In Section 2, we describe how the temporal model is constructed. In Section 3, we give some preparations such as the positivity and boundedness of solutions, as well as the existence of equilibrium points. In Section 4, we discuss the stability and bifurcations of equilibrium states. The numerical validations of the analytical findings are presented in Section 5. Conclusions and discussions are summarized to conclude this article in Section 6.

2.   Model construction

The model formulation is based on the common Leslie-Gower predator-prey model ^[3]:

where $x(t)$ and $y(t)$ represent the species densities of prey and predator at time $t$, respectively. Parameters $r$ and $s$ are the intrinsic growth rate of prey and predator, respectively. $K$ is the environmental carrying capacity, and $p$ is the linear functional response coefficient, representing the maximum per capita predation rate. Term $\frac{y(t)}{nx(t)}$ is in the sense of the 'Leslie-Gower' type, where the carrying capacity of predators is denoted by $nx$, and $n$ is a measure of the quality provided by prey as food for predator.

(1) Considering the strong Allee effect on prey, the prey equation becomes,

where $0 < A < K$ denotes the strength of Allee effect on prey species, which means the prey is subject to strong Allee effect ^[5].

(2) The hunting cooperation between predators is considered, then the prey equation is

where $\alpha$ denotes the attack rate of predator, and $\beta$ is the strength of predator cooperation in the hunting prey process. It shows that hunting cooperation has an Allee effect in predators, that is, when prey are insufficient to support the predators, the predators can still survive with the help of hunting cooperation between predators ^[18].

(3) Empirically, the reproduction of prey is observed to be greatly decreased by the predator's fear on prey, then the prey's birth rate should be changed because of the cost of fear. The effect of fear is incorporated, then the prey equation becomes,

where $\frac{r)}{1+fy(t)}$ is the birth rate with fear cost, and $f$ denotes the fear level (Wang et al. ^[41]).

We couple the predator's 'Leslie-Gower' equation and the above prey equation, then the following Leslie-Gower predator-prey model with fear effect, Allee effect on prey, and hunting cooperation is formulated:

where all parameters $r, A, \beta, s, n$ are assumed to be positive.

For brevity, let $x(t) = x, y(t) = y$, $\frac{x}{K} = \bar{x}, \beta y = \bar{y}, \bar{f} = \frac{f}{\alpha}, \bar{r} = Kr, \bar{A} = \frac{A}{K}, \bar{\beta} = \frac{\beta}{\alpha^2}$. Dropping the bars, then (2.1) can be transformed to

The initial data is $x(0) = x_0\geq0$ and $y(0) = y_0\geq0.$

3.   Preparations

3.1.   Positivity and boundedness of solutions

The existence of solutions can be derived directly by the ordinary equation theory, so we begin with the positiveness and boundedness of solutions of system (2.2).

Theorem 3.1. The solutions of system (2.2) with $x(0) > 0, y(0) > 0$ are positive and bounded for all $t\geq0.$

Proof. It is obvious that the solution $x = 0$ of the first equation of (2.2) is an invariant set, so $x(t) > 0$ for all $x(0) > 0, t\geq0.$ Similarly, from the second equation of (2.2), we conclude that $y(t) > 0$ for all $y(0) > 0.$ Therefore, all trajectory starting from the region $\{(x, y)|x > 0, y > 0\}$ cannot cross the coordinate axes. Thus, all solutions of system (2.2) with $x(0) > 0, y(0) > 0)$ are positive.

Next, we discuss the boundedness of the solutions. From the first equation of (2.2), we conclude that $x\leq1$. Since for $x > 1$, then

and there is no equilibrium point in the region $\{(x, y)|x > 1, y\leq0\}$. Thus, all positive solutions $x(t)\leq\max\{x(0), 1\}\triangleq\Theta$, where $\Theta$ represents the larger of the initial value $x(0)$ and constant 1. By the same manner, we have

Then, $y(t)\leq\max\{y(0), n\Theta\}$ for all $t\geq0.$ This completes the proof. □

3.2.   Existence of equilibrium points

It is easy to find the trivial equilibrium point $E_0(0, 0)$ and the boundary equilibria $E_{10}(1, 0)$ and $E_{20}(A, 0)$. Now, we study the existence of the coexistence equilibrium, say, $E^*(x^*, y^*)$. It follows from the predator equation that $y = nx^*$, where $x^*$ satisfies

That is, $x^*$ is the solution of the following equation:

Let

where $A_1 = \beta fn^3, A_2 = \beta n^2+fn^2+r, A_3 = n-r(r+A), A_4 = rA.$ Then by the Lemma 2.1 in ^[49], the number of positive solutions depends on the sign of the following discriminant,

Equation (3.1) has no positive if $\Delta > 0$, a unique positive solution if $\Delta = 0$, say, $x^*$, and two positive solutions if $\Delta < 0$, say, $x_3$ and $x_4$. Thus, we conclude that system (2.2) has a unique equilibrium point $E^*(x^*, y^*)$ if $\Delta = 0$, and two equilibrium points $E_3(x_3, y_3)$ and $E_4(x_4, y_4)$ if $\Delta < 0$. Numerically, we will discuss the existence of one or two solutions in Section 5.

4.   Stability and bifurcation analysis

In this section, by use of the stability theory of the dynamical system, with the help of Jacobian matrix and characteristic equations, we mainly analyze the stability of system (2.2) and some kinds of bifurcation at the equilibrium point.

4.1.   Stability analysis

(1) Stability of $E_0$

For the trivial equilibrium $E_0(0, 0)$ of system (2.2), the second equation of (2.2) is not defined along the axis $x = 0$, so we discuss the stability of the singular point by the method of topology equivalence.

Lemma 4.1. System (2.2) is topologically equivalent to the below system,

in $R_+^2 = \{(x, y)|x > 0, y > 0\}.$

Proof. Take a transformation as follows:

Then

So the transformation $\Psi$ is a diffeomorphism and preserves the orientation of time. That means (2.2) is topologically equivalent to system (4.1). This completes the proof. □

For (4.1), it is easy to extend continuously to the axis $x = 0$. By the topological equivalence, we only need to study the stability of $(0, 0)$ of system (4.1) to obtain the type of singular point $E_0(0, 0)$ of (2.2).

Theorem 4.1. The equilibrium point (0, 0) of system (4.1) is an attractor.

Proof. Due to the degenerative property of the equilibrium point (0, 0), we apply the blow-up method to discuss its stability. To start, we use a horizontal blow-up and let

and still denoting $\bar{t}$ by $t$, system (4.1) becomes,

Thus, the origin of system (4.1) is blow-up to the whole axis $M_1 = 0$. The equilibrium points in $M_1 = 0$ are $(0, 0)$ and $(0, \frac{n(s+rA)}{s}),$ respectively. Then, the Jacobian matrices at $(0, 0)$ and $(0, \frac{n(s+rA)}{s})$ are as follows:

By the sign of characteristic root, we conclude that $(0, 0)$ is a saddle and $(0, \frac{n(s+rA)}{s})$ a stable node.

Next, we perform the following transformation and consider the vertical blow-up of (4.1),

Still denoting $\bar{t}$ by $t$, system (4.1) can be rewritten as

Thus, the origin of system (4.1) is blow-up to the whole axis $N_2 = 0$. Similarly, the equilibria in $N_2 = 0$ are $(0, 0)$ and $(\frac{s}{n(s+rA)}, 0),$ respectively. Therefore, the Jacobian matrices at $(0, 0)$ and $(\frac{s}{n(s+rA)}, 0)$ are as follows:

It is clear that $(0, 0)$ is a saddle and $(\frac{s}{n(s+rA)}, 0)$ a stable node. From the horizontal and vertical blow-ups, we obtain that the equilibrium point (0, 0) of (4.1) is an attractor in $R_+^2$. This completes the proof. □

Remark 4.1. From Theorem 4.1, by taking the inverse to blow-down to system (2.2), we conclude that the trivial equilibrium point $E_0(0, 0)$ of system (2.2) is an attractor.

(2) Stability of $E_{10}$ and $E_{20}$

By an easy computation, the Jacobian matrices of (2.2) at the boundary equilibrium points $E_{10}(1, 0)$ and $E_{20}(A, 0)$ are as follows:

Since $0 < A < 1$, then it easily follows that the boundary equilibrium point $E_{10}(1, 0)$ is a saddle and $E_{20}(A, 0)$ is a source.

(3) Stability of $E^*$

By the stability theory of the dynamical system, the local asymptotic stability of $E^*(x^*, y^*)$ depends on the sign of the roots of characteristic equations. The Jacobian matrix at inner equilibrium point $E^*(x^*, y^*)$ is

where

Denote the trace and determinant of $J_{E^*}$ by $T$ and $D$, respectively, that is,

then the characteristic equation of $J_{E^*}$ can be written as

Next, we discuss the roots of Eq (4.4) in two situations.

● $D = 0$

Denote $A = A^*$ such that $D = 0$, that is,

We begin with a transformation of $E^*(x^*, y^*)$ to the origin by letting $x_1 = x-x^*, y_1 = y-y^*$. Applying the Taylor's expansion formula, system (2.2) can be rewritten as

where

Performing the transformation as

Eq (4.5) leads to

Multiplying the two sides of the first equation by $b_{10}$ and the second equation by $a_{10}$, a subtraction results in

By eliminating the term $x_2'$ of (4.6), we have

Let $(a_{10}+b_{01})dt = \bar{t}$ and drop the bar, then (4.6) turns to

where

By computation,

Due to $D = 0$, $a_{10} = -na_{01}$ and

On the other hand,

Assume that

$(H_1)\qquad \frac{r(1+A^*)}{4n} < f < \frac{3}{n},$ then $c_{20} < 0.$

Therefore, by the Theorem 7.1 in ^[50], the equilibrium point $E^*(x^*, y^*)$ is a saddle-node. Then we have the conclusion below.

Theorem 4.2. Assume that $(H_1)$ holds, then $E^*$ is a saddle-node at $A = A^*$.

Remark 4.2. If the fear is absent, then at $A = A^* = \frac{n (1+2\beta y^*)}{r}+2x^*-1$, we have $D = 0$ and $a_{11}+na_{02} = -1-3\beta y^* < 0$, so $c_{20} < 0$ and $E^*$ is a saddle-node.

● $D = 0$ and $T = 0$

Let $f = f^* = \frac{s-rx^*(1+A^*-2x^*)}{sy^*}$ such that $T = 0$. Similarly, we transform the equilibrium point $E^*(x^*, y^*)$ to the origin. Let $\tilde{x}_1 = x-x^*, \tilde{y}_1 = y-y^*$, then (2.2) becomes:

where $\tilde{a}_{10} = s, \tilde{a}_{01} = -s/n, \tilde{a}_{20} = s-\frac{rx^*}{1+f^*y^*}, \tilde{a}_{11} = -s(\frac{1}{y}-\frac{f^*}{1+fy})$, $\tilde{a}_{02} = -\frac{sf^*}{n(1+f^*y^*)}+\frac{f^*x^*(1+2\beta y^*)}{1+f^*y^*}, \tilde{b}_{10} = sn, \tilde{b}_{01} = -s$, $\tilde{b}_{20} = -\frac{ns}{x^*}, \tilde{b}_{11} = \frac{2s}{x^*}, \tilde{b}_{02} = -\frac{s}{nx^*}.$

Employing the transformation

then we have

where $\tilde{c}_{20} = -s(\frac{a_{20}}{n}+a_{11}+na_{02})$, $\tilde{c}_{11} = a_{11}-2na_{02}, \tilde{c}_{02} = -\frac{n}{s}a_{02}, \tilde{d}_{20} = -s^2(\frac{a_{20}}{n}+a_{11}+na_{02}-\frac{s}{nx})$, $\tilde{d}_{11} = s(a_{11}+2na_{02}+\frac{2s}{nx^*}), \tilde{d}_{02} = na_{02}+\frac{2s}{nx^*}.$

By the Lemma 3.3 of ^[20], (4.9) is equivalent the following system,

where $\tilde{e}_{20} = \tilde{d}_{20}$ and $\tilde{e}_{11} = \tilde{d}_{11}+2\tilde{c}_{20}$. Suppose

$(H_2)\; \; \; f^* < \frac{f^*s}{n(1+A^*)}+s(f^*)^2+2\beta.$

By computation,

Additionally,

When $s = s^\star = \frac{r(1+A^*)-4rx^*}{nf} > 0$, we have $\tilde{e}_{11} = 0$. So if $s\neq s^\star$, then $\tilde{e}_{11}\neq0$. By bifurcation theory ^[50], $E^*(x^*, y^*)$ is a cusp of the co-dimension of 2.

Furthermore, if $s = s^\star$, i.e., $\tilde{e}_{11} = 0$, we transform $E^*(x^*, y^*)$ to the origin again by letting $X = x-x^*, Y = y-y^*$, and, whence, (2.2) becomes:

where $A_{10} = s^\star, A_{01} = -\frac{s^\star}{n}, A_{20} = \frac{r}{1+f^*y^*}(1+A^*-3x^*), A_{11} = \frac{rf^*}{(1+f^*y^*)^2}(3(x^*)^2-2(1+A^*)x^*+A^*)-(1+2\beta^* y^*)$, $A_{02} = rf^*x^*(1-x^*)(x^*-A^*)\frac{f^*}{(1+f^*y^*)^3}-2\beta x^*, A_{30} = \frac{-r}{1+f^*y^*}, A_{12} = \frac{-r(f^*)^2}{3(1+f^*y^*)^3}(3(x^*)^2-2(1+A^*)x^*+A^*)-\beta, A_{40} = 0$, $B_{10} = s^\star n, B_{01} = -s^\star, B_{20} = -\frac{ns^\star}{x^*}, B_{11} = \frac{2s^\star}{x^*}, B_{02} = -\frac{s^\star}{nx^*}$, $B_{30} = \frac{ns^\star}{(x^*)^2}, B_{12} = \frac{s^\star}{n(x^*)^2}, B_{21} = \frac{2s^\star}{-(x^*)^2}, B_{40} = \frac{-ns^\star}{(x^*)^3}$, $B_{22} = \frac{-s^\star}{n(x^*)^3}, B_{13} = 0.$

Taking a transformation,

By the following substitution,

then (4.11) is as

where

Adopt the following transformation again,

Taking $dt = (1-C_{02})d\bar{t}$ and still denoting $\bar{t}$ by $t$, then (4.12) becomes:

where $D_{20} = C_{20}, D_{30} = C_{30}-2C_{02}C_{20}, D_{21} = C_{21}, D_{12} = C_{12}-C_{02}^2$, $D_{03} = C_{03}, D_{40} = C_{40}+C_{20}C_{02}^2-2C_{02}C_{30}, D_{31} = C_{31}-C_{02}C_{21}$, $D_{22} = C_{22}-C_{02}^3, D_{13} = C_{13}+C_{02}C_{03}.$

Take the following two transformations,

and

Then, we have

where $E_{20} = D_{20}, E_{30} = D_{30}, E_{12} = D_{21}$, $E_{21} = D_{12}, E_{40} = D_{40}, E_{31} = D_{31}-3D_{20}D_{03}$, $E_{22} = D_{22}$. Let $X_5 = -X_4, Y_5 = -\frac{Y_4}{\sqrt{-E_{20}}}, \bar{t} = \sqrt{-E_{20}}t$, thus

where $F_{30} = -\frac{E_{30}}{E_{20}}, F_{12} = E_{12}, F_{21} = \frac{E_{21}}{\sqrt{-E_{20}}}$, $F_{40} = \frac{E_{40}}{E_{20}}, F_{22} = -E_{22}, F_{31} = -\frac{E_{31}}{\sqrt{-E_{20}}}$.

By Lemma 3.4 of ^[20], it is equivalent to the following system:

where $\Lambda = F_{31}-F_{30}F_{21}$. If $\Lambda < 0$, then by the bifurcation theory ^[50], $E^*(x^*, y^*)$ is a cusp of co-dimension 3. We summarize the conclusion as follows.

Theorem 4.3. For $E^*(x^*, y^*)$ of system (2.2), if $A = A^*, f = f^*, s\neq s^\star$, then $E^*(x^*, y^*)$ is a cusp of the co-dimension of 2 under condition $(H_2)$. Further, $E^*(x^*, y^*)$ is a cusp of the co-dimension of 3 if $s = s^*$ and $\Lambda < 0$, where the parameters are defined as before.

Remark 4.3. By the deduction process, we can similarly get the conditions ensuring the stability of inner equilibrium points $E_3$ and $E_4$.

Remark 4.4. If the fear is absent, then at $s = s^* = rx^*(1+A^*-2x^*)$, we have $T = 0$ and

Additionally,

When $n(1+2\beta y)-2rx^*\neq0$, then $\tilde{e}_{11}\neq0$. By the similar proof, $E^*(x^*, y^*)$ is a cusp of the co-dimension of 2.

If the strong Allee effect is absent, we can derive similar results.

4.2.   Bifurcation

In this section, we will discuss the saddle-node bifurcation (SN for short), Hopf bifurcation and Bogdanov-Takens (BT) bifurcation of the inner equilibrium $E^*(x^*, y^*)$, respectively. Our discussion is divided into the following three different scenarios.

${\bf{(i)}}$ Saddle-node bifurcation

If $A = A^*$, then $D = 0$. The characteristic equation (4.4) has two roots, denoted by 0 and $\lambda = J_{11}-s(\neq0)$, respectively. By computation, the characteristic vectors of $\lambda$ corresponding to $J_{E_*}$ and $J_{E_*}^T$ are as follows respectively,

Let $F(x, y) = (f(x, y), g(x, y))^T$, then

and

Thus,

and

By the Sotomayor's theorem ^[51], for the equilibrium point $E^*$, there exists an SN bifurcation at $A = A^*$.

Theorem 4.4. For system (2.2), there exists an SN bifurcation around the equilibrium point $E^*$ at $A = A^*$.

Remark 4.5. Similarly, we can find the SN critical value of other parameters like $f$ and $\beta$, which will be shown in the simulation section. By the proof process, we find that when $f = 0$, then the SN bifurcation also exists at $A = A^* = \frac{n (1+2\beta y^*)}{r}+2x^*-1$.

${\bf{(ii)}}$ BT bifurcation

According to Theorem 4.3, we conclude that there is a BT bifurcation around the $E^*(x^*, y^*)$ under some situations. So, we choose $\beta$ and $s$ as the bifurcation parameters. Let $A = A^*, \beta = \beta^*$ such that $D = 0$ and $T = 0$. Consider a disturbance $\beta = \beta^* +\epsilon_1, s = s+\epsilon_2,$ then system (2.2) becomes:

Let $u = x-x^*, u = y-y^*$, then (4.17) becomes,

where $\hat{A}_{00} = -\varepsilon_1n^2(x^*)^3, \hat{A}_{10} = s-n^2(x^*)^2\varepsilon_1$, $\hat{A}_{01} = -\frac{s }{n}-2n(x^*)^2\varepsilon_1, \hat{A}_{11} = \frac{r}{1+fy^*}(1+A^*-3x^*)$, $\hat{A}_{20} = \frac{rf}{(1+fy^*)^2}(3(x^*)^2-2(1+A^*)x^*+A^*)-(1+2(\beta^*+\varepsilon_1) y^*)$, $\hat{A}_{02} = rfx^*(1-x^*)(x^*-A^*)\frac{f}{(1+fy^*)^3}-2\beta^* x^*.$

By using a transformation $u_1 = v, v_1 = \hat{B}_{10}u+\hat{B}_{01}v+\hat{B}_{20}u^2+\hat{B}_{11}uv+\hat{B}_{02}v^2+f_2(u, v, \epsilon)$, and let

then (4.18) becomes

where $\hat{C}_{00} = B_{10}A_{00}, \hat{C}_{10} = B_{10}A_{01}+B_{01}^2+A_{00}B_{11}-\frac{B_{01}}{B_{10}}(A_{10}B_{10})+B_{01}B_{10}+2B_{20}A_{00}$, $\hat{C}_{01} = \frac{1}{B_{10}} (A_{10}B_{10}+B_{01}B_{10}+2B_{20}B_{00})$, $\hat{C}_{20} = B_{10}A_{02}+B_{01}B_{02}+B_{11}A_{01}+2B_{02}B_{01} +\frac{B_{01}^2}{B_{10}^2}(B_{10}A_{20}+B_{01}B_{20}+2B_{20}A_{10}+B_{11}B_{10})$, $\hat{C}_{11} = \frac{1}{B_{10}}(B_{10}A_{11}+B_{01}B_{11}+2B_{20}A_{01}+B_{11}A_{10}+B_{11}B_{01}+2B_{02}B_{10})$, $\hat{C}_{02} = \frac{1}{B_{10}^2}(B_{10}A_{20}+B_{01}B_{20}+2B_{20}A_{10}+B_{11}B_{10}).$

Let

then we have

where $\hat{D}_{00} = \hat{C}_{00}, \hat{D}_{10} = \hat{C}_{10}-2\hat{C}_{00}\hat{C}_{02}$, $\hat{D}_{01} = \hat{C}_{01}, \hat{D}_{20} = \hat{C}_{20}+\hat{C}_{00}\hat{C}_{02}^2-2\hat{C}_{02}\hat{C}_{10}$, $\hat{D}_{11} = \hat{C}_{11}-\hat{C}_{01}\hat{C}_{02}.$ Make the following transformation again:

then we have

where $\hat{E}_{00} = -\frac{\hat{D}_{00}}{\hat{D}_{20}}, \hat{E}_{10} = -\frac{\hat{D}_{10}}{\hat{D}_{20}}$, $\hat{E}_{01} = \frac{\hat{D}_{01}}{\sqrt{-\hat{D}_{20}}}$, $\hat{E}_{11} = \frac{\hat{D}_{11}}{\sqrt{-\hat{D}_{20}}}.$ Take $u_4 = u_3-\frac{E_{11}}{2}, v_4 = v_3,$ then (4.21) is equivalent to

where $\hat{F}_{00} = \hat{E}_{00}+\frac{\hat{E}_{10}^2}{4}$, $\hat{F}_{01} = \hat{E}_{01}+\frac{\hat{E}_{10}\hat{E}_{11}}{2}$, $\hat{F}_{11} = \hat{E}_{11}.$ Take $u_5 = -F_{11}^2u_4, v_5 = F_{11}^3v_4, \bar{t} = -\frac{t}{F_{11}}$, then (4.22) is equivalent to

where $\mu_1 = -F_{00}F_{11}^4, \mu_2 = -F_{01}F_{11}.$ All $f_i(u_j, v_j, \epsilon)$ are $C^\infty$ functions of at least third order with $(u_j, v_j)$ for $i = 1, \cdots, 7, j = 1, \cdots, 5.$ Assume that

$(H_3)\; \left|\frac{\partial(\mu_1, \mu_2)}{\partial(\epsilon_1, \epsilon_2)}\right|_{\epsilon_1 = \epsilon_2 = 0}\neq0.$

Then by the bifurcation theory ^[51], system (2.2) goes through a BT bifurcation of co-dimension 2 when $(\epsilon_1, \epsilon_2)$ is in a neighborhood of $E_0(0, 0)$. Moreover, the three bifurcation curves are as follows,

(1) SN curve: $SN = \{(\epsilon_1, \epsilon_2)|\mu_1(\epsilon_1, \epsilon_2) = 0, \mu_2(\epsilon_1, \epsilon_2)\neq0\}$.

(2) Hopf bifurcation curve: $H = \{(\epsilon_1, \epsilon_2)|\mu_1(\epsilon_1, \epsilon_2) < 0, \mu_2 = \sqrt{-\mu_1}\}$.

(3) Homoclinic Bifurcation curve: $HL = \{(\epsilon_1, \epsilon_2)|\mu_1(\epsilon_1, \epsilon_2) < 0, \mu_2 = \frac{5}{7}\sqrt{-\mu_1}\}$.

Theorem 4.5. Assume that $(H_2)$ and $(H_3)$ hold. Then for the two bifurcation parameters $(\beta, s)$, there exists a BT bifurcation of co-dimension 2 around the equilibrium $E^*(x^*, y^*)$. The bifurcation curves are expressed as above.

Remark 4.6. The representations of bifurcation curves are very complex, so we validate them by simulation examples; see the rear Figure 7 in the simulation section. On the other hand, by the same manner, all conclusions can be extended to the inner equilibrium points $E_3$ and $E_4$, respectively.

${\bf{(iii)}}$ Hopf bifurcation

Under the condition that $D > 0$ and $T = 0$, the Jacobian matrix of $E^*(x^*, y^*)$ has a pair of pure imaginary roots. Selecting $f$ as the bifurcation parameter, we consider the Hopf bifurcation around the $E^*$.

For simplicity, we use the following transformation,

Dropping the breves, (2.2) leads to

The equilibrium point $E^*(x^*, y^*)$ is changed to $\breve{E}(1, 1)$. Let $dt = x(1+fy)d\breve{t}$ and rewrite $\breve{t}$ as $t$, then we have

The Jacobian matrix at $\breve{E}(1, 1)$ is

So, the determinant is

Now, we verify the transversality condition for the occurrence of Hopf bifurcation. By computation, we have

Next, we compute the first Lyapunov number to determine the stability of limit cycle around the inner equilibrium point $\breve{E}(1, 1)$.

Let $\tilde{u} = x-1, \tilde{v} = y-1$, then (4.25) becomes:

where $\tilde{A}_{10} = 2r(d-1)(1-A)+r (d+A-2)-2n (1+\beta)(1+f^*), \tilde{A}_{20} = 2r (d+A-2)-r +r (d-1)(1-A)+n (1+\beta)(1+f^*)$, $\tilde{A}_{11} = -2n (1+\beta)(1+f^*)-2n (f^*+\beta +2\beta f^*)$, $\tilde{A}_{30} = r(d+A-2x)-2r, \tilde{A}_{21} = n(1+\beta)(1+f^*)+ny(f^*+\beta +2\beta f^*)$, $\tilde{A}_{01} = -n (1+\beta)(1+f^*)-n (f+\beta +2\beta f^*), \tilde{A}_{02} = -\beta f^*n -n (f^*+\beta +2\beta f^*), \tilde{A}_{12} = -2\beta f^*n -2n (f^*+\beta +2\beta f^*)$, $\tilde{A}_{03} = -\beta f^*n, \tilde{B}_{10} = s (1+f^*), \tilde{B}_{20} = \tilde{B}_{30} = \tilde{B}_{21} = 0, \tilde{B}_{11} = s(1+2f^*), \tilde{B}_{01} = -s(1+f^*)$, $\tilde{B}_{02} = -2sf^*-s, \tilde{B}_{03} = -sf^*.$

Take

then (4.24) is reformed as

where

Parameters $\tilde{C}_{20} = \tilde{B}_{20}\Upsilon^2, \tilde{C}_{11} = 2\tilde{B}_{20}\Upsilon\Omega+\tilde{B}_{11}\Upsilon$, $\tilde{C}_{02} = \tilde{B}_{20}\Omega^2+\tilde{B}_{11}\Omega+\tilde{B}_{02}, \tilde{C}_{30} = \tilde{B}_{30}\Upsilon^3$, $\tilde{C}_{12} = 3\tilde{B}_{30}\Upsilon\Omega^2+\tilde{B}_{12}\Upsilon, \tilde{C}_{21} = 3\tilde{B}_{30}\Upsilon^2\Omega+\tilde{B}_{21}\Upsilon^2$, $\tilde{C}_{03} = \tilde{B}_{30}\Omega^3+\tilde{B}_{12}\Omega+\tilde{B}_{21}\Omega^2+\tilde{B}_{03}$, $\tilde{D}_{20} = \frac{1}{\Upsilon}(\tilde{A}_{20}\Upsilon^2-\tilde{B}_{20}\Upsilon^2\Omega), \tilde{D}_{11} = \frac{1}{\Upsilon}(2\tilde{A}_{20}\Upsilon\Omega+\tilde{A}_{11}\Upsilon -\Omega(2\tilde{B}_{20}\Upsilon\Omega+\tilde{B}_{11}\Upsilon))$, $\tilde{D}_{02} = \frac{1}{\Upsilon}(\tilde{A}_{20}\Omega^2+\tilde{A}_{11}\Omega+\tilde{A}_{02} -\Omega(\tilde{B}_{20}\Omega^2+\tilde{B}_{11}\Omega+\tilde{B}_{02}))$, $\tilde{D}_{30} = \frac{1}{\Upsilon}(\tilde{A}_{30}\Upsilon^3-\tilde{B}_{30}\Upsilon^3\Omega)$, $\tilde{D}_{12} = \frac{1}{\Upsilon}(3\tilde{A}_{30}\Upsilon\Omega^2+\tilde{A}_{11}\Upsilon -\Omega(3\tilde{B}_{30}\Upsilon\Omega^2+\tilde{B}_{12}\Upsilon))$, $\tilde{D}_{21} = \frac{1}{\Upsilon}(3\tilde{A}_{30}\Upsilon^2\Omega+\tilde{A}_{21}\Upsilon^2 -\Omega(3\tilde{B}_{30}\Upsilon^2\Omega+\tilde{B}_{21}\Upsilon^2))$, $\tilde{D}_{03} = \frac{1}{\Upsilon}(\tilde{A}_{30}\Omega^3+\tilde{A}_{12}\Omega+\tilde{A}_{21}\Omega^2 +\tilde{A}_{03}-\Omega(\tilde{B}_{30}\Omega^3+\tilde{B}_{12}\Omega+\tilde{B}_{21}\Omega+\tilde{B}_{03})).$

The first Liapunov number is

By the bifurcation theory ^[50], we have the following conclusion.

Theorem 4.6. For the inner equilibrium point $E^*(x^*, y^*)$ of system (4.25), if $D > 0, T = 0$, then

(1) System (4.25) undergoes a subcritical Hopf bifurcation and an unstable limit cycle appears when $\ell > 0$;

(2) System (4.25) undergoes a supercritical Hopf bifurcation and a stable limit cycle appears when $\ell < 0$;

(3) System (4.25) undergoes a degenerate Hopf bifurcation and multiple limit cycles appear when $\ell = 0$.

Remark 4.7. By the equivalence, we obtain the existence and stability of Hopf bifurcation of system (2.2) regarding the parameter of fear. Similar results about other parameters can also be deduced. In the same way, all conclusions can be extended to the inner equilibrium points $E_3$ and $E_4$, respectively.

5.   Numerical analysis

5.1.   Equilibrium and its stability

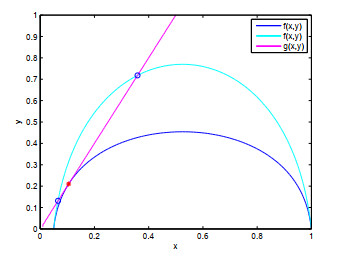
First we validate the existence of positive equilibrium points. Based on the biological feasibility, we hypothetically choose the following parameters $r = 12, f = 0.5, A = 0.05, \beta = 2, s = 1, n = 2.$ By computation under the help of Matlab, system (2.2) has two equilibrium points $E_3(0.0658, 0.1316)$ and $E_4(0.3590, 0.7580)$. Now, we change the parameter values to reveal how they affect the existence of equilibrium points. Then, we vary the values of fear from predator. If $f = 4.6709,$ then there is a unique positive equilibrium point $E^*(0.1050, 0.2101),$ see Figure 1.

By the same manner, we get the equilibrium points $E_3(0.0710, 0.1420)$ and $E_4(0.2254, 0.4509)$ when $f = 2$, and $E_3(0.0644, 0.1289)$ and $E_4(0.4656, 0.9311)$ when $f = 0$. The dynamics of all equilibrium points (see Figure 2) are summarized in Table 1.

Figure 2 shows that $E_3$ is a hyperbolic saddle and the stability of $E_4$ depends on the sign of $Tr(J(E_4))$. If $Tr(J(E_4)) < 0$ (Figure 2(a, c)), then $E_4$ is stable and unstable if $Tr(J(E_4)) > 0$ (Figure 2(b)). Figure 2(a–c) shows that there is bistable phenomenon in system (2.2), that is, the stability or extinction relies on the initial conditions. Different initial values will lead to different equilibrium states. It shows that the stability or existence of equilibria is especially sensitive to the initial conditions. Figure 2(c, f) shows that the prey and predator will be extinct, that is, the origin is globally asymptotically stable. Thus, in the biological sense, the fear is detrimental to prey and predator when the fear level increases.

Second, we change the values of Allee effect to see how it affects the existence of equilibria of (2.2). Let $r = 12, f = 2, \beta = 2, s = 1, n = 2.$ If $A = 0$, then there is a unique positive equilibrium point $E^*(0.2724, 0.5448)$. When $A = 0.001$, there are two equilibria, say $E_3(0.2717, 0.5434)$ (saddle) and $E_4(0.0012, 0.0024)$ (stable focus), and when $A = 0.01$, the equilibrium points are $E_3(0.2650, 0.5300)$ (saddle) and $E_4(0.0123, 0.0246)$ (stable focus). If $A = 0.0748,$ then the two equilibria converge to $E^*(0.2293, 0.4586),$ which is unstable leading to the extinction of both species when $A > 0.0748$.

Third, take $r = 12, f = 2, A = 0.05, s = 1, n = 2,$ then the existence of equilibria of system (2.2) with different hunting cooperation values is listed in Table 2 below.

5.2.   Sensitivity analysis

In this subsection, we focus on the sensitivity of parameters within the system, i.e., the system's response to the changes of initial conditions and parameter values. By analyzing how these variations impact system behavior, we can identify the importance of parameters in affecting the system dynamics. We utilize the sensitivity function mentioned in reference ^[52] to analyze the perturbations caused by minor parameter variations in the system. Define the following sensitivity function,

which reveals the sensitivity of prey and predator to fear perturbation, respectively. Due to the slight variation of parameter $f$, it still satisfies system (2.2), so we yield the following equations,

The sensitivity analysis for other parameters such as $A$ or $\beta$ is analogous to that of parameter $f$. To provide a more intuitive understanding of the sensitivity of system (2.2) to parameters $f$, $A$, and $\beta$, we conduct several numerical experiments. Without the other stated, we always take the following parameter values for all subsequent simulations,

By simulation, we get the sensitivity diagrams of (2.2) to parameters $f, A,$ and $\beta$ as follows.

Figure 3 shows that in the early stages, system (2.2) exhibits a subtle sensitivity to parameters $f, A$ and $\beta$, but, thereafter, it becomes very pronounced. Overall, these parameters are characterized by a high sensitivity to minor perturbations in the system, affecting its dynamic behavior significantly.

5.3.   Bifurcation

With the parameter values given in (5.1), by numerical simulation, intuitively we find that system (2.2) is unstable; see Figure 4. However, if the parameter values are changed, for example, letting $f = 2$ or $A = 0.01$ or $\beta = 1$, then system (2.2) is stable (Figure 5).

Comparing Figure 4 with Figure 5, the change of parameter values of $f, A$, or $\beta$ leads to the change of system stability. So, it is reasonable to guess that, due to the change of parameter values, bifurcation phenomenon appears around the equilibrium point of system (2.2). Next, we discuss the bifurcation scenarios of system (2.2) about parameters such as fear, Allee effect, and hunting cooperation.

(1) SN bifurcation

We begin with the SN bifurcation analysis and fix parameters $r = 12, \beta = 2, s = 1, n = 2.$ For parameter fear, we consider the cases of $A = 0$ (i.e., without Allee effect) and $A = 0.05.$ Numerically, we analyze how the equilibrium point changes with the change of fear values and plot the $x-f$ plane diagram of the prey (Figure 6(a)). It shows that system (2.2) is stable with no Allee effect, while if the Allee effect is considered, then (2.2) changes its stability and the node and saddle collide at the critical values $f = 4.6709.$ Similarly, for the simulation of parameter Allee effect, we consider the cases of $f = 0$ (i.e., without fear effect) and $f = 0.5,$ and draw the $x-A$ plane diagram (Figure 6(b)). It shows that if the fear is absent, then the SN bifurcation occurs at $A = 0.142977,$ where the prey biomass is $x = 0.2929,$ while if fear $f = 0.5$, then the SN bifurcation occurs at $A = 0.11243,$ where the prey biomass is $x = 0.2292.$ That is, the fear changes the stability of the inner equilibrium point where the prey is at a lower biomass. The $x-\beta$ plane diagrams is for the hunting cooperation effects (Figure 6(c)). The SN bifurcation appears at the critical values $\beta = 7.382380$.

(2) Hopf bifurcation

Next, we discuss the Hopf bifurcation of system (2.2). We speculate from Figures 4 and 5 that Hopf bifurcation may occur when the fear level changes. Actually, when $f = 0.2424$ or $f = 1.2903$, then $D > 0$ and $T = 0$, thus by Theorem 3.2, there exist Hopf bifurcations. We depict the Hopf bifurcation of fear $f$ (Figure 7(a)). In the same way, we can plot the Hopf bifurcations of parameter $f$ with $A = 0$, parameter $A$ with $f = 0$ or $f = 0.5$, and parameter $\beta$, see Figure 7(b–e), respectively.

Figure 7(a) shows that when $f = 0.2424$, Hopf bifurcation appears accompanied by periodic fluctuation, and system (2.2) becomes unstable from stable. However, when $f = 1.2902$, the periodic fluctuation ends and system (2.2) becomes stable again. That means multi-stability arises as fear value varies. Similarly, when $A = 0.0396$ (Figure 7(b)) or $\beta = 1.343$ (Figure 7(e)), system (2.2) becomes unstable from stable. If the fear or Allee effect is absent, then the system stability is changed. For the case of $A = 0$, system (2.2) is always stable (Figure 7(c)), but if $f = 0$, then (2.2) changes its stability at a larger critical value $A = 0.07498$ (Figure 7(d). Figure 7 indicates that the fear, Allee effect, and hunting cooperation bring serious influences to the system stability.

(3) BT bifurcation

At the end of this section, we consider the existence of BT bifurcation. By varying two parameter values simultaneously, we can get $D = 0$ and $T = 0$, so by Theorem 4.5, there exist BT bifurcations. Numerically, we vary the two parameters of fear and Allee effects at the same time, and depict the $f-A$ plane portrait; see Figure 8(a). Figure 8(a) shows that the cusp point appears at $(f, A) = (-0.507298, 0.271889),$ then as the increasing of the fear value, BT point occurs at $(f, A) = (-0.495180, 0.255084)$, and GH (generalized Hopf bifurcation) occurs at $(f, A) = (-0.373262, 0.171227)$. If $f = 1.518714$ and $A = 0.083038$, then BT point occurs again. However, from biological angle, the fear from predator is nonnegative. In view of the positiveness of the fear value, system (2.2) undergoes BT bifurcation only when $(f, A) = (1.518714, 0.083038)$. By the same way, we get the $f-\beta$ plane portrait (Figure 8(b)), where the BT point is the intersection point of the limit point curve, Hopf curve and Homoclinic curve. Rationally, we conclude that, if the parameter values are suitably chosen, then complicated dynamical phenomena such as SN bifurcation, GH and BT bifurcations, and cusp will occur in the rational biological range.

Figure 8 shows that the fear induced by predator, Allee effect, and hunting cooperation will jointly affect the dynamics of system (2.2), which is very complicated. Biologically, it is necessary to adjust the parameter value to remain the system stability or get some new equilibrium states.

6.   Conclusions and discussion

Considering the joint effects of fear induced by predator, Allee effect and hunting cooperation factors, we propose a Leslie-Gower prey-predator model. Due to $x\neq0$ in system (2.2), we study the global attractivity of the origin by topological equivalence theory (Figure 2(c, f)). By use of Jacobian matrix, characteristic equation and characteristic roots, the local stability is discussed. By Sotomayor's theorem and bifurcation theory, the SN bifurcation (Figure 5), Hopf bifurcation (Figure 6) and BT bifurcation (Figure 7) are studied, respectively. By numerical analysis, we depict some simulation graphs to intuitively validate the theoretical findings and reveal some complicated dynamical behaviors as bistability (Figure 2) and multi-stability (Figure 6(a)).

Compared with existing models, various factors such as fear induced by predator, strong Allee effect, and hunting cooperation in prey are all incorporated in our prey-predator model to reveal the complexity of the biological system. Therefore, it is difficult for us to analyze the existence of cusp of co-dimension 3 and BT bifurcation. These difficulties are overcame by constructing a series of appropriate but complex transformations. In addition, with the help of numerical simulations, we intuitively discover their existence and comprehensive impact on system stability.

Our theoretical analysis reveals the complicated dynamics of (2.2) and indicates how the fear, Allee effect and hunting cooperation seriously affect the system stability, and, in particular, how these factors jointly affect the system dynamics. They are summarized as follows.

● The existence and value of equilibrium point depend on the parameter values of fear, Allee and cooperation hunting.

● The parameter critical values of fear, Allee effect, and cooperation hunting of SN bifurcation and Hopf bifurcation are established. For the fear effect, when it increases, system (2.2) becomes unstable from stable, and then stable again, and whence, multi-stability occurs. For Allee effect and hunting cooperation, when they increase, (2.2) becomes unstable from stable companied by periodic fluctuations.

● The joint effect of fear, Allee effect and hunting cooperation leads to complicated dynamical phenomena such as SN bifurcation, generalized Hopf bifurcation and BT bifurcations.

Theoretical findings reveals that suitable parameter values are crucial for the coexistence of prey and predator and system stability. Therefore, some biological strategies may be applied to control the strength of fear and Allee effect, such as additional food supplement, establishing refuge areas, intervention in mating, and so on.

The prey-predator system is very complicated. There exist the additive predation in prey ^[53] or intraspecific competition in predator ^[54]. Similarly, the delay of biological process is popular, and the environmental fluctuation can also change the system dynamics. How these factors affect the system stability will be our future work.

Author contributions

Weili Kong: Conceptualization, Formal analysis, Methodology, Validation, Writing-original draft, Writing-review and editing; Yuanfu Shao: Conceptualization, Software, Writing-review and editing, Surpervision. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This research is supported by the Project of Education Department of Yunnan Province (2024J0943) and partially supported by Science and Technology Program of Inner Mongolia Autonomous Region (Nos. 2023YFHH0024).

Conflicts of interest

The authors declare that they have no competing interests in this paper.