Impact of the strong Allee effect in a predator-prey model

1.   Introduction

In the field of mathematical ecology, mathematical models are extensively used to explore and describe the complex interactions among individuals and between individuals and their surroundings by many scholars ^[1,2,3,4,5]. Especially, the predator-prey models have received great attention over the last one hundred years. Since the classical two species Lotka-Volterra model was put forward ^[1], there are a great many of experiments and papers investigating the interactions between predators and prey from each aspect ^[6,7,8,9,10]. Such as, in ^[7] the authors studied the complex dynamics of a predator-prey model with the nonlinear Michaelis-Menten type predator harvesting. Li et al. ^[8] proposed a Leslie-Gower predator-prey model with simplified Holling-type Ⅳ functional response. In ^[10] S. Djilali and S. Bentout proposed a delayed diffusive predator-prey model with prey social behavior and predator harvesting, and analyzed the dynamics of the deterministic model and diffusive model.

In recent years, it is widely recognized the Allee effect has important significance on the population dynamical relation and may make the dynamics more richer. Specifically, Allee effect refers to a positive correlation between population density and individual average fitness when the population is small ^[11,12]. From the view point of ecology, Allee effect on species can occur under some mechanisms, such as the change of habitat, inbreeding depression, difficulties in finding a spouse, avoiding predators, and the predation risk caused by environment conditions ^[13,14,15]. Moreover, the Allee effect is mainly divided into two forms: Strong and weak ^[16]. The strong Allee effect denotes the negative per capita growth rate when population density is below the so-called Allee threshold and the growth rate becomes positive when the population density is above this threshold ^[17]. This means, the population must surpass the threshold to grow. Contrarily, a population with a weak Allee effect has no such above threshold and the weak Allee effect means that when the species density is low, the per capita growth rate becomes small, but remains positive ^[18,19]. This implies the Allee effect may lead to much more complex dynamics and thereby affect the survival of the population. In fact in ^[20], Hilker et al. have introduced the strong Allee effect in a simple epidemic model ^[21,22] and shown that Allee effect can induce surprisingly rich dynamical behaviors, like periodic oscillations, multiple alternative steady states and homoclinic loops with the extinction of host populations. The complexity reveals, the introduction of the Allee effect in mathematical systems has important practical significance to the study of long-term species morphology and the development of species. This could have far-reaching implications in areas of biological protection.

On the other hand, there is another key objective that can also affect the dynamical behaviors of the prey-predator models: Functional response ^[23]. It refers to the average number of prey killed by each individual predator per unit of time and has two main types: Predator-dependent (as a function of prey and predators densities) and prey-dependent (as a function of the prey density) ^[24]. Exactly, functional response denotes the latter, like the famous Holling family ^[25], plays a predominant role in species dynamics models. For instance, since 1965, Holling's type Ⅱ functional response has acted as the basis for many literatures ^{[26,27,28,29,30]} on predator-prey theory.

Specially, for insect pest management, in ^[28] Sun et al. considered a prey-predator system with Holling type Ⅱ functional response in the predator:

where $x(t)$ and $y(t)$ denote the population densities of prey and predator at time $t$, respectively. $r$ is the growth rate of $x(t)$, $K$ is the environment capacity in the absence of predator. $\frac{ bx}{1+bhx}$, which is assumed to be the typical Holling type Ⅱ functional response form, gives a description of the per capita conversion rate from prey to predator. Concretely, $b$ and $h$ represent the searching rate and handling time of predator, $\lambda$ denotes the conversion efficiency. All the parameters are positive. By dynamical analysis, Sun et al. ^[28] concluded if $0 \leq h \leq \frac{\lambda}{d_1}$, system (1.1) has two saddles $P_0(0, 0)$, $P_1(K, 0)$, and a globally asymptotically stable focus $P_3\left(\frac{d_1}{b(\lambda -hd_1)}, \frac{r\left(Kb(\lambda-hd_1)-d_1 \right) }{Kb^2(\lambda-hd_1)} \right)$.

Thus, motivated by the above discussion, we naturally want to know: When an Allee effect is subject to the first species of system (1.1), what will happen to the dynamical properties? Hence, we construct the following ecological model with a strong Allee effect in prey

where $A$ is the strong Allee effect parameter and it satisfies $0 < A < K$ and other parameters are the same as system (1.1). Let $\overline{t} = Krt$, $\overline{x} = \frac{1}{K}x$ and $\overline{y} = \frac{b}{r}y,$ and drop the bars, we get

where $\alpha = \frac{A}{K}, \ \omega = \frac{\lambda b}{r}, \ \sigma = \frac{d_1}{Kr}, \ \eta = bhK$, and the strong Allee effect parameter $\alpha$ taken as $0 < \alpha < 1$.

Our main purpose aims to see how the strong Allee effect affect the dynamics of the prey-predator model with Holling type Ⅱ functional response. The layout of this paper is as follows. First, the positivity and boundedness of solution of system (1.3) are studied in Section 2. Then, in Section 3, we give the analysis of equilibria of system (1.3), including the distribution of all the possible equilibria and their stability. In Section 4, we verify the existence of transcritical bifurcation and Hopf-bifurcation. Additionally, numerical simulations and computations are carried out to explore and visualize the impact of the strong Allee effect in Section 5. Finally, this paper is concluded with a brief summary in Section 6.

2.   Preliminaries

Next, the positivity and boundedness of the solutions of system (1.3) will be shown in the region $\mathbb{R}_{+}^2 = \left\lbrace (x, y): x\geq 0, y\geq 0\right\rbrace$.

2.1.   Positivity

Lemma 2.1. For all $t\geq0$, every solution of system $(1.3)$ with initial value is positive.

Proof. Solving system (1.3) with positive initial condition $(x(0), y(0))$, we get the result:

Hence, any solution of system (1.3) starting from the interior of the first quadrant $xy$-plane still remains in it for all future times.

2.2.   Uniform boundedness

Lemma 2.2. Every solution of system $(1.3)$ with positive initial value is uniformly bounded.

Proof. Let $\varPhi = K\omega x+y$ and $\delta = \min\left\lbrace \alpha, \sigma\right\rbrace$, we have

Integrating the above inequality, we have $\varPhi(t) \leq e^{-\delta t }\varPhi(0) +\frac{\varrho}{\delta}(1-e^{-\delta t })$ and $\lim \sup \varPhi(t)\leq \varrho \delta^{-1}$, as $t \rightarrow \infty$, independently of the initial conditions. Therefore, the solutions of system (1.3) are uniformly bounded.

Remark 2.1. From the perspective of ecology, uniform boundedness of system (1.3) means that the interacting two species are ecologically well behaved and none of them can grow exponentially for a long period of time owing to limited food sources.

3.   Equilibria and stability analysis

3.1.   Existence of equilibria

Obviously, for all permissible parameters, system (1.3) always has three boundary equilibria $E_0(0, 0)$, $E_1(1, 0)$ and $E_2(\alpha, 0)$. If system (1.3) admits the positive equilibrium, then $x$ and $y$ must satisfy the equation as follows:

By some simple algebraic calculations, we obtain the system has a unique positive equilibrium $E_3\left(\frac{\sigma}{\omega-\sigma\eta}, \frac{K\left(\omega-(\eta+1)\sigma\right)\left(\sigma-\alpha(\omega-\sigma\eta)\right)}{(\omega-\sigma\eta)^2}\right)$ for $\frac{\omega\alpha}{1+\eta\alpha} < \sigma < \frac{\omega}{1+\eta}$.

3.2.   Stability of equilibria

Theorem 3.1. The trivial equilibrium $E_0$ is a hyperbolic stable node.

Proof. The Jacobian matrix at $E_0(0, 0)$ is given by

which, clearly, has two negative eigenvalues $\lambda_1(E_0) = -\alpha < 0$ and $\lambda_2(E_0) = -\sigma < 0$. Hence, the extinction equilibrium $E_0$ in the first quadrant is always a stable node.

Theorem 3.2. For the boundary equilibrium $E_1$:

(i) if $\sigma < \frac{\omega}{1+\eta}$, then $E_1$ is a hyperbolic saddle;

(ii) if $\sigma = \frac{\omega}{1+\eta}$, then $E_1$ is a non-hyperbolic saddle node. It means $S_\epsilon(E_1)$ is divided into two parts by two separatrices that tend to $E_1$ along the left and the right of $E_1$, where $S_\epsilon(E_1)$ is a neighborhood of $E_1$ with sufficient small radius $\epsilon$. One part consists of two hyperbolic sectors and another is a parabolic sector which is on the upper half plane.

(iii) if $\sigma > \frac{\omega}{1+\eta}$, then $E_1$ is a stable node.

Proof. The corresponding Jacobian matrix at $E_1(1, 0)$ is calculated as follows:

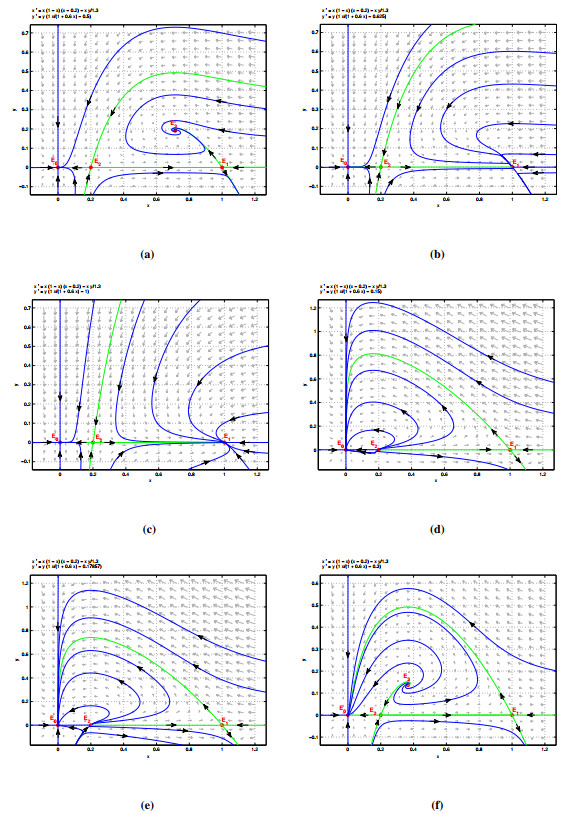
with two eigenvalues $\lambda_1(E_1) = \alpha-1 < 0$ and $\lambda_2(E_1) = \frac{\omega}{1+\eta}-\sigma$. Thus $E_1$ is a hyperbolic saddle if $\sigma < \frac{\omega}{1+\eta}$ and a stable node if $\sigma > \frac{\omega}{1+\eta}$ (see Fig. 1(a) and (c)). For $\sigma = \frac{\omega}{1+\eta}$, namely, the eigenvalue $\lambda_2(E_1) = 0$ and $E_1$ is non-hyperbolic, so we can not judge its type from the eigenvalues directly. Below we will use Theorem 7.1 in Chapter 2 in ^[31] to discuss the stability properties of $E_1$.

By letting $(\bar{x}, \bar{y}) = (x-1, y)$, we change system (1.3) into a standard form and then expand it to

where $c_1 = \frac{\omega}{(1+\eta)^2}$, $c_2 = -\frac{\omega\eta}{(1+\eta)^3}$, $c_3 = \frac{\omega\eta^2}{(1+\eta)^4}$, and $Q_0(\bar{x}, \bar{y})$ represents a power series with terms $\bar{x}^i\bar{y}^j$ $(i+j\geq5)$.

By the linear transformation

then system (3.4) becomes

where

and $Q_1(u, v)$ and $Q_2(u, v)$ represent power series with terms $u^{i}v^{j}(i+j\geq4)$.

Let $\tau = d_1t$, then system (3.6) becomes

From the implicit function theorem and $\frac{du}{d\tau} = 0$, we can obtain a unique function

which satisfies $\varphi_1(0) = \varphi_1'(0) = 0$ and $\varphi_1(v) + P(\varphi_1(v), v) = 0$. Then substituting it into the second equation of (3.7), we have that

The coefficient of $v^2$ is $-\frac{c_1}{d_1} < 0$. Thus, by using Theorem 7.1 in Chapter 2 in ^[31], we get $E_1$ is a saddle node. This means that a neighborhood of $S_{\varepsilon}(E_1)$ is divided into two parts by two separatrices that tend to $E_1$ along the left and the right of $E_1$ (see Figure 1(b)). One part consists of two hyperbolic sectors and another is a parabolic sector which is on the upper half plane.

Theorem 3.3. For the boundary equilibrium $E_2$:

(i) if $\sigma < \frac{\omega\alpha}{1+\eta\alpha}$, then $E_2$ is an unstable node;

(ii) if $\sigma = \frac{\omega\alpha}{1+\eta\alpha}$, then $E_2$ is a non-hyperbolic saddle node. This means $S_\epsilon(E_2)$ is divided into two parts by two separatrices that move away along the left and the right of $E_2$. One part consists of two hyperbolic sectors, and another is a parabolic sector which is on the upper half-plane;

(iii) if $\sigma > \frac{\omega\alpha}{1+\eta\alpha}$, then $E_2$ is a hyperbolic saddle.

Proof. The Jacobian matrix $J_{E_2}$ of $E_2(\alpha, 0)$ is

Then the eigenvalues $\lambda_1(E_2) = \alpha(1-\alpha) > 0$ and $\lambda_2(E_2) = \frac{\omega\alpha}{1+\eta\alpha}-\sigma$. Clearly, $E_2$ is an unstable node if $\sigma < \frac{\omega\alpha}{1+\eta\alpha}$ and a saddle if $\sigma > \frac{\omega\alpha}{1+\eta\alpha}$ (see Figure 1(d) and (f)). However, when $\sigma = \frac{\omega\alpha}{1+\eta\alpha}$, the eigenvalue $\lambda_2(E_2) = 0$ which indicates $E_2$ is non-hyperbolic. In order to deduce its stability, we translate $E_2$ to the origin via the translation $(\bar{x}, \bar{y}) = (x-\alpha, y)$ and then expand system (1.3) to

where $f_1 = \frac{\omega}{(1+\eta\alpha)^2}$, $f_2 = -\frac{\omega\eta}{(1+\eta\alpha)^3}$, and $M_0(\bar{x}, \bar{y})$ represents a power series in $(\bar{x}, \bar{y})$ with terms $\bar{x}^{i}\bar{y}^{j}(i+j\geq\; 4)$.

Let

be an invertible matrix. We use the following linear transformation

then system (3.10) turns into

where $e_1 = (1-\alpha)\alpha$, $e_2 = 1-2\alpha$, $e_3 = 1-3\alpha-f_1$, $e_4 = -\alpha-f_1$, $e_5 = -1$, $e_6 = f_2-1$, $e_7 = f_2-3$, and $e_8 = 2f_2-3$. $M_1(u, v)$ and $M_2(u, v)$ represent power series with terms $u^{i}v^{j}(i+j\geq 4)$.

Set $\tau = e_1t$, we attain

From $\frac{du}{d\tau} = 0$, we obtain the implicit function

which satisfies $\varphi_1(0) = \varphi_1'(0) = 0$ and $\varphi_1(v) + U(\varphi_1(v), v) = 0$. Then substituting it into the second equation of (3.13), we have

Hence, according to the Theorem 7.1 in Chapter 2 in ^[31], we have $m = 2$ and $a_m = \frac{\omega}{(1-\alpha)\alpha(1+\eta\alpha)^2} > 0$, so $E_2$ is a saddle node. That indicates a neighborhood of $S_{\varepsilon}(E_2)$ is divided into two parts by two separatrices that move away along the left and the right of $E_2$. One part consists of two hyperbolic sectors and another is a parabolic sector which is on the upper half plane (see Figure 1(e)).

Theorem 3.4. For the positive equilibrium $E_3$:

(i) if $\frac{\omega(1+\alpha)}{2+\eta(1+\alpha)} < \sigma < \frac{\omega}{1+\eta}$, then $E_3$ is locally asymptotically stable;

(ii) if $\sigma = \frac{\omega(1+\alpha)}{2+\eta(1+\alpha)}$, then $E_3$ is a center or weak focus;

(iii) if $\frac{\omega\alpha}{1+\eta\alpha} < \sigma < \frac{\omega(1+\alpha)}{2+\eta(1+\alpha)}$, then $E_3$ is unstable.

Proof. The Jacobian matrix $J_{E_3}$ of $E_3(x^{*}, y^{*})$ is

From $x^*(1-x^*)(x^*-\alpha)-\frac{1 }{K}x^*y^* = 0$, we can derive

So the determinant and the trace of Jacobian matrix $J_{E_3}$ are calculated by

When $\frac{\omega\alpha}{1+\eta\alpha} < \sigma < \frac{\omega}{1+\eta}$, $Det[J_{E_3}]$ is positive, but the sign of $Tr[J_{E_3}]$ cannot be obtained directly. If $\frac{\omega(1+\alpha)}{2+\eta(1+\alpha)} < \sigma < \frac{\omega}{1+\eta}$, then $Tr[J_{E_3}] < 0$, that is $E_3$ is locally asymptotically stable (see Figure 2(a)). If $\sigma = \frac{\omega(1+\alpha)}{2+\eta(1+\alpha)}$, then $Tr[J_{E_3}] = 0$, that implies $J_{E_3}$ has a pair of purely imaginary eigenvalues. It confirms that the equilibrium $E_3$ may be a center, a weak focus or a center focus. We also can easily show that $F(x, y) = -x^3+(1+\alpha)x^2-\frac{1}{K}xy$ and $G(x, y) = \frac{\omega xy}{1+\eta x}$, which are the nonlinear parts of system $(1.3)$, are analytic functions. Thus, from the corollary of Theorem 2.1 in Chapter 4 in ^[31], we obtain that $E_3$ is a center (see Figure 2(b), (c)) or weak focus. If $\frac{\omega\alpha}{1+\eta\alpha} < \sigma < \frac{\omega(1+\alpha)}{2+\eta(1+\alpha)}$, then $Tr[J_{E_3}] > 0$, it means $E_3$ is unstable (see Figure 2(d), (e)). Thus, this completes the proof.

4.   Bifurcation analysis

In this part, we mainly put the focus on the various bifurcation behaviors of system $(1.3)$.

4.1.   Transcritical bifurcation

Theorem 4.1. For transcritical bifurcation, the following statements are true.

(1) When the parameters satisfy $\sigma = \sigma_{TC_1} = \frac{\omega}{1+\eta}$, system $(1.3)$ undergoes a transcritical bifurcation referred as $TC_1$ at $E_{1}$;

(2) When the parameters satisfy $\sigma = \sigma_{TC_2} = \frac{\omega\alpha}{1+\eta\alpha}$, system $(1.3)$ undergoes another transcritical bifurcation referred as $TC_2$ at $E_{2}$.

Proof. (1) Now we verify the transversality condition for transcritical bifurcation by using Sotomayor's theorem ^[32,33]. If $\sigma = \sigma_{TC_1} = \frac{\omega}{1+\eta}$, then $Det[J_{E_1}] = 0$, which means one eigenvalue of the Jacobian matrix $J_{E_1}$ is zero. Let $V$ and $W$ represent the two eigenvectors corresponding to the zero eigenvalue of $J_{E_1}$ and it's transpose $J_{E_1}^T$, respectively, and they are given by

Furthermore, we have

Also

Consequently, system (1.3) undergoes a transcritical bifurcation at $\sigma = \sigma_{TC_1}$.

(2) Now we also apply Sotomayor's theorem to prove the transversality condition for another transcritical bifurcation at $\sigma = \sigma_{TC_2} = \frac{\omega\alpha}{1+\eta\alpha}$. Similar to the process of the former, the transversality condition is derived.

and

where

are the two eigenvectors corresponding to the zero eigenvalue of the Jacobian matrix $J_{E_2}$ and it's transpose $J^T_{E_2}$, respectively. Hence, we complete the proof.

In particular, from Figure 1(a), we can see that for $\sigma < \sigma_{TC_1}$, there are two equilibria $E_1$ and $E_3$. And $E_1$ is unstable and $E_3$ is stable. For $\sigma = \sigma_{TC_1}$ (see Figure 1(b)), these two equilibria coalesce. For $\sigma > \sigma_{TC_1}$(see Figure 1(c)), $E_1$ is stable and $E_3$ is unstable. In this case, $E_3$ is a negative equilibrium. Biologically, we consider the positive equilibria, so we ignore it in the corresponding phase portrait. Thus, an exchange of stability has occurred at $\sigma = \sigma_{TC_1}$, that is to say, the transcritical bifurcation at $\sigma = \sigma_{TC_1}$ occurs by the Sotomayor's theorem. Moreover, the occurrence of another transcritical bifurcation at $\sigma = \sigma_{TC_2}$ is similarly illustrated in Figure 1(d), (e), (f).

4.2.   Hopf-bifurcation and the existence of limit cycle

In this subsection, the possible occurrence of Hopf-bifurcation around the interior equilibrium $E_{3}$ about the bifurcation parameter $\sigma$ is explored. In a two dimensional system, it is concluded Hopf-bifurcation occurs as the stability of the interior equilibrium changes (from stable to unstable or vice-versa) and a periodic solution appears (or disappears). Next, we will give the proof of the existence for Hopf-bifurcation of system $(1.3)$.

4.2.1.   Hopf-bifurcation

Theorem 4.2. The conditions for occurrence of Hopf-bifurcation at the critical value $\sigma = \sigma_H = \frac{\omega(1+\alpha)}{2+\eta(1+\alpha)}$ around the positive equilibrium $E_3(x^*, y^*)$ are $\frac{\omega\alpha}{1+\eta\alpha} < \sigma < \frac{\omega}{1+\eta}$ and $\frac{d}{d\sigma}Tr[J_{E_3}]\neq0$ at $\sigma = \sigma_H$.

Proof. From the Jacobian matrix $J_{E_3}$ calculated at $E_3(x^*, y^*)$, we consider $\sigma$ as a bifurcation parameter. For occurrence of Hopf-bifurcation, the characteristic equation of $J_{E_3}$ must have a pair of purely imaginary roots. At $\sigma = \sigma_H$, $Tr[J_{E_3}] = 0$, then the characteristic equation of $J_{E_3}$ becomes

When $\frac{\omega\alpha}{1+\eta\alpha} < \sigma < \frac{\omega}{1+\eta}$, $Det[J_{E_3}] > 0$, namely the above characteristic equation has a pair of conjugated imaginary eigenvalues $\lambda_{1, 2} = \pm i\theta$, where $\theta = \sqrt{Det[J_{E_3}]}$.

Now we check the transversality condition $\frac{d}{d\sigma} \left\lbrace Re(\lambda)\right\rbrace |_{\sigma = \sigma_H}\neq0$ which confirms the eigenvalues cross the imaginary axis transversely with non-zero speed. Let $\sigma$ be any point in the neighbourhood of $\sigma_H$, the eigenvalues of the Jacobian matrix $J_{E_3}$ at $\sigma$ are $\lambda_{1, 2} = \chi(\sigma) \pm i\theta(\sigma)$, where $\chi(\sigma) = \frac{Tr[J_{E_3}]}{2}$ and $\theta(\sigma) = \sqrt{Det[J_{E_3}]-\frac{Tr^2[J_{E_3}]}{4}}$. Then

Thus the transversality condition is verified and a Hopf-bifurcation of system $(1.3)$ occurs at $\sigma = \sigma_H$.

4.2.2.   Direction of Hopf-bifurcation

In order to determine the direction of Hopf-bifurcation and the stability of the periodic solution which originates from the positive equilibrium via Hopf bifurcation, the first Lyapunov coefficient ^[33] needs to be computed.

Firstly, set $z_1 = x-x^*$ and $z_2 = y-y^*$, then system $(1.3)$ can be written as

where

By ignoring the higher order terms of degree 4 and above, then system $(4.5)$ becomes

where

The eigenvector $\bar{v}$ of $J_{E_3}$ for the eigenvalue $i\theta$ at $\sigma = \sigma_H$ is $\bar{v} = \left(\begin{array}{c} m_{01}\\ i\theta-m_{10} \end{array}\right)$.

Now we define

Let $Z = QU$, where $U = \left(\begin{array}{c} u\\ v \end{array}\right)$. Under this transformation, system $(4.6)$ becomes

Thus

where $S^{1}$ and $S^{2}$ are non-linear in $u$ and $v$ given by

with

Regarding the normal form (4.7), we calculate the first Lyapunov coefficient and obtain

Evidently, $l_1 < 0$, so that a stable Hopf-bifurcating limit cycle appears and the Hopf-bifurcation is supercritical, which indicates the stable periodic solution overlaps an unstable interior equilibrium. From view of ecology, this phenomenon means that both predators and prey reach an oscillatory coexistence state. And, in the next section, we are going to explore this phenomenon a step further with the help of numerical simulations.

5.   Numerical simulation and discussion

To verify the validity of the obtained analytical results, in this part, some numerical simulations and computations are carried out. Firstly, the phase portraits corresponding to the scenario of no positive equilibrium and one positive equilibrium are plotted in Figures 1 and 2 by varying the key parameter value $\sigma$ and keeping other fixed parameters values $\alpha = 0.2$, $K = 1.3$, $\omega = 1$ and $\eta = 0.6$. Further, using this set of parameter values and different values of $\sigma$, we also give some time series diagrams of system $(1.3)$ for a better visualization of how the strong Allee effect influence the dynamics of the model, with special attention to the stability and cyclical behavior.

Case 5.1. For $\sigma$ = 0.5, the high mortality of natural enemy predator, prey and the natural enemy populations reach a stable coexistence state because of the reduced predation pressure on prey and Allee effect (Figures 2(a) and 3).

Case 5.2. For gradually decreasing the value of $\sigma$, the positive equilibrium $E_3$ of model $(1.3)$ loses stability via a Hopf bifurcation at $\sigma_H$ = 0.441176 (Figure 2(b), (c)) and the Hopf bifurcation is supercritical as the first Lyapunov coefficient $l_1 = -0.072449680827 < 0$. Meanwhile, as shown in Figure 4, both the total populations begin to oscillate. From Figure 2(d), (e), it is found when $\sigma < \sigma_H$ slightly, a stable limit cycle from $E_3$ is bifurcated. Prey and predator populations reach an oscillation coexistence state (Figure 5). The amplitude of the oscillation is initially small, but then increases rapidly with decreasing $\sigma$, which is illustrated with a three-dimensional bifurcation diagram in Figure 6. Biologically, the populations fluctuate a lot, which corresponds to the sudden increase of prey.

Case 5.3. For small value $\sigma$ = 0.3, the low mortality of natural enemy predator, we observe that the limit cycle disappears and both prey and predator approach the extinction state for the higher predation pressure on prey and the Allee effect (Figures 1(f) and 7).

Remark 5.1. One can see that the model is sensitive to the initial condition. The strong Allee effect causes more complex dynamics, with total population density tending to either the extinction state $E_0 (0, 0)$ or coexistence state $E_3(x^*, y^*)$ depending on the selection of the initial condition. In the real world, for biological protection, our purpose is generally to maintain the sustainable survival of species rather than eradicating the species completely. Accordingly, in the above cases, we choose the initial condition $[x(0), y(0)]$ = [1, 0.1].

6.   Conclusions

In this article, a predator-prey model with strong Allee effect in prey was proposed. We investigated the classification and stability of each equilibrium of system (1.3) and fulfilled a comprehensive bifurcation analysis. Qualitative analysis shows that the model's dynamics grow more complicated when Allee effect is incorporated into the first species. More specifically, with the comparison to system (1.1) ^[28] in absence of Allee effect, we find some new dynamical properties of model (1.3).

(1) System (1.3) possesses more types of equilibria due to the strong Allee effect. The extinction equilibrium is always an attractor, whereas the stability of other two boundary equilibria and the unique interior equilibrium changes with different parameter conditions. For the system with no Allee effect, both boundary equilibria are saddles and the interior equilibrium is always globally asymptotically stable.

(2) System (1.3) exhibits more bifurcation behaviors for the existence of multiple types of equilibria. Only one transcritical bifurcation occurs for system (1.1), whereas system (1.3) undergoes two transcritical bifurcations and one Hopf-bifurcation. Also a stable limit cycle around unstable positive equilibrium $E_3$ corresponding to system (1.3) appears.

It can be clearly seen that the strong Allee effect can lead to potential changes in system dynamics. It also has a significant role in ecology. Allee effect, such as, can destabilize the coexistence steady state. From stable coexistence to oscillating coexistence, and then from oscillating coexistence to overall populations extinction state, the prey and predator populations go through multiple stability switches. Moreover, in all cases, the possibility of total species extinction in the model is caused by Allee effect. This suggests that if prey or predators are subject to Allee effect, the measures we adopt for nature preservation should take this into consideration, which is important for analyzing the long-term survival of all populations.

We just consider the impact of Allee effect in prey on the dynamical behaviors of the predator-prey system in this paper. It will be an interesting theme to study the dynamics of the model with Allee effects in both populations. We will leave this as future work.

Acknowledgments

The second author was supported by the National Natural Science Foundation of China (No.12001503) and the third author was supported by the Project of Beijing Municipal Commission of Education (KM 202110015001).

Conflict of interest

The authors declare no conflict of interest.