A two-step smoothing Levenberg-Marquardt algorithm for real-time pricing in smart grid

1.   Introduction

In the last two decades, the traditional power grid has becoming unsuitable for the electrical market, with the significantly growing demand for electricity and the shortage of electrical energy. By 2050, the global energy demand is projected to be more than double its current status. Consequently, energy conservation and the development of renewable energy sources are crucial and have attracted a lot of attention from researchers ^{[1,2,3,4,5,6]}.

The concept of smart grids and microgrids are popular in this decade, which refer to the intelligent upgrade of the power system as a whole and the energy internet in a small range, respectively. Moreover, they are both important directions for the development of renewable energy technology. The former, smart grid (SG), termed as "Grid 2.0", has a better performance in terms of reliability, self-healing, interactivity, and is proposed and recognized as the future power grid. The latter, microgrid, is a local power supply system that uses renewable energy and traditional point source energy in a small range through energy micro-net technology, which includes converting renewable energy into electricity, storing electricity through energy storage, and intelligent scheduling technology to provide users with an independent power supply. It is usually used in small commercial buildings, public facilities, residential areas, and so on.

In a smart grid, the real-time pricing (RTP) scheme is ideal for application. It is different from the common electricity pricing strategies, such as the traditional fixed price scheme, which is a simple cost allocation, and the ladder price scheme, which may lead to insufficient supply in the peak period and insufficient demand in the low period. The RTP is determined prior to the deal happening through the intercommunication between the supply and demand of electricity and it is a real-time interaction process between the user and supplier. Generally, the existing research in the field of the RTP mechanism can be divided into two categories. One is based on the game theory, which can obtain an optimal decision of multiple parties on the premise of satisfying certain rules ^[7,8,9,10], the other is based on the optimization method to solve the model, which is always either from the social welfare maximization model (SWMM) or its modified version ^{[11,12,13,14,15,16]}. In a microgrid, the computer system that assures the effective management operation is called the energy management system (EMS), which encompasses both the supply-side and demand-side management, while ensuring that system constraints are respected. EMSs are usually divided into centralized and decentralized according to their mode of operation. In the centralized mode, the management system is located in a central station and connected to the distributed energy resources (DERs) via communication lines for control and data exchange. In the decentralized model, each DER operates independently and manages itself using a local controller, thus eliminating the need for communication ^[17]. Many optimization algorithms have been proposed to handle EMS problems by far ^{[18,19,20,21]}.

In this paper, we focus on the real-time pricing in a smart grid, where some algorithms have already existed. For example, Zhang ^[11] proposed a fast distributed dual subgradient algorithm by smoothing the original dual subgradient twice. Zhu et al. ^[12] considered the relationship between the two stages of the user's electricity demand and proposed an improved simulated annealing algorithm. Wang and Gao ^[13] first transformed the SWMM into a nonsmooth system of equations based on KKT conditions, then solved the SWMM by a smoothing quasi-Newton method. Li et al. ^[14,15] proposed a smoothing Newton method based on a new smoothing approximation cosh function and a new form of the utility function. Yang et al. ^[16] proposed a new smoothing conjugate gradient method based on a smoothing Fischer-Burmeister function. These optimization methods played an important role for solving the SWMM. However, the convergence of some intelligent algorithms ^[12] could not be guaranteed, the results were feasible but may be not necessarily optimal, and there was a dual gap between the dual problem and the original problem in some Lagrangian dual methods ^[11], which may increase the direct error of the results. Recently, the smoothing algorithms are proposed. However, Refs. ^[13,16] focused on a system of equations such that

which is the approximation of a nonsmooth system transformed from the SWMM as follows

where $H_{\mu}:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ is a smoothing approximation function of the nonsmooth function $H:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$, $\mu > 0$ is called an approximating parameter, there exists gaps between the approximate smoothing system and the original nonsmooth system ^[13,16]. Refs. ^[14,15] focused on an equivalent smooth system, and proposed a smoothing Newton method, where the nonsingular property is necessary. Here, we first transform the social welfare maximization model into a smooth system of equations based on KKT conditions, then propose a two-step smoothing Levenberg-Marquardt(LM) method. The contributions of the research are as follows. $(1)$ Using the KKT conditions, we transform the optimization model into a nonlinear complementary problem, then construct an equivalent smooth system based on a symmetric perturbed smoothing function with strongly Jacobi consistency, namely, the smoothing approximation function has a better one-order approximation property than the Jacobi consistency ^[17]. $(2)$ A two-step smoothing LM method is proposed. It is worth mentioning that an adaptive parameter strategy is adopted in the proposed algorithm, which has proven effectiveness when the initial point is far from the optimal solution. $(3)$ By proving the locally Lipschitzian continuous of the corresponding function and its Jacobian matrix, we show the global convergence and locally cubic convergence under the local error bound, which is weaker than the nonsingular property. $(4)$ We adopt a new utility function based on the logistic function, which is significant for solving the real-time pricing problem of smart grids. $(5)$ We compare the proposed algorithm with the traditional fixed method, the smoothing quasi-Newton method, and one-step smoothing algorithms, and prove its effectiveness.

The outline of the paper is as follows. In Section 2, we introduce the social welfare maximization model, and its transformation from the SWMM into a smooth system based on the KKT conditions. Additionally, we investigate the locally Lipschitz continuous of the relate function, which is necessary to illustrate the local cubic convergence. In Section 3, a smoothing LM algorithm is proposed, and its global and local convergent result are discussed. In Section 4, numerical evaluations are shown to illustrate the effectiveness of the present algorithm.

2.   The social welfare maximization model and equivalent smooth system

In this section, we introduce the social welfare maximization model, and its transformation from the SWMM into an equivalent smooth system.

2.1.   RTP optimization model

Consider a smart grid system that contains one supplier and one type of users. The energy provider and all users are connected with each other through an information communication infrastructure. Divide the whole cycle into $K$ periods and let $\mathcal{N} = \{1, 2, ..., N\}$ the set of users requiring electricity, $x_{i}(k)$ represent the power consumption demand at the time slot $k$ of the $i$-${\rm th}$ users, $C_{k}(.)$ represent the cost function of the energy provider. The optimization model of SWMM ^[23,24] is as follows:

where the constraint conditions mean the electricity consumption of all users does not exceed the total generating capacity, and $L_{k}$ is the generation capacity of the residential users at the time slot $k$.

In general, the cost function $C_{k}(L_{k})$ and the utility function $U(x_{i}(k), \omega_{i}(k))$ in model (2.1) are important in economics, where $C_{k}(L_{k})$ is always adopted as a quadratic function ^[23] such that

$U(x_{i}(k), \omega_{i}(k))$ represents the relationship between the consuming utility and the number of a commodity. The utility function $U(x_{i}(k), \omega_{i}(k))$ has the properties^[16] such that

and

In this paper, we adopted the utility function as follows ^[15]:

where $\widetilde{K} > 0$ is a predetermined parameter, and $\omega_{i}(k) > 0$ varies with the time slots of the user's satisfaction in a power system.

2.2.   Equivalent nonsmooth system based on KKT conditions

Mathematically, for each period $k\in{1, 2, ..., K}$, the model (2.1) can be expressed as an optimization problem such that

which is equivalent to finding a minimum of a convex problem, since $U(x_{i}(k), \omega_{i}(k))$ is concave, $C_{k}(L_{k})$ is convex, and the constraint conditions is affine.

Denote $v_{k}: = (x_{1}(k), x_{2}(k), ..., x_{N}(k), L_{k})^{\rm T}\in\mathbb{R}^{N+1}$, and the KKT conditions of the problem (2.2) is such that

Since

is a complementarity problem, we obtain the equivalent nonsmooth system of model (2.2) as follows:

where $\varphi$ is an "nonlinear complementarity problem (NCP)" function, such as the "min" function $\varphi(a, b): = {\rm min}\{a, b\}$, the Fischer-Burmeister function $\varphi_{{\rm FB}}(a, b): = \sqrt{a^{2}+b^{2}}-a-b$ and so on ^[25,26]. It is worth mentioning that the solution $\lambda_{k}$ is the optimal price in the $k$ period, namely the shadow price in economics by virtue of Refs. ^[23,27].

2.3.   Equivalent smooth system

Using the KKT conditions, the model (2.2) is transformed into a nonsmooth system of equations. Here, we use an improved Fischer-Burmerister smoothing function to derive the equivalent smooth system of the model (2.3). Meanwhile, the Lipschitz continuous of the corresponding smoothing function is discussed, which is crucial for the proposed algorithm.

As is well known, the Fischer-Burmerister function is an NCP function, though nonsmooth at the point $(0, 0)$. According to ^[26], we adopt an improved Fischer-Burmerister smoothing function as follows:

Denote

Model (2.2) is transformed into the following smoothing system such that

It is obvious that model (2.2) is equivalent to Eq (2.3) in the sense that their solutions are coincide.

We consider the Lipschitz continuous of the function $\Phi$ as follows, which is crucial to obtain the locally convergent result.

Actually, a function $F:\mathbb{R}^{n}\longrightarrow\mathbb{R}$ is locally Lipschitz continuous if there exist $L > 0$ and $\varepsilon > 0$ such that

at any point $x\in\mathbb{R}^{n}$. The function $F$ is said to be Lipschitz continuous if there exist $L > 0$ such that

If a function $F:\mathbb{R}^{n}\longrightarrow\mathbb{R}$ is continuously differentiable, namely, smooth at $x\in\mathbb{R}^{n}$, $F$ is locally Lipschitz continuous at $x\in\mathbb{R}^{n}$ ^[22].

Assumption 2.1. The solution set $X$ of Eq (2.3) is not empty.

Lemma 2.1. Let $F = (F_{1}, F_{2}, ..., F_{n})^{\rm T}$, where $F_{i}:\mathbb{R}^{n}\rightarrow \mathbb{R}$ and locally Lipschitz continuous at $x$, and $F$ is locally Lipschitz continuous at $x\in \mathbb{R}^{n}$.

Proof. The conclusion is obvious. Suppose

where $x, y\in \mathbb{R}^{n}, L_{i}$ is a Lipschitz constant, there is

where $L = \max(L_{1}, ..., L_{n})$. The proof is completed. □

Theorem 2.1. $\Phi(.)$ and its Jacobi $J(.)$ are locally Lipschitz continuous at $y_{k}\in \mathbb{R}^{N+3}$.

Proof. Since $\Phi(y_{k})\in \mathbb{R}^{N+3}$ is smooth at $y_{k}\in \mathbb{R}^{N+3}$, it is obvious locally Lipschitz continuous at $y_{k}$. We prove the Jacobian $J(y_{k})$ are also locally Lipschitz continuous as follows.

By a straightforward calculation, we first obtain the Jacobi $J$ of $\Phi(y_{k})$ as follows:

Here, for brevity, $y_{i}$ means the $i-th$ component of $y_{k}$.

Denote $J(y_{k}): = J = (J_{1}, ..., J_{N+3})^{\rm T}$. Next, we focus on investigating the Lipschitz continuous of $J_{i}$ through its each component, where $i = 1, ..., N+3.$

(ⅰ) For $J_{1}: = (J_{1}^{(1)}, ..., J_{1}^{(N+3)}) = (e^{\mu}, ..., 0),$ we have

which implies $J_{1}$ is smooth and locally Lipschitz continuous at $y_{k}\in \mathbb{R}^{N+3}$.

(ⅱ) Consider $J_{i}: = (J_{i}^{(1)}, ..., J_{i}^{(N+3)}) = (\frac{\partial f_{i}}{\partial x_{1}}, ..., \frac{\partial f_{i}}{\partial x_{N}}, \frac{\partial f_{i}}{\partial L_{k}}, \frac{\partial f_{i}}{\partial\lambda_{k}}), i = 2, ..., N+1.$ Actually, since

we have

which implies that $J_{i}$ is smooth and locally Lipschitz continuous at $y_{k}\in \mathbb{R}^{n}$ for $i = 2, ..., N+1.$

(ⅲ) Actually, a straightforward calculation yields the following:

It is not difficult to see that $\phi_{\mu}', \phi_{a}', \phi_{b}$ are smooth. Since $g(y_{k})$ is also smooth, we obtain that $J_{N+3}$ is locally Lipschitz continuous at $y_{k}\in \mathbb{R}^{N+3}$. Then, the Jacobian $J(.)$ are locally Lipschitz continuous at $y_{k}\in \mathbb{R}^{N+3}$ by virtue of Lemma $2.1$. □

Assumption 2.2. The solution set $X\subset U$, where $U\subset \mathbb{R}^{n}$ is bounded and closed.

The bounded properties are reasonable in Assumption 2.2, since $\mu$ is an approximate parameter, which is always adopted small enough, $\lambda_{k}$ denotes the real-time pricing, and $L_{k}$ will not exceed the electricity production.

Lemma 2.2. (Borel finite covering theorem) ^[28] Suppose $U$ is bounded and closed, which is covered by a set of infinite open intervals $\Sigma$, $U$ must be covered by some finite sets of open intervals from $\Sigma$.

Theorem 2.2. $\Phi(.)$ and its Jacobi $J(.)$ are Lipschitz continuous in $U$.

Proof. By virtue of Theorem 2.1, $\Phi(.)$ and its Jacobian $J(.)$ are locally Lipschitz continuous at $y\in U$. Then, there exist $\delta_{y} > 0$ and Lipschitz constant $L_{y}$ such that

for $\forall x\in V(y; \delta_{y}).$

Set $G = \{V(y; \delta):y\in U\}$, where $V(y; \delta) = \{y'\in\mathbb{R}^{N+3}:\parallel y'-y\parallel < \delta\}$. It is obvious that $G$ is a open covering of $U$. Furthermore, there exist some finite sets such that $V(y; \delta_{y})\in G$ covering $U$ by virtue of the Borel finite covering theorem. Suppose $V(y_{i}; \delta_{y_{i}}), i = 1, 2..., m,$ covering the set $U$, we have

for $\forall x\in U,$ where $L = \max\{L_{y_{1}}, ..., L_{y_{m}}\}$, namely, $\Phi(.)$ is Lipschitz continuous in $U$. Similarly, the Jacobi $J$ is also Lipschitz continuous in $U$. □

3.   Algorithm and its convergence

3.1.   A two-step smoothing Levenberg-Marquardt method

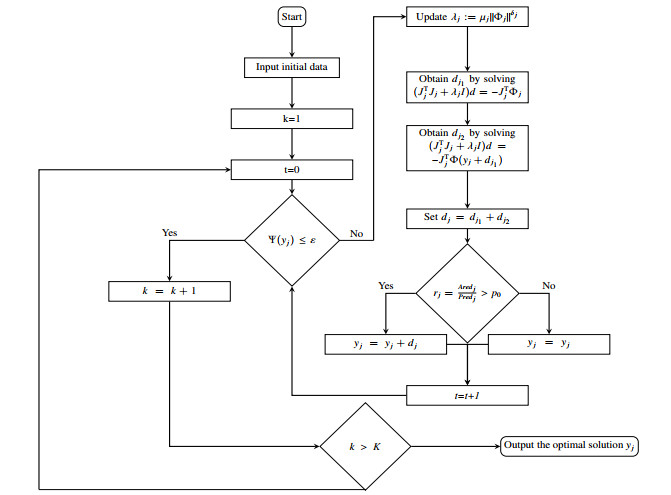
In this section, a two-step smoothing LM method is proposed to solve Eq (2.3). First, we provide the process of solving (2.3) as follows:

Step 0. If $t\in k$, during the $k$-${\rm th}$ period, one chooses the parameters based on the historical data, and computes the electricity price, the demand productions of the users, and the minimum production in the beginning of the pricing time.

Step 1. One updates the information of the user's demand, the price, and the minimum productions. In this process, the users could adjust their electricity consumption based on the price, and the electricity provider could adjust its production based on the user's demand.

Step 2. Repeat Step 1 until the supply and demand are in balance.

Denote

as the merit function of Eq (2.3). Next, we give the concrete algorithm of the aforementioned process (see Figure 3.1).

Algorithm 3.1. (SLM)

Step 0. Give an initial point $y_{0}\in\mathbb{R}^{n}$ and parameters $\varepsilon > 0, 0 < m < \mu_{0}, 0 < p_{0}\leq p_{1}\leq p_{2} < 1, j: = 0.$

Step 1. Compute $\Phi_{j}: = \Phi(y_{j})$ and $J_{j}: = J(y_{j})$, which is the Jacobi of the function $\Phi(y_{j})$. If $\Psi(y_{j})\leq \varepsilon$, stop. Otherwise, go to Step 2.

Step 2. Set $\lambda_{j}: = \mu_{j}\lVert \Phi_{j}\rVert^{\delta_{j}}$, where $\delta_{j}$ is such that

Step 3. Solve the equation such that

to obtain $d_{j_{1}}$.

Step 4. Solve the equations such that

to obtain $d_{j_{2}}$ and set $d_{j} = d_{j_{1}}+d_{j_{2}}.$

Step 5. Compute $r_{j} = \frac{Are d_{j}}{Pre d_{j}}$, where

Step 6. If $r_{j} > p_{0}$, set $y_{j+1} = y_{j}+d_{j}$, else $y_{j+1}: = y_{j}$.

Step 7. Update the parameter $\mu_{j}$ as follows:

Then, set $j: = j+1$, and go to Step 1.

Remark 3.1. The two-step LM method was proposed by Fan to solve nonlinear equations ^[29]. Different from the algorithm referenced in ^[29], a self-adaptive adjusting strategy is adopted for the LM parameter $\lambda_{j}\in (0, 2]$ to ensure that the LM step is not small, even if $\lambda_{j}$ is too large, which has proven its effectiveness during numerical evaluations.

3.2.   Convergence of Algorithm 3.1

By virtue of Theorem 2.2, we conclude that $\Phi(.)$ and its Jacobi $J(.)$ are Lipschitz continuous in $U$, where the solution set $X\subset U$. To study the global convergence, suppose there exist positive constants $L_{1}$ and $L_{2}$ such that

and

Then, by the Lipschitzness of the Jacobi, there is

based on which and Theorem 2.3 in Ref. ^[26], we obtain the sequence generated by Algorithm 3.1 converges to the stationary point of the merit function.

Theorem 3.1. (Global convergence) Algorithm 3.1 either terminates in finite iterations or satisfies $\lim\limits_{j\rightarrow \infty}$$\lVert J_{j}^{\rm T}\Phi_{j}\rVert = 0$.

Next, we give the local convergence rate of Algorithm 3.1 under the local error bound condition.

Suppose $\overline{y}_{j}\in X$, where $X$ is the solution set of Eq (2.3), the singular value decomposition (SVD) of $J(\overline{y}_{j})$, denoted as $\overline{J}_{j}$, is such that

where $\overline{\Sigma}_{j, 1} = diag(\overline{\sigma}_{j, 1}, ..., \overline{\sigma}_{j, r})$ with $\overline{\sigma}_{j, 1}\geq\overline{\sigma}_{j, 2}\geq...\geq\overline{\sigma}_{j, r} > 0.$ Similarly, the SVD of $J(\overline{y}_{j})$ denoted as $J_{j}$, is such that

where $\Sigma_{j, 1} = diag(\sigma_{j, 1}, ..., \sigma_{j, r})$ with $\sigma_{j, 1}\geq\sigma_{j, 2}\geq...\geq\sigma_{j, r} > 0,$ and $\Sigma_{j, 2} = diag(\sigma_{j, r+1}, ..., \sigma_{j, r+q})$ with $\sigma_{j, r+1}\geq\sigma_{j, r+2}\geq...\geq\sigma_{j, r+q} > 0$, when we neglect the subscription $j$ in $\Sigma_{j, i}$, $U_{j, i}$, and $V_{j, i}, i = 1, 2, 3$ for convenience, there is

Furthermore, there is

Assumption 3.1. $\lVert \Phi\rVert$ provides a local error bound on some neighborhood of $\bar{y}\in X$, i.e., there exists constants $c_{1} > 0$ and $b_{1} < 1$ such that

where ${\rm{dist}}(y, X) = \inf\limits_{ y\in X}\lVert y-\bar{ y}\rVert$ and $N(\bar{ y}, b_{1})$ is a neighborhood of $\bar{y}$.

Remark 3.1. The local error bound condition is weaker than the nonsingularity. Actually, if $J_{j}$ is nonsingular at a solution of (2.3), the solution is an isolated one, $\lVert \Phi_{j}\rVert$ provides a local error bound on its neighborhood ^[29].

Lemma 3.2. The Jacobi $J$ is Lipschitz constinous on $N(\bar{ y}, b_{1})$, which is a neighborhood of $\bar{y}\in X$, i.e.,

Moreover, there is

Proof. It is obvious by virtue of Theorem 2.2, we omit the proof here. □

Lemma 3.3. ^[29] Suppose $y_{j}, z_{j}\in N(\overline{y}_{j}, \frac{b_{1}}{2}), \overline{y}_{j}\in X$.

(ⅰ) There exists a positive constant $M > m > 0$ such that $\mu_{j}\leq M$ for $j$ large enough.

(ⅱ) There are positive constants $c_{2}, c_{3}, c_{4}$ such that

a) $\lVert U_{1}U_{1}^{\rm T}\Phi_{j}\rVert\leq c_{2}\lVert \overline{y}_{j}-y_{j}\rVert^{2}$;

b) $\lVert U_{2}U_{2}^{\rm T}\Phi_{j}\rVert\leq c_{3}\lVert \overline{y}_{j}-y_{j}\rVert^{3}$;

c) $\lVert U_{3}U_{3}^{\rm T}\Phi_{j}\rVert\leq c_{4}\lVert \overline{y}_{j}-y_{j}\rVert^{3}$.

(ⅲ) There are positive constants $c_{5}, c_{6}, c_{7}$ such that

a) $\lVert U_{1}U_{1}^{\rm T}\Phi_{j}(z_{j})\rVert\leq c_{5}\lVert \overline{y}_{j}-y_{j}\rVert^{2}$;

b) $\lVert U_{2}U_{2}^{\rm T}\Phi_{j}(z_{j})\rVert\leq c_{6}\lVert \overline{y}_{j}-y_{j}\rVert^{3}$;

c) $\lVert U_{3}U_{3}^{\rm T}\Phi_{j}(z_{j})\rVert\leq c_{7}\lVert \overline{y}_{j}-y_{j}\rVert^{3}$.

Theorem 3.2. (Local convergence) Under the conditions of Assumption 3.1, the sequence generated by Algorithm 3.1 cubically converges to some solutions of (2.3).

Proof. Suppose $y_{j}, z_{j}\in N(\overline{y}_{j}, \frac{b_{1}}{2}), \overline{y}_{j}\in X$. We divide the proof into three parts.

(ⅰ) We start the proof by proving $\lVert \lambda_{j}\Sigma_{1}^{-1}\rVert$ and $\lVert \lambda_{j}\Sigma_{1}^{-1}\rVert$ are bounded. Recalling the SVD of $J_{i}$, there is

Then, we have the following:

which is based on the theory of a matrix perturbation ^[29] and the Lipschitzness of $J_{j}$, and yields

Since ${y_{j}}$ converges to the solution set $X$ based on the global convergence, suppose $\lVert \overline{y}_{j}-y_{j}\rVert\leq\frac{\sigma}{2}$ for $j$ large enough. Then, it follows from (3.4) that

Furthermore, combining that $1 < \delta_{j}\leq 2$ for $j$ large enough, we have the following

which implies that

(ⅱ) Next, we show that $\lVert \Phi_{j}(y_{j})+J_{j}d_{j_{2}}\rVert\leq O\lVert \overline{y}_{j}-y_{j}\rVert^{3}$.

Combing (3.5), (3.6), Lemmas 3.2 and 3.3, we have

Moreover, since $\delta_{j}\in (1, 2]$ for $j$ is large enough, there is

(ⅲ) We provide the proof of the conclusion. Denote $z_{j} = y_{j}+d_{k_{1}}$. Since

and $\lVert d_{j_{1}}\rVert \lVert d_{j_{2}}\rVert\leq O(\lVert \overline{y}_{j}-y_{j}\rVert)^{3}$ by virtue of the SVD of $J_{i}$, we have the following

which implies the conclusion. □

Remark 3.3. The proof of Theorem 3.2 is similar to Theorem 3.6 in Ref. ^[29]. However, $\delta_{i}\in (0, 2]$ is adaptive here, and $\delta\in [1,2]$ is a constant in ^[29]. It is worth mentioning that Algorithm 3.1 has the local cubic convergence, which is better than Newton method.

4.   Numerical evaluation

In this section, we consider a smart grid system in a small area to illustrate the effectiveness of the two-step smoothing Levenberg-Marquardt method (SLM).

Divide a day into $24$ time slots with one hour for one slot, (i.e., $K$ = 24). Set $a_{j} = 0.01, b_{j} = c_{j} = 0$ in the cost function, and $\tilde{K} = 50, \omega_{0}(k)\in rand(0, 5)$ in the initial function. Set $\varepsilon = 1.0e-6, m = 1.0e-6, \mu_{0} = 0, p_{0} = 0.0001, p_{1} = 0.25, p_{2} = 0.75.$

Consider $N = 10$, namely $10$ users. The electricity demand $x_{j}(0)$ was chosen randomly from $[5,16], j = 1, 2, ..., 10.$. First, we compared the price and the social benefit at different times based on the present method with the traditional fixed method ^[24], where $\lambda_{j} = \max{(w_{j}(.))}-(\alpha_{j} L_{j}(.))/N$. The numerical results are shown in Figure 4.1(a), (b). Then, we adopted the approximating parameters $\mu = 0.1, \mu = 0.01$ respectively in the smoothing quasi-Newton method ^[13], and compared the real-time prices with that obtained from the two-step SLM method. The numerical results are shown in Figure 4.2(a), (b).

In Table 4.1, we adopted $N = 5, N = 10, N = 20, N = 50, N = 100$ and compared the CPU time to obtain the optimal prices between the one-step SLM and the two-step SLM at the time slots $k = 5, k = 10, k = 15, k = 20$.

From Figure 4.1(a), (b), it can be seen that the social benefit obtained by the proposed method is similar to that obtained by the fixed electricity price method. However, the electricity price calculated by the proposed method is approximately $50\%\sim70\%$ lower, which is meaningful for users to reduce their electricity consumption.

From Figure 4.2(a), (b), we find that the smaller $\mu$ is, the more approximate to the one obtained by the present algorithm. When the approximating parameter is adopted as $\mu = 0.1$, the price is a little higher than that obtained by the proposed algorithm. When the approximating parameter is adopted as $\mu = 0.01$, the price obtained tends more to coincide, which means that the proposed algorithm is more accurate and effectiveness.

From Table 4.1, we obtained that the CPU time of the present algorithm is approximately $0.25s\sim 0.65s$ than the one-step SLM method when $N = 5$ at $k = 5,$ $k = 10$, where we obtained the iterative direction by solving one LM equation. However, when the number of the users is greater, the CPU time is less than that of the one-step smoothing method. For example, take $N = 100,$ $k = 5$, the cpu time of the two-step method is $30\%$ less than the one-step method. The proposed algorithm is more suitable for large scale users.

5.   Conclusions

By transforming the social welfare maximization model into a smooth system of equations, we present a two-step LM method with the global convergence and the cubic locally convergence in this paper, which could compute the optimal electricity consumption for users, price and production for the electricity provider at the beginning of each time slot in a smart grid. It could be seen that the peak electricity ranges from $10:00$ to $13:00$, and $19:00$ to $21:00$ every day, users can turn off something that is not required and use more electricity appliances during periods of low prices, which is beneficial to peak cutting and valley filling. However, only one class of users and one electricity supply is considered here. The effectiveness of the present algorithm for multiple types of users and supplies will be discussed in our future topic.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by National Science Foundation of China (no.12101198).

Conflict of interest

All authors declare no conflicts of interest in this paper.