Dynamical analysis of an ecological aquaculture management model with stage-structure and nonlinear impulsive releases for larval predators

1.   Introduction

Fishery is a crucial industry that provides food for humanity and plays a significant role in the national economic development ^[1]. However, in recent years, the lack of comprehensive planning for fishery development and the mismanagement of marine resources have led to a drastic decline in fish populations ^[2,3,4]. For example, the Yangtze finless porpoise, sawfishes, and horseshoe crabs have been listed as endangered species due to excessive fishing. However an appropriate harvesting strategy can maintain the sustainable survival of the population such as the summer fishing moratorium policy implemented in the East China Sea, Yellow Sea, and other sea areas in China, and fishing operations are prohibited during specific time periods, allowing marine fishery resources to recuperate and rest. This promotes the stability of the marine ecosystem and the sustainable development of the fishery. Therefore, it is imperative to investigate the sufficient conditions for the sustainable survival of populations under moderate harvesting. However, biological systems are composed of numerous interacting components, and interactions such as competition and predation among biological individuals will lead to the model showing complex dynamic behaviors. In addition, human activities, such as excessive fishing, greatly disturb the biological system, making the system more complex. These realistic factors make the system become difficult to control.

An effective way to make the system controllable is to carry out appropriate intervention on it, and regulate the parameters of the system to make it favorable. Mathematical modeling is an effective tool to seek the appropriate range of intervention by turning complex biological problems into a mathematical problem with the help of mathematical modeling. Through reasoning and analysis of the model, the impact of human intervention on the biological system can be predicted, and we can get an intervention strategy that is beneficial to the biological system. The government and relevant practitioners can formulate reasonable strategies in line with the development of the aquaculture system according to the mathematical results and effectively predict and control the trend of the ecosystem.

To explore the influence of human activities on biological system, many models are formulated to study the impact of harvesting effects. For instance, many researchers ^[5,6,7,8] have developed and analyzed continuous harvesting models using ordinary differential equations. They have identified optimal harvesting strategies in predator-prey models incorporating factors such as ratio-dependent growth, disease, refuge availability, and nonlinear prey harvesting. Additionally, researchers ^[9] have investigated a Lotka-Volterra kind of model involving two prey species and one predator, with the predator population being subjected to harvesting. Other researchers ^[10] explored a predator-prey system featuring Michaelis–Menten type predator harvesting. They researched positive fixed point's stability of the system and rigorously analyzed the existence of saddle–node bifurcation and transcritical bifurcation. There are many scholars that use ordinary differential equations to perform related studies, such as ^{[11,12,13,14,15]}. These works have deepened our comprehensive to predator-prey models with harvesting.

In the aforementioned models, the authors consistently focus on continuous harvesting. However, in biological resource management, harvesting practices are often periodic and impulsive. For instance, fishing allows for the harvesting of fish at their peak economic value during the appropriate stage of production. Furthermore, by fishing in accordance with the demand cycle for different specifications of aquatic products in the market, it is possible to more effectively meet market supply needs ^{[16,17,18,19]}. Therefore, many scholars used pulses to depict this periodic phenomenon. The study on the global stability and persistence for impulsive harvesting models were conducted by ^{[20,21,22,23,24]}. Moreover, given the resource limitation, the researchers in ^[25] proposed a pest management model using biological control, in which natural enemies are released using a nonlinear impulsive method.

$x(t), y(t)$ stand for the densities of prey and predator populations at time $t$ respectively. $\tau$ denotes the pulse period. The function $g(x(t))$ represents the intrinsic growth rate of $x(t)$, and $p(x(t))$ denotes the response function of the predator. $c > 0$ is the rate of conversing prey into predator, and $D > 0$ is the death rate of the predator. $0\leq\delta < 1$ represents the maximal fatality rate, and $h > 0$ is a half saturation constant for the prey. $\theta\geq0$ is a shape parameter, $\lambda > 0$ denotes the release amount of $y(t)$, and $\frac{\lambda}{1+\theta y(t)}$ indicates the predator's release amount dependents on their populations. Reasonable utilization of resource is one of the core points of ecological aquaculture ^[26,27]. Compared to the traditional linear impulse release, the nonlinear impulse release $\frac{\lambda}{1+\theta y(t)}$ can avoid the excessive use and waste of resources, it reflects the rational utilization of resources, and highly conforms to the concept of sustainable development emphasized in ecological aquaculture.

However, only a few studies have considered adding nonlinear impulsive control and the stage structure of the population simultaneously to the ecological aquaculture modeling. Aquatic organisms typically undergo a process of growth and development, from immaturity to maturity. Different stages of aquatic organisms exhibit distinct physiological functions. For example, the juveniles of both octopus and sea bass are deficient in effective predatory capabilities, and the juveniles of aquatic animals generally do not possess reproductive competence. In addition, the mature fish always hold greater economic value in the fishing industry compared to immature fish. Therefore, it is typical to rear immature fish while harvesting mature ones. Thus, considering the stage structure of fish is helpful to assess the long-term impact of farming activities on water resources and the ecological environment. The amount and nature of the excreta and metabolites of fish at different stages are different, and the impact on water quality and ecological balance is also different. For instance, in the process of eel farming, the waste produced in the larval stage is relatively less, while the excrement in the adult stage increases. Through the consideration of the stage structure, water treatment facilities can be optimized to achieve the sustainable development of aquaculture. Consequently, investigating the survival dynamics of populations with stage-structured characteristics is more practical and has undeniable importance for realizing the maximization of economic benefits and promoting sustainable development.

On the basis of the considerations mentioned above, we develop a novel ecological aquaculture management model that integrates: (ⅰ) The predator of a system that possesses stage-structure; and (ⅱ) the larval predator in the system is released using impulsive nonlinear releasing. The structure of this paper is as follows: In Section 2, we present the formulation of our mathematical model. In Section 3, we introduce and prove key lemmas that are essential for subsequent analysis. In Section 4, we discuss the prey-vanishing periodic solution's stability and the conditions for prey-predator cohabitation, respectively. Section 5 is dedicated to numerical simulations. Finally, we give our conclusions in Section 6.

2.   Model formulation

First, we use $x(t)$ to represent the density of prey population at time $t$, and we suppose that the prey population follows the Logistical growth in the environment without predators, that is $\frac{dx}{dt} = rx(1-\frac{x}{K})$, where $r > 0$ denotes the prey's growth rate and $K > 0$ is the environmental capacity. The classic predator-prey model is

where $b > 0$ is the mortality of predator, and $k > 0$ is the rate of conversing prey into mature predators. In this paper, we divide the predator population $y(t)$ into the immature group $y_1(t)$ and the mature group $y_2(t)$. Thus, $y(t) = y_1(t)+y_2(t)$. We assume that the immature predators are young or they are fish roe so that they do not eat the prey. Since fish are vertebrates, the reaction function that conforms to the predation of vertebrates in biological literature is Holling type Ⅱ, that is $p(x) = \frac{\beta x}{1+\alpha x}(\alpha > 0, \beta > 0)$. Considering the predator population with Holling type Ⅱ functional response and the stage-structure of predators, we establish the following kind of a prey-predator system with stage structure for the predator population:

where $c > 0$ is the conversion rate of predator larvae to adults.

We assume the harvesting for mature predators at each time point $n\omega$, at which the immature predators are released simultaneously, where $\omega > 0$ represents harvesting period of mature predators and releasing period of immature predators, $n\in Z^+$. Moreover, the nonlinear function is employed to depict the release for immature predators given the resource limitation, i.e., we choose

where $\frac{u_{max}}{1+\theta y_1(t)}$ ($\theta > 0$, $u_{max}$ is the maximum release amount of larval predators and $u_{max} > 0$) represents the release amount depends on the number of the immature predator, when $y_1(t)\rightarrow0, \; \frac{u_{max}}{1+\theta y_1(t)}\rightarrow u_{max},$ when $y_1(t)\rightarrow +\infty, \; \frac{u_{max}}{1+\theta y_1(t)}\rightarrow0$. $0 < h < 1$ denotes the harvest proportion of the mature predator.

With the control measures displayed as the (2.2) and model (2.1) taken into account. Let $\triangle y_1(t) = y_1(t^+)-y_1(t)$, $\triangle y_2(t) = y_2(t^+)-y_2(t)$. We establish following ecological aquaculture management model with stage-structure and impulsive nonlinear releasing larval predators:

This model accurately reflects the predation relationship in the ecological aquaculture system. Compared with the previous models, we have simultaneously considered the stage structure of the population and the nonlinear impulse releasing strategy to reduce resource waste.

3.   The lemmas

Let $R_+$ = $[0, \infty)$, $R_+^3 = \{X\in R^3:X\geq0\}$. $X(t) = (x(t), \; y_1(t), \; y_2(t))^{'}:R_+\rightarrow R_+^3$ is the solution of system (2.3) and it is piecewise continuous. Here $f$ is the map defined by the right hand of system (2.3). According to ^[28], the smoothness of $f$ ensures that the solutions of system (2.3) possess global existence and uniqueness.

Lemma 3.1. Positivity of the solutions.

Suppose $X(0^+)\geq0$, $X(t) = (x(t), \; y_1(t), \; y_2(t))^{'}$ is a solution of (2.3) corresponding to the original value $X(0^+)$, then $x(t)\geq0, y_1(t)\geq0, y_2(t)\geq0$ for $\forall t\geq0$. Further, $x(t) > 0, y_1(t) > 0, y_2(t) > 0$ if $X(0^+) > 0$.

Proof. For $x(t)$, because $x(t)$ is continuous, we can get

Using the non-negative of the exponential function, we can know the positivity of $x(t)$ depends on the $x(0^+)$.

For $y_1(t)$, because the impulsive release will increase the population of $y_1(t)$, we only need to consider the results without pulse. Then

Thus, the positivity of $y_1(t)$ depends on the $y_1(0^+)$.

For $y_2(t)$, $\forall t > 0$, $\exists n\in Z$, such that $t \in(n \omega, (n+1)\omega].$ The following is a mathematical induction of $n$.

(1) $n = 0$, we suppose that $\exists t_1 \in (0, \omega]$ such that $y_2(t_1)\leq0.$ Let $t_1$ be the minimum time when $y_2(t) = 0$ in $(0, \omega]$. That is $\forall t\in (0, t_1)$, we have $y_2(t)\neq 0$. According to $y_2(0^+) > 0$ and the continuity of $y_2(t)$ on $(0, \omega)$, then $y_2(t) > 0, t\in(0, t_1).$ We notice that

and $\frac{d{y_2}(t)}{dt}$ is continuous at $t_1$. Thus, $\exists \delta_1 > 0$, such that $\forall t\in(t_1-\delta_1, t_1)\subset(0, t_1),$ $\frac{d{y_2}(t)}{dt} > 0$.

That is $y_2(t) < y_2(t_1) = 0$, $t\in(t_1-\delta_1, t_1)$. This is contradictory. So, $y_2(t) > 0, t\in(0, \omega].$

(2) Suppose the conclusion holds when $n = k$.

Similar to the treatment of (1), we are able to obtain the conclusion when $n = k+1$. Therefore, from mathematical induction, we have $y_2(t) > 0, \forall t > 0$. This proof is complete. □

Lemma 3.2. Eventual consistent boundedness of solutions. For all solutions of system (2.3), $\exists U > 0$ satisfies that $x(t)\leq U$, $y_1(t)\leq U$, $y_2(t)\leq U$ when $t$ is large enough.

Proof. Suppose $X(t) = (x(t), y_1(t), y_2(t))^{'}$ is a solution of (2.3). Let $V(t) = kx(t)+y_1(t)+y_2(t)$, then we can get

clearly, first equation can be limited by a positive number when $0 < \ell < b$, and the second equation can be enlarged to $V(n\omega)+u_{max}$. So, $\exists\ell_0, \; G_0 > 0$, such that

We examine the comparative system:

through simple calculation, we can get

using the comparison theorem in ^[28], then

$V(t)$ can be limited by a positive constant. So, $\exists U > 0$, for all solutions of system (2.3), we have $x(t)\leq U$, $y_1(t)\leq U,$ $y_2(t)\leq U$ when $t\rightarrow \infty$.

Suppose the prey becomes extinct, then the following subsystem can be acquired as

□

Lemma 3.3. The periodic solution of subsystem (3.4) is $\widetilde{y(t)} = (\widetilde{y_1(t)}, \widetilde{y_2(t)})^{'},$

where

and all solutions $y(t) = (y_1(t), y_2(t))^{'}$ of system (3.4) satisfy $\lvert y_1(t)-\widetilde{y_1(t)}\rvert\rightarrow0$, $\lvert y_2(t)-\widetilde{y_2(t)}\rvert\rightarrow0\; (t\rightarrow \infty).$

Proof. According to ^[25], system

exists unique periodic solution $\widetilde{y_1(t)}$ and it is globally asymptotically stable. Thus all solutions $y_1(t)$ of system (3.4) have $\lvert y_1(t)-\widetilde{y_1(t)}\rvert\rightarrow0.$ For all solutions of system (3.4), $\frac{d{y_2}(t)}{dt} = cy_1(t)-by_2(t), \frac{d{\widetilde{y_2}}(t)}{dt} = c\widetilde{y_1(t)}-b\widetilde{y_2(t)}.$ So, $\frac{d(y_2(t)-\widetilde{y_2(t)})}{dt} = c(y_1(t)-\widetilde{y_1(t)})-b(y_2(t)-\widetilde{y_2(t)}).$ Let $W(t) = y_2(t)-\widetilde{y_2(t)}$, we have

Because $\lvert y_1(t)-\widetilde{y_1(t)}\rvert\rightarrow0,$ $\forall\varepsilon > 0$, $-c\varepsilon-bW(t)\leq W^{'}(t)\leq c\varepsilon-bW(t)$ for any $n$ large enough, where $t\in(n\omega, (n+1)\omega]$. Further, we can get

for any $n$ large enough. That is $\frac{-c\varepsilon}{b(1-h)}\leq W(t)\leq \frac{c\varepsilon}{b(1-h)}$ for any $t$ large enough. Let $\varepsilon\rightarrow0$, we get $W(t)\rightarrow0$, which is $\lvert y_2(t)-\widetilde{y_2(t)}\rvert\rightarrow0,$ as $t\rightarrow \infty$. We complete the proof. □

For convenience, we suppose conditions as

(H1)

(H2)

(H3)

4.   The dynamics

Theorem 4.1. If satisfy condition $(H1)$, the periodic solution of prey-vanishing $(0, \widetilde{y_1(t)}, \widetilde{y_2(t)})^{'}$ of system (2.3) is locally asymptotically stable. If satisfy condition $(H2)$, the periodic solution of prey-vanishing $(0, \widetilde{y_1(t)}, \widetilde{y_2(t)})^{'}$ of system (2.3) is global attraction.

Proof. Defining $O(t) = x(t),$ $P(t) = y_1(t)-\widetilde{y_1(t)},$ $Q(t) = y_2(t)-\widetilde{y_2(t)}$, thus we can get the system:

Further, we obtain the linear system by Taylor expansion:

That is

and

Through simple calculation, the basic solution matrix of (4.3) can be obtained:

and the monodromy matrix of system (4.3) with respect to $\Phi(t)$ is as follows:

The eigenvalues of $\mho$ determine the stability of $(0, \widetilde{y_1(t)}, \widetilde{y_2(t)})^{'}$, and the $*$ in the matrix $\mho$ can't influence it's eigenvalues. The eigenvalues of $\mho$ are $\lambda_1 = e^{\int_{0}^{\omega}[r-\beta\widetilde{y_2(t)}dt]}$, $\lambda_2 = e^{-(c+b)\omega} \left[1-\frac{\theta u_{max}}{(1+\theta \widetilde{y_1(\omega))^2}}\right]$ and $\lambda_3 = (1-h)e^{-b \omega}$. According to the Floquet theory ^[28] and condition $(H1)$, we can get $\lvert \lambda_1 \rvert < 1$, $\lvert \lambda_2 \rvert < 1$ and $\lvert \lambda_3 \rvert < 1$. Therefore, $(0, \widetilde{y_1(t)}, \widetilde{y_2(t)})^{'}$ is locally asymptotically stable.

Next, we demonstrate the global attractiveness of the solution. We find that $\frac{d{y_2}(t)}{dt}\geq cy_1(t)-dy_2(t)$, then we examine the comparative system:

By using Lemma 3.3 and comparison theorem, we can get:

when $t$ is large enough. For avoiding the trouble brought by too many symbols, we suppose (4.7) be valid for $t\geq 0$. According to the system (2.3), we observe that

Hence, we examine the comparative system

then we can get $x(t)\leq m(t)$. $m(t)$ is the solution of Eq (4.8). We can easily calculate that $m(t) = \frac{1}{\frac{1}{K}(1-e^{-rt})+\frac{1}{m(0^+)}e^{-rt}}$, $m(t)\rightarrow K$ as $t\rightarrow \infty$. Thus, $x(t)\leq K$ when $t$ is large enough. We suppose that $0 < x(t)\leq K$ for all $t\geq0$. According to condition $(H2)$, using local sign preserving theorem of limit, we can select $\varepsilon > 0$, such that

By observing the system (2.3), we can get

We examine the system:

through simple calculus, we can get

We get $x((n+1)\omega^+)\leq x(n\omega^+)\rho$, for all $n \in Z^+$. So, $x(n\omega^+)\leq x(0^+) \rho^n$. we can derive $x(n\omega^+)\leq x(0^+) \rho^n \rightarrow0$, as $t\rightarrow \infty$. Therefore $x(t)\rightarrow0$, as $t\rightarrow \infty$.

Afterwards, we demonstrate $y_1(t)\rightarrow \widetilde{y_1(t)}$, $y_2(t)\rightarrow \widetilde{y_2(t)}$. Using the definition of the limit, we can get $\forall0 < \varepsilon < \frac{b}{k\beta}$, $\exists t_0 > 0$, $\forall t\geq t_0$, $0 < x(t) < \varepsilon$ is valid. We suppose that $0 < x(t) < \varepsilon$ for $\forall t\geq 0$. Then, according to system (2.3), we can observe that

then, it can be obtained $\varphi_1(t)\leq y_1(t) \leq \hat{\varphi}_1(t)$, $\varphi_2(t)\leq y_2(t) \leq \hat{\varphi}_2(t)$, and $\varphi_1(t)\rightarrow \widetilde{y_1(t)}$, $\varphi_2(t)\rightarrow \widetilde{y_2(t)}$, $\hat{\varphi}_1(t)\rightarrow \widetilde{\hat{\varphi}_1(t)}, \hat{\varphi}_2(t)\rightarrow \widetilde{\hat{\varphi}_2(t)}$, as $t\rightarrow \infty$. $\varphi(t) = (\varphi_1(t), \varphi_2(t))^{'}$ is the solution of

and $\hat{\varphi}(t) = (\hat{\varphi}_1(t), \hat{\varphi_2}(t))^{'}$ is the solution of

Where

and

$y_1^*$ is defined by (3.6). Then, $\forall\varepsilon_1 > 0$, $\exists t_1 > 0$, $\forall t > t_1$

Let $\varepsilon\rightarrow0$,

for $\forall t > t_1$, which implies $y_1(t)\rightarrow \widetilde{y_1(t)}$, $y_2(t)\rightarrow \widetilde{y_2(t)}$, as $t\rightarrow \infty$. This proof is complete. □

Thereafter, we examine the persistence of system (2.3). We first present the definition of system persistence.

Definition 4.1. We state a system (2.3) is persistent, if $\exists l, \; L > 0, \; \forall X(0^+) > 0\; \exists T_0 > 0, \; \forall X(t) = (x(t), y_1(t), y_2(t))^{'},$ we always can get $l\leq x(t)\leq L, l\leq y_1(t)\leq L, l\leq y_2(t)\leq L$ for all $t\geq T_0$. Where $X(t)$ is the solutions of system (2.3) corresponding to the original value $X(0^+)$.

Theorem 4.2. If condition $(H3)$ holds, system (2.3) is permanent.

Proof. Let $X(t)$ is a solution of system (2.3) corresponding to the original value $X(0^+) > 0$. By Lemma 3.2, we have demonstrated $\exists U > 0$ such that $x(t)\leqslant U, y_1(t)\leqslant U, y_2(t)\leqslant U$ when $t$ is large enough. From (4.7), we know $y_1(t)\geq\widetilde{y_1(t)}-\varepsilon, y_2(t)\geq\widetilde{y_2(t)}-\varepsilon$ when $t$ is large enough, where $\varepsilon > 0$. Thus

when $t$ is large enough. So, we only need to examine the lower bound of $x(t)$. Next, we will proceed in two steps.

Step1. According to the condition $(H3)$, $\exists m_3 > 0$, $\varepsilon_1 > 0$ such that

where

The reasons are as follows. Because $\sigma\rightarrow r\omega-\beta\left[\frac{y_1^*+y_2^*}{b}(1-e^{-b\omega})-\frac{By_1^*}{c+b}\right] > 0$, when $m_3\rightarrow 0$ and $\varepsilon_1\rightarrow 0$. Then according to the local sign preserving theorem of limit, we can always find $m_3$ and $\varepsilon_1$ that make the $\sigma > 0$ hold.

For the above $m_3$, we will prove that $\exists t_2 > 0$ such that $x(t_2)\geq m_3$. We use the method of contradiction and suppose that the proposition is not tenable. That is $x(t) < m_3,$ for any $t > 0$. Checking the comparative system:

According to the Lemma 3.3, we can obtain that $y_1(t)\leq \xi_1(t)$, $y_2(t)\leq \xi_2(t)$ and $\xi_1(t)\rightarrow \overline{\xi_1(t)}$, $\xi_2(t)\rightarrow \overline{\xi_2(t)}$, $t\rightarrow \infty$, where$(\xi_1(t), \xi_2(t))^{'}$ is the solution of (4.17).

Where

and

$y_1^*$ is defined by Eq (4.13). Therefore, we find a $t_1 > 0$ satisfies

and

for $t>T_1$. Let $N_1 \in N and N_1 \omega>T_1$, integrating (4.20) on $(n\omega, (n+1)\omega], n\geq N_1$, we get

then, $x((N_1+k)\omega)\geq e^{k\sigma}x(N_1\omega^+)\rightarrow \infty\; (k\rightarrow \infty)$. This is contrary to the boundedness of $x(t)$. Hence, $\exists t_2>0$ such that $x(t_2)\geq m_3$.

Step2. If $x(t)\geq m_3 for t>t_2$, only need to let $l = min\{m_2, \acute{m_2}, m_3\}$, then our proof is complete. If $\exists\acute{t}>t_2$ in such way that $x(\acute{t}) < m_3$, let $\overline{A} = \{t:t>t_2, x(t) < m_3\}$. Then $\overline{A}$ is not empty and has a lower bound $\acute{t}$, according to the supremum principle, $t^* = inf\overline{A} = inf\{t:t>t_2, x(t) < m_3\}$ exists. According to the continuity of $x(t)$, we have $x(t^*) = m_3$.

For above $t^*$, $\exists \vartheta_1\in Z$, such that $t^*\in (\vartheta_1\omega, (\vartheta_1+1)\omega]$. For above $\vartheta_1\in z$, we select $\vartheta_2$, $\vartheta_3\in Z^+$, such that

where $\sigma_1 = r(1-\frac{m_3}{K})-\beta U < 0$, $\xi_2^*$ is defined by Eq (3.6). Next, we assert that $\exists t_3\in(t^*, (\vartheta_1+\vartheta_2+\vartheta_3+1)\omega]$, such that $x(t_3)\geq m_3$. Otherwise $x(t) < m_3$, $t\in(t^*, (\vartheta_1+\vartheta_2+\vartheta_3+1)\omega]$. Consider (4.17) with $\xi_2((\vartheta_1+1)\omega^+) = y_2((\vartheta_1+1)\omega^+)$, we have

where $t\in (n\omega, (n+1)\omega]$, then,

where $\vartheta_1+1 \leq n\leq \vartheta_1+\vartheta_2+\vartheta_3$. Thus $y_2(t)\leq \xi_2(t) \leq \overline{\xi_2(t)}+\varepsilon_1,$ $(\vartheta_1+1+\vartheta_2)\omega \leq t\leq (\vartheta_1+1+\vartheta2+\vartheta_3)\omega$.

This indicates (4.20) is valid for $(\vartheta_1+1+\vartheta_2)\omega \leq t\leq (\vartheta_1+1+\vartheta_2+\vartheta_3)\omega$. According to the (4.21), we get

System (2.3) gives $\frac{d{x}(t)}{dt}\geq x(t)[r(1-\frac{m_3}{K})-\beta U] = x(t)\sigma_1$. Integrating it on $(t^*, (\vartheta_1+\vartheta_2+1)\omega]$, then

Thus $x((\vartheta_1+1+\vartheta_2+\vartheta_3)\omega)\geq m_3e^{\sigma_1(\vartheta_2+1)\omega}e^{\vartheta_3\sigma} > m_3$, a contradiction. Let $\widetilde{A} = \{t:t\geq t^*, x(t)\geq m_3\}$, $\widetilde{t} = inf\widetilde{A}$. Then, we get $x(\widetilde{t})\geq m_3$. For $t\in(t^*, \widetilde{t}]$, by integrating $\frac{d{x}(t)}{dt}\geq x(t)\sigma_1$ on $[t^*, t)$, we have $x(t)\geq x(t^*)e^{\sigma_1(t-t^*)}\geq m_3e^{\sigma_1(n_2+n_3+1)\omega} = m_1$. Since $x(\widetilde{t})\geq m_3$, for the part where $t > \widetilde{t}$, we can perform the same process. Hence $x(t)\geq m_1$ for $\forall t\geq t_2$. We complete the proof. □

5.   Numerical simulations

In order to validate our theoretical findings, we will carry out numerical simulations in this part. We notice that

where

We select a series of fixed parameters as follows,

5.1.   The role of the maximum release amount $u_{max}$

First, setting $h = 0.5, u_{max} = 0.1$, we can calculate that

and

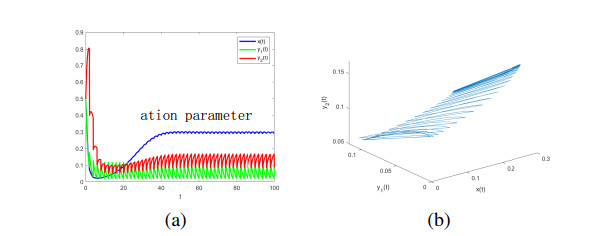
It follows from the conditions of Theorem 4.2, the system (2.3) is persistent as shown in Figure. 1.

Moreover, when we take maximum release amount $u_{max} = 0.5$, and keep the other parameters unchanged. Consequently,

and

According to the conditions of Theorem 4.1, the periodic solution of prey-vanishing of system (2.3) is globally asymptotically stable (see Figure 2).

5.2.   The role of harvesting proportion coefficient $h$

First, setting $u_{max} = 0.2$, $h = 0.7$, by calculating, we have

and

According to the conditions of Theorem 4.2, the system (2.3) is persistent (see Figure 3).

Similarly, we set $h = 0.1$ and remain other parameters remain unchanged. Then, we have

and

the periodic solution of prey-extinction of system (2.3) is globally asymptotically stable from Theorem 4.1 (see Figure 4).

From the above numerical simulations, we can increase the maximum release amount $u_{max}$ or decrease the harvest proportion coefficient $h$ may result in the vanishing of the prey in the system (2.3). The system (2.3) can persist when $u_{max}$ and $h$ take appropriate values.

To study how the nonlinear pulse $\frac{u_{max}}{1+\theta y_1(t)}$ affects the dynamical performance of the system (2.3), the bifurcation parameter graphs are used to reflect the impact of some specific parameters on the dynamical performance of the system. First, we select pulse period $\omega$ as the bifurcation parameter. We choose a series of parameters:

and let $\omega$ from 10 to 47, we obtain the bifurcation parameter diagrams (see Figure 5).

From the drawn bifurcation parameters diagrams, it can be seen that there are rich dynamical properties in the system (2.3), such as period doubling bifurcation, period halving bifurcation, chaos, and other complex phenomena. When $\omega$ increases form 10 to 36, there were three period-doubling bifurcations and period-reducing bifurcations in the system. When $\omega$ increases from 36 to 47, the dynamical properties of system (2.3) is period-doubling bifurcation $\rightarrow$ chaos $\rightarrow$ period-reducing bifurcation $\rightarrow$ period-doubling bifurcation $\rightarrow$ chaos $\rightarrow$ period-reducing bifurcation.

Next, we select the maximum release amount $u_{max}$ as the bifurcation parameter. Setting a series of parameters:

and let $u_{max}$ from 0.01 to 5, we obtain the bifurcation parameter diagrams (see Figure 6). We found that system (2.3) exhibits complex dynamical behavior. When $u_{max}$ increases from 0.01 to 0.31, complex chaotic phenomena appear in the system (2.3). When $u_{max} > 0.31$, the system enters stable $\omega$ periodic solutions. From the drawn bifurcation parameters, we found that the maximum release amount $u_{max}$ is very small, so the system will become difficult to control and predict. Moreover, when the release amount is relatively large, the dynamic behavior of the system will become controllable.

6.   Conclusions

We research the stability of a prey-vanishing periodic solution and the persistence of system (2.3) in Section 4. Through the Floquet theorem and analytical methods, we obtained the sufficient conditions for the solution's stability and system permanence. In Section 5, we verify our findings using softwares. By Theorem 4.1, if $r\omega < \beta\left[\frac{y_1^*+y_2^*}{b}(1-e^{-b\omega})-\frac{By_1^*}{c+b}\right]$, the prey-vanishing periodic solution of the system (2.3) is locally asymptotically stable. Regrettably, due to the limitations of existing mathematical tools, it is difficult to determine the local attraction domain of this periodic solution. From Theorems 4.1 and 4.2, we can see $\beta\left[\frac{y_1^*+y_2^*}{b}(1-e^{-b\omega})-\frac{By_1^*}{c+b}\right]$ is a threshold for persistence and extinction for prey populations. However this extinct threshold is a valid argument only at a local domain. Using numerical simulations, we research the effects of harvesting proportion coefficient $h$ and the maximum release amount $u_{max}$ on system (2.3), respectively. The numerical results showed that the system (2.3) can persist when $u_{max}$ and $h$ take appropriate values. Moreover, we showed that the system with nonlinear impulses has very complex dynamic properties such as chaos, period-doubling bifurcation, and period-reducing bifurcation by depicting bifurcation graphs that select $\omega$ and $h$ as bifurcation parameters, respectively. We found that if the parameter regulation is improper, that is, the artificial intervention strategy is improper, then the system will present complex dynamic behaviors, such as chaos, and thus become difficult to control. Additionally when we adopt an appropriate strategy, that is, to carry out artificial parameter regulation according to the conditions of Theorems 4.1 and 4.2, we can achieve the extinction and permanence of system populations.

In Theorem 4.2, we explored only the persistence of the system, so we were unable to further discuss whether the system would have positive periodic solutions. Thus we will utilize bifurcation theory to discuss this in the future. Future research could involve modifications to model (2.3), such as considering other functional response and exploring the effects of harvesting and releasing at distinct time points. In addition, the ecological systems in life are always affected by time delay. Considering time delay in the model will be more in line with the actual situation; this will be important research for us in the future.

In this paper, we analyzed a three-dimensional impulsive ecological aquaculture management model that incorporates: (ⅰ) The predator of a system that possesses stage-structure; and (ⅱ) the larval predator in the system are released using pulse nonlinear releasing. The sufficient conditions for coexistence between the prey and the predators and global stability of prey-vanishing periodic solutions are obtained using the Floquet theorem and other analytic tactics. Thus, we obtain the following principal results:

1) Solutions of system (2.3) are consistently and eventually bounded.

2) If system (2.3) satisfies condition $(H1)$, the periodic solution $(0, \widetilde{y_1(t)}, \widetilde{y_2(t)})^{'}$ of the system (2.3) is locally asymptotically stable.

3) If system (2.3) satisfies condition $(H2)$, the periodic solution $(0, \widetilde{y_1(t)}, \widetilde{y_2(t)})^{'}$ of the system (2.3) is globally asymptotically stable.

4) If system (2.3) satisfies condition $(H3)$, system (2.3) is permanent.

We employ numerical simulations to validate our findings. The country and aquaculture enterprises can formulate reasonable harvesting and releasing strategies with reference to these conditions to make the aquaculture ecosystem controllable. These results are expected to establish a theoretical basis for practical ecological aquaculture management.

Author contributions

Lin Wu: Conceptualization, formal analysis, writing – original draft; Zeli Zhou: Validation; Jianjun Jiao and Xiangjun Dai: Writing – review & editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This work was supported by National Natural Science Foundation of China (No.12261018), Universities Key Laboratory of Mathematical Modeling and Data Mining in Guizhou Province (No.2023013), Guizhou University of Finance and Economics Graduate Program (2024ZXSY233).

Conflict of interest

The authors declare no conflicts of interest.