Performance analysis of the convex non-convex total variation denoising model

1.   Introduction

Image denoising aims to reduce or eliminate the noise in the image degradation process while maintaining the basic features of the image ^[1]. Mathematically, the image degradation process can be expressed as

where $\theta^{*} \in \mathbb{R}^{n}$ is the original image, $y \in\mathbb{R}^n$ is the observed image, and $\varepsilon$ is the additive white Gaussian noise (AWGN) with variance $\sigma^{2}$, i.e., $\varepsilon\sim N(0, \sigma^{2}I_{n})$. The concept of total variation (TV) is a mathematical measure that quantifies the level of variation or change present in an image, measuring how rapidly the pixel intensities change across neighboring pixels. In cases where an image contains noise, its pixel intensities exhibit random fluctuations, resulting in high TV values. By minimizing the TV of an image while preserving crucial features such as edges and textures, we can effectively reduce noise and enhance its quality ^{[2,3,4,5,6,7]}. The standard TV estimator $\hat{\theta}$ can be mathematically defined as

where regularization parameter $\lambda > 0$ is used to control the trade-off between the fidelity term $\frac{1}{2n}||y-\theta||_{2}^{2}$ and the TV regularization $||\theta||_{TV}$. $n$ is the pixel size of the image. By introducing a first-order difference matrix $D\in {R}^{n\times n}$, the TV regularization $||\theta||_{TV}$ can be represented by the $\ell_1$ norm, i.e., $||\theta||_{TV} = ||D \theta||_1$.

Due to the convexity of the $\ell_1$ norm, the TV denoising model (1.2) possesses several advantages, such as having an objective function devoid of redundant local minima and ensuring a unique minimum. However, owing to the inherent property of biased estimation associated with the $\ell_1$ norm, this model may also underestimate the magnitude of signal discontinuity^[8,9,10].

The limitations of TV regularization can be overcome by employing non-convex TV regularization, which not only enhances image texture details but also sharpens edges more effectively ^[11,12,13]. This non-convex TV denoising model can be described as follows:

where $\Psi^{NC}(\cdot)$ is a non-convex function such as the $\ell_q$ norm with $0 < q < 1$^[14,15]. However, the cost function of (1.3) is usually non-convex and often has an extraneous local minimum, which brings challenges when solving.

Recently, Selesnick and Lanza et al. proposed a novel non-convex TV regularization for signal and image denoising ^[9]. This type of non-convex regularization enables the cost function to become convex by adjusting the non-convex control parameters, thereby addressing the limitations of TV regularization and avoiding unnecessary local minima in the cost function. The concept, later known as convex non-convex total variation (CNC-TV) ^[9,16,17], has been widely utilized in various fields such as medical image reconstruction^[18,19,20], fault diagnosis^[21,22], and computer vision ^[23,24]. The advantages of CNC-TV are twofold: First, the utilization of non-convex regularization not only effectively suppresses noise but also preserves image edge and texture information. Second, by adjusting the non-convexity control parameters, the global convexity of the objective function can be ensured, thereby enabling the attainment of the global optimal value through convexity optimization algorithms ^[25,26]. However, to the best of our knowledge, most of the research on CNC-TV focuses on algorithm design and applications, with a lack of theoretical analysis of performance such as ^[27]. This motivates us to conduct a thorough analysis on the performance of the CNC-TV estimator to substantiate that CNC-TV regularization surpasses TV regularization.

In this paper, we consider the following CNC-TV denoising model:

The matrix parameter $B$ in (1.4) not only controls the non-convexity of the non-convex regularization term $\Psi^{CNC}_B(D\theta)$, but also guarantees the global convexity of the cost function in (1.4).

Through rigorous theoretical analysis and comprehensive experimental evaluations, we show that the utilization of non-convex TV regularization significantly enhances the performance of the CNC-TV estimator, enabling accurate estimation of signal discontinuity. In summary, our contributions can be succinctly summarized as follows:

• Theoretically, for the CNC-TV denoising model, we first establish the conditions necessary to ensure global convexity of the cost function. Subsequently, by employing the oracle inequality, we derive an improved upper bound on performance compared to that of the standard TV denoising model.

• Algorithmically, we derive an ADMM algorithm that ensures convergence to a critical point for the proposed CNC-TV denoising model.

• Empirically, we demonstrate that the proposed CNC-TV denoising model outperforms the standard TV denoising model in both 1D and 2D denoising experiments, owing to its utilization of non-convex regularizations.

The paper is structured as follows. In Section 2, we present some preliminaries and related works related to non-convex TV regularization, performance analysis results, and convex optimization algorithms. In Section 3, we give a theoretical analysis of the performance of the CNC-TV denoising model and further propose an effective ADMM algorithm to solve it. The superiority of the proposed model is validated in Section 4 through both 1D and 2D denoising experiments. Finally, the conclusions are summarized in Section 5.

Notation: Throughout this paper, for a matrix $A$, $A^T$ and $A^{\dagger}$ represent its transpose and Moore-Penrose pseudo-inverse, respectively. $\sigma_{\text {max}}$ and $\sigma_{\text {min}}$ denote the maximum eigenvalue and minimum eigenvalue of matrix $A$. $\operatorname{ker}(A)$ and $\operatorname{ker}(A)^{\perp}$ denote the kernel space and orthogonal complement space of matrix $A$. Moreover, $0\prec A$ indicates that matrix $A$ is positive definite, while $0\preceq A$ implies that matrix $A$ is positive semi-definite. Then we use the symbol $\mathcal{O}(n)$ to indicate the efficiency or complexity of comparing different algorithms. For a set $T\subset\{1, 2, ..., n\}$, $|T|$ and $T^c$ denote its cardinality and complement. For $\theta \in \mathbb{R}^{n}$, its $\ell_1$ norm, $\ell_2$ norm, and $\ell_{\infty}$ norm can be defined as $\Vert \theta \Vert_1 = \sum_{i = 1}^{n} |\theta_i|$, $\Vert\theta \Vert_2 = \sqrt{\sum_{i = 1}^{n} \theta_i^2}$, and $\Vert\theta \Vert_{\infty} = \max_{1 \leq i \leq n} |\theta_i|$. For a function $f(\theta)$, we use $\nabla f(\theta)$ to denote the gradient or subdifferential of $f(\theta)$.

2.   Primary and related work

2.1.   Non-convex TV regularization

Standard TV denoising can be typically formulated as a convex optimization problem that incorporates an $\ell_1$ regularization term. However, it has a drawback in the sense that it tends to underestimate the magnitudes of abrupt changes in the signal. To address this limitation, non-convex $\text{TV}_q$ $(0 < q < 1)$ regularization is proposed, which can be expressed as $\Vert D \theta\Vert_q$ $(0 < q < 1)$ ^[14,15]. The effectiveness of edge preservation in $\text{TV}_q$ is further enhanced by incorporating non-convex sparse regularization. However, due to its non-convex nature, the $\text{TV}_q$ regularization introduces challenges in algorithm design as it may lead to convergence toward local optima^[28].

By leveraging the advantages of non-convex regularization and convex optimization techniques, Selesnick and Lanza et al. ^[9] proposed a CNC design strategy for designing non-convex TV regularization, thereby ensuring the global convexity of the objective function. In essence, this is achieved by subtracting its smooth version from the TV regularization, with different smoothing techniques yielding distinct forms of non-convex TV regularization^[29]. The most notable among these is the generalized Moreau envelope TV (GME-TV) regularization^[9], which can be mathematically defined as follows:

The last term in (2.1), denoted as

represents the generalized Moreau envelope of $\Vert D\theta \Vert_1$, which is a commonly used smoothing technique. The matrix parameter $B$ is utilized to adjust the smoothness of $S_B(D\theta)$ and consequently affects the non-convexity of $\Psi^{GME}_B(D\theta)$. Specifically, when $B = 0$, then $S_B(D\theta) = 0$, and $\Psi^{GME}_B(D\theta)$ reduces to the TV regularization term $\Vert D\theta \Vert_1$. When $B^T B$ is a diagonal matrix, i.e. $B = \sqrt{b}I$, then $\Psi^{GME}_B(D\theta)$ simplifies to the generalized minimax-concave TV (GMC-TV) regularization introduced in ^[30].

2.2.   Performance analysis results

In accordance with the conventions followed in the literature on image denoising ^{[27,31,32,33]}, the performance of a TV estimator $\hat{\theta}$ is evaluated by the high-probability upper bound on its mean squared error (MSE), which is defined by

The presentation of upper bounds is accomplished through the utilization of oracle inequalities, which serve as theoretical assurances for the estimator $\hat{\theta}$ in terms of its ability to capture the underlying structure of $\theta^*$ and adapt accordingly.

Let $n$ represent the total number of pixels in the image. Mammen and Van De Geer ^[31] first defined total variation by total derivatives and achieved an estimation rate of order $\mathcal{O}(n^{-3/5})$. Wang et al. ^[33] investigated the more comprehensive framework of trend filtering on graphs and obtained a rate of order $\mathcal{O}(n^{-4/5})$. Hütter and Rigollet ^[27] established sharp oracle inequalities with a rate of $\mathcal{O}(n^{-1/2})$. Sadhanala et al. ^[34] demonstrated that the penalized TVD estimator achieves an optimal near minimax rate of $\mathcal{O}(n^{-1/2})$. Chatterjee and Goswami ^[35] analyzed the recovery of piecewise rectangular images through the constrained version of 2D total variation denoising, providing a rate of $\mathcal{O}(n^{-3/4})$. Varma et al. ^[36] determined the statistical error rates associated with first-order stationary points in graph trend filtering, employing non-convex regularizations like smoothly clipped absolute deviation (SCAD) and minimax concave penalty (MCP). A more detailed summary of the oracles results on TV denoising can be found in ^[37,38,39].

The analysis of error rates in our study utilizes techniques from ^[27] that yield precise error rates through the use of oracle inequalities. Here, we present some basic definitions and conclusions from ^[27], which will also be used in the theoretical analysis of this paper.

We first give the definitions of the compatibility factor and inverse scaling factor as follows.

Definition 2.1. (^[27], Definition 1) Let $D$ be a first-order difference matrix, and the compatibility factor of $D$ for a set $T \subseteq[m]$ is defined as

Moreover, the inverse scaling factor of $D$ is defined as

Then the sharp oracle inequality for TV denoising in ^[27] is expressed as Theorem 2.1.

Theorem 2.1. (^[27], Theorem 2) Fix $\delta \in(0, 1), T \subset[m]$, and let $D$ be the first-order difference matrix. Define the regularization parameter

With this choice of $\lambda$, and for $\forall \bar{\theta} \in \mathbb{R}^n$, the TV estimator $\hat{\theta}$ satisfies

on the estimation error with a probability of at least $1-2 \delta$.

2.3.   Convex optimization algorithms

For the following optimization problem:

where $f_1(\theta)$ is convex and differentiable, $f_2(\theta)$ is a proper closed, convex, but nonsmooth regularization term. The proximal gradient descent (PGD)^[40] and alternating direction method of multipliers (ADMM)^[41] algorithms exhibit excellent performance in solving such problems, with theoretical guarantees of convergence. The iterative formulas for these algorithms for solving (2.8) are represented as

and

Furthermore, $\text{prox}_{f}(\cdot)$ is the proximal operator of $f$, which is defined as

As a special case, if $f(\theta) = \lambda \Vert \theta \Vert_1$, then its proximal operator $\text{prox}_{\lambda \Vert\cdot\Vert_1}$ is the element-wise soft thresholding function

where $\theta_i$ is the $\mathit{i}$-th element of $\theta$.

3.   CNC-TV

In this section, we analyze the CNC-TV denoising model both theoretically and algorithmically. In particular, we consider the following GME-TV denoising model:

where the GME-TV regularization $\Psi^{GME}_B(D\theta)$ is defined as (2.1), and the matrix parameter $B$ can influence the non-convexity of $\Psi^{GME}_B(D\theta)$ and further the global convexity of the cost function in (3.1).

We first give the convexity condition of the cost function in (3.1), and then we analyze the performance of the GME-TV estimator. Finally, we solve the GME-TV denoising model (3.1) by the ADMM algorithm and prove the convergence.

3.1.   Convexity condition

In this subsection, we verify that the cost function in (3.1) can be guaranteed to be convex by selecting the appropriate non-convex control parameter $B$.

Theorem 3.1. Let $\theta \in \mathbb{R}^{n}, \lambda > 0, B \in R^{p \times n}$, define the loss function of (3.1) as

Then, $f_B^{GME}(\theta)$ is convex if $D^{T} B^{T} B D \preceq (1 / \lambda) I$, and $f_B^{GME}(\theta)$ is strong convex if $D^{T} B^{T} B D\prec(1 / \lambda) I$.

Proof. We first rewrite (3.2) as follows:

Next, we analyze the convexity of each term of the last equation in (3.3). First, $-\frac{1}{n}\theta^{T} y$ is a linear function with respect to $\theta$, thus it is inherently convex. Second, $\lambda\Vert D\theta\Vert_1$ represents the $\ell_1$ norm form of $D\theta$, which is also known to be convex. Moving on to the last term, since the expression within the curly braces is affine and therefore convex with respect to $\theta$, and considering that the point-wise maximum of a set of convex functions remains convex, it can be concluded that this particular term is also convex when considered in relation to $\theta$. Consequently, the overall convexity of $f_B^{GME}(\theta)$ solely relies on the first term $\frac1{2n}\theta^{T}(I-\lambda(B D)^{T}(B D))\theta$. If $D^{T} B^{T} B D \preceq (1 / \lambda) I$ holds true, then $I-\lambda(B D)^{T}(B D)$ becomes positive semidefinite and as a result, $f_B^{GME}(\theta)$ exhibits convexity. Conversely, if $D^{T} B^{T} B D\prec(1 / \lambda) I$, then $I-\lambda(B D)^{T}(B D)$ turns out to be positive definite leading to strong convexity being displayed by $f_B^{GME}(\theta)$.

The convexity conditions mentioned above can be maintained by constructing the matrix parameter $B$. Following a similar approach as in ^[30], one simple way to determine the value of parameter $B$ is

When $0 < \zeta < 1$, then $D^{T} B^{T} B D = (\zeta / \lambda) I$ satisfies the convexity condition. When $\zeta = 0$, we have $B = 0$ and the GME-TV regularization $\Psi^{GME}_B(D\theta)$ reduce to the TV regularization $\Vert D \theta \Vert_1$. When $\zeta = 1$, (3.2) is satisfied with equality, resulting in a "maximally" non-convex regularization.

According to Theorem 3.1, we can deduce the following corollary, which is useful in our proof of algorithm convergence.

Corollary 3.1. For all $\mu\geq\lambda \sigma_{\max }I$, $\lambda\Psi^{GME}_B(D\theta) + \frac{\mu}{2}\Vert D\theta \Vert_2^2$ is convex, where the $\sigma_{\max }$ is the largest eigenvalue of $B^{T} B$.

Corollary 3.1 can be derived by replacing $\frac{\mu}{2}\Vert\theta \Vert_2^2$ with $\frac{1}{2n}\Vert y-\theta \Vert_2^2$ in (3.3), following the proof process of Theorem 3.1.

3.2.   Performance analysis

In this subsection, we analyze the performance of the GME-TV estimator (3.1), and use the oracle inequality to get an upper bound on the error rates, which is better than the upper bound of the standard TV estimator (1.2).

We consider a general GME-TV estimator (3.1), that is, the GME-TV regularization term is non-convex and does not necessarily satisfy the convexity condition given by Theorem 3.1. Due to the non-convexity, it is possible that the global minimum of the proposed GME-TV estimator cannot be achieved. Therefore, it is crucial to comprehensively understand the statistical performance of any first-order stationary points of the GME-TV estimator, making it more desirable in practical applications. We define $\hat{\theta}\in {R}^p$ as a stationary point of $F_B^{GME}(\theta)$ when it fulfills

The compatibility factor, as defined by Definition 2.1, allows us to derive the subsequent oracle inequality that is relevant to the stationary points of the GME-TV estimator (3.1).

Theorem 3.2. (Sharp oracle inequality for the GME-TV estimator) Let $D$ be the first-order difference matrix, and $\sigma_{\mathit{{max}}}$ and $\sigma_{\mathit{{min}}}$ be the maximum and minimum eigenvalues of $B^T B$, respectively. The regularization parameter $\lambda$ is set as $\lambda = \frac{1}{n} \sigma \varrho \sqrt{2 \log \left(\frac{e m}{\delta}\right)}$. For the fixed $\delta \in(0, 1)$, $0 < \mu < \frac{1}{n\Vert D\Vert_2^2}$ and $T \subset[m]$, the GME-TV estimator $\hat{\theta}$ defined in (3.1) satisfies

Proof. Since $\hat{\theta}$ is a stationary point of $f(\theta)$, according to the definition of a subgradient, we have

Furthermore, by the chain rule, we have

Then by (3.8), there exist $z \in \left\{\operatorname{sign}(D \theta)+ B^{T} B\left(D \theta-\underset{v}{\operatorname{min}}\left\{\Vert v\Vert_1+\frac{1}{2}\Vert B(D \theta-v)\Vert_2^2\right\}\right)\right\}$ such that

In particular, for $\forall \bar{\theta} \in R^n$, we have

Moreover, for a specific $\hat{\theta}$, we have

By subtracting (3.11) from (3.10) and in accordance with the definition of a subgradient, we obtain

Considering the model $y = \theta^*+\varepsilon$ and utilizing the polarization equality, i.e., $2 x^{T} y = \Vert x\Vert_2^2+\Vert y\Vert_2^2-\Vert x-y\Vert_2^2$, we can reformulate the left-hand side of (3.12) as

For $\forall \theta \in R^n$, the combination of (3.12) and (3.13) yields

Next, we will analyze each term on the right-hand side of (3.14) separately.

We first address $\varepsilon^{T}(\bar{\theta}-\hat{\theta})$. Let $\Pi$ and $I-\Pi$ denote the projection matrices onto $\operatorname{ker}(D)$ and $\operatorname{ker}(D)^{\perp}$, respectively. Moreover, we have $D^{\dagger} D = (I-\Pi)$. With the the decomposition $\varepsilon = (\Pi \varepsilon)^{T}+((I-\Pi)\varepsilon)^{T}$, we have

The last inequality in (3.15) is derived from Hölder's inequality, i.e., $x^{T} y \leq \Vert x\Vert_p + \Vert y\Vert_q$ with $1/p + 1/q = 1$.

By using the maximal inequality for Gaussian random variables ^[42], we have

and

with a probability of at least $1-2\delta$.

The substitution of (3.17) into (3.15) yields

By using $\lambda\Vert D\theta\Vert_1 \leq \lambda \Psi^{GME}_{\sqrt{\sigma_{\max}I}}(D\theta)+\frac{\mu}{2}\Vert D\theta\Vert_2^2$ and $\Vert D(\hat{\theta}-\theta)\Vert_2^2 \leq\Vert D\Vert_2^2\Vert\hat{\theta}-\theta\Vert_2^2$, we have

Substituting (3.19) into (3.14), we obtain

For the GME-TV regularization $\Psi^{GME}_B(D \bar{\theta})$, we have

and

After substituting (3.21) and (3.22) into (3.20), we can rewrite (3.20) as

Note that for any $T$, $\Psi_B(D\theta) = \Psi_B((D\theta)_T) + \Psi_B((D\theta)_{T^c})$. Consequently, by utilizing the triangular inequality and subadditivity and symmetry of $\varrho$, we obtain

For $\Psi^{GME}_{\sqrt{\sigma_{\max}I}}((D(\hat{\theta}-\bar{\theta}))_{T})$ in (3.24), we have

The last inequality is based on the definition of a compatibility factor in Definition 2.1.

Next, through the integration of (3.23)–(3.25), we can derive

By utilizing Young's inequality, i.e., $2 x y \leq \frac{x^2}{m}+{m} y^2$ for $m > 0$, with $x = \frac{1}{n}\Vert\Pi\varepsilon\Vert_2 +2\kappa_T^{-1} \sqrt{|T|}, \; y = \Vert\hat{\theta}-\bar{\theta}\Vert_2$, and $m = \frac{1}{n}-\mu\Vert D\Vert_2^2$ (with the requirement of $\mu < \frac{1}{n\Vert D\Vert_2^2}$), we can rewrite (3.26) as

The substitution of (3.27) into (3.26) results in the following equation:

The cancellation of $\frac{1}{n}\Vert\hat{\theta}-\bar{\theta}\Vert_2^2$ on both sides of (3.28) yields

By substituting $\Vert\Pi \varepsilon\Vert_2 \leq 2 \sigma \sqrt{2 \operatorname{log} e / \delta}$ and $\sigma \varrho \sqrt{2 \operatorname{log\; em} / \delta} = \lambda n$ into (3.29), we obtain

This completes the proof of Theorem 3.2. □

The oracle inequality remains valid for any $\hat{\theta}$ that satisfies the first-order optimality condition, even in the case of non-convex regularization. This mild requirement imposed on $\hat{\theta}$ represents a significant divergence from previous findings, such as Theorem 2 of ^[27], which is suitable for global minimization but challenging to ensure when employing non-convex regularizations.

The error bound to the right-hand side of (3.6) can be optimized through careful choice of $\overline{\theta}$ and $T$. When we set $\bar{\theta} = \theta^*$, then

When we set $T$ as the empty set, i.e., $T = \emptyset$, then

The error bound for the GME-TV estimator is now compared with Theorem 2.1 in the special case of setting $T = \emptyset$, i.e., (3.32). First, due to the non-convex nature of $\Psi^{GME}_B(D\theta)$, it imposes particularly strict constraints when $D\theta^*$ contains large coefficients. Therefore, we have $\Psi^{GME}_{\sqrt{\sigma_{\max }I}}(D \theta^*)\ll \Vert D\theta^* \Vert_1$ and $\Psi^{GME}_{\sqrt{\sigma_{\min }I}}(D \theta^*)-\Psi^{GME}_ {\sqrt{\sigma_{\max}I}}(D\theta^*)\ll \Vert D\theta^* \Vert_1$. Consequently, the first term in (3.32) is upper bounded by that of Theorem 2.1. Moreover, the second term in (3.32) includes $n(1-n \mu\Vert D\Vert_2^2)$ in the denominator, which establishes it as an upper bound for the second term mentioned in Theorem 2.1. In summary, the error bound of GME-TV is the upper bound from Theorem 2.1.

On the other hand, the above error gap can be reduced by adjusting the matrix parameter $B$. When we adjust $B$ such that $\Psi^{GME}_B(D\theta)$ trends to $||D \theta||_1$, the improvement in the first term of the bound can be erased.

In conclusion, the proposed GME-TV estimator ensures strong statistical guarantees for any stationary point, despite its non-convex nature.

3.3.   ADMM algorithm

In this subsection, we solve the GME-TV denoising model (3.1) by using the ADMM algorithm and prove the convergence.

By introducing an auxiliary variable $z$, problem (3.1) can be rewritten as

Furthermore, its augmented Lagrangian form can be expressed as

where $u$ represents the Lagrange multiplier and $\rho > 0$ serves as a penalty parameter.

According to ADMM iteration, solving the minimization problem (3.34) involves addressing three subproblems.

Step 1. Update $\theta^{k+1}$ while keeping $z^k$ and $u^k$ fixed.

Step 2. Update $z^{k+1}$ while keeping $\theta^{k+1}$ and $u^k$ fixed.

Equation (3.36) can be considered as the proximal operator of $\Psi^{GME}_{B}(z)$. Although this operator does not have an explicit expression, we obtain its iterative solution through the PGD iteration.

By substituting $\Psi_B^{GME}(z)$ into (3.36), we can reformulate equation (3.36) as

Let $f_1(z) = \frac{\rho}{2}\Vert z-D\theta^{k+1}+\frac{1}{\rho}u^{k}\Vert_{2}^{2} -\lambda\min\limits_{v}\left\{\Vert v\Vert_{1}+\frac{1}{2}\Vert B(z-v)\Vert_{2}^{2} \right\}$ and $f_2(z) = \lambda\Vert z\Vert_{1}$. The update of $z^{k+1}$ can be obtained through the PGD algorithm as follows:

where $\alpha$ is the step size. The main challenge of (3.38) is how to solve the gradient $\nabla f_1(z)$. According to Lemma 3 in ^[16], the last term of $f_1(z)$ is differentiable with respect to $z$. Furthermore, the gradient of $f(z)$ can be expressed as

Note that (3.39) contains an $\ell_1$ regularization problem:

which can be regarded as a proximal operator of the $\ell_1$ norm, i.e.,

where $prox_{\Vert\cdot\Vert_1}(\cdot)$ can be simply solved by the soft-thresholding operator (2.10).

By substituting (3.41) and (3.39) into (3.38), we can succinctly summarize the update of $z^{k+1}$ as follows:

Step 3. Update $u^{k+1}$.

Finally, the ADMM algorithm for GME-TV regularization can be obtained as Algorithm 1 through the rearrangement of Eqs (3.35), (3.42), and (3.43).

The total computational complexity of Algorithm 1 mainly depends on the $\theta$-subproblem, which involves the matrix inversion $(\frac{1}{n}I+{\rho}D^{T}D)^{-1}$ with a computation complexity of $\mathcal{O}(n^{3})$ for $D \in R^{n \times n}$ and $\theta \in \mathbb{R}^{n}$. Fortunately, under the periodic boundary conditions for $\theta$, $D^{T}D$ can be represented as a block circulant matrix with circulant blocks. In this scenario, solving the $\theta$-subproblem becomes feasible through one forward fast Fourier transform (FFT) and one inverse FFT, each requiring a cost of $\mathcal{O}(n\log n)$ ^[43]. Consequently, the total computational complexity of Algorithm 1 is significantly reduced to $\mathcal{O}(n\log n)$, representing a substantial improvement compared to its original complexity of $\mathcal{O}(n^{3})$.

Algorithm 1 showcases the utilization of an ADMM update with the Lagrangian introduced in Eq (3.34). Additionally, we offer convergence assurance for Algorithm 1.

Theorem 3.3. By selecting the appropriate parameter $\rho$, then the primal residual $r^{k} = \theta^{k}-z^{k}$ and the dual residual $s^{k+1} = \rho(z^{k+1}-z^{k})$ of Algorithm 1 satisfy that $\lim\limits_{k\to\infty}\Vert r^{k} \Vert_2^2 = 0$ and $\lim\limits_{k\to\infty}\Vert s^{k} \Vert_2^2 = 0$.

Proof. The proof follows the idea of proving Proposition 1 in ^[44] and Theorem 3 in ^[36].

Considering the augmented Lagrangian $L(\theta, z, u)$ with respect to $z$, while assuming the other variables are fixed, we can derive

As stated in Corollary 3.1, there exists $\mu > 0$ such that $\lambda\Psi^{GME}_{B}(D\theta)+\frac{\mu}{2}\Vert{D\theta}\Vert_2^2$ is convex. Additionally, it should be noted that the term $\frac{1}{2n}\Vert\theta-y\Vert_{2}^{2}-\frac{\rho}{2}\Vert D\theta\Vert_{2}^{2}-\rho u^{T}(D\theta)$ is independent of $z$. Therefore, by choosing $\rho \geq \mu$, we can observe the convexity of $L(\theta, z, u)$ with respect to each variable $\theta$, $u$, and $z$. The property enables us to effectively apply Theorem 5.1 in ^[45]. Consequently, Algorithm 1 converges toward the limit points $\theta^*$, $z^*$, and $u^*$. This implies that for the dual residual, we have

For the primal residual, it is worth noting that the update step for $u$ in Algorithm 1 implies that $\forall k, t \geq 0$,

For fixed $t$ and as $k\to\infty$, we have

where $\forall t\geq0$, and thus, $D \theta^*-z^* = 0$. Therefore, it follows that

Theorem 3.3 establishes the convergence of Algorithm 1 toward achieving both primal and dual feasibility in the limit. It also demonstrates the equivalence between the augmented Lagrangian form (3.34) with fixed $z$ and $u$, and the original form (3.33). Each iteration of Algorithm 1 yields a stationary point $\theta$ for (3.34) with fixed $z$ and $u$, thereby implying that $\theta^*$ is also a stationary point for (3.33).

4.   Numerical experiments

In this section, we will compare the denoising performance of the proposed GME-TV regularization with the standard TV regularization ^[46] and MC-TV regularization ^[9,17] through 1D and 2D denoising experiments.

4.1.   1D denoising

In this experiment, we evaluate the performance of different regularizations for 1D signal denoising. Initially, a piecewise constant 1D signal with a length of $n = 180$ is generated, degraded by the AWGN with a noise level of $\sigma = 0.9$. Subsequently, GME-TV, MC-TV, and standard TV regularization are applied for the purpose of denoising. The denoising accuracy is quantified using the root mean squared error (RMSE), which is defined as

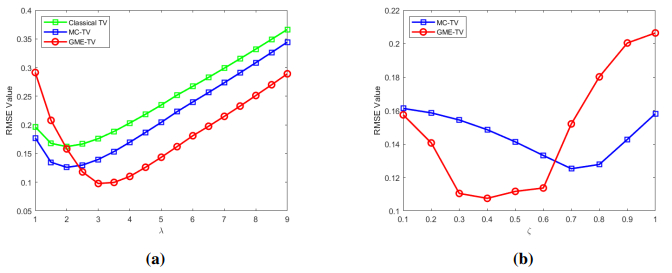
The regularization parameter $\lambda$ and the non-convex control matrix parameter $B$ play a crucial role in determining the denoising performance of GME-TV. We establish these two hyperparameters as follows: First, we plot the curve of RMSE with respect to $\lambda$, and subsequently select the optimal value of $\lambda$ that exhibits the lowest RMSE value. Second, based on (3.4), the matrix parameter $B$ is determined by $\zeta$. Therefore, once $\lambda$ is determined, we proceed to plot the curve of RMSE with respect to $\zeta$ and then choose the optimal value of $\zeta$ that exhibits the lowest RMSE value. The remaining hyperparameters $\alpha$ and $\rho$ in Algorithm 1 are simply set as $\alpha = 1$, and $\; \rho = 1$, following the strategy proposed in ^[9]. The hyperparameters $\lambda$ and $\zeta$ for MC-TV are set up in the same manner as for GME-TV. For TV, since there is no non-convex control parameter, we set $\lambda$ in the same way as for GME-TV. The remaining hyperparameters of MC-TV and TV are set by default according to ^[9] and ^[46], respectively.

The changes in RMSE values of different denoising models with $\lambda$ and $\zeta$ are illustrated in Figure 1. It can be observed that the denoising performance of the models varies with different hyperparameter values. Moreover, GME-TV demonstrates superior denoising performance compared to other models.

We set the hyperparameters of different denoising models according to the results of Figure 1, and show the denoising results of different models in Figure 2. As depicted in Figure 2, TV regularization effectively mitigates noise. However, it tends to underestimate the magnitude of certain jump-type discontinuities and lacks the piecewise constant characteristics of the original noiseless signal. In contrast, GME-TV and MC-TV regularization provide a more precise estimation of segment points in piecewise constant signals and demonstrate superior denoising performance compared to TV regularization. The RMSE values also substantiate the inherent superiority of GME-TV regularization.

4.2.   2D denoising

In this experiment, we test the performance of different regularizations on image denoising. Four commonly used denoising test images, namely "Lena", "Man", "QRcode", and "Geometric", were utilized as shown in Figures 3(a), 4(a), 5(a), and 6(a). All images have a size of $512\times512$ with grayscale values ranging from $0$ to $255$. Subsequently, all images are degraded by additive white Gaussian noise with noise level $\sigma = 0.9$. The noisy images are shown in Figures 3(e), 4(e), 5(e), and 6(e).

The image denoising accuracy is quantified by the peak signal-to-noise ratio (PSNR), which is defined as

where $\text{MAX} = 255$ is the maximum value of the images, and

where $\theta^*_{i j}$ and $\hat{\theta}_{i j}$ are the pixel values of the original image $\theta^*$ and the denoised image $\hat{\theta}$, respectively, with all images having a size of $M = N = 512$. The higher the PSNR value, the smaller the difference between the denoised image and the original image.

We employ the same strategy as the 1D denoising experiment to determine the hyperparameter values of different denoising models, and show the denoising results of each model in Figures 3–6. To enhance the visual contrast, in addition to enlarging a small patch of the local image, we also highlight the difference between the denoised image and the original one. As shown in Figures 3–6, all three denoising models can remove noise well. Compared with TV denoising results, MC-TV and GME-TV not only enhance image texture and other intricate details but also sharpen edges more efficiently for a superior visual outcome. Moreover, the PSNR values further demonstrate the superior performance of GME-TV regularization, as evidenced by the improved PSNR values for all four images compared to TV regularization and MC-TV regularization.

5.   Conclusions

In this paper, we propose CNC-TV regularization as a valuable alternative to TV regularization. This approach effectively addresses the issue of underestimation of signal discontinuity while ensuring the global convexity of the objective function. Empirical evidence is provided to demonstrate the superior performance of CNC-TV regularization compared to TV regularization. Furthermore, our theoretical analysis establishes a foundation for a deeper understanding of the estimation properties associated with CNC-TV regularization. Additionally, we demonstrate that the CNC-TV regularization exhibits superior performance on both 1D and 2D denosing experiments.

In this work, we mainly focus on the theoretical analysis of CNC-TV. In fact, these findings suggest its potential significance in future applications such as image denoising, image reconstruction, seismic data processing, etc. Furthermore, there are also some challenges in the implementation of the CNC-TV model, such as the setting strategy of the non-convex control matrix parameter $B$, which will be further studied in our following work.

Author contributions

Yating Zhu: Conceptualization, Methodology, Software, Writing–original draft; Zixun Zeng: Software, Data curation; Zhong Chen: Funding acquisition, Supervision; Deqiang Zhou: Data curation, Formal analysis; Jian Zou: Project administration, Writing–review & editing, Supervision. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This research was funded by the National Natural Science Foundation of China (grant number 62273060), and the Undergraduate Training Program of Yangtze University for Innovation and Entrepreneurship (Yz2023302).

Conflict of interest

All authors declare no conflicts of interest.