Application of ADMM to robust model predictive control problems for the turbofan aero-engine with external disturbances

1.   Introduction

The aircraft's aero-engine is a critical component. Its operation is quite complicated, and it often fluctuates depending on environmental circumstances and operating states (e.g., maximum state, cruise state, acceleration and deceleration states, etc.). As a result, optimizing the control of the aero-engine is critical in order to make it run reliably and efficiently and to achieve the best performance. Stable-state control, transition-state control, and limit control are the three main control tasks ^[1]. There are various types of aero-engines, and this study focuses on turbofan aero-engines.

Engine control adopted closed-loop feedback control from classical control theory in the early 1950s, which improved control accuracy, dynamic performance, and engine performance significantly. Because it is simple to design and implement, this approach is still utilized for many engine controllers today. Classical feedback control theory, on the other hand, cannot ensure the system's stability and dynamic performance. For this reason, modern control theories such as linear quadratic optimal control, adaptive control, robust control, LPV control, and neural network control arose in the 1960s. Classical engine linear regulators are conservative and unable to handle complex systems with output constraint protection ^[2,3]. In contrast, model predictive control (MPC) provides considerable advantages in handling engine operating restrictions explicitly ^[4,5], simplifying the engine control system structure ^[6], and performing real-time rolling optimization. MPC has received a lot of attention in the engine control industry since then ^[7,8,9,10].

The MPC algorithm is a finite-horizon optimum control algorithm that uses a time-forward rolling optimization algorithm. Its rolling implementation can compensate in time for uncertainties caused by model mis-match, time variations, and disturbances. In order for the control to remain practically optimal, the algorithm constantly builds additional optimizations in the real system ^[11]. The classical finite horizon quadratic value function is used as the objective function in the analysis of MPC problems in Ref. ^[12]. In the linear time-invariant (LTI) system, the output variables and their corresponding output constraints are disregarded. The control input is not taken into consideration in the output of the LTI system in Ref. ^[13]. In Ref. ^[14], the ADMM algorithm is used to improve the real-time performance of the aero-engine nonlinear MPC by applying it to the MPC rolling optimization. Firstly, they introduce auxiliary variables and then introduce auxiliary variable constraints. The simulation results show that the improved method is more efficient. In summary, we try to apply the ADMM algorithm to the turbofan aero-engine problem according to the previous research on MPC.

The ADMM algorithm can solve block convex optimization problems quickly, reducing the difficulty of solving them by breaking down large-scale problems into smaller chunks. The ADMM algorithm is theoretically guaranteed to converge for any convex value function and constraints. In the last ten years, the ADMM algorithm, which was originally developed to solve variational inequalities, has become widely used in optimization computing ^{[15,16,17,18,19]}. Noor proposed methods for addressing general variational inequalities ^[20,21], including projection, Wiener-Hopf equations, updating the solution, auxiliary principle, inertial proximal, penalty function, dynamical system and well-posedness. He ^[22] selects the appropriate matrix $G$ in the framework of variational inequalities and solves the convex optimization problem with linear constraints using the PPA algorithm under G-modules. The method makes the iterative process of solving subproblems easy to solve. Ref. ^[23] directly applies the PPA algorithm's powerful convergence theory to the ADMM algorithm, demonstrating that the essence of the algorithm is the same. With the further study of the ADMM algorithm, its convergence has been proved. The PPA algorithm is a fundamental algorithm for computing optimally. It was first proposed by Martinet in 1970 ^[24], and then Rockafellar did further research ^[25,26]. The PPA algorithm on Lagrangian multipliers is known as the augmented Lagrangian method (ALM) ^[27]. He ^[28] selects appropriate proximal parameters in the linear constrained convex minimization problem and solves it with the PPA algorithm. The subproblems obtained by this algorithm are easier to solve than the ones of the ALM algorithm. The PPA algorithm has received further attention in recent years, both in terms of theory and implementation ^{[29,30,31,32]}.

Model uncertainty exists in industrial processes due to factors such as model mismatch and external disturbances between the practical system and the process model. These make the performance of MPC worse and even make the system unstable. Therefore, it is critical and realistic to investigate MPC's robustness ^[33]. Within the scope of MPC, which combines the advantages of robust control with predictive control, RMPC is one of the control methods for dealing with model uncertainty. The research mainly includes predictive control algorithm robustness analysis and this algorithm robust control ^[34]. There are primarily two methods for RMPC to achieve optimal control. The first is $H_{\infty}$ control ^{[35,36,37,38,39]}, while the second is min-max optimization ^[40,41,42]. The min-max optimization commonly uses the worst-case performance function. Based on invariant set theory, the method uses linear matrix inequalities (LMI) to design the RMPC controller. The optimization problem is then converted into an LMI problem in order to solve the predictive control. Previously, the system state was thought to be quantifiable online for RMPC ^{[43,44,45,46]}. However, the system state is not always measurable in practical applications. Using the state observer, Lee ^[47] and Mayne ^[48] built the output feedback RMPC (OFRMPC) with constraints in the LTI system. The state observer's parameters are fixed in this scenario, and the control inputs are optimized online by the OFRMPC. Bemporad ^[49] used the dynamic output feedback control method to design the OFRMPC with constraints in the LTI system.

Overall, we apply the ADMM algorithm to improve the RMPC problem's rolling optimization. To increase the solving efficiency and maintain system stability, we apply the modified algorithm to the turbofan aero-engine LTI system with external disturbances. The following are the primary innovations in this paper: (1) In this paper, we investigate a more complex model by considering the dual influence of output variables and state variables on the output values; (2) We improve the algorithm by utilizing the fact that the PPA algorithm can simplify the subproblem to transform the optimization problem; (3) We use the ADMM algorithm can take full advantage of the sparsity of the problem to optimize the algorithm and improve the solution efficiency; (4) Several transformations are applied to the original optimization problem, and the suggested method is demonstrated by an example in the RMPC problem for turbofan aero-engines.

The rest of the paper is organized as follows. In Section 2, we introduce the mathematical model of the RMPC problem for the turbofan aero-engine and its augmented form. In Section 3, we derive the RMPC prediction equations in matrix form. In Section 4, we transform the optimization problem of RMPC into a form that is suitable for solving with the ADMM algorithm. In Section 5, we calculate the comparison problem of RMPC for turbofan aero-engine in ground idling and verify the effectiveness of the RMPC-ADMM algorithm in terms of robustness and solving efficiency. In Section 6, we conclude this paper and look forward to future work.

2.   RMPC model description

The model of a turbofan aero-engine with external disturbances can be described as follows:

where

The state variable $x$ denotes the deviation of the fan speed $N_{f}(r / \mathrm{min})$ and the core rotor speed $N_{c}(r / \mathrm{min})$. The output variable $y$ (also called the output constrained variable) denotes the deviation of the high-pressure compressor delivery temperature $T_{48}\left({ }^{\circ} R\right)$ and the high-pressure compressor surge margin $\operatorname{SmHPC} (\%)$. The control variable $u$ denotes the deviation of the fuel flow rate $W_{f}(kg / \mathrm{s})$, the variable stator vane angle $\operatorname{VSV}\left({ }^{\circ}\right)$, and the variable bleed valve opening $\mathrm{VBV}$. $A_{d}$, $B_{d}$, $C_{d}$, and $D_{d}$ denote the input and output matrices of the corresponding variables. The external disturbance variable $w(k)$ is bounded.

We now introduce the augmented state matrix $x_{a}(k) = \left[\begin{array}{ll}x(k)^{T} & u(k-1)^{T}\end{array}\right]^{T}$, which has the advantages of low computational effort, high computational accuracy, and strong computational stability. By applying $x_{a}(k)$ to (2.1), we can get the following augmented model:

The compact form can be written as:

where

$x_{a}$ denotes the augmented state variable. $\Delta u$ denotes the new control variable. When solving practical problems, we usually depend on whether it is the tracking variable ($\Delta N_{f}$) or the output constrained variable ($\Delta T_{48}$, $\Delta \mathrm{S m H P C}$) to use different matrix coefficients. As a result, we express these two types of variables, respectively, to fulfill our practical needs. The equivalent model equation can be written as follows:

where $C_{0} = \left[\begin{array}{lllll}1 & 0 & 0 & 0 & 0\end{array}\right]$, $y(k)$ denotes the expression of $\Delta N_{f}$, and $p(k)$ denotes the expression of $\Delta T_{48}$ and $\Delta \mathrm{S m H P C}$.

3.   RMPC prediction equation

In order to reduce the number of independent variables in the optimization problem and improve the algorithm efficiency, we introduce the control horizon $n_{u}$, the prediction horizon $n_{y}$, and the control variable $\Delta u(k+i), i = 0, 1, 2, \cdots, n_{y}-1$.

Since predict the control system needs control inputs throughout the prediction horizon, we make the following assumptions:

Assumption 1. The control horizon $n_{u}$ is not larger than the prediction horizon $n_{y}$, and the control variable $\Delta u(k+i)$ is constant in the later times of the control horizon $n_{u}$. That is,

By iterating the first equation of Eq (2.4), the prediction state columns can be obtained as:

By iterating the second equation of Eq (2.4), the prediction tracking columns can be obtained as:

where $(k+i \mid k), i = 1, \cdots, n_{y}$ in Eqs (3.1) and (3.2) denotes the prediction of $k+i$ times at the current time $k$.

Equations (3.1) and (3.2) can be simplified into matrix form as follows:

where

4.   RMPC optimization problem

During engine operation, it is necessary to guarantee that the fan speed reaches the specified reference value and that the control system remains stable at all times. Therefore, we design the value function to ensure that the tracking variable is close to the reference input variable and that the control variable's fluctuation is as small as possible. The value function is as follows:

where $e(k) = r(k)-\hat{y}(k)$, $r(k)$ denotes the reference input (i.e., the given fan speed deviation value). The first term is expressed as the sum of the squares of the differences between the tracking variable and the reference input variable in the prediction horizon $n_{y}$. $a$ denotes the scalar weight (i.e., the weighting factor). At each prediction time, the larger the weighting factor $a$, the smaller the fluctuation of the control variable is. We use a consistent weighting factor to simplify the value function. The second term is expressed as the sum of the squares of the control variation during the control horizon $n_{u}$.

When solving the RMPC optimization problem, the system needs to satisfy the assumptions as follows:

Assumption 2. The control variable $u$, the output constraint variable $p$, and the external disturbances $w$ are maintained within the allowed range. That is,

where $\underline{U}, \overline{U}, \underline{P}( = \underline{Y}), \overline{P}( = \overline{Y}), \underline{w}$ and $\overline{w}$ denote the upper and lower bound vectors of the control variable, the output constraint variable, and the external disturbances, respectively.

When the disturbances of the system are bounded, we can take the maximum value of the disturbances to solve the minimum value of the optimization problem. As a result, the optimization problem can be expressed in terms of the worst-case performance function on a finite horizon.

Problem 1.

The optimization variables of Problem 1 are $\Delta \hat{u}$ and $\hat{w}$, but they are not explicit in the value function, and the variables in the constraints are with respect to $u$, $p$ and $w$. Therefore, it is necessary to unify the variables of both value function and constraints as $\Delta \hat{u}$ and $\hat{w}$. The transformations are shown as follows:

(1) For value function

where

Since $J_{0}$ is a constant at the current time $k$, it can be ignored.

(2) For constraints

$({\rm{i}})$ Constraints for the variable $u$

Let $i = 0$ and subtract $u(k-1)$ from both sides of the inequality simultaneously:

Set $k = k+1$, and then substitute $u(k)-u(k-1) = \Delta u(k)$:

Still let $k = k+1$, and then substitute $u(k)-u(k-1) = \Delta u(k)$:

Similarly, we can obtain:

Then, it can be expressed in matrix form:

Let

Then the matrix form can be expressed as:

$({\rm{ii}})$ Constraints for the variable $p$

According to the derivation process (3.2), the prediction equation for the output constraint variable $p$ can be obtained in the same way:

where

According to Eqs (4.2) and (4.13), we can obtain:

Substitute Eq (4.12) into Eq (4.14),

it can be simplified as,

where $\overline{d_{p}} = \hat{p}_{\max }-E_{c} x_{a}(k)-G_{c} \hat{w}$ and $\underline{d_{p}} = -\hat{p}_{\min }+E_{c} x_{a}(k)+G_{c} \hat{w}$.

In summary, the constraint can be denoted as:

where $\Psi = \left[\begin{array}{l}C_{c} \\ H_{c}\end{array}\right]$.

$({\rm{iii}})$ Constraints for the variable $w$

For $\underline{w} \leq w(k+i) \leq \overline{w}, i = 0, 1, 2, \cdots, n_{y}-1$, the direct deformation yields:

Based on the above transform, Problem 1 can be converted as:

Problem 2.

where $\theta_{1}(\Delta \hat{u}) = \frac{1}{2} \Delta \hat{u}^{T} W \Delta \hat{u}+c^{T} \Delta \hat{u}$ and $\theta_{2}(\hat{w}) = \frac{1}{2} \hat{w}^{T} S \hat{w}+b^{T} \hat{w}$.

Solving optimization problems in the framework of variational inequalities can bring great convenience ^[50,51], therefore, we transform Problem 2 into the form of variational inequalities as follows:

Problem 3. Solve for $\left(\Delta \hat{u}^{*}, \hat{w}^{*}\right) \in \Lambda$ such that it satisfies:

where

It can effectively exploit the simplicity of the objective function by applying the PPA algorithm to solve this problem. So, based on the study of linear constrained convex optimization problems in the papers ^[22,28], we use the PPA algorithm to solve Problem 3.

For given $\left(\Delta \hat{u}^{v}, \hat{w}^{v}\right)$, the subproblems of $\Delta \hat{u}$ and $\hat{w}$ can be denoted as:

where $r_{1}$ and $s_{1}$ are constants.

Simplifying Eq (4.20), we can obtain the following problem.

Problem 4.

where

By solving Eq (4.20), we can obtain:

It can be observed that the subproblems of Eq (4.20) are all quadratic programming problems with high-dimension block matrices, and there is a solution order among the subproblems, so the Problem 4 is hard to solve. Considering that the ADMM algorithm has the property of distributed optimization, we apply it to the rolling optimization of the 4 to increase the solution efficiency.

Firstly, we introduce the slack variable $z_{1}(>0)$ to Problem 4:

Applying the ADMM algorithm yields the iteration equation:

where $\left(\hat{w}^{q}, z_{1}^{q}, \lambda_{1}^{q}\right)$ denotes the current iteration point. $L_{\beta}$ denotes the augmented Lagrangian function and can be expressed as:

Simplifying Eq (4.24) yields:

Iterate until the termination condition is satisfied. We can get the optimal solution $\widetilde{\hat{w}}^{v}$ of Eq (4.21). Next, we substitute $\widetilde{\hat{w}}^{v}$ into the expression of $e_{1}$. Similarly, the optimal solution $\Delta \tilde{\hat{u}}^{v}$ of Eq (4.22) can be obtained. In conclusion, we can obtain the proximal point $\left(\Delta \widetilde{\hat{u}}^{v}, \widetilde{\hat{w}}^{v}\right) \in \Lambda$.

After that, the next iteration point is updated to $\left(\Delta \hat{u}^{v+1}, \hat{w}^{v+1}\right)$. The iteration equation can be denoted as:

We determine whether the iterative process satisfies the accuracy requirements. The iteration continues if it is not fulfilled. If it is met, the solution $\left(\Delta \hat{u}^{*}, \hat{w}^{*}\right)$ of Eq (4.19), which is also the optimal solution $(\Delta \hat{u}, \hat{w})$ of Eq (4.18), can be achieved.

According to the system model Eq (2.4), the state variable $x(k+1)$ and the output variable $y(k+1)$ at time $k+1$ can be obtained. We continue the procedures above until the whole simulation horizon $\mathrm{Simhor}$ has been finished, where $\mathrm{Simhor}$ denotes the time range ($\mathrm{Simhor} \leq n_{y} \leq n_{u}$) for solving the actual problem. In Algorithm 1, the specific solution stages are presented.

5.   Simulation example

The simulation example studies the CMAPSS-40k turbofan aero-engine in ground idling. We want to reach the required fan speed response $\Delta N_{f} = 100 \mathrm{r} / \mathrm{min}$ in the shortest time possible when the control variable and the output constraint variable are kept within the permitted range. For the sake of simplicity, we choose $\Delta N_{f} = 100 \mathrm{r} / \mathrm{min}$, $n_{u} = 3$, $n_{y} = 7$, $\mathrm{Simhor} = 30$. The remaining values of variables($A_{d}$, $B_{d}$, $C_{d}$, $D_{d}$, $\overline{U}$, $\underline{U}$, $\overline{Y}$, $\underline{Y}$, $\overline{w}$, $\underline{w}$) are all consistent with the ones used in ^[4].

5.1.   Comparison of the results of MPC-ADMM algorithm and RMPC-ADMM algorithm

To prove the stability of the improved algorithm, we solve the two problems with and without disturbances while keeping the common parameter values constant ($\beta = 2.5$, $\gamma = 1.5$, $a = 0.01$).

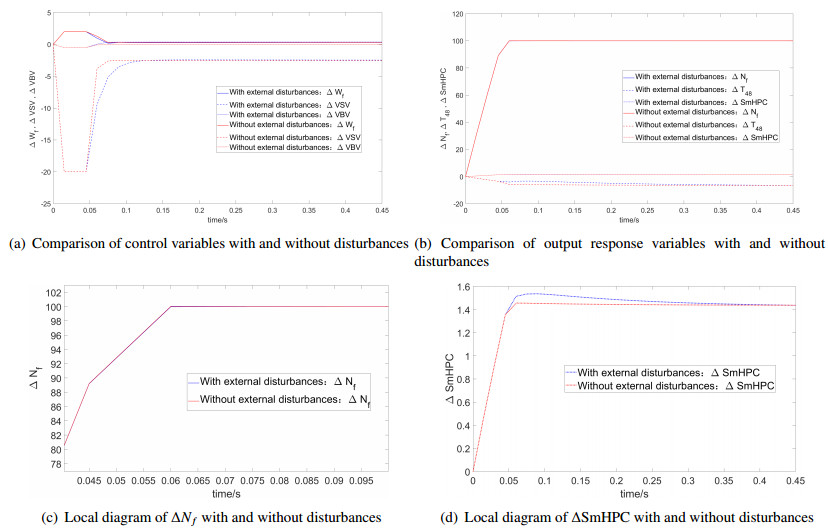
In Figure 1(a) and 1(b), the RMPC system can reach the target tracking value when the constraints are satisfied. Furthermore, there is little difference in the fluctuation of the two system variables. In Figure 1(c), both systems are almost approaching the specified fan speed response value at the same time. The difference in surge margin and numerical fluctuation between the two systems is small in Figure 1(d). These results show that the system is always in stable condition. In conclusion, by using the improved method to solve the RMPC problem, the system can reach the target value rapidly and steadily. Section 5.1 illustrates the robustness of the RMPC-ADMM algorithm.

5.2.   Comparison of the results of RMPC-QP algorithm and RMPC-ADMM algorithm

In this section, to prove the effectiveness of the RMPC-ADMM algorithm, we calculate the same RMPC problem by using the QP algorithm (interior point method) and the ADMM algorithm, respectively. The prediction horizon $n_{y}$ and the control horizon $n_{u}$ may affect the predictive control performance. Too small $n_{y}$ may result in failure to satisfy stability and constraints ^[52], while too large may affect the dynamic characteristics ^[53,54]. So we will discuss it in two cases.

Case 1. $n_{u} = n_{y}$.

Firstly, we take $n_{u} = n_{y}\leq 15$. The results are shown in Table 1.

As can be seen in Table 1, the ADMM algorithm can reduce the solution time by more than 50% when $n_{u} = n_{y}\leq 15$. This is because the ADMM algorithm keeps the KKT coefficient matrix and penalty parameters fixed during the iterations. Therefore, the ADMM algorithm needs to calculate the matrix decomposition only once in each iteration. In contrast, the interior-point method requires the inverse or decomposition of the KKT matrix in each iteration. Assuming that the solution requires $M$ iterations, the matrix decomposition time takes $t_{1}$, and the KKT system solution back takes $t_{2}$, then the solution time of the ADMM algorithm takes $t_{1}+Mt_{2}$, and the solution time of the interior point method takes $M(t_{1}+t_{2})$. In summary, as compared to the interior-point, the ADMM algorithm applied in this paper reduces the computational effort and improves the real-time performance.

Next, we further prove the effectiveness of the improved algorithm by computing the case $n_{u}$ = $n_{y} > 15$, and the results are shown in Table 2.

Case 2. $n_{u}\neq n_{y}$.

This section proves that the improved algorithm still has good results when $n_{u} \neq n_{y}$. We assume $n_{u} = \frac{1}{2} n_{y}$, and the results are shown in Table 3.

6.   Conclusions

In this paper, we aim to solve a practical optimization problem quickly and stably. Considering that the control system in the practical problem is always uncertain, this uncertainty is divided into external uncertainty (i.e., external disturbances) and internal uncertainty (e.g., measurement error, parameter estimation error, model mismatch, etc.). As a result, we introduce the external disturbance $w(k)$ (which is also a general method) and obtain the RMPC problem in order to solve the practical problem accurately.

We study the RMPC problem for turbofan aero-engines. We take the original optimization problem as an entry point and transform it into the variational inequality. The PPA algorithm, the ADMM algorithm, the splitting contraction algorithm, and the projection contraction algorithm can all solve the variational inequality problem, the first three of which are known to have simple mechanisms and can be used with great importance in the engineering field and related disciplines. We use the PPA algorithm to transform it into problem that is applicable for the ADMM algorithm to solve. Finally, the ADMM algorithm is applied to the rolling optimization to improve its effectiveness. The application of the RMPC-ADMM algorithm to the ground idling example demonstrates that the system can still obtain the objective value while maintaining stability. Furthermore, the time it takes to solve a problem is cut in half. The research has implications for turbofan aero-engine control optimization, and further work has to be done to increase the solution efficiency. In general, it is easier to solve the variational inequality problem using the projection contraction algorithm. However, due to the high dimensionality of this practical problem, the solution is not satisfactory. In our subsequent research, we will try to solve the problem using this algorithm. Meanwhile, we will concentrate our efforts on improving the classical ADMM algorithm and increasing its solution efficiency.

Acknowledgments

The authors sincerely thank the anonymous referees for their valuable comments and detailed suggestions, which led to considerable improvement in the article. This work was supported by the National Natural Science Foundation of China (Grant Nos.12161076, 61890920, 61890921) and the Fundamental Research Funds for the Central Universities (Grant No. DUT21LAB301).

Conflict of interest

All authors declare no conflicts of interest in this paper.