Adaptive predefined-time robust control for nonlinear time-delay systems with different power Hamiltonian functions

1.   Introduction

Actual nonlinear systems are subject to a wide variety of unknown disturbances, parameter uncertainties and delay phenomena ^[1,2]. Robust control and adaptive control methods have been proven successful at addressing these issues ^{[3,4,5,6,7,8,9,10,11,12,13,14]}. For nonlinear time-delay systems (NTDSs) with variable powers, ^[4] solved the adaptive robust tracking control problem. Taking into account the disturbance and time-varying delay of nonlinear Lipschitz systems, ^[5] designed a class of delay-dependent $H_\infty$ dynamic observers. The literature ^[6] investigated the global adaptive state feedback control issue of stochastic NTDSs with unknown disturbances and time-dependent delays. A new adaptive tracking controller with minimum learning parameters was designed to solve an adaptive tracking issue in finite time caused by full-state constrained NTDSs under input saturation ^[8]. The Lyapunov-Krasovskii functional method was applied to investigate the adaptive robust control problem on finite time of NTDSs subject to uncertainty and disturbances ^[10]. For NTDSs with the triangular form, the robust output tracking control problem is solved by neural network ^[11]. For stochastic NTDSs with partially known jump rates, ^[12] investigated the continuous gain-scheduled robust fault detection issue. The above results developed several good infinite-time and finite-time methods. Although the finite-time control scheme presented above achieves faster convergence and greater robustness than the infinite-time scheme, its convergence time is determined by giving the initial state. Namely, its convergence time has an uncertain upper bound.

As a result, a predefined-time control method is presented. As is well known, a closed-loop system (CLS) operated under a predefined-time strategy will maintain its convergence time uncorrelated with its initial state, and the upper bound of its convergence time is set beforehand, which improves the control accuracy of the CLS and compensates for the limitations of the finite-time control scheme. Consequently, the predefined-time control approach has received considerable focus from scholars, and some excellent results have been produced ^{[15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]} on the mechanical system, time-varying system and uncertain system. Meanwhile, many effective predefined-time control methods have also been proposed like optimal control ^[16], time-varying feedback ^[17,18,19], backstepping ^[20], high-gain approach ^[26] and so on. Among them, the Lyapunov-like theorem proposed in ^[25] ensured that such dynamic systems reached stability in a predefined time and also constituted a framework based on predefined-time stability analysis. By introducing time transformations with terminal time terms, ^[26] investigated the stability in a predefined time of the nonlinear uncertain system. With a new scale-free backstepping method, ^[28] solved the predefined-time mean-square stability as well as the inverse optimality issues of nonlinear stochastic systems. By designing a double time-varying gain, ^[29] presented a new predefined-time adaptive control method and solved the predefined-time control problems involved in triangular NTDSs having unknown parameters. Even so, there are few predefined-time control results of NTDSs except ^[29]. Particularly, as far as the authors know, no predefined-time control result has been published regarding the NTDSs with external disturbances and parameter uncertainty simultaneously, which inspired the present work.

As is well known, it is a very difficult task to study nonlinear systems due to lack of an effective research tool. Recently, the Hamiltonian method, as an important nonlinear research tool, has received much attention in the academic community and has been used to solve succesfully a large number of nonlinear problems. In fact, one of the advantages of using the Hamiltonian function method is that the Hamiltonian function in a Hamiltonian system can be chosen as a candidate Lyapunov function, which effectively overcomes the difficulty of constructing Lyapunov functions. Moreover, several well-established techniques for the design of Hamiltonian systems are given in the literature ^[34,35,36]. Among them, the authors also develop many strategies to obtain their Hamiltonian forms for given nonlinear systems. These methods are presented so that one can easily convert the system under study into its Hamiltonian version. However, the fact that the powers of the Hamiltonian functions in the literature ^[9,14,37,38] are the same for each state implies that the results have greater limitations.

In the paper, we investigate a general class of NTDSs with uncertain parameter and external disturbance, and propose several predefined-time $H_\infty$ and adaptive robust control results by applying the Hamiltonian function method with different powers. Here are some of the main contributions of this paper: (1) Contrary to the available results of infinite-time control as well as finite-time control, our predefined-time controller is capable of ensuring the CLS converges to zero within any given predefined constant number, and its convergence time cannot be affected by the initial state, making the system behavior better determined. (2) In contrast with the previous NTDS control results using the Hamiltonian approach (with the same power Hamiltonian form), this paper develops several more general results with different power Hamiltonian function forms, implying that these results have broader applications. (3) Compared with the recent predefined-time control result on the delay system in ^[29] (considering only the triangular form and unknown parameter), this paper examines a general class of NTDSs subject to uncertainties and disturbances and designs its predefined-time $H_\infty$ controller and adaptive robust controller by applying different power Hamiltonian forms. As expected, the results are more in line with reality.

The remaining sections of the paper are listed below. In Section 2, we present several preliminaries. Section 3 gives our main findings, Section 4 illustrates a case of river pollution that supports our new result and Section 5 is the conclusion.

2.   Preliminaries

Consider the system

where $f: \mathbb{R}_{+} \times \mathbb{R}^{n}\times \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ indicates a nonlinear function, $x \in \mathbb{R}^{n}$ represents the system state, $h > 0$ is the constant delay, $\rho$ denotes an uncertain constant parameter with appropriate dimension, and $t$ indicates time variable defined on $\left[t_{0}, \infty\right)$, where $t_{0} \in \mathbb{R}_{+} \cup\{0\}$, $x_{0} = x\left(t_{0}\right)$ is the initial condition.

In some practical cases, it would be desirable if the system (2.1) could achieve its original point in a given time $T_{a}$, where $T_{a}$ is a constant and can be defined beforehand.

Assume that $M (\subset R^{n})$ is a non-empty set. If any solution $x(t, x_{0})$ reaches $M$ in $t \leq t_0+T_{a}$, then the predefined time $T_{a}$ gets defined.

Lemma 2.1. Suppose that $V(t, x_t): = V$ is a continuous radial unbounded function with $V(t, 0) = 0$ such that

holds, then $M$ is predefined-time attractive, where $x_{t}$ is a delay function segment defined as $x_{t}: = x(t+\varrho), \varrho \in[-h, 0]$ with $h > 0$, the constant $0 < q \leq 1$ and $T_{a}$ is the predefined time.

Proof. From Eq (2.2), it is easy to obtain:

To give the upper boundary of $t$, using $V(t, 0) = 0$, we can obtain

where $V_{x_{0}}$ denotes the initial value of $V$. From Eq (2.4), and $0 < \exp \left(-(V_{x_{0}})^{q}\right) \leq 1$, we have

implying $T_{a}$ is the predefined time. Therefore, it has been proved.

Lemma 2.2. ^[39] For real matrices $\digamma_{a}, \digamma_{b}$ and a positive real number $\tau$, the following equation holds:

Lemma 2.3. ^[35] When a scalar function $g(x)$ has continuous partial derivatives of order $n$ and $g(0) = 0\left(x \in \mathbb{R}^{n}\right)$, then $g(x)$ may be characterized as $g(x) = l_{1}(x) x_{1}+\cdots+ l_{n}(x) x_{n}$ with $l_{i}(x)(i = 1, 2, \cdots, n)$ also being scalar functions.

Assuming $k(x)\left(\in \mathbb{R}^{n}\right)$ is a smooth function and $k(0) = 0$, then $k(x): = M(x) x =$

Lemma 2.4. ^[13] For any given real number $d\geq1$, the inequality holds:

3.   Main results

3.1.   Robust stabilization result

Consider the following NTDS

where the state vector is $x(t) (\in \Omega)$, $\Omega$ represents the bounded convex neighborhood of the zero point inside the space $\mathbb{R}^{n}$, inverse symmetric structure matrix $J(x)(\in \mathbb{R}^{n \times n})$ and positive definite symmetric matrix $R(x)(\in\mathbb{ R}^{n\times n})$ are given, $\tilde{x} : = x(t-h)$, Hamiltonian function $H(x)$ reaches its minimum when $x = 0$ that is $H(0) = 0$, the gradient vector of $H(x)$ is denoted by $\nabla_{x}^\mathrm{T}H(x)$, $T(x)\in \mathbb{R}^{n \times n}$ with $T(0) = 0$, $g_1(x)$ and $g_2(x)$ are the weighted matrices, $u$ represents system input, $\omega$ denotes outside disturbance, and $\varphi(\eta)$ denotes a vector-valued initial value function. Moreover, assume that $g_{1} (x)$ has full column rank.

To present several predefined-time control results on the Hamiltonian system (3.1), we assume that

and $y = g_{1}^\mathrm{T}(x)\nabla_{x}H(x)$ is the system output signal.

Remark 3.1. Note that the Hamiltonian function of the present paper has different powers, which is different from the existing results on the Hamiltonian system ^[9,14,37,38]. It should be mentioned as well that we presume the Hamiltonian function takes the form (3.2) so as to get certain predefined-time control outcomes on the Hamiltonian system (3.1). Obviously, a real system cannot satisfy the form. For a specific system, we have the following methods to develop its Hamiltonian form: the orthogonal decomposition method ^[40], Hamiltonian functional method ^[40], the energy shaping approach ^[40], the vector field decomposition method ^[41] and so on. In this section, we only present a theory result. Once the theory result is obtained, then one can design a suitable controller and apply the energy shaping approach to convert the general form to the form (3.2). Please refer to Section $4$ for more details.

Assumption 3.1. The disturbance $\omega$ satisfies

where $\mu > 0$ is a given positive constant.

For the purpose of analysis, the set $\Omega$ is selected in the following form:

where $\alpha_{j}(j = 1, 2, \cdots, n)$ are known constant vectors, which describe n edges of $\Omega$.

We begin by defining the predefined-time $H_\infty$ stabilization issue.

The predefined-time $H_\infty$ stabilization is to: Design a controller $u = a(x)$ so that the CLS is stable for a predefined time when $\omega$ disappears. Meanwhile, when $\omega\in\Lambda$ is not zero, the zero-state response $(\varphi(\eta) = 0$, $\eta\in[-h, 0])$ meets

where positive constant $\gamma$ represents the disturbance suppression level, while $z$ denotes the penalty signal described by

with the weighted matrix $h(x)$ having the appropriate dimension.

Now, the main results of our study are presented.

Theorem 3.1. Considering the system (3.1) under Assumption 3.1, for $T_{a} > 0$ and $\gamma > 0$, if

(1) constant matrices $L < 0$, $P > 0$ and constant numbers $\epsilon > 0$, $0 < r \leq \gamma^{2}$ exist, the following inequalities hold:

(2) real numbers $s > 0$ and $\mu > 0$ exist and

then a predefined-time $H_\infty$ controller of the NTDS (3.1) could be constructed as follows:

where $\delta: = \max\{c^{\frac{2 \alpha_{min}-2}{2 \alpha_{min}-1}}, \; c^{\frac{2 \alpha_{max}-2}{2 \alpha_{max}-1}}\}$ with $c: = \max \left\{\left\|x\right\|: x \in \Omega\right\}$, $\sigma : = W^{\frac{1}{\alpha_{max}}-\frac{1}{\alpha_{min }}}$ with $H(x)\leq W$ when $x \in \Omega$, $\alpha_{min }$ represents the minimum value of $\alpha_{i}$, $\alpha_{max }$ represents the maximum value of $\alpha_{i}$, and $\Phi(x)$ is the predefined-time stabilizing function that follows

Proof. To prove the system (3.1) is a predefined-time $H_\infty$ stabilization, we first show (3.5) holds for $\omega \neq 0$, and then prove its stability in a predefined time when $\omega$ disappears.

The Lyapunov function is constructed in the following form:

Based on Lemma 2.2, one can derive

Computing the derivative of $V(x)$ and using ${\nabla_{x}}^\mathrm{T}H(x)J(x)\nabla_{x}H(x) = 0$, one can obtain

Noting that $\frac{2 \alpha_{i}}{2 \alpha_{i}-1} = \frac{1}{1-\frac{1}{2 \alpha_{i}}}$ is a decreasing function, we have

Next, when $x \in \Omega$, let $H(x)\leq W$. Since $H(x)\leq W$, we can obtain that $\dfrac{1}{W}\sum_{i = 1}^{n}\left(x_{i}\right)^{\frac{2 \alpha_{i}}{2 \alpha_{i}-1}} < 1$. From that and Lemma 2.4, we get

Note that the monotonicity of $W^{\frac{1}{\alpha_{i}}-\frac{1}{\alpha_{min }}}$ is related to the value range of $W$. When $0 < W\leq1$, $W^{\frac{1}{\alpha_{i}}-\frac{1}{\alpha_{min }}}$ is an increasing function of $\alpha_i$, then $W^{\frac{1}{\alpha_{i}}-\frac{1}{\alpha_{min }}}\geq W^{\frac{1}{\alpha_{min}}-\frac{1}{\alpha_{min }}} = 1$ and if $W > 1$, $W^{\frac{1}{\alpha_{i}}-\frac{1}{\alpha_{min }}}$ is a decreasing function on $\alpha_i$, we have $W^{\frac{1}{\alpha_{i}}-\frac{1}{\alpha_{min }}}\geq W^{\frac{1}{\alpha_{max}}-\frac{1}{\alpha_{min }}}$. Combining these two cases, we have $W^{\frac{1}{\alpha_{i}}-\frac{1}{\alpha_{min }}}\geq\min\{1, \; W^{\frac{1}{\alpha_{max}}-\frac{1}{\alpha_{min }}}\} = W^{\frac{1}{\alpha_{max}}-\frac{1}{\alpha_{min }}} : = \sigma$ with $\sigma$ being a positive constant. Substituting it into Eq (3.16), we have $\sum_{i = 1}^{n}\left(\frac{2 \alpha_{i}}{2 \alpha_{i}-1}\right)^{2}\left(x_{i}^{2}\right)^{\frac{1}{2 \alpha_{i}-1}}\geq\sigma\left(\frac{2 \alpha_{max }}{2 \alpha_{max }-1}\right)^{2}(H(x))^{\frac{1}{\alpha_{min }}}$, namely,

Substituting (3.17) into (3.14), one can get

Now, we prove (3.5) holds.

By letting $\Gamma(t, x) = V(x)+\int_{0}^{t}(\parallel z(s) \parallel^{2}-\gamma^{2}\parallel \omega(s) \parallel^{2})ds$, we next indicate that $\Gamma(t, x)\leq0$.

Noting that $r \leq \gamma^{2}$, we obtain

Using the condition of zero-state response and integrating (3.19) over $0$ and $t$ result in

Since $V(x)\geq0$, one obtains

In addition, noting that $\frac{\alpha_{i}}{2 \alpha_{i}-1} < 1$ and $x^{T} x = \sum_{i = 1}^{n}\left(x_{i}\right)^{2}$, we have $x^{T}x = c^{2} \sum_{i = 1}^{n}\left(\frac{x_{i}}{c}\right)^{2} \leq c^{2} \sum_{i = 1}^{n}\left[\left(\frac{x_{i}}{c}\right)^{2}\right]^{\frac{\alpha_{i}}{2 \alpha_{i}-1}} = \frac{c^{2}}{c^{\frac{2 \alpha_{i}}{2 \alpha_{i}-1}}} \sum_{i = 1}^{n}\left(x_{i}^{2}\right)^{\frac{\alpha_{i}}{2 \alpha_{i}-1}} = c^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}} H(x)$ holds on $\Omega$.

The monotonicity of $c^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}$ is related to the value range of $c$. When $0 < c\leq1$, $c^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}$ is a decreasing function of $\alpha_i$, then $c^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}\leq c^{\frac{2 \alpha_{min}-2}{2 \alpha_{min}-1}}$ and if $c > 1$, $c^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}$ is an increasing function of $\alpha_i$, we have $c^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}\leq c^{\frac{2 \alpha_{max}-2}{2 \alpha_{max}-1}}$. Combining these two equations, we can reach the conclusion that $c^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}\leq\max\{c^{\frac{2 \alpha_{min}-2}{2 \alpha_{min}-1}}, \; c^{\frac{2 \alpha_{max}-2}{2 \alpha_{max}-1}}\} : = \delta$, from which we have $x^{T}x\leq\delta H(x)$.

Noting Assumption 3.1 and (3.20), we have $x^{T}x\leq \delta H(x) = \frac{1}{2}\delta V\left(t, x\right) \leq \delta \frac{\gamma^{2}}{2} \int_{0}^{T}\|w(s)\|^{2} d s \leq \frac{\delta \gamma^{2}}{2 \mu^{2}}$, namely, $\|x\|^{2} \leq \frac{\delta \gamma^{2}}{2 \mu^{2}}$.

Afterward, it is shown that $x(t) \in \Omega$ holds when $\forall t > 0$, $\varphi = 0$, $\omega \in \Lambda$. With (3.4), it must be demonstrated that

From ^[42], we have

which indicates that (3.9) holds with free scalar $s > 0$ introduced by the S-procedure and $\zeta = \left[1, x^{T}\right]^{T}$.

Thus, we conclude that $x(t)$ remains in $\Omega$ for all $t > 0$, $\varphi = 0$, $\omega\in \Lambda$.

Next, we demonstrate the stability in a predefined time for the CLS (3.1) when $\omega$ disappears.

Noting (3.18), we get

It implies Lemma 2.1 holds. Thus, it has been proved.

In Theorem 3.1, the controller (3.10) contains the delay term. Next, we present a controller without containing the delay term for the NTDS (3.1).

Theorem 3.2. Consider the NTDS (3.1) under Assumption 3.1. For the presented $T_{a} > 0$ and $\gamma > 0$, if

(1) constant matrices $L < 0, P > 0$ and constant numbers $\epsilon > 0$, $r > 0$ exist such that $e^{\left(h \lambda_{\max }\{P\}\right) \chi^{2}}r\leq \gamma^{2}$,

(2) real numbers $s > 0$ and $\mu > 0$ exist, and

where $\delta: = \max\{\chi^{\frac{2 \alpha_{min}-2}{2 \alpha_{min}-1}}, \; \chi^{\frac{2 \alpha_{max}-2}{2 \alpha_{max}-1}}\}$ with $\chi: = \max \left\{\left\|x_{t}\right\|: x \in \Omega\right\}$, then a predefined-time $H_\infty$ controller of the NTDS (3.1) could be constructed as follows:

where $\sigma : = W^{\frac{1}{\alpha_{max}}-\frac{1}{\alpha_{min }}}$ with $H(x)\leq W$ when $x \in \Omega$, $\alpha_{min }$ and $\alpha_{max }$ are similar to these in Theorem 3.1, and $\Phi(x)$ is the predefined-time stabilizing function that follows

and $G(t): = e^{\int_{t-h}^{t} \nabla_{x}^{T} H(x(s)) P \nabla_{x} H(x(s)) d s}$.

Proof. To prove the system (3.1) has predefined-time $H_\infty$ stability, we first show

holds for $\omega \neq 0$.

Construct the Lyapunov function as:

Computing the derivative of $V(t, x_{t})$ and using $\nabla_{x}^\mathrm{T}H(x)J(x)\nabla_{x}H(x) = 0$, one can obtain

From that and using (3.17), one obtains

Now, we prove (3.5) holds. Do so by letting $\Gamma_{1}(t, x) = V(t, x_{t})+\int_{0}^{t}(\parallel z(s) \parallel^{2}-\gamma^{2}\parallel \omega(s) \parallel^{2})ds$. We next indicate that $\Gamma_{1}(t, x)\leq0$.

Assuming that $\left\|x_{t}\right\| \leq \chi$, it follows that $G(t) \leq e^{\left(h \lambda_{\max }\{P\}\right) \chi^{2}}$. Substituting $\dot{V}(t, x_{t})$ into $\dot{\Gamma}_{1}(t, x)$, and noting that $e^{\left(h \lambda_{\max }\{P\}\right) \chi^{2}}r \leq \gamma^{2}, G(t)\geq1$, one gets

The condition of zero-state response and the integration of $\dot{\Gamma}_{1}(t, x)$ over $0$ and $t$ result in

and under $V(t, x_{t})\geq0$, one obtains

Using $\frac{\alpha_{i}}{2 \alpha_{i}-1} < 1$ as well as $x^{T} x = \sum_{i = 1}^{n}\left(x_{i}\right)^{2}$, we have $x^{T} x = \chi^{2} \sum_{i = 1}^{n}\left(\frac{x_{i}}{\chi}\right)^{2} \leq \chi^{2} \sum_{i = 1}^{n}\left[\left(\frac{x_{i}}{\chi}\right)^{2}\right]^{\frac{\alpha_{i}}{2 \alpha_{i}-1}} = \frac{\chi^{2}}{\chi^{\frac{2 \alpha_{i}}{2 \alpha_{i}-1}}} \sum_{i = 1}^{n}\left(x_{i}^{2}\right)^{\frac{\alpha_{i}}{2 \alpha_{i}-1}} = \chi^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}} H(x)$ holds on $\Omega$.

The monotonicity of $\chi^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}$ is related to the value range of $\chi$. When $0 < \chi\leq1$, $\chi^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}$ is a decreasing function, then $\chi^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}\leq \chi^{\frac{2 \alpha_{min}-2}{2 \alpha_{min}-1}}$ and if $\chi > 1$, $\chi^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}$ is an increasing function, we have $\chi^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}\leq \chi^{\frac{2 \alpha_{max}-2}{2 \alpha_{max}-1}}$. Combining these two equations, we can conclude that $\chi^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}}\leq\max\{\chi^{\frac{2 \alpha_{min}-2}{2 \alpha_{min}-1}}, \; \chi^{\frac{2 \alpha_{max}-2}{2 \alpha_{max}-1}}\} : = \delta$, from which we have $x^{T}x\leq\delta H(x)$.

Noting Assumption 3.1, Eq (3.36) and $G(t)\geq1$, one has $x^{T}x\leq \delta H(x)\leq G(t)\delta H(x) = \frac{1}{2}\delta V\left(t, x_{t}\right) \leq \delta \frac{\gamma^{2}}{2} \int_{0}^{T}\|\omega(s)\|^{2} d s \leq \frac{\delta \gamma^{2}}{2 \mu^{2}}$, namely, $\|x\|^{2} \leq \frac{\delta \gamma^{2}}{2 \mu^{2}}$.

Afterward, it is shown that $x(t) \in \Omega$ holds when $\forall t > 0$, $\varphi = 0$, $\omega \in \Lambda$. With (3.4), it must be demonstrated that

From ^[42], we have

which indicates that (3.27) holds with free scalar $s > 0$ introduced by the S-procedure and $\xi = \left[1, x^{T}\right]^{T}$. Thus, we conclude that $x(t)$ remains in $\Omega$ when all $t > 0$, $\varphi = 0$, $\omega\in \Lambda$.

As the remainder of the proof is similar to Theorem 3.1, it is omitted.

3.2.   Adaptive robust stabilization result

Now, we present an adaptive robust stabilization result with external disturbance and uncertainty.

Consider the NTDS

where $p$ represents constant bounded uncertainty, inverse symmetric structure matrix $J(x, p)$ and symmetric matrix $R(x, p)$ are given, $J (x, 0) = J (x)$, $R (x, 0) = R (x)$, $J (x, p) = J (x) + \Delta J (x, p)$, $R (x, p) = R (x) + \Delta R (x, p)$, Hamiltonian function $H_{1}(x)$, which is smooth, reaches its minimum when $x = 0$ that is $H_{1}(0) = 0$, $H_{1} (x, 0) = H_{1} (x)$, $\nabla_{x}H_{1} (x, p) = \nabla_{x}H_{1}(x) + \Delta H_{1} (x, p)$, $u \in \mathbb{R}^{m_{1}}$ represents system input, $\omega \in \mathbb{R}^{q}$ indicates the external interference satisfying $\int_{0}^{\infty}\omega^\mathrm{T}(t)\omega(t)dt < \infty$, and $\varphi(\eta)$ denotes a vector-valued initial value function. Moreover, assume that $g_{1} (x)$ has full column rank.

Assumption 3.2. ^{[14,43,44,45]} Assume $\phi(x)$ satisfies

for $\forall x\in\Omega$, where $\theta \in R^{m_{2}}$ indicates the constant vector determined by the uncertain parameter $p$ and assume the constant $k > 0$ exists such that $\|\theta\|\leq k$.

Under Assumption 3.2, noting that $J (x, p) = J (x) + \Delta J (x, p)$, $R (x, p) = R (x) + \Delta R (x, p)$, the system (3.40) can be transformed into:

where $G(x, p): = [\triangle J(x, p)-\triangle R(x, p)] \nabla_{x} H_{1}(x)$.

Based on the NTDS (3.40) and Lemma 2.3, we can easily know that matrix $M(x) \in \mathbb{R}^{n \times n}$ as well as positive constant $\varpi$ exist such that $\nabla_{x}H_{1}(x) = M (x) x$, and

where

To investigate the predefined-time stabilizing issue, we need to convert the Hamiltonian function $H_{1}(x)$ into:

To do this, the controller $u$ is designed as

where $v$ represents a new input, $\iota > 0$, and $\iota^{2} = dH(x)$ with $d$ being a positive constant, $H_{2}(x) : = H(x)-H_{1}(x), v = v_{1}+v_{2}$ with $v_1$ and $v_2$ being determined later.

Substituting (3.46) into (3.42), system (3.42) is expressed as

Consider the system (3.47), set $\gamma > 0$ as disturbance suppression level, and choose penalty signal $z = h(x)g_{1}^\mathrm{T}(x)\nabla_{x}H(x)$, where $h(x)$ denotes the weight matrix of the appropriate dimension.

Theorem 3.3. Consider the NTDS (3.40) under Assumptions 3.1 and 3.2. For the presented $T_{a} > 0$ and $\gamma > 0$, if

(1) constant matrices $L$, $P > 0$, $Q\geq\frac{1}{2}k^{2}I_{n}$ and constant numbers $r > 0$, $b > 0$ exist such that $e^{\left(h \lambda_{\max }\{P\}\right) a^{2}}r\leq \gamma^{2}$,

where $k > 0$, $\varpi$ and $\iota$ are given in Assumption 3.2, (3.44) and (3.46), respectively, $N(x): = \operatorname{Diag}\left\{(\frac{2 \alpha_{1}-1}{2 \alpha_{1}})x_{1}^{\frac{2 \alpha_{1}-2}{2 \alpha_{1}-1}}, (\frac{2 \alpha_{2}-1}{2 \alpha_{2}})x_{2}^{\frac{2 \alpha_{2}-2}{2 \alpha_{2}-1}}, \cdots, (\frac{2 \alpha_{n}-1}{2 \alpha_{n}})x_{n}^{\frac{2 \alpha_{n}-2}{2 \alpha_{n}-1}}\right\}$, and

(2) real numbers $s > 0$ and $\mu > 0$ exist, and

where $\delta: = \max\{a^{\frac{2 \alpha_{min}-2}{2 \alpha_{min}-1}}, \; a^{\frac{2 \alpha_{max}-2}{2 \alpha_{max}-1}}\}$ with $a: = \max \left\{\left\|x_{t}\right\|: x \in \Omega\right\}$, then a predefined-time adaptive robust controller of the NTDS (3.47) could be constructed as

where $\sigma : = \min\{1, \; W^{\frac{1}{\alpha_{max}}-\frac{1}{\alpha_{min }}}\}$ with $H(x)\leq W$ when $x \in \Omega$, $\alpha_{min }$ and $\alpha_{max }$ are similar to these in Theorem 3.1, and $\Phi(x)$ is given in (3.30).

Proof. $V(t, x_{t})$ is set as follows:

When we compute the derivative of $V(t, x_{t})$ and use ${\nabla_{x}}^\mathrm{T}H(x)J(x)\nabla_{x}H(x) = 0$, one can obtain

There exists a matrix $N(x): = \operatorname{Diag}\left\{(\frac{2 \alpha_{1}-1}{2 \alpha_{1}})x_{1}^{\frac{2 \alpha_{1}-2}{2 \alpha_{1}-1}}, (\frac{2 \alpha_{2}-1}{2 \alpha_{2}})x_{2}^{\frac{2 \alpha_{2}-2}{2 \alpha_{2}-1}}, \cdots, (\frac{2 \alpha_{n}-1}{2 \alpha_{n}})x_{n}^{\frac{2 \alpha_{n}-2}{2 \alpha_{n}-1}}\right\}$ such that $x: = N(x)\nabla_{x}H(x)$ holds, and using (3.43), one can get

Substituting (3.56) and (3.17) into (3.55), we have

Noting that $\parallel \theta\parallel^{2}\leq k^{2}$ and $Q\geq\frac{1}{2}k^{2}I_{n}$, one can obtain that $-2Q\leq-k^{2}I_{n}\leq-\theta^{\mathrm{T}}\theta I_{n}$, which is

Substituting (3.58) into (3.57), and noting (3.48) and (3.50), one can get

First, we prove (3.5) holds by letting $D\left(t, x\right) = V(t, x_{t})+\int_{0}^{t}(\parallel z(s) \parallel^{2}-\gamma^{2}\parallel \omega(s) \parallel^{2})ds$. Then we indicate that $D\left(t, x\right)\leq0$.

Substituting (3.59) into $\dot{D}\left(t, x\right)$, we get

Assuming that $\left\|x_{t}\right\| \leq a$, it follows that $G(t) \leq$ $e^{\left(h \lambda_{\max }\{P\}\right) a^{2}}$, from which we obtain $\dot{D}\left(t, x\right)\leq$ $-\frac{\alpha_{min}}{T_{a}(\alpha_{min}-1)}\exp[(2G(t)H(x))^{1-\frac{1}{\alpha_{min}}}](2G(t)H(x))^{\frac{1}{\alpha_{min}}}+(e^{\left(h \lambda_{\max }\{P\}\right) a^{2}}r-\gamma^{2})\parallel \omega \parallel^{2}+(-G(t)+1)\parallel z \parallel^{2}.$

Noting that $e^{\left(h \lambda_{\max }\{P\}\right) a^{2}}r \leq \gamma^{2}$ and $G(t)\geq1$, one gets

The condition of zero-state response and the integration of $\dot{D}\left(t, x\right)$ over $0$ and $t$ result in

and with $V(t, x_{t})\geq0$, we get

Furthermore, using $\frac{\alpha_{i}}{2 \alpha_{i}-1} < 1$ and $x^{T} x = \sum_{i = 1}^{n}\left(x_{i}\right)^{2}$, it is easy to obtain that $x^{T} x = a^{2} \sum_{i = 1}^{n}\left(\frac{x_{i}}{a}\right)^{2} \leq a^{2} \sum_{i = 1}^{n}\left[\left(\frac{x_{i}}{a}\right)^{2}\right]^{\frac{\alpha_{i}}{2 \alpha_{i}-1}} = \frac{a^{2}}{a^{\frac{2 \alpha_{i}}{2 \alpha_{i}-1}}} \sum_{i = 1}^{n}\left(x_{i}^{2}\right)^{\frac{\alpha_{i}}{2 \alpha_{i}-1}} = a^{\frac{2 \alpha_{i}-2}{2 \alpha_{i}-1}} H(x)$ holds on $\Omega$.

Similar to Theorem 3.1, we can get $x^{T}x\leq\delta H(x)$.

Noting Assumption 3.1 and Eq (3.62), we have $x^{T}x\leq \delta H(x)\leq G(t)\delta H(x) = \frac{1}{2}\delta V\left(t, x_{t}\right) \leq \delta \frac{\gamma^{2}}{2}\\\times \int_{0}^{T}\|\omega(s)\|^{2} d s \leq \frac{\delta \gamma^{2}}{2 \mu^{2}}$, namely, $\|x\|^{2} \leq \frac{\delta \gamma^{2}}{2 \mu^{2}}$.

Afterward, it is shown that $x(t) \in \Omega$ holds when $\forall t > 0$, $\varphi = 0$, $\omega \in \Lambda$. With (3.4), it must be demonstrated that

From ^[42], we have

which indicates that (3.64) holds with free scalar $s > 0$ introduced by the S-procedure and $\zeta = \left[1, x^{T}\right]^{T}$. Thus, we conclude that $x(t)$ remains in $\Omega$ for all $t > 0$, $\varphi = 0$, $\omega\in \Lambda$.

Next, we demonstrate the stability in the predefined time for the NTDS (3.47) when $\omega$ disappears.

Noting (3.59), one obtains

which implies that Lemma 2.1 holds when $\omega = 0$. Thus, it has been proved.

4.   Illustrative example

Take into account the following pollution control system with the single delay for rivers ^[46,47]:

where $A_{1} = \beta_{0} \eta_{2} I_{2}$, $\Delta A_{1}(t) = \Delta \beta \eta_{2} I_{2}$, $B = \operatorname{Diag}\left\{\eta_{1}, 1\right\},$ $\begin{array}{c} A_{0} = \left[\begin{array}{cc} -k_{10}-\eta_{1}-\eta_{2} & 0 \\ -k_{30} & -k_{20}-\eta_{1}-\eta_{2} \end{array}\right], \Delta A_{0}(t) = \left[\begin{array}{cc} -\Delta k_{1}(t) & 0 \\ -\Delta k_{3}(t) & -\Delta k_{2}(t) \end{array}\right]. \end{array}$

From Ref. ^[47], we are aware that $\triangle A_{0}(t) = B \Psi(t)$, $\bar{\omega}(t) = B \omega(t)$ and constants $\rho_{i}(i = 1, 2) > 0$, where $\|\Psi(t)\| \leq \sqrt{\rho_{1}}, \; \|\omega(t)\| \leq \sqrt{\rho_{2}}$. Ref. ^[46] explains the physical meaning of the above parameters (for more details, please see Ref. ^[46]). Furthermore, assume that $x = \left[x_{1}, x_{2}\right]^{T} \in \Omega = \left\{\left(x_{1}, x_{2}\right):\left|x_{1}\right| \leq 2.5, \left|x_{2}\right| \leq 2.5\right\}$ and $\triangle A_{0}(t) = \left[\begin{array}{ll}p \; & 0 \\ p \; & p\end{array}\right]$.

First, the Hamiltonian form of system (4.1) is expressed as follows:

where $H_{a}(x) = 0.5\left(x_{1}^{2}+x_{2}^{2}\right)$, $T = A_{1}+\triangle A_{1}(t)$, $g_{1} = g_{2} = B$ and $J-R = : A_{0}.$ Besides, since $\|G(x, p)\| = 0$, we can easily see that (3.43) holds on $\Omega$ with $\varpi = 0$.

In the following, we can obtain

where $\theta = p$ and $\phi(x) = \left[\frac{1}{\eta_{1}} x_{1}, x_{1}+x_{2}\right]$. Substituting (4.3) into (4.2), one gets

Next, design the controller in the following manner:

where $v$ represents a new input, $\iota: = (dH(x))^{\frac{1}{2}} = (0.0001H(x))^{\frac{1}{2}}$, and $H_{b}(x): = H(x)- H_{a}(x)$ with $H(x) = x_{1}^{\frac{4}{3}}+x_{2}^{\frac{6}{5}}(\alpha_{1} = 2, \alpha_{2} = 3)$. Noting that $H(x)\leq W$ when $x \in \Omega$ and selecting $W = 8$, one can obtain $\sigma : = \min\{1, \; W^{\frac{1}{\alpha_{max}}-\frac{1}{\alpha_{min }}}\} = \dfrac{\sqrt{2}}{2}$. As a result, the system (4.4) can be expressed as follows:

In addition, set $\gamma = 0.19$ as disturbance suppression level, and choose penalty signal $z = h(x) g_{1}^{T} \nabla_{x} H(x) = \frac{4 \eta_{1}}{3} x_{1}^{\frac{1}{3}}+ \frac{6}{5} x_{2}^{\frac{1}{5}}$, where $h(x) = [1,1]$ denotes the weight matrix of the appropriate dimension.

Now, we demonstrate that all conditions of Theorem 3.3 hold for the system by choosing $k_{10} = 19$, $k_{20} = 5$, $k_{30} = 10$, $\beta_{0} = 0.6$, $\triangle\beta = 0.02$, $\eta_{1} = 0.3$, $\eta_{2} = 0.7$, and then we can obtain $J(x) = \left[\begin{array}{cc} 0 \; & 5 \\ -5 \; & 0 \end{array}\right], R(x) = \left[\begin{array}{cc} 20 \; & 5 \\ 5 \; & 6 \end{array}\right]$, $T = 0.434 I_{2}$.

Meanwhile, set the parameters as follows: $T_{a} = 0.1s$ and $0.05s$, respectively, $k = 4$, $b = 0.1661$, $r = 0.035$, $P = 0.15 I_{2}$, $Q = 10 I_{2}$. From $x: = N(x)\nabla_{x}H(x)$, we have $N = \operatorname{Diag}\left\{\dfrac{3}{4}x_{1}^{\frac{2}{3}}, \dfrac{5}{6}x_{2}^{\frac{4}{5}}\right\}$. Then, condition (1) holds for $0 < h < 0.5$.

Selecting $\alpha_{j} = 0.1(j = 1, 2)$, $s = 10$ and $\mu = 0.06$, the equations $\alpha_{j}\left|x_{j}\right| \leq 1$ and (3.51) are valid. It follows that condition (2) of Theorem 3.3 holds.

For this system, Theorem 3.3 is fulfilled when $0 < h < 0.5$. Based on Theorem 3.3, we design a adaptive robust controller in the predefined time for the system (4.2) as

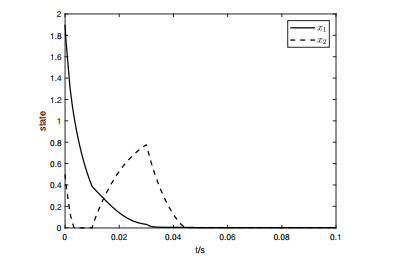
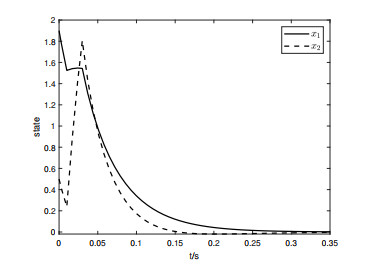
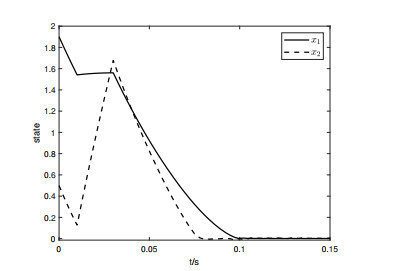
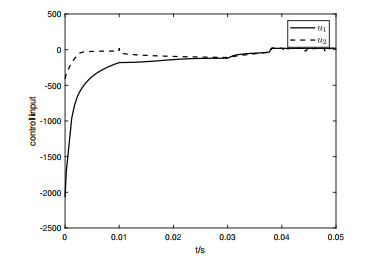
Choose $h = 0.5$ and $p = 0.5$. To assess how robust the controller (4.7) is against disturbances from outside, a disturbance with magnitude $[120, \; 120]^{T}$ is introduced into our system in the time interval $[0.01s \sim 0.03s]$. Figures 1–4 are the simulation results.

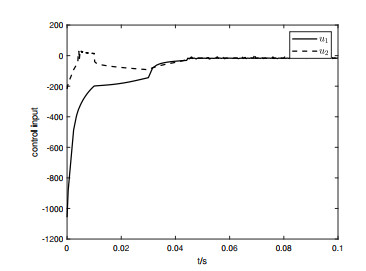
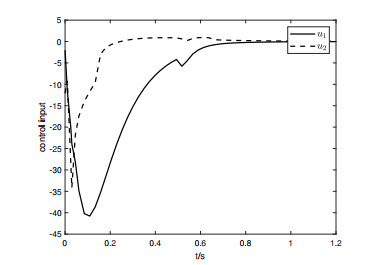
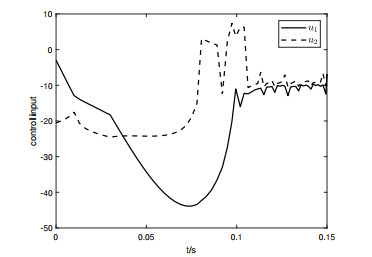
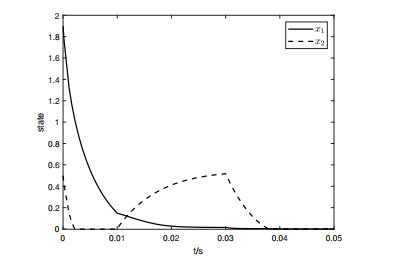
Applying the predefined-time adaptive robust controller (4.7) to the system (4.2) with $\varphi = (1.9, 0.5)$, $T_{a} = 0.05s$ and $T_{a} = 0.1s$, the simulation outcomes can be seen in Figure 1 as well as 2, and the behaviors of the corresponding control inputs are shown in Figures 5 and 6, indicating the system converges to zero within $0.05s$ and $0.1s$. In addition, when the infinite-time controller designed in ^[34] is applied to the system (4.6) with the same initial conditions and disturbance, the result is shown in Figure 3, and the behavior of the corresponding control inputs is shown in Figure 7, and it is obvious that the system states converge to zero in $0.35s$.

In addition, we also give a comparison with the finite-time controller from ^[14] with the same initial conditions and disturbance, Figure 4 illustrates the simulation result, and Figure 8 shows the behavior of the corresponding control inputs. According to Figure 4, the states stabilize within $0.15s$.

Comparing Figures 1 and 2, Figures 3 and 4, the predefined-time, infinite-time and finite-time control schemes were applied to the same system (4.6) under the same initial conditions, the same applied perturbations and the same parameters, respectively, and the comparison results are shown in Table 1. Through Table 1, we can find that the system converges faster under predefined-time control. Moreover, under the same disturbances, the CLS with the above-mentioned predefined-time controller has a smaller amplitude and returns to equilibrium rapidly after the perturbation ends. Consequently, the controller presented in this paper is shown that is very effective for robust stabilization calming.

5.   Conclusions

Throughout the work, we have studied the predefined-time control problem for NTDSs based on the Hamiltonian function approach. By choosing a suitable Hamiltonian form of different powers and constructing appropriate Lyapunov functions, we have presented two corresponding predefined-time control results, namely, $H_\infty$ control and adaptive robust control ones, which have guaranteed the systems to be quickly calibrated in a predefined time and have shortened the calibration time and improved the control accuracy. The simulation results have indicated that the predefined-time adaptive robust scheme presented here has quicker convergence and greater robustness over existing infinite-time and finite-time control schemes. Moreover, unlike the results of existing Hamiltonian systems (where the powers are the same), this paper uses a more realistic form of different power Hamiltonian functions, implying its wider application.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This article received support from the National Natural Science Foundation of China (G61773015), the Natural Science Foundation of Shandong Province (ZR2023MF019), the Research Leader Studio of Jinan (202228119).

Conflict of interest

All the authors declare no conflict of interest.