Fixed/predefined-time generalized synchronization for stochastic complex dynamical networks with delays

1.   Introduction

With the continuous advancement of science and technology, complex dynamical networks (CDNs) have become a research hotspot in recent years. CDNs are composed of edges and nodes, each of which exhibits complex dynamical behaviors. Many real-world networks can be modeled by CDNs, such as the internet ^[1], social networks ^[2], and so on. In addition, CDNs are widely used in various fields, such as physics, engineering, and automatic control ^[3,4,5].

Synchronization is a common non-linear phenomenon between CDNs. Its has been a subject of study since Huygens's pendulum experiment in 1655. Synchronization has potential application value in many aspects, such as information transmission ^[6], pattern recognition ^[7], and secure communication ^[8]. Therefore, more and more scholars pay attention to synchronization between systems ^[9]. The phenomenon of synchronization can occur inside or outside of the systems, which is called "inside synchronization" or "outside synchronization". Generalized synchronization (GS), as a typical external synchronization, is realized by mapping nonlinear smooth vector functions to the drive system and the response system ^[10]. In ^[11], Chen et al. realized the GS of CDNs by using impulsive control methods. In ^[12], the GS of CDNs with different dimensions and nodes was explored. In addition, some scholars have extended it to the field of complex numbers. Shen et al. explored the GS of delayed complex-valued dynamical networks (DCVDNs) by using hybrid controllers in ^[13].

It is worth noting that, due to the complexity of the structures of networks, oscillation and chaos will occur in system. Therefore, many researchers have created viable controllers to synchronize the networks, such as distributed impulsive control, adaptive control, and pinning control, etc. In ^[7], Guan et al. realized the synchronization of CDNs through distributed impulsive control. In ^[14], Zhou et al. investigated local and global adaptive synchronization of uncertain CDNs with time-varying delays by using an adaptive controller. In ^[15], Ren et al. explored fixed-time synchronization (FTS) of DCVDNs with random perturbations under impulsive pinning control. In ^[16], Feng et al. discussed pinning synchronization in general CDNs through pinning control strategies.

In practical applications, people often hope that the controlled system can achieve the expected goal within fixed time or predefined time, to reduce the control cost. Fixed-time is determined based on the designed controller parameters and is independent of the initial system values. To our delight, there have been many reports on fixed-time synchronization results. In ^[17,18], the fixed time stabilization and synchronization of neural networks is studied. The FTS of complex networks with random noise is explored by using pinning control ^[19,20]. Hu et al. explored the FTS of complex networks with time delays ^[21]. Predefined-time is determined solely by the actual requirements of the systems, and is not influenced by any initial values or parameters. In ^[22], the authors studied the synchronization of fuzzy neural networks by designing a controller that does not contain linear terms, and obtained sufficient conditions for FTS and predefined-time synchronization (PDTS). In addition, some scholars have extended single-layer networks to double-layer networks. In ^[23], the authors explored the FTS/PDTS of complex-valued BAM neural networks. In ^[24], the authors used a non-jitter adaptive control strategy to realize the FTS/PDTS of discontinuous neutral competitive networks. For further interesting results, see ^{[25,26,27,28,29]}. The research of general synchronization is implemented on the basis of infinite running time, but FTS/PDTS can greatly reduce the running time, thus reducing the control cost. Synchronization within a fixed/predefined time reduces control cost. In ^[30], Liu et al. explored the cluster synchronization of uncertain CDNs in prescribed-time by using a pinning control technique. In ^[31], the problem of finite/prescribed-time cluster synchronization for switching CDNs with proportional delays is studied by using pinning control. In ^[32], Xiao et al. studied FTS/PDTS of memory neural networks based on state variable index coefficients. In ^[33], Ruan et al. studied the FTS/PDTS on complex networks in light of the T-S fuzzy system. In real networks, delays and random noise interference are not negligible, so it is necessary to discuss FTS/PDTS between SCDNs with delays. This is one of the motivations for this article.

As we know, due to the limited information transmission speed and processing time between systems, the system will inevitably have time delays and random disturbances. The existence of disturbance factors will cause the system to lose stability ^[34]. In practical scenarios, the nodes or endpoints of complex networks may have delays, which brings complexity into the analysis of complex networks. Random noise will cause the system to lose synchronization. In recent years, many researchers have developed a keen interest in the synchronization of CDNs with stochastic perturbations. In ^[35], the synchronization of stochastic CDNs (SCDNs) with time delays is discussed. In ^[36], Li et al. explored the synchronization of SCDNs by using adaptive coupling control methods. In ^[20], Zhang et al. explored the FTS of complex networks with nonidentical nodes and random perturbations. The above works consider general synchronization rather than GS between CDNs with delays and random perturbations. GS is the extension of general synchronization, so this is an second driving force of this paper.

This paper is devoted to the FTGS/PDTGS of SCDNs with delays.

1). In this paper, the synchronization of CDNs with time delays and random disturbances is considered. If time delays and random disturbances are not considered, the networks may not be able to accurately describe the dynamic relationship between nodes. Therefore, considering the time delays and random disturbances, the real network's model can be truly described.

2). Compared with previous literature ^[22,23], this paper extends the FTSt lemma of stochastic systems, so that the system ST is not subject to $\eta$. Therefore, the results of this paper are more general.

3). By designing a feedback controller without linear terms, the SCDNs can achieve fixed/predefined time synchronization.

4). The sufficient conditions for synchronization of the SCDNs are derived by using stochastic analysis methods and inequality techniques.

The structure of this paper is as follows: Section II introduces the models, controllers, definitions, theorems, and lemmas. Section III derives the sufficient conditions for achieving the FTGS/PDTGS of SCDNs. Section IV provides an example. Finally, we provide a conclusion for this paper.

2.   Preliminaries and model

2.1.   Notation

Let $||\ast ||$ be the Euclidean norm. If $P$ is a matrix, its transpose is expressed as $P^T.$ If $P$ is a symmetric matrix, its maximum and minimum eigenvalues are expressed as $\lambda_{\max}(P)$ and $\lambda_{\min}(P)$. $\otimes$ is the Kronecker product. $\omega_{i}$ is the Brownian motion defined on a complete probability space $(\Omega, \mathcal{F}, \left\{\mathcal{F}_{t} \right\}_{t\geq 0}, \mathcal{P})$. $PC([-\vartheta, 0], R^{M})$ is a set of functions $\varphi_{1}: ([\vartheta, 0], R^{M})$ continuous everywhere.

2.2.   Problem formulation

Consider the following mathematical model of SCDNs with delays:

where $\psi_{i}(t) = {(\psi _{i1}(t), \psi _{i2}(t), \dots, \psi _{iM}(t))}^T\in R^{M}$ is the state vector of the $i$-th node, $\Theta _{i}: R^{M}\times R^{M}\rightarrow R^{M}$ is the activation function, and $\vartheta _{1}$ and $\vartheta _{2}$ represent the internal delays and the transmission delays, respectively. $A\in R^{M\times M}, \mathfrak{V} = {(b_{ij })}_{M\times M}\in R^{M\times M}$ and $\mathfrak{Y} = {(\backepsilon _{ij })}_{M\times M}\in R^{M\times M}$ are coupling matrices, where $b_{ij }(\backepsilon _{ij })$ is defined as follows: from node $i$ to $j \ (i\neq j)$, then the coupling strength $b_{ij }\neq 0\ (\backepsilon _{ij }\neq 0)$; otherwise, $b_{ij } = 0\ (\backepsilon _{ij } = 0)$, and the matrices $\mathfrak{V}$ and $\mathfrak{Y}$ satisfy

$\ell _{i}$ denotes the noise intensity function. Suppose the initial value of system (2.1) is $\psi_{i}(t) = \varphi _{i}(t) \in PC([-\vartheta, 0], R^{M})$, $t\in[-\vartheta, 0]$, and $\vartheta = \max\left\{\vartheta _{1}, \vartheta _{2}\right\}$.

Remark 1. Because CDNs typically consist of many interconnected nodes, the relationships between these nodes change over time. If time delays and random disturbances are not considered, the model of networks may not be able to accurately describe the dynamic relationship between nodes. For example, in the intelligent transportation system, the communication between vehicles needs to consider time delays and random disturbances to ensure that the information transmission between vehicles is reliable. If delays and random perturbations are ignored, they can lead to communication failures between vehicles, affecting traffic flow and safety.

Select system (2.1) as the master system. Then, the slave system can be described as

where $p_{i}(t) = {(p_{i1}(t), p_{i2}(t), \dots, p_{iM}(t))}^T\in R^{M}$, $K_{i}(t)$ is the controller. Denote $p_{i}(t) = \psi _{i}(t) \in PC([-\vartheta, 0], R^{M})$, $t\in[-\vartheta, 0]$ as initial condition of system (2.2). Let $\varphi _{i} = (\varphi _{i1}, \varphi _{i2}, \dots, \varphi _{iM})\in R^M$ and the Jacobian matrix of $\varphi _{i}(p_{i}(t))$ is given by:

Let $\hbar_ {i}(t) = \psi_{i}(t)-\varphi p_{i}(t)$. The error systems can be described as follows:

where $\Theta _{i}(t, \hbar_ {i}(t-\vartheta _{1})) = \Theta _{i}(t, \psi_{i}(t-\vartheta _{1}))-\Theta _{i}(t, \varphi _{i}(p_{i}(t-\vartheta _{1})))$.

To achieve FTGS in systems (2.1) and (2.2), the controller is designed in the following manner:

where $\lambda _{1} > 0, \lambda _{2} > 0$, $\iota > 1, 0 < \beta < 1$. $sign(\cdot)$ is the sign function.

Remark 2. Compared with ^[13], we further consider the effect of external random noise on the system. In addition, the controller in this paper does not contain linear terms, so the results obtained are more general.

Substituting controller (2.4) into the error system (2.3), we get

Remark 3. The phenomenon of synchronization refers to the existence of multiple interrelated components or processes in a system, which can maintain the same or similar state. Studying synchronization can help us better understand complex behaviors in nature, such as communication systems. It is worth noting that, when studying synchronization phenomena, we need to consider the stability of the error system. By studying the stability of error system, we can understand the degree of influence of error on system synchronization, so as to design a more stable and reliable system. That is, the synchronization of systems (2.1) and (2.2) can be translated into the stability of the error system (2.5).

We now present the necessary definitions, assumptions, and lemmas.

Definition 1. CDNs (2.1) and (2.2) can realize the GS if

where $\varphi _{i}:R^{M}\to R^{M}$ is a holomorphic map with an inverse map $\varphi _{i}^{-1}$, and $T_{\varepsilon }$ is the settling time (ST).

Remark 4. In Definition 1, if $\varphi _{i}(p_{i}(t)) = \rho p_{i}(t), \rho\in R$, called projective synchronization. If $\varphi _{i}(p_{i}(t)) = p_{i}(t)$, it is called fully synchronization. If $\varphi _{i}(p_{i}(t)) = -p_{i}(t)$, it is called anti-synchronization. If $\varphi _{i}(p_{i}(t)) = p_{i}(t-\sigma)$, it is called lag synchronization, where $\sigma$ is time lag.

Assumption 1. For $\forall \psi, p \in R^M,$ suppose that $\exists l _{i} > 0,$ satisfies the Lipschitz condition and

holds.

Assumption 2. For $\forall z_1, z_2 \in R^M$, and the noise function $\ell_{i} (t, z_1, z_2),$ and $\exists \mu _{i} > 0,$ satisfying

where $\ell_{i} (t, 0)\equiv 0, \ i = 1, 2, \dots, M$.

The main results are obtained through the following lemma.

Lemma 1. ^[37] Let $k_{i}\geq 0\ (i = 1, 2, \dots, M)$, $0 < r < 1, \varrho > 1.$ Then, the following inequalities hold:

To obtain the main results presented in the next section, we introduce some necessary concepts regarding stochastic differential equations.

Given is a stochastic nonlinear network in consideration ^[18]:

with

(i). $\psi (t)\in R^M$ is the state of (2.6),

(ii). Continuous function $\Theta : R^{M}\to R^{M}$ and $\Theta _1: R^{M}\to R^{M\times M}$ satisfy $\Theta (t, 0) = 0$ and $\Theta _1(t, 0) = 0$, respectively,

(iii). $\omega(t)$ is the Brownian motion.

Denoted by $\psi (t, \psi _{0})$ is the root of (2.6) with initial condition $\psi _{0}$. When $t\geq T$, $\psi (t, \psi _{0}) = 0$, and the ST function is given by

Definition 2. Suppose $\mathcal{C} ^{2, 1}(R^{M}\times R_{+}, R_{+})$ is the family of all non-negative functions $\mathsf{V}$ on $R^{M}\times R_{+}$ which are continuously twice differentiable in $\psi$ and once differentiable in $t$. For $\mathsf{V} \in \mathcal{C} ^{2, 1}(R^{M}\times R_{+}, R_{+})$, define the operator $\mathcal{L}\mathsf{V}$ related to system (2.6) given by

Definition 3. ^[18] Assume the following conditions hold:

(i). $\lim_{t \to T_{\varepsilon }}||E(\psi (t))||^{2} = 0$.

(ii). $||\psi (t)||^2\equiv 0$ for $t\geq T_{\varepsilon }$.

Then, system (2.6) is said to be globally stochastically FTSt.

Definition 4. ^[38] System (2.6) can achieve stochastic FTSt in probability$,$ if $\exists T_{\varepsilon } > 0, T_{\max} > 0$, such that, $\forall \bar\zeta (s), s\in [t_0-\vartheta, t_0]$ and

(i). The origin achieves global stochastic FTSt in probability.

(ii). The mean value of ST function $T (\bar\zeta (s), \omega)$ is independent of the initial value of the network, and its upper bound is bounded by $T_{\max} > 0$. That is,

Lemma 2. ^[38] Let $\mathsf{V}: R^{M}\to R_{+}$ be a nonnegative definite and radially unbounded function, and $\eta _{1} > 0, \eta_{2} > 0$, $\iota > 1, 0 < \beta < 1$, satisfying$,$

Then, network (2.6) is FTGS, and the ST can be estimated as

where $\tau = \frac{1-\beta}{\iota-\beta}, \gamma = \eta_{1}+\eta_{2}-\eta$. When $\iota+\beta = 2$, the ST can be more accurately estimated as $T(\psi, \omega) < \tilde{T}_{\varepsilon }$, where

where $\Delta = 4\eta_{1}\eta_{2}-\eta^{2}$.

Lemma 3. Let $\mathsf{V}: R^{M}\to R_{+}$ be a nonnegative definite and radially unbounded function, and $\eta _{1} > 0$, $\eta_{2} > 0$, $\iota > 1, 0 < \beta < 1$, satisfying,

If $\iota+\beta = 2$, $\eta > 2\sqrt{\eta_{1}\eta_{2}}$, then network (2.6) is FTGS, and the ST can be estimated as

Proof. Similar to the proof in ^[39], we choose the following integral function:

Now, we use variable substitution, which is $w = w_{1}^{\gamma-1}$, when $\eta > 2\sqrt{\eta_{1}\eta_{2}}$, and we get

If $\eta > 2\sqrt{\eta_{1}\eta_{2}}$, then $\eta^2-4\eta_{1}\eta_{2} > 0$, and one has

The proof is complete. □

Remark 5. In ^[22,23], $\eta$ is restricted to $\eta < 2\sqrt{\eta_{1}\eta_{2}}$. In Lemma 2 of this paper, we further extend the constraint on $\eta$ to $\eta > 2\sqrt{\eta_{1}\eta_{2}}$ and prove it by constructing integral functions. In comparison to the current findings, Lemma 3 in this paper has wider applicability. The system can better cope with diversity and complexity, and thus be more stable and reliable.

Lemma 4. ^[38]. Let $\mathsf{V}(\psi)$ be a C-regular function on $R^M\to R$ that satisfies the following inequality:

where $\eta < \min\left\{\eta_{1}, \eta_{2}\right\}$. Then, system (2.3) is FTS within PDTS $T_{d} > 0$, where

3.   Main results

Now, we will discuss the FTGS/PDTGS of SCDNs with delays. Based on the controller (2.4), the error system (2.5) to achieve the FTGS is our main control objective.

3.1.   Fixed-time generalized synchronization

Denote $\eta_i = L+\lambda _{\max}\big(2||\mathfrak{V} \otimes A||+||\mathfrak{Y} \otimes A||\big)+\mu _{i}$, and in the controller (2.4) will get the following results.

Theorem 1. Let Assumptions 1 and 2 hold$.$ Then, CDNs (2.1) and (2.2) can be realized FTGS under controller (2.4)$,$ if the following conditions are satisfied:

where $L = \max\left\{l_{i}\right\}$, $\eta = \max\left\{\eta_i\right\}$, $\lambda _{1} > 0, \lambda _{2} > 0,$ and $\breve{\lambda }_{1} = \lambda _{1}(Mm)^{\frac{1-\iota }{2}}$, and the ST is estimated by $T_{\varepsilon }$ defined in Lemma 2.

Proof. Select the Lyapunov function as follows:

The operator $\mathcal{L}$ defined in (2.7) onto the derivative of $\mathsf{V}$ in system (2.5) can be computed as

From Assumption 1,

where $L = \max\left\{l_{i}\right\}, i = 1, 2, \dots, M$.

Furthermore, based on the definition of $b_{ij }$ and $\backepsilon _{ij }$, we have

and

From Lemma 1,

Based on Assumption 2,

Substituting (3.4)–(3.9) into (3.3),

From (3.10),

By utilizing the Cauchy-Schwarz inequality,

Let $\hat{\eta} = L+\lambda _{\max}||\mathfrak{Y} \otimes A||\leq 0$, that is, under conditions (3.1) and (3.2) of Theorem 1, one has

If (3.1) and (3.2) hold, then $\mathsf{V}(t)\to 0, (t\to \infty)$, which means that $||\hbar_ {i}(t)||\to 0, (t\to \infty), i$ = $1, 2, \dots, M$. Based on Lemmas 2 and 3, CDN (2.5) is FTGS and the ST can be derived from Lemma 2.

The proof is finished. □

Remark 6. Using Lemmas 2 and 3, the FTGS/PDTGS of SCDNs with real domain delays are discussed. The work in this paper is a complementary extension of reference ^[13]. It provides a good basis for considering the FTGS/PDTGS of DCVDNs with random impulsive disturbance in the next stage.

Corollary 1. Let Assumptions 1 and 2 and inequality (3.2) hold. If $\iota +\beta = 2$ and $\eta > 2\sqrt{\eta_{1}\eta_{2}}$, then systems (2.1) and (2.2) can be FTGS with the ST $\tilde{T}_{\varepsilon }$ defined in Lemma 2.

When the error system gradually approaches zero, the system may fluctuate due to the presence of a sign function in the controller (2.4). In order to avoid such fluctuations, a continuous controller will be used below to achieve the FTS of systems (2.1) and (2.2).

where $\lambda _{1}\geq 0, \lambda _{2}\geq 0$, $\iota_{1}, \iota_{2}, \beta_{1}, \beta_{2}$ are integers satisfying $\iota_{1} < \iota_{2}, \beta_{1} > \beta_{2}$. So, we have the following Corollary 2.

Corollary 2. Let Assumptions 1 and 2 and inequality (3.2) hold. Then, systems (2.1) and (2.2) can be FTGS under controller (3.14), with the ST $T_{\varepsilon }$ defined in Lemma 2. If $\frac{\iota_{1}}{\iota_{2}} +\frac{\beta_{1}}{\beta_{2}} = 2$ and $\eta > 2\sqrt{\eta_{1}\eta_{2}}$, then systems (2.1) and (2.2) can be FTGS under controller (3.14), with the ST $\tilde{T}_{\varepsilon }$, where, $\eta_{1} = 2\lambda_{1}$, $\eta_{2} = 2\lambda_{2}M^{\frac{\beta_{2}-\beta_{1}}{2\beta_{2}}}, \iota = \frac{\iota_{1}+\iota_{2}}{2\iota_{2}}, \beta = \frac{\beta_{1}+\beta_{2}}{2\beta_{2}}$. The remaining symbols are explained in Theorem 1.

Proof. Similar to Theorem 1, the Lyapunov function is constructed as $\mathsf{V}(t) = \sum_{i = 1}^{M} \hbar_ {i}^{T}(t)\hbar_ {i}(t)$, and one has

From Lemma 1,

and

By combining (3.5)–(3.7), (3.10), (3.17), and (3.18), we can get

where $\eta = \max\left\{\eta_i\right\}$.

According to Lemmas 2 and 3, systems (2.1) and (2.2) can achieve FTS under controller (3.14), where ST can be estimated by $T_{\varepsilon }$. □

3.1.1.   Predefined-time generalized synchronization

In this section, we discuss the PDTS of systems (2.1) and (2.2) through some control methods. To this end, we give the following controller:

where

where

Theorem 2. Let Assumptions 1 and 2 and inequality (3.2) hold, and when $\frac{\iota_{1}}{\iota_{2}} +\frac{\beta_{1}}{\beta_{2}} \neq 2$ or $\eta > 2\sqrt{\eta_{1}\eta_{2}}$ when $\frac{\iota_{1}}{\iota_{2}} +\frac{\beta_{1}}{\beta_{2}} \neq 2$, then systems (2.1) and (2.2) can be realized to be PDTGS by controller (3.19), and the ST is $T_{d}$.

Proof. Similarly to Corollary 2, we choose the Lyapunov function as $\mathsf{V}(t) = \sum_{i = 1}^{M} \hbar_ {i}^{T}(t)\hbar_ {i}(t)$,

The symbols are the same as in Corollary 2.

According to Lemma 4, systems (2.1) and (2.2) can implement PDTGS under controller (3.19). □

Remark 7. We know that sign functions in the controller cause the system to vibrate. In practical engineering applications, system jitter may make the system more difficult to maintain and inevitably increase the control. Therefore, in Corollary 2, we use a continuous feedback controller (3.19) to effectively avoid system jitter.

4.   Numerical example

To demonstrate the usefulness of FTGS and PDTGS strategies, an example is given in this section.

Example. Consider the following SCDNs with two nodes:

Let $\Theta (t) = \tanh(t), \ell _{i}(\psi) = 0.4, \vartheta _{1} = 0.150, \vartheta _{2} = 1.070$. Choose as $A = 0.2I_{2}$, where $I_{2}$ represents the $2\times 2$ identity matrix. $B$ and $C$ represent the external coupling configuration matrix without delays and with delays, respectively, and can be expressed as

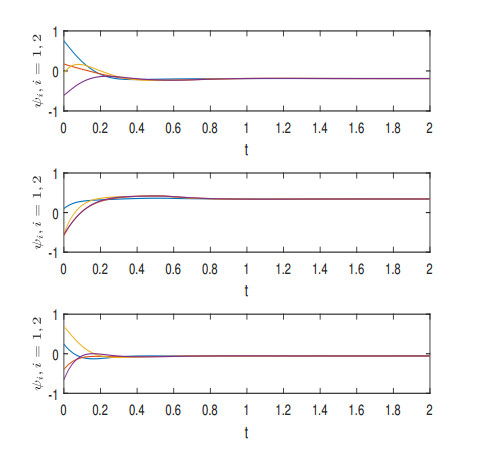
where the initial values of system (4.1) are chosen as $\psi_{1}(t) = -0.15$, $\psi_{2}(t) = 1.15$. Figure 1 shows the state of system (4.1).

Remark 8. CDNs often change with the change of time and environment in practical applications, so the control strategy is very important. The stability of the drive system (4.1) under the feedback controller (2.4) is shown in Figure 1. The greater the control intensity over time, the faster the system tends to stabilize.

System (4.1) is the master system, and the corresponding slave system is

where the symbols are defined in systems (2.1) and (2.2). The map $\varphi _{i}$ is defined as follows:

Then, the inverse map is

The feedback controller is

where $\hbar_ {i}(t) = \psi_{i}(t)-\varphi p_{i}(t), i = 1, 2$, and $\varphi _{i}(t)$ is the Jacobian matrix defined in (2.2). The error system of systems (4.2) and (4.3) is

Let $\eta _{1} = 6.032, \eta _{2} = 8.202$, $\big|\Theta (t, \psi (t))-\Theta (t, p(t))\big|\leq \big|\psi (t)-p(t)\big|$, that is, $l_{i} = 1$, and select $\mu = 0.5$, satisfying Assumptions 1 and 2. Due to $\eta = \max\left\{\eta _{1}, \eta _{2}\right\} = 8.202$, $\lambda_{1} = 3.1, \lambda_{2} = 3.1, \iota = 0.01, \beta = 2.1$, and we satisfy inequality (3.2). Therefore, from Theorem 1, it can be concluded that systems (4.2) and (4.3) can achieve FTGS and ST $T_{\varepsilon}^{3} = 11.513$. The synchronization error behavior of systems (4.2) and (4.3) is shown in Figure 2. The ST $T_{\varepsilon}^{1}$ can be easily calculated by MATLAB.

Figure 3 shows the evolution curve of $\iota = 0.9, \beta = 1.1$ for systems (4.2) and (4.3) in Corollary 1. Figure 4 shows the evolution curve of $\iota_{1} = 5, \iota_{1} = 6, \beta_{1} = 7, \beta_{2} = 6$ (i.e., $\frac{\iota_{1}}{\iota_{2}}+\frac{\beta_{1}}{\beta_{2}} = 2$) for systems (4.2) and (4.3) in Corollary 2. From Figure 5, the ST of the fixed time lemma generalized in this paper is more accurate than that in the previous literature. Figure 6 illustrates the state of the error system (4.5) when $T_{d} = 0.863, \iota = 0.310, \beta = 0.611$. The numerical results show that the estimated settlement time in this paper is reasonable and more widely applicable, which provides theoretical support for the analysis of complex systems.

Remark 9. In ^{[22,23,24,25,26,27]}, the FTS/PDTS for $\eta < \sqrt{\eta_{1}\eta_{2}}$ is discussed. However, it will make the accuracy of estimating ST more conservative. This paper further discusses the case of $\eta > \sqrt{\eta_{1}\eta_{2}}$, which makes the results of this paper more general. It is more resistant to parameter disturbance, external interference and uncertainty, more suitable for different situations and environments, and enhances the robustness of the system.

5.   Conclusions

This paper focuses on the FTGS/PDTGS of SCDNs with delays, studied by a feedback controller without linear terms. First, based on the fixed/predefined-time stability lemma of stochastic differential equations, we optimize the ST of the system. Since there is no linear term in the controller, the results of this paper are more general. In addition, we use an inequality technique to analyze the fixed/predefined-time synchronization of CDNs for the first time, and derive sufficient conditions for ensuring the FTGS/PDTGS of SCDNs. We believe that the findings of this research result provide theoretical support for studying and creating complex networks. In the future, our work will further analyze the GS of fractional order CDNS with reaction-diffusion terms or impulsive effects. At the same time, we try to use less conservative Lipschitz conditions to study CDNs, making the network more stable and thus easier to achieve synchronization.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare no conflict of interest.