Cluster synchronization of coupled complex-valued neural networks with leakage and time-varying delays in finite-time

1.   Introduction

In contrast to conventional neural networks (NNs) ^[1], coupled NNs (CNNs) are often susceptible to exhibit complex dynamical properties due to sub-network contact and cooperation ^[2,3,4,5]. CNNs are becoming important because of their potential in various application domains, e.g., electrical grid, medical science, image processing, and compression coding ^[6,7]. Although complex-valued signals are common in real-world applications, CNNs are unable to process them since real-valued signals are involved, e.g., in coupled real-valued neural networks (CRVNNs) ^[3,4,5,6].

In order to deal with complex-valued data ^[8,9,10,11], coupled complex-valued neural network (CCVNNs) are introduced. They can provide efficient and complex characteristics by incorporating complex variables as network elements ^{[12,13,14,15,16,17,18]}. The activation function selection poses the biggest challenge for a complex-valued neural network. There are two different activation functions in complex-valued neural networks (CVNNs): amplitude/phase activation and real/imaginary activation. The node activation function in a real case is often a smooth, bounded, nonconstant function. These constraints on the activation function are quite simple, so choosing a real function that satisfies them is not hard. In a complex valued neural network, any regular analytic function cannot be bounded unless it reduces to a constant. This is known as Liouville's theorem ^[19]. That is to say, activation functions in complex-valued neural networks cannot be both bounded and analytic. As a result, the primary difficulty for complex-valued neural networks is the activation functions. compared with CRVNNs, CCVNNs can solve various practical issues, e.g, a neuron with complex signal and orthogonal decision boundary can efficiently handle the XOR and symmetry detection problems ^[20,21]. In ^[22], CCVNNs can accurately represent optical wave fields of phase-conjugate resonators, since their phase and amplitude characteristics can be interpreted by complex-valued signals. Furthermore, CCVNNs have a number of advantages, including faster learning and reliability as well as powerful computing capabilities. Therefore, CCVNNs have attracted attention pertaining to their dynamic studies for real-world applications.

Many stability and synchronization studies have been reported, e.g., finite-time Mittag-Leffler stability ^[23], global stability ^[24,26], input-to-state stability ^[27] and lag synchronization, complete synchronization, anti-synchronization ^{[28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]}. Among these, CNN synchronization has been popular due to its effectiveness in various applications, e.g, image encryption, image protection, and secure communication ^[45]. In cluster synchronization (CS), the elements in a network are grouped into various clusters. In this respect, the elements from the same cluster are completely synchronized, while those in different clusters are desynchronized. For example, two subgroups will be naturally formed in social networks when a crowd of people chooses to accept or reject an opinion according to their preference. Subtasks will divide the robot network into communities when a collection of robots is to complete a complex task, and consensus should be reached within each community. Many research studies on CS have been conducted since this phenomenon exists in many different systems, and it is applicable to different complex networks including cellular and metabolic networks, social networks, electrical power grid networks, biological NNs, and telephone cell graphs ^{[2,3,46,47,48,49]}. Liu et al. ^[50] considered the fractional-ordered linearly coupled system consisting of $N$ NNs. Zhang et al. ^[51] explored CS of delayed CNNs with fixed and switching coupling topologies by employing Lyapunov theory and differential inequalities method. Yang et al. ^[52] discussed the CS issue of fractional-order networks subject to nonlinear coupling in finite time with complex variables based on the decomposition method. While CS of complex networks has received substantial attention, research on CS of complex-valued networks is new, despite its potential use. In ^[52], CS of a complex variable dynamical complex network was studied, but without considering time delays. Therefore, the problem of CS for complex variable networks in finite time requires further investigation.

The majority of studies focused mostly on asymptotic or exponential synchronization of networks through traditional control techniques. However, in reality, the networks might always be expected to achieve synchronization as quickly as possible, particularly in engineering fields. To achieve a faster convergence rate in time-delay complex networks, an effective method is to use finite-time (FT) synchronization control techniques. FT synchronization means the optimality in convergence time. Investigation of finite-time CS (FTCS) of CCVNNs is useful from a practical perspective. FTCS denotes the ability of the controlled systems to achieve synchronization in a predetermined amount of time with the assistance of some suitable controllers. Comparing with asymptotic synchronization, which occurs as the time approaches omit infinity, in certain instances synchronization in FT not only improves synchronization speed but also has the advantage of low disruption and perseverance in the presence of uncertainty. Therefore, it is worthwhile to investigate the CS of CCVNNs in FT. Yu et al. ^[53] analyzed FTCS pertaining to coupled dynamical systems without time delays. Concerning the prescribed-time stability for nonlinear PWS systems, two novel lemmas are established in ^[42], where the stable time can be arbitrarily specified and is independent of any control settings and initial values. The global fixed-time convergence principle of nonlinear systems with semi-Markovian switching is developed in ^[49], to ensure the cluster synchronization in finite/fixed time for a semi-Markovian switching complex dynamical network with discontinuous dynamic nodes. He et al. ^[54] studied adaptive CS in FT based on a neutral type of CNN models with mixed delays. FTCS for a coupled fuzzy cellular NNs was investigated in ^[55]. These studies are generally based on the premise that the parameters of complex networks are in the real domain. There are very few results on the CS of CCVNNs in FT. Furthermore, it is well understood that time delays are unavoidable in NN models, which can result in oscillations or asynchronization ^[56]. As a result, it is essential to examine time delays affect on CNNs. Furthermore, several studies have reported that constant time delays and time-varying delays in NNs can result in chaotic behaviors. In many real-world problems, leakage delays appear as negative feedback terms in a system, which can have a substantial impact on the dynamics of NNs ^{[57,58,59,60,61]}. Because of the impact on many real-world systems such as automatic control systems, it is important to investigate synchronization of NNs with time-varying delays and leakage delays ^[62,63,64]. We investigate asymptotic and CS of CCVNNs in FT with leakage and time-varying delays, and provide several useful criteria in this paper. Our research contributions include:

${\rm{(i) }}$ Examining CCVNN models with leakage and time-varying delays, which constitute a class of coupling systems. Finding a suitable activation function subject to complex functions is the primary goal of many studies on CVNNs. We employ the real and imaginary types of activation functions in this paper. In addition, it is useful to divide them into their corresponding real and imaginary parts of models for the analysis of FT synchronization of the drive-response CCVNN model with leakage time delays.

${\rm{ (ii)}}$ Deriving the sufficient conditions with respect to asymptotical synchronization of the drive-response CCVNN model with time delays. This is achieved by constructing some non-negative functions, along with inequality techniques. Moreover, the CS criteria are presented.

${\rm{(iii)}}$ Formulating the conditions in terms of nonsingular M-matrices for determining asymptotic and FTCS of the CCVNN model. Comparing with other conditions such as the Linear Matrix Inequalities (LMIs), the main benefit of the adequate condition includes non-singularity of the M-matrix ^[65,66,67]. Unlike recent studies on CS in FT with nonlinear coupling and no time delay of CVNN models^[52], our method is applicable to CVNN models with both leakage and time variable delays. As such, our results are more general, as compared with those in the existing literature.

2.   Model description and preliminaries

Graph theory. Consider a graph $\mathbb{G} = (\mathcal{V}, \mathcal{E}, G)$ with a set of nodes $\mathcal{V} =$ $\{1, \ldots, V\}(V > 2$), $\mathcal{E} \subseteq \mathcal{V} \times \mathcal{V}$, and coupling matrix $\mathbb{J} = \left[\jmath_{i j}\right]_{V \times V} \in \mathbb{R}^{V \times V}$ with $\jmath_{i i} = -\sum_{j = 1, j \neq i}^{V} \jmath_{i j}$ for $i = 1, \ldots, V$, where $\jmath_{i j} > 0$ if there is an interaction between nodes $i$ and $j$, or else $\jmath_{i j} = 0$. Denote $\left\{\mathcal{C}_{1}, \mathcal{C}_{2}, \ldots, \mathcal{C}_{M}\right\}$ with $\mathcal{C}_{k} =$ $\left\{l_{k-1}+1, l_{k-1}+2, \ldots, l_{k}\right\}$ as a set of partitions of nodes $\mathcal{V}$ with non-empty subset $M$ such that $(2 \leq M < V)$.

Consider a linear CCVNN model consisting of $V$ CVNNs with both leakage and time-varying delays. Referring to the $i$th node, its dynamics can be represented by:

where $i \in \mathcal{C}_{k}$ with $k \in$ $\{1, \ldots, M\}, \ z_{i}(t) = \left(z_{i 1}(t), \ldots, z_{i n}(t)\right)^{T} \in \mathbb{C}^{n}$ denotes the $i$th CCVNN's state vector (2.1) at time $t$; $\tau(t)$ is the time-varying delay; $\delta$ is the leakage term; $f\left(z_{i}(t)\right) =$ $\left(f_{1}\left(z_{i 1}(t)\right), \ldots, f_{n}\left(z_{i n}(t)\right)\right)^{T}$ denotes the vector of neuron activations; $A_{i} = \operatorname{diag}\left(a_{1}^{i}, a_{2}^{i}, \ldots, a_{n}^{i}\right) >$ $0; C_{i} = \left[c_{l r}^{i}\right]_{n \times n} \in \mathbb{C}^{n \times n}$ and $D_i = \left[d_{l r}^{i}\right]_{n \times n} \in \mathbb{C}^{n \times n}$ are the interconnection weight matrices, $l, r = 1, 2, \ldots, n$; $\hat{I}_{i} = (\hat{I}_{1}^{i}, \ldots, \hat{I}_{n}^{i})^{T} \in \mathbb{C}^{n}$ denotes an external input source. We will design the control law $u_i(t)$ later. The initial states that correspond to (2.1) are:

where $\varphi_{i}(s) = \left(\varphi_{i 1}(s), \ldots, \varphi_{i n}(s)\right)^{T} \in \mathbb{C}^{n}$ is continuous.

Remark 2.1. The terms $f(z_i(t-\tau(t)))$ and $f(z_i(t))$ are referred to as activation functions with and without time delay, respectively. There are significant time delays in every biological process. Time delay occurs in the propagation of action potentials along the axon and transmitting signals across the synapse for connected neurons. Discrete delays reflect the system's centralized effects of delays, whereas distributed delays have effects on neural networks at some duration or period relative to the discrete point of delays. Further research using discrete and distributed delays on this model will be carried out in the near future.

Assumption 2.1. Let any given $k = 1, 2, \ldots, M$, $A_{l_{k-1}+1} =$ $A_{l_{k-1}+2} = \cdots = A_{l_{k}}$$= \bar{A}_{k}, C_{l_{k-1}+1} = C_{l_{k-1}+2}$$= \cdots = C_{l_{k}} = \bar{C}_{k}, D_{l_{k-1}+1} = D_{l_{k-1}+2} = \cdots =$ $D_{l_{k}} = \bar{D}_{k}$, and $\hat{I}_{l_{k-1}+1} = \hat{I}_{l_{k-1}+2} = \cdots = \hat{I}_{l_{k}} = \bar{I}_{k}$.

The activation function in $(2.1)$ is Lipschitz continuous throughout this study.

Assumption 2.2. For $z(t) = a^R(t)+ib^I(t) \in \mathbb{C}, a^R(t), b^I(t) \in \mathbb{R}, f_k(z_k(t))$ is divided into its real and imaginary parts: $f_k(z_k(t)) = f_k^R(a_k^R(t))+if_k^I(b_k^I(t)), k = 1, 2, \dots, n.$ With the existence of some constants $\hat{\kappa}_k^-, \check{\kappa}_k^-, \hat{\kappa}_k^+, \check{\kappa}_k^+, k = 1, \ldots, n$ such that for any $u, v \in \mathbb{R}$ and $u \neq v,$ $f^R_k(\cdot), f^I_k(\cdot), g^R_k(\cdot), g^I_k(\cdot)$ satisfies the following:

Remark 2.2. The proposed generalized activation function class in this paper can describe the activation functions more flexibly and more specifically. The constants $\hat{\kappa}_k^{-}, \check{\kappa}_k^{-}$ and $\hat{\kappa}_k^{+}, \check{\kappa}_k^{+}$ in Assumption 2.2 may be positive, negative, or zero, as illustrated in ^[68]. Especially, when $\hat{\kappa}_k^{-} = \check{\kappa}_k^{-} = 0$ and $\hat{\kappa}_k^{+} > 0, \check{\kappa}_k^{+} > 0$ Assumption 2.2 describes the class of globally Lipschitz continuous and monotone nondecreasing activation functions. And when $\hat{\kappa}_k^{+} > \hat{\kappa}_k^{-} > 0$ and $\check{\kappa}_k^{+} > \check{\kappa}_k^{-} > 0$ Assumption 2.2 describes the class of globally Lipschitz continuous and monotone increasing activation functions. Obviously, sigmoid and piecewise linear neuron activation functions are special cases of the functions meeting Assumption 2.2.

Assumption 2.3. Assume that the coupling matrix $\mathbb{J}$ satisfies the following:

where $\mathbb{J}_{k k} \in \mathbb{R}^{\left(l_{k}-l_{k-1}\right) \times\left(l_{k}-l_{k-1}\right)}$ is a zero row-sum matrix consisting of non negative off-diagonal values. $\mathbb{J}_{k r} \in$ $\mathbb{R}^{\left(l_{k}-l_{k-1}\right) \times\left(l_{r}-l_{r-1}\right)}(k \neq r)$, $k, r = 1, \ldots, M$ is a zero row-sum matrix.

Definition 2.1. The CCVNN model in (2.1) is said to achieve CS in FT with partition $\left\{\mathcal{C}_{1}, \mathcal{C}_{2}, \ldots, \mathcal{C}_{M}\right\}$, if $t^{*} > t_{0}$ such that for any $i \in \mathcal{C}_{k}, k = 1, 2, \ldots, M$

and the following equation is satisfied by $R_{k}(t) = \hat{a}_k^R(t)+i\hat{b}_k^I(t)$.

Assumption 2.3 and (2.3) are combined. As such, for any $i \in \mathcal{C}_{k}, k = 1, 2, \ldots, M$

Lemma 2.1. ^[69] Consider the following differential inequality with time delay:

where $\tau > 0, x(t) \in \mathbb{R}$ is continuously differential and non-negative function. If $a > b > 0,$ then $\lim\limits_{t \rightarrow +\infty}x(t) = 0.$

Remark 2.3. In ^[70], different dynamical behaviors for RVNN models with time-varying delays were examined using Lyapunov stability theory. Here, we study CVNN models, i.e the states, connection weights and external inputs belong to the complex domain. Therefore, the derived theoretical results are complementary to those in ^[70].

3.   Main results

3.1.   Asymptotic CS of CVNN models

The new criteria for asymptotic and CS in FT for CCVNN models are established. Let $e_{i}(t) = z_{i}(t)-R_{k}(t)$ for $i \in \mathcal{C}_{k}$. As such, the control laws $\mathcal{U}^R(t)$ and $\mathcal{U}^I(t)$ can be devised as:

It follows that the error dynamical models are characterized by $(2.1), (2.4)$ and Assumption 2.1

where $i \in \mathcal{C}_{k},$ $f^R(e^R, e^I), f^I(e^R, e^I), f^R(e_{\tau}^R, e_{\tau}^I), f^I(e_{\tau}^R, e_{\tau}^I),$ $e_{i}^R(t_\delta), e_{i}^I(t_\delta)$ are real and imaginary parts of $f(e_i(t)) = f(z_i(t)-f(R_k(t))),$ $f(e_i(t)) = f(z_i(t-\tau(t))-f(R_k(t-\tau(t)))),$ $e_i(t-\delta(t) = z_i(t-\delta)-R_k(t-\delta)$, respectively.

Denote $\bar{\Lambda} =$ $\operatorname{diag}\left(\bar{\lambda}_{1}, \ldots, \bar{\lambda}_{M}\right), \bar{A} = \operatorname{diag}\left(a_{\min }^{1},\ldots, a_{\min }^{M}\right)$ with $a_{\min }^{k} =$ $\min\limits_{1 \leq j \leq n}\left\{a_{l}^{i} \mid l = 1, \ldots, n, i \in \mathcal{C}_{k}\right\}$ for $k = 1, 2, \ldots, M,$

Theorem 3.1. If Assumptions 2.1–2.3 hold, the CCVNN model in (2.1) with $t_0 = 0$ can achieve CS asymptotically under controller (3.1) if $\tilde{\Lambda}+\tilde{A}-\tilde{C}-\tilde{D}-\tilde{\mathbb{J}}$ is a non-singular M-matrix.

Proof: Since $\tilde{\Lambda}+\tilde{A}-\tilde{C}-\tilde{D}-\tilde{\mathbb{J}}$ is a non-singular $M$-matrix, there exists a positive vector $\mathcal{J} = (\mathcal{J}_1, \dots\mathcal{J}_{M})^T \in \mathbb{C}^M$ such that $(\tilde{\Lambda}+\tilde{A}-\tilde{C}-\tilde{D}-\tilde{\mathbb{J}})\mathcal{J}\geq 0,$ where,

As most of the majority of neural network stability criteria are derived from the Lyapunov theory, they are all conservative. Reducing the conservatism has been the topic of much research. The reduction can be achieved with the Lyapunov stability theory primarily through two phases: a) choosing the suitable Lyapunov functional and b) estimating its derivative. Therefore, we constructed the following non-negative function as follows:

The derivative of $V(t)$ along the solution of model (3.2) gives

As such, from Assumption 2.2

Similarly

and

On the other hand, since

we obtain the following results based on the characteristics of matrix $\mathbb{J}$,

and

As a result of (3.7), it follows that

Similarly, we can have

From (3.7)–(3.11) we have,

where

As a result of $(\tilde{\Lambda}+\tilde{A}-\tilde{C}-\tilde{D}-\tilde{\mathbb{J}})\mathcal{J}\geq 0$, $a_{\min} > b_{\max} > 0$. Then according to Lemma 2.1, one can obtain that $\lim_{t \rightarrow +\infty} V(t) = 0,$ which implies that the coupled complex-valued neural networks (2.1) can achieve cluster synchronization asymptotically. This completes the proof of Theorem 8.

Remark 3.1. CS is a more feasible collective behavior than complete synchronization, is thought to be important in biological research and communication engineering ^[71]. Generally, if all of the neurons in neural networks are separated into many clusters, nodes within the same cluster can achieve complete synchronization, but there is no uniform behavior between various clusters. In this paper, we investigate cluster synchronization of the model (2.1) using the synchronization manifold method described in ^[72]. It should be noted that we do not assume the coupling matrix is symmetric or diagonal. However, the majority of previous works on network synchronization are predicated on this assumption ^[73,74]. Moreover, only the simple Lyapunov function is used in this paper. As a result, the conditions of Theorems are strict. To further reduce the conservativeness and improve the conditions for this cluster synchronization problem, a delay partitioning approach or the free-weight matrix method ^[75,76] could be used. However, these methods will significantly increase the complexity of the proof procedure. Therefore, it is omitted here. In the near future, this model will be subjected to additional research using the delay partitioning approach or the free-weight matrix method.

3.2.   CS of CVNN models in FT

In the following, the solution of model (2.1) is designed in the sense of Filippov. As such, the control inputs $\mathcal{U}^R(t), \mathcal{U}^I(t)$ to be constructed is discontinuous and the differential inclusion can be written as:

where $\mathbb{K}[\mathcal{U}_i(t)]$ represents the closure of the convex hull of $\mathcal{U}_i(t)$. There exists a measurable function $\mathcal{S} _i(t) \in \mathbb{K}[\mathcal{U}_i(t)]$ when the measurable selection theorem is applied such that

From ^[77,78], it is straightforward to establish that if Assumption 2.2 holds, then there exists a solution $z(t)$ for the IVP combined with (2.1) on [$t_0, \infty$) with controller inputs $\mathcal{U}_i^R(t), \mathcal{U}_i^I(t)$ for given initial condition (2.2). Consider the controller inputs in the following form:

From Assumption 2.1 as well as (2.1) and (2.4), the synchronization errors become

and the set valued map $\mathcal{U}_i(t)$ is denoted by

Then there exists $\mathcal{O}_i(t) \in K[sgn(e_i(t))]$ such that $t\geq t_0$

Definition 3.1. ^[79] The response model of (2.3) is said to be synchronized with the drive model of (2.1) in FT under a suitable designed controller (3.15), if a constant $T^{*} > 0$ exists such that $\left\|e\left(T^{*}\right)\right\|_{1} = 0$ and $\|e(t)\|_{1} \equiv 0$ for $t > T^{*}$, where $\|e(t)\|_{1} = \sum_{i = 1}^{n} |e_{i}(t)|, e(t) = (e^R(t), e^I(t))^T$. Note that $T$ is denoted as the settling time of synchronization if $T = \inf \left\{T^{*} \geq 0\right.$ for $\left.t \geq T^{*}\right\}.$

Based on the above account, a theorem is put forward, as follows.

Theorem 3.2. Based on Assumptions 2.1 and 2.2, if $\eta^{R_1}_k \geq ||\bar{d}_k^R\theta^{RR}||_1-$$||\bar{d}_k^I\theta^{IR}||_1, \eta^{I_1}_k$$\geq ||\bar{d}_k^R\theta^{RI}||_1-$$||\bar{d}_k^I\theta^{II}||_1, \eta^{R_2}_k$$\geq ||\bar{d}_k^R\theta^{IR}||_1+$$||\bar{d}_k^I\theta^{RR}||_1, \eta^{I_2}_k$$\geq ||\bar{d}_k^R\theta^{II}||_1+$$||\bar{d}_k^I\theta^{RI}||_1, \bar{\mathcal{Y}}$$\geq 0,$ for $k = 1, \ldots, M$ and $\tilde{\Lambda}+\tilde{A}-\tilde{C}-\tilde{\mathbb{J}}$ is a non singular $M-$matrix, i.e, there exists a positive vector $\mathcal{Y} = (\mathcal{Y}_1, \ldots, \mathcal{Y}_{2M})^T \in \mathbb{R}^{2M}$ such that $(\tilde{\Lambda}+\tilde{A}-\tilde{C}-\tilde{\mathbb{J}}) \mathcal{Y} > 0 \in \mathbb{R}^{2M}$, then the coupled CVNN model of (3.13) can realize FTCS under controller (3.15).

Proof: Leveraging on the non-singularity of $\mathbb{J}$ matrix

We can obtain

According to $\eta^{R_1}_k \geq ||\bar{d}_k^R\theta^{RR}||_1-$$||\bar{d}_k^I\theta^{IR}||_1, \eta^{I_1}_k$$\geq ||\bar{d}_k^R\theta^{RI}||_1-$$||\bar{d}_k^I\theta^{II}||_1, \eta^{R_2}_k$$\geq ||\bar{d}_k^R\theta^{IR}||_1+$$||\bar{d}_k^I\theta^{RR}||_1, \eta^{I_2}_k$$\geq ||\bar{d}_k^R\theta^{II}||_1+$$||\bar{d}_k^I\theta^{RI}||_1$ for $k = 1, \ldots, M,$ (3.6), (3.21) and (3.22), one can obtain

The above equations yield

where $\bar{\alpha}_{ki} = \alpha_{k}$ if $e_i^{R}(t)\neq 0$, $e_i^{I}(t)\neq 0$ otherwise $\bar{\alpha}_{ki} = 0$.

Integrating both sides of the above inequality from $0$ to $t$ gives

Note that as $||e(t)||_1 \geq 0$, it indicates that

It then follows from (3.25) that $\lim _{t \rightarrow +\infty} V(t) = -\infty$, which contradicts $V(t) > 0$, for $t \in(0, +\infty). \quad$ Hence there exists $T^{*} \in(0, +\infty)$ such that $V\left(T^{*}\right) = 0$, which implies that

Next, we show that $\|e(t)\|_{1} \equiv 0$ for $\forall t \geq T^{*}$. Otherwise, suppose that there exists $T_{1} > T^{*}$ such that $\left\|e\left(T_{1}\right)\right\|_{1} > 0.$ Let

It then follows from the fact $\left\|e\left(T^{*}\right)\right\|_{1} = 0$ that $T_{s}$ is nonempty. Notice that $T_{s} < T_{1}, \left\|e\left(T_{s}\right)\right\|_{1} = 0$ and $\|e(t)\|_{1} > 0$ for all $t \in\left(T_{s}, T_{1}\right].$ As such, there exists $T_{2} \in\left[T_{s}, T_{1}\right]$ such that $\left.\dot{V}(t)\right|_{t = T_{2}} > 0$, otherwise, $\forall t \in\left[T_{s}, T_{1}\right], \dot{V}(t) \leq 0.$ Then $V(t)$ is monotone increasing, we obtain $0 = V\left(T_{s}\right) \geq V\left(T_{1}\right) > 0$, which is a contradiction. Therefore, there exists $T_{2} \in\left(T_{s}, T_{1}\right]$ such that $\left.\dot{V}(t)\right|_{t = T_{2}} > 0.$ On the other hand, note that $\left\|e\left(T_{2}\right)\right\|_{1} > 0$ implies that

It follows from inequality (3.25) that $\dot{V}\left(T_{2}\right) < 0$, which is also a contradiction. As such, $\|e(t)\|_{1} \equiv 0, \forall t \geq T^{*}.$ Consequently, based on Definition 3.1, response model (2.1) is synchronized with drive model (2.3) in FT under controller (3.15). The proof of is completed.

Remark 3.2. Different from ^[70] in this study, 1-norm of vectors is used to construct the real and imaginary types of Lyapunov functions. The necessary sufficient criterion is derived in the form of a non-singular M-matrix using the constructed Lyapunov function (3.4), which can be easily verified. In addition, other Lyapunov functions that prove CS of different NN models are available, e.g., Euclidean norm or positive-definite quadratic form. Nonetheless, the resulting adequate conditions are in the form of LMIs or eigenvalues, which are more difficult to be verified.

Remark 3.3. Referring to Theorems 8 and 10, when $a_i^R(t) = b_i^I(t), \hat{a}_k^R(t) = \hat{b}_k^I(t),$

we can establish new adequate conditions for asymptotic CS and FTCS for NN models described by differential equations. Therefore, the results can be used for analyzing FTCS of NN models with a differential equation as well as with two differential equations.

Remark 3.4. In ^[52], the dynamical properties of ordinary difference equations in the real domain were studied. However, very few results on coupled network models in the complex domain are available. Different from the existing literature, we investigate CCVNN models and analyze their dynamical behaviours in this study.

4.   Numerical example

A simulation example to demonstrate the usefulness of the theoretical results is presented.

Example 4.1. Consider a two-neuron coupled CVNN model of (2.1) with leakage and time varying delays, where $f(\cdot) =$ $\left(f_{1}(\cdot), f_{2}(\cdot)\right)^{T} = (\tanh (\cdot), \tanh (\cdot))^{T}, \tau(t) = 2, M = 3$ and

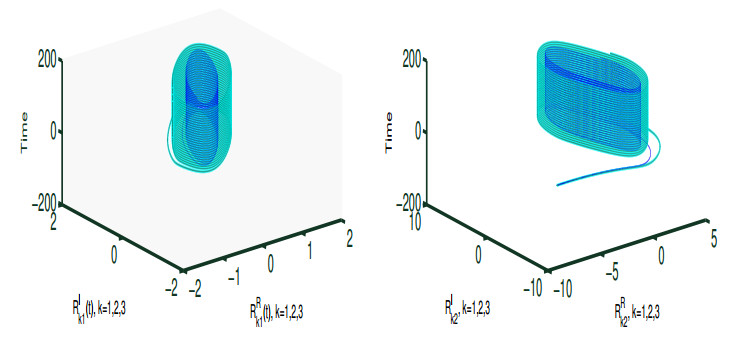
The initial values for $k = 1, 2, 3$ are $R_{k}(t) = (0.8, -8)^{T}$ for $t \in[-1, 0]$. The phase portraits are shown in Figure 1, demonstrating their chaotic behaviors.

The coupling matrix $G$ for CCVNN model (2.1) is

Then, model (2.1) can be separated into three clusters $\mathcal{C}_{1} =$ $\{1, 2, 3\}, \mathcal{C}_{2} = \{4, 5\}$, and $\mathcal{C}_{3} = \{6, 7\}.$ With the above-mentioned settings, we can obtain $A =$ $\operatorname{diag}(1, 1, 1),$$\mu^{RR} = \mu^{RI} = \mu^{IR} =$$\mu^{II} = \theta^{RR} =$$\theta^{RI} = \theta^{IR} = \theta^{II} =$$\operatorname{diag}(1, 1, 1),$$\bar{C}^{RR} = \bar{C}^{RI} =$$\bar{C}^{IR} =$$\bar{C}^{II} = \operatorname{diag}(14, 14.2, 14),$$\bar{D}^{RR} =$$\bar{D}^{RI} =$$\bar{D}^{IR} = \bar{D}^{II} =$$\operatorname{diag}(5.2, 5.1, 5)$, and

Case 1 : Let $\bar{\Lambda} = \operatorname{diag}(20, 19, 20)$, one can achieve

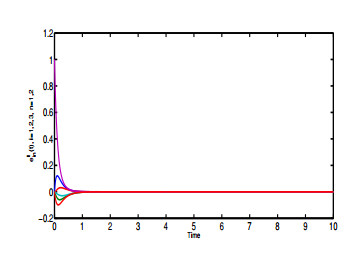
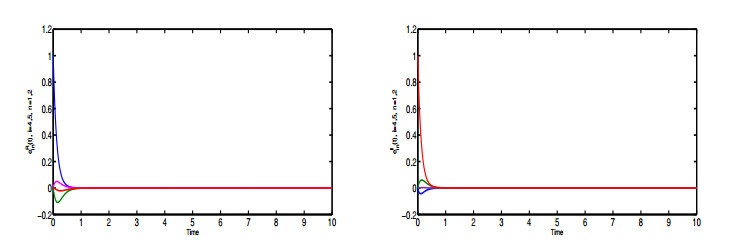
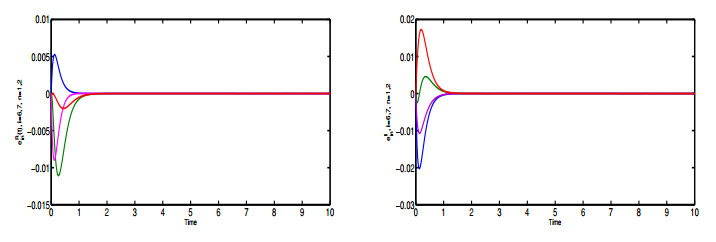
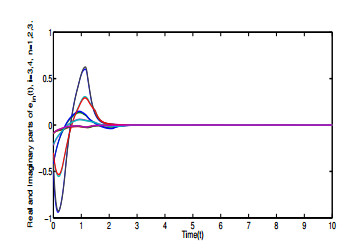
which is a non-singular $M$-matrix. Based on Theorem 8, CCVNN model (2.1) can realize CS asymptotically under (3.1) with respect to $\mathcal{C}_{1}, \mathcal{C}_{2}, \mathcal{C}_{3}$. To analyze the CS process, the error in each cluster is

For $k = 1, 2, 3$ in Figures 2–4, we have ${e}_{k}(t) \rightarrow 0$ when $t \rightarrow +\infty$, which implies that all states achieve CS asymptotically.

Case 2: Let $\bar{\Lambda} = \operatorname{diag}(19, 18, 18), \beta_{1} = 3, \beta_{2} = 2.73, \beta_{3} =$ 2.5, $\alpha_{1}^R = \alpha_{2}^R = \alpha_{3}^R = 1, \alpha_{1}^I = \alpha_{2}^I = \alpha_{3}^I = 1$. As such, the control law (3.15) follows that

implying that $\tilde{\Lambda}+\tilde{A}-\tilde{C}-\tilde{\mathbb{J}} =$ is a strictly diagonally dominant matrix.

Case 3: In this case, we take three neurons instead of two neurons in above two cases, the three dimensional interconnection weight matrices are taken as follows:

Then activation functions $f(z_i(t))$ and $f(z_i(t-\tau(t)))$ in (2.1) can be selected as $f(z_i(t)) = \tanh(z_i(t)), f(z_i(t-\tau(t))) = \tanh(z_i(t-\tau(t)))$ and the transmission time-varying delay is $\tau(t) = \frac{e^t}{e^t+1}$.

For the existence of the constants $\hat{\kappa}_k^- = 0.5, \check{\kappa}_k^- = 0.5, \hat{\kappa}_k^+ = 1, \check{\kappa}_k^+ = 1$ Assumption 3.2 is satisfies for the activation functions $f(z_i(t)) = \tanh(z_i(t)), f(z_i(t-\tau(t))) = \tanh(z_i(t-\tau(t))).$

The leakage term is selected as $\delta = 1.2$. The initial conditions associated with model (2.1) is chosen as $z_1(0) =$$(0.51-i0.32, -0.29-i0.31,$$0.01+0.01)^T,$$z_2(0) =$$(-0.32-i0.3, -0.3-i0.31,$$0.01+i0.01)^T,$$z_3(0) =$$(-0.311-i0.3, -0.31-i0.32,$$0.01+i0.01)^T,$$z_4(0) =$$(-0.2-i0.3, -0.32-i0.31,$$0.01+i0.01)^T.$ The coupling matrix $G$ for CCVNN model (2.1) is

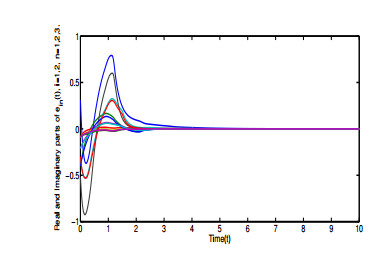
Then, model (2.1) can be separated into two clusters $\mathcal{C}_{1} =$ $\{1, 2\}$ and $\mathcal{C}_{2} = \{3, 4\}$. From the above findings we can easily show that the matrix $\tilde{\Lambda}+\tilde{A}-\tilde{C}-\tilde{D}-\tilde{\mathbb{J}}$ is a non-singular matrix for suitable $\tilde{\Lambda}$. Based on Theorem 8, CCVNNs (2.1) can realize CS asymptotically under the controller (3.1) with respect to $\mathcal{C}_{1}, \mathcal{C}_{2}$. To analyze the CS process, the error in each cluster is

For $k = 1, 2$ in Figures 5–6, we have ${e}_{k}(t) \rightarrow 0$ when $t \rightarrow +\infty$, which implies that all states achieve CS asymptotically.

5.   Conclusions

This study has examined the FT asymptotic and CS problem of delayed CVNN models with leakage delay. By utilizing the Lyapunov theory for differential systems and the Filippov regularization framework, new sufficient conditions to ensure the FT asymptotic and the CS for the considered drive-response coupled complex-valued models have been obtained. The conditions are formulated in terms of non-singular M-matrices for determining FT asymptotic and CS of CCVNN models. A simulation example with two cases has been given to validate the theoretical results. Although there exist many studies on CS ^[2,3,47,50] of CNNs and network control methods such as adaptive control ^[50], investigations on adaptive control schemes to realize adaptive and CS CCVNN models are limited. In this study, asymptotic CS of CCVNN models has been realized under adaptive control. The obtained results can extend further to those in the existing literature ^[2,3,47,50]. For further research, the dynamics of coupled delayed CVNN models with stochastic disturbances and impulsive effects will be investigated.

Acknowledgements

This research is made possible through financial support from the Rajamangala University of Technology Suvarnabhumi, Thailand. The authors are grateful to the Rajamangala University of Technology Suvarnabhumi, Thailand for supporting this research.

Conflict of interest

The authors declares no conflicts of interest.