Some Hermite-Hadamard and midpoint type inequalities in symmetric quantum calculus

1.   Introduction and preliminaries

Calculus is a major field of mathematics which mainly deals with the study of functions and their continuous changes. In the 17th century, Isaac Newton and Gottfried Wilhelm Leibniz contributed to its modern development. After the 17th century, Euler (1707–1783) was the first person who gave the idea of quantum calculus (a calculus which the concept of a limit excludes) which builds a connection between mathematics and physics. In the early 20th century, F. H. Jackson and others further advanced quantum calculus. Time-scale calculus has a subbranch called quantum calculus, which deals with the study of difference equations and solves many problems in dynamical systems. Quantum calculus can be further divided into two types: $\mathrm{q}$-calculus/$\mathrm{q}$-deformed calculus and $\mathrm{h}$-calculus. Moreover, we can say that the derivative and integration of classical calculus can be generalized in $\mathrm{q}$-calculus, and when $\mathrm{q \rightarrow 1}$, we recapture the classical results. The $\mathrm{q}$-parameter was first introduced in Newton's infinite series by the eminent mathematician Euler (1707–1783), who also developed $\mathrm{q}$-calculus. To define the $\mathrm{q}$-integral and $\mathrm{q}$-derivative of continuous functions on the interval $(0, \infty)$, popularly known as calculus without limits, Jackson ^[1] extended Euler's idea in 1910. The ideas of $\mathrm{q}$-fractional integral inequalities and $\mathrm{q}$-Riemann-Liouville fractional integral inequalities were investigated by Al-Salam ^[2] in 1966. The main and fundamental principles of $\mathrm{q}$-calculus were summarized by Kac and Cheung in their book ^[3]; see also ^[4,5,6]. Later, Tariboon and Ntouyas, in particular, presented the $\mathrm{q}$-integral and $\mathrm{q}$-derivative of continuous functions on finite intervals in ^[7]. Moreover, in recent years, some authors have studied the existence theory for $\mathrm{q}$-boundary value problems ^[8,9,10].

In the following, we summarize definitions and a basic introduction to the $\mathrm{q}$-calculus. In this paper, let $\mathrm{q}$ be a constant with $0 < \mathrm{q} < 1$, and $[\mathrm{b}_{0}, \mathrm{b}_{1}]\subseteq \mathbb{R}$ with $\mathrm{b}_{0} < \mathrm{b}_{1}$. The quantum analog of any number $n$ can be given as

Definition 1.1. ^[7] The $\mathrm{q}$-derivative on $[\mathrm{b}_{0}, \mathrm{b}_{1}]$ for a continuous function $\mathfrak{f}: [\mathrm{b}_{0}, \mathrm{b}_{1}] \to \Re$ is defined by

A function $\mathfrak{f}$ is stated to be ${}_{\mathrm{b}_{0}}\mathrm{q}$-differentiable if ${}_{\mathrm{b}_{0}}D_{\mathrm{q}}\mathfrak{f}(\mathrm{x})$ exists.

Putting $\mathrm{b}_{0} = 0$ in Definition 1.1, then (1.1) takes the form

It is a derivation operator provided by Jackson. For more information, see ^[1].

Definition 1.2. ^[7] Let $\mathfrak{f}: [\mathrm{b}_{0}, \mathrm{b}_{1}] \to \Re$ be a continuous function. Then, a $_{\mathrm{b}_{0}}\mathrm{q}$-integral on $[\mathrm{b}_{0}, \mathrm{b}_{1}]$ can be defined as

for $\mathrm{x}\in [\mathrm{b}_{0}, \mathrm{b}_{1}].$ A function $\mathfrak{f}$ is called $_{\mathrm{b}_{0}}\mathrm{q}$-integrable if $\int_{\mathrm{b}_{0}}^{\mathrm{x}}{\mathfrak{f}(\mathrm{t})}\; d_{\mathrm{q}}\mathrm{t}$ exists for all $x \in [\mathrm{b}_{0}, \mathrm{b}_{1}]$.

Substituting $\mathrm{b}_{0} = 0$ into Definition 1.2, (1.2) can then be given as

This is a $q$-integral provided by Jackson. For more information, see ^[1]. Moreover, Jackson ^[1] introduced the $\mathrm{q}$-Jackson integral on the interval $[\mathrm{b}_{0}, \mathrm{b}_{1}]$ as

Using the above fundamentals of quantum theory, Tariboon and Ntouyas presented numerous well-known inequalities, namely Hermite-Hadamard, trapezoid, Ostrowski, Cauchy-Bunyakovsky-Schwarz, Grüss, and Grüss-Cebyvsev for $\mathrm{q}$-calculus in ^[11]. However, Alp et al. in 2018 introduced the first corrected version of the $\mathrm{q}$-Hermite-Hadamard inequality in ^[12] by considering support lines and the geometrical concept of convex functions as follows:

Theorem 1.3. Let $\mathfrak{f}:\left[ \mathrm{b}_0, \mathrm{b}_1\right] \rightarrow \Re$ be a convex function on $\left[ \mathrm{b}_0, \mathrm{b}_1\right]$. Then, we have

where ${{\mathrm{q}}} \in (0, 1)$.

Another useful approach was introduced by Bermudo et al. in 2020 in the context of quantum calculus in ^[13]. They not only provided new definitions of the quantum derivative and quantum integrals, but also employed these notions to obtain a new interpretation of the Hermite-Hadamard inequality.

Definition 1.4. ^[13] If $\mathfrak{f}:\left[ \mathrm{b}_0, \mathrm{b}_1\right] \rightarrow \Re$ is an arbitrary function, then an $^{\mathrm{b}_1}\mathrm{q}$-definite integral on $\left[ \mathrm{b}_0, \mathrm{b}_1\right]$ is given by

Definition 1.5. ^[13] If $\mathfrak{f}:\left[ \mathrm{b}_0, \mathrm{b}_1\right] \rightarrow \Re$ is an arbitrary function, then $^{\mathrm{b}_1}\mathrm{q}$-derivative of $\mathfrak{f}$ at $\mathrm{t} \in \left[ \mathrm{b}_0, \mathrm{b}_1\right]$ is defined by

Theorem 1.6. ^[13] Let $\mathfrak{f}:\left[ \mathrm{b}_{0}, \mathrm{b}_{1}\right] \rightarrow \Re$ be a convex function on $\left[ \mathrm{b}_{0}, \mathrm{b}_{1}\right]$. Then, we have the following new variant of the ${\mathrm{q}}$-Hermite-Hadamard inequalities

where ${{\mathrm{q}}}\in (0, 1)$.

There is a large amount of literature is presented regarding the development of useful inequalities in quantum calculus. Noor et al. established some inequalities of trapezoid type for $_{\mathrm{b}_0}\mathrm{q}$-integrals in ^[14]. On the other hand, Budak et al. presented several midpoint and trapezoid type inequalities for $^{\mathrm{b}_1}\mathrm{q}$-integrals in ^[15,16]. Some Simpson and Newton type quantum inequalities can be seen in ^{[17,18,19,20]}; for the coordinate case, see ^[21,22]. Many mathematicians have conducted research in the fascinating area of quantum calculus. Interested readers can check ^{[23,24,25,26]}.

In this paper, we will derive Hermite-Hadamard inequalities in the symmetrical quantum sense. The idea of symmetric quantum calculus was first introduced by Da Cruz et al. ^[27]. The $\mathrm{q}$-symmetric calculus plays an important role in quantum mechanics. It has a key role in the development of basic hypergeometric functions, the generalized linear Schr$\ddot{o}$dinger equation, and quantum dynamical equation, in quantum mechanics^[28]. We can write $\mathrm{q}$-differentials and $\mathrm{h}$-differentials in the symmetrical sense, which are mentioned in ^[3], for $\mathrm{q \neq 1}$, $\mathrm{h \neq 0}$,

Definition 1.7. ^[29] Let $\mathfrak{f}:[\mathrm{b}_{0}, \mathrm{b}_{1}]\subset\Re \rightarrow \Re$ be a continuous function. Then, the $\tilde{\mathrm{q}}$-derivative or ${}_{\mathrm{b}_{0}} \mathrm{q}$-symmetric derivative at $\mathrm{x}\in [\mathrm{b}_{0}, \mathrm{b}_{1}]$ is formulated as

which implies that

Definition 1.8. ^[29] Let $\mathfrak{f}:[\mathrm{b}_{0}, \mathrm{b}_{1}] \subset \Re\rightarrow \Re$ be a continuous function. Then, the $_{\mathrm{b}_{0}}\tilde{\mathrm{q}}$-definite integral on $[\mathrm{b}_{0}, \mathrm{b}_{1}]$ is given as

Here, $\mathrm{x}\in [\mathrm{b}_{0}, \mathrm{b}_{1}]$, or

If we take $\mathfrak{f}(\mathrm{t}) = 1$, then (1.6) becomes

If we take $\mathrm{b}_{0} = 0$ in (1.6), then

or

and is simply called $\tilde{q}$-integral.

If $\mathrm{u}\in(\mathrm{b}_{0}, \mathrm{x})$, then the $_{\mathrm{b}_{0}}\tilde{\mathrm{q}}$-definite integral on $[\mathrm{u}, \mathrm{x}]$ can be written as

Motivated by the idea of Bermudo et al. in ^[13], one can define the $^{\mathrm{b}_{1}}\tilde{\mathrm{q}}$-definite integral at $\mathrm{b}_{1} \in [\mathrm{b}_{0}, \mathrm{b}_{1}] \subset \Re$ as follows:

Definition 1.9. Let $\mathfrak{f}:[\mathrm{b}_{0}, \mathrm{b}_{1}] \rightarrow \Re$ be a continuous function. Then, the $^{\mathrm{b}_{1}}\tilde{\mathrm{q}}$-definite integral on $[\mathrm{b}_{0}, \mathrm{b}_{1}]$ is given as

for each $\mathrm{x}\in [\mathrm{b}_{0}, \mathrm{b}_{1}]$, or

Remark 1.10. It is pertinent to mention here that the monotonicity property

is not always true in quantum calculus for all $\mathrm{t} \in [\mathrm{b_{0}}, \mathrm{b_{1}}]$. In ^[30], one can find a counter-example in the context of Hahn calculus so that, if $\mathfrak{f} \leqslant \mathfrak{g}$ on an interval $[\mathrm{b_{0}}, \mathrm{b_{1}}]$, we have

Some recent investigations in this direction were pursued by Cardoso et al. in ^[31], where the authors give other generalizations of the Hahn difference operator by using $\beta$-integrals. Therefore, in order to avoid this ambiguity in this paper, in all our theorems, we will consider the monotonicity property for all functions in the context of symmetric $\mathrm{q}$-calculus, i.e., if $\mathfrak{f}(\mathrm{t}) \leqslant \mathfrak{g}(\mathrm{t})$, then

for all $\mathrm{t} \in [\mathrm{b_{0}}, \mathrm{b_{1}}]$.

2.   Hermite-Hadamard inequalities in symmetric $\mathrm{q}$-calculus

In this section, we introduce the Hermite-Hadamard inequality in symmetric $\mathrm{q}$-calculus at $\mathrm{b_{0}}\in [\mathrm{b_{0}}, \mathrm{b_{1}}]\subset\Re$, which is a different variant. Note that, in all theorems of this section, the monotonicity property, given in Remark 1.10, is satisfied for the function $\mathfrak{f}:[\mathrm{b_{0}, b_{1}}]\subset\Re \rightarrow \Re$.

Theorem 2.1. If $\mathfrak{f}:[\mathrm{b_{0}, b_{1}}]\subset\Re \rightarrow \Re$ is a convex differentiable function on $(\mathrm{b_{0}, b_{1}})$, then

holds for $0 < \mathrm{q} < 1$.

Proof. Since the line of support of the given function at the point $\dfrac{ (1-\mathrm{q}+\mathrm{q}^{2})\mathrm{b_{0}}+\mathrm{q}\mathrm{b_{1}}}{1+\mathrm{q}^{2}}\in (\mathrm{b_{0}, b_{1}})$ can be written as

Due to convexity of $\mathfrak{f}$ on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$,

for all $\mathrm{x} \in[\mathrm{b_{0}}, \mathrm{b_{1}}]$.

Taking the $_{\mathrm{b_{0}}}\tilde{\mathrm{q}}$-Integral on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$, we write

Hence,

Moreover, the secant line with end points ($\mathrm{b_{0}}, \mathfrak{f}(\mathrm{b_{0}})$) and ($\mathrm{b_{1}}, \mathfrak{f}(\mathrm{b_{1}})$) can also be written in terms of the function $\mathfrak{S}(\mathrm{x}) = \mathfrak{f}(\mathrm{b_{0}})+ \frac{\mathfrak{f}(\mathrm{b_{1}})-\mathfrak{f}(\mathrm{b_{0}})}{\mathrm{b_{1}}-\mathrm{b_{0}}}(\mathrm{x}-\mathrm{b_{0}})$. Using the convexity of $\mathfrak{f}$ on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$,

holds for all $\mathrm{x} \in$ [$\mathrm{b_{0}}, \mathrm{b_{1}}$].

Taking the $\mathrm{_{b_{0}}}\tilde{\mathrm{q}}$-Integral on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$, we can write

A combination of (2.2) and (2.3) gives (2.1). □

Remark 2.2. If $\mathrm{q} \rightarrow 1^{-}$ in Theorem 2.1, then it becomes the classical Hermite-Hadamard inequality, i.e.,

which was first introduced in ^[32].

Now we choose the point $\dfrac{\mathrm{q}\mathrm{b_{0}}+(1-\mathrm{q}+\mathrm{q}^{2})\mathrm{b_{1}}}{1+\mathrm{q}^{2}}$ instead of $\dfrac{ (1-\mathrm{q}+\mathrm{q}^{2})\mathrm{b_{0}}+\mathrm{q}\mathrm{b_{1}}}{1+\mathrm{q}^{2}}$, and we will get a different inequality which will be proved in the next theorem.

Theorem 2.3. For a convex differentiable function $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ on $(\mathrm{b_{0}}, \mathrm{b_{1}})$,

holds for all $\mathrm{x} \in [\mathrm{b_{0}}, \mathrm{b_{1}}]$.

Proof. Since the line of support of the given function at the point $\dfrac{\mathrm{q}\mathrm{b_{0}}+(1-\mathrm{q}+\mathrm{q}^{2})\mathrm{b_{1}}}{1+\mathrm{q}^{2}} \in(\mathrm{b_{0}}, \mathrm{b_{1}})$ can be written as $\mathfrak{t}_{1}(\mathrm{x}) = \mathfrak{f}\left(\dfrac{\mathrm{q}\mathrm{b_{0}}+(1-\mathrm{q}+\mathrm{q}^{2})\mathrm{b_{1}}}{1+\mathrm{q}^{2}}\right) +\mathfrak{f}^{\prime}\left(\dfrac{\mathrm{q}\mathrm{b_{0}}+(1-\mathrm{q}+\mathrm{q}^{2})\mathrm{b_{1}}}{1+\mathrm{q}^{2}}\right) \left(\mathrm{x}-\dfrac{\mathrm{q}\mathrm{b_{0}}+(1-\mathrm{q}+\mathrm{q}^{2})\mathrm{b_{1}}}{1+\mathrm{q}^{2}}\right)$, due to the convexity of $\mathfrak{f}$ on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$, we have

for all $\mathrm{x} \in[\mathrm{b_{0}}, \mathrm{b_{1}}]$.

Taking the $\mathrm{_{\mathrm{b_{0}}}\tilde{q}}$-Integral from $\mathrm{b_{0}}$ to $\mathrm{b_{1}}$, we get

Combining (2.6) and (2.3), we get (2.5), and hence the theorem is proved. □

Moreover, if we choose the midpoint of the interval [$\mathrm{b_{0}}, \mathrm{b_{1}}$] instead of $\dfrac{\mathrm{q}\mathrm{b_{0}}+(1-\mathrm{q}+\mathrm{q}^{2})\mathrm{b_{1}}}{1+\mathrm{q}^{2}}$, then we obtain another inequality which will be described in the next theorem.

Theorem 2.4. For a convex differentiable function $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ on $(\mathrm{b_{0}}, \mathrm{b_{1}})$,

holds for $0 < \mathrm{q} < 1$.

Proof. Since the line of support of the given function at the point $\dfrac{\mathrm{b_{0}}+\mathrm{b_{1}}}{2} \in(\mathrm{b_{0}}, \mathrm{b_{1}})$ can be written as $\mathfrak{t_{2}}(\mathrm{x}) = \mathfrak{f}\left(\dfrac{\mathrm{b_{0}}+\mathrm{b_{1}}}{2}\right)+ \mathfrak{f}^{\prime}\left(\dfrac{\mathrm{b_{0}}+\mathrm{b_{0}}}{2}\right)\left(\mathrm{x}-\dfrac{\mathrm{b_{0}}+\mathrm{b_{1}}}{2}\right)$, due to the convexity of $\mathfrak{f}$ on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$,

holds for all $\mathrm{x} \in[\mathrm{b_{0}}, \mathrm{b_{1}}]$.

Taking $\mathrm{_{\mathrm{b_{0}}}\tilde{q}}$-Integral from $\mathrm{b_{0}}$ to $\mathrm{b_{1}}$, we get

Now, combining (2.3) and (2.8), we get (2.7). □

We can also generalize the following results.

Theorem 2.5. For any convex differentiable function $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ on $(\mathrm{b_{0}}, \mathrm{b_{1}})$,

holds for $0 < \mathrm{q} < 1$, where

Proof. A combination of (2.1), (2.5), and (2.7) gives (2.9). Thus, the proof is complete. □

Using the same methodology and (1.7), we can derive the Hermite-Hadamard inequality and its types at the point $\mathrm{b_{1}}$ of the interval [$\mathrm{b_{0}}, \mathrm{b_{1}}$]. These results are in the following theorems.

Theorem 2.6. For any convex differentiable function $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ on $(\mathrm{b_{0}}, \mathrm{b_{1}})$,

Proof. We can prove it in the same way as in Theorem 2.1. □

Remark 2.7. If $\mathrm{q} \rightarrow 1^{-}$ in Theorem 2.6, we will get the classical Hermite-Hadamard inequality (2.4) again.

Corollary 2.8. If we add (2.1) and (2.10), then the following inequalities can be obtained:

and

Theorem 2.9. Let $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ be a function which is convex and differentiable on $(\mathrm{b_{0}}, \mathrm{b_{1}})$. Then,

holds.

Proof. The proof is similar to that of Theorem 2.3. □

Theorem 2.10. Let $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ be a function which is convex and differentiable on $(\mathrm{b_{0}}, \mathrm{b_{1}})$. Then,

Proof. The proof is similar to that of Theorem 2.4. □

Theorem 2.11. Let $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ be a function which is convex and differentiable on $(\mathrm{b_{0}}, \mathrm{b_{1}})$. Then,

holds for $0 < \mathrm{q} < 1$, where

Proof. A combination of (2.10), (2.11), and (2.12) gives (2.13). □

Now, we will investigate a function which does not hold for the Hermite-Hadamard inequality in $\mathrm{q}$-calculus. See Example 5 in ^[12].

Example 2.12. Let $\mathfrak{f}(\mathrm{x}) = 1-\mathrm{x}$, set $[\mathrm{b_{0}}, \mathrm{b_{1}}] = [0, 1]$, and for the value of $\mathrm{q}$ choose from (0, 1) in Theorem 2.1. Then, we have

Remark 2.13. In Example 2.12, we can see that $\mathrm{q}$-symmetric analogues of the Hermite-Hadamard inequality becomes equality for $\mathfrak{f}(\mathrm{x}) = 1-\mathrm{x}$ given as in Example 5 of ^[12].

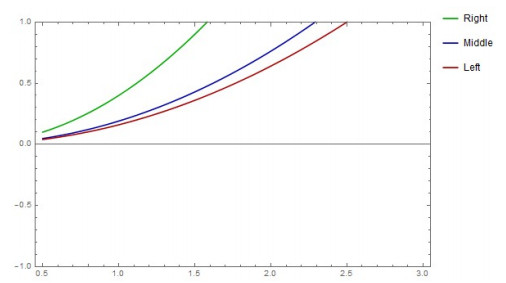
Example 2.14. Now, we choose $\mathfrak{f}(\mathrm{x}) = \mathrm{x}^{2}$ and $[\mathrm{b_{0}}, \mathrm{b_{1}}] = [0, 1]$, and we then get the following inequalities:

Case 1: We fix $\mathrm{b_{0}} = 0, \mathrm{b_{1}} = 1$, and the value of $\mathrm{q}$ is chosen from (0, 1) in Theorem 2.1. Then, the inequalities become:

Case 2: If we fix $\mathrm{q} = \dfrac{1}{2}$ and assume that $\mathrm{b_{0}}$ varies from 2 to 2.1 and $\mathrm{b_{1}}$ varies from 3 to 5 in Theorem 2.1, then the inequalities become

Since

inequality (2.15) becomes

Graphical representations of (2.14) and (2.16) are given in Figures 1 and 2.

3.   Midpoint type inequalities in symmetric q-calculus

In this section, we will construct a lemma and, with the help of this lemma, we will prove the midpoint type inequalities for the convex function in symmetric $\mathrm{q}$-calculus at $\mathrm{b_{0}}$. Also, note that in all theorems of this section, the monotonicity property, given in Remark 1.10, is satisfied for the function $\mathfrak{f}:[\mathrm{b_{0}, b_{1}}]\subset\Re \rightarrow \Re$.

Lemma 3.1. For any convex ${}_\mathrm{b_{0}}\mathrm{q}$-symmetric differentiable function $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ on $(\mathrm{b_{0}}, \mathrm{b_{1}})$, if its first ${}_\mathrm{b_{0}}\mathrm{q}$-symmetric derivative is continuous and integrable on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$, then

holds for $\mathrm{q} \in$ (0, 1).

Proof. Using the definition of the $\tilde{\mathrm{q}}$-derivative, we have

From the right-hand side of (3.1), we get

which completes the proof. □

Remark 3.2. If $\mathrm{q}$ approaches 1 in Lemma 3.1, it will reduce to Lemma 11 in ^[12], and Lemma 3.1 will help us to prove the midpoint type inequality in symmetric $\mathrm{q}$-calculus.

Theorem 3.3. For any ${}_\mathrm{b_{0}}\mathrm{q}$-symmetric differentiable function $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ on $(\mathrm{b_{0}}, \mathrm{b_{1}})$, if its first ${}_\mathrm{b_{0}}\mathrm{q}$-symmetric derivative is continuous and integrable on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$ and if $\mathfrak{|{}_\mathrm{b_{0}}\tilde{D}_{q}f}|$ is convex on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$, then the $\mathrm{q}$-symmetric midpoint type inequality holds:

where

Proof. Taking the modulus in Lemma 3.1, we have

Adding (3.3), (3.4), (3.5), and (3.6) and then putting in (3.2), we get the required result. □

Remark 3.4. If $\mathrm{q}$ approaches 1 in Theorem 3.3, it will become Corollary 14 in ^[12].

Theorem 3.5. For any ${}_\mathrm{b_{0}}\mathrm{q}$-symmetric differentiable function $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ on $(\mathrm{b_{0}}, \mathrm{b_{1}})$, if its first ${}_\mathrm{b_{0}}\mathrm{q}$-symmetric derivative is continuous and integrable on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$ and if $|{}_\mathrm{b_{0}}\tilde{D}_{\mathrm{q}}\mathfrak{f}|$ is convex on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$, then the $\mathrm{q}$-symmetric midpoint type inequality holds:

where

and

Proof. We have

Using (3.3)–(3.6) from Theorem 3.3, we get required result. □

Remark 3.6. If $\mathrm{q}$ approaches 1 in Theorem 3.5, it will become Corollary 17 in ^[12].

Theorem 3.7. For any ${}_\mathrm{b_{0}}\mathrm{q}$-symmetric differentiable function $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ on $(\mathrm{b_{0}}, \mathrm{b_{1}})$, if its first ${}_\mathrm{b_{0}}\mathrm{q}$-symmetric derivative is continuous and integrable on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$ and if $|{}_\mathrm{b_{0}}\tilde{D}_{\mathrm{q}}\mathfrak{f}|$ is convex on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$, then the $\mathrm{q}$-symmetric midpoint type inequality holds:

where

Proof. We have

Using $\tilde{\mathrm{q}}$-integration, we may write

and

Putting (3.8)–(3.11) into (3.7), we get the desired results. □

Remark 3.8. If $\mathrm{q}$ approaches 1 in Theorem 3.7, we will get Corollary 19 in ^[12].

Theorem 3.9. For any ${}_\mathrm{b_{0}}\mathrm{q}$-symmetric differentiable function $\mathfrak{f}:[\mathrm{b_{0}}, \mathrm{b_{1}}] \rightarrow \Re$ on $(\mathrm{b_{0}}, \mathrm{b_{1}})$, if its first ${}_\mathrm{b_{0}}\mathrm{q}$-symmetric derivative is continuous and integrable on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$ and if $|{}_\mathrm{b_{0}}\tilde{D}_{\mathrm{q}}\mathfrak{f}|$ is convex on $[\mathrm{b_{0}}, \mathrm{b_{1}}]$, then the $\mathrm{q}$-symmetric midpoint type inequality holds:

where

and

Proof. Using Lemma 3.1, estimate

Using (3.3)–(3.6) from Theorem 3.3, we get required result. □

Remark 3.10. If $\mathrm{q}$ approaches 1 in Theorem 3.9, then we will get Corollary 22 of ^[12].

4.   Conclusions

In this work, we constructed new results of Hermite-Hadamard and midpoint-type inequalities using the basic definition of symmetric quantum calculus. We also analyzed that, when $q \to 1$, the newly acquired inequalities transformed into classical Hermite-Hadamard and midpoint-type inequalities. Examples were considered to verify the newly acquired inequalities. These inequalities may be more helpful to obtain new results in symmetric quantum calculus for further publications.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (PSAU/2023/01/90102).

Conflict of interest

The authors declare no conflicts of interest.