A high accuracy compact difference scheme and numerical simulation for a type of diffusive plant-water model in an arid flat environment

1.   Introduction

Ecological and environmental desertification began to emerge as a prominent issue in the late 1960s and early 1970s. Due to a lack of rainfall, the Sahara region in western Africa experienced severe drought, causing serious harm to local ecosystems, people's livelihoods, and the global ecology^[1]. At present, desertification is a comprehensive issue related to economy, society, and ecology. The areas where desertification occurs are in arid and semi-arid regions, and the result is desertification.Therefore, preventing desertification has become a hot and core issue in global research, and plant and water play a crucial role in preventing desertification. In arid and semi-arid regions, the rainfall is relatively low, and the feedback between vegetation and water acts as a feedback effect between vegetation and water, resulting in a regular distribution of vegetation in time and space. This distribution is called vegetation pattern^[2,3,4]. Many domestic scholars have conducted extensive research on the spatiotemporal dynamics of vegetation in arid and semi-arid regions based on diffusion type nonlinear partial differential equations^[5,6,7,8,9]. However, obtaining precise and accurate solutions for nonlinear equations is generally challenging. In contrast, numerical solutions are relatively easier to obtain and can also reveal the spatiotemporal dynamics of the system.

How to effectively solve nonlinear partial differential equations has been a long-standing concern for researchers, and various numerical methods for solving this equation include finite volume method, finite element method, lattice Boltzmann method, spectral method, finite difference method, etc.^{[10,11,12,13,14,15,16,17,18,19]}. The finite difference method is widely used due to its simplicity, strong operability, easy access to high order numerical formats, and ease of programming. The high order finite difference method, after years of development, has achieved rich research success^[20,21,22]. Furthermore, research has shown that high-precision methods are superior in improving the reliability and effectiveness of model numerical simulations.

This article focuses on the plant-water model in a flat environment of one-dimensional space^[23], as follows:

Where $W$ represents the density of water, and $N$ represents the density of plant biomass. $A$ is rainfall rate, $M$ is plant mortality, $L$ is the rate of evaproation of water. $J$ is plant conversion rate, and $R$ denotes water penetration rate. $T$ represents the time and $N_{x x}, W_{x x }$ represent second-order partial derivatives in one-dimensional space. In this literature, the author applied the branch theory of reaction diffusion equations to study the spatiotemporal dynamics of model (2.1), and it is necessary to demonstrate the spatiotemporal distribution of vegetation and water from a numerical simulation perspective.

This paper is organized as follows: In section 2, a high-precision compact difference scheme is constructed using the finite difference method for a model (2.1) that satisfies homogeneous Neumann boundary conditions. In section 3, we proved the stability of the high-precision compact difference scheme in model (2.1). In section 4, numerical examples are constructed to verify the convergence and accuracy of the high-precision compact difference scheme. By utilizing Matlab for numerical simulation, we obtain spatial distribution maps of vegetation and water under small disturbances with varying parameters. By analyzing their variation patterns, the impact of small changes in parameters on the spatiotemporal dynamics of the vegetation water model is revealed. In section 5, a summary of the results of this study and prospects for future research are presented.

2.   High order difference scheme for a class of plant water models

In this paper. Consider the plant-water model (1.1) in one-dimensional space on flat environment. The following dimensionless transfromation is perfromed for system (1.1):

● $\omega = \frac{\sqrt{R} J}{\sqrt{L}} W, \quad n = \frac{\sqrt{R}}{\sqrt{L}} N, \quad a = \frac{\sqrt{R} J}{L \sqrt{L}} A, \quad t = L T,$

● $x = \frac{\sqrt{L}}{\sqrt{D_{1}}} X, \quad m = \frac{M}{L}, \quad \mu = \frac{D_{2}}{D_{1}},$

We obtain the initial conditions on an interval $(0, l\pi)$ and the following system with Neumann boundary:

For the sake of convenience and to ensure consistency with the symbol representations used in this paper, Eq (2.1) can be reformulated into the form presented in Eq (2.2).

Now we identify $n$ with $u$, $\omega$ with $v$, $\omega n^{2}-m$ with $f(u, v)$, $a-\omega-\omega n^{2}$ with $g(u, v)$, ${d}_{1} = 1$, $\mu$ with ${d}_{2}$. In order to establish a high-order compact difference scheme, we rewrite (2.2) in the form, which is a nonlinear diffusion reaction system:

where

The reaction term $\mathrm{R}(\mathrm{W})$ represents a non-linear function associated with the variable $W$.

2.1.   High order compact difference scheme

In order to construct a high order compact difference scheme for solving (2.3)–(2.5), the region divides $[0, l \pi] \; \times \; [0, T]$ into a uniform meshed. Take positive integers $N$ and $M$, divide the interval $[0, l \pi]$ into $N$ equal parts, and $[0, T]$ into $M$ equal parts. Define $\mathrm{h} = \frac{\mathrm{l \pi}}{\mathrm{N}}$, $\tau = \frac{\mathrm{T}}{\mathrm{M}}$; $\mathrm{x}_{\mathrm{i}} = \mathrm{0}+\mathrm{ih}$, $0 \leq \mathrm{i} \leq \mathrm{N}$; $\mathrm{t}_{\mathrm{n}} = \mathrm{n} \tau$, $0 \leq \mathrm{n} \leq \mathrm{M}$; $\Omega_{\mathrm{h}} = \left\{\mathrm{x}_{\mathrm{i}} \mid 0 \leq \mathrm{i} \leq \mathrm{N}\right\}$; $\Omega_{\tau} = \left\{\mathrm{t}_{\mathrm{n}} \mid 0 \leq \mathrm{n} \leq \mathrm{M}\right\}$; $\Omega_{\mathrm{h} \tau} = \Omega_{\mathrm{h}} \times \Omega_{\tau}$. Define the grid function $v = \left\{\mathrm{v}_{\mathrm{i}}^{\mathrm{n}} \mid 0 \leq \mathrm{i} \leq \mathrm{N}, 0 \leq \mathrm{n} \leq \mathrm{M}\right\}$ on $\Omega_{\mathrm{h} \tau}$, define

2.1.1.   Interior scheme

In developing a high-precision compact difference scheme for interior points, we refer to the work presented by Wei JianYing in 2022 ^[24]. Define grid functions $\mathrm{U}=\left\{\mathrm{U}_{\mathrm{i}}^{\mathrm{n}} \mid 0 \leq \mathrm{i} \leq \mathrm{N}, 0 \leq \mathrm{n} \leq \mathrm{M}\right\}$ and $\mathrm{U}_{\mathrm{x}}=\left\{\mathrm{U}_{\mathrm{xi}}^{\mathrm{n}} \mid 0 \leq \mathrm{i} \leq \mathrm{N}, 0 \leq \mathrm{n} \leq \mathrm{M}\right\}$ on $\Omega_{\mathrm{h} \tau}=\Omega_{\mathrm{h}} \times \Omega_{\tau}$, in which $\mathrm{U}_{\mathrm{i}}^{\mathrm{n}}=\mathrm{W}\left(\mathrm{x}_{\mathrm{i}}, \mathrm{t}_{\mathrm{n}}\right)$, $\mathrm{U}_{\mathrm{xi}}^{\mathrm{n}}=\mathrm{W}_{\mathrm{x}}\left(\mathrm{x}_{\mathrm{i}}, \mathrm{t}_{\mathrm{n}}\right)$, At nodes $(\mathrm{x}_{\mathrm{i}},\mathrm{t}_{\mathrm{n}})$, considering Eq (2.3) with

The second derivative term $\mathrm{W}_{\mathrm{xx}}$ in space is approximated using a fourth-order compact difference method for calculation

which $\mathrm{i} = 1, \cdots, \mathrm{N}-1$, Bringing (2.7) into (2.6) can obtain

Where $\delta_{\mathrm{x}}$ and $\delta_{\mathrm{x}}^{2}$ represent the central difference operators of the first and second derivative terms of the space, The definitions of $\delta_{\mathrm{t}}^{+} \mathrm{U}_{\mathrm{i}}^{\mathrm{n}}$, $\delta_{\mathrm{x}} \mathrm{U}_{\mathrm{xi}}^{\mathrm{n}}$ and $\delta_{\mathrm{x}}^{2} \mathrm{U}_{\mathrm{xi}}^{\mathrm{n}}$ are the same as $\delta_{\mathrm{t}}^{+} \mathrm{v}_{\mathrm{i}}^{\mathrm{n}}$, $\delta_{\mathrm{x}} \mathrm{v}_{\mathrm{xi}}^{\mathrm{n}}$, and $\delta_{\mathrm{x}}^{2} \mathrm{v}_{\mathrm{xi}}^{\mathrm{n}}$.

For the first order derivative term regarding time in (2.8), the Taylor series expansion method can be used to obtain:

In order to obtain a finite difference compact scheme with second-order accuracy in the time direction, it is necessary to process $\mathrm{W}_{\mathrm{tt}}$ in Eq (2.9). Take the first order partial derivative of Eq (2.3) with respect to the variable ${\mathrm{t}}$ on both sides simultaneously. Then we get:

Considering the value of Eq (2.10) at discrete nodes (such as node $(\mathrm{x}_\mathrm{i}, \mathrm{t}_\mathrm{n})$). For the right end term of Eq (2.10), the first order derivative term in time is discretized using forward difference, and the second order derivative term in space is discretized using Eq (2.8), obtained

Now, substituting Eq (2.11) into Eq (2.9) and replace $\mathrm{W}_{\mathrm{tt}}$ yields

Bringing Eq (2.12) into Eq (2.8) and replacing $\mathrm{W}_{\mathrm{t}}\left(\mathrm{x}_{\mathrm{i}}, \mathrm{t}_{\mathrm{n}}\right)$, we obtain the following:

The high order term is represented by $\mathrm{S}_{\mathrm{i}}^{\mathrm{n}}$, and the high-order term in Eq (2.13) is replaced by $\mathrm{S}_{\mathrm{i}}^{\mathrm{n}}$, we get:

Where $1 \leq \mathrm{i} \leq \mathrm{N}-1$, $0 \leq \mathrm{n} \leq \mathrm{M}$, such that

Note the boundary conditions (2.4) and initial conditions (2.5) of system (2.3), and discretize the initial boundary conditions to obtain:

Omit the higher-order term $\mathrm{S}_{\mathrm{i}}^{\mathrm{n}}$ in Eq (2.14), replace $\mathrm{U}_{\mathrm{i}}^{\mathrm{n}}$ with $\mathrm{W}_{\mathrm{i}}^{\mathrm{n}}$, and replace $\mathrm{U}_{\mathrm{xi}}^{\mathrm{n}}$ with $\mathrm{W}_{\mathrm{xi}}^{\mathrm{n}}$. Then, the following difference format can be established for problems (2.3)–(2.5):

Denote $R(\mathrm{W}_{\mathrm{i}}^{\mathrm{n}})$ as $\mathrm{R}_{\mathrm{i}}^{\mathrm{n}}$. Equation (2.17) can also be expressed as:

Using the fourth order Pade scheme^[24] for the spatial first derivative term $\mathrm{W}_{\mathrm{xi}}$ appearing in Eq (2.20):

Moreover, we have

Where

The difference scheme (2.20) is a two-layer compact implicit scheme, and the calculation of unknown time layers only involves three grid points. From the above derivation process, it can be seen that the truncation error of the format is $\mathrm{O}\left(\tau^{2}+\mathrm{h}^{4}\right)$, and when $\tau = \mathrm{O}\left(\mathrm{h}^{2}\right)$, this format has second-order accuracy in the temporal direction and fourth-order accuracy in the spatial direction.

2.1.2.   Boundary scheme

The value of $\mathrm{W}_{\mathrm{x}}$ at the boundary point is given by the Neumann boundary condition of Eq (2.15). In order to ensure the overall fourth order accuracy of the difference scheme (2.20), the calculation formula for $\mathrm{W}$ at the boundary points is derived using the five point fourth order differential formula of $\mathrm{W}_{\mathrm{x}}$ and combined with homogeneous Neumann boundary conditions.

Let $\eta\left(\mathrm{x}\right)$ be a function defined on interval $C^{1}\left[x_{0}, x_{4}\right]$, and $\eta_{\mathrm{x}}\left(\mathrm{x}_{0}\right) = 0$, given that the function value of $\eta\left(\mathrm{x}\right)$ at node $\mathrm{x}_{0} < \mathrm{x}_{1} < \mathrm{x}_{2} < \mathrm{x}_{3} < \mathrm{x}_{4}$ is $\eta\left(\mathrm{x}_{\mathrm{k}}\right), (\mathrm{k} = 0, 1, 2, 3, 4)$. Let $\mathrm{x}_{0}$, $\mathrm{x}_{1}$, $\mathrm{x}_{2}$, $\mathrm{x}_{3}$ and $\mathrm{x}_{4}$ be equidistant nodes, assume $\mathrm{x}_{\mathrm{k}+1}-\mathrm{x}_{\mathrm{k}} = \mathrm{h}, (\mathrm{k} = 0, 1, 2, 3)$. On the interval $\left[x_{0}, x_{4}\right]$, perform a quartic Largerange interpolation function on $\eta\left(\mathrm{x}\right)$ and take the derivative of the interpolation remainder. Using the method of undetermined coefficients^[25], we can obtain

Since $\zeta \in\left[\mathrm{x}_{0}, \mathrm{x}_{4}\right]$, ignoring the higher-order term in (2.22), it can be inferred from the homogeneous Neumann boundary condition that $\eta_{\mathrm{x}}\left(\mathrm{x}_{0}\right) = 0$, transfer available:

Similarly, if $\eta\left(\mathrm{x}\right)$ is defined as a function on the interval $C^{1}\left[x_{N-4}, x_{N}\right]$, $\eta_{\mathrm{x}}\left(\mathrm{x}_{N}\right) = 0$, then

From this, the computation formula for the unknown function $\mathrm{W}$ at the boundary point can be obtained:

3.   Stability analysis

The Fourier analysis method is used to analyze the stability of the difference schemes (2.17)–(2.20), and by accurately establishing the $\mathrm{R}(\mathrm{W})$ term, the difference scheme (2.20) can be further transformed

At grid points $(\mathrm{x}_{i}, \mathrm{t}_{n})$, set

Where $\mathrm{I} = \sqrt{-1}$, $\beta^{\mathrm{n}}$, $\alpha^{\mathrm{n}}$ are the amplitudes of the Nth layer, $\theta = \frac{2\pi \mathrm{I}}{\lambda }$ is the phase angle in the $\mathrm{x}$ direction, and $\lambda$ is the wavelength. By substituting (3.2) into Eq (3.1) and simplifying it, it can be obtained that:

For the sake of simplicity, we will not consider the impact of $\mathrm{W}_{\mathrm{x}}$ the calculation format on the stability of the difference scheme at the boundary. Simplify Eq (3.2) by substituting it into Eq (2.21) to obtain:

Substitute formula (3.4) into Eq (3.3) and simplify it to obtain:

Simplify one term of Eq (3.5): $2 \mathrm{D} \frac{\cos (\theta)-1}{\mathrm{\; h}^{2}}+\frac{\mathrm{D}}{2} \frac{3 \sin ^{2}(\theta)}{\mathrm{h}^{2}(2+\cos (\theta))}$ = $\frac{\mathrm{D}\left(4 \cos (\theta)+\cos ^{2}(\theta)-5\right)}{2 \mathrm{\; h}^{2}(2+\cos (\theta))}$. Thus, the error amplification factor $\mathrm{Z} = \frac{\alpha^{\mathrm{n}+1}}{\alpha^{\mathrm{n}}} = \frac{\frac{1}{\tau}+\mathrm{G}}{\frac{1}{\tau}-\mathrm{G}}$ is obtained, where

From Eq (3.6), it can be seen that $\mathrm{G}\le 0$, thus the square of the error amplification factor modulus $\|\mathrm{Z}\|^{2} = \frac{\left(\frac{1}{\tau}+\mathrm{G}\right)^{2}}{\left(\frac{1}{\tau}-\mathrm{G}\right)^{2}} \leq 1$, i.e., the difference scheme (2.20) is unconditionally stable.

4.   Numerical simulation

The vegetation-water model (2.1) does not yield an exact solution. Therefore, in this paper, we construct a diffusion system with an exact solution to validate the convergence and accuracy of our difference scheme.

We verify the accuracy and convergence of the high-precision compact difference scheme by solving the following numerical examples. We use the $\mathrm{L}_{2}$ norm error to measure the accuracy of the differential schemes, The definitions of the error:

● $\mathrm{L}_{2} = \sqrt{\mathrm{h} \sum_{\mathrm{i}}\left(\mathrm{u}_{\mathrm{i}}^{\text {exact }}-\mathrm{u}_{\mathrm{i}}^{\text {num }}\right)^{2}}.$

The definition of convergence rate is:

● $\text { Rate } = \frac{\log \left(\mathrm{E}_{1} / \mathrm{E}_{2}\right)}{\log \left(\mathrm{h}_{1} / \mathrm{h}_{2}\right)}$.

in which $\mathrm{E}_{1}$ and $\mathrm{E}_{2}$ represent the errors corresponding to the different spatial step-lengths $\mathrm{h}_{1}$ and $\mathrm{h}_{2}$, respectively.

As an example, let us consider a one-dimensional diffusion system as follows:

The initial condition is

The boundary conditions of the variables are Neumann boundary conditions, i.e.,

Which, $\mathrm{D}_{11} = \mathrm{D}_{21} = \beta$ are the diffusion coefficient, $\mathrm{D}_{12}$ and $\mathrm{D}_{12}$ are constants. The analytical solution is

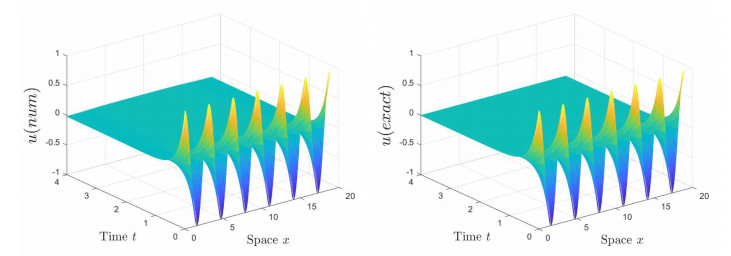
In this paper, the differential scheme (2.20), (2.21) and (2.25) are used to solve the model (4.1), when $T = 4$, $\tau = 0.005$, $\beta = 1$. The numerical solutions of $\mathrm{u(x, t)}$ and $\mathrm{v(x, t)}$ obtained through the differential scheme computation, as well as the visual comparison of their evolution in space and time with the exact solution, are presented in Figures 1 and 2, respectively. From the figures, it can be observed that the numerical results closely match the analytical results. Both $\mathrm{u(x, t)}$ and $\mathrm{v(x, t)}$ eventually stabilize over time, while exhibiting periodic variations in the spatial dimension. The $\mathrm{L}_{2}$ errors and convergence orders of $\mathrm{u(x, t)}$ and $\mathrm{v(x, t)}$ obtained from the scheme calculation are presented in Table 1. From the table, it can be seen that the $\mathrm{L}_{2}$ error of $\mathrm{u(x, t)}$ achieves fourth-order accuracy in the spatial dimension, and similarly, the $\mathrm{L}_{2}$ error of $\mathrm{v(x, t)}$ also achieves fourth-order accuracy in the spatial dimension. The computational results indicate that the difference scheme method used in this study exhibits good convergence. By employing this system as a reference, we assess the performance of our difference scheme and compare the results against the known exact solution. Through this verification process, we demonstrate the convergence and accuracy of our framework. Our findings contribute to the validation and reliability of our proposed methodology for modeling vegetation-water systems, enhancing our understanding and facilitating informed decision-making in the field of environmental science.

Next, with respect to model (2.1), reference ^[23] applied bifurcation theory to analyze the emergence of Hopf branches, Turing branches, and Turing Hopf branches near steady-state solutions, providing necessary conditions for their occurrence. Two disturbance parameters $\varepsilon = \left(\varepsilon_{1}, \varepsilon_{2}\right) \in \mathbb{R}^{2}$ are selected as control parameters to study the impact of disturbances on the dynamic behavior of plant and water. It can be roughly divided into four states: spatial non-homogeneous steady-state, spatial homogeneous steady-state, spatial homogeneous periodic solution, and spatial non-homogeneous periodic solution. Thus, where $\varepsilon_{2}$ is the perturbation of parameter $\mu$, and the calculation formula for the steady-state solution is ^[23]:

Next, we select parameters different from the original text, use the difference schemes (2.20), (2.21), and (2.25) to solve the model (2.1), and give the spatio-temporal dynamic distribution of vegetation and water. The calculation area is $\mathrm{x} \in[0, 30 \pi], \mathrm{T} \in[0, 1500]$, the space step size is $\mathrm{h} = \frac{30 \pi}{150}$, the time step is $\tau = 0.05$, the initial values are set to random perturbations of $\left(\mathrm{n}^{*}\left(\varepsilon_{1}\right), \omega^{*}\left(\varepsilon_{1}\right)\right)$ and $\mu_{*} = \mu-\varepsilon_{2}$, Other parameter values: $m = 3$, $\mu = 3$, Figures 1–4 are the numerical simulation result of model (2.1).

Figure 3 shows that system (2.1) has a stable solution, Figure 4 shows that system (2.1) has a stable spatially homogeneous periodic solution, Figure 5 shows that system (2.1) has a spatially non homogeneous periodic solution, Figure 6 shows that the system (2.1) converges to a spatially non-uniform steady state. Minor changes in parameters can cause switching between four different states: uniform state, temporal periodic state, spatially non-uniform steady state, and spatially non-uniform periodic state. This essentially indicates that vegetation in arid environments is fragile, and if precipitation decreases, the area where the vegetation is located will become desertification. The numerical results also show that vegetation biomass and water density are negatively correlated in space, and the places with more vegetation biomass have less water density, while the places with less vegetation biomass have more water density.

5.   Conclusions

In this paper, we present a high-precision compact difference scheme for a vegetation water model in a flat environment. The proposed scheme achieves fourth-order accuracy in the spatial direction and second-order accuracy in the temporal direction for both the interior point and boundary point formulations of the model. First, the Fourier analysis method is used to prove that the high-precision compact difference scheme is unconditionally stable. Second, the convergence and accuracy of the scheme are verified through numerical examples. Then, the model is numerically solved and simulated, and the effects of parameter perturbations on vegetation and hydrodynamic systems are obtained, causing the dynamic system to switch in four different state. This will also provide guidance for desertification warning and control in arid and semi-arid areas. The highly refined finite difference scheme plays an important role in solving vegetation water models. In the future, high-precision compact difference schemes for vegetation water models will be established in two-dimensional regions, and further analysis of system (2.1) will be conducted.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This study is supported by National Natural Science Foundation of China under Grant No. 11761005.

Conflict of interest

All authors declare no conflicts of interest in this paper.