On The oscillatory behavior of solutions to a class of second-order nonlinear differential equations

1.   Introduction

Chemical kinetics deals with chemistry experiments and interprets them in terms of a mathematical model. The experiments are done on chemical reactions with the passage of time. The models are differential equations for the rates at which reactants are consumed and products are produced. Chemists are able to understand how chemical reactions take place at the molecular level by combining models with investigation. Molecules react in steps to lead to the overall stoichiometric reaction which is reaction mechanism for collection of reactions. The set of reactions specifies the path (or paths) that reactant molecules take to finally arrive at the product molecules. All species in the reaction appear in at least one step and the sum of the steps gives the overall reaction. The govern the rate of the reaction which leads directly to the mechanism of differential equations ^[1]. Many processes and phenomena in chemistry generally in sciences can be designated by first-order differential equations. These equations are the most important and most frequently used to describe natural laws. The following examples are discussed: the Bouguer-Lambert-Beer law in spectroscopy, time constants of sensors, chemical reaction kinetics, radioactive decay, relaxation in nuclear magnetic resonance, and the RC constant of an electrode ^[2]. The induced kinetic differential equations of a reaction network endowed with mass action type kinetics are a system of polynomial differential equations ^[3]. We review the basic ideas of fractional differential equations and their applications on non-linear biochemical reaction models. We apply this idea to a non-linear model of enzyme inhibitor reactions ^[4].

The fractional-order, which involves integration and transect differentiation using fractional calculus is helping to better understand the explanation of real-world problems than ordinary integer order, as well as in the modeling of real phenomena due to a characterization of memory and hereditary properties in ^[5,6]. Riemann Liouville developed the concept of fractional derivative, which is based on power law, ^[7,8] offers a novel fractional derivative that makes use of the exponential kernel. Several issues include the non-singular kernel fractional derivative, which covers the trigonometric and exponential functions, and ^[9,10,11,12] illustrates some relevant techniques for epidemic models. This virus's suggested outbreak efficiently catches the timeline for the COVID-19 disease conceptual model ^[13]. In the literature, many fractional operators are employed to solve real-world issues ^[14,15].

In this paper, section 1 is introduction and section 2 consists of some basic fractional order derivative which are helpful to solve the epidemiological model. Section 3 and 4 consists of generalized from of the model, uniqueness and stability of the model. Fractal Fractional techniques with exponential decay kernel and Mittag-Leffler kernel respectively in section 5. Results and conclusion are discussed in section 6, and 7 respectively.

2.   Basic definitions

Following are the basic definitions ^[7,8,14,15] used for analysis and solution of the problem.

Definition 1: Sumudu transform for any function $\phi \left(t\right)$ over a set is given as,

is defined by

Definition 2: For a function $g\left(t\right)\in {W}_{2}^{1}\left(\mathrm{0, 1}\right), b > a\ and\ \sigma \in \left(\mathrm{0, 1}\right],$ the definition of Atangana–Baleanu derivative in the Caputo sense is given by

where

By using Sumudu transform (ST) for (1), we obtain

Definition 3: For a function $g\left(t\right)\in {W}_{2}^{1}\left(\mathrm{0, 1}\right), b > a\ and\ {\alpha }_{1}\in \left(\mathrm{0, 1}\right],$ the definition of Atangana–Baleanu derivative in the Caputo sense is given by

where

Definition 4: Suppose that $g\left(t\right)$ is continuous on an open interval $(a, b),$ then the fractal-fractional integral of $g\left(t\right)$ of order ${\alpha }_{1}$ having Mittag-Leffler type kernel and given by

3.   Hires problem with fractional operator

Robertson introduces this chemical process in ^[19,20]. Schafer pioneered the following chemical reactions method in 1975 ^[19,20]. It represents the high irradiance response (HIRES) of photomorphogenesis based on phytochrome. A stiff system of eight non-linear ordinary differential equations is used to create the following mathematical model.

Here ${M}_{1} = 1.7, {M}_{2} = 0.43, {M}_{3} = 8.32,$ ${M}_{4} = 0.0007, {M}_{5} = 8.75,$ ${M}_{6} = 10.03, {M}_{7} = 0.035,$ ${M}_{8} = 1.71, {M}_{9} = 1.12, {M}_{10} = 1.745,$ ${M}_{11} = 280, {M}_{12} = 0.69, {M}_{13} = 1.81.$ The initial values can be represented by $y = {\left(\mathrm{1, 0}, \mathrm{0, 0}, \mathrm{0, 0}, \mathrm{0, 0.0057}\right)}^{T}$. By using Atangana-Baleanu in Caputo sense for system (1), we get

Here ${}_{O}{}^{ABC}{D}_{t}^{\alpha }$ is the Atanagana-Baleanue Caputo sense fractional derivative with $0 < \alpha \le 1$.

With given initial conditions

Theorem 3.1: The solution of the proposed fractional-order model (1) along initial conditions is unique and bounded in R₊⁸.

Proof: In (1), we can get its existence and uniqueness on the time interval (0, ∞). Afterwards, we need to show that the non-negative region R₊⁸ is a positively invariant region. For this

If (${y}_{1}$(0)), (${y}_{2}$(0)), (${y}_{3}$(0)), (${y}_{4}$(0)), (${y}_{5}$(0)), (${y}_{6}$(0)), (${y}_{7}$(0)), (${y}_{8}$(0)) $\epsilon$ ${R}_{+}^{8}$, then from above expression, the solution cannot escape from the hyperplane. Also on each hyperplane bounding the non-negative orthant, the vector field points into ${R}_{+}^{8}$, i.e., the domain ${R}_{+}^{8}$ is a positively invariant set.

Now, with the help of Sumudu transform definition, we get

Where $Q = \frac{M\left(\alpha \right)\alpha \mathrm{\Gamma }\left(\alpha +1\right)}{1-\alpha }$

Rearranging, we get

Using the inverse Sumudu transform on both sides of the system (5), we obtain

We next obtain the following recursive formula.

Where $H = \frac{1-\alpha }{M\left(\alpha \right)\alpha \mathrm{\Gamma }\left(\alpha +1\right){E}_{\alpha }\left(-\frac{1}{1-\alpha }{P}^{\alpha }\right)}$

And the solution of system is provided by

4.   Fixed-point theorem for stability analysis of iteration method

Theorem 4.1: Define K be a self-map is given by

Proof: By using triangular inequality with the definition of norms, we get

Hence satisfied given conditions.

Hence the system is stable.

Theorem 4.2: Unique singular solution with the iterative method for the special solution of system $\left(2\right).$

Proof: Considering the Hilbert space $H = {L}^{2}\left(\left(p, q\right)\times \left(0, T\right)\right)$ which can be defined as

For this purpose, we consider the following operator

By using inner product, we get

Where

$({{y}_{1}}_{\left(11\right)}-{{y}_{1}}_{\left(12\right)}, {{y}_{2}}_{\left(21\right)}-{{y}_{2}}_{\left(22\right)}, {{y}_{3}}_{\left(31\right)}-{{y}_{3}}_{\left(32\right)},$ ${{y}_{4}}_{\left(41\right)}-{{y}_{4}}_{\left(42\right)}, {{y}_{5}}_{\left(51\right)}-{{y}_{5}}_{\left(52\right)},$ ${{y}_{6}}_{\left(61\right)}-{{y}_{6}}_{\left(62\right)},$ ${{y}_{7}}_{\left(71\right)}-{{y}_{7}}_{\left(72\right)},$ ${{y}_{8}}_{\left(81\right)}-{{y}_{8}}_{\left(82\right)}),$ are the special solutions of the system. Taking into account the inner function and the norm, we have

In the case for large number ${e}_{1}, {e}_{2}, {e}_{3}, {e}_{4}, {e}_{5}, {e}_{6}, {e}_{7}and{e}_{8},$ both solutions happen to be converged to the exact solution. Employing the topology concept, we can obtain eight positive very small parameters $\left({\chi }_{{e}_{1}}, {\chi }_{{e}_{2}}, {\chi }_{{e}_{3}}, {\chi }_{{e}_{4}}, {\chi }_{{e}_{5}}, {\chi }_{{e}_{6}}, {\chi }_{{e}_{7}}and{\chi }_{{e}_{8}}\right).$

Where

But, it is obvious that

where $||{V}_{1}||, ||{V}_{2}||, ||{V}_{3}||, ||{V}_{4}||, ||{V}_{5}||, ||{V}_{6}||, ||{V}_{7}||, ||{V}_{8}||\ne 0$.

Therefore, we have

Which yields that

This completes the proof of uniqueness.

An operator $B:Z\to Z$ can be defined as:

If $£ \left(t, \varphi \left(t\right)\right)$ satisfies the Lipschitz condition and the following extension then

● For every $\varphi \in Z$ there exists constants ${L}_{£ } > 0$ and ${M}_{£ }$ such that

● For every $\varphi, \overline{\varphi }\in Z$, there exists a constant ${M}_{£ } > 0$ such that

Theorem 4.2: If the condition of (11) holds then for the function $£ :[0, T]\times Z\to R$ there exists at least one solution for the (1).

Proof: Since $£$ in (10) is continuous function, so $B$ is also a continuous. Assume $M = \left\{\varphi \in \left|\left|\varphi \right|\right|\le R, R > 0\right\}$, then for $\varphi \in Z,$ we have

Hence, $B$ is uniformly bounded, and $M\left(\mathsf{μ}, {\alpha }_{1}\right)$ is a beta function. For equicontinuity of $B$, we take ${t}_{1} < {t}_{2}\le T,$ then consider

If ${t}_{1}\to {t}_{2}$ then $\left|\left|B\left(\varphi \right)\left({t}_{2}\right)-B\left(\varphi \right)\left({t}_{1}\right)\to 0\right|\right|$ Consequently $\left|\left|B\left(\varphi \right)\left({t}_{2}\right)-B\left(\varphi \right)\left({t}_{1}\right)\to 0\right|\right|, as{t}_{1}\to {t}_{2}.$ Hence $B$ is equicontinous. Thus, by Arzela-Ascoli theorem $B$ is completely continuous. Consequently, by the result of Schauder's fixed point, it has at least one solution.

Theorem 4.3: If $\eta = \frac{\mathsf{μ} {T}^{\mathsf{μ} -1}\left(1-{\alpha }_{1}\right)}{\mathrm{A}\mathrm{B}\left({\alpha }_{1}\right)}+\frac{\mathsf{μ} {\alpha }_{1}}{\mathrm{A}\mathrm{B}\left({\alpha }_{1}\right)\mathrm{\Gamma }\left({\alpha }_{1}\right)}{T}^{\mathsf{μ} +{\alpha }_{1}-1}M\left(\mathsf{μ}, {\alpha }_{1}\right){M}_{£ } < 1$ and the condition (12) holds, then $\eta$ has a unique solution.

Proof: For $\varphi, \overline{\varphi }\in Z$, we have

Hence, $B$ is a contraction. So, by the principle of Banach contraction, it has a unique solution.

Ulam-Hyres stability

The proposed model is Ulam-Hyres stable if there exists ${B}_{\mathsf{μ}, {\alpha }_{1}}\ge 0$ such that for every $\varepsilon > 0$ and for every $\varphi \in (L\left[0, T\right], R)$ satisfies the following inequality ${{}^{FFM}J}_{0, t}^{\mathsf{μ}, {\alpha }_{1}}\left(\varphi \left(t\right)\right)-£ \left(t, \varphi \left(t\right)\right)\le \varepsilon, t\in \left[0, T\right]$ such that $\left|\varphi \left(t\right)-£ \left(t\right)\right|\le {B}_{\mathsf{μ}, {\alpha }_{1}}\varepsilon, t\in \left[0, T\right]$.

Suppose a perturbation $\omega \in L\left[0, T\right], R$ then $\omega \left(0\right) = 0$ and

● For every $\varepsilon > 0 \exists \omega \left(t\right)\le \varepsilon |$

● ${{}_{0}{}^{FFM}J}_{t}^{\mathsf{μ}, {\alpha }_{1}}\left(\varphi \left(t\right)\right) = £ \left(t, \varphi \left(t\right)\right)+\omega \left(t\right).$

Lemma 4.4: The solution of the perturbed model ${{}_{0}{}^{FFM}J}_{t}^{\mathsf{μ}, {\alpha }_{1}}\left(\varphi \left(t\right)\right) = £ \left(t, \varphi \left(t\right)\right)+\omega \left(t\right), \varphi \left(0\right) = {\varphi }_{0}$ fulfills the relation

Where ${{\alpha }_{1}}_{{\alpha }_{1}, \mathsf{μ} }^{*}\varepsilon = \frac{\mathsf{μ} {T}^{\mathsf{μ} -1}\left(1-{\alpha }_{1}\right)}{\mathrm{A}\mathrm{B}\left({\alpha }_{1}\right)}+\frac{\mathsf{μ} {\alpha }_{1}}{\mathrm{A}\mathrm{B}\left({\alpha }_{1}\right)\mathrm{\Gamma }\left({\alpha }_{1}\right)}{T}^{\mathsf{μ} +{\alpha }_{1}-1}M\left(\mathsf{μ}, {\alpha }_{1}\right).$

Lemma 4.5: By using condition (12) with lemma (4.4), proposed model is Ulam-Hyres stable if $\eta < 1.$

Proof: Suppose ${\alpha }_{1}\in Z$ be a solution and $\varphi \in Z$ be any solution of (1), then

Consequently,

So, we can write it as

Where ${B}_{{\alpha }_{1}, \mathsf{μ} }\varepsilon = \frac{{{\alpha }_{1}}_{{\alpha }_{1}, \mathsf{μ} }^{*}}{1-\eta }.$ Hence the solution is Ulam-Hyres stable.

5.   Fractal-fractional operator for hires problem

In this section, we present the Hires problem model $\left(1\right)$ using fractal-fractional Atangana-Baleanu derivative. We have

With initial conditions

We present the numerical algorithm for the fractal-fractional Hires problem model (13). The following is obtained by integrating the system (13).

Let

Then system (14) becomes

At ${t}_{n+1} = \left(n+1\right)\Delta t,$ we have

Also, we have

In general, approximating the function $k\left(\tau, y\left(\tau \right)\right),$ using the Newton polynomial, we have

Using Eq (18) into system (17) we have

Rearranging the above equation, we have

Writing further system (20) we have

Now, calculating the integrals in system (21) we get

Inserting them into system (21) we get

Finally, we have the following approximation:

6.   Results and discussions

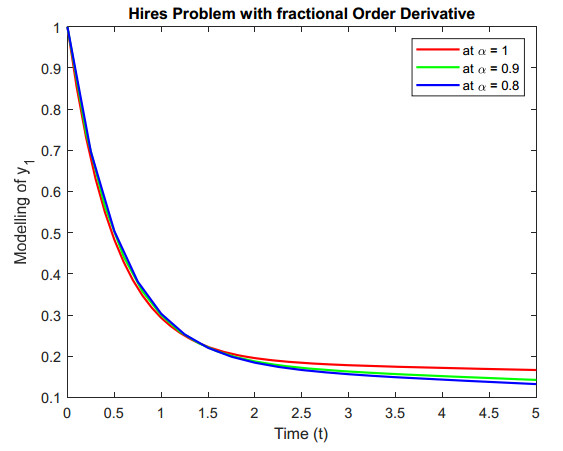
A fractional-order model is proposed for analysis and simulation, to observe the concentration of chemicals in chemistry kinematics problems with a stiff differential equation. For this purpose, we used ABC with Mittage-Lefffier law, Atangana-Tufik scheme, and fractal fractional derivative for hires problem with given initial conditions. Details of parameters values of real data are also given in ^[18,19] which will consider for simulation analysis for the proposed study. Solution of compartment shows in Figures 1 to 8 with fractional fractal operator at different order. Effect of fraction order can easily be observed in simulation of the compartments having a concentration of chemical reaction with stiff differential equations. The concentration ${y}_{1}$ and ${y}_{8}$ of the chemical species start decreasing by decreasing fractional values respectively while concentration ${y}_{2}, {y}_{3}$, ${y}_{4}$, ${y}_{5}$, ${y}_{6}$ and ${y}_{7}$ of the chemical species start increasing by decreasing fractional values. These concentrations of chemical species converge to our desired value according to steady state by decreasing the fractional values which shows that it provides us appropriate results at non integer value. We can get better concentration of the components by using the fractional derivative which are very important for chemical problem to check the actual behavior of the concentration of the chemical with smallest changes in derivative with respect to time. It is also very important for solutions of nonlinear problems which are commonly used researcher and scientist in kinetics chemistry.

7.   Conclusions

We examine the hires problems with stiff systems of nonlinear ordinary equations that rely on the concentration of chemical reaction of components in this study. The advanced techniques of fractional operator have been implemented for initial value problem arising from chemical reactions composed of large systems of stiff ordinary differential equations. The arbitrary derivative of fractional order has been taken with Atangana-Toufik scheme and fractal fractional derivative. Solutions have been obtained efficiently within limited time which shows the actual behavior of kinetic chemical reactions. Existence and uniqueness of results have been verified by fixed point theorem. Simulations are carried out for different fractional values. New chemical reactions can be done with the help of these analyses. These concepts are very important to use for real life problems like Brine tank cascade, Recycled Brine tank cascade, pond pollution, home heating and biomass transfer problem.

Acknowledgments

Research Supporting Project number (RSP-2021/167), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

No conflict of interest.