Single index regression for locally stationary functional time series

1.   Introduction

In recent decades, there has been a burgeoning interest in statistical issues related to the analysis of functional random variables, particularly those taking values in infinite-dimensional spaces. This surge is driven by the increasing availability of data collected on ever more refined temporal and spatial grids, common in fields such as meteorology, medicine, satellite imagery, and various other research domains. Consequently, the statistical modeling of these data, conceptualized as random functions, has engendered numerous challenging theoretical and computational research questions. Several monographs can be consulted for a comprehensive understanding of both theoretical and practical aspects of functional data analysis. Specifically, the researchers in ^[14] examined linear models for random variables within a Hilbert space, while the researchers in ^[75] provide insights into scalar-on-function and function-on-function linear models, functional principal component analysis, and parametric discriminant analysis. For those interested in nonparametric methods, particularly kernel-type estimation for scalar-on-function nonlinear regression models, ^[43] offers an extensive exploration, extending these methodologies to classification and discrimination analysis. Additionally, the researchers in ^[55] discuss extending several pivotal statistical concepts—such as goodness-of-fit tests, portmanteau tests, and change detection—to the functional data framework. The researchers in ^[85] focus on the analysis of variance for functional data, and the researcher in ^[77] delves into regression analysis for Gaussian processes. The literature also encompasses semiparametric models, including but not limited to projection pursuit models ^[31], partial linear models ^[3], and functional sliced inverse regression ^[45]. The authors of ^[40] investigated functional expectile regression as a framework for modeling spatial financial risk, proposing a nonparametric estimator tailored to the FSIR structure. In ^[15], the researchers addressed the intricate task of estimating the regression function operator and its partial derivatives for stationary mixing random processes using local higher-order polynomial fitting, achieving a key result in establishing the joint asymptotic normality of the estimators. Moreover, ^[26] focused on the weak convergence of the conditional empirical process indexed by a suitable function class and the $k$-NN conditional $U$-processes in the context of functional explanatory variables, that is extented in ^[18]. A notable contribution of this work was the establishment of sharp, almost uniform consistency in the number of neighbors for the proposed estimator. Finally, estimators for the single-index conditional $U$-statistics operator, designed to accommodate the nonstationary nature of the data-generating process, were analyzed in the time series framework in ^[19] and extended to spatial data in ^[17], building on the foundational work of ^[27]. For more recent insights and surveys on functional data modeling and analysis, readers can refer to ^{[2,4,23,25,28,29,30,33,47,67]}.

Literature strongly advocates for regression models that incorporate dimension reduction techniques. Single-index models, widely employed for this purpose, assume that the influence of predictors on the response can be simplified to a single index. This index, representing a projection in a specified direction, is combined with a nonparametric link function. By doing so, these models reduce the predictors to a single-variable index while retaining crucial characteristics. Notably, the nonparametric link function operates solely on a one-dimensional index, mitigating issues associated with high dimensionality, often referred to as the curse of dimensionality. The single-index model extends the concept of linear regression by incorporating a link function equivalent to the identity function (see ^{[12,50,54,59,80]}). Advances in functional data analysis underscore the need for models addressing dimensionality effects (see ^[33,48,61] for recent surveys, and ^[2,24] for related studies). Semiparametric approaches naturally emerge as suitable candidates for such models. In this context, ^[44] and ^[1] investigated the functional single-index model (FSIM). The researchers in ^[56] introduced functional single-index composite quantile regression, estimating the unknown slope function and link function using $B$-spline basis functions. The researchers in ^[70] proposed a compact functional single-index model with a coefficient function that is nonzero only in a subregion. The researchers in ^[86] focused on estimating a general functional single-index model, where the conditional distribution of the response depends on the functional predictor through a functional single-index structure. The researchers in ^[81] developed a new estimation procedure that combines functional principal component analysis of the functional predictors, $B$-spline modeling for parameters, and profile estimation of unknown parameters and functions in the model.

Additionally, ^[62,63] investigated the estimation of the functional single-index regression model with missing responses at random for strongly mixing time series data. The researchers in ^[42] introduced a functional single-index varying coefficient model, with the functional predictor forming the single-index part. Utilizing functional principal component analysis and basis function approximation, they obtained estimators for the slope function and coefficient functions, proposing an iterative estimation procedure. ^[71] developed an automatic and location-adaptive procedure for estimating regression in an FSIM based on $k$-Nearest Neighbors ($k$NN) ideas. Motivated by the analysis of imaging data, ^[58] proposed a novel functional varying-coefficient single-index model for regression analysis of functional response data on a set of covariates of interest. The researchers in ^[5] and ^[7] investigated a functional Hilbertian regressor for nonparametric estimation of the conditional cumulative distribution with a scalar response variable in the single-index structure. In particular, the authors of the last reference tackled the challenge of nonparametric estimation for the regression function within the FSIM under a random censoring framework for the i.i.d. data. In an alternative approach, ^[31] extended their methodology to the multi-index case, avoiding anchoring the true parameter to a prespecified sieve. They provided a detailed theoretical analysis of a direct kernel-based estimation scheme, establishing a polynomial convergence rate. For references on the subject, we refer to ^{[6,28,30,68,74]}.

The common assumption of stationarity in time series modeling has led to the development of numerous models, techniques, and methodologies. However, this assumption is often inappropriate for spatio-temporal data, even after applying detrending and deseasonalization methods. Many key time series models exhibit nonstationarity, as observed in various physical phenomena and economic data, rendering traditional stationary approaches inadequate. To address this issue, ^[79] introduced the concept of the locally stationary random process, which approximates a nonstationary process by treating it as stationary over short time intervals. This notion of local stationarity has been further explored in the works of ^{[35,36,69,72,76]}, among others. Notably, the seminal work by ^[35] provides a strong theoretical foundation for inference on locally stationary processes.

1.1.   Paper contribution

In ^[64], the author examined the asymptotic properties of nonparametric regression for dependent functional data, focusing on stationary processes. Building on this foundation, our work extends the framework to accommodate nonstationary processes, leveraging more advanced techniques in a more realistic setting. Specifically, we introduce the concept of local stationarity to model time-dependent functional data in the single index setting. While ^[64] established the convergence rate for a Nadaraya-Watson-type estimator, we broaden the scope by deriving this rate not only for that estimator but also for a wider class of kernel estimators. Both studies consider semi-metric spaces for strongly mixing data; however, the approaches differ significantly: The researcher in ^[64] employed the norm, whereas we utilize the inner product. This distinction enhances the adaptability of our results, making them applicable to a broader range of scenarios, particularly in the single-index setting. Additionally, ^[57] explored nonstationary functional time series within a semi-metric space defined by a norm for mixing data, obtaining similar results. However, our use of an inner-product-based semi-metric generalizes their findings, particularly as ^[57] did not address the single-index direction $\theta$. Our work further advances the field by providing detailed proofs of asymptotic normality, expanding upon the methodology in ^[64], and reinforcing the theoretical foundations of our approach. Our primary aim of this paper is to establish a comprehensive framework for the single-index model in a nonparametric setting, with a focus on regression involving functional covariates and the challenges posed by the potential nonstationarity of functional time series. We conduct a rigorous theoretical analysis to address the complexities of this setting, including the unbounded nature of the functional space, which necessitates intricate and extensive proofs. Finally, the theoretical results are supported by a simulation study, demonstrating the finite-sample performance of our proposed method and underscoring its practical relevance and robustness.

1.2.   Paper organization

The structure of the paper is as follows: In Section 2, we introduce the concept of local stationarity for functional time series, which take values in a semi-metric space equipped with the semi-metric $d_\theta(\cdot, \cdot)$, where $\theta$ is a single index from a Hilbert space $\mathscr{H}$. The novelty of this work lies in the incorporation of a single-index $\theta \in \mathscr{H}$, which serves as a filter and effectively represents the explanatory variables $X_{t, T}$ that influence the response variable $Y_{t, T}$. This section also covers the dependence structure of the functional time series considered in the study.

In Section 3, we present the derivation of uniform convergence rates for general kernel estimators, along with results on uniform convergence and asymptotic normality for the Nadaraya-Watson estimator of the regression function. In particular, we observe that the general kernel estimator converges uniformly to its mean at the rate $\sqrt{\dfrac{\log T}{T h \phi_{\theta}(h)}}$. For the Nadaraya-Watson estimator, we establish a convergence rate with two distinct components: One addressing the stochastic part and the other addressing the bias part. Following a decomposition similar to ^[64] and ^[57], we obtain our convergence result based on the proof structure of Theorem 3.1. However, we incorporate the impact of the single-index $\theta$, reflected in the dependence structure in the second part of the proof of Proposition 2, which is essential for proving Theorem 3.1. The small-ball probability $\phi_{\theta}(h)$ provides insight into the concentration of random variables as governed by the semi-metric $d_{\theta}(\cdot, \cdot)$, highlighting the contribution of this work. This section concludes with the derivation of asymptotic normality for the Nadaraya-Watson estimator. The proof begins by showing that the bias term converges to zero, followed by establishing the asymptotic normality of the variance term. The argument is completed using Bernstein's blocking technique, along with key tools such as Davydov's Lemma, the Volkonski-Rosanov inequality, and the Lindeberg-Feller theorem for finite normality, supplemented by appropriate truncation arguments. In Section 4, we present comprehensive simulation results to evaluate the finite-sample properties of the proposed approach. Concluding remarks and discussions on potential future research are provided in Section 5. For clarity and coherence, all proofs are collected in Appendix-A, with relevant technical results included in the Appendix-B.

1.3.   Notations

Let $\{a_n\}$ and $\{b_n\}$ be arbitrary sequences of positive numbers. Throughout this paper, we adopt the notation $a_n \lesssim b_n$ to signify that there exists a constant $C > 0$, independent of $n$, such that $a_n \leq C b_n$ for all $n$. When $a_n \lesssim b_n$ and $b_n \lesssim a_n$ hold simultaneously, we write $a_n \sim b_n$, indicating that the two sequences are asymptotically comparable. In cases where $\frac{a_n}{b_n} \to 0$ as $n \to \infty$, we use the notation $a_n \ll b_n$. For any real numbers $a$ and $b$, the expressions $a \vee b$ and $a \wedge b$ denote the maximum and minimum of $a$ and $b$, respectively, i.e., $a \vee b = \max\{a, b\}$ and $a \wedge b = \min\{a, b\}$. Furthermore, we denote convergence in distribution by $\stackrel{d}{\to}$. Finally, for any real number $x$, $\lfloor x \rfloor$ represents the integer part of $x$, also known as the floor function.

2.   Settings

In this section, we present an advanced framework for analyzing locally stationary functional time series, incorporating the concept of a semi-metric $d_\theta(\cdot, \cdot)$ that depends on a single-index parameter $\theta \in \mathscr{H}$, where $\mathscr{H}$ denotes a Hilbert space. This approach broadens the original notion of local stationarity as introduced by ^[35] while extending the developments on locally stationary functional series by ^{[17,19,27,57]}. In this expanded framework, we examine not only the structural properties of local stationarity but also delve into the dependence structures inherent in the functional time series, providing a comprehensive view of the interplay between stationarity and dependence within this context.

2.1.   Model

The semi-metric $d_{\theta}(\cdot, \cdot)$ associated to the single-index $\theta \in \mathscr H$, a Hilbert space, defined by:

Let $\{Y_{t, T}, X_{t, T}\}_{t = 1}^{T}$ be random variables where $Y_{t, T}$ is real-valued and $X_{t, T}$ takes values in some semi-metric space $\mathscr{H}$ with a semi-metric $d_\theta(\cdot, \cdot)$. In this study, we consider the following model:

where $\{\varepsilon_{t}\}_{t \in \mathbb{Z}}$ is a sequence of independent and identically distributed random variables that is independent of $\{X_{t, T}\}_{t = 1}^{T}$, $m(\cdot, \cdot)$ is the regression function allowed to change smoothly over time and $\sigma(\cdot, \cdot)$ is the variance function. For notational convenience, we use $\varepsilon_{t, T}$ to denote $\sigma\left({\frac{t}{T}}, \langle\theta, X_{t, T}\rangle\right)\varepsilon_{t}$. For the identifiability issue, we assume that the regression function is differentiable and $\langle\theta, e_{1}\rangle = 1$, where $e_{1}$ is the first element of the orthonormal basis of $\mathscr{H}$. Observe that $m\left({\frac{t}{T}}, \langle\theta_1, x\rangle\right) = m\left({\frac{t}{T}}, \langle\theta_2, x\rangle\right)$ implies that $\theta_{1}\equiv \theta_{2}$. We also assume that $\{X_{t, T}\}$ is a locally stationary functional time series, and the regression function $m$ is allowed to change smoothly over time.

2.2.   Local stationarity

A functional time series $\{X_{t, T}\}_{t = 1}^{T}$, where $T \to \infty$, is intuitively regarded as locally stationary if it exhibits approximate stationarity within localized time intervals. This concept implies that while the series may display non-stationary characteristics over its entirety, within any sufficiently small time window, its behavior can be approximated as stationary. For an in-depth discussion on the theoretical framework and broader applications of locally stationary time series, we refer to the works of ^[37] and ^[38]. Furthermore, investigations into the concept of local stationarity for time series in a Hilbert space setting are available in ^[82] and ^[8]. Local stationarity at each normalized time point $u$ can be characterized by stochastically approximating the original process $\{X_{t, T}\}$ with a stationary functional time series $\{X_{t}^{(u)}\}$. The following formal definition captures this idea rigorously.

Definition 2.1. ^[82] The $\mathscr{H}$-valued stochastic process $\{X_{t, T}\}_{t = 1}^{T}$ is locally stationary if for each rescaled time point $u \in [0, 1]$, there exists an associated $\mathscr{H}$-valued process $\{X_{t}^{(u)}\}_{t \in \mathbb{Z}}$ with the following properties:

(ⅰ) $\{X_{t}^{(u)}\}_{t \in \mathbb{Z}}$ is strictly stationary.

(ⅱ) It holds that

for all $1 \leq t \leq T$, where $\{U_{t, T}^{(u)}\}$ is a process of positive variables satisfying $\mathbb{E}[(U_{t, T}^{(u)})^{\rho}] < C$ for some $\rho > 0$ and $C < \infty$ that are independent of $u, t$, and $T$.

We extend the concept of local stationarity for real-valued time series introduced by ^[35] and for local functional time series studied by ^[57] by introducing a new semi-metric $d_{\theta}(\cdot, \cdot)$ associated with a single index $\theta$ in a Hilbert space $\mathscr{H}$ (see Definition 2.1). This semi-metric $d_{\theta}(\cdot, \cdot)$ is defined similarly to that in ^[63], where $\theta \in \Theta_{\mathscr{H}}$ and $\Theta_{\mathscr{H}}$ is a compact subset of $\mathscr{H}$. In their work, they applied the semi-metric to data exhibiting arithmetic strong mixing with identical distributions. Furthermore, our Definition 2.1 corresponds to Definition 2.1 of ^[57], where they used the semi-metric $d(u, v) = \|u - v\|$ in a Banach or Hilbert space $\mathscr{H}$ with norm $\|\cdot\|$. Moreover, when $\mathscr{H}$ is the Hilbert space $L_{\mathbb{R}}^{2}([0, 1])$ of all real-valued, square-integrable functions on the unit interval $[0, 1]$, our definition aligns with Definition 2.1 of ^[82]. In their study, they used the $L_{2}$-norm for $f, g \in L_{\mathbb{R}}^{2}([0, 1])$, defined as

Observe that if we choose $\theta \in L_{\mathbb{R}}^{2}([0, 1])$ defined by

assuming $f(t) - g(t) > 0$ almost everywhere, then

Therefore,

This demonstrates that, in this particular case, the semi-metric $d_{\theta}(\cdot, \cdot)$ reduces to the absolute value of the inner product of $f$ and $g$, thereby generalizing the $L_{2}$-norm.

Remark 2.1. ^[82] generalizes the definition of local stationary processes, initially proposed by ^[34], to the functional setting in the frequency domain. This extension is made under the following assumptions:

(A1) (ⅰ) $\left\{\varepsilon_i\right\}_{i\in \mathbb{Z}}$ is a weakly stationary white noise process taking values in $\mathscr H$ with a spectral representation given by

where $Z_\omega$ is a $2 \pi$-periodic orthogonal increment process taking values in $\mathcal H_{\mathbb{C}} = L_{\mathbb{C}}^2([0, 1])$;

(ⅱ) the functional process $X_{i, n}$ with $i = 1, \ldots, n$ and $n \in \mathbb{N}$ is given by

with the transfer operator $\mathcal{A}_{j, \omega}^{(n)} \in \mathcal{B}_p$ and an orthogonal increment process $Z_\omega$.

(A2) There exists $\mathcal{A}:[0, 1] \times[-\pi, \pi] \rightarrow S_p\left(\mathcal H_{\mathbb{C}}\right)$ with $\mathcal{A}_{u, \cdot} \in \mathcal{B}_p$ and $\mathcal{A}_{u, \omega}$ being continuous in $u$ such that for all $n \in \mathbb{N}$

They have proved in [82, Proposition 2.2] that:

Proposition 2.1. Suppose that Assumptions (A1) and (A2) hold. Then, $\left\{X_{i, n}\right\}$ is a locally stationary process in $\mathscr H$.

2.3.   Mixing condition

Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space, and let $\mathcal{A}$ and $\mathcal{B}$ be subfields of $\mathcal{F}$. Define

Moreover, for an array $\{Z_{t, T}: 1\leq t\leq T\}$, define the coefficients

where $\sigma(Z)$ is the $\sigma$-field generated by $Z$. The array $\{Z_{t, T}\}$ is said to be $\alpha$-mixing (or strongly mixing) if $\alpha(k) \to 0$ as $k \to \infty$.

Among the various mixing conditions explored in the literature, $\alpha$-mixing is a relatively weak but widely applicable property, satisfied by a broad range of stochastic processes, including numerous time series models. The researchers in ^[49] and ^[84] established the conditions required for a linear process to exhibit $\alpha$-mixing. Under minimal assumptions, the linear autoregressive and more general bilinear time series models demonstrate strong mixing properties with exponentially decaying mixing coefficients. Furthermore, the researchers in ^[9] provided valuable insights into the role of $\alpha$-mixing (including geometric ergodicity) in identifying nonlinear time series models (see also ^[20,21,22]). Similarly, the researchers in ^[32] showed that functional autoregressive processes attain geometric ergodicity under specific conditions. Additionally, ^[65,66] demonstrated that, with mild assumptions, both autoregressive conditional heteroscedastic processes and nonlinear additive autoregressive models with exogenous variables are stationary and $\alpha$-mixing.

3.   Main results

We provide the main results of this paper in this section by first considering general kernel estimators as represented in Section 3.1. Correspondingly, we derived the uniform convergence rate as seen in Proposition 3.1. Furthermore, some results on uniform convergence rate and asymptotic normality of the Nadaraya-Watson estimator for the regression function in Model (2.1) are provided in the succeeding subsections (see Theorems 3.1 and 3.2, respectively).

3.1.   Kernel estimation for regression functions

As mentioned, we consider the following kernel estimator for $m\big(u, \langle \theta, x\rangle\big) = m_{\theta}(u, x)$ in Model (2.1):

where $K_{1}(\cdot)$ and $K_{2}(\cdot)$ denote one-dimensional kernel functions. Here, for $j = 1, 2$, we used the notations $K_{j, h}(v) = K_{j}(v/h)$. Moreover, $h = h_{T}$ is a bandwidth satisfying $h \to 0$ as $T \to \infty$. The estimator defined in (3.1) differs from the traditional NW estimator, typically used in strictly stationary settings, by incorporating an additional kernel along the time dimension. Consequently, smoothing is applied not only in the direction of the covariates $X_{t, T}$ but also across time, accounting for variations in the regression function over time.

Remark 3.1. In the finite-dimensional framework, the researcher in ^[83] provided a detailed study of the following model:

where $Y_{t, T}$ and $X_{t, T}$ are random variables of dimensions 1 and $d$, respectively, and the noise satisfies $\mathbb{E}\left[\varepsilon_{t, T} \mid X_{t, T}\right] = 0$. The NW estimator for the regression function in model (3.2) is expressed as:

Furthermore, the researchers in ^[83] explored structured models where the regression function decomposes into time-varying additive components. In ^[83], it is demonstrated that a locally stationary sequence can be effectively approximated by decomposing it into a stationary time series component and a time-varying trend function. Specifically, this representation is expressed as:

where $\vartheta_1\left(\frac{t}{T}\right)$, $\vartheta_2\left(\frac{t}{T}\right)$, are unknown time-varying functions and $({X}_t^*, Y_t^*)$ are assumed to be strictly stationary. In contrast, the present paper focuses on a different framework: The functional single-index model. This setting introduces new challenges and requires distinct conditions to derive the asymptotic properties.

We first enumerate the model and kernel assumptions which are important in deriving our main results. Mentioned assumptions are made for Model (2.1) and the kernel functions therein. These assumptions are standard, and similar assumptions are made among others by ^{[57,63,64,82]}.

Assumption 3.1. (Model assumptions)

(M1) The process $\{X_{t, T}\}$ is locally stationary, that is, $\{X_{t, T}\}$ satisfies Definition 2.1.

(M2) Let $B_\theta(x, h) = \{y \in \mathscr{H}: d_\theta(x, y)\leq h\}$ denote the ball of radius $h$ centered in $x \in \mathscr{H}$. We assume that there exist positive constants $c_d,$ and $C_d$ where $c_{d} < C_{d}$, such that for all $u \in [0, 1]$, all $x \in \mathscr{H}$, and all $h > 0$,

where $\phi_{\theta, x}(h) = \mathbb{P}\left(X_{t}^{(u)} \in B_\theta(x, h)\right) > 0,$ $\phi_{\theta}(h) \to 0$ as $h \to 0$, and $f_{1}(x)$ is a nonnegative functional in $x \in \mathscr{H}$. Moreover, there exist constants $C_{\phi} > 0$ and $\varepsilon_{0} > 0$ such that for any $0 < \varepsilon < \varepsilon_{0}$,

(M3) $\sup\limits_{s, t, T}\sup\limits_{s \neq t}\mathbb{P}((X_{s, T}, X_{t, T}) \in B_\theta(x, h)\times B_\theta(x, h))\leq \psi_\theta(h)f_{2}(x)$, where $\psi_\theta(h) \to 0$ as $h \to 0$, and $f_{2}(x)$ is a nonnegative functional in $x \in \mathscr{H}$. We assume that the ratio $\psi_\theta(h)/\phi_{\theta}^{2}(h)$ is bounded.

(M4) $m_{\theta}(u, x)$ is twice continuously partially differentiable with respect to $u$. We also assume that

for all $x, y \in \mathscr{H}$ for some $c_{m} > 0$ and $\beta > 0$.

Assumption 3.1 formalizes the local stationarity property of the process $\{X_{t, T}\}$ as seen in condition (M1), while the distributional behavior of the rescaled random variable $X_t^{(u)}$ is described in the second condition (M2). Also, condition (M2) ensures that through the function $\phi_{\theta}(h)$, the behavior of the small-ball probability is controlled around zero. Furthermore, condition (M2) is consistent with the ones made by ^[64] and ^[46]. The former used this assumption for strongly mixing processes while the latter in the context of density estimation for functional data. For strongly mixing processes in the locally functional time series setting, one may see ^[57].

Observe that similar to what ^[64] employed in their paper, we can satisfy the Condition (3.3) for fractal-type processes by defining $\phi_{\theta}(\varepsilon) \sim \varepsilon^{\tau}$ as $\varepsilon \to 0$ for some $\tau > 0$, with some change of notation but of similar meaning. Considering a separable Hilbert space $\mathscr{H}$, it can be expected that as $h\to 0,$ $\phi_{\theta}(h)$ diminishes to 0 as in ^[46]. Since $\phi_{\theta}(h)$ is defined similarly as $\phi(h)$ by previously mentioned authors and more specifically by ^[64], we exemplify its form by $\phi_{\theta}(\varepsilon) = \varepsilon^\delta \exp (-C/\varepsilon^a)$ with $\delta, a\geq 0.$ The case when $\phi_{\theta}(\varepsilon) = \exp (-C/\varepsilon^2)$ refers to the Ornstein-Uhlenbeck and general diffusion processes. Also, $\phi_{\theta}(\varepsilon) = \varepsilon^\delta \exp (-C)$ with $\delta > 0$ corresponds to the fractal processes. Excellent references detailing fractal-type processes and on concepts relating to the small ball probability $F_{u}(h; x)$ include those of ^[13] and ^[43]. Extending condition (M2) gives us $(d_{\theta}(X_{s, T}, x), d_{\theta}(X_{t, T}, x))$ that describes the behavior of the joint distribution near the origin. Thus, condition (M3). Consistent with the assumptions made by ^[43,57,64], we have included (M3) and (M4) in this study. To deal with the regression function $m_\theta(u, x)$ with respect to $u$ and $x$, we have condition (M4) to handle the smoothness and continuity properties, respectively.

We impose the following conditions on $\sigma$ (Assumption 3.2) and for kernel functions (Assumption 3.3). These conditions are similar to those made and assumed by ^{[19,43,57,63,64,83]}.

Assumption 3.2. (Conditions on $\sigma$)

($\Sigma$ 1) $\sigma:[0, 1]\times \mathscr{H} \to \mathbb{R}$ is bounded by some constant $C_{\sigma} < \infty$ from above and by some constant $c_{\sigma} > 0$ from below, that is, $0 < c_{\sigma}\leq\sigma\big(u, \langle\theta, x\rangle\big)\leq C_{\sigma} < \infty$ for all $u$ and $x$.

($\Sigma$ 2) $\sigma$ is Lipschitz continuous with respect to $u$.

($\Sigma$ 3) $\sup\limits_{u \in [0, 1]}\sup\limits_{y:d_\theta(x, y)\leq h}\big|\sigma\big(u, \langle\theta, x\rangle\big)-\sigma\big(u, \langle\theta, y\rangle\big)\big| = o(1)$ as $h \to 0$.

Assumption 3.3. (Kernel assumptions)

(KB1) The kernel $K_{1}(\cdot)$ is symmetric around zero, bounded, and has a compact support, that is, $K_{1}(v) = 0$ for all $|v| > C_{1}$ for some $C_{1} < \infty$. Moreover, $\int K_{1}(z)dz = 1$ and $K_{1}(\cdot)$ is Lipschitz continuous, that is, $|K_{1}(v_{1}) - K_{1}(v_{2})| \leq C_{2}|v_{1} - v_{2}|$ for some $C_{2} < \infty$ and all $v_{1}, v_{2} \in \mathbb{R}$.

(KB2) The kernel $K_{2}(\cdot)$ is nonnegative, bounded, and has support in $[0, 1]$ such that $0 < K_{2}(0)$ and $K_{2}(1) = 0$. Moreover, $K'_{2}(v) = dK_{2}(v)/dv$ exists on $[0, 1]$ and satisfies $C'_{1}\leq K'_{2}(v) \leq C'_{2}$ for two real constants $-\infty < C'_{1} < C'_{2} < 0$. Moreover, suppose that $K_2(\cdot)$ is a Lipschitz continuous function.

In line with the assumptions made by ^[57,83], we define conditions ($\Sigma$1) and ($\Sigma$2). Along with the notational convention $\sigma(u, \langle \theta, x \rangle)$, we employ condition ($\Sigma$3) to investigate the asymptotic properties of the variance of $\hat{m}(u, x)$ and establish its asymptotic normality. Evaluating $Th \phi_{\theta}(h) \, \text{Var}\left(\hat{g}_{\theta}^{(1)}(u, x) \right)$ in Eq (A.9) is essential to demonstrate the existence of the variance $V_{\theta}(u, x) > 0$.

Moreover, the assumptions on the kernel functions $K_1(\cdot)$ and $K_2(\cdot)$ are standard in the literature and are satisfied by popular kernels such as the (asymmetric) triangle and quadratic kernels. Condition (KB1) ensures that $K_1(\cdot)$ is bounded and has compact support. Additionally, its symmetry property implies that $K_1(\cdot)$ can be any symmetric kernel, such as the box, triangle, quadratic, or Gaussian kernel. Condition (KB2) indicates that $K_2(\cdot)$ is a Type Ⅱ kernel function as defined in ^[43]. For a comprehensive introduction and detailed discussion of these assumptions, please refer to ^[43]. In our study, Assumption 3.3 aids in determining the upper bounds of the kernel functions, as demonstrated in the initial steps of the proof of Proposition 3.1 and in certain parts of the proof of Theorem 3.2.

3.2.   Uniform convergence rates for kernel estimators

Our goal here is to establish the asymptotic properties of the estimator given in (3.1). We first investigate the mentioned properties for the general kernel estimator provided below. For an array of one-dimensional random variables $\{W_{t, T}\}$, we define

Several representations of (3.4) can be made using kernel estimators including the Nadaraya-Watson (NW) estimator. For the purposes of this study, we use the results with $W_{t, T} = 1$ and $W_{t, T} = \varepsilon_{t, T}$.

To show the desired claim, we will derive the uniform convergence rate of $\hat{\psi}_\theta(u, x) - \mathbb{E}[\hat{\psi}_\theta(u, x)]$. We assume the following (Assumptions 3.4 and 3.5) for the components of $\hat{\psi}_\theta(u, x)$ in Eq (3.4). Assumption 3.4 relates to the mixing assumptions attributed to the array of random variables $\{X_{t, T}, W_{t, T}\}$ while Assumption 3.5 concerns the regularity conditions on $h$ and $\phi_{\theta}(h)$.

Assumption 3.4. (Mixing assumptions)

(E1) It holds that $\sup\limits_{t, T}\sup\limits_{x \in \mathscr{H}}\mathbb{E}[|W_{t, T}|^{\zeta}|X_{t, T} = x] \leq C$ for some $\zeta > 2$ and $C < \infty$.

(E2) The $\alpha$-mixing coefficients of the array $\{X_{t, T}, W_{t, T}\}$ satisfy $\alpha(k) \leq Ak^{-\gamma}$ for some $A > 0$ and $\gamma > 3$. We also assume that $\delta+1 < \gamma(1-{\frac{2}{\nu}})$ for some $\nu > 2$ and $\delta > 1-{\frac{2}{\nu}}$, and

as $T \to \infty$, where $\lambda_{T} = [(\phi_{\theta}(h))^{-(1-{\frac{2}{\nu}})/\delta}]$.

To prove Theorem 3.2, which establishes the asymptotic normality of $\hat{m}_\theta(u, x)$, we need to apply condition (3.5) specified in (E2) of Assumption 3.4. This condition also aids in demonstrating the asymptotic negligibility of the bias of $\hat{m}_\theta(u, x)$. Similar assumptions for conditions (E1) and (E2) were made by ^[57]; however, we employ a slightly different version of condition (E2) in our work. Comparable conditions to Assumption 3.4 have also been utilized in other studies, such as ^[64,83].

In the following section, we present the regularity conditions concerning $h$ and $\phi_{\theta}(h)$, specified in Assumption 3.5.

Assumption 3.5. (Regularity assumptions)

As $T \to \infty$,

(R1) $\frac{\big(\log T\big)^{\frac{\gamma-1}{2}+\zeta_0(\gamma+1)}}{T^{\frac{\gamma-1}{2}-1-\frac{\gamma+1}{\zeta}}h^{\frac{\gamma-1}{2}+1}\big(\phi_{\theta}(h)\big)^{\frac{\gamma-1}{2}}} \to 0$ for some $\zeta_{0} > 0$, and

(R2) $Th^{3}, Th\phi_{\theta}(h) \to \infty$,

where $\zeta$ and $\gamma$ are positive constants that appear in Assumption 3.4.

To obtain the convergence rate of the general estimator $\hat{\psi}_\theta(u, x),$ we use an exponential inequality for $\alpha$-mixing sequence in Lemma B.3, and impose the regularity assumption (R1). Consequently, the same is done for the Nadaraya-Watson estimator $\hat{m}_\theta(u, x)$. Considering the same values forS $\gamma$ and $\zeta$ in Assumption 3.4, condition (R1) holds since $\gamma > \frac{2+3\zeta}{\zeta-2}$ and that the $\lim_{\zeta\to \infty}\frac{2+3\zeta}{\zeta-2} = 3.$ Moreover, we use the second regularity condition (R2) in dealing with the bias and in computing the convergence rate of the general estimator. Also, it can be noted that (R2) holds by considering $h\leq CT^{-\zeta}$ (see ^[83]), and $\phi_{\theta}(h)\sim h^\tau, \tau > 0.$

The succeeding result (Proposition 3.1) suggests a generalization of the work of ^[83] on the uniform convergence results to a functional time series. Comparably, we provide a more general result than those obtained by ^[63], wherein the convergence is obtained for identically distributed random variables, and extended the work of ^[57] that uses the measure $d(u, v) = \|u-v\|$. As a recall, we use the measure $d_{\theta}(u, v) = |\langle\theta, u-v\rangle|.$

Proposition 3.1. Assume that Assumptions 3.1 (M1), (M2), 3.3, 3.4, and 3.5 are satisfied. Then, the following result holds for any $x \in \mathscr{H}$:

Using Proposition 3.1, we established that our general estimator $\hat{\psi}_{\theta}(u, x)$ achieves a uniform convergence rate of $\sqrt{\dfrac{\log T}{T h \phi_{\theta}(h)}}$. This result is comparable to the convergence rates for general estimators in nonstationary functional data settings reported by ^[57] (see Proposition 3.1 therein). The key distinction in our approach is the use of $\phi_{\theta}(h)$ instead of $\phi(h)$, which enables us to incorporate the single index $\theta$ into the semi-metric $d_{\theta}(\cdot, \cdot)$ utilized in our study.

Moreover, in the context of strictly stationary functional time series, ^[43] derived a pointwise convergence rate for the nonparametric regression function that aligns with the rate we obtained in Proposition 3.1.

Building on these results, we will now determine the uniform convergence rate of the kernel estimator $\hat{m}_{\theta}(u, x)$ using Theorem 3.1 below.

Theorem 3.1. Suppose that Assumptions 3.1–3.3, and 3.5 are satisfied and that Assumption 3.4 is satisfied with $W_{1, T} = 1$ and $W_{t, T} = \varepsilon_{t, T}$. Then, the following result holds for any $x \in \mathscr{H}$:

In our proof, the stochastic component is of order $O_{\mathbb{P}}\left(\sqrt{\dfrac{\log T}{T h \phi_{\theta}(h)}} \right)$, which relies heavily on the results obtained in Proposition 3.1. The bias component is shown to be of order $O_{\mathbb{P}}\left(h^{2 \wedge \beta} \right)$. Similar to the convergence results obtained by ^[57], and in contrast to ^[83] (see Theorem 4.2 therein), we do not encounter a bias term arising from the approximation error of $X_{t, T}$ by $X_{t}^{(u)}$. Under our assumptions, this approximation error is $O\left(T^{-1} h^{(1 \wedge \beta) - 1} \phi_{\theta}^{-1}(h) \right)$, which is negligible compared to $h^{2 \wedge \beta}$. Furthermore, by introducing a single-index $\theta$ in our framework, we generalized the pointwise convergence results from ^[43] and extended the findings for strictly stationary functional time series in ^[64]. This generalization is achieved through Theorem 3.1 presented above. To illustrate our result, refer to Remark 3.2 below. While ^[57] derived a convergence rate of order $O_{\mathbb{P}}\left(\left(\dfrac{\log T}{T} \right)^{\frac{\beta}{2\beta + \tau + 1}} \right)$ for fractal-type processes $\{X_{t}^{(u)}\}$ with $\beta \leq 2$, we have obtained a comparable convergence rate in our setting. According to ^[43] (see page 208), the bandwidth selection scheme corresponding to regression estimation is $h \sim \left(\dfrac{\log T}{T} \right)^{\frac{1}{2\beta + \tau}}$. This observation leads to the following remark.

Remark 3.2. For a fractal-type process $\{X_{t}^{(u)}\}$, the right-hand side of (3.1) with $\beta \leq 2$ is optimized by choosing $h \sim \left({\frac{\log T}{T}}\right)^{\frac{1 }{ 2\beta+\tau}}$, and the optimized rate is

3.3.   Asymptotic normality for kernel estimators

We provide the central limit theorem for our Nadaraya-Watson estimator $\hat{m}_\theta(u, x)$ in this section. We need Assumption 3.6 to establish the asymptotic normality of the NW estimator $\hat{m}_\theta(u, x)$. We are aided by the Bernstein's big-block and small-block procedure to accomplish the proof of Theorem 3.2 along with the assumptions considered therein. To simplify the proof, we set $K_{2}(\cdot)$ as the asymmetrical triangle kernel. That is, $K_{2}(x) = (1-x)\mathbb{1}_{(x \in [0, 1])}$.

Assumption 3.6. There exists a sequence of positive integers $\{v_{T}\}$ satisfying $v_{T}\to \infty$, $v_{T} = o\Big(\sqrt{Th\phi_{\theta}(h)}\Big)$ and $\sqrt{\frac{T }{ h\phi_{\theta}(h)}}\alpha(v_{T}) \to 0$ as $T \to \infty$.

Observe that

where

Under the same assumption in Theorem 3.1, we can show that

See the proof of Theorem 3.2 for details. Then, we have

where $B_{T, \theta}(u, x) = \frac{\mathbb{E}[\hat{g}^{B}_\theta(u, x)]}{\mathbb{E}[\hat{m}_{\theta}^{(1)}(u, x)]}$ is the "bias" term and $\frac{\hat{g}_{\theta}^{(1)}(u, x)}{\hat{m}_{\theta}^{(1)}(u, x)}$ is the "variance" term.

Theorem 3.2. Assume that Assumptions 3.1–3.3, 3.5, and 3.6 are satisfied and that Assumption 3.4 is satisfied for both $W_{1, T} = 1$ and $W_{t, T} = \varepsilon_{t, T}$. Then as $T\to \infty$, the following result holds for any $x \in \mathscr{H}$:

where $B_{T, \theta}(u, x) = O\left(h^{2\wedge \beta}\right)$ and

Remark 3.3. Theorem 3.2 is an extension of the results in ^[64,83], and ^[57] to a locally stationary functional time series with a semi metric $d_{\theta}(\cdot, \cdot)$ associated with a single index $\theta$ from a Hilbert space $\mathscr{H}$. It is noteworthy that we use a decomposition containing the expressions $B_{T, \theta}(u, x)$ and $V_\theta(u, x)$ that are very similar to those in ^[57]. Moreover, we use a similar proof procedure to that of ^[64] and of ^[57] and obtain very similar results. It is important to note that the asymptotic negligibility of the bias part is achieved by requiring

This is satisfied whenever we have $h = T^{-\xi}$ and $\phi_{\theta}(h) = h^c$ for

Remark 3.4. The single functional index $\theta \in \mathscr{H}$ is typically unknown and must be estimated in practical applications. This challenge has been addressed in the literature on single functional regression models, where estimation approaches using cross-validation or maximum-likelihood methods have been explored, as in ^[1] and references therein. An alternative approach, adopted in this section, involves selecting $\theta(t)$ among the eigenfunctions of the covariance operator $\mathbb{E}\left[\left(X^{\prime}-\mathbb{E}\left(X^{\prime}\right)\right)\langle X^{\prime}, \cdot \rangle_{\mathcal{H}}\right]$, where $X(t)$ is a diffusion-type process on a real interval $[a, b]$ and $X^{\prime}(t)$ denotes its first derivative (see ^[5,7,40], for example). Given a training sample $\mathcal{L}$, the covariance operator can be estimated using its empirical version $(1 /|\mathcal{L}|) \sum_{i \in \mathcal{L}}\left(X_i^{\prime}-\mathbb{E} X^{\prime}\right)^t\left(X_i^{\prime}-\mathbb{E} X^{\prime}\right)$. Subsequently, a discretized version of the eigenfunctions $\theta_i(t)$ can be obtained via principal component analysis.

3.4.   The bandwidth selection criterion

Several methods have been established in the literature for bandwidth selection criteria. For instance, ^[78] lists various approaches for choosing the smoothing parameter $h$, which is crucially important in kernel density estimation for both univariate and multivariate data. In the univariate case, a natural method is the researcher's subjective choice, involving the plotting of multiple curves and selecting an estimate that aligns with prior beliefs about the density. Other methods involve referencing a particular standard distribution. Specifically, when using a Gaussian kernel, the optimal bandwidth is given by $h_{\text{opt}} = 1.06\, \sigma\, n^{-1/5}$, where $\sigma$ can be the sample standard deviation or a more robust estimator. To avoid oversmoothing in multimodal populations, one may use the interquartile range $R$ and set $h_{\text{opt}} = 0.79\, R\, n^{-1/5}$. Corresponding suggested optimal values of the smoothing parameter for multivariate data can also be found in Chapter 4 of ^[78]. Additionally, we refer to ^[51,53,73] for bandwidth selection rules concerning nonparametric kernel estimators, including the Nadaraya-Watson regression estimators. A suitable selection of the smoothing parameter $h$ that works for both finite and infinite-dimensional cases must be chosen. We define our local cross-validation criterion as follows:

where $\hat{m}^{[s]}_{\theta}(\cdot)$ represents the leave-one-out estimator of $\hat{m}_{\theta} (\cdot)$, based on the sample $\left(X_{1, T}, Y_{1, T} \right), \ldots, \left(X_{T, T}, Y_{T, T} \right)$ excluding the pair $\left(X_{s, T}, Y_{s, T} \right)$. Our goal is to minimize the criterion (3.6) by selecting a bandwidth $\hat{h}_T \in [a_T, b_T]$ among $h \in [a_T, b_T]$.

Following the idea introduced by ^[10] and used by ^[16], we replace the global weights $\tilde{\mathscr{W}}(X_{s, T})$ with local weights $W(x, X_{s, T})$, which are independent of $T$. Thus, $CV_{\theta, x}(h_T)$ in (3.6) becomes

In practice, for $i \in \{1, \ldots, T\}$, one may utilize uniform global weights $\tilde{\mathscr{W}}(X_{i, T}) = 1$ and define the local weights as

4.   Numerical experiment

In this section, we present the results of a numerical simulation study designed to illustrate the finite-sample behavior of the proposed estimator within the context of a single-index regression model for functional time series. The estimator for $m_\theta(u, x)$ is defined as

where $K_{1, h}(\cdot)$ and $K_{2, h}(\cdot)$ are kernel functions with bandwidth $h$, and $d_\theta(\cdot, \cdot)$ is the semi-metric associated with the single index $\theta$. We consider the Hilbert space $\mathscr{F}$ of square-integrable functions on $[0, 1]$:

equipped with the inner product

for all $f, g \in \mathscr{F}$, and the associated $L^2$-norm

Let $\mathcal{L}: \mathscr{F} \to \mathscr{F}$ be a linear operator. An operator $\mathcal{L}$ is said to be compact if it maps bounded sets to relatively compact sets. Since $\mathscr{F}$ is a separable Hilbert space, any compact operator $\mathcal{L}$ admits a singular value decomposition with a sequence of nonnegative singular values $\{ s_n(\mathcal{L}) \}_{n \in \mathbb{N}}$ decreasing to zero. The operator $\mathcal{L}$ can thus be represented as

where $\{ \phi_n \}$ and $\{ \psi_n \}$ are orthonormal sequences in $\mathscr{F}$. For $p \in [1, \infty]$, the Schatten $p$-class $S_p(\mathscr{F})$ consists of compact operators $\mathcal{L}$ for which the Schatten $p$-norm $\| \mathcal{L} \|_p$ is finite:

Simulation steps:

Step 1: Generating the functional sample $X_{t, T}$. We generate the functional time series $X_{t, T}$ as a functional autoregressive process of order 1 (FAR(1)), following the method outlined in ^[82]:

where $B_{t/T}$ is a time-varying linear operator, and $\epsilon_t(\tau)$ are innovation functions. The innovations $\epsilon_t$ are constructed using Fourier basis functions $\{ \psi_j \}_{j \in \mathbb{N}}$, specifically sine and cosine functions, with coefficients $\langle \epsilon_t, \psi_j \rangle$ that are independent Gaussian random variables with mean zero and variance $\sigma_j^2 = [\pi (j -1.5)]^{-2}$:

In practice, we truncate the infinite series at a finite number $J$ to obtain an approximate representation:

Substituting into Eq (4.2) and exploiting the linearity of $B_{t/T}$, we derive the finite-dimensional recursion:

where $\mathit{\boldsymbol{X}}_t^{(T)} = \left(\langle X_{t, T}, \psi_1 \rangle, \ldots, \langle X_{t, T}, \psi_J \rangle \right)^\top$, $\mathit{\boldsymbol{\epsilon}}_t = \left(\langle \epsilon_t, \psi_1 \rangle, \ldots, \langle \epsilon_t, \psi_J \rangle \right)^\top$, and $\mathit{\boldsymbol{B}}_{t/T}$ is a $J \times J$ matrix with entries $b_{ij} = \langle B_{t/T} \psi_i, \psi_j \rangle$. To construct $\mathit{\boldsymbol{B}}_{t/T}$, we generate a $J \times J$ matrix $\mathit{\boldsymbol{A}}_u$ with entries $a_{ij}$ being independent Gaussian random variables with variance

where $u = t/T$, $c = 3$, and $i, j = 1, \ldots, J$. The operator $B_{t/T}$ is then represented by normalizing $\mathit{\boldsymbol{A}}_u$ using the operator norm:

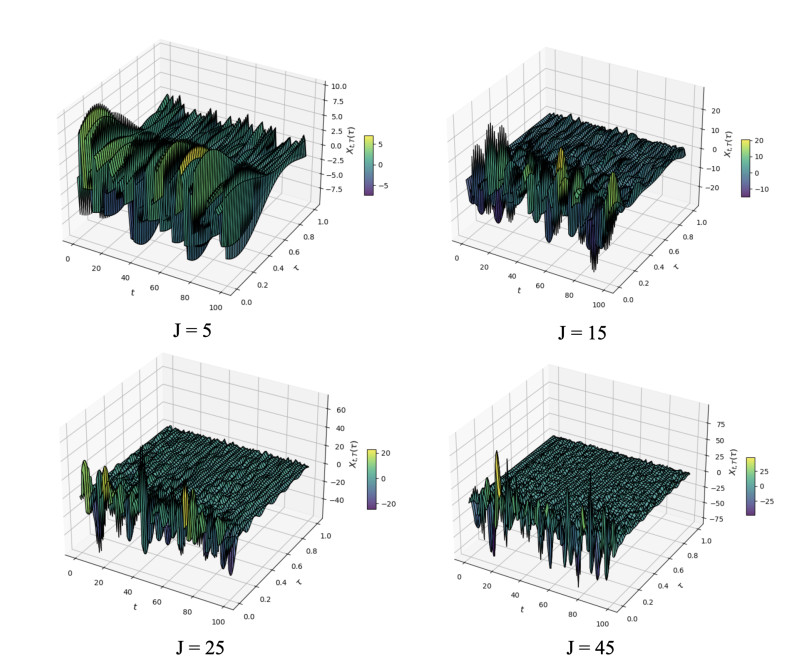
where $\eta = 0.4$. In this step, we have adopted the parameter values for $\eta$ and $c$ as proposed by ^[82]. The parameter $c$ plays a crucial role in modulating the decay rate of the variance for the entries $a_{ij}$, thereby significantly influencing the overall structure of the functional data, as illustrated in Figure 1. Moreover, the parameter $\eta$ primarily affects the scale of $X_{t, T}$, allowing us to adjust the influence of $B_{t, T}$ on the updates to $X_{t, T}$ at each time step. By tuning $\eta$, we can regulate the extent of each update to $X_{t, T}$, with smaller values of $\eta$ serving to mitigate potential over-amplification in these updates. For our simulations, we have adopted these parameter values, not only to align with the cited work, but also to enhance computational efficiency. Readers interested in further analysis might consider examining how variations in $\eta$ and $c$ impact the dynamics of the model. Additionally, we utilize the following Fourier basis functions for the terms $X_{t, T}(\tau)$ and $\epsilon_t(\tau)$ for each $t = 1, \dots, T$ and $\tau \in [0, 1]$:

These basis functions help define the structural form of each functional term, enhancing the representational fidelity of the model.

Step 2: Generating the single index $\theta(\tau)$. We generate the single index function $\theta(\tau)$ as a linear combination of basis functions, following ^[63]:

where the basis functions are defined as

Step 3: Generating the scalar response variable $Y_{t, T}$. We generate the scalar response variable $Y_{t, T}$ according to the model

where $\varepsilon_{t, T}$ are independent standard normal random variables. The regression function $m_\theta(u, x)$ is specified as

Step 4: Selecting the Bandwidth $h$. We select the bandwidth $h$ using the cross-validation criterion, minimizing the cross-validation score

where $\hat{m}_{\theta}^{[s]}(\cdot)$ is the leave-one-out estimator of $\hat{m}_{\theta}(\cdot)$, computed without the $s$-th observation.

Visualization. Figure 1 displays samples of 100 curves $X_{t, T}$ over the interval $[0, 1]$ for different numbers of basis functions $J = 5, 15, 25,$ and $45$. Each panel illustrates realizations of the time-varying functional process $X_{t, T}$ for $t = 1, \ldots, 100$.

4.1.   Point-wise mean square convergence

To demonstrate the pointwise convergence of the estimator $\hat{m}_{\theta}(u, x)$ to the true regression function $m_{\theta}(u, x)$, we conducted simulations with $T = 1000$ observations and evaluated the estimator at various rescaled time points $u = 0.25, 0.50,$ and $0.95$. We selected $x = X_{3, T}$ as the covariate point of interest.

Recall that the Nadaraya-Watson estimator is defined as

where $h > 0$ is the bandwidth parameter, $d_\theta(\cdot, \cdot)$ is the semi-metric associated with the single index $\theta$, and $K_1(\cdot)$ and $K_2(\cdot)$ are kernel functions. In our simulations, we employed the uniform kernel for $K_1(\cdot)$ and the Gaussian kernel for $K_2(\cdot)$. Specifically, the uniform kernel $K_1(\cdot)$ is defined as

which provides equal weighting to observations within the bandwidth and zero weight outside. The Gaussian kernel $K_2(\cdot)$ is given by

as described in ^[43]. Notably, we utilized an asymmetric version of $K_2(\cdot)$ by considering only non-negative values of $w$, reflecting the non-negativity of the semi-metric $d_\theta(x, X_{t, T})$. It is worth noting that while our simulation study employed the uniform and gaussian kernels for $K_1(\cdot)$ and $K_2(\cdot)$, respectively, one may also explore utilizing other kernel functions satisfying Assumption 3.3. A comparison with regards to the estimator's mean squared errors (MSEs) across various choices of kernel functions may be investigated. The MSE values computed from the simulations using the uniform and gaussian kernels are summarized in Table 1, illustrating the estimator's performance at the specified time points. These results confirm the theoretical convergence properties of $\hat{m}_{\theta}(u, x)$ as established in our asymptotic analysis.

The analysis explores the impact of varying the number of basis functions, $J = 5, 15, 25,$ and $45$, along with the various rescaled time points. For each of the results obtained (for both the MSEs and the optimal bandwidths), we set $T = 1000$, $100$ replications, and 100 candidate optimal bandwidths to choose from, ranging between 0.01 to 0.99. The MSE values observed at each rescaled time $u$ display minimal variation across the different values of $J$, suggesting that the choice of basis functions within this range has negligible influence on the results. The table further suggests that for the rescaled time points $u = 0.25$, and $u = 0.95$, we obtain relatively higher MSEs compared to that at $u = 0.50$. These findings suggest that for the subsequent analysis of the estimator $\hat{m}_\theta(u, x)$'s performance as $T$ increases, we focus on $u = 0.50$, using a bandwidth of $h = 0.426549$ and $J = 5$ basis functions. We have demonstrated the performance of the mentioned estimator at varying values of $T = 100,500, 1000,$ and $1500$. Although not displayed in Figure 2, we have computed the mean values of the MSEs which are $0.0260923, 0.00506145, 0.00264353,$ and $0.00182452$ for $T = 100,500, 1000,$ and $1500$, respectively. Hence, our assertion concerning decreasing approximation errors induced by our estimator as $T$ increases. As is common in inferential contexts, larger sample sizes generally yield better performance. Simple inspection of the results in Figure 2 shows that larger sample sizes $T$ lead to smaller MSEs. More precisely, Figure 2 shows a steady decrease in approximation error as $T$ grows, supporting the inference that as $T$ becomes larger and larger, the MSE values become smaller and smaller. These empirical findings are thus in alignment with the theoretical results outlined in Theorem 3.1.

4.2.   Asymptotic normality

As imposed in the previous subsection, we also consider the rescaled time point $u = 0.50$, with a bandwidth of $h = 0.426549$, $T = 1500$, and $J = 5$ basis functions to illustrate the asymptotic normality of our estimator. In this setting, we employ a quadratic kernel for $K_1(\cdot)$ and an asymptotic uniform kernel for $K_2(\cdot)$. The uniform kernel is defined analogously to that introduced in the previous subsection, but with support on the interval $[0, 1]$. The quadratic kernel is defined as $\frac{3}{4}(1-u^2)\mathbb{1}_{[-1, 1]}(u)$ (see ^[43]). While selecting a bandwidth $h$ tailored to these kernels would be preferable, for the purpose of our simulations—specifically, to illustrate asymptotic normality—we consider an approximate optimal bandwidth of $h = 0.426549$. Our results suggest that this choice yields similar conclusions, provided that the assumptions on $K_1(\cdot)$ and $K_2(\cdot)$ stated in Assumption 3.3 hold. Therefore, our primary aim here is to demonstrate that the theoretical results remain valid irrespective of the particular choices of $K_1(\cdot)$ and $K_2(\cdot)$, as long as they satisfy Assumption 3.3 and the other required conditions. Thus, we proceed with the simulation by first recalling the following quantities $\hat{m}_\theta(u, x)$, $m_\theta(u, x)$, $B_{T, \theta}(u, x)$, and $\hat{g}^B_\theta(u, x)$ in Assumption 3.6 and suppose that

where

Here, with $B_{T, \theta}(u, x) = O\left(h^{2\wedge \beta}\right)$ as per results obtained, we will demonstrate that $S_\theta(u, x)$ can be approximated by the normal distribution. That is,

where

To estimate $\text{Var}\left(\hat{g}_{\theta}^{(1)}(u, x)\right)$ and $\phi_{\theta}(h)$ by $\hat{\sigma}(u, x)$ and $\hat{\phi}_{\theta}(h)$, respectively, please see ^[63]. That is, we have

We confirm our theoretical results by taking 100 copies of the random variable $S_\theta(u, x)$ and creating the corresponding histogram and $Q$-$Q$ plot. See Figure 3 for an illustration. The histogram illustrates that our data can be approximated by a normal distribution (the distribution we theorized) with its shape forming like a bell. The presented $Q$-$Q$ plot supports our claim since the points closely align with the diagonal line. This indicates that our simulated statistics approximate a normal distribution.

5.   Concluding remarks

In this paper, we develop an asymptotic theory for single-index nonparametric regression models applied to locally stationary functional time series under $\alpha$-mixing dependent observations. We begin by defining a semi-metric $d_{\theta}(\cdot, \cdot)$ associated with a single index $\theta$ in a Hilbert space $\mathscr{H}$, where $d_{\theta}(u, v) : = |\langle \theta, u - v \rangle|$ for all $u, v \in \mathscr{H}$. We consider and investigate the model

where $\{Y_{t, T}, X_{t, T}\}_{t = 1}^{T}$ are random variables, $Y_{t, T}$ is real-valued, and $X_{t, T}$ takes values in the semi-metric space $\mathscr{H}$ equipped with the semi-metric $d_\theta(\cdot, \cdot)$. Moreover, we construct an estimator for the nonparametric regression operator within this model and derive its asymptotic properties under mild conditions. Specifically, we obtain uniform convergence rates for both the general kernel estimator and the NW estimator of the regression function. Our results demonstrate that, under sufficient conditions, the general kernel estimator $\hat{\psi}_\theta(u, x)$ converges to its mean $\mathbb{E}[\hat{\psi}_\theta(u, x)]$ at the rate

and the NW estimator $\hat{m}_\theta(u, x)$ converges to $m_\theta(u, x)$ at the rate

The convergence rate of the NW estimator comprises two components: The first term relates to the variability of the estimate and depends on the concentration of the random variables $X_{t, T}$ as characterized by the small-ball probability $\phi_{\theta}(h)$, while the second term pertains to the bias of the estimate, which is influenced by the smoothness condition imposed on the operator $m_\theta(u, x)$. Specifically, the bias term depends on the parameter $\beta$ and results from the application of the Lipschitz assumption. To achieve a more efficient estimator for $m_\theta(u, x)$, it is crucial to minimize the dispersion of the functional data, thereby increasing the concentration of the random variables and maximizing the small-ball probability $\phi_{\theta}(h)$. A higher value of $\phi_{\theta}(h)$ leads to a faster convergence rate.

Consistent with the approaches of ^[57] and ^[83], one may explore the uniform convergence rate of $\hat{m}_\theta(u, x)$ over the domain $(1 -C_1 h, 1] \times \{x\}$ for forecasting purposes. This can be achieved by employing boundary-corrected kernels or one-sided kernels, assuming they are compactly supported and Lipschitz continuous to satisfy the present theoretical framework. It is important to note that achieving a high concentration value $\phi_{\theta}(h)$ is directly linked to the structure of the underlying space, which can be optimized by defining an appropriate semi-metric, such as the $d_\theta(\cdot, \cdot)$ introduced above. This optimization is further enhanced by selecting $k(\theta) = \arg\min_{k \in \{1, 2, \ldots, N_{\theta, T}\}} \|\theta - \theta_k\|$ for $\theta$, as demonstrated in the proof of Proposition 3.1. Consequently, the choice of $\theta$ plays a pivotal role in controlling $\phi_{\theta}(h)$. Additionally, employing an estimator $\theta(t) \in \mathscr{H}$ may provide more effective estimates and yield more reliable forecasting results. A pertinent reference for such an estimator is found in ^[63] (page 672).

Finally, we refer to Section 4 to illustrate the finite-sample behavior of the estimator. Our simulation study supports the pointwise convergence of $\hat{m}_\theta(u, x)$ to $m_\theta(u, x)$, as demonstrated using a first-order functional autoregressive process $X_{t, T}$. The asymptotic tightness of the estimator is evidenced by Figure 2, where the box plots shrink as $T$ increases, indicating that the mean squared error (MSE) becomes asymptotically negligible for large $T$, which is consistent with our theoretical findings. Additionally, Figure 3 corroborates Theorem 3.2 by demonstrating the asymptotic normality of the estimator. To provide methodological recommendations for using the proposed estimators, it would be beneficial to conduct extensive Monte Carlo experiments comparing our procedures with other alternatives in the literature. However, this is beyond the scope of the present paper.

Author contributions

Breix Michael Agua and Salim Bouzebda: Conceptualization, methodology, investigation, writing–original draft, writing–review & editing. All authors of this article have been contributed equally. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The author(s) declare(s) that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Mr. Agua's research is supported by the Department of Science and Technology - Science Education Institute (DOST-SEI) of the Philippine Government in partnership with Campus France through the PhilFrance-DOST Scholarship grant, which are greatly acknowledged. The authors extend their sincere gratitude to the Editor-in-Chief, the Associate Editor, and the three referees for their invaluable feedback. Their insightful comments have greatly refined and focused the original work, resulting in a markedly improved presentation.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Salim Bouzebda is the Guest Editor of special issue "Advances in Statistical Inference and Stochastic Processes: Theory and Applications" for AIMS Mathematics. Salim Bouzebda was not involved in the editorial review and the decision to publish this article.

A.   Appendix-A

In this section, we present detailed proofs of the conjectures under investigation. We begin by proving Proposition 3.1. The proof starts by decomposing $\hat{\psi}_{\theta}(u, x)$ into two terms: $\hat{\psi}^{(1)}_{\theta}(u, x)$ and $\hat{\psi}^{(2)}_{\theta}(u, x)$.

Proof of Proposition 3.1. We first define $B = [0, 1]$, $\alpha_T = \sqrt{\frac{\log T}{Th\phi_{\theta}(h)}}$, and $\tau_T = \rho_T T^{1/\zeta}$ with $\rho_T = (\log T)^{\zeta_o}$ for some $\zeta_o > 0.$ Now, define

Clearly,

From this, we outline the proof of Proposition 3.1 into two steps as follows:

(ⅰ) $\sup\limits_{\theta \in \Theta_{\mathscr{H}}}\sup\limits_{x\in S_{\mathscr{H}} }\sup\limits_{u \in [0, 1]}\Big|\hat{\psi}_{\theta}^{(2)}(u, x)-\mathbb{E}\left[\hat{\psi}_{\theta}^{(2)}(u, x)\right]\Big| = O_\mathbb{P}(\alpha_T)$, and

(ⅱ) $\sup\limits_{\theta \in \Theta_{\mathscr{H}}}\sup\limits_{x\in S_{\mathscr{H}} }\sup\limits_{u \in [0, 1]}\Big|\hat{\psi}_{\theta}^{(1)}(u, x)-\mathbb{E}\left[\hat{\psi}_{\theta}^{(1)}(u, x)\right]\Big| = O_\mathbb{P}(\alpha_T)$.

Step (ⅰ): We first tackle $\hat{\psi}_{\theta}^{(2)}(u, x)-\mathbb{E}\big[\hat{\psi}_{\theta}^{(2)}(u, x)\big].$ Observe that

Now, using Assumptions 3.1 (M1) and (M4), and Assumption 3.3 (KB2), we obtain

where by using the elementary properties of summations and by the definition of $d_\theta (\cdot, \cdot)$, we get

Hence, combining the above results, we have

Consequently, we obtain

By Lemma B.2, we have

Inferring from the last result, we get

Step (ⅱ): We are left to show that

To achieve the desired result, assume that $S_{\mathscr{H}}$ and $\Theta_{\mathscr{H}}$ are compact subsets of $\mathscr{H}.$ Suppose also that $N_{S, T},$ and $N_{\theta, T}$ are the minimal number of balls in $\mathscr{H}$ with radius $h$ necessary to cover $S_{\mathscr{H}}$ and $\Theta_{\mathscr{H}}$ with centers $x_1, \ldots, x_{N_{S, T}},$ and $\theta_1, \ldots, \theta_{N_{\theta, T}},$ respectively such that $N_{S, T}\cdot N_{\theta, T}\leq C\cdot \frac{1}{\alpha_T}$ balls

More discussion on the covering numbers may be found in ^[11]. We further suppose that with $N_{B_{i, T}}\leq C \frac{1}{h\alpha_T}$ balls $B_{i, T}$, B is covered. Here,

where $u_i$ is the midpoint of $B_{i, T}.$ Now, assume that for $(w, v)\in \mathbb{R}^2$,

With a sufficiently large $T$ and for $u\in B_{i, T},$ we obtain

where $K^{*}_h(v) = K^{*}(v/h).$ We now define $\bar{\psi}_{\theta}^{(1)}(u_i, x)$ as

Now, we write $t(x) = \arg \min_{t\in\{1, 2, \ldots, N_{S, T}\}}\|x-x_t\|,$ and $k(\theta) = \arg \min_{k\in \{1, 2, \ldots, N_{\theta, T}\}}\|\theta-\theta_k\|,$ and use a similar decomposition in ^[63] which is given as follows

We first deal with the term $Q_{3, \theta}.$ Since for sufficiently large $M,$ and

for any $x\in \mathscr{H}$, we get

Thus, we have

where

and

Before proceeding with the further parts of the proof, we first lay down some important notations. For $t = 1, 2, \ldots, T,$ and $\mathbb{1}_{A}(\cdot)$ is an indicator function of a set $A,$ we write

We now go back to showing the bound of $Q_{3, 1, T, \theta},$ and $Q_{3, 2, T, \theta}.$ Observe that they can be analyzed in an almost similar manner. Thus, we focus our attention to $Q_{3, 1, T, \theta}.$ Now, for $t = 1, \ldots, T,$

Note that for each $(u, x_{t(x)})$, the array $\{ Z_{t, T, 1, \theta}(u_i, x_{t(x)}) \}$ is $\alpha$-mixing with mixing coefficients $\alpha_{Z, T, k(\theta)}(k)$ satisfying

We set $\varepsilon = M \alpha_T T h \phi_{\theta}(h)$, $b_T = C \tau_T$ for a sufficiently large constant $C > 0$, and $S_T = \dfrac{1}{\alpha_T \tau_T}$, and apply Lemma B.3. Moreover, with a constant $C'$ independent of $(u, x)$, Theorem 2 of ^[64] can be extended to show that

Therefore, for any $(u, x_{t(x)})$ and sufficiently large $T$, we obtain

The last inequality holds by picking a very large $M > C^{'}.$ We can then show that

That is,

for sufficiently large $M > 0 \left(\text{i.e., } M > 64+\frac{8}{3}C\right)$, and the fact that $\phi_{\theta}(h) \to 0$ as $h\to 0,$ and $\log(T)\to \infty$ as $T\to \infty.$ On the other hand, we have

using the first regularity condition (R1) in Assumption 3.5. The desired result is achieved by imposing

That is, $\gamma > 3$ just as Assumption 3.5 requires. This means that

We now treat the term $Q_{1, \theta}.$ Let

We observe that asymptotically

Observe that

We now deal $I_{Q_{1, \theta}}$. Then, we infer that

where

Observe that $Z_{t, T, 1, \theta}$ is an alpha-mixing sequence. Therefore, by selecting the same parameter values for $\varepsilon, b_T, S_T,$ and $\sigma^2_{S_T, T}$ as those used for $Z_{t, T, 1, k(\theta)}$, and utilizing the corresponding constants $C, C',$ and $M$ defined therein, we can apply a similar proof strategy as employed for $Q_{3, \theta}$. Specifically, by invoking Lemma B.3, we have

It can also be shown that

by employing proof techniques analogous to those used for $Q_{1, \theta}$ and $Q_{3, \theta}$, we obtain the desired result for the $\alpha$-mixing variable

The parameters are chosen as $\varepsilon = M \alpha_T T h \phi_{\theta}(h)$ (for a sufficiently large $M > C'$), $b_T = C \tau_T$ (with $C > 0$ sufficiently large), and

Here, $C'$ is a constant independent of $(u, x)$, and the variance satisfies

It remains to establish the convergence of $Q_{4, \theta}$ and $Q_{5, \theta}$. Note that $Q_{4, \theta}$ can be addressed similarly to $Q_{2, \theta}$ since

Thus, we have

Finally,

since $Q_{5, \theta}\leq \mathbb{E}[Q_{1, \theta}]$ by proving in a similar fashion as $Q_{4, \theta}.$ The preceding results together with the result in step (i) complete the proof of Proposition 3.1. □

Proof of Theorem 3.1. To prove Theorem 3.1, we use a similar decomposition used by ^[57]. That is, we have

where

The proof is completed by showing the following four results:

(ⅰ) $\sup_{\theta \in \Theta_{\mathscr{H}}}\sup_{x\in S_{\mathscr{H}}}\sup_{u\in[0, 1]}\left|\hat{g}_{\theta}^{(1)}(u, x)\right| = O_{\mathbb{P}}\left(\sqrt{\frac{\log T}{Th\phi_{\theta}(h)}}\right),$

(ⅱ) with $\hat{g}_{\theta}^{B}(u, x) = \hat{g}_{\theta}^{(2)}(u, x)-m_{\theta}(u, x)\hat{m}_{\theta}^{(1)}(u, x),$

(ⅲ) using $\hat{g}_{\theta}^{B}(u, x)$ in (ⅱ),

(ⅳ) and $\frac{ 1}{ \inf_{\theta \in \Theta_{\mathscr{H}}}\inf_{x\in S_{\mathscr{H}}}\inf_{u\in[C_1h, 1-C_1h]}\hat{m}_{\theta}^{(1)}(u, x)} = O_{\mathbb{P}}(1).$

Using Proposition 3.1, the first two can be shown by picking $\varepsilon_{t, T},$ and $m_{\theta}\left(\frac{t}{T}, X_{t, T}\right)-m_{\theta}(u, x)$ for $W_{t, T},$ respectively. We now prove (ⅳ). Thus, we have

Putting $W_{t, T} = 1,$ we get

uniformly in $u$ using Proposition 3.1. Furthermore, since $K_2(\cdot)$ is Lipschitz, and by using Definition 2.1 and Lemma B.2, we have

where, by the regularity assumption (R2) in Assumption 3.5, we have $\frac{1}{Th\phi_{\theta}(h)}\to 0$ as $T\to \infty.$ Consequently, using (A.2), we have

uniformly in $u$. Now, using Assumption 3.1,

uniformly in $u.$ Therefore,

Hence, the assertion. For the proof of (ⅲ), with support $[0, q]$ for some $q > 1,$ we suppose that $K_0:[0, 1]\rightarrow \mathbb{R}$ is a Lipschitz continuous function such that $K_0(x) = 1$ for all $x\in[0, 1]$. Notice that

where

such that

Now, observe that

Now, we obtain the bound $h^{1 \wedge \beta}$ using Assumption 3.1. That is,

Furthermore, since $K_2(\cdot)$ is Lipschitz continuous from Assumption 3.3 and that

as previously shown, we have

uniformly in $u.$ The cases for $P_{2, \theta}(u, x)$ and $P_{3, \theta}(u, x)$ can be proved in a similar fashion as $P_{1, \theta}(u, x).$ Hence, we have

and

Finally, leveraging Assumption 3.1 and Lemma B.1, we derive

However, we have

We then infer that

Hence, we obtain

Finally, given our assumptions, our proof is complete with an approximation error of

Hence the proof is complete. □

Proof of Theorem 3.2. We begin our proof for this theorem by showing

that is, from

we define

Now, we infer

where

Then, we readily obtain

We now discuss $V_{1, T, \theta}^{B}$ by first noting that

using integration by parts, change of variables, and the model and kernel assumptions in Assumptions 3.1 and 3.3, respectively, and using the fact that $K_{2, h}(x) = (1-x)\mathbb{1}_{x\in [0, 1]}$ is an asymmetrical triangle kernel. On the other hand, since $K_2(\cdot)$ is Lipschitz and by Definition 2.2, we have

Moreover, by the smoothness of $m_\theta$ in Assumption 3.1, we get

Therefore, it follows that

We now consider $V_{2, T, \theta}^{B}$ and write

where

Observe that from our previous calculations, we can deduce

and that by Assumption 3.1,

Therefore, $V_{2, 1, T, \theta}^{B}$ becomes

where by Assumption 3.1, $\frac{\psi_\theta(h)}{\phi_{\theta}^{2}(h)} < \infty,$ and

since $Th^3\to \infty$ by Assumption 3.5. Here, the goal is to pick $\lambda_T$ such that $\left|V_{2, 1, T, \theta}^{B}\right| \to 0$ as $T\to \infty.$ Thus, using Lemma B.4, and the fact that $K_2(\cdot)$ is bounded as in Assumption 3.1, we have

For $V_{2, 2, T, \theta}^{B},$ we use the preceding calculations and obtain

As previously mentioned, we pick $\lambda_T$ that makes our expression approach to zero. That happens if we choose

and hence the use of Assumption 3.4. Therefore, the results from (A.7) and (A.8) suggest that

Consequently,

as we desired. Thus, the above results together with (A.3), (A.4), and the fact that $\lim\limits_{T\to \infty}\mathbb{E}\left[\hat{m}_{\theta}^{(1)}(u, x)\right] > 0$ give us

We now work with $Th\phi_{\theta}(h)\text{Var} \left(\hat{g}_{\theta}^{(1)}(u, x)\right)$ which concerns the first part of the previous equation. In this part of the proof, we will show that

Here, we utilize the Assumption 3.2, and the result in (A.5). Also, consider a sequence of independent random variables $\{\varepsilon_t\}_{t\in \mathbb{Z}},$ independent of $\{X_{t, T}\}_{t = 1}^{T}.$ Thus, we have

The final part of the proof covers the asymptotic normality of $\tilde{g}_{\theta}^{(1)}(u, x)$ which is derived from

where

That is, we want to show that

To demonstrate the distributional convergence of $\tilde{g}_{\theta}^{(1)}(u, x)$, we will employ Bernstein's big-block and small-block method. We begin by partitioning the index set $\{1, \ldots, T\}$ into $2k_T + 1$ subsets, consisting of large blocks of size $a_T$ and small blocks of size $v_T$, such that

Using Assumption 3.6, there exists a sequence of positive integers $\{q_T\}, q_T\to \infty,$ such that

Consequently, setting $a_T = \left \lfloor \frac{\sqrt{Th\phi_{\theta}(h)}}{q_T}\right\rfloor$, we have

Thus, the decomposition of $\tilde{g}_{\theta}^{(1)}(u, x)$ would be

where

First, we show that the summation over the small-blocks $\Big(\tilde{g}_{\theta}^{(12)}(u, x)\Big),$ and over the remainder-blocks $\Big(\tilde{g}_{\theta}^{(13)}(u, x)\Big)$ are asymptotically negligible. That is, as $T\to \infty,$

We first prove

We have

Dealing $F_1$, we have

We have

using the results in (A.9) and (A.10). We next handle $F_2.$ That is, with $\Delta^{'}_{t}(u, x; \theta) = K_{1, h}\Big(u-\frac{t}{T}\Big)K_{2, h}\big(d_{\theta}(x, X_{t, T})\big),$

where $\lambda_k = ja_T+(j-1)v_T.$ Since $i\neq j, |\lambda_i-\lambda_j+l_1-l_2|\geq v_T,$ we have

Using Davydov's lemma (see Lemma B.4), Assumption 3.3, and the results in (A.5) and (A.6), we get

Therefore, with

and using Assumption 3.4, we obtain

Hence,

We next show that

We again use $\Delta^{'}_{t}(u, x; \theta)$ for simplicity of notations to denote $K_{1, h}\Big(u-\frac{t}{T}\Big)K_{2, h}\big(d_{\theta}(x, X_{t, T})\big).$ Thus,

Note that

implies that

We are left to show the bound of $G_2.$ Now, setting $\lambda_i = k_T(a_T+v_T),$ we have

The third equality follows from the fact that since $i\neq j,$

Moreover, the preceding proof procedure follows similarly as that in $|F_2|$ making use of Davydov's lemma, Assumptions 3.3 and 3.4, the results in (A.5) and (A.6), and picking again

We then infer that

as $T\to \infty.$ Finally, we will prove the last part of the decomposition (A.11). First, we will show that the summation in $\tilde{g}_{\theta}^{(11)}(u, x)$ are asymptotically independent. This ensures us the use of the conditions of Lindeberg-Feller for finite normality. To establish this, we first note that the processes $(Y_{t, T}, X_{t, T})$ are strongly mixing and apply the Volkonskii and Rosanov inequality in Lemma B.5. Then, for a $\mathscr{F}_{i_a}^{j_a}-$measurable $\eta_a$ where

we have

which tends to zero using (A.10) implying that the asymptotic independence is achieved. We now find the variance of $\tilde{g}_{\theta}^{(11)}(u, x).$ We obtain

Now, we can see that

This means that

since $\frac{k_Ta_T}{T}\to 1.$ On the other hand, similar to our previous calculations, we can deduce with $\Delta^{'}_{t}(u, x; \theta) = K_{1, h}\Big(u-\frac{t}{T}\Big)K_{2, h}\big(d_{\theta}(x, X_{t, T})\big)$ that

where $\lambda_T$ is as defined in Assumption 3.4. Therefore, we conclude that

To complete the proof for the finite-dimensional convergence, we need to show that for sufficiently large $T,$

Observe that using A.10,

Hence, when $T$ is large enough, the set

is empty proving (A.12). This further implies that

where

To prove the general case, we employ a truncation argument since the response variable $Y_{t, T}$ is not necessarily bounded. With $L$ being the truncation point, we set

Recall that

and define

where $\mu_T^L$ is the mean of the first term on the right side, and

so that for each $L > 0,$

We have

We also define

Now, we can infer by (A.13), setting $\eta^L_j(u, x; \theta)$ as defined in (A.11), and the fact that $\Delta^{'}_{t}(u, x; \theta)$ is bounded, we have by replacing $\tilde{Z}_{t, T}$ by $\tilde{Z}^L_{t, T}$,

This means that

The final part of the proof intends to show that

We have

Note that by (A.15), $I \to 0$ as $T\to \infty$ for every $L > 0.$ Also, by (A.16), $II \to 0$ as first $T\to \infty$ and then $L\to \infty.$ Last, since as $L\to \infty,$

we have $III \to 0$ using (A.14). Hence, we are left to prove (A.16). Observe that $\bar{S}^L_T$ has the same structure as $S_T$ by replacing $Y_t$ with $Y_t\mathbb{1}_{\{|Y_t| > L\}}.$ We can use similar proof procedure as in (A.14), and obtain

which converges to 0. By dominated convergence, the right side converges to 0 as $L$ tends to infinity. This completes the proof for Theorem 3.2. □

B.   Appendix-B

This section provides a detailed overview of the essential lemmas underpinning the primary results of this study. Lemmas B.1 and B.2, both found in ^[57], play a crucial role in deriving the convergence results outlined in Proposition 3.2. Specifically, ^[60] established Lemma B.3, which introduces an exponential inequality for strongly mixing sequences, detailed in Theorem 2.1 of his paper. This lemma is instrumental in demonstrating the convergence of the second term in the decomposition of the general kernel estimator. Further, Lemma B.4, attributed to ^[39] (with the proof presented in Corollary A.2 of ^[52]), is central to proving the asymptotic negligibility of covariance terms within the decomposition of $\hat{g}_{\theta}^{(1)}(u, x)$, as specified in Eq (A.11). Last, Lemma B.5 is pivotal in establishing the asymptotic independence of the term $\tilde{g}_{\theta}^{(11)}(u, x)$, which represents the first term in Eq (A.11). For a comprehensive introduction, refer to Proposition 2.6 in ^[41].

Lemma B.1. Suppose that the kernel $K_1(\cdot)$ satisfies Assumption 3.3 (KB1). Then, for $k = 0, 1, 2,$

Lemma B.2. Suppose that the kernel $K_1(\cdot)$ satisfies Assumption 3.3 (KB1) and let $g:[0, 1]\times \mathscr{H}\rightarrow \mathbb{R}$ such that $(u, x)\mapsto g(u, x)$ be continuously differentiable with respect to u. Then,

Lemma B.3. Let $Z_{t, T}$ be a zero-mean triangular array such that $|Z_{t, T}|\leq b_T$ with $\alpha-$mixing coefficient $\alpha(k).$ Then, for any $\varepsilon > 0$ and $S_T\leq T$ with $\varepsilon > 4S_Tb_T,$

where

Lemma B.4. (Corollary 2 in ^[52]) Suppose that $X$ and $Y$ are random variables which are $\mathscr{G}-$ and $\mathscr{H}-$measurable, respectively, and that $\mathbb{E}|X|^p < \infty, \mathbb{E}|Y|^q < \infty,$ where $p, q > 1, \frac{1}{p}+\frac{1}{q} < 1.$ Then

Lemma B.5. (Proposition 2.6 in ^[41]) Suppose that $\{X_t: t = 0, \pm 1, \pm 2, \ldots \}$ Let $\mathscr{F}_{i}^{j}$ denote the $\sigma-$algebra generated by $\{X_t: i\leq t \leq j\}$ and

Let $\xi_1, \ldots, \xi_k$ be complex-valued random variables measurable with respect to the $\sigma-$algebras $\mathscr{F}_{i_1}^{j_1}, \ldots, \mathscr{F}_{i_k}^{j_k},$ respectively. Suppose that $i_{l+1}-j_l\geq n$ for $l = 1, \ldots, k-1$ and $j_l \geq i_l$ and $\mathbb{P}(|\xi_l|\leq 1) = 1$ for $l = 1, \ldots, k.$ Then