An accelerated adaptive two-step Levenberg–Marquardt method with the modified Metropolis criterion

1.   Introduction

Let $m$ and $n$ be two positive integers with $m\geq 2$ and $n\geq 2$, $[n] = \{1, 2, \ldots, n\}$, $\mathbb{R}$ be the set of all real numbers, ${\mathbb{R}}^{n}$ be the set of all $n$-dimensional real vectors. Let $x = (x_1, x_2, \ldots, x_m)\in\mathbb{R}^{m}$ and $y = (y_1, y_2, \ldots, y_n)\in\mathbb{R}^{n}$. If a fourth-order tensor $\mathcal{A} = (a_{ijkl})\in\mathbb{R}^{[m]\times [n]\times [m]\times [n]}$ satisfies the properties

then we call $\mathcal{A}$ a partially symmetric tensor.

It is well know that the tensor of the elastic modulus of elastic materials is just partially symmetrical ^[11]. And the components of a fourth-order partially symmetric tensor $\mathcal{A}$ can be regarded as the coefficients of the following biquadratic homogeneous polynomial optimization problem ^[6,19]:

The optimization problem plays a great role in the analysis of nonlinear elastic materials and the entanglement problem in quantum physics ^[5,6,8,9,26]. To solve the problem, we would establish a new version based on the following definition:

Definition 1.1. ^[11,20,21] Let $\mathcal{A} = (a_{ijkl})\in\mathbb{R}^{[m]\times [n]\times [m]\times [n]}$ be a partially symmetric tensor. If there are $\lambda\in\mathbb{R}$, $x\in {\mathbb{R}}^{m}\setminus\{0\}$ and $y\in {\mathbb{R}}^{n}\setminus\{0\}$ such that

where

then we call $\lambda$ an M-eigenvalue of $\mathcal{A}$, $x$ and $y$ the left and right M-eigenvectors associated with $\lambda$, respectively. Let $\sigma(\mathcal{A})$ be the set of all M-eigenvalues of $\mathcal{A}$ and $\lambda_{\max}(\mathcal{A})$ be the largest M-eigenvalue of $\mathcal{A}$, i.e.,

In 2009, Wang, Qi and Zhang ^[24] pointed out that Problem (1.1) is equivalently transformed into calculating the largest M-eigenvalue of a fourth-order partially symmetric tensor. Based on this, Wang et al. ^[24] presented an algorithm (WQZ-algorithm) to find the largest M-eigenvalue of a fourth-order partially symmetric tensor.

WQZ-algorithm [24,Algorithm 4.1]:

Initial step: Input $\mathcal{A} = (a_{ijkl})\in\mathbb{R}^{[m]\times [n]\times [m]\times [n]}$ and unfold it into a matrix $A = (A_{st})\in\mathbb{R}^{[mn]\times [mn]}$ by mapping $A_{st} = a_{ijkl}$ with $s = n(i-1)+j, \; \; \; \; t = n(k-1)+l.$

Substep 1: Take

and set

where $\mathcal{I} = (\delta_{ijkl})\in\mathbb{R}^{[m]\times [n]\times [m]\times [n]}$ with $\delta_{ijkl} = 1$ if $i = k$ and $j = l,$ otherwise, $\delta_{ijkl} = 0.$ Then unfold $\overline{\mathcal{A}} = (\overline{a}_{ijkl})\in\mathbb{R}^{[m]\times [n]\times [m]\times [n]}$ into a matrix $\overline{A} = (\overline{A}_{st})\in\mathbb{R}^{[mn]\times [mn]}.$

Substep 2: Compute the unit eigenvector $w = (w_i)_{i = 1}^{mn}\in\mathbb{R}^{mn}$ of matrix $\overline{A}$ associated with its largest eigenvalue, and fold vector $w$ into the matrix $W = (W_{ij})\in\mathbb{R}^{[m]\times [n]}$ in the following way:

set $i = \lceil k/n \rceil, \; \; \; j = (k-1)\text{modn}+1, \; \; \; \forall\; k = 1, 2, \cdots, mn.$

Substep 3: Compute the singular vectors $u_1$ and $v_1$ corresponding to the largest singular value $\sigma_1$ of the matrix $W$. Specifically, the singular value decomposition of $W$ is

where $\sigma_1\geq\sigma_2\geq\cdots\geq\sigma_r$ and $r$ is the rank of $W$.

Substep 4: Take $x_0 = u_1, y_0 = v_1,$ and let $k = 0.$

Iterative step: Execute the following procedures alternatively until certain convergence criterion is satisfied and output $x^\ast, y^\ast:$

Final step: Output the largest M-eigenvalue of the tensor $\mathcal{A}$:

where

and the associated M-eigenvectors: $x^\ast, y^\ast$.

The M-eigenvalues of tensors have a close relationship with the strong ellipticity condition in elasticity theory, which guarantees the existence of the solution to the fundamental boundary value problems of elastostatics ^[3,5,16]. However, when the dimensions $m$ and $n$ of tensors are large, it is not easy to calculate all M-eigenvalues. Thus, the problem of M-eigenvalue localization have attracted the attention of many researchers and many M-eigenvalue localization sets are given; see ^{[2,4,13,14,15,17,18,23,27]}.

For this, Wang, Li and Che ^[23] presented the following M-eigenvalue localization set for a partially symmetric tensor:

Theorem 1.1. [23,Theorem 2.2] Let $\mathcal{A} = (a_{ijkl})\in\mathbb{R}^{[m]\times [n]\times [m]\times [n]}$ be a partially symmetric tensor. Then

where

From the set $\mathcal{H}(\mathcal{A})$ in Theorem 1.1, we can obtain an upper bound of the largest M-eigenvalue $\lambda_{\max}(\mathcal{A})$, which can be taken as an parameter $\tau$ in WQZ-algorithm. From Example 2 in ^[15], it can be seen that the smaller the upper bound of $\lambda_{\max}(\mathcal{A})$, the faster WQZ-algorithm converges. In view of this, this paper intends to provide a smaller upper bound based on a new inclusion set and take this new upper bound as a parameter $\tau$ to make WQZ-algorithm converges to $\lambda_{\max}(\mathcal{A})$ faster.

The remainder of this paper is organized as follows. In Section 2, we provide an M-eigenvalue localization set for a partially symmetric tensor $\mathcal{A}$ and prove that the new set is tighter than some existing M-eigenvalue localization sets. In Section 3, based on the new set, we provide an upper bound for the largest M-eigenvalue of $\mathcal{A}$. As an application, in order to make the sequence generated by WQZ-algorithm converge to the largest M-eigenvalue of $\mathcal{A}$ faster, we replace the parameter $\tau$ in WQZ-algorithm with the upper bound. In Section 4, we conclude this article.

2.   A shaper M-eigenvalue localization set of a fourth-order partially symmetric tensor

In this section, we provide a new M-eigenvalue localization set of a fourth-order partially symmetric tensor and prove that the new M-eigenvalue localization set is tighter than that in Theorem 1.1, i.e., Theorem 2.2 in ^[23]. Before that, the following conclusion in ^[1,25] is needed.

Lemma 2.1. Let $x = (x_1, x_2, \ldots, x_n)^{\top}\in\mathbb{R}^{n}$ and $y = (y_1, y_2, \ldots, y_n)^{\top}\in\mathbb{R}^{n}$. Then

a) If $\parallel x\parallel_{2} = 1$, then $|x_{i}||x_{j}|\leq\frac{1}{2}$ for $i, j\in[n]$, $i\neq j$;

b) $\Big(\sum\limits_{i\in[n]}x_{i}y_{i}\Big)^{2}\leq\sum\limits_{i\in[n]}x_{i}^2\sum\limits_{i\in[n]}y_{i}^2$.

Theorem 2.1. Let $\mathcal{A} = (a_{ijkl})\in\mathbb{R}^{[m]\times [n]\times [m]\times [n]}$ be a partially symmetric tensor. Then

where

and

Proof. Let $\lambda$ be an M-eigenvalue of $\mathcal{A}$, $x\in \mathbb{R}^{m}\backslash\{0\}$ and $y\in\mathbb{R}^{n}\backslash\{0\}$ be its left and right M-eigenvectors, respectively. Then $x^{\top}x = 1$. Let $|x_t| = \max\limits_{i\in [m]}|x_i|$. Then $0 < |x_t|\leq 1$. For any given $s\in[m]$ and $s\neq t$, by the $t$-th equation of (1.2), we have

Taking the modulus of the above equation and using the triangle inequality and Lemma 2.1, one has

i.e.,

By (2.1), we have $(|\lambda|-\widetilde{r}_{t}^{s}(\mathcal{A}))|x_{t}|\leq r_{t}^{s}(\mathcal{A})|x_{t}|$, which leads to that $|\lambda|\leq \widetilde{r}_{t}^{s}(\mathcal{A})+ r_{t}^{s}(\mathcal{A})$, i.e., $\lambda\in\overline{\Upsilon}_{t, s}(\mathcal{A})$.

If $|x_{s}| > 0$, then by the $s$-th equation of (1.2), we have

Taking the modulus of the above equation and using the triangle inequality and Lemma 2.1 yield

i.e.,

When $|\lambda|\geq \widetilde{r}_{t}^{s}(\mathcal{A})$ or $|\lambda|\geq r_{s}^{s}(\mathcal{A})$, multiplying (2.1) and (2.2) and eliminating $|x_{t}||x_{s}| > 0$, we have

which implies that

When $|\lambda| < \widetilde{r}_{t}^{s}(\mathcal{A})$ and $|\lambda| < r_{s}^{s}(\mathcal{A})$, it holds that

It follows from (2.4) and (2.5) that

If $|x_s| = 0$ in (2.1), then $|\lambda|\leq \widetilde{r}_{t}^{s}(\mathcal{A})$. When $|\lambda| = \widetilde{r}_{t}^{s}(\mathcal{A})$, then (2.3) holds and consequently, (2.4) holds. When $|\lambda| < \widetilde{r}_{t}^{s}(\mathcal{A})$, if $|\lambda|\geq r_{s}^{s}(\mathcal{A})$, then (2.3) and (2.4) hold. If $|\lambda| < r_{s}^{s}(\mathcal{A})$, then (2.5) holds. Hence, (2.6) holds. By the arbitrariness of $s\in[m]$, and $s\neq t$, we have

therefore, the assertion is proved.

Next, we give the relationship between the localization set $\mathcal{H}(\mathcal{A})$ given in Theorem 1.1 and the set $\Upsilon(\mathcal{A})$ given in Theorem 2.1.

Theorem 2.2. Let $\mathcal{A} = (a_{ijkl})\in\mathbb{R}^{[m]\times [n]\times [m]\times [n]}$ be a partially symmetric tensor. Then

Proof. For any $i, s\in[m]$ and $i\neq s$, it holds that

and

Let $z\in\Upsilon(\mathcal{A})$. By Theorem 2.1, there is an index $i\in [m]$ such that for any $s\in[m]$, $i\neq s$, $z\in\Upsilon_{i, s}(\mathcal{A})$, which means that $z\in\widehat{\Upsilon}_{i, s}(\mathcal{A})$, or $z\in\widetilde{\Upsilon}_{i, s}(\mathcal{A})$ and $z\in\overline{\Upsilon}_{i, s}(\mathcal{A})$.

Let $z\in\widehat{\Upsilon}_{i, s}(\mathcal{A})$, i.e., $|z| < \widetilde{r}_{i}^{s}(\mathcal{A})$ and $|z| < r_{s}^{s}(\mathcal{A})$. By (2.7) and (2.8), we have $|z|\leq R_{i}(\mathcal{A})-R_{i}^{s}(\mathcal{A})$ and $|z|\leq R_{s}^{s}(\mathcal{A})$, therefore, $z\in\widehat{\mathcal{H}}_{i, s}(\mathcal{A})$.

Let $z\in\widetilde{\Upsilon}_{i, s}(\mathcal{A})$ and $z\in\overline{\Upsilon}_{i, s}(\mathcal{A})$, i.e.,

and

By (2.7), (2.8) and (2.10), one has $|z| < \widetilde{r}_{i}^{s}(\mathcal{A})+r_{i}^{s}(\mathcal{A})\leq R_{i}(\mathcal{A})$, which means that $z\in\Gamma_{i}(\mathcal{A})$. When $|z|\geq R_{i}(\mathcal{A})-R_{i}^{s}(\mathcal{A})$ and $|z|\geq R_{s}^{s}(\mathcal{A})$, by (2.7), (2.8) and (2.9), we have

then

i.e.,

which means that $z\in\overline{\mathcal{H}}_{i, s}(\mathcal{A})$. Thus, whether $R_{i}(\mathcal{A})-R_{i}^{s}(\mathcal{A})\leq |z|\leq R_{s}^{s}(\mathcal{A})$ or $R_{s}^{s}(\mathcal{A})\leq |z|\leq R_{i}(\mathcal{A})-R_{i}^{s}(\mathcal{A})$, (2.11) also holds. When $|z|\leq R_{i}(\mathcal{A})-R_{i}^{s}(\mathcal{A})$ and $|z|\leq R_{s}^{s}(\mathcal{A})$, it follows that $z\in\widehat{\mathcal{H}}_{i, s}(\mathcal{A})$. i.e.,

From the arbitrariness of $s\in[m]$, and $s\neq i$, we have

i.e., $z\in\mathcal{H}(\mathcal{A})$. Therefore, $\Upsilon(\mathcal{A})\subseteq\mathcal{H}(\mathcal{A})$.

In order to show the validity of the set $\Upsilon(\mathcal{A})$ given in Theorem 2.1, we present a running example.

Example 1. Let $\mathcal{A} = (a_{ijkl})\in\mathbb{R}^{[2]\times [2]\times [2]\times [2]}$ be a partially symmetric tensor with entries

By Theorem 1.1, we have

By Theorem 2.1, we have

It is easy to see that $\Upsilon(\mathcal{A})\subseteq\mathcal{H}(\mathcal{A})$ and all M-eigenvalues are in $[-20.0035, 20.0035]$. In fact, all different M-eigenvalues of $\mathcal{A}$ are $-1.2765$, 0.0710, 0.1242, 0.2765, 0.3437 and 15.2091.

3.   A sharp upper bound for the M-spectral radius of a partially symmetric tensor

In this section, based on the set in Theorem 2.1, we provide an upper bound for the largest M-eigenvalue of a fourth-order partially symmetric tensor $\mathcal{A}$. As an application, we apply the upper bound as a parameter $\tau$ to the WQZ-algorithm to make the sequence generated by the WQZ-algorithm converges to the largest M-eigenvalue of $\mathcal{A}$ faster.

Theorem 3.1. Let $\mathcal{A} = (a_{ijkl})\in\mathbb{R}^{[m]\times [n]\times [m]\times [n]}$ be a partially symmetric tensor. Then

where

and

Proof. By Theorem 2.1 and $\rho(\mathcal{A})\in \sigma(\mathcal{A})$, it follows that there exists an index $i\in[m]$ such that for any $s\in[m]$ and $s\neq i$, $\rho(\mathcal{A})\in\widehat{\Upsilon}_{i, s}(\mathcal{A})$, or $\rho(\mathcal{A})\in(\widetilde{\Upsilon}_{i, s}(\mathcal{A})\cap\overline{\Upsilon}_{i, s}(\mathcal{A}))$. If $\rho(\mathcal{A})\in\widehat{\Upsilon}_{i, s}(\mathcal{A})$, that is, $\rho(\mathcal{A}) < \widetilde{r}_{i}^{s}(\mathcal{A})$ and $\rho(\mathcal{A}) < r_{s}^{s}(\mathcal{A})$, then

If $\rho(\mathcal{A})\in(\widetilde{\Upsilon}_{i, s}(\mathcal{A})\cap\overline{\Upsilon}_{i, s}(\mathcal{A}))$, that is,

and

Solving Inequality (3.3), we have

Combining (3.2) and (3.4), we have

Hence, by (3.1) and (3.5), we have

Furthermore, by the arbitrariness of $s$, we have

Since we do not know which $i$ is appropriate to $\rho(\mathcal{A})$, we can only conclude that

This proof is complete.

Remark 3.1. In Theorem 3.1, we obtain an upper bound $\Omega(\mathcal{A})$ for the largest M-eigenvalue of a fourth order partially symmetric tensor $\mathcal{A}$. Now, we take $\Omega(\mathcal{A})$ as the parameter $\tau$ in WQZ-algorithm to obtain a modified WQZ-algorithm. That is, the only difference between WQZ-algorithm and the modified WQZ-algorithm is the selection of $\tau$, in particular, $\tau = \sum\limits_{1\leq s\leq t\leq mn}|A_{st}|$ in WQZ-algorithm and $\tau = \Omega(\mathcal{A})$ in the modified WQZ-algorithm.

Next, we take $\Omega(\mathcal{A})$ and some existing upper bounds of the largest M-eigenvalue as $\tau$ in WQZ-algorithm to calculate the largest M-eigenvalue of a fourth-order partially symmetric tensor $\mathcal{A}$.

Example 2. Consider the tensor $\mathcal{A}$ in Example 4.1 of ^[24], where

By (1.3), we have $\tau = \sum\limits_{1\leq s\leq t\leq 9}|A_{st}| = 23.3503.$ By Corollary 1 of ^[17], we have

By Theorem 3.5 of ^[23], we have

By Corollary 2 of ^[17], we have

By Corollary 1 of ^[15], where $S_{m} = S_{n} = 1$, we have

By Corollary 2 of ^[15], where $S_{m} = S_{n} = 1$, we have

By Theorem 3.1, we have

From ^[24], it can be seen that $\lambda_{\max}(\mathcal{A}) = 2.3227$.

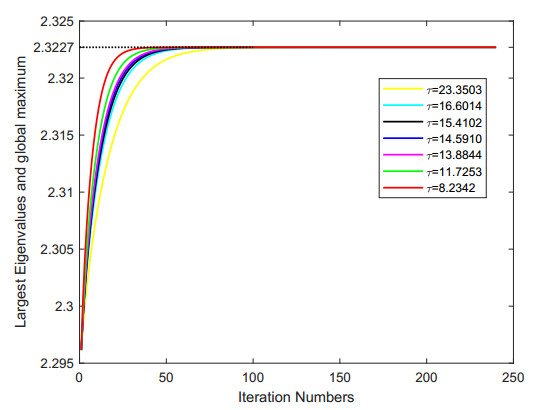
Taking $\tau = 23.3503$, 16.6014, 15.4102, 14.5910, 13.8844, 11.7253 and 8.2342 respectively, numerical results obtained by the WQZ-algorithm are shown in Figure 1.

Numerical results in Figure 1 shows that :

1) When we take $\tau = 8.2342$, the sequence more rapidly converges to the largest M-eigenvalue $\lambda_{\max}(\mathcal{A})$ than taking $\tau = 23.3503$, $\tau = 16.6014$, $\tau = 15.4102$, $\tau = 14.5910$, $\tau = 13.8844$ and $\tau = 11.7253$, respectively.

2) When we take $\tau = 23.3503$, 16.6014, 15.4102, 14.5910, 13.8844, 11.7253 and 8.2342, the WQZ-algorithm can get the largest M-eigenvalue $\lambda_{\max}(\mathcal{A})$ after finite iterations. However, under the same stopping criterion, if we take $\tau = \; 23.3503$, 16.6014, 15.4102, 14.5910, 13.8844 and 11.7253, it can be seen that the WQZ-algorithm needs more iterations to obtain the largest M-eigenvalue, and when $\tau = 8.2342$, WQZ-algorithm can obtain the largest M-eigenvalue $\lambda_{\max}(\mathcal{A})$ faster.

3) The choice of the parameter $\tau$ in WQZ-algorithm has a significant impact on the convergence speed of the WQZ-algorithm. When $\tau$ is larger, the convergence speed of WQZ-algorithm is slower. When $\tau$ is smaller and $\tau$ is greater than the largest M-eigenvalue, the WQZ-algorithm converges faster. In other words, the faster the largest M-eigenvalue can be obtained.

4) The numerical result of the upper bound of the M-spectral radius obtained by Theorem 3.1 is of great help to the WQZ-algorithm. Therefore, it shows that the results we get have a certain effect.

Now, we consider a real elasticity tensor, which is derived from the study of self-anisotropic materials ^[10] for explanation.

In anisotropy materials, the components of the tensor of elastic moduli $\mathcal{C} = (c_{ijkl})\in\mathbb{R}^{[3]\times [3]\times [3]\times [3]}$ satisfy the following symmetry:

which is also called an elasticity tensor. After a lot of research, we know that there are many anisotropic materials, of which crystal is one of its typical examples. We classify from the crystal homologues ^[22], the elasticity tensor $\mathcal{C} = (c_{ijkl})\in\mathbb{R}^{[3]\times [3]\times [3]\times [3]}$ of some crystals for trigonal system, such as $CaCO_3$ and $HgS$ also satisfy

This shows that the triangular system of anisotropic materials has only 7 elasticities. In fact, $CaMg(CO_3)_2$-dolomite and $CaCO_3$-calcite have similar crystal structures, in which the atoms along any triplet are alternated with magnesium and calcium. In ^[22], we can know that the elasticity tensor of $CaMg(CO_3)_2$-dolomite is as follows.

Next, we transform the elastic tensor $\mathcal{C}$ into a partially symmetric tensor $\mathcal{A}$ through the following double mapping, and the M-eigenvalue of $\mathcal{A}$ after transformation is the same as the M-eigenvalue of $\mathcal{C}$ ^[7,12]:

In order to illustrate the validity of the results we obtained, we take the above-mentioned partial symmetry tensor of the $CaMg(CO_3)_2$-dolomite elasticity tensor transformation as an example.

Example 3. Consider the tensor $\mathcal{A}_2 = (a_{ijkl})\in\mathbb{R}^{[3]\times [3]\times [3]\times [3]}$ in Example 3 of ^[17], where

and other $a_{ijkl} = 0$.

The data results of Example 2 show that the upper bound of the largest M-eigenvalue in Theorem 3.1 is sharper than the existing results.Here, we only calculate the upper bound of the largest M-eigenvalue of $\mathcal{A}_2$ by Theorem 3.1, and use it as the parameter $\tau$ in the WQZ-algorithm to calculate the largest M-eigenvalue of $\mathcal{A}_2$. Here, in order to distinguish different values of $\tau$, we calculate the result by Theorem 3.1 and record it as $\tau_2$, that is, WQZ-algorithm $\tau = \tau_2$.

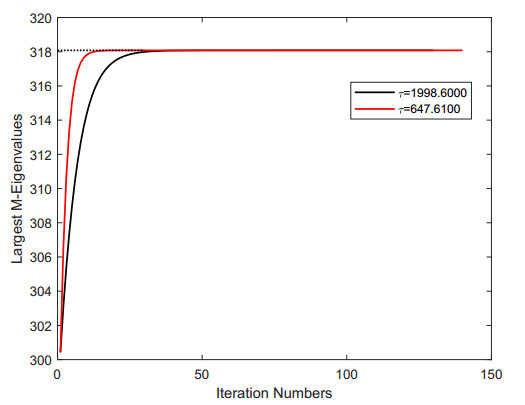
By Theorem 3.1, we can get $\tau_2 = 647.6100$.

By Eq (1.3), we can get

In the WQZ-algorithm, when we take $\tau = 1998.6000$ and 647.6100 respectively, the numerical results we get are shown in Figure 2.

As we can see in Figure 2, in the WQZ-algorithm, when we regard $\tau_2$ as $\tau$, it makes the convergence sequence in the WQZ-algorithm converges faster than $\tau = \sum\limits_{1\leq s\leq t\leq 9}|A_{st}|$, so that the largest M-eigenvalue can be calculated faster.That is to say, in this article, the result we provide as the parameter $\tau$ in the WQZ-algorithm can speed up the convergence speed, so that the largest M-eigenvalue can be calculated quickly.

4.   Conclusions

In this paper, we first in Theorem 2.1 provided an M-eigenvalue localization set $\Upsilon(\mathcal{A})$ for a fourth-order partially symmetric tensor $\mathcal{A}$, and then proven that the set $\Upsilon(\mathcal{A})$ is tighter than the set $\mathcal{H}(\mathcal{A})$ in Theorem 2.2 of ^[23]. Secondly, based on the set $\Upsilon(\mathcal{A})$, we derived an upper bound for the M-spectral radius of $\mathcal{A}$. As an application, we took the upper bound of the M-spectral radius as a parameter $\tau$ in the WQZ-algorithm to make the sequence generated by this algorithm converge to the largest M-eigenvalue of $\mathcal{A}$ faster. Finally, two numerical examples are given to show the effectiveness of the set $\Upsilon(\mathcal{A})$ and the upper bound $\Omega(\mathcal{A})$.

Acknowledgments

The author sincerely thanks the editors and anonymous reviewers for their insightful comments and constructive suggestions, which greatly improved the quality of the paper. The author also thanks Professor Jianxing Zhao (Guizhou Minzu University) for guidance. This work is supported by Science and Technology Plan Project of Guizhou Province (Grant No. QKHJC-ZK[2021]YB013).

Conflict of interest

The author declares no conflict of interest.