Eisenstein field BCH codes construction and decoding

1.   Introduction

Algebraic coding theory is a subset of coding theory that uses algebraic structures, especially finite fields, and linear algebra to make error-correcting codes and study how they work. The theory is based on linear codes, in which code words are shown as linear combinations of a given set of vectors called "basis vectors". These codes' minimal distance and error correction capabilities may be studied and enhanced using algebraic methods. The field is important for telephony, data storage and information security, which makes it a key part of current code theory. "Algebraic Codes for Data Transmission" by Richard ^[1] is a complete introduction to algebraic coding theory. It covers the basics of finite fields, linear codes and decoding methods. It is good for both newbies and more experiencecoders who want to learn more about algebra. "Modern Coding Theory" by Tom and Urbanke ^[2] is a book about advanced topics in coding theory, such as algebraic codes and iterative decoding methods. It shows how mathematical methods and current ways of coding are related, which makes it an important resource for experts in the field. Algebraic coding theory is a key part of designing and analyzing error-correcting codes, which makes it possible to make communication systems that work well and are reliable. Using algebraic structures, researchers can come up with strong coding schemes and build the theoretical frameworks needed for error correction in channels that are busy and not very reliable.

Ring-linear coding theory employs finite rings or modules as the basic alphabet. This field has grown tremendously. Assmus and Mattson (1963) ^[3] were among the first to suggest using ring elements for linear codes in their landmark book. An excellent starting point for learning about linear and cyclic codes-based fields is Augot et al. ^[4]. The Ring-linear coding theory was advanced by Blake ^[5,6]. He started linear codes based on some special rings and moved on to the main integer residue rings. Blake also introduced Hamming, Reed-Solomon and BCH code analogs. Using group algebra, Spiegel ^[7,8] linear codes over the integer ring modulo n. With the use of the Chinese Remainder Theorem, Blake was able to use these rings for BCH. In 1958, BCH codes over Galois fields existed. Shah et al. ^[9] utilized the semigroup ring to encode. In ^[10,11,12], the authors introduced DNA cyclic codes over ${F}_{2}\left[u\right]/({u}^{4}-1)$. Kim et al. In ^[13], the authors defined quasi-cyclic self-orthogonal codes that can go on forever. Recently, Zullo ^[14] developed another type of cyclic code. The fundamental binary and ternary BCH code hulls were investigated by Lei et al. ^[15]. In ^[16], Liu et al. constructed ${2}^{m}+1$ binary BCH codes.

Eisenstein integers, named after the German mathematician Ferdinand Eisenstein ^[17], are a special subset of complex numbers that have a significant impact on algebraic number theory. They are expressed as $a+b\omega$, where $a$ and $b$ are integers, and ω is a complex number known as the cube root of unity. The cube root of unity, ω, satisfies the equation ${\omega }^{3} = 1$. Eisenstein integers exhibit intriguing properties, including a hexagonal lattice structure when represented on the complex plane. They are closely related to triangular numbers and have applications in various mathematical areas, such as elliptic curves and modular forms. The unique factorization of Eisenstein integers is also of great interest in algebraic number theory, making them a crucial element in studying and understanding number theory concepts.

Error-correcting codes are an essential component of today's sophisticated communication systems because they enable the detection and correction of errors that may occur while data is being sent. BCH codes, which are circular codes, have been studied extensively and are used in real life. BCH codes are made to handle random errors, which makes them good for busy lines of communication. Research on BCH codes has usually been about making and studying codes over limited Galois fields ^[18]. The authors have created codes using Vectorial Algebra and have also utilized these codes in cryptography ^{[19,20,21,22,23]}. Huber ^[24] presented a two-dimensional modular distance and associated codes. These codes, known as consta-cyclic codes, feature simple constructions and can be classified as a subset of Ⅰ-cyclic (Ideal cyclic) codes. Notably, Ⅰ-cyclic codes include error-correcting Mannheim codes. In addition, Eisenstein fields offer a generalized concept of finite Galois fields with a more intricate structure. Eisenstein's fields have numerous applications, including cryptography, error-correcting codes, communications, etc.

BCH codes are extremely valuable for securing data and providing efficient error correction capabilities. Important ideas for decoding BCH codes center on the polynomials used to find errors and evaluate their severity, as well as the critical key equation that these polynomials meet. There are numerous methods for solving the key equation, each of which provides a decoding algorithm. The Euclidean algorithm ^[25], BMA ^[26] and Sugiyama's algorithm (SA) ^[27] are three of the most effective algorithms. Authors in ^{[28,29,30,31]} defined some algebraic structures and its applications in algebraic coding theory and algebraic cryptography. Sajjad et al. ^[32], constructed Gaussian field-based BCH codes decoding. In this situation, we will use a tweaked version of the Berlekamp-Massey method to fix errors in BCH codes. Due to their superior performance, the EF-based BCH is an area of study.

We have dual objectives. To answer the question, what is Eisenstein's field? To construct BCH codes that operate over the Eisenstein field. BMA-modified BCH codes decoding over the Eisenstein field. Then, we compare the BCH codes' Eisenstein and Galois field findings.

2.   Eisenstein field and the extensions of Eisenstein field

2.1.   Eisenstein field

Let $\omega$ be the cube root of unity $({\omega }^{3} = 1)$ and $1+\omega +{\omega }^{2} = 0.$ Let $\mathbb{Z}\left[\omega \right] = \left\{u+v\omega :u, v\in \mathbb{Z}\right\}$ be the Euclidean domain (ED) of the Eisenstein integers (EI) [17, Section 1]. Accordingly, ${\mathbb{Z}}_{p}\left[\omega \right] = \left\{u+v\omega :u, v\in {\mathbb{Z}}_{p}\right\}$ is a commutative ring with identity. ${\mathbb{Z}}_{p}\left[\omega \right]$ is the Eisenstein field (EF) if $p\equiv 2\left(mod3\right)$ [17, Corollary 14].

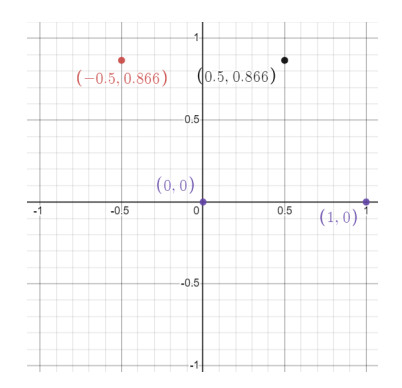
Illustration 1. Let ${\mathbb{Z}}_{2}\left[\omega \right] = \{\mathrm{0, 1}, \omega , 1+\omega \}$ be the Eisenstein field because every nonzero element of ${\mathbb{Z}}_{2}\left[\omega \right]$ is a unit element and the cardinality of ${\mathbb{Z}}_{2}\left[\omega \right]$ is ${2}^{2} = 4.$ Elements of ${\mathbb{Z}}_{2}\left[\omega \right]$ are given in Figure 1.

Illustration 2. Let

be an Eisenstein field, because every nonzero element of ${\mathbb{Z}}_{5}\left[\omega \right]$ is unit element and the cardinality of ${\mathbb{Z}}_{5}\left[\omega \right]$ is ${5}^{2} = 25.$ Elements of ${\mathbb{Z}}_{5}\left[\omega \right]$ are shown in Figure 2.

Remark 1. ${\mathbb{Z}}_{p}\left[\omega \right]$ has ${p}^{2}$ elements if $p\equiv 2\left(mod3\right).$

Remark 2. Let ${\mathbb{Z}}_{p}{\left[\omega \right]}^{*}$ denote the units in ${\mathbb{Z}}_{p}\left[\omega \right]$ if $p\equiv 2\left(mod3\right)$ with cardinality ${p}^{2}-1.$

2.2.   Eisenstein field extension

Let ${\mathbb{Z}}_{2}\left[\omega \right]$ be the Eisenstein field $.$ While ${\mathbb{Z}}_{2}\left[\omega \right]\left[x\right]$ is an ED.

2.2.1.   The Eisenstein field extension ${\mathbb{Z}}_{2}{\left[\mathrm{\omega }\right]}^{2}$

For the extension of EF ${\mathbb{Z}}_{2}{\left[\omega \right]}^{2},$ the quotient ring (QR)

where $< H\left(x\right) >$ is the maximal ideal generated by an irreducible polynomial (IP) $H\left(x\right)$ of degree $2$ in ${\mathbb{Z}}_{2}\left[\omega \right]\left[x\right]$. Let $\gamma$ is the coset $x+\left(H\right(x\left)\right)$, then $H\left(\gamma \right) = 0$ and

Hence ${\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ is a 2-degree extension field of the EF ${\mathbb{Z}}_{2}\left[\omega \right],$ and ${\mathbb{Z}}_{2}{{\left[\omega \right]}^{*}}^{2} = {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}\backslash \left\{0\right\}$ is a cyclic group (CG) of order ${2}^{4}-1 = 15.$

Illustration 3. Let the ideal

generated by the primitive IP $H\left(x\right) = {x}^{2}+x+\omega$ over ${\mathbb{Z}}_{2}\left[\omega \right]$ and $\gamma$ be the root of $H\left(x\right)$ in extension field ${\mathbb{Z}}_{2}\left[\omega \right]\left[x\right]$, then $H\left(\gamma \right) = 0$ as ${\gamma }^{2}+\gamma +\omega = 0.$ Thus $, {\gamma }^{2} = \gamma +\omega$ and ${\mathbb{Z}}_{2}{{\left[\omega \right]}^{*}}^{2} = {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}\backslash \left\{0\right\}$ is a CG of order ${2}^{2\left(2\right)}-1 = 15$ in Table 1.

2.2.2.   The Eisenstein field extension ${\mathbb{Z}}_{2}{\left[\boldsymbol{\omega }\right]}^{{\bf{3}}}$

For the extension of EF ${\mathbb{Z}}_{2}{\left[\omega \right]}^{3},$ the QR

where $< H\left(x\right) >$ is the maximal ideal generated by an IP $H\left(x\right)$ of degree $3$ in ${\mathbb{Z}}_{2}\left[\omega \right]\left[x\right]$. Let $\gamma$ is the coset $x+\left(H\right(x\left)\right)$, then $H\left(\gamma \right) = 0$ and

Hence ${\mathbb{Z}}_{2}{\left[\omega \right]}^{3}$ is a 3-degree extension field of the EF ${\mathbb{Z}}_{2}\left[\omega \right],$ and ${\mathbb{Z}}_{2}{{\left[\omega \right]}^{*}}^{3} = {\mathbb{Z}}_{2}{\left[\omega \right]}^{3}\backslash \left\{0\right\}$ is a CG of order ${2}^{6}-1 = 63.$

Illustration 4. Let the ideal

generated by the primitive IP $H\left(x\right) = {x}^{3}+{x}^{2}+x+\omega$ over ${\mathbb{Z}}_{2}\left[\omega \right]$ and $\gamma$ be the root of $H\left(x\right)$ in extension field ${\mathbb{Z}}_{2}\left[\omega \right]\left[x\right]$, then $H\left(\gamma \right) = 0$ as ${\gamma }^{3}+{\gamma }^{2}+\gamma +\omega = 0.$ Thus, ${\gamma }^{3} = {\gamma }^{2}+\gamma +\omega$ and ${\mathbb{Z}}_{2}{{\left[\omega \right]}^{*}}^{3} = {\mathbb{Z}}_{2}{\left[\omega \right]}^{3}\backslash \left\{0\right\}$ is a CG of order ${2}^{6}-1 = 63$ in Table 2.

2.2.3.   The Eisenstein field extension ${\mathbb{Z}}_{2}{\left[\mathrm{\omega }\right]}^{\mathrm{m}}$

For the extension of EF ${\mathbb{Z}}_{2}{\left[\omega \right]}^{m},$ the QR

where $< H\left(x\right) >$ is the maximal ideal generated by an IP $H\left(x\right)$ of degree $m$ in ${\mathbb{Z}}_{2}\left[\omega \right]\left[x\right]$. Let $\gamma$ is the coset $x+\left(H\right(x\left)\right)$, then $H\left(\gamma \right) = 0$ and

${\mathbb{Z}}_{2}{\left[\omega \right]}^{m}$ is a $m$ degree extension field of the EF ${\mathbb{Z}}_{2}\left[\omega \right],$ and ${\mathbb{Z}}_{2}{{\left[\omega \right]}^{*}}^{m} = {\mathbb{Z}}_{2}{\left[\omega \right]}^{m}\backslash \left\{0\right\}$ is a cyclic group of order ${2}^{2m}-1.$

Furthermore, let ${\mathbb{Z}}_{5}\left[\omega \right]$ be an Eisenstein field. In fact, ${\mathbb{Z}}_{5}\left[\omega \right]\left[x\right]$ is an ED and the EF extension is given below.

2.2.4.   The Eisenstein field extension ${\mathbb{Z}}_{5}{\left[\mathrm{\omega }\right]}^{2}$

For the extension of EF ${\mathbb{Z}}_{5}{\left[\omega \right]}^{2},$ the QR

where $< H\left(x\right) >$ is the maximal ideal generated by an IP $H\left(x\right)$ of degree $2$ in ${\mathbb{Z}}_{5}\left[\omega \right]\left[x\right]$. Let $\gamma$ is the coset $x+\left(H\right(x\left)\right)$, then $H\left(\gamma \right) = 0$ and ${\mathbb{Z}}_{5}{\left[\omega \right]}^{2} = \left\{{u}_{0}+{u}_{1}\gamma :\forall {u}_{0}, {u}_{1}\in {\mathbb{Z}}_{5}\left[\omega \right]\right\}.$ Hence ${\mathbb{Z}}_{5}{\left[\omega \right]}^{2}$ is a 2-degree extension field of the EF ${\mathbb{Z}}_{5}\left[\omega \right],$ and ${\mathbb{Z}}_{5}{{\left[\omega \right]}^{*}}^{2} = {\mathbb{Z}}_{5}{\left[\omega \right]}^{2}\backslash \left\{0\right\}$ is a CG of order ${5}^{4}-1 = 624.$

2.2.5.   The Eisenstein field extension ${\mathbb{Z}}_{5}{\left[\mathrm{\omega }\right]}^{3}$

For the extension of EF ${\mathbb{Z}}_{5}{\left[\omega \right]}^{3},$ the QR

where $< H\left(x\right) >$ is the maximal ideal generated by an IP $H\left(x\right)$ of degree $3$ in ${\mathbb{Z}}_{5}\left[\omega \right]\left[x\right]$. Let $\gamma$ is the coset $x+\left(H\right(x\left)\right)$, then $H\left(\gamma \right) = 0$ and

Hence, ${\mathbb{Z}}_{5}{\left[\omega \right]}^{3}$ is a 3-degree extension field of the EF ${\mathbb{Z}}_{5}\left[\omega \right],$ and ${\mathbb{Z}}_{5}{{\left[\omega \right]}^{*}}^{3} = {\mathbb{Z}}_{5}{\left[\omega \right]}^{3}\backslash \left\{0\right\}$ is a CG of order ${5}^{6}-1 = 15625.$

2.2.6.   The Eisenstein field extension ${\mathbb{Z}}_{5}{\left[\mathrm{\omega }\right]}^{\mathrm{m}}$

For the extension of EF ${\mathbb{Z}}_{5}{\left[\omega \right]}^{m},$ the QR

where $< H\left(x\right) >$ is the maximal ideal generated by an IP $H\left(x\right)$ of degree $m$ in ${\mathbb{Z}}_{5}\left[\omega \right]\left[x\right]$. Let $\gamma$ is the coset $x+\left(H\right(x\left)\right)$, then $H\left(\gamma \right) = 0$ and

Hence, ${\mathbb{Z}}_{5}{\left[\omega \right]}^{m}$ is a m-degree extension field of the EF ${\mathbb{Z}}_{5}\left[\omega \right],$ and ${\mathbb{Z}}_{5}{{\left[\omega \right]}^{*}}^{m} = {\mathbb{Z}}_{5}{\left[\omega \right]}^{m}\backslash \left\{0\right\}$ is a CG of order ${5}^{2m}-1.$

In a similar way, Eisenstein field extension ${\mathbb{Z}}_{p}\left[\omega \right],$ if $p\equiv 2\left(mod3\right)$ is given below.

2.2.7.   The Eisenstein field extension ${\mathbb{Z}}_{\mathrm{p}}{\left[\mathrm{\omega }\right]}^{2}\mathrm{i}\mathrm{f}\;\mathrm{p}\equiv 2\left(\mathrm{m}\mathrm{o}\mathrm{d}\;3\right)$

For the extension of EF ${\mathbb{Z}}_{p}{\left[\omega \right]}^{2},$ the QR

where $< H\left(x\right) >$ is the maximal ideal generated by an IP $H\left(x\right)$ of degree $2$ in ${\mathbb{Z}}_{p}\left[\omega \right]\left[x\right]$. Let $\gamma$ is the coset $x+\left(H\right(x\left)\right)$, then $H\left(\gamma \right) = 0$ and

Hence, ${\mathbb{Z}}_{p}{\left[\omega \right]}^{2}$ is a 2-degree extension field of the EF ${\mathbb{Z}}_{p}\left[\omega \right],$ and ${\mathbb{Z}}_{p}{{\left[\omega \right]}^{*}}^{2} = {\mathbb{Z}}_{p}{\left[\omega \right]}^{2}\backslash \left\{0\right\}$ is a CG of order ${p}^{4}-1.$

2.2.8.   The Eisenstein field extension ${\mathbb{Z}}_{\mathrm{p}}{\left[\mathrm{\omega }\right]}^{3}\mathrm{i}\mathrm{f}\;\mathrm{p}\equiv 2\left(\mathrm{m}\mathrm{o}\mathrm{d}\;3\right)$

For the extension of EF ${\mathbb{Z}}_{p}{\left[\omega \right]}^{3},$ the QR

where $< H\left(x\right) >$ is the maximal ideal generated by an IP $H\left(x\right)$ of degree $3$ in ${\mathbb{Z}}_{p}\left[\omega \right]\left[x\right]$. Let $\gamma$ is the coset $x+\left(H\right(x\left)\right)$, then $H\left(\gamma \right) = 0$ and

Hence, ${\mathbb{Z}}_{p}{\left[\omega \right]}^{3}$ is a 3-degree extension field of the EF ${\mathbb{Z}}_{p}\left[\omega \right],$ and ${\mathbb{Z}}_{p}{{\left[\omega \right]}^{*}}^{3} = {\mathbb{Z}}_{p}{\left[\omega \right]}^{3}\backslash \left\{0\right\}$ is a CG of order ${p}^{6}-1.$

2.2.9.   The Eisenstein field extension ${\mathbb{Z}}_{\mathrm{p}}{\left[\mathrm{\omega }\right]}^{\mathrm{m}}\mathrm{i}\mathrm{f}\;\mathrm{p}\equiv 2\left(\mathrm{m}\mathrm{o}\mathrm{d}\;3\right)$

For the extension of EF ${\mathbb{Z}}_{p}{\left[\omega \right]}^{m},$ the QR

where $< H\left(x\right) >$ is the maximal ideal generated by an IP $H\left(x\right)$ of degree $m$ in ${\mathbb{Z}}_{p}\left[\omega \right]\left[x\right]$. Let $\gamma$ be the coset $x+\left(H\right(x\left)\right)$, then $H\left(\gamma \right) = 0$ and

${\mathbb{Z}}_{p}{\left[\omega \right]}^{m}$ is an m-degree extension field of the EF ${\mathbb{Z}}_{p}\left[\omega \right],$ and ${\mathbb{Z}}_{p}{{\left[\omega \right]}^{*}}^{m} = {\mathbb{Z}}_{p}{\left[\omega \right]}^{m}\backslash \left\{0\right\}$ is a CG of order ${p}^{2m}-1.$

Remark 3. The cardinality of ${\mathbb{Z}}_{p}{\left[\omega \right]}^{m}is$ ${p}^{2m}.$

Theorem 1. Let $\gamma$ be the element of the extension field ${\mathbb{Z}}_{p}{\left[\omega \right]}^{m}$ if $p\equiv 2\left(mod3\right),$ then $\gamma , {\gamma }^{{p}^{2}}, {{\gamma }^{p}}^{4}, \dots ,$ have the same minimal polynomial over the EF ${\mathbb{Z}}_{p}\left[\omega \right]$.

Proof. Straightforward [18, Theorem 4.4.2].

In this section, we will construct BCH codes over the EF by following [16, Section 4.4].

3.   Encoding of BCH codes over Eisenstein field

Let $c, n, q, d > 0$, such that $q$ is a some prime power, $2\le d\le n-1$, and $gcd(n, q) = 1.$ Let a least positive integer $m$ such that ${p}^{2m}\equiv 1\left(modn\right)$ [By Euler's theorem, ${p}^{2\varphi \left(n\right)}\equiv 1\left(modn\right),$ then $m$ divides $\varphi \left(n\right)$]. Thus $n$ divides ${p}^{2m}-1$.

Let $\gamma$ be the element of the extension field ${\mathbb{Z}}_{p}{\left[\omega \right]}^{m}.$ Consider the minimal polynomials ${m}_{i}\left(X\right)\in {\mathbb{Z}}_{p}\left[\omega \right]\left[X\right]$ of ${\gamma }^{i}.$ The least common multiple $\left(lcm\right)$ of all distinict minimal polynomials ${m}_{i}\left(X\right), i = c, c+1, ... , c+d-2$ is known as the generator polynomial $g\left(X\right)$ that is,

Since all minimal polynomials divides ${X}^{n}-1$, So generator polynomial divides ${X}^{n}-1$. Let $C$ be the cyclic code generated by $g\left(X\right)$ in the ring ${\mathbb{Z}}_{p}\left[\omega \right]{\left[X\right]}_{n}$. Then $C$ is called a BCH code of length $n$ over EF ${\mathbb{Z}}_{p}\left[\omega \right]$ with designed distance $d$.

Remark 4. If the code is full length $n = {p}^{2m}-1$ then it is primitive.

Remark 5. If the code is narrow sense, then $c = 1.$

Remark 6. The cardinality of the code $C$ over EF is ${p}^{2k}.$

Illustration 5. Construct a $(15, k, 3)$ BCH code over the EF ${\mathbb{Z}}_{2}\left[\mathrm{\omega }\right].$

Let $\gamma \in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then by Theorem 1, $\gamma , {\gamma }^{{2}^{2}}$ have the same minimal polynomial

Let ${\gamma }^{2}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{2}\left(X\right)$ can be found by ${\gamma }^{2}, {\gamma }^{8}$,

The generator polynomial $g\left(X\right)$ is,

The degree of $g\left(X\right)$ is 4, and the dimension $k$ is $11.$ Hence, we get $(15, 11, 3)$ BCH code over EF ${\mathbb{Z}}_{2}\left[\omega \right].$

Illustration 6. Construct a $(15, k, 5)$ BCH code over the EF ${\mathbb{Z}}_{2}\left[\mathrm{\omega }\right].$

Let $\gamma \in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then by Theorem 1, $\gamma , {\gamma }^{{2}^{2}}$ have the same minimal polynomial

Let ${\gamma }^{2}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{2}\left(X\right)$ can be found by ${\gamma }^{2}$ and ${\gamma }^{8}$,

Let ${\gamma }^{3}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{3}\left(X\right)$ can be found by ${\gamma }^{3}$ and ${\gamma }^{12}$,

Let ${\gamma }^{4}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{4}\left(X\right)$ can be found by ${\gamma }^{4}$ and ${\gamma }^{1}$,

The generator polynomial $g\left(X\right)$ is,

The degree of $g\left(X\right)$ is 6, and the dimension $k$ is $9.$ Hence, we get $\left(15, 9, 5\right)$ BCH codes over EF ${\mathbb{Z}}_{2}\left[\omega \right].$

Illustration 7. Construct a $\left(15, k, 7\right)$ BCH code over the EF ${\mathbb{Z}}_{2}\left[\mathrm{\omega }\right].$

Let $\gamma \in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then by Theorem 1, $\gamma , {\gamma }^{{2}^{2}}$ have the same minimal polynomial

Let ${\gamma }^{2}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{2}\left(X\right)$ can be found by ${\gamma }^{2}$ and ${\gamma }^{8}$,

Let ${\gamma }^{3}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{3}\left(X\right)$ can be found by ${\gamma }^{3}$ and ${\gamma }^{12}$,

Let ${\gamma }^{4}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{4}\left(X\right)$ can be found by ${\gamma }^{4}$ and ${\gamma }^{1}$,

Let ${\gamma }^{5}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{5}\left(X\right)$ can be found by ${\gamma }^{5}$,

Let ${\gamma }^{6}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{6}\left(X\right)$ can be found by ${\gamma }^{6}$ and ${\gamma }^{9}$,

The generator polynomial $g\left(X\right)$ is,

The degree of $g\left(X\right)$ is 9, and the dimension $k$ is $6.$ Hence, we get $\left(15, 6, 7\right)$ BCH codes over EF ${\mathbb{Z}}_{2}\left[\omega \right].$

Illustration 8. Construct a $\left(15, k, 9\right)$ BCH code over the EF ${\mathbb{Z}}_{2}\left[\mathrm{\omega }\right].$

Let $\gamma \in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then by Theorem 1, $\gamma , {\gamma }^{{2}^{2}}$ have the same minimal polynomial

Let ${\gamma }^{2}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{2}\left(X\right)$ can be found by ${\gamma }^{2}$ and ${\gamma }^{8}$,

Let ${\gamma }^{3}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{3}\left(X\right)$ can be found by ${\gamma }^{3}$ and ${\gamma }^{12}$,

Let ${\gamma }^{4}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{4}\left(X\right)$ can be found by ${\gamma }^{4}$ and ${\gamma }^{1}$,

Let ${\gamma }^{5}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{5}\left(X\right)$ can be found by ${\gamma }^{5}$,

Let ${\gamma }^{6}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{6}\left(X\right)$ can be found by ${\gamma }^{6}$ and ${\gamma }^{9}$,

Let ${\gamma }^{7}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{7}\left(X\right)$ can be found by ${\gamma }^{7}$ and ${\gamma }^{13}$,

Let ${\gamma }^{8}\in {\mathbb{Z}}_{2}{\left[\omega \right]}^{2}$ then ${m}_{8}\left(X\right)$ can be found by ${\gamma }^{8}$ and ${\gamma }^{2}$,

The generator polynomial $g\left(X\right)$ is,

The degree of $g\left(X\right)$ is 11, and the dimension $k$ is $4.$ Hence, we get $\left(15, 4, 9\right)$ BCH codes over EF ${\mathbb{Z}}_{2}\left[\omega \right].$

4.   Decoding algorithm-based EF

This section is for the comprehensive decoding procedure of BCH codes based that are superimposed on an EF with length $n$ using modified BMA.

The subsequent theorem is a merely restatement of [27, Section V, Theorem 2].

Theorem 2. Let $C$ be a $n$ length BCH code that is superimposed over a GF ${\mathbb{Z}}_{p}\left[\omega \right]$ if $\left(p\equiv 2\right)\left(mod3\right)$ with a distance d that has been created. Then the code $C$ is the null space of the matrix $H.$

Proof. Straightforward ^[28].

Let $c$ be a code word of the $(n, k, d)$ narrow sense BCH code, received word $r$ and design distance $d$. Then the error corrections of the BCH codes have the following steps.

Step 1: Let ${S}_{i}$ for $i = c, c+1, \dots , c+d-2$ be the syndromes with the help of $H$ and $r$ as;

OR ${S}_{i} = r\left({\gamma }^{i}\right) = {a}_{0}+{a}_{1}{\gamma }^{i}+\dots +{a}_{n-1}{\gamma }^{\left(n-1\right)i}$ for $i = c, c+1, \dots , c+d-2.$

If all ${S}_{i}$ are zeros then $c = r.$ However, if at least one ${S}_{i}$ is nonzero then the error occurs. So, we will move to the next step.

Step 2: Apply modified BMP to find ${\Delta }^{n}\left(y\right).$

Where ${\vartheta }_{n}$ is the discrepancy, degree $\left({\Delta }^{n}\left(y\right)\right) = {u}_{n}$ and $t$ is the upper bound of the number of errors. There are two cases for ${\Delta }^{n}\left(\mathrm{y}\right)$;

Case 1: If ${\vartheta }_{n} = 0,$ then ${\Delta }^{n+1}\left(\mathrm{y}\right) = {\Delta }^{n}\left(\mathrm{y}\right)$ and ${u}_{n} = {u}_{n+1}.$

Case 2: If ${\vartheta }_{n}\ne 0, \;\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{n}$ for $m\le n-1$ and $n-{u}_{m}$ have the largest value in $n-{u}_{n}.$ So, from ${\vartheta }_{n}-z{\vartheta }_{m} = 0,$ we get $z$. Thus, ${\Delta }^{n+1}\left(y\right) = {\Delta }^{n}\left(y\right)-z{y}^{n-m}{\Delta }^{m}\left(y\right).$ Then,

Step 3: Find the reciprocal function $g\left(\mathrm{y}\right)$ of ${\Delta }^{n}\left(\mathrm{y}\right)$, then ${y}_{j}$ represents the roots of $g\left(\mathrm{y}\right).$ Let ${x}_{j} = {\rho }^{j}$ are error locations if it satisfies the $\left({x}_{j}-{y}_{j}\right) = 0,$ where $1\le j\le n-1.$

Step 4: Find an elementary symmetric function (ESF) for the possible errors that occur in the received word.

where ${x}_{\mathrm{j}}$, $j = \mathrm{1, 2}, \dots , v$ and $v$ is the total number of the roots of $g\left(y\right).$

Step 5: The magnitude of the errors can be found by Forney's procedure ^[29] as;

Start with ${\Delta }_{0} = {\Delta }_{i, 0} = 1.$ Where ${\Delta }_{i, j} = {\Delta }_{j}+{x}_{i}.{\Delta }_{i, j-1};j = 1, \;2, \;3, \dots , v-1$ and $i = 1, 2, \dots , v.$

Step 6: The cord word $c$ can be corrected by $c = r-e,$ where $e$ is the error vector.

Illustration 9. Let $(15, 11, 3)$ BCH code over the EF ${\mathbb{Z}}_{2}\left[\omega \right]$ and the received vector $r = {\left(\mathrm{0, 0}, \omega , \dots , 0\right)}_{1\times 15}.$ Find the corrected cord word if possible.

Let

Where ${S}_{1} = {\gamma }^{7}$ and ${S}_{2} = {\gamma }^{9}$ are two syndromes. Find ${\Delta }^{2}\left(y\right)$ by modified BMA by the following iterations.

Iteration 1. The first nonzero syndrome is $1+\omega +\gamma \omega$. Apply step 2 (case Ⅱ) of the BMA because ${\vartheta }_{0}\ne 0,$ $-1 = -1,$ and $0-{u}_{-1} = 0$ is the higher value of the last column. Then, ${\vartheta }_{0}-z{\vartheta }_{-1} = 0,$ then

So the polynomial

Iteration 2. ${\vartheta }_{1}\ne 0$ in Iteration 1, $0 = 1-1$ and $1-{u}_{0} = 1-0 = 1$ is the higher value of the last column. Thus, ${\vartheta }_{1}-z{\vartheta }_{0} = 0,$ then

So, the polynomial

The results of the iterations are given in Table 4.

The reciprocal function of ${\Delta }^{2}\left(y\right) = 1+{\gamma }^{2}y$ is $g\left(y\right) = {\gamma }^{2}+y.{\gamma }^{2}$ is the root of $g\left(y\right).$ Hence ${y}_{1} = {\gamma }^{2},$ so an error occurred in second place of $r.{\Delta }_{0}{\mathrm{y}}^{v}+{\Delta }_{1} = \mathrm{y}-{\gamma }^{2}$ is an ESF. The error magnitude is

where ${\Delta }_{0} = 1, {\Delta }_{1} = {\mathrm{\gamma }}^{2}$ and $v = 1$. Corrected code word $c = a-e = {\left(0, \;0, \;0, \dots , \;0\right)}_{1\times 15}.$ Hence $c$ is the corrected code word of the $(15, 11, 3)$ BCH code $C.$

Illustration 10. Let $(15, 11, 3)$ BCH code over the EF ${\mathbb{Z}}_{2}\left[\omega \right]$ and the received vector $r = r = {\left(\mathrm{1, 1}, \omega , \mathrm{0, 1}, 0, \dots , 0\right)}_{1\times 15}.$ Find the corrected cord word if possible.

Let

Where ${S}_{1} = {\gamma }^{7}$ and ${S}_{2} = {\gamma }^{9}$ are two syndromes. Find ${\Delta }^{2}\left(y\right)$ by modified BMA by the following iterations.

Iteration 1. The first nonzero syndrome is $1+\omega +\gamma \omega$. Apply step 2 (case Ⅱ) of the BMA because ${\vartheta }_{0}\ne 0,$ $-1 = -1$ and $0-{u}_{-1} = 0$ is the higher value of the last column. Thus, ${\vartheta }_{0}-z{\vartheta }_{-1} = 0,$ then

So, the polynomial

Iteration 2. ${\vartheta }_{1}\ne 0$ in Iteration 1, $0 = 1-1$ and $1-{u}_{0} = 1-0 = 1$ is the higher value of the last column. Thus, ${\vartheta }_{1}-z{\vartheta }_{0} = 0,$ then $z = \frac{{\vartheta }_{1}}{{\vartheta }_{0}} = \frac{1+\gamma }{1+\omega +\gamma \omega } = 1+\gamma +\gamma \omega = {\gamma }^{12}.$ So, the polynomial

The results of the iterations are given in Table 5.

The reciprocal function of ${\Delta }^{2}\left(y\right) = 1+{\gamma }^{2}y$ is $g\left(y\right) = {\gamma }^{2}+y.{\gamma }^{2}$ is the root of $g\left(y\right).$ Hence ${y}_{1} = {\gamma }^{2},$ so an error occurred in second place of $r.{\Delta }_{0}{\mathrm{y}}^{v}+{\Delta }_{1} = \mathrm{y}-{\gamma }^{2}$ is an ESF. The error magnitude is

where ${\Delta }_{0} = 1, {\Delta }_{1} = {\mathrm{\gamma }}^{2}$ and $v = 1$. Corrected code word $c = a-e = {\left(0, \;0, \;0, \dots , \;0\right)}_{1\times 15}.$ Hence $c$ is the corrected code word of the $(15, 11, 3)$ BCH code $C.$

Illustration 10. Let $(15, 11, 5)$ BCH code over the EF ${\mathbb{Z}}_{2}\left[\omega \right]$ and the received vector $r = {\left(1\omega \omega 1 1 0 0\dots 0\right)}_{1\times 15}.$ Find the corrected cord word if possible.

Let

Let ${S}_{1} = 1+\mathrm{\gamma }+\mathrm{\gamma }\omega = {\mathrm{\gamma }}^{12}, {S}_{2} = 1+\mathrm{\gamma }+\omega +\mathrm{\gamma }\omega = {\mathrm{\gamma }}^{14}, {S}_{3} = 1+\mathrm{\gamma }+\mathrm{\gamma }\omega = {\mathrm{\gamma }}^{12}$ and ${S}_{4} = 1+\omega +\mathrm{\gamma }\omega = {\mathrm{\gamma }}^{7}$. Find ${\Delta }^{4}\left(y\right)$ by modified BMA by the following iterations.

Iteration 1. The first nonzero syndrome is $1+\mathrm{\gamma }+\mathrm{\gamma }\omega$. Apply step 2 (case Ⅱ) of the BMA because ${\vartheta }_{0}\ne 0,$ $-1 = -1$ and $0-{u}_{-1} = 0$ is the higher value of the last column. Thus, ${\vartheta }_{0}-z{\vartheta }_{-1} = 0,$ then

So, the polynomial

Iteration 2. ${\vartheta }_{1}\ne 0$ in Iteration 1, $0 = 1-1$ and $1-{u}_{0} = 1-0 = 1$ is the higher value of the last column. Thus, ${\vartheta }_{1}-z{\vartheta }_{0} = 0,$ then

So, the polynomial

Iteration 3. ${\vartheta }_{2}\ne 0$ in Iteration 2, $1 = 2-1$ and $2-{u}_{1} = 2-1 = 1$ is the higher value of the last column. Thus, ${\vartheta }_{2}-z{\vartheta }_{1} = 0,$ then

So, the polynomial

Iteration 4. ${\vartheta }_{3}\ne 0$ in Iteration 3, $2 = 3-1$ and $3-{u}_{2} = 3-1 = 2$ is the higher value of the last column. Thus, ${\vartheta }_{3}-z{\vartheta }_{2} = 0,$ then $z = \frac{{\vartheta }_{3}}{{\vartheta }_{2}} = \frac{\gamma +\omega +\gamma \omega }{1+\gamma \omega } = \omega = {\gamma }^{5}.$ So, the polynomial

The results of the iterations are given in Table 6.

The reciprocal function of ${\Delta }^{4}\left(y\right) = 1+{\gamma }^{3}y+{\mathrm{\gamma }}^{10}{y}^{2}$ is $g\left(y\right) = {y}^{2}+{\mathrm{\gamma }}^{3}y+{\mathrm{\gamma }}^{10}.\mathrm{\gamma }$ and ${\gamma }^{9}$ are the roots of $g\left(y\right).$ Hence ${y}_{1} = \mathrm{\gamma }$ and ${y}_{2} = {\mathrm{\gamma }}^{9}$, so the errors appeared in first and ninth place in

is an ESF. The error magnitudes are as;

As ${\Delta }_{\mathrm{1, 1}} = {{\Delta }_{1}+\Delta }_{\mathrm{1, 0}}.{y}_{1} = {\mathrm{\gamma }}^{9},$ therefore

Corrected code word

Hence $c$ is the corrected code word of the $(15, 11, 5)$ BCH code $C.$

5.   Comparison

We compare the narrow sense BCH code and decoding method on a GF and an EF. BCH-codes base $GF\left({p}^{m}\right)$ are defined with detail in [7, Section 4.4], including their length $(n = {p}^{m}-1)$, design distances $\left(d\right)$, dimension $\left({k}_{1}\right)$, code rates $({R}_{1} = {k}_{1}/({p}^{m}-1)$ and words of $C$ $\left({p}^{{k}_{1}}\right)$. Here, the authors provide BCH codes of length $(n = {p}^{2m}-1)$, design distance $\left(d\right)$, dimension ${k}_{2}$, code rate $({R}_{2} = {k}_{2}/({p}^{2m}-1)$ and the words of $C$ over the EF ${\mathbb{Z}}_{p}\left[\omega \right]$ are ${p}^{2{k}_{2}}$, and their decoding technique. Comparisons between BCH codes based on GF and EF are given in Tables 7 and 8.

For comparison we take a one GF and one EF. Based on the results of [9, Exercise 4.4 (10)], length of the code $n$ is ${p}^{m}-1 = {2}^{4}-1,$ design distance $d$, dimension ${k}_{1}$, coding rate ${R}_{1}$ and the code words ${p}^{{k}_{1}}$ are given in Table 7.

In a similar way, the length of the code $n = {p}^{2m}-1 = {2}^{4}-1 = 15$, dimension ${k}_{2},$ designed distance $d$, code rate ${R}_{2}$ and the words of $C$ are ${p}^{2{k}_{2}}$ over the EF ${\mathbb{Z}}_{p}\left[\omega \right] = {\mathbb{Z}}_{2}\left[\omega \right]$ given in Table 8.

Figure 3 shows the BCH coding rate ${R}_{1}$ over a Galois field (GF) and ${R}_{2}$ over the Eisenstein field with designed distance d from Tables 7 and 8. Figure 4 shows the BCH code dimension ${k}_{1}$ over a Galois field and ${k}_{2}$ over an Eisenstein field with designed distance $d$.

6.   Discussion for shortcoming

When the BCH codes-based GF and their decoding algorithm are compared with the EF and their decoding method for the same length and designed distance, the following observations are achieved. In the Eisenstein field, the code rates and dimensions are greater than in the Galois field. The BCH code over the Eisenstein field has a lot number of code words than the Galois field. The decoding algorithm over the GF is a specific algorithm for error correction, whereas the Eisenstein field decoding algorithm is a general algorithm for error correction.

7.   Conclusions and future direction

The Eisenstein field and its extension are covered in this article. Additionally, the construction of BCH codes based on the EF ${\mathbb{Z}}_{p}\left[\omega \right]$, for $p\equiv 2\left(mod3\right)$ has been provided. Furthermore, a slightly modified version of the BMA was used to decode these codes. It has been demonstrated that the performance of the BCH codes over the EF ${\mathbb{Z}}_{p}\left[\omega \right]$ for $p\equiv 2\left(mod3\right)$ and their decoding technique is superior to that of the BCH codes over the $GF\left({p}^{m}\right)$.

In future directions, BCH codes based on EF ${\mathbb{Z}}_{p}\left[\omega \right]$ and its decoding technique may extend across Eisenstein local rings ${\mathbb{Z}}_{{p}^{k}}\left[\omega \right]$, for $p\equiv 2\left(mod3\right)$, which may improve performance of the BCH codes using symbols from ${\mathbb{Z}}_{p}\left[\omega \right]$.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Researchers Supporting Project number: RSPD 2023R650, King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declared that they had no conflicts of interest.