Crossing cubic Lie algebras

1.   Introduction

Algebraic structures are a crucial aspect of pure and applied mathematics, and other domains, with an enormous variety of applications in computer science ^[1,2,3], theoretical physics ^[4], coding theory ^[5], and other domains. The idea of Lie algebra was initially discovered by Sophus Lie ^[6] as continued transformation groups (now referred to as Lie groups). The inception of this idea of Lie algebras was presented when Sophus Lie tried to distinguish certain "smooth" subgroups of general linear groups. Many scholars have focused on Lie algebras over the years, creating a variety of structural concepts pertaining to the theory of groups, rings, fields, and other algebraic aspects. Lie groups, Lie similarities and Lie algebras are fundamental notions in mathematics.

The inception of the notion of fuzziness structures was performed by a well-known mathematician, Zadeh in 1965 ^[7]. After him, the concept has undergone plenty of additions, improvements and developments by numerous researchers who adopted further advanced and novel kinds and aspects of the notion, such as interval-valued fuzziness structures ^[8], cubic structures ^[9], and $\mathcal{N}$-structures ^[10]. For the results on algebraic structures with uncertainty (see works by the authors of ^{[11,12,13,14,15,16,17]}).

In the fuzzification of Lie algebras and bringing together the concepts of fuzziness structure and Lie subalgebrs or ideals, the thought of fuzziness structure was connected with Lie algebras by Yehia ^[18]. A lot of researchers concentrated on Lie algebras in fuzziness structures (see works by the authors of ^[19,20,21]). Applying the idea of interval-valued fuzziness structures to Lie algebras, Akram ^[22] extended the work of ^[18] and studied the conception of interval-valued fuzziness Lie subalgebras and Lie ideals. In the intutionistic fuzziness Lie algebras, Akram and Shum ^[23] applied intuitionistic fuzziness structures to Lie algebras by merging the notions of intuitionistic fuzziness structures and Lie algebras. They proposed and discussed the idea of intuitionistic fuzzy Lie subalgebras and investigated some of their characteristics and properties in a Lie algebra. As an extension of the results in ^[18,23], Akram et al. ^[24] developed single-valued neutrosophic Lie subalgebras and ideals. They described some significant results of single-valued neutrosophic Lie ideals.

In terms of the case of $\mathcal{CCS}s$, Jun et al. ^[25] were the first one presenting this concept. They defined the same or opposite direction order, $S$-intersection (union), and $O$-intersection (union) of $\mathcal{CCS}s,$ and discussed their related properties. On a nonempty set $\mathscr{L},$ a $\mathcal{CCS}$ indicates a map known as the membership function

The introduction of $\mathcal{CCS}s$ is based on the ideas of interval-valued fuzziness structure indicates a map known as the membership function

and the negative version of fuzziness structures (say, $\mathcal{N}$-structures) indicates a map known as the membership function

In ^[26], Jun and Song applied this notion to BCK and BCI-algebras. They implemented the notions of $\mathcal{CC}$ ideals in a BCK/BCI-algebra, $\mathcal{CC}$ $\circ$-subalgebras of a BCK-algebra with the condition ($S$), and investigated certain characterizations and translations of $\mathcal{CC}$ subalgebras and ideals. $\ddot{O}$zt$\ddot{u}$rk et al. ^[27] applied this notion to commutative BCK-algebras and semigroups. Mostafa et al. ^[28] proposed $(\widetilde{\alpha}, \alpha)$-$\mathcal{CC}$ QS-ideals of QS-algebras, and discussed certain related characteristics and results.

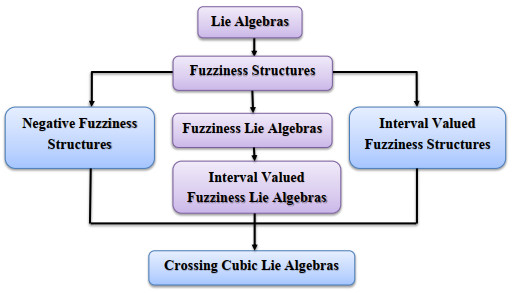
To convey the novelty of this framework, Figure 1 depicts a novel hybrid modification of interval-valued fuzziness Lie algebras and a negative version of fuzziness Lie algebras known as $\mathcal{CC}$ Lie algebras.

This study is the initial effort to discuss and utilize the $\mathcal{CCS}s$ in Lie algebras. The overall structure of the manuscript is as follows: In Section 2, we review the definitions of Lie subalgebra, Lie ideal, and homomorphism. We present the definitions of fuzziness Lie subalgebra and Lie ideal of Lie algebras. Moreover, we propose the notion of $\mathcal{CCS}s$ with their level cuts. In Section 3, we develop the concepts of $\mathcal{CC}$ Lie subalgebras, $\mathcal{CC}$ Lie ideals, and homomorphism. We discuss the Cartesian product of $\mathcal{CC}$ Lie subalgebras. Also, we describe certain significant results of $\mathcal{CC}$ Lie ideals. In Section 4, we provide a construction of a quotient Lie algebra via the $\mathcal{CC}$ Lie ideal in a Lie algebra. Also, the $\mathcal{CC}$ isomorphism theorems are presented. Lastly, the conclusions and certain potential future studies of the current article are proposed in Section 5.

2.   Preliminaries

Here, we initially review some fundamental aspects that are significant for this manuscript. Throughout this manuscript, $\mathscr{L}$ is a Lie algebra.

A Lie algebra is presented as a pair $(\mathscr{L}, [\cdot, \cdot]),$ where $\mathscr{L}$ is a vector space over a field ${F}$ (${\mathbb{R}}$ or ${\mathbb{C}}$) and $[\cdot, \cdot]: \mathscr{L} \times \mathscr{L} \rightarrow \mathscr{L}$ is denoted by $(l_1, l_2) \rightarrow [l_1, l_2]$ achieving the axioms below:

(A1) $[l_1, l_2]$ bilinear;

(A2) $[l_1, l_2] = 0$ $\forall l_1 \in \mathscr{L};$

(A3) $[[l_1, l_2], l_3]+ [[l_2, l_3], l_1]+ [[l_3, l_1], l_2] = 0$ $\forall l_1, l_2, l_3 \in \mathscr{L}.$

We note that the operation "." in $\mathscr{L}$ is anti-commutative, i.e., $[l_1, l_2] = -[ l_2, l_1].$ But it is not associative, i.e., $[[l_1, l_2], l_3] \neq [l_1, [ l_2, l_3]].$ Now, we recall the concepts of a Lie subalgebra and a Lie ideal.

● A Lie subalgebra is a subspace $\mathscr{K}$ of $\mathscr{L}$ that is closed under "$[\cdot, \cdot]$".

● A Lie ideal is a subspace $\mathscr{I}$ of $\mathscr{L}$ with the property $[\mathscr{I}, \mathscr{L}] \subseteq\mathscr{I}$.

● Any Lie ideal $\mathscr{I}$ is a Lie subalgebra.

Let $\varpi$ be a fuzzy structure on $\mathscr{L}, i.e., \varpi: \mathscr{L} \rightarrow [0, 1].$ Then, $\varpi$ is a fuzzy Lie subalgebra ^[29] of $\mathscr{L}$ if the following identities are satisfied: $\forall l_1, l_2 \in \mathscr{L}, \alpha \in {F},$

(S1) $\varpi(l_1 + l_2)\geq min\{\varpi(l_1), \varpi(l_2)\},$

(S2) $\varpi(\alpha l_1)\geq \varpi(l_1),$

(S3) $\varpi([l_1, l_2])\geq min\{\varpi(l_1), \varpi(l_2)\}.$

A fuzzy structure $\varpi$ is a fuzzy Lie ideal ^[29] of $\mathscr{L}$ if (S1), (S2), and $\varpi([l_1, l_2])\geq \varpi(l_1)$ are satisfied $\forall l_1, l_2 \in \mathscr{L}, \alpha \in {F}.$

Consider the interval number $\widetilde{\xi} = [\xi^-, \xi^+]$ of $[0, 1],$ where $\xi^-, \xi^+ \in [0, 1]$ and $\xi^- \leq \xi^+.$ $\mathbb{P}[0, 1]$ denotes the set of all interval numbers. For the interval numbers $\widetilde{\xi_i} = [\xi_i^-, \xi_i^+], \widetilde{\tau_i} = [\tau_i^-, \tau_i^+] \in \mathbb{P}[0, 1],$ where $i\in \Lambda.$ We give:

● $\widetilde{min}\{\widetilde{\xi_i}, \widetilde{\tau_i}\} = [ min\{\xi_i^-, \tau_i^-\}, min\{\xi_i^+, \tau_i^+\}],$

● $\widetilde{max}\{\widetilde{\xi_i}, \widetilde{\tau_i}\} = [ max\{\xi_i^-, \tau_i^-\}, max\{\xi_i^+, \tau_i^+\}],$

● $\widetilde{\xi_1} \preceq \widetilde{\xi_2} \Leftrightarrow \xi^-_1 \leq \xi^-_2$ and $\xi^+_1 \leq \xi^+_2,$

● $\widetilde{\xi_1} = \widetilde{\xi_2} \Leftrightarrow \xi^-_1 = \xi^-_2$ and $\xi^+_1 = \xi^+_2.$

To say that $\widetilde{\xi_1} \prec \widetilde{\xi_2}$ (resp. $\widetilde{\xi_1} \succ \widetilde{\xi_2}),$ we mean $\widetilde{\xi_1} \preceq \widetilde{\xi_2}$ and $\widetilde{\xi_1} \neq \widetilde{\xi_2}$ (resp. $\widetilde{\xi_1} \succeq \widetilde{\xi_2}$ and $\widetilde{\xi_1} \neq \widetilde{\xi_2}).$

$\mathcal{F}(\mathscr{L}, [-1, 0])$ indicates the collection of maps from a set $\mathscr{L} \neq \phi$ to $[-1, 0].$ An object of $\mathcal{F}(\mathscr{L}, [-1, 0])$ is a negative-valued map from $\mathscr{L}$ to [-1, 0] (simply, an $\mathcal{N}$-functionon $\mathscr{L}$). $(\mathscr{L}, \pi)$ is an $\mathcal{N}$-structure, where $\pi$ is an $\mathcal{N}$-function on $\mathscr{L}.$

Definition 2.1 (^[25]). Let $\mathscr{L}$ be a non-empty set. A $\mathcal{CCS}$ of $\mathscr{L}$ is a structure having the shape:

where $\widetilde{\varpi}_{\mathscr{C}}: \mathscr{L} \rightarrow \mathbb{P}[0, 1]$ is an interval valued fuzziness structure on $\mathscr{L}$ and $\pi_{\mathscr{C}}: \mathscr{L} \rightarrow [-1, 0]$ is an $\mathcal{N}$-function on $\mathscr{L}.$

For the sake of simplicity, we shall use the symbol $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ for the $\mathcal{CCS}$ $\mathscr{C} = \{\langle l, \widetilde{\varpi}_{\mathscr{C}}(l), \pi_{\mathscr{C}}(l) \rangle \mid l \in \mathscr{L}\}$.

Definition 2.2 (^[25]). Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ be a $\mathcal{CCS}$ of $\mathscr{L}$. Then, $(\widetilde{\nu}, \gamma)$-level of $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is the crisp set in $\mathscr{L}$ denoted by $\Upsilon \Big(\mathscr{C}; (\widetilde{\nu}, \gamma)\Big)$ and is defined as

where $\widetilde{\nu} \in \mathbb{P}[0, 1]$ and $\gamma \in [-1, 0].$

For $\widetilde{\nu} \in \mathbb{P}[0, 1]$ and $\gamma \in [-1, 0].$ The $\widetilde{\nu}$-level $\Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}\Big)$ and $\gamma$-level $\Upsilon \Big(\pi_{\mathscr{C}}; \gamma \Big)$ subsets of $\mathscr{C}$ can be defined as:

3.   Crossing cubic Lie subalgebras and ideals

In the current section, we originate the concepts of $\mathcal{CC}$ Lie sub-algebra, ideal, and homomorphism. Also, we investigate some features of these notions.

Definition 3.1. A $\mathcal{CCS}$ $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie subalgebra of $\mathscr{L}$ if it meets the following identities:

(A) $(\forall l_1, l_2 \in \mathscr{L})$ $\left(\begin{array}{c} \widetilde{\varpi}_{\mathscr{C}}(l_1 + l_2)\succeq \widetilde{min}\{\widetilde{\varpi}_{\mathscr{C}}(l_1), \widetilde{\varpi}_{\mathscr{C}}(l_2)\}, \\ \pi_{\mathscr{C}}(l_1+ l_2)\leq max\{\pi_{\mathscr{C}}(l_1), \pi_{\mathscr{C}}(l_2)\}\\ \end{array} \right),$

(B) $(\forall l_1\in \mathscr{L}, \alpha \in {F})$ $\left(\begin{array}{c} \widetilde{\varpi}_{\mathscr{C}}(\alpha l_1)\succeq \widetilde{\varpi}_{\mathscr{C}}(l_1), \\ \pi_{\mathscr{C}}(\alpha l_1)\leq \pi_{\mathscr{C}}(l_1)\\ \end{array} \right),$

(C) $(\forall l_1, l_2 \in \mathscr{L})$ $\left(\begin{array}{c} \widetilde{\varpi}_{\mathscr{C}}([l_1, l_2])\succeq \widetilde{min}\{\widetilde{\varpi}_{\mathscr{C}}(l_1), \widetilde{\varpi}_{\mathscr{C}}(l_2)\}, \\ \pi_{\mathscr{C}}([l_1, l_2])\leq max\{\pi_{\mathscr{C}}(l_1), \pi_{\mathscr{C}}(l_2)\}\\ \end{array} \right).$

Note that for all $l\in L$, $\widetilde{\varpi}_{\mathscr{C}}(0)\succeq \widetilde{\varpi}_{\mathscr{C}}(l)$ and $\pi_{\mathscr{C}}(0)\leq \pi_{\mathscr{C}}(l).$ If $\alpha \neq 0, \widetilde{\varpi}_{\mathscr{C}}(\alpha l) = \widetilde{\varpi}_{\mathscr{C}}(l),$ since $\widetilde{\varpi}_{\mathscr{C}}(\alpha l)\succeq \widetilde{\varpi}_{\mathscr{C}}(l) = \widetilde{\varpi}_{\mathscr{C}}(\alpha^{-1}(\alpha l))\succeq \widetilde{\varpi}_{\mathscr{C}}(\alpha l)$. Similarly, $\pi_{\mathscr{C}}(\alpha l) = \pi_{\mathscr{C}}(l).$

Definition 3.2. A $\mathcal{CC}$ Lie subalgebra $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ of $\mathscr{L}$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L}$ if it meets the conditions (A) and (B) of Definition 3.1, respectively, and the condition (E), where

(E) $(\forall l_1, l_2 \in \mathscr{L})$ $\left(\begin{array}{c} \widetilde{\varpi}_{\mathscr{C}}([l_1, l_2])\succeq \widetilde{\varpi}_{\mathscr{C}}(l_1), \\ \pi_{\mathscr{C}}([l_1, l_2])\leq \pi_{\mathscr{C}}(l_1)\\ \end{array} \right).$

The Next two examples illustrate the above two definitions.

Example 3.1. Let $\mathscr{L} = \mathbb{R}^3 = \{(n, y, m) : n, y, m \in \mathbb{R} \}.$ Then, $(\mathbb{R}^3, [\cdot, \cdot])$ is a real Lie algebra, where the bracket $[\cdot, \cdot]$ is defined as $[l_1, l_2] = l_1 \times l_2$ (the usual cross product). We define a $\mathcal{CCS}$ as:

It is clear that, $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie subalgebra of $\mathbb{R}^3.$ But it is not a $\mathcal{CC}$ Lie ideal, since $\widetilde{\varpi}_{\mathscr{C}}([(1, 1, 1), (1, 2.4)]) = \widetilde{\varpi}_{\mathscr{C}}((2, -3, 1)) = [0.6, \; 0.8] \nsucceq [0.7, \; 0.9] = \widetilde{\varpi}_{\mathscr{C}}((1, 1, 1))$.

Example 3.2. Let $\mathscr{L} = \mathbb{R}^3 = \{(n, y, m) : n, y, m \in \mathbb{R} \}.$ Then, $(\mathbb{R}^3, [\cdot, \cdot])$ is a real Lie algebra, where the bracket $[\cdot, \cdot]$ is defined as $[l_1, l_2] = l_1 \times l_2$ (the usual cross product). We define a $\mathcal{CCS}$ as:

Clearly, one can obtain that $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie ideal of $\mathbb{R}^3.$

Theorem 3.3. Any $\mathcal{CC}$ Lie ideal is a $\mathcal{CC}$ Lie subalgebra.

Proof. The proof is obvious. □

The converse of Theorem 3.3 does not hold in general.

Example 3.3. Let $\mathscr{L} = \mathbb{R}[n]$ be the set of all polynomials with coefficients in $\mathbb{R}.$ Then, $(\mathbb{R}[n], [\cdot, \cdot])$ is a real Lie algebra over $\mathbb{R},$ where the bracket $[\cdot, \cdot]$ is defined as

We define a $\mathcal{CCS}$ as :

Note that, for any $p(n), q(n)\in \mathbb{R}[n],$ and $\alpha\in \mathbb{R}$:

It is clear that, $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie subalgebra of $\mathbb{R}[n],$ but it is not a $\mathcal{CC}$ Lie ideal, since

Theorem 3.4. A $\mathcal{CCS}$ $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie subalgebra (ideal) if and only if

are Lie subalgebras (ideals) of $\mathscr{L}$ for any $(\widetilde{\nu}, \gamma) \in Im(\widetilde{\varpi}_{\mathscr{C}}) \times Im(\pi_{\mathscr{C}}),$ where $\widetilde{\nu} \in \mathbb{P}[0, 1]$ and $\gamma \in [-1, 0].$

Proof. Assume that $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie subalgebra, and let $\widetilde{\nu} \in Im(\widetilde{\varpi}_{\mathscr{C}})$ and $\gamma \in Im(\pi_{\mathscr{C}})$. Let $l_1, l_2\in \Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}\Big)$ and $\alpha \in F$. Then $\widetilde{\varpi}_{\mathscr{C}}(l_1) \succeq \widetilde{\nu}$ and $\widetilde{\varpi}_{\mathscr{C}}(l_2) \succeq \widetilde{\nu}$. It follows that

and hence, $l_1+l_2, \; \alpha l_1, \; [l_1, \; l_2]\in \Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}\Big).$ Thus, $\Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}\Big)$ is a Lie subalgebra of $\mathscr{L}.$ The proof of $\Upsilon \Big(\pi_{\mathscr{C}}; \gamma\Big)$ is similar.

Conversely, suppose that $\Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}\Big) \text{ and } \Upsilon \Big(\pi_{\mathscr{C}}; \gamma\Big)$ are Lie subalgebras of $\mathscr{L}$ for any $\widetilde{\nu} \in Im(\widetilde{\varpi}_{\mathscr{C}}), \gamma\in Im(\pi_{\mathscr{C}})$. Let $l_1, l_2\in L$ and $\alpha \in F$. Taking

Thus, $l_1, l_2\in \Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}\Big)$. Then, we have $l_1+l_2\in \Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}\Big)$, which means

Similarly, we can show that:

In a similar way, we use the fact that $\Upsilon \Big(\pi_{\mathscr{C}}; \gamma\Big)$ is a Lie subalgebras of $\mathscr{L}$ to show:

Hence, $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie subalgebra. The proof of the Lie ideal is similar. □

Theorem 3.5. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ be a $\mathcal{CC}$ Lie subalgebra. Define a binary relation $\bowtie$ on $\mathscr{L}$ by

Then, $\bowtie$ is an equivalence relation on $\mathscr{L}.$

Proof. Clearly, the reflexiveness and symmetry of $\bowtie$ are trivial. So, we only need to demonstrate that $\bowtie$ is transitive. Let $l_1, l_2, L_3 \in \mathscr{L},$ If $l_1 \bowtie l_2$ and $l_2 \bowtie l_3$, then $\widetilde{\varpi}_{\mathscr{C}}(l_1 - l_2) = \widetilde{\varpi}_{\mathscr{C}}(0), \widetilde{\varpi}_{\mathscr{C}}(l_2 - l_3) = \widetilde{\varpi}_{\mathscr{C}}(0)\text{ and } \pi_{\mathscr{C}}(l_1- l_2) = \pi_{\mathscr{C}}(0), \pi_{\mathscr{C}}(l_2- l_3) = \pi_{\mathscr{C}}(0).$ Thus, it follows that

and

Hence, $\bowtie$ is an equivalence relation on $\mathscr{L}.$ □

Theorem 3.6. Let $\mathscr{H}_\circ \subset \mathscr{H}_1 \subset... \subset \mathscr{H}_n = \mathscr{L}$ be a chain of Lie algebra $\mathscr{L}.$ Then, there exists a $\mathcal{CC}$ Lie subalgebras $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ for which the level subsets

$(\widetilde{\nu_k}, \gamma_k) \in Im(\widetilde{\varpi}_{\mathscr{C}}) \times Im(\pi_{\mathscr{C}}),$ where $\widetilde{\nu_k} \in \mathbb{P}[0, 1]$ and $\gamma_k \in [-1, 0]$, $1 \leq k\leq n$ coincide with this chain.

Proof. Take $\widetilde{\nu_k}$ and $\gamma_k, \; k = 0, 1, ..., n$ such that

and

We can choose $\widetilde{\nu_k} = [0, \frac{1}{1+k}]$ and $\gamma_k = \frac{-1}{1+k}, \; k = 0, 1, ..., n$. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ be a $\mathcal{CCS}$ of $\mathscr{L}$ defined by

We first prove that $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie subalgebra of $\mathscr{L}$. Let $l_1, l_2\in \mathscr{L}$ and $\alpha\in F$. Suppose that $l_1\in \mathscr{H}_{i}-\mathscr{H}_{i-1}$ and $l_2\in \mathscr{H}_{j}-\mathscr{H}_{j-1}$ for some $i, j.$ We may assume that $j \leq i$. Then, we have $l_1, l_2\in \mathscr{H}_{i}$. Thus, $l_1+l_2, \; \alpha l_1, \; [l_1, \; l_2]\in \mathscr{H}_{i}$. It follows that

and

So, $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie subalgebra of $\mathscr{L}$ and all its level sets are Lie algebras, since $Im(\widetilde{\varpi}_{\mathscr{C}}) = \{\widetilde{\nu_0}, \widetilde{\nu_1}, ...\widetilde{\nu_n}\}$ and $Im(\pi_{\mathscr{C}}) = \{\gamma_0, \gamma_1, ...\gamma_n\}$ are level subsets of $\mathscr{C}$ form chains:

and

respectively. We now prove that

Clearly, $\mathscr{H}_k \subseteq \Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu_k}\Big)$ and $\mathscr{H}_k \subseteq \Upsilon \Big(\pi_{\mathscr{C}}; \gamma_k\Big)$. If $l\in \Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu_k}\Big),$ then $\widetilde{\varpi}_{\mathscr{C}}(l)\succeq\widetilde{\nu_k}$ and so $\widetilde{\varpi}_{\mathscr{C}}(l) = \widetilde{\nu_i}$ for some $i\leq k$. Thus, $l\in \mathscr{H}_i$. Since $\mathscr{H}_i\subseteq \mathscr{H}_k$, it follows that $l\in \mathscr{H}_k$. Consequently, $\mathscr{H}_k = \Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu_k}\Big)$. The proof of $\Upsilon \Big(\pi_{\mathscr{C}}; \gamma\Big)$ is similar. □

Definition 3.7. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CCS}s$ on $\mathscr{L}.$ If $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ relation on $\mathscr{L}$, then $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is called a $\mathcal{CC}$ relation on $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ if $\widetilde{\varpi}_{\mathscr{C}}(l_1, l_2)\preceq \widetilde{min}\{\widetilde{\varpi}_{\mathscr{D}}(l_1), \widetilde{\varpi}_{\mathscr{D}}(l_2)\}$ and $\widetilde{\pi}_{\mathscr{C}}(l_1, l_2)\geq max\{\widetilde{\pi}_{\mathscr{D}}(l_1), \widetilde{\pi}_{\mathscr{D}}(l_2)\}$ for all $l_1, l_2 \in \mathscr{L}.$

Definition 3.8. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CCS}s$ on $\mathscr{L}.$ Then, the generalized Cartesian product $\mathscr{C} \times \mathscr{D}$ is presented as:

where $(\widetilde{\varpi}_{\mathscr{C}} \times \widetilde{\varpi}_{\mathscr{D}})(l_1, l_2) = \widetilde{min}\{\widetilde{\varpi}_{\mathscr{C}}(l_1), \widetilde{\varpi}_{\mathscr{D}}(l_2)\}$ and $(\pi_{\mathscr{C}} \times \pi_{\mathscr{D}})(l_1, l_2) = max\{\widetilde{\pi}_{\mathscr{C}}(l_1), \widetilde{\pi}_{\mathscr{D}}(l_2)\}$ for all $(l_1, l_2) \in \mathscr{L} \times \mathscr{L}.$ It is clear that the generalized Cartesian product $\mathscr{C} \times \mathscr{D}$ is always a $\mathcal{CC}$ structure on $\mathscr{L} \times \mathscr{L}.$

The proof of the next theorem is trivial, so it is omitted.

Theorem 3.9. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CCS}s$ on $\mathscr{L}.$ Then,

(1) $\mathscr{C} \times \mathscr{D}$ is a $\mathcal{CC}$ relation on $\mathscr{L}.$

(2) $\Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}} \times \widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}\Big) = \Upsilon \Big(\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}\Big) \times \Upsilon \Big(\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}\Big) \ and\ \Upsilon \Big(\pi_{\mathscr{C}} \times \pi_{\mathscr{D}}; \gamma\Big) = \Upsilon \Big(\pi_{\mathscr{C}}; \gamma\Big) \times \Upsilon \Big(\pi_{\mathscr{D}}; \gamma\Big)$

$\forall \widetilde{\nu} \in \mathbb{P}[0, 1],$ $\gamma \in [-1, 0].$

Theorem 3.10. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CC}$ Lie subalgebras on $\mathscr{L}.$ Then, $\mathscr{C} \times \mathscr{D}$ is a $\mathcal{CC}$ Lie subalgebra on $\mathscr{L}\times \mathscr{L}.$

Proof. Let $l = (l_1, l_2), n = (n_1, n_2)\in \mathscr{L} \times \mathscr{L}.$ Then,

Also,

and

Hence, $\mathscr{C} \times \mathscr{D}$ is a $\mathcal{CC}$ Lie subalgebra on $\mathscr{L}\times \mathscr{L}.$ □

Definition 3.11. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CC}$ Lie ideals of $\mathscr{L}.$ Then, $\mathscr{C}$ is the same type of $\mathscr{D}$ if $\mathscr{C} = \mathscr{D} \circ \Psi$ for some $\Psi \in Aut{\mathscr{L}},$ i.e., $\widetilde{\varpi}_{\mathscr{C}}(l) = \widetilde{\varpi}_{\mathscr{D}}(\Psi(l))$ and $\pi_{\mathscr{C}}(l) = \pi_{\mathscr{C}}(\Psi(l))$ for all $l\in \mathscr{L}.$

Theorem 3.12. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CC}$ Lie ideals of $\mathscr{L}.$ Then, $\mathscr{C}$ is isomorphic to $\mathscr{D}$ if and only if $\mathscr{C}$ is a $\mathcal{CC}$ Lie ideal having the same type of $\mathscr{D}.$

Proof. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CC}$ Lie ideals of $\mathscr{L}.$ If $\mathscr{C}$ is isomorphic to $\mathscr{D},$ then clearly $\mathscr{C}$ is a crossing Lie ideal having the same type of $\mathscr{D}.$ Now, suppose that $\mathscr{C}$ is a crossing Lie ideal having the same type of $\mathscr{D}.$ Then, $\exists \Psi \in Aut({\mathscr{L}})$ such that

for any $l_1 \in \mathscr{L}.$ Let $\Omega: \mathscr{C}(\mathscr{L})\rightarrow \mathscr{D}(\mathscr{L})$ be a map presented by:

for any $l_1 \in \mathscr{L}.$ That is,

for any $l_1 \in \mathscr{L}.$ Then, it is obvious that $\Omega$ is surjective. Since $\Omega(\widetilde{\varpi}_{\mathscr{C}}(l_1)) = \Omega(\widetilde{\varpi}_{\mathscr{C}}(l_2)$ for any $l_1, l_2 \in \mathscr{L},$ then $\widetilde{\varpi}_{\mathscr{D}}(\Psi(l_1)) = \widetilde{\varpi}_{\mathscr{D}}(\Psi(l_2))$ and therefore $\widetilde{\varpi}_{\mathscr{C}}(l_1) = \widetilde{\varpi}_{\mathscr{C}}(l_2).$ Similarly, $\Omega(\pi_{\mathscr{C}}(l_1)) = \Omega(\pi_{\mathscr{C}}(\Psi(l_2)))$ for any $l_1, l_2 \in \mathscr{L},$ then $\widetilde{\varpi}_{\mathscr{D}}(\Psi(l_1)) = \pi_{\mathscr{D}}(\Psi(l_2))$ and therefore $\pi_{\mathscr{C}}(l_1) = \pi_{\mathscr{C}}(l_2).$ Now, for any $l_1, l_2 \in \mathscr{L},$ we have

and

Similarly,

and

Therefore, $\Omega$ is a homomorphism. Thus, $\mathscr{C}$ is isomorphic to $\mathscr{D}.$ □

Theorem 3.13. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be a $\mathcal{CC}$ Lie ideals of $\mathscr{L}.$ If $\mathscr{C}$ is s $\mathcal{CC}$ Lie ideal having the same type of $\mathscr{D},$ then $\Psi \in Aut(\mathscr{L})$ such that $\widetilde{\varpi}_{\mathscr{C}} \circ \Psi = \widetilde{\varpi}_{\mathscr{D}}$ and $\pi_{\mathscr{C}} \circ \Psi = \pi_{\mathscr{D}}.$

Proof. The proof is obvious from the Definition 3.11. □

Definition 3.14 Let $\Psi: \mathscr{L}_1 \rightarrow \mathscr{L}_2$ be a homomorphism Lie algebras. For any $\mathcal{CC}$ structure $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ on $\mathscr{L}_2,$ we present a $\mathcal{CC}$ structure $\mathscr{C}^{\Psi} = \langle \widetilde{\varpi}_{\mathscr{C}}^{\Psi}, \pi_{\mathscr{C}}^{\Psi} \rangle$ on $\mathscr{L}_1,$ where $\mathscr{C}^{\Psi}(l) = \mathscr{C}(\Psi(l))$ for any $l \in \mathscr{L}_1.$ That is, $\widetilde{\varpi}_{\mathscr{C}}^{\Psi}(l) = \widetilde{\varpi}_{\mathscr{C}}(\Psi(l))$ and $\pi_{\mathscr{C}}^{\Psi}(l) = \pi_{\mathscr{C}}(\Psi(l))$ for any $l \in \mathscr{L}_1.$

Theorem 3.15. Let $\Psi: \mathscr{L}_1 \rightarrow \mathscr{L}_2$ be a homomorphism Lie algebras. If $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L}_2,$ then $\mathscr{C}^{\Psi} = \langle \widetilde{\varpi}_{\mathscr{C}}^{\Psi}, \pi_{\mathscr{C}}^{\Psi} \rangle$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L}_1.$

Proof. Let $l_1, l_2 \in \mathscr{L}_1$ and $\alpha \in {F}.$ Then,

and

Similarly, $\pi_{\mathscr{C}}^{\Psi}(l_1 + l_2)\leq max\{\pi_{\mathscr{C}}^{\Psi}(l_1), \pi_{\mathscr{C}}^{\Psi}(l_2))\},$ $\pi_{\mathscr{C}}^{\Psi}(\alpha l_2) \leq \pi_{\mathscr{C}}^{\Psi}(l_1)$ and $\widetilde{\varpi}_{\mathscr{C}}^{\Psi}([l_1 + l_2])\leq \widetilde{\varpi}_{\mathscr{C}}^{\Psi}(l_1).$ Thus, $\mathscr{C}^{\Psi} = \langle \widetilde{\varpi}_{\mathscr{C}}^{\Psi}, \pi_{\mathscr{C}}^{\Psi} \rangle$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L}_1.$ □

Theorem 3.16. Let $\Psi: \mathscr{L}_1 \rightarrow \mathscr{L}_2$ be an epimorphism of Lie algebras. If $\mathscr{C}^{\Psi} = \langle \widetilde{\varpi}_{\mathscr{C}}^{\Psi}, \pi_{\mathscr{C}}^{\Psi} \rangle$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L}_1,$ then $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L}_2.$

Proof. Since $\Psi$ is surjective, then for any $l_1, l_2 \in \mathscr{L}_2,$ there are $n_1, n_2 \in \mathscr{L}_2$ such that $l_1 = \Psi(n_1)$ and $l_2 = \Psi(n_2).$ Hence, $\widetilde{\varpi}_{\mathscr{C}}(l_1) = \widetilde{\varpi}_{\mathscr{C}}^{\Psi} (n_1),$ $\widetilde{\varpi}_{\mathscr{C}}(l_2) = \widetilde{\varpi}_{\mathscr{C}}^{\Psi} (n_2),$ $\pi_{\mathscr{C}}(l_1) = \pi_{\mathscr{C}}^{\Psi} (n_1)$ and $\pi_{\mathscr{C}}(l_2) = \pi_{\mathscr{C}}^{\Psi} (n_2).$ Now,

and

Similarly, $\pi_{\mathscr{C}}(l_1 + l_2)\leq max\{\pi_{\mathscr{C}}(l_1), \pi_{\mathscr{C}}(l_2)\},$ $\pi_{\mathscr{C}}(\alpha l_1) \leq \pi_{\mathscr{C}}(l_1)$ and $\pi_{\mathscr{C}}([l_1 + l_2])\leq \pi_{\mathscr{C}}(l_1).$ Thus, $\mathscr{C}^{\Psi} = \langle \widetilde{\varpi}_{\mathscr{C}}^{\Psi}, \pi_{\mathscr{C}}^{\Psi} \rangle$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L}_1.$ □

In Theorems 3.17–3.20 below, let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CC}$ Lie ideals of $\mathscr{L}.$

Theorem 3.17. If $\widetilde{\varpi}_{\mathscr{C}} \circ \Psi = \widetilde{\varpi}_{\mathscr{D}}$ and $\pi_{\mathscr{C}} \circ \Psi = \pi_{\mathscr{D}}$ for some $\Psi \in Aut(\mathscr{L}),$ then $g(\widetilde{\varpi}_{\mathscr{C}}) = \widetilde{\varpi}_{\mathscr{D}}$ and $g(\pi_{\mathscr{C}}) = \pi_{\mathscr{D}}.$

Proof. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be $\mathcal{CC}$ Lie ideals of $\mathscr{L}.$ Assume that $\exists \Psi \in Aut(\mathscr{L})$ such that $\widetilde{\varpi}_{\mathscr{C}} \circ \Psi = \widetilde{\varpi}_{\mathscr{D}}$ and $\pi_{\mathscr{C}} \circ \Psi = \pi_{\mathscr{D}},$ then $\widetilde{\varpi}_{\mathscr{C}}(\Psi(l_1)) = \widetilde{\varpi}_{\mathscr{D}}(l_1)$ and $\pi_{\mathscr{C}}(\Psi(l_1)) = \pi_{\mathscr{D}}(l_1).$ Thus,

and

for all $l_1 \in \mathscr{L}.$ If $g = \Psi^{-1},$ then $g\in Aut({\mathscr{L}}),$ therefore $g(\widetilde{\varpi}_{\mathscr{C}}) = \widetilde{\varpi}_{\mathscr{D}}$ and $g(\pi_{\mathscr{C}}) = \pi_{\mathscr{D}}.$ □

Theorem 3.18. If $g(\widetilde{\varpi}_{\mathscr{C}}) = \widetilde{\varpi}_{\mathscr{D}}$ and $g(\pi_{\mathscr{C}}) = \pi_{\mathscr{D}}$ for some $g \in Aut(\mathscr{L}),$ then $\exists h \in Aut(\mathscr{L})$ such that $h(\widetilde{\varpi}_{\mathscr{D}}) = \widetilde{\varpi}_{\mathscr{C}}$ and $h(\pi_{\mathscr{D}}) = \pi_{\mathscr{C}}.$

Proof. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CC}$ Lie ideals of $\mathscr{L}.$ Suppose that $g(\widetilde{\varpi}_{\mathscr{C}}) = \widetilde{\varpi}_{\mathscr{D}}$ and $g(\pi_{\mathscr{C}}) = \pi_{\mathscr{D}}$ for some $g \in Aut(\mathscr{L}),$ then

and

Thus,

and

for any $l_1\in \mathscr{L}.$ If $h = g^{-1},$ then $h\in Aut({\mathscr{L}})$ and therefore $h(\widetilde{\varpi}_{\mathscr{D}}) = \widetilde{\varpi}_{\mathscr{C}}$ and $h(\pi_{\mathscr{D}}) = \pi_{\mathscr{C}}.$ □

Theorem 3.19. If $h(\widetilde{\varpi}_{\mathscr{D}}) = \widetilde{\varpi}_{\mathscr{C}}$ and $h(\pi_{\mathscr{D}}) = \pi_{\mathscr{C}}$ for some $h \in Aut(\mathscr{L}),$ then $\Upsilon (\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}) = h(\Upsilon (\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}))$ and $\Upsilon (\pi_{\mathscr{C}}; \gamma) = h(\Upsilon (\pi_{\mathscr{D}}; \gamma))$ for all $\widetilde{\nu} \in \mathbb{P}[0, 1]$ and $\gamma \in [-1, 0].$

Proof. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be a $\mathcal{CC}$ Lie ideals of $\mathscr{L}.$ Suppose that $h(\widetilde{\varpi}_{\mathscr{D}}) = \widetilde{\varpi}_{\mathscr{C}}$ and $h(\pi_{\mathscr{D}}) = \pi_{\mathscr{C}}$ for some $h \in Aut(\mathscr{L}),$ then

and

for any $l_1 \in \mathscr{L}.$ Now, let $\widetilde{\nu} \in \mathbb{D}[0, 1]$ and $\gamma \in [-1, 0].$ If $l_1 \in \Upsilon (\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}) \cap \Upsilon (\pi_{\mathscr{C}}; \gamma),$ then

and

which implies that $h^{-1}(l_1) \in \Upsilon (\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}) \cap \Upsilon (\pi_{\mathscr{D}}; \gamma),$ i.e., $x \in h(\Upsilon (\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}) \cap \Upsilon (\pi_{\mathscr{D}}; \gamma)).$ Hence, $\Upsilon (\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}) \subseteq h(\Upsilon (\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}))$ and $\Upsilon (\pi_{\mathscr{C}}; \gamma) \subseteq h(\Upsilon (\pi_{\mathscr{D}}; \gamma)).$ Now, let $l_1 \in h(\Upsilon (\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}))\cap h(\Upsilon (\pi_{\mathscr{D}}; \gamma)).$ Then, $h^{-1}(l_1) \in h(\Upsilon (\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}))\cap h(\Upsilon (\pi_{\mathscr{D}}; \gamma)).$ Therefore,

and

It follows that $l_1 \in \Upsilon (\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}) \cap \Upsilon (\pi_{\mathscr{C}}; \gamma).$ Hence, $h(\Upsilon (\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}))\subseteq \Upsilon (\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu})$ and $h(\Upsilon (\pi_{\mathscr{C}}; \gamma)) \subseteq \Upsilon (\pi_{\mathscr{C}}; \gamma).$ Thus, $\Upsilon (\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}) = h(\Upsilon (\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}))$ and $\Upsilon (\pi_{\mathscr{C}}; \gamma) = h(\Upsilon (\pi_{\mathscr{C}}; \gamma))$ for all $\widetilde{\nu} \in \mathbb{P}[0, 1]$ and $\gamma \in [-1, 0].$ □

Theorem 3.20. If $\exists h\in Aut{\mathscr{L}}$ such that $\Upsilon (\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}) = h(\Upsilon (\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}))$ and $\Upsilon (\pi_{\mathscr{C}}; \gamma) = h(\Upsilon (\pi_{\mathscr{C}}; \gamma))$ for all $(\widetilde{\nu}, \gamma) \in \mathbb{P}[0, 1]\times [-1, 0],$ then $\mathscr{C}$ is s crossing structure having the same type of $\mathscr{D}.$

Proof. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CC}$ Lie ideals of $\mathscr{L}.$ Assume that $\exists h \in Aut{\mathscr{L}}$ such that $\Upsilon (\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}) = h(\Upsilon (\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu}))$ and $\Upsilon (\pi_{\mathscr{C}}; \gamma) = h(\Upsilon (\pi_{\mathscr{C}}; \gamma))$ for all $(\widetilde{\nu}, \gamma) \in \mathbb{P}[0, 1]\times [-1, 0].$ Let $\widetilde{\varpi}_{\mathscr{D}}(\mathscr{L}^{-1}(l_1)) = \widetilde{\nu}$ and $\omega_{\mathscr{D}}(\mathscr{L}^{-1}(l_1)) = \gamma.$ Then, $h^{-1}(l_1) \in \Upsilon (\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}) \cap \Upsilon (\pi_{\mathscr{D}}; \gamma).$ Hence, $l_1 \in h(\Upsilon (\widetilde{\varpi}_{\mathscr{D}}; \widetilde{\nu})) \cap h(\Upsilon (\pi_{\mathscr{D}}; \gamma)) = \Upsilon (\widetilde{\varpi}_{\mathscr{C}}; \widetilde{\nu}) \cap \Upsilon (\pi_{\mathscr{C}}; \gamma).$ Thus, $\widetilde{\varpi}_{\mathscr{C}}(l_1) \succeq \widetilde{\nu} = \widetilde{\varpi}_{\mathscr{D}}(h^{-1}(l_1))$ and $\omega_{\mathscr{C}}(l_1) \leq \gamma = \widetilde{\varpi}_{\mathscr{D}}(h^{-1}(l_1))$ for all $l_1 \in \mathscr{L}.$ Therefore, $\mathscr{C}$ is s crossing structure having the same type of $\mathscr{D}.$ □

4.   Crossing cubic quotient Lie algebras

Here, we give a construction of a quotient Lie algebra via $\mathcal{CC}$ Lie ideal $\mathscr{L}.$ Then, we present the $\mathcal{CC}$ isomorphism theorems.

Theorem 4.1. Let $\mathscr{I}$ be a Lie ideal of $\mathscr{L}.$ If $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L},$ then a $\mathcal{CCS}$ $\overline{\mathscr{C}} = \langle \overline{\widetilde{\varpi}_{\mathscr{C}}}, \overline{\pi_{\mathscr{C}}} \rangle$ is a $\mathcal{CC}$ Lie ideal of the quotient Lie algebra $\mathscr{L}/\mathscr{I},$ where $\overline{\widetilde{\varpi}_{\mathscr{C}}} = \sup_{k\in \mathscr{I}}(l_1 + k)$ and $\overline{\pi_{\mathscr{C}}} = \inf_{k \in \mathscr{I}}(l_1 + k).$

Proof. Straightforward, $\overline{\mathscr{C}}$ is well defined. Let $(l_1 + \mathscr{I}), (l_2 + \mathscr{I}) \in \mathscr{L}/\mathscr{I},$ then

and

Also,

and

Hence, $\overline{\mathscr{C}}$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L}/\mathscr{I}.$ □

Theorem 4.2. Let $\Psi: \mathscr{L_1} \rightarrow \mathscr{L_2}$ be an epimorphism of a Lie algebra $\mathscr{L_1}$ onto a Lie algebra $\mathscr{L_2}.$ Then, the following statements hold:

(i) If $\mathscr{C}$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L_1},$ then $\Psi(\mathscr{C})$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L_2}.$

(ii) If $\mathscr{D}$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L_2},$ then $\Psi^{-1}(\mathscr{D})$ is a $\mathcal{CC}$ Lie ideal of $\mathscr{L_1}.$

Proof. Straightforward. □

An equivalence relation $\bowtie$ in Theorem 3.5 is a congruence relation. To verify that $\bowtie$ is a congruence relation on $\mathscr{L}.$ Let $l_1 \bowtie l_2$ and $l_2 \bowtie l_3$, then $\widetilde{\varpi}_{\mathscr{C}}(l_1 - l_2) = \widetilde{\varpi}_{\mathscr{C}}(0), \widetilde{\varpi}_{\mathscr{C}}(l_2 - l_3) = \widetilde{\varpi}_{\mathscr{C}}(0), \pi_{\mathscr{C}}(l_1- l_2) = \pi_{\mathscr{C}}(0) \text{ and }\pi_{\mathscr{C}}(l_2- l_3) = \pi_{\mathscr{C}}(0).$ Now, let $n_1, n_2, m_1, m_2 \in \mathscr{L},$ we have

Also,

That is, $n_1 + n_2 \bowtie m_1 + m_2, \alpha n_1 \bowtie \alpha m_1$ and $[n_1, n_2] \bowtie [m_1, m_2].$ Thus, $\bowtie$ is a congruence relation on $\mathscr{L}.$

The set of all equivalence classes $\mathscr{C}[\mathscr{L_1}]$ is denoted by $\mathscr{L}/\mathscr{C}.$ It is a Lie algebra under the following operations:

Next, we present the $\mathcal{CC}$ isomorphism theorems over Lie algebras.

Theorem 4.3. Let $\Psi: \mathscr{L_1} \rightarrow \mathscr{L^{'}}$ be an epimorphism, where $\mathscr{L}$ and $\mathscr{L^{'}}$ are Lie algebras. If $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ is a $\mathcal{CC}$ Lie ideal in $\mathscr{L^{'}},$ then $\mathscr{L}/\Psi^{-1}(\mathscr{C}) \cong \mathscr{L^{'}}/\mathscr{C}.$

Proof. Define $\Omega: \mathscr{L}/\Psi^{-1}(\mathscr{C}) \rightarrow \mathscr{L^{'}}/\mathscr{C}$ as:

$\forall l\in \mathscr{L}$ and for any collection of the $\mathcal{CCS}s$ of $\mathscr{L^{'}}.$ Hence, $\Omega$ is an isomorphism. □

Theorem 4.4. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CC}$ Lie ideals in $\mathscr{L},$ with $\widetilde{\varpi}_{\mathscr{C}}(0) = \widetilde{\varpi}_{\mathscr{D}}(0)$ and $\pi_{\mathscr{C}}(0) = \pi_{\mathscr{D}}(0).$ Then, $(\mathscr{L}_{\mathscr{C}} + \mathscr{L}_{\mathscr{D}}) /\mathscr{D} \cong \mathscr{L}_{\mathscr{C}}/(\mathscr{C}\cap \mathscr{D}).$

Proof. Clearly, $\mathscr{L}_{\mathscr{C}} + \mathscr{L}_{\mathscr{D}}$ and $\mathscr{L}_{\mathscr{C}}/(\mathscr{C}\cap \mathscr{D})$ are $\mathcal{CC}$ Lie ideals in $\mathscr{L}.$ For every $l\in (\mathscr{L}_{\mathscr{C}} + \mathscr{L}_{\mathscr{D}}), l = a+b,$ where $a\in \mathscr{L}_{\mathscr{C}}$ and $b \in \mathscr{L}_{\mathscr{D}}.$ Let $\mathscr{C}$ and $\mathscr{D}$ have a congruence relation $\propto$ on $\mathscr{L},$ defined as:

for all $\mathscr{C}$ and $\mathscr{D}$. Define $\Omega: (\mathscr{L}_{\mathscr{C}} + \mathscr{L}_{\mathscr{D}}) /\mathscr{D} \rightarrow \mathscr{L}_{\mathscr{C}}/(\mathscr{C}\cap \mathscr{D})$ as:

and

Then, $\Omega$ is an isomorphism. □

Theorem 4.5. Let $\mathscr{C} = \langle \widetilde{\varpi}_{\mathscr{C}}, \pi_{\mathscr{C}} \rangle$ and $\mathscr{D} = \langle \widetilde{\varpi}_{\mathscr{D}}, \pi_{\mathscr{D}} \rangle$ be two $\mathcal{CC}$ Lie ideals in $\mathscr{L},$ with $\widetilde{\varpi}_{\mathscr{C}}(0) = \widetilde{\varpi}_{\mathscr{D}}(0),$ $\pi_{\mathscr{C}}(0) = \pi_{\mathscr{D}}(0)$ and $\mathscr{C} \subseteq \mathscr{D}.$ Then, $(\mathscr{L}/\mathscr{C})/ (\mathscr{L}_{\mathscr{D}})/\mathscr{C}) \cong \mathscr{L}/(\mathscr{D}.$

Proof. Clearly, $(\mathscr{L}/\mathscr{C})/ (\mathscr{L}_{\mathscr{D}})/\mathscr{C})$ is a $\mathcal{CC}$ Lie ideal over $\mathscr{L}.$ Define

as:

$\forall l \in \mathscr{L}.$ Then, the proof is straightforward. □

5.   Conclusions

As discussed earlier, the $\mathcal{CC}$ structure is a parallel concept between interval-valued and negative versions of fuzziness structures. The idea of the $\mathcal{CC}$ structure is an extension of the fuzziness structure of two polarities (positive and negative). In this paper, we develop the concepts of $\mathcal{CC}$ Lie subalgebras, $\mathcal{CC}$ Lie ideals, and homomorphism. We discussed the Cartesian product of $\mathcal{CC}$ Lie subalgebras. Also, we described some interesting results of $\mathcal{CC}$ Lie ideals. In addition, we provided a construction of a quotient Lie algebra via the $\mathcal{CC}$ Lie ideal in a Lie algebra and presented the $\mathcal{CC}$ isomorphism theorems.

The idea of $\mathcal{CC}$ structure is a topic of great interest, and it is a task to apply this logical concept to problems in theoretical physics, coding theory, and quantum mechanics. Further, the results of this study can be utilized in a variety of algebraic frameworks, for instance Hom-Lie algebras, Hom-Lie bi-algebras, semirings, $\Gamma$-semirings, and QS/UP/KU-algebras.

Author contributions

Anas Al-Masarwah: Conceptualization and Methodology. Nadeen Kdaisat and Majdoleen Abuqamar: Investigation and Writing-original draft. Anas Al-Masarwah and Kholood Alsager: Writing-review and editing. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

The Researchers would like to thank the Deanship of Graduate Studies and Scientific Research at Qassim University for financial support (QU-APC-2024-9/1).

Conflict of interest

The authors declare that they have no competing interests.