Some integral inequalities for harmonical $cr$-$h$-Godunova-Levin stochastic processes

1.   Introduction

Interval analysis offers a variety of practical strategies for working with ambiguous data. This approach can be applied to models with data that are inaccurate because they were collected using unreliable measurement techniques. Interval analysis is a type of set-valued analysis that is used in mathematical analysis and general topology. We can handle interval uncertainty in some deterministic real-world phenomena using this technique. For the first time in numerical analysis, interval analysis was introduced in Moore's acclaimed book the mathematics of numerical analysis, see Ref. ^[1]. There has been the extensive application of interval analysis over the last fifty years in a variety of fields, such as the following: computer graphics^[2], interval differential equation^[3], automatic error analysis^[4], and neural network output optimization^[5], etc.

The concept of convexity is fundamental to many branches of mathematics and science, such as probability theory, economics, optimal control theory, fuzzy analysis, and natural and applied sciences. Furthermore, generalized convexity can also be a powerful tool for solving a variety of nonlinear analysis, applied analysis, and math and physics problems. The optimality conditions of diffeomorphic functions are characterised by variational inequalities, whose origins can be traced back to Euler, Lagrange, and Newton. As a counterpart to the arithmetic means, we have harmonic means. Among other applications, harmonic means are found in electrical circuit theory. By adding up the reciprocals of the individual resistance values of parallel resistors and considering the reciprocal of their combined value, we can obtain the total resistance of the set. In addition, harmonic means are used in parallel algorithms that solve a wide range of issues, see Ref.^[6]. The study of convexity with integral problems is a particularly fascinating field. Integral inequalities have recently proven helpful for both qualitative and quantitative assessments of convexity. In mathematics, the Hermite-Hadamard inequality is well known for being the first geometric interpretation of convex maps. A famous double inequality is defined as follows:

where $\Phi:I\subseteq \mathbf{R}\rightarrow \mathbf{R}$ be a convex function on interval $I$ and $f, g\in\ I$ with $f < g$. This function, which has been improved, generalized, and utilizing h-convexity, covers convexity classes of different sorts, see Refs. ^{[7,8,9,10,11,12,13,14,15,16,17]}. There is a class of convex functions called harmonic convex which were introduced by Anderson et al. ^[18]. Using the harmonic variational inequality, Noor ^[19] has shown that the optimality conditions of the differentiable harmonic convex functions on the harmonic convex set. A number of generalizations of integral inequalities apply to harmonic convex functions with applications across a variety of dimensions, see Refs. ^{[20,21,22,23,24,25,26,27,28]}. Furthermore, stochastic convexity must be understood in order to construct numerical estimates of existing probabilistic quantities, which is crucial in statistics and probability. In the beginning, Nikodem's 1980 work on convex stochastic processes, see Ref. ^[29]. Numerous examples of stochastic convexity applications were provided by Shaked et al. in ^[30]. In 1992, Skowronski revised the authors' earlier findings once more while also introducing some fresh ideas on convex stochastic processes and obtaining some additional findings, see Ref. ^[31]. In 2012, Kotrys extended a well-known double inequality called $\mathcal{H.H}$ inequality to convex stochastic processes, see Ref. ^[32]. In 2015, Nelson Merentes and his co-authors utilized Varoşanec ^[33], concept of h-convexity and updated earlier findings generated by many writers in the context of h-convex stochastic processes. By describing h-convex stochastic processes, they develop $\mathcal{H.H}$, Schur, and Jensen type inequalities in that work, see Ref. ^[34]. These inequalities for convex stochastic processes have undergone some recent developments, see Refs. ^{[35,36,37,38,39,40,41,42]}. Furthermore, Mevlut Tunc and the authors listed in ^[43,44] created inequalities of the Ostrowski type for both h-convexity and h-convex stochastic processes, respectively.

Bhunia ^[45] developed the center-radius order in 2014 based on the radius and midpoints of the interval. Based on the ideas of center-radius order, the following authors created these inequalities for harmonical cr-h-convex and cr-h-Godunova-Levin functions in 2022, see Refs. ^{[46,47,48,49,50,51]}. By providing interesting examples, center-radius order relations about harmonical cr-h-Godunova-Levin functions can provide more precise inequality terms and can be demonstrated to be valid. The application of total order relations to convexity and inequality is therefore crucial for understanding. This order relation is somewhat different to calculate compared to the other order relations used in interval analysis to create inequalities; we can compute it using the midpoint and centre of the interval.

The novelty of the present study is the first time stochastic processes have been used in conjunction with interval analysis; it serves as a starting point for researchers interested in this field. We also observe that by applying this approach, the inequality term derived from the center-radius order relations using stochastic processes provides much more precise results than other partial order relations of this type. In order to verify the validity of our claim, we analyze interesting examples in which the interval difference between the end points is much closer. More importantly, we know that stochastic processes can be applied to interval analysis in many different ways, see Refs. ^{[52,53,54,55,56]}. Researchers examined gradient descent as an optimal method for strongly convex stochastic optimization in ^[57]. When considering terminal wealth with budget constraints, a continuous-time financial portfolio selection model with expected utility maximization boils down to solving a convex stochastic optimization problem, see Ref. ^[58].

Inspired by Refs. ^{[34,43,44,49,51]}. We create various $\mathcal{H.H}$ inequalities in the context of $\mathcal{IVFS}$ by fusing center-radius order relation with harmonic h-$\mathcal{GL}$-convex stochastic process. The study provides several examples in addition to the conclusions.

2.   Backgrounds and preliminaries

As it relates to concepts that have been utilised but not defined, see Refs. ^[7,49]. It will be very helpful if you are familiar with a few fundamental arithmetic ideas related to interval analysis as you process the remaining portions of the article.

and

where ${\delta} \in \mathbf{R}$.

Let $\mathbf{R}_I$ and $\mathbf{R}^+_I$ be the collection of all and positive intervals of $\mathbf{R}$, respectively. The following will discuss several algebraic properties of interval arithmetic.

Let ${\Omega} = [\underline{{\Omega}}, \bar{{\Omega}}] \in \mathbf{R}_{I}$, then ${\Omega}_{c} = \frac{\overline{{\Omega}}+\underline{{\Omega}}}{2}$ and ${\Omega}_{r} = \frac{\overline{{\Omega}}-\underline{{\Omega}}}{2}$ are basically the center and radius of interval ${\Omega}$. A cr form of interval ${\Omega}$ can be expressed as:

The formulas we employ to establish an interval's radius and centre are as follows:

Definition 2.1. (See ^[49]) The cr-order relation for ${\Omega} = [\underline{{\Omega}}, \overline{{\Omega}}] = \langle {\Omega}_{c}, {\Omega}_{r} \rangle$, ${\iota} = [\underline{{\iota}}, \overline{{\iota}}] = \langle {\iota}_{c}, {\iota}_{r} \rangle \in \mathbf{R}_{I}$ represented as (see Figure 1).

For these intervals ${\Omega}, {\iota}\in\mathbf{R}_{I}$, we have either ${\Omega}\preceq_{cr}{\iota}$ or ${\iota}\preceq_{cr}{\Omega}$. Riemann integral for $\mathcal{IVFS}$ are represented as:

Definition 2.2. (See ^[49]) Let $\Theta:[{f}, {g}]$ be an $\mathbf{IVF}$ such that $\Theta = [\underline{\Theta}, \overline{\Theta}]$. Then $\Theta$ is Riemann integrable ($\mathbf{IR}$) on $[{f}, {g}]$ iff $\underline{\Theta}$ and $\overline{\Theta}$ are $\mathbf{IR}$ on $[{f}, {g}],$ that is,

The pack of all $(\mathbf{IR})$ $\mathcal{IVFS}$ on $[{f}, {g}]$ is represented by $\mathbf{IR}_{([{f}, {g}])}$. The pack of all center-radius order $\mathcal{IVFS}$ are denoted by cr-$\mathcal{IVFS}$.

Theorem 2.1. (See ^[49]) Let $\Theta, \Phi:[{f}, {g}]$ be $\mathcal{IVFS}$ given by $\Theta = [\underline{\Theta}, \overline{\Theta}]$ and $\Phi = [\underline{\Phi}, \overline{\Phi}]$. If $\Theta(\mathrm{s})\preceq_{cr}\Phi(\mathrm{s})$, for all $s\in [{f}, {g}]$, then

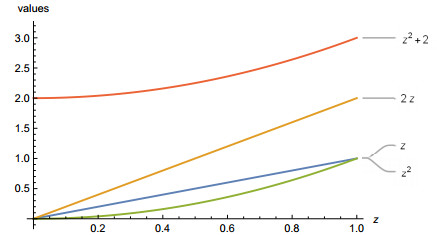
We will now give an example and a few thought-provoking instances to back up the aforementioned theorem (see Figure 2).

Example 2.1. Conider $\Theta = [{z}^{2}, {z}^{2}+2]$ and $\Phi = [z, 2z]$, then, $\forall \; {z}\in[0, 1]$.

From Definition 2.1, we have $\Phi({z})\preceq_{{cr}}\Theta({z})$, $\forall \; {z}\in[0, 1]$.

Since,

and

From Theorem 2.1, we have

Some novel definitions and properties

Definition 2.3. Define $({\Omega}, \mathbb{A}, \mathcal{P})$ be a probability space ($\mathbf{PBS}$). A function $\Phi:\Omega\rightarrow \mathbf{R}$ is said to be random variable if they satisfy the axioms of $\mathbb{A}$-measurable. A function $\Phi:I\times \Omega\rightarrow \mathbf{R}$ where $I\subseteq \mathbf{R}$ is known as stochastic process if, $\forall \; f\in I$ the function $\Phi(f, .)$ is a random variable.

Properties of stochastic process

A stochastic process $\Phi:I\times\Omega\rightarrow \mathbf{R}$ is

● Continuous in interval $I$, if $\forall \; f_o\in I$, we have

where $P-\lim$ represent the limit in probability space.

● Mean square continuous over interval $I$, if $\forall \; f_o\in I$, we have

where $\mathbf{E}\left[\Phi(f, .)\right]$ represent the expectation of random variable $\Phi(f, .)$.

● Mean-square differentiable at some point $f$, if one has random variable $\Phi':I \times \Omega\rightarrow \mathbf{R}$, then this holds

● Mean square integral in interval $I$, if $\forall \; f\in I$, with $\mathbf{E}\left[\Phi(f, .)\right] < \infty$. Let $[f, g]\subseteq I$, $f = s_o < s_1 < s_2... < s_k$ is a partition of $[f, g]$. Consider $\eta_n\in[s_{n-1}, s_n], \, \forall\, n = 1, ..., k$. A random variable $S:\Omega\rightarrow \mathbf{R}$ is mean-square integral of the stochastic process $\Phi$ over interval $[f, g]$, if this holds

In that case, we write it as

Definition 2.4. (See ^[49,51]) Consider $h:[0, 1]\rightarrow \mathbf{{R}^{+}}.$ We say that $\Phi: [f, g] \rightarrow \mathbf{{R}^{+}}$ is called h-convex function, or that $\Phi \in SX($cr-h$, [f, g], \mathbf{{R}^{+}})$, if $\forall \; f_1, g_1\in [f, g]$ and $\delta\in [0, 1],$ we have

In (2.2), if "$\leq$" is replaced with "$\geq$", then it is called $h$-concave function or ${\Phi}\in SV($cr-h$, [f, g], \mathbf{{R}^{+}}).$

Definition 2.5. (See ^[49,51]) Consider $h:(0, 1)\rightarrow \mathbf{{R}^{+}}.$ We say that $\Phi: [f, g] \rightarrow \mathbf{{R}^{+}}$ is called h-$\mathcal{GL}$ function, or that $\Phi \in SGX \; ($cr-h$, [f, g], \mathbf{{R}^{+}})$, if $\forall \; f_1, g_1\in [f, g]$ and $\delta\in [0, 1],$ we have

In (2.3), if "$\leq$" is replaced with "$\geq$", then it is called $h$-$\mathcal{GL}$ concave function or ${\Phi}\in SGV($cr-h$, [f, g], \mathbf{{R}^{+}}).$

Definition 2.6. (See ^[34,51]). Consider $h:[0, 1]\rightarrow \mathbf{{R}^{+}}.$ We say that $\Phi: I\times \Omega \rightarrow \mathbf{{R}^{+}}$ is called h-convex stochastic process, or that $\Phi \in SPX($cr-h$, I, \mathbf{{R}^{+}})$, if $\forall \; f_1, g_1\in I$ and $\delta\in (0, 1),$ we have

In (2.4), if "$\leq$" is replaced with "$\geq$", then it is called $h$-concave stochastic process or ${\Phi}\in SPV($cr-h$, I, \mathbf{{R}^{+}}).$

Definition 2.7. (See ^[34,51]) Consider $h:(0, 1)\rightarrow \mathbf{{R}^{+}}.$ We say that $\Phi: I\times \Omega \rightarrow \mathbf{{R}^{+}}$ is called h-$\mathcal{GL}$ convex stochastic process, or that $\Phi \in SGPX($cr-h$, I, \mathbf{{R}^{+}})$, if $\forall \; f_1, g_1\in I$ and $\delta\in (0, 1),$ we have

In (2.5), if "$\leq$" is replaced with "$\geq$", then it is called $h$-$\mathcal{GL}$-concave stochastic process or ${\Phi}\in SGPV($cr-h$, I, \mathbf{{R}^{+}}).$

Definition 2.8. (See ^[49,51]) Consider $h:[0, 1]\rightarrow \mathbf{{R}^{+}}.$ We say that $\Phi = [\underline{\Phi}, \overline{\Phi}]: [f, g] \rightarrow \mathbf{{R}_{I}^{+}}$ is called cr-h-convex function, or that $\Phi \in SX($cr-h$, [f, g], \mathbf{{R}_{I}^{+}})$, if $\forall \; f_1, g_1\in [f, g]$ and $\delta\in [0, 1],$ we have

In (2.6), if "$\preceq_{cr}$" is replaced with "$\succeq_{cr}$", then it is called cr-$h$-concave function or ${\Phi}\in SV($cr-h$, [f, g], \mathbf{{R}_{I}^{+}}).$

Definition 2.9. (See ^[49,51]) Consider $h:(0, 1)\rightarrow \mathbf{{R}^{+}}.$ We say that $\Phi = [\underline{\Phi}, \overline{\Phi}]: [f, g] \rightarrow \mathbf{{R}_{I}^{+}}$ is called cr-h-$\mathcal{GL}$ convex function, or that $\Phi \in SGX($cr-h$, [f, g], \mathbf{{R}_{I}^{+}})$, if $\forall \; f_1, g_1\in [f, g]$ and $\delta\in (0, 1),$ we have

In (2.7), if "$\preceq_{cr}$" is replaced with "$\succeq_{cr}$", then it is called cr-$h$-$\mathcal{GL}$-concave function or ${\Phi}\in SGV($cr-h$, [f, g], \mathbf{{R}_{I}^{+}}).$

Definition 2.10. (See ^[49,51]). Consider $h:(0, 1)\rightarrow \mathbf{{R}^{+}}.$ We say that $\Phi = [\underline{\Phi}, \overline{\Phi}]: [f, g] \rightarrow \mathbf{{R}_{I}^{+}}$ is called harmonic cr-h-$\mathcal{GL}$ convex function, or that $\Phi \in SGX($cr-h$, [f, g], \mathbf{{R}_{I}^{+}})$, if $\forall \; f_1, g_1\in [f, g]$ and $\delta\in (0, 1),$ we have

In (2.8), if "$\preceq_{cr}$" is replaced with "$\succeq_{cr}$", then it is called harmonic cr-$h$-$\mathcal{GL}$-concave function or ${\Phi}\in SGV($cr-h$, [f, g], \mathbf{{R}_{I}^{+}}).$

Remark 2.1. Geometric interpretation

Now let's take a look at harmonic Godunova-Levin convex functions from a geometric perspective. Consider $f_1, g_1$ from the domain of $\Phi$, and consider the point $\frac{f_1g_1}{\delta f_1+(1-\delta)g_1}$, with $\delta\in (0, 1)$. We will notice that $(1-\delta)\Phi(f_1)+\delta \Phi(g_1)$ gives us the weighted average of $\Phi(f_1)$ and $\Phi(g_1)$, where $\Phi \left(\frac{f_1g_1}{\delta f_1+(1-\delta)g_1}\right)$ gives the output at the point $\frac{f_1g_1}{\delta f_1+(1-\delta)g_1}$. So, for harmonic Godunova-Levin convex function $\Phi$ the value of the function $\Phi$ at $\frac{f_1g_1}{\delta f_1+(1-\delta)g_1}$ whose initial point is $f_1$ and terminal point is $g_1$ is less than or equal to the chord joining the points $\left(f_1, \Phi(f_1)\right)$ and $\left(g_1, \Phi(g_1)\right)$.

Remark 2.2. In comparison with ordinary convex functions, harmonic Godunova-Levin functions behave quite differently and have more properties. For clarity, see the following three examples, which are not convex but are harmonically Godunova-Levin convex on the interval $(0, \infty)$. As a result, we conclude that this is a more generalized and also larger class of convex functions that cover a broader range of functions (see Figure 3).

Now let's introduce the concept for stochastic process for cr-$\mathcal{IVFS}$.

Definition 2.11. (See ^[34,51]) Consider $h:[0, 1]\rightarrow \mathbf{{R}^{+}}.$ We say that stochastic process $\Phi = [\underline{\Phi}, \overline{\Phi}]: I\times\Omega \rightarrow \mathbf{{R}_{I}^{+}}$ where $[f, g]\subseteq I$ is called h-convex stochastic process for cr-$\mathcal{IVFS}$ or that $\Phi \in SPX($cr-h$, [f, g], \mathbf{{R}_{I}^{+}})$, if $\forall \; f_1, g_1\in [f, g]$ and $\delta\in [0, 1],$ we have

In (2.9), if "$\preceq_{cr}$" is replaced with "$\succeq_{cr}$", then it is called h-concave stochastic process for cr-$\mathcal{IVFS}$ or ${\Phi}\in SPV($cr-h$, [f, g], \mathbf{{R}_{I}^{+}}).$

Definition 2.12. (See ^[34,51]) Consider $h:(0, 1)\rightarrow \mathbf{{R}^{+}}.$ We say that stochastic process $\Phi = [\underline{\Phi}, \overline{\Phi}]: I\times\Omega \rightarrow \mathbf{{R}_{I}^{+}}$ where $[f, g]\subseteq I$ is called harmonic h-$\mathcal{GL}$-convex stochastic process for cr-$\mathcal{IVFS}$ or that $\Phi \in SGHPX($cr-h$, [f, g], \mathbf{{R}_{I}^{+}})$, if $\forall \; f_1, g_1\in [f, g]$ and $\delta\in (0, 1),$ we have

In (2.10), if "$\preceq_{cr}$" is replaced with "$\succeq_{cr}$", then it is called harmonic h-$\mathcal{GL}$-concave stochastic process for cr-$\mathcal{IVFS}$ or ${\Phi}\in SGHPV($cr-h$, [f, g], \mathbf{{R}_{I}^{+}}).$

Remark 2.3. (i) If $h = 1$, Definition 2.12 becomes a stochastic process for harmonical-cr-P-function.

(ii) If $h(\delta) = \frac{1}{h(\delta)}$, Definition 2.12 becomes a stochastic process for harmonical-cr-convex function.

(iii) If $h(\delta) = \delta$, Definition 2.12 becomes a stochastic process for harmonical cr-$\mathcal{GL}$ function.

(iv) If $h = {{\delta}^{s}}$, Definition 2.12 becomes a stochastic process for harmonical cr-s-$\mathcal{GL}$ function.

3.   Hermite-Hadamard inequality for harmonical cr-h-$\mathcal{GL}$ stochastic process

This section developed the $\mathcal{H.H}$ inequalities for a harmonically stochastic process for center-radius interval order relation for the class of Godunova-Levin function.

Theorem 3.1. Let ${h}:(0, 1)\rightarrow \mathbf{R}^{+}$ and $h\left(\frac{1}{2}\right)\neq0.$ A function $\Theta:I\times \Omega\rightarrow {\mathbf{R}_I}^{+}$ is h-$\mathcal{GL}$-convex stochastic process as well as mean square integrable for cr-$\mathcal{IVFS}$. For every f, g $\in[f, g]\subseteq I$, $(f < g)$, if $\Theta\in SGHPX(cr$-$h, [f, g], {\mathbf{R}_I}^{+})$ and $\Theta\in\ \mathbf{IR}_{I}.$ Almost everywhere, the following inequality is satisfied

Proof. Since $\Theta\in SGHPX($cr-h$, [f, g], {R_I}^{+})$, we have

With integration over $(0, 1)$, we have

By Definition 2.12, we have

With integration over (0, 1), we have

Accordingly,

Adding (3.2) and (3.3), results are obtained as expected

Remark 3.1. ● If $h(\varrho) = 1$, Theorem 3.1 becomes result for stochastic process harmonically cr- P-function:

● If $h(\varrho) = \frac{1}{\varrho}$, Theorem 3.1 becomes result for stochastic process harmonically cr-convex function:

● If $h(\varrho) = \frac{1}{(\varrho)^s}$, Theorem 3.1 becomes result for stochastic process harmonically cr-s-convex function:

Example 3.1. Let $[f, g] = [1, 2]$, ${h}(\varrho) = \frac{1}{\varrho}$, $\forall \; \varrho\in\ (0, 1). \; \Theta:[f, g]\rightarrow {R_I}^{+}$ is defined as

where

As a result,

This verifies the Theorem 3.1.

Theorem 3.2. Let ${h}:(0, 1)\rightarrow \mathbf{R}^{+}$ and $h\left(\frac{1}{2}\right)\neq0.$ A function $\Theta:I\times \Omega\rightarrow {\mathbf{R}_I}^{+}$ is h-$\mathcal{GL}$-convex stochastic process as well as mean square integrable for cr-$\mathcal{IVFS}$. For every f, g $\in[f, g]\subseteq I$, $(f < g)$, if $\Theta\in SGHPX(cr$-$h, [f, g], {\mathbf{R}_I}^{+})$ and $\Theta\in\mathbf{IR}_{I}.$ Almost everywhere, the following inequality is satisfied

where

Proof. Consider $\left[f, \frac{2fg}{f+g}\right]$, we have

Integration over $(0, 1)$, we have

Similarly for interval $\left[\frac{2fg}{f+g}, g\right]$, we have

Adding inequalities (3.4) and (3.5), we get

Now,

Example 3.2. Let $[f, g] = [1, 2]$, ${h}(\varrho) = \frac{1}{\varrho}$, $\forall \; \varrho\in\ (0, 1). \; \Theta:[f, g]\rightarrow {R_I}^{+}$ is defined as

where

Thus, we obtain

This verify the the Theorem 3.2.

Theorem 3.3. Let ${h_1, h_2}:(0, 1)\rightarrow \mathbf{R}^{+}$ and $h_1, h_2\neq0.$ A functions $\Theta, \Phi:I\times \Omega\rightarrow {\mathbf{R}_I}^{+}$ are harmonic h-Godunova-Levin stochastic process as well as mean square integrable for cr-$\mathcal{IVFS}$. For every f, g $\in I$, $(f < g)$, if $\Theta\in SGHPX(cr$-$h_1, [f, g], {\mathbf{R}_I}^{+})$, $\Phi\in SGHPX(cr$-h$_2, [f, g], {\mathbf{R}_I}^{+})$ and $\Theta, \Phi\in\mathbf{IR}_{I}.$ Almost everywhere, the following inequality is satisfied

where

Proof. Conider $\Theta\in SGHPX(cr$-$h_1, [f, g], {R_I}^{+})$, $\Phi\in SGHPX(cr$-$h_2, [f, g], {R_I}^{+})$ then, we have

Then,

Integration over (0, 1), we have

It follows that

Theorem is proved.

Example 3.3. Let $[f, g] = [1, 2]$, ${h_1}(\varrho) = {h_2}(\varrho) = \frac{1}{\varrho}$, $\forall \; \varrho\in\ (0, 1)$. $\Theta, \Phi:[f, g]\rightarrow {R_I}^{+}$ be defined as

Then,

It follows that

This verifies the Theorem 3.3.

Theorem 3.4. Let ${h_1, h_2}:(0, 1)\rightarrow \mathbf{R}^{+}$ and $h_1, h_2\neq0.$ A functions $\Theta, \Phi:I\times \Omega\rightarrow {\mathbf{R}_I}^{+}$ are harmonic h-Godunova-Levin stochastic process as well as mean square integrable for cr-$\mathcal{IVFS}$. For every f, g $\in I$, $(f < g)$, if $\Theta\in SGHPX(cr$-$h_1, I, {\mathbf{R}_I}^{+})$, $\Phi\in SGHPX(cr$-$h_2, I, {\mathbf{R}_I}^{+})$ and $\Theta, \Phi\in\mathbf{IR}_{I}.$ Almost everywhere, the following inequality is satisfied

Proof. Since $\Theta\in SGHPX(cr$-$h_1, [f, g], {R_I}^{+})$, $\Phi\in SGHPX(cr$-$h_2, [f, g], {R_I}^{+})$, we have

Then,

Integration over $(0, 1)$, we have

Multiply both sides by $\frac{h_1\left(\frac{1}{2}\right)h_2\left(\frac{1}{2}\right)}{2}$ above equation, we get required result

Example 3.4. Recall the Example 3.3, we have

It follows that

This verifies the Theorem 3.4.

4.   Conclusions

This paper introduces a center-radius order relation for $\mathcal{IVFS}$ by using harmonic-Godunova-Levin stochastic processes in the setting of $\mathcal{IVFS}$. Using these ideas, we created some variants of $\mathcal{H.H}$ inequalities. The fact that inequality terms derived from this order relation produce precise results is one of its distinguishing features. Furthermore, in this article, we generalise the findings of the following authors ^[34,49,51], which is a novel approach for future research. Furthermore, the study provides interesting examples to demonstrate the validity of theorems. These ideas can be used to push convex optimization to new heights. This concept should be useful to scientists working in a variety of fields. Future research may investigate the use of different integral operators for determining equivalent inequalities.

Acknowledgments

We would like to thank the reviewers for their valuable comments and suggestions, which helped us to improve the quality of the manuscript.

This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).

Conflict of interest

The authors declare that there is no conflict of interest in publishing this paper.