Generalized first-order second-moment method for uncertain random structures

1.   Introduction

Structural reliability, which reflects the level of use safety and potential risk of the structure, is one of the most important properties of structural systems ^[1,2]. In this sense, a precise assessment of structural reliability plays a vital role in structural design and analysis ^[3,4,5]. Since the structure usually involves uncertain environments, a key issue in the structural reliability assessment is to reasonably quantify the various uncertainties.

In most practical situations, aleatory uncertainty and epistemic uncertainty simultaneously influence structures. Among them, aleatory uncertainty refers to the inherent randomness of the physical world, while epistemic uncertainty refers to the uncertainty coming from the lack of knowledge about the structure ^[6,7]. For example, the geometric parameters of link mechanism would exhibit dispersion because of the manufacturing tolerances, reflecting the effect of aleatory uncertainty. The epistemic uncertainty of a link mechanism might be reflected in insufficient knowledge of material characters due to new material applications, or unclear load parameters due to unknown use scenarios. In existing literature, most of the current reliability assessment methods focus only on a single type of uncertainty, and there is a lack of research on the structural reliability assessment with hybrid uncertainties. Faced with this demand, this paper will propose a new structural reliability method for the structures influenced by both aleatory uncertainty and epistemic uncertainty.

Intuitively, quantification of single type of uncertainty is the necessary basis for the study of quantification of hybrid uncertainties. In the past few decades, the structural reliability assessment method subject to aleatory uncertainty has been well studied, which is also called limit state probability analysis method. In this method, probability theory is used to quantify the uncertainty, and structural parameters are expressed as random variables. Reliability R is represented by taking integral over all basic variables in the safe domain ^[8]. Under this definition, calculating reliability directly is often difficult because multiple integral operation is quite complex and the computing resource of Monte Carlo method is often too enormous to be accepted ^[9]. Therefore, a first-order second-moment (FOSM) method was proposed to overcome these difficulties in reliability calculation ^[10,11,12]. Through representing basic variables by their first two moments, FOSM method obviates the multiple integral operation utilizing the properties of the normal distribution and characterizes structural reliability approximatively using Cornell reliability index $\beta$. Due to its convenience and effectiveness, FOSM method has been widely applied to structural reliability assessment ^[13,14,15].

Although probability theory is thought to be the best mathematical tool for aleatory uncertainty, it cannot handle epistemic uncertainty very well, especially when the collected data is real limited ^[7,16]. Therefore, some non-probabilistic mathematical methods are introduced into structural reliability assessment with epistemic uncertainty. Cremona and Gao applied possibility measure to the structural reliability assessment ^[17]. Ben-Haim and Elishakoff used interval variables to describe basic variables, and proposed a convex model for structural reliability assessment ^[18]. Bae et al. proposed a reliability analysis method based on evidence theory ^[19]. Recently, many researchers have introduced uncertainty theory to deal with epistemic uncertainty in reliability assessment. Zeng et al. established a series of reliability metrics and indexes to characterize systems' reliability from different aspects ^[20]. Wang et al. presented a reliability index as the ratio of expected value to standard deviation based on uncertain measure, and showed its effectiveness as a representation of structural reliability ^[21]. As stated by Kang et al., the possibility measure may cause counter-intuitive results since the sum of reliability and unreliability is not 1, and the interval-based methods (convex model and evidence theory-based model) may exhibit interval extension problems. Therefore, uncertainty theory is viewed as a more reasonable mathematical theory to model epistemic uncertainty in reliability fields ^[7] and this paper will adopt uncertainty theory to describe the effect of epistemic uncertainty.

The above review indicates that in the problem of structural reliability assessment, probability theory and uncertainty theory are utilized as the mathematical tools for uncertainty quantifications. To handle the hybrid conditions with both aleatory and epistemic uncertainties, chance measure, which is defined as a mixture of probability measure and uncertain measure, is further adopted ^[22]. Till now, the chance theory has been applied to a wide range of fields ^[23,24,25], demonstrating its effectiveness in dealing with hybrid uncertainties. The application of chance theory in structural reliability is still in its infancy. Zhang et al. tried to propose a reliability assessment method for hybrid uncertainties by defining a new reliability index based on chance measure ^[26]. They defined this hybrid reliability index as the form of the ratio of expected value and standard deviation of limit state function just like Cornell reliability index. However, they failed to present an available general calculation methodology for arbitrary structural limit state functions because multiple integral operation is still not obviated in calculation. Thus, this method has strong limitations in engineering. How to assess structural reliability under hybrid uncertainties in a feasible way remains a problem to be solved.

For convenience, since the two types of uncertainties are described with "random" variables and "uncertain" variables, respectively, and the epistemic uncertainty is a newly considered elements with great importance, in this paper, the structures influenced by hybrid uncertainties are called the "uncertain random structures". Random structures and uncertain structures are two special cases of the uncertain random structures, which refer to structures only influenced by single aleatory or epistemic uncertainty, respectively. For the reliability of uncertain random structures, this paper will establish a systematic and effective reliability assessment method on the basis of chance theory. A hybrid reliability index will be first presented, which is proved to have good properties assuring feasibility and effectiveness. Further, a general calculation method of the new hybrid reliability index will be developed by utilizing the first two moments of basic variables and first-order Taylor expansion. Therefore, this paper names the new method as generalized first-order second-moment (GFOSM) method. The new method provides a feasible way to assess reliability rapidly for arbitrary uncertain random structures.

The remainder of this paper is organized as follows. Detailed introduction of the new hybrid reliability index and GFOSM method will be presented in Section 2. Two numerical applications will be studied utilizing the GFOSM method in Section 3. In addition, some fundamental definitions and theorems will be given in the appendix, which is the important mathematical foundation of the method presented in this paper.

2.   Generalized first-order second-moment method

As elaborated before, practical structures are usually influenced by both aleatory uncertainty and epistemic uncertainty. For uncertain random structures, this section will propose a new hybrid reliability index based on chance theory (see its introduction in Appendix A) and construct a generalized first-order second-moment (GFOSM) method to analyze and calculate this index. Some good properties of this index are also pointed out via theorems and proofs.

2.1.   Hybrid reliability index for uncertain random structures

The calculation of reliability inevitably faces the problem of large-scale computation. Thus, a new reliability index is needed to characterize the reliability of uncertain random structures efficiently. To better provide a reliability index that meets the practical needs of uncertain random structures, it is necessary to first discuss the fundamental criteria of the index:

Ⅰ. Simplicity criterion: The calculation of the reliability index should avoid large-scale computing. Simplicity criterion is obviously necessary because the original purpose of presenting a new index is to assess reliability rapidly with limited computing resources and time.

Ⅱ. Correlation criterion: The reliability index should be positively related to the reliability measure. Correlation criterion ensures that the new reliability index could characterize structural reliability well.

Ⅲ. Fusion criterion: The index should be compatible with both uncertain conditions and random conditions. Fusion criterion provides the foundation of uniform reliability measurement for different types and different levels of uncertainty.

Although Cornell reliability index $\beta$ can meet the first two criteria, it does not meet the fusion criterion. Thus, it is necessary to propose a new reliability index that can meet the all three criterion. In retrospect of the classical Cornell reliability index $\beta$, its geometrical significance plays an important role in reliability analysis and calculation. $\beta$ corresponds to the shortest distance from the origin in standard normal probability space to the limit state surface. In order to satisfy fusion criterion, the new reliability measure index should have the similar geometrical significance to Cornell reliability index.

We assume that each individual basic variable is affected only by the same class of uncertainty, where variables affected only by aleatory uncertainty are described by random variables and variables affected only by epistemic uncertainty are described by uncertain variables. Since the geometric meaning of Cornell reliability index is given in the standard probability space, the new hybrid index needs to be studied in the standard chance space in order to be able to use the properties in the standard space. Fortunately, both random variables and uncertain variables have the same standardizing formulas ^[27] as

where ${X_i}$ denotes a random variable or uncertain variable, $\overline {{X_i}}$ denotes the standardized form of ${X_i}$, $E(\cdot)$ denotes the expected value and $V(\cdot)$ denotes the variance. Therefore, it can be ensured that geometric measures in different dimensions are uniform after standardizing random variables and uncertain variables in a certain chance space. This uniformity provides necessary condition to establish a new hybrid reliability index for uncertain random structures utilizing geometrical significance. This paper will consider different classes of uncertainty of the basic variables in the probability space and uncertainty space, respectively, and then fuses them in the chance space.

Due to the good nature of the normal distribution ^[8,28], in this paper, a basic variable would be viewed as a normal random variable if it is influenced by aleatory uncertainty, and would be viewed as a normal uncertain variable if it is influenced by epistemic uncertainty.

We here first give the concepts of standardized limit state function and chance checking point as follows, which are necessary foundations to define the new hybrid reliability index.

Definition 2.1. (Standardized limit state function). Let ${\bf{ \pmb{\mathsf{ η}} }} = \left({{\eta _1}, {\eta _1}, \cdots, {\eta _m}} \right)$ be a normal random vector, ${\bf{ \pmb{\mathsf{ τ}} }} = \left({{\tau _1}, {\tau _2}, \cdots, {\tau _n}} \right)$ be a normal uncertain vector and $G({\bf{ \pmb{\mathsf{ η}} }}, {\bf{ \pmb{\mathsf{ τ}} }})$ be the limit state function of an uncertain random structure. If ${\bf{ \pmb{\mathsf{ η}} }}$ and ${\bf{ \pmb{\mathsf{ τ}} }}$ are standardized into $\overline {\bf{ \pmb{\mathsf{ η}} }}$ and $\overline {\bf{ \pmb{\mathsf{ τ}} }}$ respectively, then the equivalent limit state function $\overline G \left({\overline {\bf{ \pmb{\mathsf{ η}} }}, \overline {\bf{ \pmb{\mathsf{ τ}} }} } \right)$ is called standardized limit state function.

Example 2.1. Let $G\left({{x_1}, {x_2}, {x_3}} \right) = {x_1} - {x_2}{x_3}$ be a limit state function of an uncertain random structure, where the expected value of ${x_i}$ is ${\mu _i}$ and the variance of ${x_i}$ is ${\sigma _i}^2$. Then the standardized limit state function of $G\left({{x_1}, {x_2}, {x_3}} \right)$ is

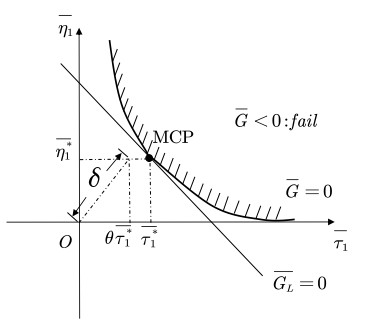
Definition 2.2. (Chance Checking Point). Let $\overline G \left({\overline {\bf{ \pmb{\mathsf{ η}} }}, \overline {\bf{ \pmb{\mathsf{ τ}} }} } \right)$ be a standardized limit state function of an uncertain random structure, then the point on limit state surface $\overline G \left({\overline {\bf{ \pmb{\mathsf{ η}} }}, \overline {\bf{ \pmb{\mathsf{ τ}} }} } \right) = 0$ with the closest distance to the origin is called Chance Checking Point (CCP), denoted as $\left({\overline {{{\bf{ \pmb{\mathsf{ η}} }}^*}}, \overline {{{\bf{ \pmb{\mathsf{ τ}} }}^*}} } \right)$.

Remark 2.1. CCP's significance is similar to Most Probable Point (MPP), which makes the most significant contribution to the nominal failure chance. Both CCP and MPP take the role of "Checking Point", an intuitively appealing linearization point.

On the basis of the above concepts, the hybrid reliability index can be then defined in the standard chance space with a linearization of the limit state function at the CCP. The definition of the index is given as follows:

Definition 2.3. (Hybrid reliability index). Let $\overline G \left({\overline {\bf{ \pmb{\mathsf{ η}} }}, \overline {\bf{ \pmb{\mathsf{ τ}} }} } \right)$ be a standardized limit state function of an uncertain random structure, $\left({\overline {\eta _1^*}, \overline {\eta _2^*}, \cdot \cdot \cdot, \overline {\eta _m^*}, \overline {\tau _1^*}, \overline {\tau _2^*}, \cdot \cdot \cdot, \overline {\tau _n^*} } \right)$ be the coordinate of CCP and $\overline {{G_L}} \left({\overline {\bf{ \pmb{\mathsf{ η}} }}, \overline {\bf{ \pmb{\mathsf{ τ}} }} } \right)$ be the first order Taylor expansion of $\overline G \left({\overline {\bf{ \pmb{\mathsf{ η}} }}, \overline {\bf{ \pmb{\mathsf{ τ}} }} } \right)$ on CCP denoted as

where $a_i^\prime$ and $b_j^\prime$ are the coefficients of $\overline {{\eta _i}}$ and $\overline {{\tau _j}}$ in $\overline {{G_L}} \left({\overline {\bf{ \pmb{\mathsf{ η}} }}, \overline {\bf{ \pmb{\mathsf{ τ}} }} } \right)$, respectively. Then the hybrid reliability index $\delta$ of the uncertain random structure is defined by

where

This definition seems to be very complex mathematically, so we tend to explain it more clearly with its geometric meaning in the chance space, as shown in Figure 1. Without loss of generosity, Figure 1 shows the geometric meaning of hybrid reliability index $\delta$ in the case of $m = n = 1$. The given coordinate system represents a standardized chance space, which is essentially the Cartesian product of a standardized probability space and a standardized uncertainty space. As m and n increase, $\overline G = 0$ and $\overline {{G_L}} = 0$ will become a hypersurface and a hyperplane in an multi-dimension chance space, respectively. According to the definition of the hybrid reliability index given in Eq (1), the point associated with $\delta$ is shifted toward the standardized uncertain space with respect to the CCP since $\theta < 1$. This shift reflects the effect of epistemic uncertainty on structural reliability. In other words, the reliability prediction results given by $\delta$ are more conservative compared to treating all variables as random variables.

This hybrid reliability index has obvious advantages, which we will subsequently illustrate by proposing algorithms and quantitative mathematical derivations.

2.2.   Generalized first-order second-moment algorithm

In this section, a calculating method of the hybrid reliability index $\delta$ called generalized first-order second-moment (GFOSM) algorithm is elaborated, which means the first-order Taylor expansion and first two moments of basic variables are used in the calculation.

In this method, a critical task is to find the position of CCP. In the traditional FOSM method, the HLRF algorithm is widely used to search for MPP ^[8,11,12]. Since the HLRF algorithm is independent of mathematical measure, it can also be used to search CCP in uncertain random structures legitimately. Then, according to the definition of the hybrid reliability index $\delta$, we hereby provide the GFOSM algorithm, whose process is summarized as Algorithm 2.1. Among them, the mean and variance of random variables can be obtained by probability statistics, while the mean and variance of uncertain variables can be obtained by the graduation formula ^[29]. It can be found that the GFOSM algorithm avoids multiple integration operations, ensuring computational efficiency.

In addition, when the basic variables are known not to obey normal distribution, the equivalent normalization method can be utilized. Equivalent normalization means replacing the original distribution with a normal distribution so that cumulative distribution function value and its derivative value at the CCP of the original distribution are the same as that normal distribution. Then the obtained normal distribution function can be used as input to the GFOSM algorithm.

2.3.   Properties of the hybrid reliability index

Since the hybrid reliability index is defined in a completely new space, it presents many unique properties and also shows its flexibility, especially in the multidimensional case. This section provides a quantitative analysis of these properties to illustrate their potential application in structural reliability.

In practical engineering, epistemic uncertainty and aleatory uncertainty are interchangeable with the development of people's knowledge and the change of external environment. For example, with the application of a structure, more actual data can be collected for the basic variables, allowing us to estimate their distributions more accurately. In this case, the relevant uncertain variables may be transformed into random variables as the knowledge increases. On the other hand, if new materials or new molding techniques are used in the structure, the relevant basic variables may be transformed from random variables to uncertain variables as cognitive level decreases. The hybrid reliability index should be able to distinguish the effects of different types of uncertainty and give a reasonable estimation when the transformation happens. To elaborate this, the following theorems are provided and proved.

Theorem 2.1. For a certain structure with given limit state function and first two moments of basic variables, as uncertain variables transform into random variables, the hybrid reliability index $\delta$ will increase.

Proof. According to the definition of the hybrid reliability index, $\theta$ is a constant with the given limit state function and the first two moments of basic variables. Further, we have

Let $Y = \sum\limits_{i = 1}^m {a_i^{\prime 2}} + \sum\limits_{j = 1}^n {b_j^{\prime 2}}$, $Z = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\left| {a_i^\prime } \right|} } \cdot \left| {b_j^\prime } \right|$. Then, Y and Z are obviously positive numbers, and thus we have

Since θ is a positive number, we have

Without loss of generality, consider an uncertain random structure with p basic variables, among those there are ${n_1}$ uncertain variables with two parts denoted as ${\tau _1}, {\tau _2}, \cdots, {\tau _{{n_1} - t}}, {\rho _1}, {\rho _2}, \cdots, {\rho _t}$ and $p - {n_1}$ random variables denoted as ${\eta _1}, {\eta _2}, \cdots, {\eta _{p - {n_1}}}$, where $0 < t⩽{n}_{1} < p$. According to Eq (1), hybrid reliability index for this structure can be denoted by

Assume that variables ${\rho _1}, {\rho _2}, \cdots, {\rho _t}$ have transformed into random variables, then hybrid reliability index would be denoted by

According to Eq (2), we have ${\delta _2} > {\delta _1}$. The theorem is proved.

Theorem 2.2. For a certain structure with given limit state function and first two moments of basic variables, as random variables transform into uncertain variables, hybrid reliability index $\delta$ will decrease.

Proof. Without loss of generality, consider an uncertain random structure with p basic variables, among those there are ${m_1}$ random variables ${\eta _1}, {\eta _2}, \cdots, {\eta _{{m_1} - t}}, {\rho _1}, {\rho _2}, \cdots, {\rho _t}$ and $p - {m_1}$ uncertain variables ${\tau _1}, {\tau _2}, \cdots, {\tau _{p - {m_1}}}$, where $0 < t \le {m}_{1} < p$. According to Eq (1), hybrid reliability index for this structure is denoted by

Assume that variables ${\rho _1}, {\rho _2}, \cdots, {\rho _t}$ have transformed into uncertain variables, then hybrid reliability index would be denoted by

According to Eq (2), we have ${\delta _2} < {\delta _1}$. The theorem is proved.

The above properties are obviously intuitive. The higher our cognitive level about the structure, the less epistemic uncertainty and the higher quantitative index value we tend to give to the event of "the structure is reliability".

Theorem 2.3. Hybrid reliability index $\delta$ will degenerate into the Cornell reliability index $\beta$ when the structures are random structures.

Proof. According to Eq (1), hybrid reliability index for random structures with p basic variables can be denoted by

which means the distance from the origin to CCP. Since there are all random variables in limit state function, the chance space in which the hybrid reliability index is defined degenerates to the probability space, i.e., the Cartesian product of the probability space of each random variable. Therefore, CCP here is accordingly degraded to the MPP in traditional FOSM method. Thus, ${\delta _R}$ represents the distance from the origin to MMP in the standard normal probability space, which has the same meaning as the Cornell reliability index $\beta$ ^[8]. The theorem is proved.

Definition 2.4. (Uncertain reliability index ^[21]). Let ${\bf{ \pmb{\mathsf{ τ}} }} = \left({{\tau _1}, {\tau _2}, \cdots, {\tau _n}} \right)$ be an uncertain vector and $G({\bf{ \pmb{\mathsf{ τ}} }})$ be the limit state function of an uncertain structure. The uncertain reliability index $\gamma$ is defined as

where $E(G)$ is the expected value of G, $V(G)$ is the variance of G.

Theorem 2.4. Hybrid reliability index will degenerate into uncertain reliability index $\gamma$ when the structures are uncertain structures.

Proof. For arbitrary nonlinear limit state function G, it should be first transformed into linear function via first order Taylor expansion, thus the next proof procedure is only for the case after linearization.

Let the linear limit state function of an uncertain structure be

According to the operational law of the expected value and variance of normal uncertain variables ^[27], we have

where $E(G)$ is the expected value of G, $V(G)$ is the variance of G, ${\mu _{{\tau _j}}}$ is the expected value of ${\tau _j}$ and ${\sigma _{{\tau _j}}}^2$ is the variance of ${\tau _j}$.

Therefore, according to Eqs (3)–(5), uncertain reliability index can be written as

According to Eq (1), hybrid reliability index for uncertain structures with p basic variables can be denoted by

Let $D = {\left({\sum\limits_{j = 1}^p {{{\overline {\tau _j^*} }^2}} } \right)^{\frac{1}{2}}}$. Apparently, D represents the distance from the origin to CCP in the standard normal uncertainty space. On the basis of HLRF algorithm ^[11,12], we have

Then according to Eqs (6)–(8), we have

The theorem is proved.

These theorems indicate that the hybrid reliability index $\delta$ defined by Eq (1) can be viewed as a unified assessment for random structures, uncertain structures and uncertain random structures since it is compatible with all three types of structures. Therefore, compared with FOSM method, GFOSM method is a more universal method suitable for structures influenced by both aleatory uncertainty and epistemic uncertainty, which is also compatible with the FOSM method.

3.   Case study

In this section, two cases will be studied to illustrate the effectiveness of the GFOSM method. Case 1 will investigate the stress-strength interference model and discuss the effect of the uncertainty type of the basic variables on the hybrid reliability index. Case 2 will study a simple beam structure and explore the relationship between the hybrid reliability index and the structural reliability.

3.1.   Basic stress-strength interference case

The basic structural reliability problem considers only one load effect S resisted by one resistance R. Then the limit state function is written as $G = R - S$. In this section, this basic linear problem will be studied via GFOSM method. The different combinations of uncertainty types for R and S will be discussed.

In practical engineering, the amount of information or data that people have about R and S varies, making it possible for R and S to contain multiple forms of uncertainty types. R may be mainly affected by aleatory uncertainty when people have a comprehensive amount of information about the structure, while it may be mainly affected by epistemic uncertainty when people do not have enough information about the structure. This is also true for the stresses to which the structure is subjected, which also affect the type of uncertainty in S. Thus, there would be four kinds of circumstances considering different combinations of uncertainty types with given expected values and variances of R and S:

Ⅰ. R and S are both influenced by aleatory uncertainty;

Ⅱ. R and S are both influenced by epistemic uncertainty;

Ⅲ. R is influenced by aleatory uncertainty; S is influenced by epistemic uncertainty;

Ⅳ. R is influenced by epistemic uncertainty; S is influenced by aleatory uncertainty.

As explained before, the basic variable should be viewed as a random variable or an uncertain variable according to the uncertainty types it is influenced by, i.e., random variable for aleatory uncertainty and uncertain variable for epistemic uncertainty. Hybrid reliability index of basic stress-strength interference case for four combinations of uncertainty types could be calculated via GFOSM algorithm respectively. The evaluated results are shown in Table 1.

Table 1 shows that ${\delta _{\text{I}}}$ is the largest while ${\delta _{{\text{II}}}}$ is the smallest under the same first two moments with different uncertainty types, indicating the reliability assessment for uncertain structures would be more conservative than that for random structures. This is due to the use of the axiomatic system of uncertainty theory, and it is also consistent with the practical situation that we tend to give more conservative assessment results when epistemic uncertainty is high. Moreover, since Condition Ⅰ contains only random variables, its assessment result is actually the same as that of the traditional FOSM method.

Besides, comparison between ${\delta _{{\text{II}}}}$ and ${\delta _{{\text{III}}}}$ and between ${\delta _{{\text{II}}}}$ and ${\delta _{{\text{IV}}}}$ show that the ${\delta _i}$ increases when either of R and S is transformed from an uncertain variable to a random variable. This is because, with equal first two moments, using random variables for the basic variables means that we collect more data or information than using uncertain variables, thus giving us more knowledge about the reliability of the structure. This is in line with the actual judgment of the reliability of the structure.

3.2.   Beam structure case

In this case, the reliability assessment of a beam structure with a point load F and gravitational effect in Figure 2 will be studied by GFOSM method. The correlativity and sensitivity between hybrid reliability index and basic variables will be analyzed as well.

The beam structure's limit state function is nonlinear, which can be written as

where b is the breadth, h is the height, L is the length, $\sigma$ is the material strength and $\rho$ is the material gravity density. Considering the situation that the material used in this beam is newly developed, the material strength and gravity density are effected by epistemic uncertainty because there is no enough information or data about this material. For this reason, the material strength $\sigma$ and gravity density $\rho$ should be expressed as uncertain variables, while other basic variables would be expressed as random variables.

The parameters information including variable types, expected values and variances are summarized in Table 2.

According to Eq (1) where $m = 4$, $n = 2$, the hybrid reliability index will be $\delta {\text{ = }}3.1041$ for this beam structure.

In order to further verify the effectiveness and robustness of GFOSM method, the reliability assessment results of the structure are investigated when the first two moments of the basic variables vary within a certain range. As comparison to the GFOSM method, the reliability is calculated using the uncertain random simulation algorithm proposed by Zhang ^[30]. The results are shown in Figure 3. Obviously, the trend of hybrid reliability index $\delta$ is consistent with reliability R, verifying that GFOSM method can effectively characterize the reliability.

Furthermore, sensitivity analysis of structural parameters is conducted for hybrid reliability index $\delta$ and reliability R. Sensitive factors of $\delta$ and R are defined respectively as follow:

where $X_i^{(1)}$ is the low level expected value of the i-th basic variable, $X_i^{(2)}$ is the high level expected value of the i-th basic variable, ${S_\delta }\left({{X_i}} \right)$ is the sensitive factor of $\delta$ for the i-th basic variable and ${S_R}\left({{X_i}} \right)$ is the sensitive factor of R for the i-th basic variable. The values of $X_i^{(1)}$ and $X_i^{(2)}$ are taken as 90% and 110% in Table 2 respectively, as shown in Table 3. It should be noted that the sensitive factor here considers only the local sensitivity, i.e., when calculating the sensitive factor of one certain basic variable, the value of the others should be fixed as Table 2.

Tables 4 and 5 show the sensitive factors of $\delta$ and R calculated via Eq (9), respectively. The results indicates that structural basic variables' sensitivity ranking for $\delta$ and R is consistent, which means that changes in the expected value of any basic variable affect the structural reliability and hybrid reliability index to the same extent. Therefore, the hybrid reliability index can effectively characterize structural reliability. The validity of the hybrid reliability index is further verified.

4.   Conclusions

As an efficient assessment method for structures influenced by hybrid uncertainties is needed, this paper has presented a new reliability assessing method for uncertain random structures, named GFOSM method. The contributions of this paper are concluded as follows.

1) A new hybrid reliability index has been proposed as well as some important properties. These properties indicate that the new hybrid reliability index satisfies the fusion criterion.

2) Traditional FOSM method has been extended into GFOSM method to adapt reliability assessment for uncertain random structures. Compared to the calculation of reliability, large-scale computing is avoided in GFOSM algorithm, verifying the simplicity criterion.

3) Two cases have been studied to further illustrate the GFOSM method proposed. It has been shown that the GFOSM method has the sufficient practicability for uncertain random structures and satisfies the correlation criterion.

The GFOSM method has very high computational efficiency and relative accuracy, which makes it very suitable for applications with rapid reliability evaluation needs, such as reliability-based design optimization. Therefore, the application of GFOSM method in structural design optimization problem would be studied in the future work.

Acknowledgments

This work was supported by National Natural Science Foundation of China [Grant No. 62073009], Stable Supporting Project of Science and Technology on Reliability and Environmental Engineering Laboratory [Grant No. WDZC20220102], Funding of Science and Technology on Reliability and Environmental Engineering Laboratory [Grant No. 6142004210102] and Yunnan Province Science and Technology Innovation Talent Training Target Project [Grant No. 202205AD160001].

Conflict of interest

The authors disclosed no conflicts of interest in publishing this paper.

Appendix A: Preliminary on uncertainty and chance theory

Some basic axioms, definitions and theorems in uncertainty theory vital for this paper will be presented in this section.

Let $\mathcal{L}$ be a nonempty set, and $\Gamma$ a $\sigma$-algebra over $\Gamma$. Each element $\Lambda \in \mathcal{L}$ is called an event. Each event $\Lambda$ will obtain a number $\mathcal{M}\{ \Lambda \} \in [0, 1]$, i.e., uncertain measure, to indicate the belief degree that the event $\Lambda$ occurs. Uncertain measure $\mathcal{M}$ must satisfy the following axioms that was suggested by Liu ^[27,31]:

Axiom A.1. (Normality Axiom). $\mathcal{M}\{ \Lambda \} = 1$ for the universal set $\Gamma$.

Axiom A.2. (Duality Axiom). $\mathcal{M}\{ \Lambda \} + \mathcal{M}\left\{ {{\Lambda ^c}} \right\} = 1$ for any event $\Lambda$.

Axiom A.3. (Subadditivity Axiom). For every countable sequence of events ${\Lambda _1}, {\Lambda _2}, \cdots,$ we have

Axiom A.4. (Product Axiom). Let $\left({{\Gamma _k}, {\mathcal{L}_k}, {\mathcal{M}_k}} \right)$ be uncertainty spaces for $k = 1, 2, \cdots$. The product uncertain measure $\mathcal{M}$ is an uncertain measure satisfying

where ${\Lambda _k}$ are arbitrarily chosen events from ${\mathcal{L}_k}$ for $k = 1, 2, \cdots$, respectively.

Definition A.1. (Uncertainty space ^[27]). Let $\Gamma$ be a nonempty set, $\mathcal{L}$ an $\sigma$-algebra over $\Gamma$ and $\mathcal{M}$ an uncertain measure. Then the triplet $(\Gamma, \mathcal{L}, \mathcal{M})$ is called an uncertainty space.

Definition A.2. (Uncertain variable ^[27]). An uncertain variable $\xi$ is a measurable function from an uncertainty space $(\Gamma, \mathcal{L}, \mathcal{M})$ to the set of real numbers, i.e., for any Borel set B of real numbers, the set

is an event.

Definition A.3. (Uncertainty distribution ^[27]). The uncertainty distribution $\Phi$ of an uncertain variable $\xi$ is defined by

for any real number x.

Definition A.4. (Normal uncertain variable ^[27]). An uncertain variable $\xi$ is called normal if it has a normal uncertainty distribution

denote by $\mathcal{N}(e, \sigma)$ where $e$ and $\sigma$ are real numbers with $\sigma > 0$.

Since human epistemic uncertainty and objective randomness often coexist in practice, Liu defined a new measure to describe this phenomenon combining probability measure and uncertain measure, called chance measure ^[22].

Definition A.5. (Chance space ^[22]). Let $(\Gamma, \mathcal{L}, \mathcal{M})$ be an uncertainty space, and $(\Omega, \mathcal{A}, \Pr)$ be a probability space. Then, $(\Gamma, \mathcal{L}, \mathcal{M}) \times (\Omega, \mathcal{A}, \Pr)$ is called a chance space.

Definition A.6. (Uncertain random variable ^[22]). An uncertain random variable is a function $\xi$ from a chance space $(\Gamma, \mathcal{L}, \mathcal{M}) \times (\Omega, \mathcal{A}, \Pr)$ to the set of real numbers such that $\{ \xi \in B\}$ is an event in $\mathcal{L} \times \mathcal{A}$ for any Borel set $B$ of real numbers

Definition A.7. (Chance measure ^[22]). Let $(\Gamma, \mathcal{L}, \mathcal{M}) \times (\Omega, \mathcal{A}, \Pr)$ be a chance space, and let $\Theta \in \mathcal{L} \times \mathcal{A}$ be an event. Then, the chance measure of $\Theta$ is defined as