The unit generalized log Burr XII distribution: properties and application

1.   Introduction

Statistical distributions bounded on (0, 1) are useful tools to describe uncertainty phenomena. For modeling proportions, percentages, indices, rates and ratios measured on the unit interval, many new continuous unit distributions have been developed. In statistical literature, the most famous unit distribution is the beta distribution, since it is a convenient and useful model in many areas of statistics. However, its data modeling ability may be insufficient to explain the data. So, there are some alternative distributions to beta distribution in the literature such as the Johnson S_B distribution ^[1], Topp-Leone distribution ^[2], the unit-Gamma distribution ^[3,4], the Kumaraswamy distribution ^[5], the Arcsine distribution ^[6], the unit-Logistic distribution ^[7], the Simplex distribution ^[8], the unit-Birnbaum-Saunders distribution ^[9], the unit-Weibull distribution ^[10], the unit-Gompertz distribution ^[11], the unit-Lindley distribution ^[12], the unit-improved second-degree Lindley distribution ^[13], the unit-inverse Gaussian distribution ^[14], the unit half normal distribution ^[15], the logit slash distribution ^[16], the arc-secant hyperbolic normal distribution ^[17] and the TURQ distribution ^[18]. Many of the above mentioned distributions have been obtained via transforming of the base distribution and they have given better results than beta distribution in terms of the data modeling.

We aim to propose a new unit distribution with many sub-models on (0, 1) interval in order to obtain flexible density function with various shapes and skewed forms in the unit interval. The UGLBXII distribution is important due to (i) it has simple and closed form expressions for the cumulative distribution function and quantile function; (ii) it can provide increasing, bathtub, N-shaped and bimodal hazard rate and (iii) it can provide better fits than other well-known distributions defined on the unit interval. Further, We focus on the following motivations: (i) to develop distributions with various density shaped model as well as high kurtosis; (ii) to have monotone and non-monotone failure rate function; (iii) to derive mathematical properties such as random number generator, sub-models, ordinary moments, generalized TL moments, conditional moments, reliability measures, uncertainty measures and characterizations; (iv) to present the bivariate and multivariate‐type distributions; (v) to estimate the precision of the different estimators via simulation studies; (vi) to illustrate the potentiality of the UGLBXII model; (vii) to employ as the preeminent substitute model to the other existing models and (viii) to deliver a better fit model than other models.

The content of the article is prepared as follows. In Section 2, we derive the UGLBXII distribution. We also study basic structure related properties like random number generator and sub-models. Section 3 presents certain mathematical properties such as ordinary moments, generalized TL moments, conditional moments, reliability and uncertainty measures. We also present the bivariate‐ and multivariate‐type distributions. Section 4 provides certain characterizations of the UGLBXII distribution via innovative techniques. In Section 5, we adopt six estimation methods to estimate its unknown parameters. We carry out simulation studies on the basis of the graphical results to see the performance of the above estimators. In Section 6, we consider two applications to illustrate the potentiality of the UGLBXII model. Concluding remarks are given in Section 7.

2.   The UGLBXII distribution

We derive the probability density function (pdf) of the UGLBXII distribution and discuss its basic structural properties.

2.1.   Development of the UGLBXII distribution

In this sub-section, we derive the pdf of the UGLBXII distribution using the Pearson differential equation given by

For transformation $x = {e^{ - t}}$, Pearson differential equation is

Taking $m = n = 2 {\rm{ \mathsf{ β} }} + 1$, ${a_0} = \left( {2 {\rm{ \mathsf{ β} }} - 1} \right){{\rm{ \mathsf{ λ} }} ^{2 {\rm{ \mathsf{ β} }} }}$, ${a_1} = - {{\rm{ \mathsf{ λ} }} ^{2 {\rm{ \mathsf{ β} }} }}$, ${a_2} = {a_3}...{a_{m - 2}} = 0$, ${a_{m - 1}} = - \left( {2{\rm{ \mathsf{ α} }} {\rm{ \mathsf{ β} }} + 1} \right)$, ${a_m} = - 1$, ${b_0} = 0$ ${b_1} = {{\rm{ \mathsf{ λ} }} ^{2 {\rm{ \mathsf{ β} }} }}$, ${b_0} = {b_2} = {b_3}... = {b_{n - 1}} = 0, {b_n} = 1$, we arrive at

Integrating (3), we obtain

Using condition $\int\limits_0^1 {f\left( x \right)dx = 1} \,$, the normalizing constant is $k = \frac{{2{\rm{ \mathsf{ α} }} {\rm{ \mathsf{ β} }} }}{{\rm{ \mathsf{ λ} }} }$ and the pdf of UGLBXII distribution is

The cdf corresponding to (4) is

2.2.   Relationship between the exponential and gamma variable

Here, we derive the UGLBXII distribution from a relationship between the exponential and gamma random variables, i.e., ${W_1} \sim \exp \left( 1 \right)$ and ${W_2} \sim gamma\left( {{\rm{ \mathsf{ α} }} , 1} \right)$. ${W}_{1}and$ ${W}_{2}$ independently distributed

Lemma (i). Let ${W_1} \sim \exp \left( 1 \right)$ and ${W_2} \sim gamma\left( {{\rm{ \mathsf{ α} }} , 1} \right)$ $be$ independently distributed, then for ${W_1} = {\left( { - \frac{{\ln X}}{{\rm{ \mathsf{ λ} }} }} \right)^{2 {\rm{ \mathsf{ β} }} }}{W_2}$, we have $X = \exp \left[ { - {\rm{ \mathsf{ λ} }} {{\left( {\frac{{{W_1}}}{{{W_2}}}} \right)}^{\frac{1}{{2 {\rm{ \mathsf{ β} }} }}}}} \right]$ ~ UGLBXII $\left( {{\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }} } \right)$.

Proof. Let ${W_1} \sim \exp \left( 1 \right)$ i.e., $f\left( {{w_1}} \right) = {e^{ - {w_1}}}\, , \, {w_1} > 0$, and ${W_2} \sim gamma\left( {{\rm{ \mathsf{ α} }} , 1} \right)$, i.e., $f\left( {{w_2}} \right) = \frac{{{w_2}^{{\rm{ \mathsf{ α} }} - 1}{e^{ - {w_2}}}}}{{\Gamma \left( {\rm{ \mathsf{ α} }} \right)}}, \, \, \, {w_2} > 0$. The joint density of ${W_1}, \, \, {W_2}$ is $f\left( {{w_1}, {w_2}} \right) = \frac{{{w_2}^{{\rm{ \mathsf{ α} }} - 1}{e^{ - {w_2}}}{e^{ - {w_1}}}}}{{\Gamma \left( {\rm{ \mathsf{ α} }} \right)}}, \, \, \, {w_1} > 0, \, \, {w_2} > 0$. Let ${W_1} = {\left( { - \frac{{\ln X}}{{\rm{ \mathsf{ λ} }} }} \right)^{2 {\rm{ \mathsf{ β} }} }}{W_2}$, the joint density of $X\,$ and ${W_2}$ is

The marginal density of $X$ is

After simplification, we have

which is the UGLBXII density.

2.3.   Structural properties

If X~ UGLBXII $\left( {{\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }} } \right)$, the survival function, failure rate function, cumulative hazard function, reverse hazard function and elasticity are given, respectively, by

and

The quantile function of the UGLBXII distribution for $0 < q < 1$ is $x = \exp \left[ { - λ {{\left( {{q^{ - \frac{1}{α }}} - 1} \right)}^{\frac{1}{{2 β }}}}} \right]$.

The random number generator of the UGLBXII distribution for $U$ ~Uniform (0, 1) is given by

2.4.   Sub models of the UGLBXII distribution

i). For $λ = 1$, the UGLBXII distribution reduces to the unit log Burr XII (ULBXII) distribution.

ii). For $β = 0.5$, the UGLBXII distribution reduces to the unit log Lomax (ULL) distribution.

iii). For $α \to \infty , \, λ = \gamma {α ^{\frac{1}{{2 β }}}}$, the UGLBXII distribution becomes the unit log generalized Weibull (UGLW) distribution.

iv). For $α \to \infty , \, λ = \gamma {α ^{\frac{1}{{2 β }}}}, β = 0.5$, the UGLBXII distribution becomes the unit log-exponential distribution.

v). For ${X^{ - 1}}$, the UGLBXII distribution reduces to the generalized log Burr XII (GLBXII) distribution ^[19].

vi). For ${X^{ - 1}}$ and $λ = 1$, the UGLBXII distribution reduces to the log Burr XII (LBXII) distribution.

2.5.   Plots of the UGLBXII density and failure rate functions

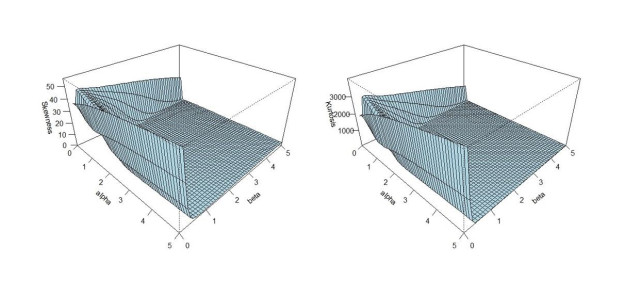
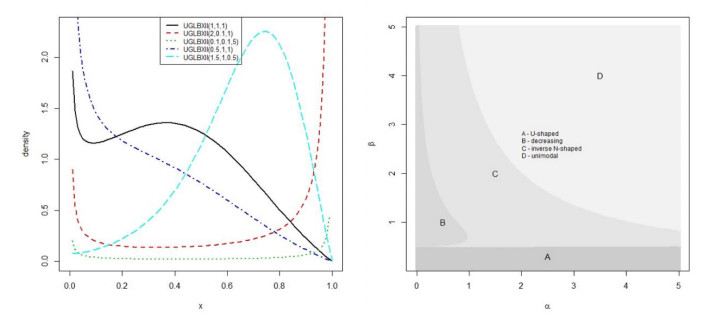
We plot the pdf and failure rate functions of the UGLBXII distribution to the selected parameters values. Figure 1 displays that the UGLBXII density can take various shapes such as decreasing, unimodal, U-shaped, decreasing-increasing-decreasing (inverse N-shaped) and the possible pdf's regions of the UGLBXII density with $λ = 1$ . On the other hand, Figure 2 shows that failure rate function can be increasing, bathtub, N-shaped and bimodal. Therefore, the UGLBXII distribution is quite flexible and can be applied for numerous data sets.

3.   Mathematical properties

We present some properties such as ordinary moments, generalized TL moments, conditional moments, reliability and uncertainty measures. We also present the bivariate and multivariate‐type distributions.

3.1.   Moments

The moments are significant tools for statistical analysis in pragmatic sciences. The r^th ordinary moment of X is

Setting ${\left( { - \frac{{\ln x}}{ {\rm{ \mathsf{ λ} }} }} \right)^{2 {\rm{ \mathsf{ β} }} }} = w$, we can write

The Mellin transformation ${\rm M}\left\{ {f\left( x \right);s} \right\} = {f^*}\left( s \right) = E\left[ {{X^{s - 1}}} \right]$ is applied to get the moments of X as

The r^th central moment $\left( {{{\rm{ \mathsf{ μ} }} _r}} \right)$, coefficients of skewness (${{\rm{ \mathsf{ γ} }} _1}$) and kurtosis (${{\rm{ \mathsf{ γ} }} _2}$) of X are

The numerical values for the mean $\left( {{{{\rm{ \mathsf{ μ} }} '}_1}} \right)$, median $\left( {\tilde {\rm{ \mathsf{ μ} }} } \right)$, standard deviation $\left( \sigma \right)$, skewness $\left( {{{\rm{ \mathsf{ γ} }} _1}} \right)$ and kurtosis $\left( {{{\rm{ \mathsf{ γ} }} _2}} \right)$ of the UGLBXII distribution for selected values of ${\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }}$ are listed in Table 1. Figure 3 shows the skewness and kurtosis of the distribution for the selected parameters values with $λ = 1.$

3.2.   The generalized TL-moments

Elamir and Seheult ^[20] developed generalized TL-moments. The expression for r^th generalized TL-moment is

where ${\rm{ \mathsf{ λ} }} _r^{\left( {m, n} \right)}$ is a function of $E\left( {{X_{r + m - \ell \, \, \, :\, \, \, \, r + m + n}}} \right)$ and m and n are the probable trimming lowermost and uppermost values, respectively.

The pdf of ( $r + m - \ell$ )^th order statistic ${X_{r + m - \ell \, \, \, :\, \, \, \, r + m + n}}$ for the UGLBXII distribution is

The k^th moment about the origin of ${X_{r + m - \ell \, \, \, :\, \, \, \, r + m + n}}$ for the UGLBXII model is

Letting $\, \, {\left( { - \frac{{\ln x}}{ {\rm{ \mathsf{ λ} }} }} \right)^{2 {\rm{ \mathsf{ β} }} }} = w$, we arrive at

Mean of ${X_{r + m - \ell \, \, \, :\, \, \, \, r + m + n}}$ for the UGLBXII distribution is

The r^th generalized TL-moment is obtained as

The r^th generalized TL-moment can be used to obtain the r^th L-moment (0, 0), LL-moments (0, n), TL-moment (1, 1) and LH-moment (m, 0) for the UGLBXII distribution. The first two moments $λ _1^{\left( {m, n} \right)}$ and $λ _2^{\left( {m, n} \right)}$ are employed to compute the location and dispersion of the data, respectively. $L - CV = \frac{{ λ _2^{\left( {m, n} \right)}}}{{ λ _1^{\left( {m, n} \right)}}}$ is coefficient of variation. ${\tau _r} = \frac{{ λ _r^{\left( {m, n} \right)}}}{{ λ _2^{\left( {m, n} \right)}}}$, $r \geqslant 3$, ${\tau _3} = \frac{{ λ _3^{\left( {m, n} \right)}}}{{ λ _2^{\left( {m, n} \right)}}}$ and ${\tau _4} = \frac{{ λ _4^{\left( {m, n} \right)}}}{{ λ _2^{\left( {m, n} \right)}}}$ are measures for skewness and kurtosis, respectively.

3.2.1.   The TL-moments (1, 1)

When only the extreme observations are trimmed from the array sample, then the r^th generalized TL-moment befits r^th TL-moment (m = n = 1). The r^th TL-moment is obtained as follows

3.2.2.   The L-moments ^[21]

When no value is trimmed from the array sample, then the r^th generalized TL-moment becomes r^th L-moment (m = n = 0). L-moments are used for estimation of the parameters. The r^th L-moment for the UGLBXII distribution is

3.2.3.   The LH-moments ^[22]

When lowermost m values are trimmed from the array sample, then the r^th generalized TL-moment becomes r^th LH-moment (m, 0). The r^th LH-moments (m, 0) gives more weight to the upper part of data. The r^th LH-moment for the UGLBXII distribution is

3.2.4.   The LL-moments ^[23]

When the uppermost n values are trimmed from the array sample, then the r^th generalized TL-moment becomes r^th LH-moment (0, n). The r^th LL-moments (0, n) gives more weight to the lowermost part of data. The r^th LL-moment for the UGLBXII distribution is

3.3.   Conditional moments

The r^th conditional moment of X is $E\left( {\left. {{X^k}} \right|X > z} \right) = \frac{1}{{S\left( z \right)}}\left[ {{E_{X > z}}\left( {{X^k}} \right)} \right]$. The k^th incomplete upper moment about the origin for X is

where $S\left( z \right)$ is survival function and $B\left( {z;., .} \right)$ is the incomplete beta function. The k^th conditional moment of X is

The r^th reversed conditional moment of X is $E\left( {\left. {{X^k}} \right|X \leqslant z} \right) = \frac{1}{{F\left( z \right)}}\left[ {{E_{X \leqslant z}}\left( {{X^k}} \right)} \right]$. The k^th incomplete lower moment about the origin for X is

where $F\left( z \right)$ is cdf and $B\left( {z;., .} \right)$ is the incomplete beta function. The k^th reversed conditional moment of X is

The mean deviation about the mean $\left( {{\delta _1} = E\left| {X - μ } \right|} \right)$ and about the median $\left( {{\delta _2} = E\left| {X - \tilde μ } \right|} \right)$ can be written as ${\delta _1} = 2μ F\left( μ \right) - 2μ \, {M'_1}\left( μ \right)$ and ${\delta _2} = μ - 2{M'_1}\left( {\tilde μ } \right)$, respectively, where $μ = E\left( X \right)$ and $\tilde μ = {x_{0.5}}$.The quantities ${M'_1}\left( μ \right)$ and ${M'_1}\left( {\tilde μ } \right)$ can be obtained from (6). For specific probability p, Lorenz and Bonferroni curves are computed as $L(p) = \frac{{{{M'}_1}\left( q \right)}}{{μ '}}$ and $B(p) = \left. {L(p)} \right|p$, where $q = Q\left( p \right)$.

3.4.   Reliability in multicomponent stress-strength model

Consider a system with $\kappa$ identical elements, out of which s elements are operative. Let ${X_i}, i = 1, 2...\kappa$ represent strengths of $\kappa$ elements with the cdf F while, the stress Y enforced on the elements has the cdf G. The strengths ${ X}_{i}$ and stress Y are independently and identically distributed (i.i.d.). The probability that system operates properly, is the reliability of the system, i.e.,

Then, we can write this probability (from ^[24]) as follows:

Let X~UGLBXII $\left( {{{\rm{ \mathsf{ α} }} _1}, {\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }} } \right)$, Y~ UGLBXII $\left( {{{\rm{ \mathsf{ α} }} _2}, {\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }} } \right)$ with unknown ${{\rm{ \mathsf{ α} }} _1}\, \, and\, {{\rm{ \mathsf{ α} }} _2}$, common ${\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }}$ where $\mathrm{X}$ and $\mathrm{Y}$ are independently distributed. The reliability in multicomponent stress-strength model for the UGLBXII distribution is

Setting $\omega = {\left[ {1 + {{\left( { - \frac{{\ln y}}{ {\rm{ \mathsf{ λ} }} }} \right)}^{2 {\rm{ \mathsf{ β} }} }}} \right]^{ - {{\rm{ \mathsf{ α} }} _2}}}$, we obtain ${R_{s, \kappa }} = \sum\limits_{\varsigma = s}^\kappa {\left( \begin{gathered} \kappa \\ \varsigma \\ \end{gathered} \right)} \int\limits_0^1 {{{\left( {1 - {\omega ^\vartheta }} \right)}^\varsigma }\, {\omega ^{\vartheta \left( {\kappa - \varsigma } \right)}}\, d\omega , }$ where $\vartheta = \frac{{{{\rm{ \mathsf{ α} }} _1}}}{{{{\rm{ \mathsf{ α} }} _2}}}$.

Letting $\, u = {\omega ^\vartheta }\, \, ,$

The probability in (7) is called the reliability in a multicomponent stress-strength model.

For s $= \kappa$ = 1, the multicomponent stress-strength model reduces to the stress-strength model ^[25] as

3.5.   Uncertainty measures

The measure of uncertainty of a random variable (rv) is called entropy. Rényi entropy generalizes Hartley, Min, Shannon and collision entropies. Entropies are useful to study daily temperature instabilities (climatic), abnormal diffusion, DNA structures, information content gestures, heart rate variability (HRV) and cardiac autonomic neuropathy (CAN). Here, we study Shannon entropy, Awad entropy, Rényi, Q, Havrda, Chavrat and Tsallis-entropies.

Claude Shannon ^[26] measured expected information in a message. Shannon entropy is given by

where $\psi \left( {\rm{ \mathsf{ α} }} \right) = \frac{d}{{dp}}\left[ {\ln \Gamma {\rm{ \mathsf{ α} }} } \right]$ is the digamma function.

Awad and Alawneh ^[27] provided the extension of Shannon entropy as $A\left( X \right) = - \int\limits_1^\infty {f\left( x \right)} \ln \frac{{f\left( x \right)}}{\delta }dx$.

For X~UGLBXII $\left( {{\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }} } \right),$ the Awad entropy is given by

For X~UGLBXII $\left( {{\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }} } \right),$ Rényi entropy ^[28] is given by

Now taking

Considering $\int\limits_0^1 {{x^{ - {\rm{ \mathsf{ ν} }} }}{{\left( { - \frac{{\ln x}}{ {\rm{ \mathsf{ λ} }} }} \right)}^{2 {\rm{ \mathsf{ β} }} \ell }}^{ + 2 {\rm{ \mathsf{ β} }} {\rm{ \mathsf{ ν} }} - {\rm{ \mathsf{ ν} }} }} dx$ and letting $\left( { - \frac{{\ln x}}{b}} \right) = w$, we arrive at

The Q-entropy for the UGLBXII distribution is

The Havrda and Chavrat entropy ^[29] for the UGLBXII distribution is

The Tsallis-entropy ^[30] for the UGLBXII distribution is

3.6.   Bivariate and multivariate extensions of the UGLBXII distribution

Here, we derive the bivariate UGLBXII model via Morgenstern (Mor) family and via Clayton family ^[31].

3.6.1.   Bivariate UGLBXII distribution via Mor family

The cdf of the bivariate UGLBXII model via Mor family for random vector $\left( {{W_1}, {W_2}} \right)$ is

where ${F_1}\left( {{w_1}} \right) = {\left[ {1 + {{\left( { - \frac{{\ln {w_1}}}{{{ {\rm{ \mathsf{ λ} }} _1}}}} \right)}^{2{ {\rm{ \mathsf{ β} }} _1}}}} \right]^{ - {{\rm{ \mathsf{ α} }} _1}}}$ and ${F_2}\left( {{w_2}} \right) = {\left[ {1 + {{\left( { - \frac{{\ln {w_2}}}{{{ {\rm{ \mathsf{ λ} }} _2}}}} \right)}^{2{ {\rm{ \mathsf{ β} }} _2}}}} \right]^{ - {{\rm{ \mathsf{ α} }} _2}}},$ then we have seven dimension parameter model.

3.6.2.   Bivariate UGLBXII distribution via Clayton family

The cdf of the bivariate UGLBXII model via Clayton family for random vector $\left( {{\text{U}}, {\text{V}}} \right)$ is

Let ${W_1}$ ~ UGLBXII $\left( {{{\rm{ \mathsf{ α} }} _1}, { {\rm{ \mathsf{ β} }} _1}, { {\rm{ \mathsf{ λ} }} _1}} \right)$ and ${W_2}$ ~ UGLBXII $\left( {{{\rm{ \mathsf{ α} }} _2}, { {\rm{ \mathsf{ β} }} _2}, { {\rm{ \mathsf{ λ} }} _2}} \right)$. Then, setting

The cdf of the bivariate UGLBXII distribution via Clayton family for random vector (W1, W2) is

3.6.3.   The multivariate extension

Here, we derive the multivariate UGLBXII distribution. A straightforward d-dimensional extension from the above will be

In future works, we could study various characteristics of the bivariate and the multivariate extensions of the UGLBXII model.

4.   Characterizations

In this section, we characterize the UGLBXII distribution via; (i) ratio of truncated moments; (ii) reverse hazard function and (iii) Elasticity function.

4.1.   Ratio of truncated moments

We employ ratio of truncated moments of X using a Theorem due to Glänzel ^[32] to characterize the UGLBXII distribution.

Proposition 4.1.1. Let ${\rm{X:}}\Omega \to \left( {0,1} \right)$ be a continuous rv and let

According to the Glänzel Theorem, the rv X has pdf (4), iff the function $\upsilon \left( x \right)$ has the form

Proof. For the rv X with the pdf (4), we have

and

Therefore, in light of Theorem of Glänzel ^[32], X has pdf (4).

Corollary 4.1.1. Let ${\rm{X:}}\Omega \to \left( {0,1} \right)$ be a continuous rv and let

Then, X has pdf (4) iff the functions $\upsilon \left( x \right)\,$ and ${\xi _1}\left( x \right)$ satisfy the differential equation

Remark 4.1.1. The general solution of (8) is

where D is a constant.

4.2.   Reverse Hazard function

Definition 4.2.1. Let ${\rm{X:}}\Omega \to \left( {0,1} \right)$ be a continuous rv with a twice continuously differential cdf $F(x)$. Then, the reverse hazard function $r_F$ satisfies the differential equation

Proposition 4.2.1. Let ${\rm{X:}}\Omega \to \left( {0,1} \right)$ be continuous rv. The pdf of X is (4) iff its reverse hazard function, $r_F$ satisfies the first order differential equation

Proof. If X has pdf (4), then (10) holds. Now if (10) holds, then

or

which is the reverse hazard function of the UGLBXII distribution.

4.3.   Elasticity function

Definition 4.3.1. Let ${\rm{X:}}\Omega \to \left( {0,1} \right)$ be a continuous rv with a twice continuously differential cdf $F(x)$. Then, the elasticity function ${{\rm{ \mathsf{ η} }} _F}\left( x \right)$ satisfies the differential equation

Proposition 4.3.1. Let ${\rm{X:}}\Omega \to \left( {0,1} \right)$ be continuous rv. The pdf of X is (4), if and only if its elasticity function, ${\rm{ \mathsf{ η} }}_F (x)$ satisfies the first order differential equation

Proof. If X has pdf (4), then (12) holds. Now if (12) holds, then

or

which is the elasticity function of the UGLBXII distribution.

5.   Different estimation methods

In this section, we propose various estimators for estimating the unknown parameters of the UGLBXII distribution. We discuss maximum likelihood, maximum product spacings, least squares, weighted least squares, Cramer-von Mises and Anderson-Darling estimation methods and compare their performances on the basis of a simulated sample from the UGLBXII distribution. The details are as follows.

5.1.   Maximum likelihood estimation

In this subsection we estimate the parameters of the UGLBXII distribution via the method of maximum likelihood estimation (MLE). Let ${X_1}, {X_2}, \ldots {X_n}$ be a random sample from the UGLBXII distribution with observed values ${x_1}, {x_2}, \ldots {x_n}$ and ${\bf{\Xi }} = {\left( {{\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }} } \right)^T}$ be the vector of the model parameters. The log likelihood function for ${\bf{\Xi }}$ may be expressed as

The elements of the score vector, $U\left( {\bf{\Xi }} \right) = \tfrac{{\partial \ell }}{{\partial {\bf{\Xi }}}} = {\left( {\tfrac{{\partial \ell }}{{\partial {\rm{ \mathsf{ α} }} }}, \tfrac{{\partial \ell }}{{\partial {\rm{ \mathsf{ β} }} }}, \tfrac{{\partial \ell }}{{\partial {\rm{ \mathsf{ λ} }} }}} \right)^T}$, are given as

and

We can obtain the estimates of the unknown parameters by setting the score vector to zero, $U\left( {{\bf{\hat \Xi }}} \right) = {\bf{0}}$. Solving these equations simultaneously gives the MLEs, say ${\hat {\rm{ \mathsf{ α} }} _{MLE}}$, ${\hat {\rm{ \mathsf{ β} }} _{MLE}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{MLE}}$, of the ${\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }}$ and ${\rm{ \mathsf{ λ} }}$ parameters. Since, these equations include non-linear equation systems, they must be solved with numerically methods. The equation (13) can be directly maximized by the different packet programs such as R, S-Plus, Mathematica and SAS.

Moreover, for the UGLBXII distribution, all the second order derivatives exist. The interval estimation of the model parameters requires the $3 \times 3$ observed information matrix $J\left( {\bf{\Xi }} \right) = \left\{ {{J_{ij}}} \right\}$ for $i, j = {\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }}$. The multivariate normal ${N_3}\left( {0, J{{\left( {{\bf{\hat \Xi }}} \right)}^{ - 1}}} \right)$ distribution, under standard regularity conditions, can be used to provide approximate confidence intervals for the unknown parameters, where $J\left( {{\bf{\hat \Xi }}} \right)$ is the total observed information matrix evaluated at ${\bf{\hat \Xi }}$. Then, approximate $100\left( {1 - \delta } \right)\%$ confidence intervals for ${\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }}$ and ${\rm{ \mathsf{ λ} }}$ can be determined by: ${\hat {\rm{ \mathsf{ α} }} _{MLE}} \pm {z_{\delta /2}}\sqrt {{{\hat J}_{{\rm{ \mathsf{ α} }} {\rm{ \mathsf{ α} }} }}}$, ${\hat {\rm{ \mathsf{ β} }} _{MLE}} \pm {z_{\delta /2}}\sqrt {{{\hat J}_{ {\rm{ \mathsf{ β} }} {\rm{ \mathsf{ β} }} }}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{MLE}} \pm {z_{\delta /2}}\sqrt {{{\hat J}_{ {\rm{ \mathsf{ λ} }} {\rm{ \mathsf{ λ} }} }}}$ where ${z_{\delta /2}}$ percentile of the standard normal model and The ${\hat J_{ii}}$ s are the i th diagonal elements of the $J{\left( {{\bf{\hat \Xi }}} \right)^{ - 1}}$, which is the estimated variance-covariance matrix, for $i = {\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }}$. The elements of the $J\left( {{\bf{\hat \Xi }}} \right)$ and $J{\left( {{\bf{\hat \Xi }}} \right)^{ - 1}}$ can be requested from the authors.

5.2.   Maximum product spacing estimates

The maximum product spacing (MPS) method is an alternative method to MLE for parameter estimation. This method was proposed by Cheng and Amin ^[33,34] as well as independently developed by Ranneby ^[35] as an approximation to the Kullback-Leibler measure of information. This method is based on the idea that differences (spacings) between the values of the cdf at consecutive data points should be identically distributed. Let ${X_{\left( 1 \right)}}, {X_{\left( 2 \right)}}, \ldots , {X_{\left( n \right)}}$ be ordered sample of size n from UGLBXII distribution. The geometric mean of the differences is given by

where, the difference ${D_i}$ is defined as

The maximum product spacing estimates (MPSEs), say ${\hat {\rm{ \mathsf{ α} }} _{MPS}}, {\hat {\rm{ \mathsf{ β} }} _{MPS}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{MPS}}$ of the ${\rm{ \mathsf{ α} }} , \, \, {\rm{ \mathsf{ β} }}$ and ${\rm{ \mathsf{ λ} }}$ are obtained by maximizing the geometric mean of the differences. Substituting cdf of the UGLBXII distribution in Eq (14) and taking logarithm of the above expression, we have

where, $F\left( {{x_{\left( 0 \right)}}} \right) = 0$ and $F\left( {{x_{\left( {n + 1} \right)}}} \right) = 1$. By maximizing $MPS\left( {\bf{\Xi }} \right)$, the ${\hat {\rm{ \mathsf{ α} }} _{MPS}}, {\hat {\rm{ \mathsf{ β} }} _{MPS}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{MPS}}$ can be obtained as the simultaneous solution of the following non-linear equations:

and

respectively, where

and

5.3.   Least squares estimates

Let ${X_{\left( 1 \right)}}, {X_{\left( 2 \right)}}, \ldots , {X_{\left( n \right)}}$ be ordered sample of size ${\text{n}}$ from UGLBXII distribution. Then, the expectation of the empirical cumulative distribution function is defined as

The least square estimates (LSEs) say, ${\hat {\rm{ \mathsf{ α} }} _{{\text{LSE}}}}, {\hat {\rm{ \mathsf{ β} }} _{LSE}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{LSE}}$, of ${\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }}$ and ${\rm{ \mathsf{ λ} }}$ are obtained by minimizing

Therefore, ${\hat {\rm{ \mathsf{ α} }} _{{\text{LSE}}}}, {\hat {\rm{ \mathsf{ β} }} _{LSE}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{LSE}}$ can be obtained as the simultaneous solution of the following non-linear equations:

and

where the ${F'_{\rm{ \mathsf{ α} }} }\left( x \right)$, ${F'_ {\rm{ \mathsf{ β} }} }\left( x \right)$ and ${F'_ {\rm{ \mathsf{ λ} }} }\left( x \right)$ are defined before.

5.4.   Weighted least squares estimates

Let ${X_{\left( 1 \right)}}, {X_{\left( 2 \right)}}, \ldots , {X_{\left( n \right)}}$ be ordered sample of size ${\text{n}}$ from the UGLBXII distribution. The variance of the empirical cumulative distribution function is defined as

Then, the weighted least square estimates (WLSEs) say, ${\hat {\rm{ \mathsf{ α} }} _{{\text{WLSE}}}}, {\hat {\rm{ \mathsf{ β} }} _{WLSE}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{WLSE}}$, of ${\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }}$ and ${\rm{ \mathsf{ λ} }}$ are obtained by minimizing

Therefore, ${\hat {\rm{ \mathsf{ α} }} _{{\text{WLSE}}}}, {\hat {\rm{ \mathsf{ β} }} _{WLSE}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{WLSE}}$ can be obtained as the simultaneous solution of the following non-linear equations:

and

5.5.   Anderson-Darling estimation

This estimator is based on Anderson-Darling goodness-of-fits statistics which was introduced by Anderson and Darling ^[36]. The Anderson-Darling (AD) minimum distance estimates, ${\hat {\rm{ \mathsf{ α} }} _{{\text{AD}}}}, {\hat {\rm{ \mathsf{ β} }} _{{\text{AD}}}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{{\text{AD}}}}$, of ${\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }}$ and ${\rm{ \mathsf{ λ} }}$ are obtained by minimizing

Therefore, ${\hat {\rm{ \mathsf{ α} }} _{{\text{AD}}}}, {\hat {\rm{ \mathsf{ β} }} _{{\text{AD}}}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{{\text{AD}}}}$ can be obtained as the simultaneous solution of the following non-linear equations:

and

5.6.   The Cramer-von Mises estimations

The Cramer-von Mises (CVM) minimum distance estimates, ${\hat {\rm{ \mathsf{ α} }} _{{\text{CVM}}}}, {\hat {\rm{ \mathsf{ β} }} _{{\text{CVM}}}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{{\text{CVM}}}}$, of ${\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }}$ and ${\rm{ \mathsf{ λ} }}$ are obtained by minimizing

Therefore, the ${\hat {\rm{ \mathsf{ α} }} _{{\text{CVM}}}}, {\hat {\rm{ \mathsf{ β} }} _{{\text{CVM}}}}$ and ${\hat {\rm{ \mathsf{ λ} }} _{{\text{CVM}}}}$ can be obtained as the simultaneous solution of the following non-linear equations:

and

We refer the interested readers to Chen and Balakrishnan ^[37] for AD and CVM goodness-of-fits statistics. To solve the above equations, Eqs (13), (15), (16)–(19) can be optimized either directly by using the R (optim and maxLik functions), SAS (PROC NLMIXED) and Ox package (sub-routine Max BFGS) or the non-linear optimization methods such as the quasi-Newton procedure to numerically optimize the $\ell \left( {\bf{\Xi }} \right)$, $MPS\left( {\bf{\Xi }} \right)$, $LSE\left( {\bf{\Xi }} \right)$, $WLSE\left( {\bf{\Xi }} \right)$, $AD\left( {\bf{\Xi }} \right)$ and $CVM\left( {\bf{\Xi }} \right)$ functions.

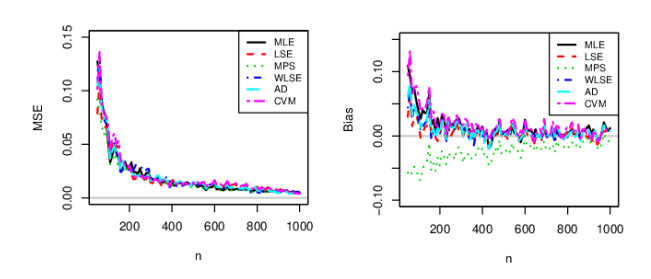
5.7.   Simulation experiments

In this Section, we perform a simulation study by using the UGLBXII to see the performance of the above estimators corresponding to this distribution and obtain the graphical results. We generate N = 1000 samples of size n = 20, 25, …, 1000 from the UGLBXII distribution with true parameter values ${\rm{ \mathsf{ α} }} = 1, {\rm{ \mathsf{ β} }} = 3$ and ${\rm{ \mathsf{ λ} }} = 0.5$. The random numbers generation is obtained by its quantile function. In this simulation study, we calculate the empirical bias and mean square errors (MSEs) of all estimators to compare in terms of their biases and MSEs with varying sample size. The empirical bias and MSE are calculated by (for $h = {\rm{ \mathsf{ α} }} , {\rm{ \mathsf{ β} }} , {\rm{ \mathsf{ λ} }}$)

and

respectively. We expect that the MSEs and biases are near zero. All results related to estimations were obtained using optim-CG routine in the R programme.

The results of this simulation study are shown in Figures 4–6. These figures show that all estimators are to be consistent, since the MSE and biases decrease with increasing sample size. It is clear that the estimates of parameters are asymptotically unbiased. For all parameters estimations, the performances of all estimators are close.

6.   Data Applications

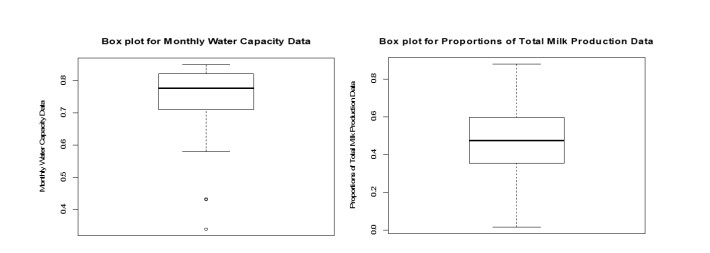
We verify the potentiality of the UGLBXII model via two real data sets. The first data set represents monthly water capacity ^[38,39] for February (1991 to 2010) at Shasta reservoir (California, USA). The second data set is about the proportion of total milk production in the first birth of 107 cows (Carnaúba farm, Taperoá, Brazil) from SINDI race ^[40]. Both data sets are converted to the interval (0, 1) using a transformation $\left( {{\text{data}} - {\text{dat}}{{\text{a}}_{\min }}} \right) \div \left( {{\text{dat}}{{\text{a}}_{{\text{max}}}} - {\text{dat}}{{\text{a}}_{\min }}} \right)$. We compare the UGLBXII distribution with models such as unit Log Burr XII (ULBXII), unit Log Lomax (ULLOM), unit modified Burr XII (UMBXII), Kumaraswamy (Kum), unit Weibull (UW), unit inverse Weibull (UIW), unit Gompertz (UGP) and beta. For the selection of the best fit distribution, we compute the estimate of likelihood ratio statistic ($- 2\, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\ell }$), Akaike information criterion (AIC), corrected Akaike information criterion (CAIC) and Bayesian information criterion (BIC) and Hannan-Quinn information criterion (HQIC) for all competing and sub-models. We also compute the MLEs along with their standard errors (SEs) in parentheses. Table 2 reports some descriptive measures for two data sets.

Table 2 shows that the monthly water capacity data set is significantly left-skewed, with high positive kurtosis. About the proportions of total milk production data set, it is left-skewed, with somewhat positive kurtosis.

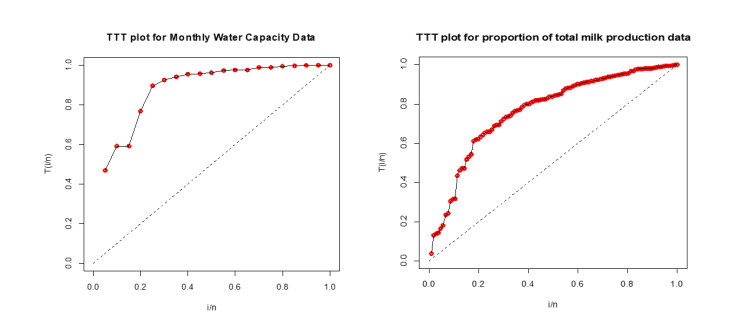
Figure 7 shows that both data sets are left-skewed. The nature of the two data sets differs in numerous features. Here, we study the statistical analysis by total time on test (TTT) for the two data sets in Figure 8.

In Figure 8, the TTT plots for both data sets are concave which suggests increasing failure intensity. So, the UGLBXII distribution is suitable to model these data sets.

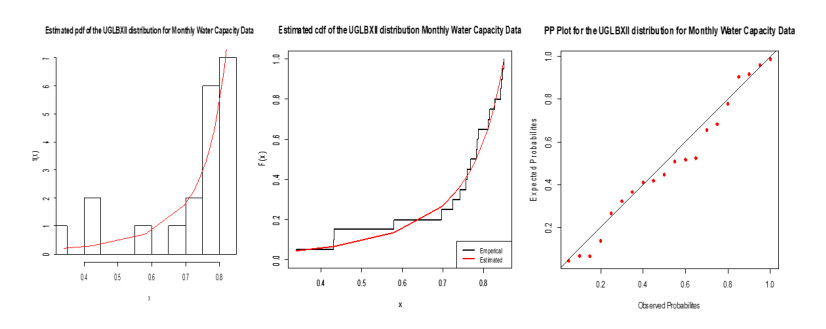
6.1.   Data set I: water capacity

Table 3 reports the MLEs, SEs (in parentheses) and measures W*, A*, K-S (p-values) for monthly water capacity data. Table 4 displays measures $- 2\, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\ell }$, AIC, CAIC, BIC and HQIC for water capacity data.

From the results presented in Tables 3 and 4, we see that the UGLBXII distribution is considered as the best model for monthly water capacity data because the values of all statistics are smaller for the proposed model. Figure 9 confirms this claim via the graphical display of fitted pdf, estimated cdf and PP plots of the UGLBXII distribution. From this figure, we can infer that the proposed model is closely fitted to monthly water capacity data.

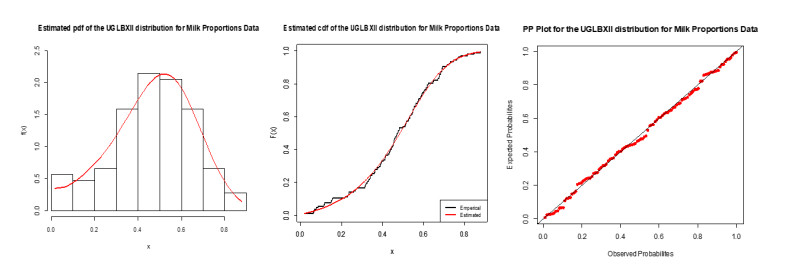
6.1.   Data set II: milk production

Table 5 reports the MLEs, SEs (in parentheses) and measures W*, A*, K-S (p-values) for milk production data. Tables 6 displays measures $- 2\, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\ell }$, AIC, CAIC, BIC and HQIC for proportions of total milk production data.

From the results presented in Tables 5 and 6, we see that the UGLBXII distribution is considered as the best model for proportions of total milk production data because the values of all statistics are smaller for the proposed model. Figure 10 confirms this claim via the graphical display of fitted pdf, estimated cdf and PP plots of the UGLBXII distribution. From this figure, we can infer that the proposed model is closely fitted to proportions of total milk production data.

7.   Conclusions

We derive and study the UGLBXII distribution. Some mathematical properties such as random number generator, sub-models, ordinary moments, generalized TL moments, conditional moments, reliability, uncertainty measures and characterizations are presented. We employ six different estimation methods to estimate the model parameters. We perform simulation studies on the basis of the graphical results to see the performances of the estimators of the UGLBXII distribution. We verify the potentiality of the UGLBXII distribution via two applications. In conclusion, it is expected that the UGLBXII model is the best fit for the monthly water capacity and the proportions of total milk production data analysis. The potentiality of the UGBLXII model illustrates that it is flexible, competitive and parsimonious to other existing distributions. Therefore, it should be included in the distribution theory to facilitate the researchers. Further, as perspective of future projects, we may consider several intensive subjects (i) statistical inferences using different sampling schemes such as simple random sampling (SRS) and rank set sampling (RSS); (ii) reliability analysis using SRS and RSS; (iii) Bayesian estimation of the UGLBXII parameters via SRS and RSS under different loss functions (iv) unit modified log Burr XII; (v) various characteristics of the bivariate and the multivariate extensions of the UGLBXII; (vi) Bayesian estimation of the UGLBXII parameters via complete and censored samples under different loss functions and (vi) the study of the complexity of the UGLBXII via Bayesian methods.

Conflict of interest

The authors declare no conflict of interest.