Stabilization of discrete-time positive switched T-S fuzzy systems subject to actuator saturation

1.   Introduction

The variational inequality problem (VIP) was introduced by Stampacchia ^[1] and provided a very useful tool for researching a large variety of interesting problems arising in physics, economics, finance, elasticity, optimization, network analysis, medical images, water resources, and structural analysis, see for example (^{[2,3,4,5,6,7,8,9,10,11,12,13,14,15]}) and references therein.

Let $\mathcal{H}$ be a real Hilbert space with inner product $\langle\cdot, \cdot\rangle$ and norm $\|\cdot\|$, respectively. Let $\mathcal{C}$ be a nonempty closed convex subset of $\mathcal{H}$. Let $\mathcal{B}:\mathcal{C}\longrightarrow \mathcal{H}$ be an operator.

In this article, our study is related to a classical variational inequality problem (VIP) which aims to find an element $x^{\dagger}\in \mathcal{C}$ such that

It is well known that $x^{\sharp}\in VI(\mathcal{B}, \mathcal{C})$ if and only if $x^{\sharp} = \mathcal{P}_{\mathcal{C}}(x^{\sharp}-\zeta \mathcal{B}x^{\sharp})$, where $\zeta > 0$, in other words, the VIP is equivalent to the fixed point problem (see ^[16]). Supposing that $\mathcal{B}$ is $\eta$-strongly monotone and $L$-Lipschitz continuous with $0 < \zeta < \frac{2\eta}{L^{2}}$, the following sequence $\{x_{n}\}$ of Picard iterates:

converges strongly to a point $x^{\dagger}\in VI(\mathcal{B}, \mathcal{C})$ due to the fact that $\mathcal{P}_{\mathcal{C}}(I-\zeta \mathcal{B})$ is a contraction on $\mathcal{C}$. However, in general, the algorithm (1.2) fails when $\mathcal{B}$ is monotone and $L$-Lipschitz continuous (see ^[17]). In ^[7], Korpelevich put forward an extragradient method which provided an important idea for solving monotone variational inequality:

where $f$ is monotone, $L$-Lipschitz continuous in the finite dimensional Euclidean space $R^{n}$ and $\lambda\in(0, \frac{1}{L})$.

The another motivation of this article is the split common fixed point problem which aims to find a point $u\in \mathcal{H}_{1}$ such that

The split common fixed point problem can be regarded as a generalization of the split feasibility problem. Recall that the split feasibility problem is to find a point satisfying

where $\mathcal{C}$ and $\mathcal{Q}$ are two nonempty closed convex subsets of real Hilbert spaces $\mathcal{H}_{1}$ and $\mathcal{H}_{2}$, respectively and $\mathcal{A}:\mathcal{H}_{1}\rightarrow \mathcal{H}_{2}$ is a bounded linear operator. Inverse problems in various disciplines can be expressed as the split feasibility problem and the split common fixed point problem. Problem (1.4) was firstly introduced by Censor and Segal ^[18]. Note that solving (1.4) can be translated to solve the fixed point equation:

Whereafter, Censor and Segal proposed an algorithm for directed operators. Since then, there has been growing interest in the split common fixed point problem (see ^{[19,20,21,22]}).

Censor et al. ^[23] first proposed split variational inequality problems by combining the variational inequality problem and the split feasibility problem. Very recently, in 2017, Tian and Jiang ^[24] considered the following split variational inequality problem: finding an element $u$ such that

where $\mathcal{T}:\mathcal{H}_{2}\rightarrow \mathcal{H}_{2}$ is nonexpansive, $\mathcal{B}:\mathcal{H}_{1}\rightarrow \mathcal{H}_{2}$ is a bounded linear operator with its adjoint $\mathcal{B}^{\ast}$, and $\mathcal{A}:\mathcal{C}\rightarrow \mathcal{H}_{1}$ is a monotone and $L$-Lipschitz continuous mapping. Then they presented the following iteration method by combining the extragradient method with CQ algorithm for solving the (1.6):

Algorithm 1.1. Choose an arbitrary initial value $x_{1}\in \mathcal{C}$. Assume $x_{n}$ has been constructed. Compute

They proved that the iterative sequence $\{x_{n}\}$ defined by Eq (1.7) converges weakly to an element $z\in\Gamma$, where $\Gamma$ is the set of solutions of the problem (1.6). However, Algorithm 1.1 fails, in general, to converge strongly in the setting of infinite-dimensional Hilbert spaces. We also notice that Algorithm 1.1 is involved with three metric projections in each iteration, which might seriously affect the efficiency of the method.

Motivated and inspired by the above works, in the present paper, we consider variational inequality problems and split common fixed point problems for finding an element $u$ such that

where $\{\mathcal{T}_{n}\}^{\infty}_{n = 1}:\mathcal{H}_{2}\rightarrow \mathcal{H}_{2}$ is an infinite family of nonexpansive mappings, $\mathcal{B}:\mathcal{H}_{1}\rightarrow \mathcal{H}_{2}$ is a bounded linear operator with its adjoint $\mathcal{B}^{\ast}$, and $\mathcal{A}:\mathcal{H}_{1}\rightarrow \mathcal{H}_{1}$ is a monotone and $L$-Lipschitz continuous mapping. In contrast to Tian and Jiang ^[24], we consider the common fixed points of an infinite family of nonexpansive mappings instead of only the fixed points of a nonexpansive mapping. The efficiency of the algorithm is also improved by removing the projection operator in the first iteration which might affect the efficiency of the method to a certain extent. Finally, we present a very simple modification to extragradient method, which makes our algorithm have the strong convergence. It is well known that the strong convergence theorem is always more convenient to use.

This paper is organized as follows: In Section 2, we give some definitions and key lemmas which are used in this paper. Section 3 consists of our algorithms and provides the strong convergence theorems. In Section 4, numerical examples are provided for illustration. Finally, this paper is concluded in Section 5.

2.   Preliminaries

Let $\mathcal{H}$ be a real Hilbert space with inner product $\langle\cdot, \cdot\rangle$ and norm $\|\cdot\|$, respectively. Let $\mathcal{C}$ be a nonempty closed convex subset of $\mathcal{H}$. Let $\mathcal{T}:\mathcal{C}\longrightarrow \mathcal{C}$ be an operator. We use $\mathrm{Fix}(\mathcal{T})$ to denote the set of fixed points of $\mathcal{T}$, that is, $\mathrm{Fix}(\mathcal{T}) = \{x^{\dagger} |x^{\dagger} = Tx^{\dagger}, x^{\dagger} \in \mathcal{C}\}.$ First, we give some definitions and lemmas related to the involved operators.

Definition 2.1. An operator $T:C\longrightarrow C$ is said to be nonexpansive if $\|Tu - Tv\|\leq\|u - v\|$ for all $u, v \in C$.

Definition 2.2. An operator $\mathcal{A:C\longrightarrow H}$ is said to be monotone if $\langle \mathcal{A}x-\mathcal{A}y, x-y\rangle\geq0$ for all $x, y \in \mathcal{C}$.

A monotone operator $\mathcal{R}:\mathcal{H}\rightrightarrows2^{\mathcal{H}}$ is called maximal monotone if the graph of $\mathcal{R}$ is a maximal monotone set.

Definition 2.3. An operator $\mathcal{T:C\longrightarrow H}$ is said to be $L$-Lipschitzian if there exists $L > 0$ such that $\|\mathcal{T}x - \mathcal{T}y\|\leq L\|x - y\|$ for all $x, y \in \mathcal{C}$.

Usually, the convergence of fixed point algorithms requires some additional smoothness properties of the mapping $\mathcal{T}$ such as demi-closedness.

Definition 2.4. An operator $\mathcal{T}$ is said to be demiclosed if, for any sequence $\{u_{n}\}$ which weakly converges to $u^{*}$, and if $\mathcal{T}u_{n}\longrightarrow w$, then $\mathcal{T}u^{*} = w$.

Recall that the (nearest point or metric) projection from $\mathcal{H}$ onto $\mathcal{C}$, denoted by $\mathcal{P}_{\mathcal{C}}$, assigns to each $u\in \mathcal{H}$, the unique point $\mathcal{P}_{\mathcal{C}}u\in \mathcal{C}$ with the property:

The metric projection $\mathcal{P}_{\mathcal{C}}$ of $\mathcal{H}$ onto $\mathcal{C}$ is characterized by

for all $u\in \mathcal{H}, v\in \mathcal{C}$. It is well known that the metric projection $\mathcal{P}_{\mathcal{C}}:\mathcal{H}\rightarrow \mathcal{C}$ is firmly nonexpansive, that is,

for all $u, v\in \mathcal{H}$. More information on the metric projection can be found, for example, in Section 3 of the book by Goebel et al. (see ^[25]).

For all $u, v \in H$, the following conclusions hold:

and

Let $\{\mathcal{T}_{n}\}^{\infty}_{n = 1}:\mathcal{H}\rightarrow \mathcal{H}$ be an infinite family of nonexpansive mappings and $\lambda_{1}, \lambda_{2}, ...$ be real numbers such that $0\leq\lambda_{i}\leq1$ for each $i\in\mathbb{N}$. For any $n\in\mathbb{N}$, define a mapping $\mathcal{W}_{n}$ of $\mathcal{C}$ into $\mathcal{H}$ as follows:

Such a mapping $\mathcal{W}_{n}$ is called the $\mathcal{W}$-mapping generated by $\mathcal{T}_{1}, \mathcal{T}_{2}, ..., \mathcal{T}_{n}$ and $\lambda_{1}, \lambda_{2}, ..., \lambda_{n}$. We have the following crucial Lemma concerning $\mathcal{W}_{n}$:

Lemma 2.1. ^[26] Let $\mathcal{H}$ be a real Hilbert space. Let $\{\mathcal{T}_{n}\}^{\infty}_{n = 1}:\mathcal{H}\rightarrow \mathcal{H}$ be an infinite family of nonexpansive mappings such that $\bigcap^{\infty}_{n = 1}\mathrm{Fix}$$(\mathcal{T}_{n})\neq\emptyset$. Let $\lambda_{1}, \lambda_{2}, ...$ be real numbers such that $0\leq\lambda_{i}\leq b < 1$ for each $i\geq1$. Then we have the following:

(1) For any $x\in\mathcal{H}$ and $k\geq1$, the limit $\lim_{n\rightarrow \infty}\mathcal{U}_{n, k}x$ exists;

(2) $\mathrm{Fix}$$(\mathcal{W}) = \bigcap^{\infty}_{n = 1}\mathrm{Fix}$$(\mathcal{T}_{n})$, where $\mathcal{W}x = \lim_{n\rightarrow \infty}\mathcal{W}_{n}x = \lim_{n\rightarrow \infty}\mathcal{U}_{n, 1}x, \ \forall x\in\mathcal{C};$

(3) For any bounded sequence $\{x_{n}\}\subset \mathcal{H}$, $\lim_{n\rightarrow \infty}\mathcal{W}x_{n} = \lim_{n\rightarrow \infty}\mathcal{W}_{n}x_{n}$.

Lemma 2.2. ^[27] Assume that $\{\alpha_{n}\}$ is a sequence of nonnegative real numbers such that

where $\{\gamma_{n}\}$ is a sequence in $(0, 1)$ and $\{\delta_{n}\}$ is a sequence such that

(1) $\sum^{\infty}_{n = 1}\gamma_{n} = \infty$;

(2) $\limsup_{n\rightarrow \infty}\frac{\delta_{n}}{\gamma_{n}}\leq0$ or $\sum^{\infty}_{n = 1}|\delta_{n}| < \infty.$ Then $\lim_{n\rightarrow \infty}\alpha_{n} = 0.$

Lemma 2.3. ^[28] Let $\{\varpi_{n}\}$ be a sequence of real numbers. Assume there exists at least a subsequence $\{\varpi_{n_{k}}\}$ of $\{\varpi_{n}\}$ such that $\varpi_{n_{k}}\leq\varpi_{n_{k+1}}$ for all $k\geq0$. For every $n\geq N_{0}$, define an integer sequence $\{\tau(n)\}$ as:

Then, $\tau(n) \rightarrow \infty$ as $n\rightarrow \infty$ and for all $n\geq N_{0}$, we have $max\{ \varpi_{\tau(n)}, \varpi_{n}\}\leq\varpi_{\tau(n)+1}$.

3.   Main results

In this section, we introduce our algorithm and prove its strong convergence. Some assumptions on the underlying spaces and involved operators are listed below.

$(R_{1})$ $\mathcal{H}_{1}$ and $\mathcal{H}_{2}$ are two real Hilbert spaces and $\mathcal{C}\subset\mathcal{H}_{1}$ is a nonempty closed convex subset.

$(R_{2})$ $\mathcal{B}:\mathcal{H}_{1}\rightarrow \mathcal{H}_{2}$ is a bounded linear operator with its adjoint $\mathcal{B}^{\ast}$.

$(R_{3})$ $\mathcal{A}:\mathcal{H}_{1}\rightarrow \mathcal{H}_{1}$ is a monotone and $L$-Lipschitz continuous mapping.

$(R_{4})$ $\Omega = \{\hat{x}|\hat{x}\in VI(\mathcal{A}, \mathcal{C})$ and $\mathcal{B}\hat{x}\in \bigcap^{\infty}_{n = 1} \mathrm{Fix}(\mathcal{T}_{n})\}$, where $\Omega$ is the set of solutions of the problem (1.8).

Next, we present the following iterative algorithm to find a point $\hat{x}\in\Omega$.

Algorithm 3.1. Choose an arbitrary initial value $x_{1}\in \mathcal{H}$. Assume $x_{n}$ has been constructed. Compute

where $\{\alpha_{n}\}$ is a sequence in $(0, 1)$, $\varsigma_{n}$ is a sequence in $(0, \frac{1}{L})$, and $\tau_{n}$ is a sequence in $(0, \frac{1}{\|\mathcal{B}\|^{ 2}})$.

Theorem 3.1. If $\Omega\neq\emptyset$ and the following conditions are satisfied:

($C_{1}$) $\lim_{n\rightarrow \infty}\alpha_{n} = 0\ and\ \sum^{\infty}_{n = 0}\alpha_{n} = \infty$;

($C_{2}$) $0 < \liminf_{n\rightarrow \infty}\varsigma_{n}\leq \limsup_{n\rightarrow \infty}\varsigma_{n} < \frac{1}{L}$;

($C_{3}$) $0 < \liminf_{n\rightarrow \infty}\tau_{n}\leq \limsup_{n\rightarrow \infty}\tau_{n} < \frac{1}{\|\mathcal{B}\|^{ 2}}$.

Then, the iterative sequence $\{x_{n}\}$ defined by Eq (3.1) strongly converges to the minimum-norm solution $\hat{x}( = \mathcal{P}_{\Omega}\theta)$.

Proof. Set $z = \mathcal{P}_{\Omega}\theta$. We can obtain that

It follows from (2.1) that

We also observe that

On the other hand, we have that

Hence, we can derive that

Owing to the assumption ($C_{2}$), it follows from (3.6) that

and so

which implies that the sequence $\{x_{n}\}$ is bounded. In view of (3.2) and (3.7), we obtain that

CASE $\mathbb{I}$. Suppose that there exists $m > 0$ such that the sequence $\{\|x_{n}-z\|\}$ is decreasing when $n\geq m$. Then, $\lim_{n\rightarrow \infty}\|x_{n}-z\|$ exists. Consequently, according to the assumptions ($C_{1}$) and ($C_{3}$), we deduce that

In virtue of the boundedness of the sequence $\{\mathcal{B}x_{n}\}$ and Lemma 2.1, we get that

This together with (3.24) implies that

It follows from (3.6) that

Thanks to the boundedness of the sequence $\{x_{n}\}$, we derive that

In view of (3.30), we can also get that

Combining (3.14) and (3.15), we obtain that

On the other hand, we get that

Hence, by (3.14), it turns out that

and consequently, according to (3.16), we have that

Next, we can take a subsequence $\{n_{i}\}$ such that

By the boundedness of the real sequence $\{x_{n_{i}+1}\},$ we may assume that $x_{n_{i}+1}\rightharpoonup x^{\dagger}.$ Since $\mathcal{W}$ is nonexpansive, we can derive that $\mathcal{B}x^{\dagger} = \mathcal{W}\mathcal{B}x^{\dagger}$(see Corollary 4.28 in ^[29]), that is, $\mathcal{B}x^{\dagger}\in Fix(\mathcal{W}) = \bigcap^{\infty}_{n = 1}Fix(\mathcal{T}_{n})$.

Now, we show that $x^{\dagger}\in VI(\mathcal{A}, \mathcal{C})$. Let

where $\mathcal{N}_{\mathcal{C}}(v)$ is the normal cone to $\mathcal{C}$ at $v$. According to Reference ^[30], we can easily derive that $\mathcal{R}$ is maximal monotone. Let $(v, w)\in G(\mathcal{R})$. Since $w -Av \in\mathcal{N}_{\mathcal{C}}(v)$ and $x_{n}\in \mathcal{C}$, we have that

Noting that, due to $v\in \mathcal{C}$, we get

It follows that

Thus, we can deduce that

As $i\rightarrow \infty$, we obtain that

By the maximal monotonicity of $\mathcal{R}$, we derive that $x^{\dagger}\in\mathcal{R}^{-1}0$. Hence, $x^{\dagger}\in VI(\mathcal{A}, \mathcal{C})$. Therefore, $x^{\dagger}\in\Omega$. Since the norm of the Hilbert space $\mathcal{H}_{1}$ is weakly lower semicontinuous(see Lemma 2.42 in ^[29]), we have the following inequality:

and therefore

From (3.7), we observe that

Thanks to $z = \mathcal{P}_{\Omega}\theta$ and $x^{\dagger}\in\Omega$, we can deduce that

Applying Lemma 2.2 to (3.23), we derive that $\lim_{n\rightarrow \infty}\|x_{n}-z\| = 0$, which implies that the sequence $\{x_{n}\}$ converges strongly to $z$.

CASE $\mathbb{II}$. For any $n_{0}$, there exists an integer $m\geq n_{0}$ such that $\|x_{m}-z\|\leq\|x_{m+1}-z\|$. At this case, we set $\varpi_{n} = \|x_{n}-z\|$. For $n\geq n_{0}$, we define a sequence $\{\tau_{n}\}$ by

It is easy to show that $\tau(n)$ is a non-decreasing sequence such that

and

This together with (3.9) implies that

Employing techniques similar to CASE $\mathbb{I}$, we have

and

Since $\varpi_{\tau(n)}\leq\varpi_{\tau(n)+1},$ we have

By (3.25), we obtain that

and so

By Eq (3.26), we also obtain

In the light of the last inequality and Eq (3.28), we derive that

Applying Lemma 2.3, we obtain

Therefore, we get that $\varpi_{n}\rightarrow0$, that is, $x_{n}\rightarrow z$. This completes the proof. □

Algorithm 3.2. Choose an arbitrary initial value $x_{1}\in \mathcal{C}$. Assume $x_{n}$ has been constructed. Compute

where $\{\alpha_{n}\}$ is a sequence in $(0, 1)$, $\varsigma_{n}$ is a sequence in $(0, \frac{1}{L})$, and $\tau_{n}$ is a sequence in $(0, \frac{1}{\|\mathcal{B}\|^{ 2}})$.

Theorem 3.2. If $\hat{\Omega}\neq\emptyset$ and the following conditions are satisfied:

($C_{1}$) $lim_{n\rightarrow \infty}\alpha_{n} = 0\ and\ \sum^{\infty}_{n = 0}\alpha_{n} = \infty$;

($C_{2}$) $0 < \liminf_{n\rightarrow \infty}\varsigma_{n}\leq \limsup_{n\rightarrow \infty}\varsigma_{n} < \frac{1}{L}$;

($C_{3}$) $0 < \liminf_{n\rightarrow \infty}\tau_{n}\leq \limsup_{n\rightarrow \infty}\tau_{n} < \frac{1}{\|\mathcal{B}\|^{ 2}}$.

Then, the iterative sequence $\{x_{n}\}$ defined by Eq (3.29) strongly converges to the minimum-norm solution $\hat{x}( = \mathcal{P}_{\hat{\Omega}}\theta)$, where

Algorithm 3.3. Choose an arbitrary initial value $x_{1}\in \mathcal{C}$. Assume $x_{n}$ has been constructed. Compute

where $\{\alpha_{n}\}$ is a sequence in $(0, 1)$ and $\varsigma_{n}$ is a sequence in $(0, \frac{1}{L})$.

Theorem 3.3. If $\hat{\Omega}\neq\emptyset$ and the following conditions are satisfied:

($C_{1}$) $lim_{n\rightarrow \infty}\alpha_{n} = 0\ and\ \sum^{\infty}_{n = 0}\alpha_{n} = \infty$;

($C_{2}$) $0 < \liminf_{n\rightarrow \infty}\varsigma_{n}\leq \limsup_{n\rightarrow \infty}\varsigma_{n} < \frac{1}{L}$;

Then, the iterative sequence $\{x_{n}\}$ defined by Eq (3.30) strongly converges to the minimum-norm solution $\hat{x}( = \mathcal{P}_{\Omega}\theta)$, where $\hat{\Omega} = \{\hat{x}|\hat{x}\in VI(\mathcal{A}, \mathcal{C})\}\neq\emptyset.$

4.   Numerical illustrations

In this section, we present some numerical examples to illustrate our main results. The MATLAB codes run in MATLAB version 9.5 (R2018b) on a PC Intel(R) Core(TM)i5-6200 CPU @ 2.30 GHz 2.40 GHz, RAM 8.00 GB. In all examples $y$-axes shows the value of $\|x_{n+1}-x_{n}\|$ while the $x$-axis indicates to the number of iterations.

Example 4.1. Let $\mathcal{H}_{1} = \mathcal{H}_{2} = R^{n}$. The feasible set is defined as:

Let $G:R^{n}\rightarrow R^{n}$ is a linear operator defined by:

for all $x\in R^{n}$, where $G = (g_{ij})_{1\leq i, j \leq n}$ is a matrix in $R^{n\times n}$ whose terms are given by:

It is obvious that $\mathcal{A}$ is $\|G\|$-Lipschitz continuous. By a direct calculation, we also have that $\langle \mathcal{A}x, x\rangle = \langle Gx, x\rangle = 0$ and so, $\mathcal{A}$ is monotone. Let $\mathcal{B}$ be a matrix in $R^{n\times n}$ which is randomly generated.

Taking cognizance of the difference of the problems handled by Algorithm 3.1 and Algorithm in Tian and Jiang ^[24], in order to comparing these two algorithms, we make a very small modification to the one in ^[24] such that it can also solve the problem (1.8). The modified algorithm can be written as follows:

Algorithm 4.1.

According to the proof of Theorem 3.1, we can easily verify that this modified algorithm works for solving (1.8). The values of control parameters in these two Algorithms are $\varsigma_{n} = \frac{1}{2\|G\|}$, $\tau_{n} = \frac{1}{2\|B\|^{2}}$, $\alpha_{1} = \frac{1}{2}$, $\alpha_{n} = \frac{1}{n}$(for all $n\geq2$), $\lambda_{n} = \frac{1}{n+1}$ and $x_{1} = (1, \cdots, 1)^{T}$, and the infinite family of nonexpansive mappings $\{\mathcal{T}_{k}\}^{\infty}_{k = 1}:R^{n}\rightarrow R^{n}$ is defined by:

for all $x\in R^{n}$, where $\{M_{k}\}$ is a sequence of diagonal matrixes in $R^{n\times n}$:

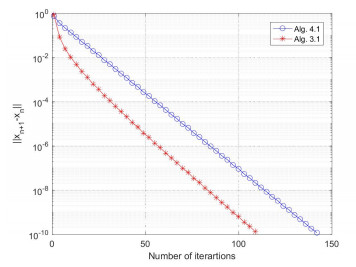
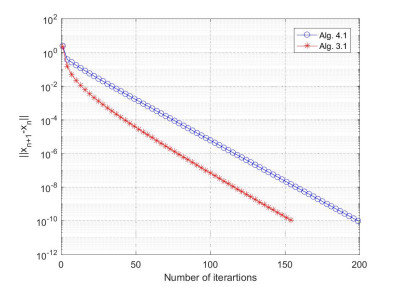
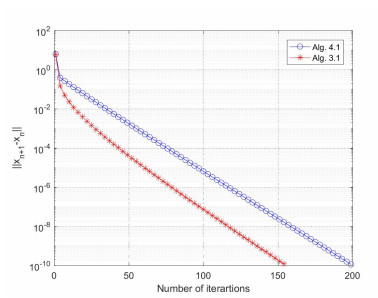
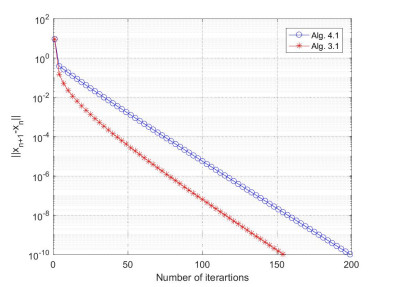
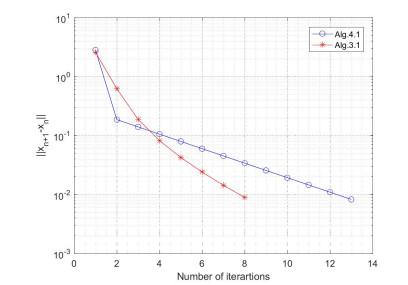
The numerical results of the Example 4.1 are reported in Table 1 and Figures 1–4 by using the stopping criterion $\|x_{n+1}-x_{n}\|\leq10^{-10}$.

Example 4.2. Let $\mathcal{H}_{1} = \mathcal{H}_{2} = L^{2}([0, 1])$ with the inner product:

and the induced norm:

The feasible set is defined as:

The mapping $\mathcal{A}:L^{2}([0, 1])\rightarrow L^{2}([0, 1])$ is defined by:

It is easy to see that

and

Therefore, the operator $\mathcal{A}$ is monotone and $2$-Lipschitz continuous. Let $\mathcal{W}_{n} = \mathcal{I}$(Identity mapping). The values of control parameters for Algorithm 4.1 and Algorithm 3.1 are $\varsigma_{n} = \frac{1}{4}$, $\alpha_{1} = \frac{1}{2}$, $\alpha_{n} = \frac{1}{n}$(for all $n\geq2$), $\lambda_{n} = \frac{1}{n+1}$ and $x_{1} = 8t^{2}$. It can be seen easily that $\{x_{n}\}$ strongly converges to the zero vector $\theta(\in L^{2}([0, 1])).$ The numerical results of the Example 4.2 are reported in Table 2 and Figures 5 by using the stopping criterion $\|x_{n+1}-x_{n}\|\leq\varepsilon = 0.01$.

Remark 4.1. The numerical results of Example 4.1 and Example 4.2 show that the performance of Algorithm 3.1 is better than Algorithm 4.1 both in CPU time and the number of iterations. Algorithm 3.1 is more effective in both finite and infinite dimensional spaces and especially in conditions involving complex projection calculations, see Tables 1, 2 and Figures 1–5. In Example 4.1, we observe that the number of iterations tends to be stable, while the CPU time increases, as $n$ increasing.

5.   Conclusions

In the present paper, we consider variational inequality problems and split common fixed point problems. We construct an iterative algorithm for solving Eq (1.8) which can be regard as a modification and generalization of Algorithm 1.1 with fewer metric projection operators. Under some mild restrictions, we demonstrate the strong convergence analysis of the presented algorithm. We also give some numerical examples to illustrate our main results. Noticeably, in our article, $\mathcal{A}$ is assumed to a monotone and $L$-Lipschitz continuous mapping. A natural question arises: how to weaken this assumption?

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by National Natural Science Foundation of China under Grant (No. 62103289), National Natural Science Foundation of China (No. 11761074), Project of Jilin Science and Technology Development for Leading Talent of Science and Technology Innovation in Middle and Young and Team Project (No. 20200301053RQ), and Natural Science Foundation of Jilin Province(No. 2020122336JC).

Conflict of interest

The authors declare no conflict of interest.