Phase transition for piecewise linear fibonacci bimodal map

1.   Introduction

The dynamical properties of unimodal interval maps have been extensively studied recently, for backgrounds and history, see for example ^[14,17] and the references therein. Major breakthroughs were the complete solution of Milnor's attractor problem for smooth unimodal maps with small critical order and the proof of Palis' conjecture for real analytic unimodal maps.

From a modern perspective, it is essential (for both of the two problems) to study the local geometry around the critical point of a non-renormalizable map. A useful tool is the so-called principal nest. Let $f: [0, 1]\to [0, 1]$ be a (smooth) unimodal map. Let $I^0 = (\hat q, q)$ where $q \in (0, 1)$ is the orientation reversing fixed point of $f$ and $f (\hat q) = f(q)$. Let $I^0 \supset I^1 \supset I^2 \supset \ldots$ be the principal nest of $f$. The scaling factor of $f$ is defined as $\mu_n : = |I^{n+1}|/|I^n|$. One of the main studies in interval dynamics is the classification of the asymptotic property of $\lambda_n$ when $n$ tends to $\infty$. It is well-known, see ^[12], that decay of geometry property, which means $\mu_{n_i}$ decreases to 0 exponentially fast for a subsequence $\{ n_i\}$, excludes the existence of wild attractor. It was proved in ^[6] that if $\mu_n$ is sufficiently small for all $n$ large enough, then $f$ has an acip. On the other hand, a wild attractor occurs for a unimodal map $f$ with very large critical order and specific combinatorics including Fibonacci combinatorics. We remark here that a wild attractor is a Cantor attractor of a non-renormalizable map with full Lebesgue measure attraction of basin but is of the first Baire category. It is a metric attractor, but fails to be a topological one in the sense of Milnor.

Fibonacci unimodal maps can be treated as the prototype of non-renormalizable unimodal maps. A unimodal map $f$ has Fibonacci combinatorics if the first return time $s_n$ of the critical point $c$ to the principal nest $I^n$ coincides with that Fibonacci numbers. Fibonacci combinatorics were first introduced by Branner and Hubbard ^[1] for cubic polynomials with one critical point escaping to infinity, and by Hofbauer and Keller ^[7] for unimodal maps with slow recurrence. Existence of wild attractor for Fibonacci unimodal map with sufficiently high critical order was verified in ^[3]. It is quite interesting that the geometry and metic properties of a Fibonacci unimodal map will change as the critical order grows. To be precise, let $f$ be the unique map from the family $x \to a (1 - |2 x -1|^{\ell})$ with Fibonacci combinatorics. It is now well-known that: if $\ell \in (1, 2]$, then $f$ possess decay of geometry and admits an absolutely continuous (respect to Lebesgue measure) invariant probability measure (acip for short) ^[10,11]; if $\ell \in (2, \infty)$, then $f$ possess bounded geometry in the sense that $\mu_n$ is uniformly bounded from above and below by constants depending only on $\ell$ ^[8,12]; if $\ell$ is sufficient large, then $f$ has a wild attractor and a dissipative $\sigma$-finite acim, ^[3] (Here an acim means an absolutely continuous (respect to Lebesgue measure) invariant measure).

But what about multimodal maps? Even for the simplest case, the cubic bimodal maps, is rarely known. A conceptual dichotomy was due to Shen ^[15] where he showed that a polynomial possesses either 'decay of geometry' or 'essentially bounded geometry'. A concrete example of a non-renormalizable bimodal cubic polynomial with bounded geometry was given by Świtiek and Vargas in ^[18]. Principal nest is a useful tool when studying geometric properties of interval maps, but seems not convenient to treat about metric problems in the multimodal case. Unlike in the unimodal case, the scaling factors fail to give distortion control of the first return map of the principal nest, because the critical branches may fold many times. However, in ^[19] Vargas constructed the Fibonacci bimodal map by use of the natural symmetry of bimodal maps using twin principal nest (see subsection 2.1). It was proved by Vargas (unpublished) and the authors ^[9] that the cubic Fibonacci polynomial possesses decay of geometry. Actually, we proved such a property for a general class of maps.

A natural question arises now: What are the metric properties of the Fibonacci bimodal map when the critical order grows? It is quite a difficult question, for we do not even have 'a priori bounds' (or real bounds) in this settings. We cannot adapt the proofs in ^[9] to do so because the complex tools used there rely heavily on the fact that the two critical points are locally quasi-quadratic. Despite difficulties we study Fibonacci bimodal maps under a restrictive condition in this paper. We aim to give a somewhat hypothetical picture of smooth Fibonacci bimodal maps, in particular when the critical order changes. We first study the combinatorics of the Fibonacci bimodal map in the context of kneading map. We also give an equivalent description of Fibonacci combinatorics. And by doing this we can construct an induced Markov map over such a map naturally. The metric property of the original map depends on the conservative and dissipative behaviors of the induced Markov map. To avoid the difficulty of distortion control, we construct a countably piecewise linear bimodal map $f$ with Fibonacci combinatorics which is also an odd function. By carefully choosing the slope, we show that the induced Markov map $F$ is also piecewise linear on each branches in forms of $[z_{j-1}, z_j]$ or $[y_j, y_{j-1}]$, where $z_j$ and $y_j$ are closest precritical points. We let $z_j$ tends to the critical points in a geometric manner ($|z_j-c| = O(\lambda^j)$) so that $f$ depends solely on the single parameter $\lambda \in (0, 1)$. The change of $\lambda$ will be reflected on the change of the critical order. Then we will show that the one-parameter family $f_{\lambda}$ has a phase transition from Lebesgue conservative to dissipative behaviors.

The Main Theorem is stated as follows. Note that in this non-differentiable setting, the critical order $\ell$ is defined by the property that $C^{-1} |x-c|^{\ell} \leq |f(x)-f(c)|\leq C|x-c|^{\ell}$ for some $C > 0$ and all $x\in [-1, 0]$. We use a single symbol $\ell$ here since the critical order of the two critical points are equal. Our theorem yields the precise values of critical orders $\ell = \ell(\lambda)$, where each of the different behaviors occurs.

Main Theorem. The piecewise linear bimodal map $f_\lambda$ (i.e., with a geometric manner defined in Sect. 3) satisfies the following properties:

(1) The critical order $\ell = 3+\frac{2\log(1-\lambda)}{\log \lambda}$.

(2) If $\lambda \in (\frac{1}{2}, 1)$, i.e., $\ell > 5$, then $f_\lambda$ has a wild attractor.

(3) If $\lambda \in [\frac{2}{3+\sqrt5}, \frac{1}{2}]$, i.e., $4 \leq \ell \leq 5$, then $f_\lambda$ has no wild attractor, but an infinite $\sigma$-finite acim.

(4) If $\lambda \in (0, \frac{2}{3+\sqrt5})$, i.e., $3 < \ell < 4$, then $f_\lambda$ has an acip.

This paper is organized as follows. In Section 2 we study the topological properties of the Fibonacci bimodal map in the context of kneading map. We also give an equivalent description of Fibonacci combinatorics and construct the induced Markov map. In Section 3 we construct the piecewise linear bimodal map $f$ which is an odd function and has the Fibonacci combinatorics. In Section 4 we let the closest precritical points tend to the critical points in a geometric manner and turn the original system into a one-parameter family. In Section 5 we use a random walk argument to prove the Main Theorem.

2.   Combinatorics

2.1.   Fibonacci bimodal map

Denote $I = [-1, 1]$. A continuous map $f: I \to I$ is called bimodal if $f(\{-1, 1 \}) = \{-1, 1 \}$ and $f$ has exactly one local maximum and one local minimum in $(-1, 1)$. The two extreme points specified by $c < d$ are called turning points and $f$ is strictly monotone on subintervals determined by these points. If the points $\{-1, 1 \}$ are fixed then we say that the bimodal map $f$ is positive and in the case that these points are permuted we say that $f$ is negative.

Definition 2.1. A bimodal map $f$ is called combinatorially symmetric if there exists an orientation-reversing homeomorphism $h : I \to I$ such that $h \circ f = f \circ h$.

Let $\mathscr B$ denote the collection of bimodal maps $f : I \to I$ which have no wandering intervals and no attracting periodic cycles. Let $\mathscr B^+$ and $\mathscr B^-$ denote, respectively, the subset of positive and negative bimodal maps from class $\mathscr B$. Let $\mathscr B_*$ denote the collection of maps from $\mathscr B$ which are combinatorially symmetric. If a bimodal map $f \in \mathscr B_*$, then there is a fixed point $p$ between $c$ and $d$ with three preimages $\{ p, p_1, p_2\}$ specifying by $p_1 < p < p_2$. Define $I^0 = (p_1, p)$, $J^0 = (p, p_2)$.

Assume that both $c$ and $d$ are recurrent and define

inductively such that, for $k\geq 1$, the intervals $I^{k}$ and $J^{k}$ are components of the domain of the first return map $\phi_k$ to $I^{k-1} \cup J^{k-1}$, which are called critical domains of $\phi_k$. The critical return times $s_k$ are defined by $\phi_k(c) = f^{s_k}(c)$ and $\phi_k(d) = f^{s_k}(d)$. The first return map $\phi_k$ is called central return if $\phi_k(c) \in I^k \cup J^k$ or $\phi_k(d) \in I^k \cup J^k$; otherwise $\phi_k$ is called non-central return.

Definition 2.2. A bimodal map $f \in \mathscr B$ has Fibonacci combinatorics if and only if $s_k$ is well-defined for all $k \geq 1$ and coincide with the Fibonacci sequence $2, 3, 5, \ldots.$

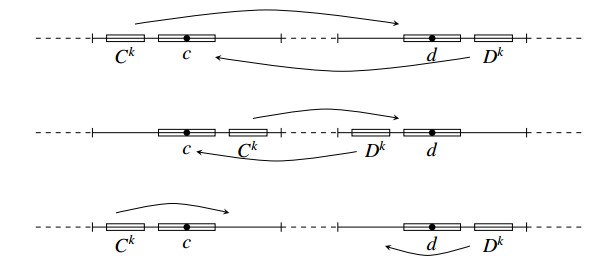
According to ^[19], Fibonacci bimodal map is combinatorially symmetric and has no central return. Then for each $k \geq 1$, let $C^k \subset I^{k-1}$ and $D^k \subset J^{k-1}$ be the return domains intersecting $\{ \phi_k(c), \phi_k(d)\}$, which are called post critical domains. Note that the post critical branches $\phi_k|C^k$ and $\phi_k|D^k$ are monotone and onto. The Fibonacci combinatorics implies some constraints on the position of the post-critical domains and their images. This leads us to consider the three types of first return map $\phi_k$ below:

● Type $\mathcal A$: if $\phi_k(C^k) = J^{k-1}$, $\phi_k(I^k) \subset J^{k-1}$ and $\phi_k(D^k) = I^{k-1}$, $\phi_k(J^k) \subset I^{k-1}$;

● Type $\mathcal B$: if $\phi_k(C^k) = J^{k-1}$, $\phi_k(I^k) \subset I^{k-1}$ and $\phi_k(D^k) = I^{k-1}$, $\phi_k(J^k) \subset J^{k-1}$;

● Type $\mathcal C$: if $\phi_k(C^k) = I^{k-1}$, $\phi_k(I^k) \subset J^{k-1}$ and $\phi_k(D^k) = J^{k-1}$, $\phi_k(J^k) \subset I^{k-1}$.

Figure 1 illustrates a possible position but still without the orientation. Furthermore, the Fibonacci combinatorics shows that the sequence of first return maps $\phi_1, \phi_2, \phi_3, \ldots$ exhibits a specific sequence of types as in Fact 2.1 below. This together with an analysis of the orientation and the precise position of the branches of their first return maps will determine the topological properties of a Fibonacci bimodal map. So for each type $\mathcal A$, $\mathcal B$ and $\mathcal C$, subdivide in subtypes $\mathcal A^{ij}$, $\mathcal B^{ij}$ and $\mathcal C^{ij}$ with $i, j \in \{ +, - \}$. Where $i = +$ or $i = -$ if the post critical branches of $\phi_k$ are orientation-preserving or orientation-reversing; and $j = +$ or $j = -$ if $\phi_k$ is local maximal or minimal at $c$.

Fact 2.1. ^[9,19] If $f \in \mathscr B$ has Fibonacci combinatorics, then for all $k \geq 1$ the following holds:

(1) $\phi_k(I^k \cup J^k) \supset I^k \cup J^k$.

(2) Denote $s_0 = 1$, $s_1 = 2$ and $s_{n+1} = s_n +s_{n-1}$ for $n \geq 1$. Then $\phi_k|I^k$ and $\phi_k|J^k$ equal to $f^{s_k}$, while $\phi_k|C^k$ and $\phi_k|D^k$ equal to $f^{s_{k-1}}$. Furthermore, $\phi_k|I^k \cup J^k = \phi_{k-1}^2$ while $\phi_k|C^k \cup D^k = \phi_{k-1}$.

(3) The sequence $\phi_1, \phi_2, \phi_3, \ldots$ of the first return maps exhibits the sequence of types

or

depending respectively on $f \in \mathscr B^+$ or $f \in \mathscr B^-$. See Figure 2.

2.2.   Cutting time

The definition of Fibonacci combinatorics for bimodal maps was stated in the sense of generalized renormalization. In the unimodal case, the Fibonacci unimodal map can be understood in the context of both generalized renormalization and kneading theory (including kneading invariants and kneading map). Kneading map (which was introduced by Hofbauer and Keller) and the associated Hofbauer tower construction are very useful tools to study metric properties for unimodal maps. But these tools seem to be of no use in multimodal case. For example, it is rather difficult to give a proper definition. However, since we only consider maps which are combinatorially symmetric, it is still possible to describe the kneading map for such maps, especially for specific combinatorics. For the Fibonacci bimodal map, we will give an equivalent description.

Let $I^0$ and $J^0$ be defined as above. For $x \in I^0$ or $x \in J^0$, the involution of $x$, denoted $\hat x$, is defined as the point in $I^0 \cup J^0$ and such that $f(x) = f(\hat x)$.

We may assume that $f(c) > d$ and $f(d) < c$ when $f \in \mathscr B^+$ and $f(c) < c$ and $f(d) > d$ when $f \in \mathscr B^-$. For otherwise, one can show that $f^j(c), f^j(d) \in (f^{j-1}(c), f^{j-1}(d))$ for all $j \geq 1$, hence the orbits of $c$ and $d$ both converge to the fixed point $p$. Then either $c$ or $d$ has two preimages inside $I^0 = (p_1, p)$. Denote ${\rm{Crit}} : = \{c, d \}$. Define $S_0 : = 1$, define

Define inductively,

and

$S_k$ are called cutting times while $z_k$ and $y_k$ are called the closest precritical points. If $S_k < n \leq S_{k+1}$, then $(z_k, c)$, $(c, \hat z_k)$, $(\hat y_k, d)$ and $(d, y_k)$ are maximal intervals on which $f^n$ is monotone. Let $A_k : = (z_{k-1}, z_k)$ and $B_k : = (y_k, y_{k-1})$ for $k \geq 1$. Let $\hat A_k : = (\hat z_k, \hat z_{k-1})$ and $\hat B_k : = (\hat y_{k-1}, \hat y_k)$.

By construction, $f^{S_{k-1}}(z_k)$ has the form $f^{-m}(\rm{Crit})$ and is contained in $(z_r, \hat z_r)$ or $(\hat y_r, y_r)$ for some $r \geq 0$, see Figure 3. Hence $S_k -S_{k-1}$ is still a cutting time. The kneading map of a bimodal map $f \in \mathscr B_*$ is defined as

It follows that

The kneading map determines the combinatorics of the map. By Figure 3 and the construction of the closest preimages,

This is true for all $k \geq 1$. If $Q(k) = 0$, then $f^{S_{k-1}} (c)$ and $f^{S_{k-1}} (d)$ are outside $(z_0, \hat z_0) \cup (\hat y_0, y_0)$. Notice also that $f^{S_k}$ maps $(z_{k-1}, c) \to (b, f^{S_k}(c))$ is monotone and onto, where $b \in \{ f^{S_{Q(k)}}(c), f^{S_{Q(k)}}(d)\}$, and its image contains one turning point $c$ or $d$. See Figure 4 for one possible case.

Lemma 2.1. If $f$ has no periodic attractor, then $Q(k) < k$ for all $k \geq 1$.

Proof. Consider $f^{S_{k-1}}$ on $(z_{k-1}, c)$. We may assume that $f^{S_{k-1}} : (z_{k-1}, c) \to (d, f^{S_{k-1}}(c))$ is monotone and increasing. Then $f^{S_{k-1}}(c) \in (y_{Q(k)}, y_{Q(k)-1})$. If $Q(k) > k$, then $f^{S_{k-1}}(c) \in (d, y_{k-1})$. Hence $f^{S_{k-1}} \circ f^{S_{k-1}}$ maps $(z_{k-1}, c)$ into itself, yields a periodic attractor. Contradiction.

Lemma 2.1 also implies the fact that if $f$ has no periodic attractor, then the cutting times are well-defined for all $k \geq 1$.

2.3.   Topological properties

In this subsection we will state some topological properties of the Fibonacci bimodal map in terms of kneading map. For simplicity, we only focus on positive Fibonacci bimodal maps. The case of negative maps is analogous.

Suppose $f \in \mathscr B^+$ has Fibonacci combinatorics. Let $\{I^n \}_{n \geq 0}$ and $\{J^n \}_{n \geq 0}$ be its twin principal nest. Denote $I^n : = (u_n, \hat u_n)$ with $u_n < c$ and $J^n : = (\hat v_n, v_n)$ with $d < v_n$. Note that $\hat u_0 = \hat v_0 = p$, $u_0 = p_1$ and $v_0 = p_2$.

Proposition 1. The cutting times $S_k$ and the critical return times $s_k$ are coincident, the kneading map is clarified as $Q(k) = \max\{k-2, 0\}$. Moreover, for $k \geq 0$,

(1) $z_k \in (u_k, u_{k+1})$ and $y_k \in (v_{k+1}, v_k)$.

(2) If $k \equiv 0, 1 \mod 3$, then $z_k \in f^{-S_k}(d)$ and $y_k \in f^{-S_k}(c)$.

(3) If $k \equiv 2 \mod 3$, then $z_k \in f^{-S_k}(c)$ and $y_k \in f^{-S_k}(d)$.

Proof. We prove this lemma by induction. For $k = 0$, statement (2) holds by the chosen of $z_0$ and $y_0$. By Fact 2.1 $\phi_1$ is of type $\mathcal A^{++}$, then $f^{s_1} = f^2 : u_{1} \to p$. In particular, $C^1 = (u_0, u_1)$ and $f^{s_0} = f : (u_0, u_1) \to J^0$ is monotone and onto. Hence statement (1) holds.

We now assume that the lemma holds for $k$ and prove that it holds for $k+1$. Without loss of generality, we may assume that $\phi_k$ is of type $\mathcal C^{++}$ and $\phi_{k+1}$ is of type $\mathcal A^{++}$. Since $s_k = S_k$ and $\phi_{k+1} |C^{k+1} = f^{s_k}$ with $C^{k+1}$ is on the left side of $c$, we have $z_k \in C^{k+1}$. Since $\phi_{k+1}(I^{k+1}) = f^{s_{k+1}}(I^{k+1}) \supset J^{k+1} \ni d$, $s_{k+1}$ is a cutting time. Now it suffices to show that there is no cutting time between $s_k$ and $s_{k+1}$. Let $s_k < n < s_{k+1}$, consider $f^n|(z_k, c)$. Firstly note that $f^{s_k} : (z_k, c) \to (d, f^{s_k}(c))$ where $f^{s_k}(c) \in D^k \subset J^{k-1}$. Since $\phi_{k-1}|J^{k-1} = f^{s_{k-1}}$ is the first return map, $f^j(J^{k-1}) \cap (I^{k-1} \cup J^{k-1}) = \emptyset$ for $1 \leq j \leq s_{k-1}$. This implies $f^n((z_k, c)) \cap \{ c, d\} = \emptyset$ for all $s_k < n < s_{k+1}$. Hence $s_{k+1} = S_{k+1}$. Since $\phi_{k+1}(I^{k+2}) \subset D^{k+1}$, $z_{k+1} \in I^{k+1} \setminus I^{k+2}$. This proves statement (1). Statements (2) and (3) follow from Fact 2.1 immediately. This finishes the proof.

Combining this with Fact 2.1, we can prove the following lemma by induction.

Lemma 2.2. For $k \geq 2$, we have

(1) If $k \equiv 0, 1 \mod 3$, then $f^{S_{k-1}}(z_k) \in \{y_{k-2}, \hat y_{k-2} \}$ and $f^{S_{k-1}}(y_k) \in \{z_{k-2}, \hat z_{k-2} \}$;

(2) If $k \equiv 2 \mod 3$, then $f^{S_{k-1}}(z_k) \in \{z_{k-2}, \hat z_{k-2} \}$ and $f^{S_{k-1}}(y_k) \in \{y_{k-2}, \hat y_{k-2} \}$.

Moreover, for $k \geq 1$, we have

(3) If $k \equiv 0, 1, 2, 4, 9, 11 \mod 12$, then $f^{S_k}$ is increasing on $(z_k, c)$ and $(d, y_k)$;

(4) If $k \equiv 3, 5, 6, 7, 8, 10 \mod 12$, then $f^{S_k}$ is decreasing on $(z_k, c)$ and $(d, y_k)$.

Actually, by Eq (1) and Proposition 1 we can state the position of $f^{S_k}(c)$ and $f^{S_k}(d)$ in more details.

Since $f : (-1, u_0) \to (-1, \hat u_0) = (-1, p)$ is increasing and onto, $c$ has a preimage $z_{-1} \in (-1, u_0)$. Similarly, $d$ has a preimage $y_{-1} \in (v_0, 1)$.

Figure 5 illustrates one possible possition for points and their images under $f^{S_{k-1}-1}$ for $k \equiv 2 \mod 12$.

Lemma 2.3. Suppose that $f \in \mathscr B^+$ has Fibonacci combinatorics. Then $f$ satisfies the following starting condition:

(1) $f(c) \in (y_{-1}, 1)$ and $f(d) \in (-1, z_{-1})$;

(2) $f^2(c), f^2(d) \in I^0 \cup J^0$;

(3) $f^4(c), f^4(d) \notin I^0 \cup J^0$.

Proof. By Fact 2.1, the first return map $\phi_1$ is of type $\mathcal A^{++}$. Then $\phi_1 : I^1 \to J^0$ is local maximal at $c$ with $\phi_1|I^1 = f^{S_1} = f^2$. Statement 2 follows immediately. Since $\phi_1(I^1) \supset J^1$, $f^2(c) > d$, hence $f(c) \in (y_{-1}, 1)$. Similarly we have $f(d) \in (-1, z_{-1})$. To prove statement 3, note that $f^3(c) = f^{S_2}(c) \in I^1$. Recall that $I^1 = (u_1, \hat u_1)$ with $f(u_1) = v_0$. Then $f: (u_0, u_1) \to J^0$ is monotone and onto. Since $f$ is increasing on $(-1, c)$, $f(I^1) \subset (v_0, 1)$, hence $f^4(c) \notin I^0 \cup J^0$.

For any $x \in [-1, 1]$, let $x^f : = f(x)$ and $x_i : = f^i(x)$. Furthermore, for $k \geq 1$, let $\alpha_k : = \{f^{S_k}(c), f^{S_k}(d) \} \cap (-1, p)$ and $a_k : = \{f^{S_k}(c), f^{S_k}(d) \} \cap (p, 1)$. Similarly, let $\beta_k : = \{f^{S_k + S_{k+2}}(c), f^{S_k + S_{k+2}}(d)\} \cap (-1, p)$ and $b_k : = \{f^{S_k + S_{k+2}}(c), f^{S_k + S_{k+2}}(d)\} \cap (p, 1)$.

Lemma 2.4. The points $u_{k-1}^f, \alpha_k^f, z_{k-1}^f, \beta_k^f, u_k^f$ are ordered in the following way (we state the ordering near $c^f$ rather than near $c$ so that we do not need to be careful about on which side of $c$ these points lie):

Proof. Firstly note that $\alpha_k \in C^k$ by the chosen of $C^k$. By Proposition 1, $z_{k-1} \in (u_{k-1}, u_k)$, hence $u_{k-1}^f < z_{k-1}^f < u_k^f < c^f$. In particular, since $f^{S_{k-1}} | C^k$ is monotone and onto $I^{k-1}$ or $J^{k-1}$, $z_{k-1}$ or $\hat z_{k-1} \in C^k$. We claim that $z_{k-1} \in (\alpha_k, \hat \alpha_k)$.

Indeed, without loss of generality, we may assume that $\phi_k$ is of type $\mathcal A^{++}$. Then $C^k$ is on the left side of $I^k$ and $\phi_k : C^k \to J^{k-1}$ is increasing. Moreover, $\alpha_k = f^{S_k}(d)$ and $f^{S_{k-1}} : \alpha_k \to f^{S_{k+1 }}(d) \in D^{k+1}$. Since $\phi_{k+1}$ is of type $\mathcal B^{-+}$, $D^{k+1}$ is on the left side of $J^{k+1}$, then $\beta_{k+1} < d$ and hence $\alpha_k < z_{k-1}$. This proves the claim.

Since $\phi_{k+2}$ is of type $\mathcal C^{–}$, $f^{S_{k+2}}(c) \in D^{k+2} \subset J^{k+1}$. Recall that $f^{S_k} : J^k \to I^{k-1}$ and hence $f^{S_k} (J^{k+1}) \subset C^k$. Therefore $f^{S_k+S_{k+2}}(c) \in C^k$. Furthermore, $f^{S_{k-1}} \circ f^{S_k+S_{k+2}}(c) = f^{S_{k+3}}(c) \in D^{k+3}$ which is on the right side of $d$. Hence $f^{S_k+S_{k+2}}(c) \in (z_{k-1}, \hat z_{k-1})$. This finishes the proof.

The following proposition gives an equivalent description of Fibonacci combinatorics for bimodal maps.

Proposition 2. Suppose that $f \in \mathscr B^+$ has kneading map $Q(k) = \max\{k-2, 0\}$ and satisfies the starting condition stated in Lemma 2.3, then $f$ has Fibonacci combinatorics.

Proof. We prove this by induction. Firstly note that the kneading map $Q(k) = \max\{k-2, 0\}$ shows that $S_0 = 1$, $S_1 = 2$, $S_2 = 3$ and $\{ S_k \}_{k \geq 1}$ is the Fibonacci sequence.

From the starting condition, $f(d) \in (-1, z_{-1})$. Since $f$ is positive and $f(z_{-1}) = c$, $f^2(d)$ is on the left side of $c$. Hence $f^2(d) \in I^0 = (u_0, \hat u_0)$ (recall that $I^0$ and $J^0$ are always well-defined). By equation (1), $f^2(d)$ is outside $(z_0, \hat z_0)$, hence $f^2(d) \in (u_0, z_0)$. Since the first return time of $c$ and $d$ to $I^0 \cup J^0$ is 2, $I^1$ and $J^1$ are well-defined. To be precise, since $S_1 = 2$, by the chosen of $z_1$ and $y_1$ we have $f(y_1) = z_{-1}$ and $f(z_1) = y_{-1}$. Then $f:(z_0, z_1) \to (d, y_{-1})$ which contains $v_0$. Let $u_1 \in f^{-1}(v_0) \cap (z_0, z_1)$. Then $f^2 : u_1 \to p = \hat v_0$. Indeed, $I^1 = (u_1, \hat u_1)$. Furthermore, $f^2 = f^{S_1} : I^1 \to J^0$ is local maximal at $c$. Since $f: (u_0, u_1) \to J^0$ is monotone and onto, $f^{S_2}(d) = f^3(d) \in J^0$. By equation (1), $f^3(d) \in (\hat y_0, \hat y_1) \cup (y_1, y_0)$. We claim that $f^3(d) \in (\hat v_1, \hat y_1) \cup (y_1, v_1)$. For otherwise, since $f: (v_1, y_0) \to (u_0, c)$ is monotone and onto, we have $f^4(d) \in I^0$ and which contradicts the starting condition. Moreover, since $f|(u_0, z_0)$ is increasing, we have $f^3(d) < d$ and hence $f^3(d) \in (\hat v_1, \hat y_1)$. Since $f^{S_1} : J^1 \to I^0$, $f^{S_3}(d) = f^{S_1+S_2}(d) \in I^0$. Since $S_3$ is a cutting time, $(f^{S_1}(d), f^{S_3}(d))$ contains $c$, then $f^{S_3}(d)$ is on the right side of $c$. This implies $f^4(d) = f^{S_0 + S_2}(d) \in (z_{-1}, u_0)$.

For the induction step, assume that the first return times of $c$ and $d$ to $I^{k-1} \cup J^{k-1}$ equal to $S_k$ and the following induction hypothesis holds:

Then $I^k$ and $J^k$ are well-defined such that the first return times to $I^{k-1} \cup J^{k-1}$ are $S_k$. Since $f^{S_{k-1}} : z_{k-1} \to c \mbox{ or } d$, the return time of $z_{k-1}$ to $I^{k-1} \cup J^{k-1}$ is not larger that $S_{k-1}$. Hence $z_{k-1} \notin I^k$. For simplicity, we may assume that $f^{S_k} : I^k \to I^{k-1}$ is local maximal at $c$. Since $S_k$ is a cutting time, $f^{S_k} |(z_{k-1}, c)$ is monotone and increasing. Since $f^{S_k}((z_{k-1}, c))$ contains the critical point $c$, $f^{S_k}(c) > c$ and hence $f^{S_k} (I^k) \ni c$. Then $z_k \in I^k$. This shows that $z_{k-1}^f < u_k^f < z_k^f$. Moreover, since $\alpha_k^f < z_{k-1}^f$, $f^{S_k}(c) \notin I^k$ and then $f^{S_k}(I^k) \supset I^k$. This implies that $z_k$ is contained in a return domain to $I^k$ with return time $S_k$.

For simplicity, we may assume that $f^{S_{k-1}} : I^{k-1} \to J^{k-2}$ is local maximal at $c$. (Keep in mind that this is the case when $\phi_{k-1}$ is of type $\mathcal A^{++}$ and $\phi_k$ is of type $\mathcal B^{-+}$). By the induction hypothesis, $f^{S_{k-1}}(c)$ is on the right side of $d$. Then $f^{S_{k+1}}(c)$ is on the left side of $d$. By equation (1), $f^{S_{k+1}}(c) \in (\hat y_{k-1}, \hat y_k)$.

Now let $R_{k-1}$ be the first return domain to $I^{k-2} \cup J^{k-2}$ which contains $y_{k-2}$. Then the return time on $R_{k-1}$ is $S_{k-2}$. Since we assume that $f^{S_{k-1}} : I^{k-1} \to J^{k-2}$ is local maximal at $c$, it is clear that by the induction hypothesis, $d < f^{S_{k+1} + S_{k-1}}(c) < y_{k-2} < f^{S_{k-1}}(c)$. Since $f^{S_{k-2}} \circ f^{S_{k-1}}(c) = f^{S_k}(c) \in I^{k-2} \cup J^{k-2}$, $f^{S_{k-1}}(c) \in R_{k-1}$. Also since $f^{S_{k-2}} \circ f^{S_{k+1} + S_{k-1}}(c) = f^{S_{k+2}}(c) \in I^{k-2} \cup J^{k-2}$, $f^{S_{k+1} + S_{k-1}}(c) \in R_{k-1}$. Then $f^{S_{k-1}}(I^k) \cap R_{k-1} \neq \emptyset$. In particular, $f^{S_{k-1}} : \partial I^k \to \partial R_{k-1}$. This fact implies that $f^{S_{k+1}}(c) \in I^k$ and hence $z_{k-1}^f < \alpha_{k+1}^f < z_k^f$.

Finally, by Eq (1) $\alpha_{k+2} \in (z_k, z_{k+1}) \cup (\hat z_{k+1}, \hat z_k)$. Consider $f^{S_k}|(z_k, z_{k+1})$ which is monotone and increasing. Since $S_{k+1}$ is a cutting time, then $f^{S_k} : (z_k, z_{k+1}) \to (c, z_{k-1})$. This shows $\beta_k \in (c, z_{k-1})$. Since $f^{S_{k-1}}(\beta_k) \in I^{k-1} \cup J^{k-1}$, $\beta_k \notin I^k$. This is because the return times are different. This shows $z_{k-1}^f < \beta_k^f < u_k^f$ and proves the induction hypothesis. The proof is now complete.

2.4.   Induced Markov map

Inducing schemes is a standard tool for interval maps that relates the dynamics to Markov chains. In order to prove, among other things, the existence of invariant measures, mixing rates and stochastic laws. We will first construct a countable interval partition, and then the induced Markov map for the Fibonacci bimodal map $f$.

The partition of $I = [-1, 1]$ is defined as the following. Denote

For $j \geq -1$, define $\hat W_j$ and $\hat V_j$ so that

The induced Markov map $F$ is defined as the following.

Clearly, $F$ is monotone on each state $W_k$ and $V_k$. Moreover, $F$ preserves the partition, hence is a Markov map. To be precise, for $j = -3, -2, -1, 0, 1$ we have

and due to the symmetry

For $j \geq 2$, by Proposition 1 and Lemma 2.2 we have the following.

Fact 2.2.

(1) For $j = 2$, $F(W_2) = F(\hat W_2) = \cup_{j \geq 0} V_j$ and $F(V_2) = F(\hat V_2) = \cup_{j \geq 0} W_j$;

(2) For $j \geq 3$, we have

(2.1) if $j \equiv 1, 2, 5, 10 \mod 12$, then $F(W_j) = F(\hat W_j) = \cup_{k \geq j-1} V_k$ and $F(V_j) = F(\hat V_j) = \cup_{k \geq j-1} W_k$;

(2.2) if $j \equiv 4, 7, 8, 11 \mod 12$, then $F(W_j) = F(\hat W_j) = \cup_{k \geq j-1} \hat V_k$ and $F(V_j) = F(\hat V_j) = \cup_{k \geq j-1} \hat W_k$;

(2.3) if $j \equiv 0, 3 \mod 12$, then $F(W_j) = F(\hat W_j) = \cup_{k \geq j-1} \hat W_k$ and $F(V_j) = F(\hat V_j) = \cup_{k \geq j-1} \hat V_k$;

(2.4) if $j \equiv 6, 9 \mod 12$, then $F(W_j) = F(\hat W_j) = \cup_{k \geq j-1} W_k$ and $F(V_j) = F(\hat V_j) = \cup_{k \geq j-1} V_k$.

3.   The piecewise linear model

In this section we will construct a piecewise linear bimodal map which is an odd function and has Fibonacci combinatorics. The idea comes from the unimodal model studied in ^[5]. The induced Markov map $F$ over $f$ is countably piecewise linear with definite slope on each domain. The construction proceeds along the following steps:

${\bf I:}$ Fix the Fibonacci sequence $S_j$ such that $S_0 = 1, S_1 = 2$ and $S_{j+1} = S_{j} + S_{j-1}$ for $j\geq 1$.

${\bf II:}$ Choose $0 < q < p < 1$. For $j \geq -1$, choose a strictly increasing sequences of points $z_j \nearrow c = -p/2$ satisfying $z_{-1} < -p < z_0 < -q < z_1$. For $j \geq 0$, set $\hat z_j = -p -z_j \searrow -p/2$. Finally, set $y_j = -z_j$ for $j \geq -1$ and $\hat y_j = - \hat z_j$ for $j \geq 0$. Clearly, $y_j \searrow p/2$ satisfying $y_1 < q < y_0 < p < y_{-1}$. These points $\{ z_j\}_{j \geq -1}$ and $\{ y_j \}_{j \geq -1}$ will play the role of the closest precritical points. The points $-p$ and $-q$ should be treated as $u_0$ and $u_1$. Then we have a partition of the interval $[-1, 1]$ as in subsection 2.4. Set

Note that ${\hat W}_{-3}, {\hat W}_{-2}, {\hat V}_{-3}$ and ${\hat V}_{-2}$ have no sense. Therefore we have

${\bf III:}$ Define

These numbers will turn out to be the absolute values of the slopes of $F|W_j$ for the induced Markov map.

${\bf IV:}$ For $j \geq -3$, define $k_j > 0$ that will denote the slope of $f|W_j$. Let

${\bf V:}$ Let $f$ be the unique continuous bimodal map such that

so that $|f(W_j)| = k_j \epsilon_j, j\geq -3$ and each interval $f(W_j)$ is adjacent to $f(W_{j+1})$.

${\bf VI:}$ Comparing Lemma 2.3, Lemma 2.4 and Proposition 2, we need some additional conditions on the sequence $\{ \epsilon_j \}$ to ensure that $f$ has Fibonacci combinatorics:

and

Actually, in the next section, we will let $\epsilon_j$ tends to $0$ in a geometric manner so that $f$ depends solely on a parameter $\lambda \in (0, 1)$, and we will check these conditions are satisfied under the geometric manner.

${\bf VII:}$ The induced Markov map $F:[-1, 1]\rightarrow [-1, 1]$ is defined the same as in subsection 2.4.

Proposition 3. Let $f$ be the map constructed above. Then $f$ is well-defined and has kneading map $Q(k) = \max\{k-2, 0 \}$. The induced map $F$ is linear on each set $W_j, {\hat W}_j, {\hat V}_j$ and $V_j$, having slope $\pm s_j$.

Proof.

$({\rm{I}})$ For $j = -3, -2, -1, 0.$ We check directly that

From the definition of the induced Markov map $F$, it is clear that $F$ is linear on $W_j$ and has slope $s_j$ for $j = -3, -2, -1, 0$.

$({\rm{II}})$ For $j = 1.$ Since $f(-q) = p, k_1 = \frac{s_1}{s_{-2}}$, we have

It follows that $f(W_1) = f((-q, z_1)) = (p, y_{-1}) = V_{-2}$. Therefore

is linear with slope $k_{-2}k_1 = s_1$. Moreover, $c^f \in (y_{-1}, 1) = V_{-3}$.

$({\rm{III}})$ For $j = 2$. Since $(z_1^f, c^f)\subset V_{-3}$, ${{f^{S_1-1}|}}{(z_1^f, c^f)} = {f|}{(z_1^f, c^f)}$ is linear (and also increasing) with slope $k_{-3} = s_{-3}$. Hence ${F|}{W_2} = {{f^{S_1}}|}{W_2}$ is increasing and linear with slope $k_2 \cdot s_{-3} = s_2$. Furthermore,

and

Since $z_2^f > z_1^f, (z_2^f, c^f) \subset V_{-3}$. By Eq (4), we have

It follows that $f^{S_1}(c) \in V_{-1} = (y_0, p)$.

$({\rm{IV}})$ For $j = 3$. Since $(z_2^f, c^f) \subset V_{-3}$, $f|(z_2^f, c^f)$ is increasing and linear with slope $k_{-3} = s_{-3}$. See from above that $f = f^{S_1-1} : (z_2^f, c^f) \to (y_0, f^{S_1}(c)) \subset V_{-1}$. Therefore $f^{S_2-1}|(z_2^f, c^f) = f \circ f^{S_1-1}|(z_2^f, c^f)$ is increasing and linear with slope $k_{-1} \cdot k_{-3} = s_{-1} \cdot s_{-3} = \frac{s_3}{k_3}$. Hence $F|W_3 = f^{S_2}|W_3$ is increasing and linear with slope $s_3$. Furthermore, we have

and

By Eq (4) again,

It follows that $f^{S_2}(c) \in {\hat W}_1$. Recall that $f : \hat W_1 \to V_{-2}$ is monotone and onto. Then $f^{S_0+ S_2}(c) \in V_{-2}$.

$({\rm{V}})$ For $j \geq 4$, we argue by induction, using the induction hypothesis:

From the first statement, it immediately follows ${F|}{W_j} = {f^{S_{j-1}}|}{W_j}$ is linear with slope $\pm s_j$. Then by the second statement, for $j \geq 4$,

$({\rm{VI}})$ For $j = 4$. Since $(z_3^f, c^f) \subset (z_2^f, c^f)$, ${{f^{S_2-1}|}}{(z_3^f, c^f)}$ is increasing and linear with slope $\frac{s_3}{k_3}$. Since $f^{S_2}(z_3) = {\hat z}_1$ and $f^{S_2}(c) \in {\hat W}_1$, $f^{S_2-1}((w_3^f, c^f)) \subset {\hat W}_1$. Note that $f^{S_1}|{\hat W}_1$ is decreasing and has slope $-s_1$. Then $f^{S_3-1}|(z_3^f, c^f) = f^{S_1} \circ f^{S_2-1} | (z_3^f, c^f)$ is decreasing with slope $- s_1 \cdot \frac{s_3}{k_3} = - \frac{s_4}{k_4}$. Therefore $F|W_4 = f^{S_3}|W_4$ is decreasing and linear with slope $-s_4$. Furthermore,

and

By Eq (4),

This shows $f^{S_3}(c)\in {\hat V}_2$.

$({\rm{VII}})$ For $j = 5$. We have

Since $(z_4^f, c^f) \subset (z_3^f, c^f)$, $f^{S_3-1}|(z_4^f, c^f)$ is decreasing and linear with slope $-\frac{s_4}{k_4}$. Since $f^{S_3}(c)\in {\hat V}_2$, $f^{S_3-1} : (z_4^f, c^f) \to (f^{S_3}(c), \hat y_2) \subset {\hat V}_2$. Since $f^{S_1} |\hat V_2$ has slope $-s_2$. We have

is increasing and linear with slope $s_2 \cdot \frac{s_4}{k_4}$. By Eq (5),

Therefore $f^{S_1+S_3}(c) - z_0 \leq \epsilon_0$, hence $(z_0, f^{S_1+S_3}(c)) \subset W_0$. Since $f|W_0$ is increasing and linear with slope $k_0$, we have $f^{S_4-1}|(z_4^f, c^f)$ is linear with slope $k_0 \cdot s_2 \frac{s_4}{k_4} = \frac{s_5}{k_5}$. Hence $F|W_5 = f^{S_4}|W_5$ is increasing and linear with slope $s_5$. Furthermore,

and

By Eq (4),

This shows $f^{S_4}(c)\in V_3$.

$({\rm{VIII}})$ For $j \geq 6$. Now assume that the induction hypothesis (${\rm{IH}}_{\rm{i}}$) holds for $5 \leq i < j$, we will prove that (${\rm{IH}}_{\rm{j}}$) holds.

Consider

Since $(z_{j-1}^f, c^f) \subset (z_{j-2}^f, c^f)$, using (${\rm{IH}}_{{\rm{j}}-1}$), we have $f^{S_{j-2}-1}|(z_{j-1}^f, c^f)$ is linear with slope $\pm \frac{s_{j-1}}{k_{j-1}}$. By Eq (4),

Then $f^{S_{j-2}}(c) \in W_{j-3}$ or ${\hat W}_{j-3}$ or $V_{j-3}$ or ${\hat V}_{j-3}$. It follows that

is linear with slope $\pm s_{j-3} \frac{s_{j-1}}{k_{j-1}}$. Using (${\rm{IH}}_{{\rm{j}}-1}$) and (${\rm{IH}}_{{\rm{j}}-3}$),

By Eq (5), the length of the interval

is $s_{j-3} \cdot \frac{s_{j-1}}{k_{j-1}}|c^f - z_{j-1}^f|\leq s_{j-3} \frac{\epsilon_{j-4}}{s_{j-3}} = \epsilon_{j-4}$. Then

Using (${\rm{IH}}_{{\rm{j}}-4}$), $F = f^{S_{j-5}}$ is linear on these sets with slope $\pm s_{j-4}$. It follows that $f^{S_{j-1}-1}|(z_{j-1}^f, c^f)$ is linear with slope $\pm s_{j-4} \cdot s_{j-3} \cdot \frac{s_{j-1}}{k_{j-1}} = \pm \frac{s_j}{k_j}$.

For simplicity, we may assume that $f^{S_{j-1}}(z_{j-1}) = c$ and $f^{S_{j-1}-1}|(z_{j-1}^f, c^f)$ is increasing and linear with slope $\frac{s_j}{k_j}$. Then

By Eq (4),

Hence $f^{S_{j-1}}(c) \in {\hat W}_{j-2}$. This concludes the induction.

The following proposition shows that the map $f$ constructed as above has Fibonacci combinatorics.

Proposition 4. Let $f$ be the map constructed as above. Then $f$ has Fibonacci combinatorics.

Proof. It follows from the proof of Proposition 3 that $f$ satisfies

(1) $f(c) \in V_{-3}$ and $f(d) \in W_{-3}$;

(2) $f^2(c) = f^{S_1}(c) \in V_{-1} \subset J^0$ and $f^2(d) = f^{S_1}(d) \in W_{-1} \subset I^0$;

(3) $f^4(c) = f^{S_0 + S_2}(c) \in V_{-2}$ and $f^4(d) = f^{S_0 + S_2}(d) \in W_{-2}$, hence $f^4(c), f^4(d) \notin I^0 \cup J^0$.

Then $f$ satisfies the starting condition. Now this proposition follows from the fact that $f$ has kneading map $Q(k) = \max\{ k-2, 0\}$ and Proposition 2.

4.   A geometric manner of the model

In smooth interval dynamics, the uniform expansion of a map was mainly described in two ways: the expansion of derivatives along critical orbits and the local geometry around the critical points. In the latter case, the local geometry was often clarified by the ratio between principal nest (in our setting we use twin principal nest instead). In other words, the uniform expansion of a map depends on the asymptotic properties of its scaling factor, i.e. the sequences $\frac{|u_n-c|}{|u_{n-1}-c|}$ and $\frac{|v_n-c|}{|v_{n-1}-c|}$.

In this section, we let $\epsilon_j$ tends to 0 in a geometric manner. To be precise, set

where $\lambda \in (0, 1)$. Then $f$ depends solely on a single parameter $\lambda$ and we can calculate $s_j$ and $k_j$ under this geometric manner. Since we use the preimages of the critical points instead of the preimages of the fixed point $p$ to construct the induced Markov map, the ratio $\frac{|z_{j}-c|}{|z_{j-1}-c|}$ (which equals $\lambda$ for $j \geq -1$) plays the same role as the scaling factor. Figures 6 and 7 show the partial graphs of $f$ and $F$ under this geometric manner.

By formula (2),

Using formula (3) we obtain

Let us check that formulas (4) and (5) in Step Ⅵ are true for all $\lambda \in (0, 1)$.

Lemma 4.1.

and

are true for all $\lambda \in (0, 1)$ under the geometric manner.

Proof. For simplicity, we write $\epsilon_j = C_1 \lambda^j$, $j\geq-1$, $k_j = C_2 \omega^j$, $j\geq6$, where $C_1 = \frac{\lambda(1-\lambda)}{4}, C_2 = \frac{1}{2\lambda^5(1-\lambda)^7}, \omega = \lambda^2(1-\lambda)^2$, then $C_2 \sum_{i = 6}^{\infty} (\lambda \omega)^i = \frac{\lambda^{13}(1-\lambda)^5}{2(1-\lambda^3(1-\lambda)^2)}$. Let us first check formula (4.1).

● For $j = 2$,

● For $j = 3$,

● For $j = 4$,

Figure 8 shows the graphs of functions $x^3 + x^6(1-x) + x^{10}(1-x)^3+\frac{x^{14}(1-x)^5}{1-x^3(1-x)^2} -1$, $x^4 + x^8(1-x)^2 +\frac{x^{12}(1-x)^4}{1-x^3(1-x)^2} -1$ and $x^5(1-x)+ \frac{x^{9}(1-x)^3}{1-x^3(1-x)^2} -1$.

● For $j = 5$,

● For $j \geq 6$,

Figure 9 shows the graphs of functions $\frac{x^{5}(1-x)}{1-x^3(1-x)^2} -1$ and $\frac{x^4 (1-x)}{1-x^3(1-x)^2} -1$.

These are true for all $\lambda \in (0, 1)$. Now we check formula (4.2).

● For $j = 4$,

● For $j = 5$,

● For $j \geq 6$,

Figure 10 shows the graphs of functions $x^5+ \frac{x^{9}(1-x)^2}{1-x^3(1-x)^2} -1$, $\frac{x^{5}}{1-x^3(1-x)^2} -1$ and $\frac{x^4}{1-x^3(1-x)^2} -1$.

Again, these are true for all $\lambda \in (0, 1)$.

5.   random walk governed by F

In this section, we prove the Main Theorem. We first compute the critical order $\ell$ of $f$ in terms of $\lambda$. This is statement (1) of the Main Theorem.

Proof of statement (1) of the Main Theorem. Note that by formula (8) we have $|Df(x)| = k_j = O(\lambda^{2j}(1-\lambda)^{2j})$. Then by formula (6) and the fact that $\sum_{i \geq j+1} \epsilon_i \leq |x-c| \leq \sum_{i \geq j} \epsilon_i$, $|x-c| = O(\lambda^j)$ if $x\in W_j$ for $j \geq 5$. On the other hand, by definition, $|Df(x)| = O(|x-c|^{\ell-1})$. Hence

This finishes the proof.

5.1.   Acip for $f$

Now we will compute the values of $\lambda$ for which there is an $F_{\lambda}$-invariant probability measure which is an acip. For simplicity, we will consider the following system instead.

Given any $\lambda \in (0, 1)$, let $V_n = (\lambda^n, \lambda^{n-1}]$ for $n \geq 1$. Then $V_n$ form a Markov partition of the interval $(0, 1]$. Define the countably piecewise linear interval map $T_{\lambda} : (0, 1] \to (0, 1]$ as:

For the graph of $T_{\lambda}$, see Figure 11.

Note that the system $F_{\lambda}$ and $T_{\lambda}$ are not semi-conjugate. This is because there are infinitely branches $F|W_n$ and $T|V_n$ with different orientations. However, one can show that $F_{\lambda}$ admits an acip whenever $T_{\lambda}$ does. Moreover, if $T_{\lambda}$ admits an acip $\mu$, then $F_{\lambda}$ admits an acip $\nu$ satisfying $\nu(W_n) = \frac{1}{4}\mu(V_n)$ for all $n \geq 1$.

To continue, we will consider a random walk governed by $T_{\lambda}: (0, 1] \to (0, 1]$. When there is no confusion, we will omit the parameter $\lambda$ and use $F$ and $T$ for instead. To describe the random walk, let $\alpha_k (x) = n$ if $T^k(x) \in V_n$. Then the sequence of random variables $\alpha_0, \alpha_1, \alpha_2, \ldots$ can be considered as a Markov chain with the following transition probability:

where $Leb(\dots)$ denotes the Lebesgue measure of the set.

Let $(A_{i, j})_{i, j}$ be the transition matrix corresponding to $T_{\lambda}$, one can compute that in matrix form

Now write $y_{n, k} = Leb(\{ \alpha_k = n\}) = Leb(T^{-k}(V_n))$. Let $\vec{v}_k = (y_{1, k}, y_{2, k}, y_{3, k}, \ldots, y_{n, k}, \ldots)$ be a row vector.

Lemma 5.1. For $k \geq 1$, we have

Proof. Choose $n \geq 4$. Note that $T^{-1}(V_n)$ has $n+1$ connected components. Let $J_i \subset V_i$, $1 \leq i \leq n+1$, denote these components. Now let $J$ be any components of $T^{k-1}$ such that $T^{k-1} (J) = V_i$. Since $T$ is piecewise linear, we have

Summing over all $J$ and $1 \leq i \leq n+1$, we have

The cases for $n = 1, 2, 3$ are similar. Now this lemma follows from formulas $(6)$ and $(7)$.

For $\lambda \in (0, \frac{1}{2})$, take

The functions $v_i(\lambda)$ and $k(\lambda)$ remain positive. Figure 12 shows the graphs of $v_i(\lambda)$ and $k(\lambda)$.

For $i \geq 5$, we set $v_i = k(\frac{\lambda}{1- \lambda})^i$. One can check that $\vec v = (v_1, v_2, \ldots, v_i, \ldots)$ is the left eigenvector of the matrix $(A_{i, j})_{i, j}$ with eigenvalue 1. In fact, $k$ and $v_i$, $1 \leq i \leq 4$ are the solutions of the following equations:

Lemma 5.2. If $\lambda \in (0, \frac{1}{2})$, then the system $((0, 1], T_{\lambda})$ admits an acip $\mu$. Furthermore, for $i \geq 5$

Proof. We will use the result by Straube ^[16] claiming that $T$ has an acip if (and only if) for any $\eta \in (0, 1)$, there exists $\delta > 0$ such that for every measurable set $A$ of measure $Leb(A) < \delta$ holds $Leb(T^{-k}(A)) < \eta$ for all $k \geq 1$.

To check the Straube's condition, we will prove by induction that $y_{n, k} \leq C \cdot v_n(\lambda)$ for all $n, k \geq 0$. For fixed $\lambda$, take $C = C(\lambda)$ large enough such that $0 < y_{n, 0} \leq C \cdot v_n$ for all $n$. This is possible because

for all $n \geq 5$. Since $\vec{v}$ is the left eigenvector, now this claim follows from Lemma 5.1.

Now take $\eta \in (0, 1)$. Since $y_{n, k}$ is exponentially small in terms of $n$, pick $n_1$ large enough such that $\sum_{n \geq n_1} y_{n, k} < \eta/2$. Assume that $A \subset V_i$ for some $1 \leq i < n_1$. Since $T$ is piecewise linear, we have

provided $Leb(A) < \delta$ is sufficiently small. It follows that if $A \subset \bigcup_{i < n_1} V_i$ has sufficiently small measure, then $Leb(T^{-k}(A)) < n_1 \eta/(2n_1) = \eta/2$. This concludes the verification of Straube's condition.

Since $T$ has an acip $\mu$, it can be written as $\mu(A) = \lim_{n \to \infty} \frac{1}{n} \sum_{i = 0}^{n-1}Leb(T^{-i}(A))$. Therefore,

Indeed, one can show that $\vec{\mu} = (\mu(V_1), \mu(V_2), \ldots, \mu(V_n), \ldots)$ is also an eigenvector of $(A_{i, j})_{i, j}$ with eigenvalue 1 and satisfying $\sum_n \mu(V_n) = 1$. Argue as ^[4][Theorem 1] shows that $\mu(V_n) \sim (\frac{\lambda}{1-\lambda})^n$ for all $n \geq 5$.

Proof of statement (4) of the Main Theorem. By a standard pullback argument, the original map $f$ has acip if and only if

And when it fails, then $f$ has an absolutely continuous $\sigma$-finite measure. This follows because $f$ is conservative and $\omega(c) = \omega(d)$ is a Cantor set with 0 Lebesgue measure. See ^[13] [Lemma 3.1] and ^[7] [Theorem 1].

Note that $\{S_j\}$ is Fibonacci so $S_{j-1} \sim \gamma^{j-1}$, where $\gamma = \frac{1+\sqrt5}{2}$ is the golden mean. Since $\mu(W_i) \sim (\frac{\lambda}{1-\lambda})^i$ for $i \geq 5$, then

This corresponds to the critical order $3 < \ell < 4$. If $\frac{2}{3+\sqrt5} \leq \lambda < \frac{1}{2}$, the series divergence, $f$ has an absolutely continuous $\sigma$-finite measure. This corresponds to the critical order $4 \leq \ell < 5$.

When $\lambda = \frac{1}{2}$, the proof is quite different and is somewhat out of the context of this paper. However, one can argue as ^[4] [Lemma 3] to show that $T_{\lambda}$ (equivalently $F_{\lambda}$) is null recurrent w.r.t. Lebesgue measure and hence is conservative with a $\sigma$-finite measure.

5.2.   Wild attractor for $f$

In this subsection we prove that $f_{\lambda}$ has a wild attractor when $\lambda \in (\frac{1}{2}, 1)$, which is equivalent to show that $F_{\lambda}$ (and also $T_{\lambda}$) is dissipative.

The main tool in the proof of the existence of wild Cantor attractor is a random walk. In this subsection we will use a random walk governed by the system $F_{\lambda}$ which is somewhat similar with the argument used in the previous subsection. To describe the random walk, write $\varphi_n(x) = k$ if $F^n(x) \in W_k \cup \hat W_k \cup \hat V_k \cup V_k$. In principle, if a point $x$ escapes to infinity under iteration of $F$, then $x$ tends to $\omega(c)$ under $f$. And if a positive Lebesgue set points escape to infinity, then $\omega(c)$ is a wild attractor. We will have to calculate the probabilities from one state to another.

The asymptotic behavior of the random variable $\varphi_n$ can be computed from the expectation $\mathbb E(\varphi_n - \varphi_{n-1})$, taken with respect to normalized Lebesgue measure on $[-\frac{1}{2}, \frac{1}{2}]$. If $E(\varphi_n - \varphi_{n-1}) \geq \epsilon > 0$, then one can expect that $\lim_n \varphi_n = \infty$. To prove this we will use the conditional expectation. We also need the boundedness of the variance. The drift of the random walk is defined as the conditional expectation

Such a concept was first used in the study of Fibonacci unimodal maps in ^[3]. The second moment ${\rm Var} (\varphi_n-k | \varphi_{n-1} = k)$ is clarified as

Lemma 5.3. Let $F_{\lambda}$ be the induced Markov map over $f_{\lambda}$ under the geometric manner. If there exists $k \in \mathbb N$ and $\delta > 0$ such that

(1) $\mathbb E(\varphi_n-k | \varphi_{n-1} = k) \geq \delta$;

(2) ${\rm Var} (\varphi_n-k | \varphi_{n-1} = k)$ is uniformly bounded from above.

Then $\lim_{n \to \infty} \varphi_n(x) = \infty$ for Lebesgue a.e. $x$.

Proof. The proof is just a modification of ^[2] [Theorem 5.2] since in our case the system has strong symmetry.

Proof of statement (2) of Main Theorem. Now the statement follows from the remark before and Lemma 5.3.

Remark 5.1. For a general smooth bimodal map $f$ with Fibonacci combinatorics, even in the case that the two critical points are non-flat with the same critical order $\ell$, it is quite difficult to show that $f$ has a wild attractor when $\ell$ is sufficiently large. A crucial step in the proof is to estimate the upper and lower bounds of the derivatives along the orbit of the critical points $Df^{S_n}(f(c))$. Suppose that $n \equiv 0, 1 \mod 3$, $f^{S_n}(c) \in J^{n-1}$. Then by the standard argument,

But in fact we do not have any estimate of $|J^n|/|I^n|$. However, if the Fibonacci bimodal map is also an odd function, one can show that its metric properties are essentially the same as those of the Fibonacci unimodal map. Since in this case we always have $|I^n| = |J^n|$ and $Df^n(f(c)) = Df^n(f(d))$ for all $n \geq 1$. One can use the topological properties stated in Lemma 2.4 and the formulas in ^[10] to do so.

Remark 5.2. One possible way to find a Fibonacci bimodal map which is an odd function is by topology. If we can find a one-parameter family of odd polynomials with two critical points and show that such a family is a 'full family' (see ^[13]) for any combinatorially symmetric combinatorics (note that it is never a full family for any combinatorics since non symmetric combinatorics cannot appear in this family), then the family must contain the Fibonacci combinatorics. Another possible way is by renormalization. Note that the first return map $g_n$ restricted on the four return domains is a special class of box mapping. Rescaling $g_n$ to the same scale and obtaining a new map, such a step is called 'generalized renormalization'. The Fibonacci bimodal map is clearly infinitely renormalizable in this sense. Denote the $n$-th renormalization by $\mathcal R^n f$. If the renormalization sequence $\mathcal R^n f$ converges to a periodic cycle (this is reasonable by Fact 2.1), then any limit map is an odd function and has Fibonacci combinatorics. We emphasize here that the 'bounded geometry' property plays essential way in the renormalization theory, see ^[8].

6.   Conclusions

We study Fibonacci bimodal maps under a restrictive condition and show that the one-parameter family $f_{\lambda}$ has a phase transition from Lebesgue conservative to dissipative behaviors in this paper.

In Section 2, we study the topological properties of the Fibonacci bimodal maps in the context of kneading map and give an equivalent description of Fibonacci combinatorics. In Proposition 1, we show that the cutting times $S_k$ and the critical return times $s_k$ are coincident, the kneading map is clarified as $Q(k) = \max\{k-2, 0\}$. And, in Proposition 2, we prove that if $f \in \mathscr B^+$ has kneading map $Q(k) = \max\{k-2, 0\}$ and satisfies the starting condition stated in Lemma 2.3, then $f$ has Fibonacci combinatorics. Therefore we can study the Fibonacci combinatorics for bimodal maps by two equivalent descriptions.

In Section 3, we construct a piecewise linear bimodal map $f$ which is an odd function and has Fibonacci combinatorics. After construction, we prove in Proposition 3 and Proposition 4 that $f$ is well-defined and has kneading map $Q(k) = \max\{k-2, 0 \}$. The induced map $F$ is linear on each set $W_j, {\hat W}_j, {\hat V}_j$ and $V_j$, having slope $\pm s_j$.

In Section 4, we let $\epsilon_j$ tends to 0 in a geometric manner, where $\epsilon_j$ only depends on $\lambda$. Then $f$ depends solely on a single parameter $\lambda$. We denote $f$ by $f_{\lambda}$ for emphasizing $\lambda$ and calculate $s_j$ and $k_j$ under this geometric manner. In Lemma 4.1 we show that the additional conditions VI in Section 3 are true for all $\lambda \in (0, 1)$.

In Section 5, we first compute the critical order $\ell$ of $f$ in terms of $\lambda$. In Subsection 5.1, we compute the values of $\lambda$ for which there is an $F_{\lambda}$-invariant probability measure which is an acip, using a random walk govered by $T_{\lambda}: (0, 1] \to (0, 1]$. Finally, in Subsection 5.2, we prove that $f_{\lambda}$ has a wild attractor when $\lambda \in (\frac{1}{2}, 1)$, which is equivalent to show that $F_{\lambda}$ is dissipative.

Conflict of interest

All authors declare no conflicts of interest in this paper.