A stabilized multiple time step method for coupled Stokes-Darcy flows and transport model

1.   Introduction

Recently, Adams, Ehlting, and Edwards ^[1] developed a model of phenylalanine metabolism in plants that involved two mechanisms by which a plant may prioritize primary over secondary metabolism when input is low, while allowing secondary metabolism to operate at very high levels when there is sufficient input. The importance of these mechanisms lies in the fact that the input is the same for both primary and secondary metabolism, and there is a branch point in the sequences of biochemical reaction pathways, one of which leads to output (efflux) that drives primary metabolism, and the other, secondary. It is not obvious at first glance how a plant can shut down secondary metabolism but maintain primary metabolism when input is low, while allowing secondary output to be very large when input levels are high. The two mechanisms proposed by Adams and colleagues are

1. Threshold Separation, and

2. The Precursor Shutoff Valve (PSV).

While differences in thresholds are common in biochemical network models, the PSV was a new term and concept introduced in the paper by Adams and colleagues. The model for the phenylpropanoid network developed there was a reduced model from a more complex and more realistic network that tracks all the reactions in the relevant pathways, but a reduction that retains the essential structure and the gradual-but-saturated (Michaelis-Menten) nature of the reaction kinetics. Nevertheless, it consisted of a system of four nonlinear differential equations, analysis of which is not straightforward. It was shown that both mechanisms on their own contributed to the desired effect of prioritizing primary metabolism only at a low input level, but that the effect was enhanced when both mechanisms were present. In particular, thresholds for primary and secondary branches had to be widely (orders of magnitude) separated to be effective in the absence of the PSV, but much less so in the presence of the PSV, and even the PSV on its own was somewhat effective.

The simple structural nature of these mechanisms suggested that they might underlie similar behaviour in other systems with different reaction kinetics --- for example, steeper than Michaelis-Menten. On the other hand, the analysis of these highly nonlinear systems becomes difficult in high dimensions (when many variables are involved), and it would be advantageous to have a simpler class of equations that approximate the biochemical kinetics in a way that retains essential structures such as the two mechanisms involved in the phenylpropanoid network, but in a way that facilitates analysis. A first step in this direction was taken by Glass and Edwards ^[10], who showed that the Threshold Separation mechanism also functions in systems with infinitely steep reaction kinetics (Heaviside switches instead of Michaelis-Menten functions), related to and motivated by Glass networks, which are used as qualitative models of gene regulatory systems. The effect of the mechanism there was stronger than in Michaelis-Menten systems, such that thresholds do not have to be widely separated, but simply need to be unequal.

The idea to use step functions as approximations of steep sigmoidal reaction functions to produce qualitatively similar systems that are more tractable to analysis was first introduced by Glass and Kauffman ^[11,12]. The analysis of the resulting systems, called Glass networks since 2000 ^[7], has been extensively developed since, mainly to model gene regulatory networks (for references, see the recent review by Glass and Edwards ^[10]). A number of specific systems have been modelled by this approach, such as the gene networks for flower morphogenesis in Arabidopsis thaliana ^[17], for the initiation of sporulation in Bacillus subtilis ^[4], for carbon starvation response in Escherichia coli ^[6,8,14,21], for the yeast cell cycle ^[3], and for immune cell function ^[2]. Other examples are cited by Glass and Edwards ^[10]. Glass networks include a degradation term for each variable, which is appropriate in the context of gene regulation, where the molecules are large: proteins and mRNA. Glass and Edwards ^[10] discuss the possibility of using such analysis in models of biochemical networks that may not include degradation.

Here, we investigate the viability of the two mechanisms (Threshold Separation and the PSV) for branch prioritization in networks with steep reaction functions, but without degradation. Analysis in such systems is easier than in systems with Michaelis-Menten functions or Hill functions with higher exponents. We will show that while Threshold Separation is highly effective and sensitive in sharply-switching networks (even more so than in networks with Michaelis-Menten functions), the PSV is not at all effective in this context, adding nothing to the prioritization effect. Thus, the value of the PSV for prioritization depends on the switching being less steep, while the Threshold Separation is effective to some degree in a wider variety of systems, though the separation may have to be extreme if the switching function is not steep. It is the gradual nature of switching that is exploited by the PSV to enhance prioritization.

The work we present here is also a case study in the analysis of networks with steep activation functions that (unlike Glass networks) do not have degradation terms.

In Section 2, we present the structure we use for comparison of systems and mechanisms, the simplest structure in which both mechanisms can operate, slightly simpler than the one that occurs in the phenylpropanoid network model. This PSV motif, with or without Threshold Separation, can of course exist as a component of many larger systems. In Section 3, we extend the earlier analysis of step function systems to include the PSV, without many restrictions on parameters, and we compare the behaviour with and without each of the two mechanisms. The implications are discussed briefly in Section 4.

2.   A structure for the threshold separation and PSV motifs

2.1.   The PSV motif

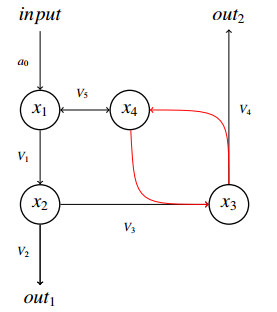
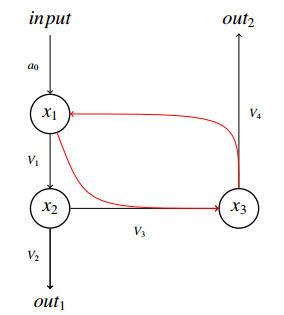
The simplest structure that includes the PSV motif is shown in Figure 1. This is a reduced version the phenylpropanoid network model of Adams and colleagues ^[1], but here we wish to consider it as a generic structure (motif) that might occur in many specific biochemical systems. The corresponding dynamical equations are

where $V_1$ through $V_4$ are the fluxes, which in that model were given by Michaelis-Menten functions, so that the full system could be written

where the corresponding flux terms are written in the same positions in Equations (2.1) and (2.2), and each $a_i$ is what is usually called the maximum flux parameter for flux $V_i$. We assume that $a_0 \geq 0$ and all other parameters in (2.2) are positive. We say that $x_1$ is the concentration of the precursor, which is upstream from the branching point at $x_2$, but which is also required to activate the secondary pathway, by producing the compound whose concentration is $x_3$. For brevity, we will sometimes loosely say that $x_1$ is "the precursor", rather than "the concentration of the precursor", and say "producing $x_i$", instead of "producing the molecule whose concentration is $x_i$, " and the like.

In the phenylpropanoid network of Adams et al. ^[1], the precursor is shikimate, which produces phenylalanine via a sequence of reactions. Phenylalanine then serves as the branching point, since it is used both in producing proteins that are needed in primary metabolism, and in producing compounds that are used in the complex set of reactions for secondary metabolism. These compounds are shikimate esters, and shikimate (the precursor) is required to make this chain of reactions go, so the precursor has the ability to shut off the secondary metabolism when the shikimate ester loop is inactivated.

The model of Adams and colleagues had an additional variable that can be thought of as separating the precursor into two populations: one, $x_1$, that participates in producing $x_2$ and another, $x_4$, that combines with $x_2$ to produce $x_3$. Shikimate exists in two cellular compartments: plastid and cytosol. The chain of reactions by which phenylalanine ($x_2$) is produced from shikimate occurs in plastid, while the binding of shikimate to a downstream product of phenylalanine to produce shikimate esters occurs in cytosol. However, the division of shikimate molecules into two populations is not necessary in principle for the PSV to operate, so here our precursor is represented only by $x_1$.

For comparison, the 4-dimensional model of Adams and colleagues ^[1] is as shown in Figure 2, where the concentrations of plastidial and cytosolic shikimate are represented by $x_1$ and $x_4$, respectively (we have changed the labelling from Adams and colleagues, reversing $x_3$ and $x_4$, $V_2$ and $V_5$ and corresponding parameters of those fluxes). The equations are given by

which are equivalent to

This model had an additional parameter, $b$, which allowed for an inhibitory effect of phenylalanine concentration ($x_2$) on the conversion of plastidial shikimate ($x_1$) to phenylalanine. Adams and colleagues considered mainly the case in which $b = 0$. They reported on simulations with $b > 0$ to show that the essential behaviour is not changed for small positive values of $b$, so we will not include this in our reduced form of the PSV motif. System (2.2) is obtained from (2.4) by eliminating the fluxes between $x_1$ and $x_4$ and combining them into a single variable. To show that the results of Adams et al. hold in this case, one need only take $K_5^- = K_5^+ = K_5$ and $a_5^- = a_5^+ = a_5$, and for non-equilibrium situations take $a_5$ arbitrarily large, so that shikimate moves arbitrarily rapidly between cytosolic and plasmidial pools, and acts effectively as a single pool (note that the index here was $2$ and not $5$ in the paper by Adams et al.).

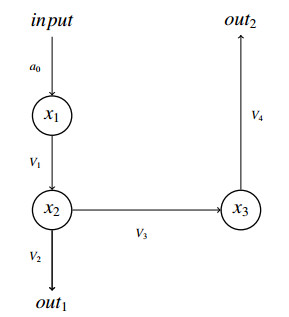
2.2.   Structure without the PSV

When the PSV (the involvement of the precursor in the secondary pathway) is removed, system (2.2) becomes

as shown in Figure 3. With Michaelis-Menten control functions for the reactions, this becomes

Again, the biochemical context requires $a_0 \geq 0$ and all other parameters $> 0$.

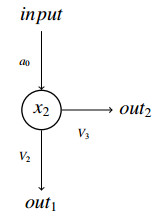
While this system allows for the most direct comparison to the system with the PSV, it is more complicated than necessary for the operation of the Threshold Separation motif, which depends only on the difference between thresholds for primary and secondary pathways at the branching point. Glass and Edwards ^[10] studied this motif in a two-dimensional context, that can be obtained from system (2.6) by removing $x_1$ and feeding the input $a_0$ directly into $x_2$, since the only role of $x_1$ now is to feed the input into $x_2$. In fact, the Threshold Separation is really a one-variable phenomenon, acting at the branching point, so it could be reduced still further by removing $x_3$ and considering the flux $V_3$ as the secondary output flux (see Figure 4).

3.   Sharply-switching systems

3.1.   Analysis of sharply-switching systems

Glass and Edwards ^[10] show how the system

as a general framework for sharply-switching networks without degradation, relates to

in the limit as the degradation rates $\gamma_i\to 0$, where the $F_i$ is a scalar that depends on the Boolean State vector X ($X_i = 0$ if $x_i < \theta_i$ and $X_i = 1$ if $x_i > \theta_i$), $\theta_i$ is a threshold concentration, and $N$ is the number of chemical species. In the context of gene regulation, these species are protein products of genes, $\gamma_i > 0$, and this is a Glass network. Each $x_i$ is bounded within the interval $[0, \max_{\bf X} (F_i)/\gamma_i]$. In more generality, if a gene regulates more than one other gene it can do so at different thresholds, so one has $X_{ij} = 0$ if $x_i < \theta_{ij}$ and $X_{ij} = 1$ if $x_i > \theta_{ij}$. Note that $X_{ij}$ is not so far defined at $x_i = \theta_{ij}$, but we will deal with these discontinuities by considering the sharp switching of $X_{ij}$ as a limit of steep but smooth sigmoidal functions, so that $X_{ij}$ will take values in $[0, 1]$ at $x_i = \theta_{ij}$. The idea of Glass and Edwards was to consider systems without degradation, but with sharp switching, as occurs when there is high cooperativity in reactions. It is not necessary to take a limit as hypothetical degradation terms go to $0$; one can simply start with Eq (3.1).

Glass and Edwards ^[10] use as an example a sharply-switching version of the phenylpropanoid system to explain the prioritization of primary over secondary metabolism in plants when input is low. They considered only the operation of the Threshold Separation mechanism in the sharply-switching context, showing that it was effective in prioritizing primary metabolism, as in the original Michaelis-Menten reaction system, but even more distinctly. Here, we consider the PSV mechanism in the sharply-switching context. One may anticipate that the PSV is a mechanism that could be present in a wide variety of biochemical systems, and it is desirable to determine in what types of system it is effective and in what types of system it is not.

When there is no degradation, it is possible for the system to blow up. The model of Adams, et al. is an open one: there is an input flux and there are two output fluxes. Conditions on the input in relation to other parameters in the system must be met to ensure that no variable goes to infinity (which would not be very plausible in biochemical systems). For example, the maximum output capacity must exceed the input. From the point of view of sharply-switching systems, like Glass networks, the phase space is divided into rectangular regions (boxes) bounded by the threshold values, and the vector field is piecewise linear within each box. In fact, when we have no degradation terms, the vector fields are piecewise constant within each box. Flow is unbounded if in a box where one or more variable is above its highest threshold the flow is constrained to that box and away from that highest threshold, or if the flow cycles between a set of boxes above the highest threshold of one variable such that the net movement is away from that highest threshold. $F_i$ can be negative, though not when $x_i$ is below its lowest threshold (since it is not possible for any variable to go below $0$.

The solution to system (3.1) in a given box with constant $F_i$ is

If a trajectory exits the box at $x_i(t^*) = \theta_{ik}$, then the time at which this occurs is given by

and the other coordinates of the exit point are clearly

Trajectories in boxes are parallel, rather than converging towards a focal point, as they do in Glass networks. Maps from switching point to switching point can be calculated, but it is not possible to have a fixed point in the interior of a box. Fixed points can exist, but only in threshold domains.

Within a box, $x_i$ is increasing if $F_i > 0$ and is decreasing if $F_i < 0$. When $F_i = 0$, strictly speaking $x_i$ remains fixed, but if we consider $X_i$ or $X_{ik}$ to be a steep and strictly monotonic sigmoidal function, instead of a step function, then $F_i$ will not usually be exactly zero, and the form of its dependence on $X_i$ will determine whether it is slightly positive or slightly negative.

If there are $N$ variables in a system, then the $(N-1)$-dimensional boundaries between the $N$-dimensional boxes in phase space are sometimes called walls, and a black wall occurs between two boxes in which the flow is directed in towards the wall from both sides ^[19]. It will be typical in these networks for flows to be constrained to threshold domains such as black walls, or more generally, threshold intersections. To handle flows in such domains rigorously, we must resort to Filippov solutions ^[13], or else singular perturbation analysis ^[19]. We generally prefer the latter, as it avoids possible non-uniqueness that can arise in the Filippov approach, though in most situations encountered (such as in black walls), the two methods give the same solutions. The singular perturbation approach considers the step functions as infinitely steep limits ($q\to 0$) of Hill functions:

In a threshold domain in which a subset, $S$, of the variables are at their threshold value, and the variables in the complementary subset, $\bar{S}$, are not, we describe the fast flow of the switching variables by transforming from $x_s$ to $X_s$ in Equation (3.1) for all $s\in S$, to get

where ${\bf X}_{\bar{S}}\in \{0, 1\}^{|\bar{S}|}$ and $\tau = t/q$ is the fast time variable. When this has an asymptotically stable equilibrium ${\bf X}_S^*\in (0, 1)^{|S|}$, we can then use the fixed point to determine the dynamics of the slow variables ($i\in \bar{S}$) and obtain the sliding flow in the threshold domain:

Full details may be found in ^[19], where a degradation term is always included, but this can simply be taken to be $0$, as here. Note that Hill functions are natural in this context but any other class of strictly monotone sigmoidal functions with a step function limit would be expected to produce qualitatively the same results. More general sigmoids are considered in some of the literature on gene networks ^[11,18,20].

3.2.   Sharply-switching system with the PSV

Figure 1 shows the system to be modelled. In the model of Adams et al., the variables $x_1, x_2$, and $x_3$ represent concentrations of shikimate, phenylalanine, and shikimate esters, respectively. In general, $x_1$ is the precursor, $x_2$ feeds into both primary and secondary pathways, and $x_3$ is a complex involving the precursor.

The switching system version of the model is:

where the parameter $a_0$ represents the input flux, while $a_1, a_2, a_3,$ and $a_4$ represent the maximum fluxes for each of the four fluxes in the system, $V_1, V_2, V_3,$ and $V_4$. Each flux is now considered to turn on sharply when the relevant variables are above a threshold. Thus, the switching variables are $X_{11}, X_{12}, X_{21}, X_{22},$ and $X_3$ where:

We have chosen to index the thresholded variables in this way to enforce that $\theta_{11} < \theta_{12}$ and $\theta_{21}\le \theta_{22}$. That is, $x_1$ becomes available to combine with $x_2$ at a lower concentration than it becomes available for conversion into $x_2$, and, as its name suggests, the primary output pathway cannot have a higher threshold than the secondary pathway (or at least the first step of the secondary pathway). The reason for the ordering of thresholds for $x_1$ will be discussed further below, after the proof of Proposition 1.

3.3.   Assumptions on parameters

In order for Equations (3.4) to represent a realistic biochemical system, it should not be possible for any variable to grow arbitrarily large. Since it is an open system, if the input were to exceed the maximum possible output, then unbounded growth would be inevitable. The following Proposition shows that the input must be bounded in various ways in relation to maximum flux parameters.

Proposition 1. Consider Equations (3.4) with $\theta_{11} < \theta_{12}$ and $\theta_{21} \le \theta_{22}$. If any of the following three conditions holds, then the system has unbounded growth:

● $a_0 > a_1$,

● $a_0 > a_2+a_3$,

● $a_0 > a_2+a_4$.

Proof. First, note that all variables remain non-negative if initially non-negative: When $x_1 = 0$, $\dot{x}_1 = a_0+a_4X_3\ge 0$; when $x_2 = 0$, $\dot{x}_2 = a_1X_{12} \ge 0$; when $x_3 = 0$, $\dot{x}_3 = a_3X_{11}X_{22}\ge 0$. Now, suppose $a_0 > a_1$. Then

so $(x_1+x_3)\to \infty$ as $t\to\infty$. Since both $x_1$ and $x_3$ must remain non-negative, either $x_1\to\infty$ or $x_3\to\infty$ or both. Now suppose $a_0 > a_2+a_3$. Then

so $(x_1+x_2+x_3)\to \infty$. Finally, suppose $a_0 > a_2+a_4$. Then

so $(x_1+x_2+2x_3)\to \infty$.

If $a_0 < \min \{ a_1, a_2+a_3, a_2+a_4 \}$, we will see below that the system is bounded when $\theta_{21} < \theta_{22}$, but if these are equal, another condition will be required. The situation is more complicated if $\theta_{12} < \theta_{11}$, where further conditions are needed to ensure boundedness. Adams and colleagues ^[1] found in their more complicated model that an ordering of thresholds similar to $\theta_{11} < \theta_{12}$ was needed to produce biologically sensible behaviour, so we do not consider the opposite ordering further here.

The following are assumptions on parameters made to reflect the functioning of realistic processes.

Assumption 1. The parameters of system (3.4) satisfy

● $a_0 \geq 0$ (System influx cannot be negative)

● $a_1, a_2, a_3, a_4 > 0$ (All rate parameters must be positive)

● $a_0 < a_1$ (First step of the pathway must have capacity to handle maximum input)

● $a_0 < a_2 + a_3$ (Total output from branch point must have capacity to handle maximum input)

● $a_0 < a_2 + a_4$ (Total system output must have capacity to handle maximum input)

● $\theta_{11} < \theta_{12}$ (Precursor can be used to facilitate secondary pathway whenever that is active)

● $\theta_{21}\le \theta_{22}$ (Secondary pathway is not prioritized, or it would not be secondary)

3.4.   Threshold separation

As for Adams, et al. ^[1], we are interested in the ability of a system to prioritize the primary output when input is low by two mechanisms. Glass & Edwards ^[10] dealt with a model without the PSV, and considered the Threshold Separation mechanism by studying the system's behaviour when the thresholds for the two pathways were separated and when they were not. Here we study the system with the PSV and again consider separated thresholds and equal thresholds. The two thresholds are those for flux $V_2$ into the primary pathway and flux $V_3$ into the beginning of the secondary pathway. In each case, we consider low input ($a_0 < a_2$) and high input ($a_0 > a_2$). The goal is to locate the equilibrium in each case with each input level, and to show that it is globally stable, in order to determine which pathways are "switched on".

● The PSV model with Threshold Separation: $\theta_{21} < \theta_{22}$

● The PSV model without Threshold Separation: $\theta_{21} = \theta_{22} = \theta_2$

First, we deal with the separated threshold PSV structure.

3.5.   The PSV model with threshold separation

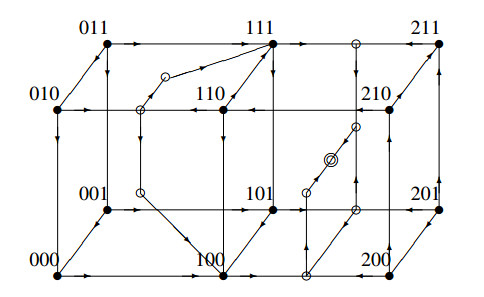
The phase space is divided into regions (boxes) where each variable is above or below each of its thresholds. Let us label these boxes by a string of integers, 0, 1, or 2, given for each variable by $X_{i1}+X_{i2}$ for $i = 1$ or $2$, and $X_i$ for $i = 3$. Thus, 120 represents the box where $\theta_{11} < x_1 < \theta_{12}$, $x_2 > \theta_{22}$ and $x_3 < \theta_3$, or equivalently, where $X_{11} = 1, X_{12} = 0, X_{21} = 1, X_{22} = 1$, and $X_3 = 0$. In general, $abc$ represents the box where $X_{11}+X_{12} = a, X_{21}+X_{22} = b$, and $X_3 = c$.

We assume throughout that $a_0 < \min\{ a_1, a_2+a_3, a_2+a_4\}$ so that unbounded growth is not guaranteed by Proposition 1. The flow in each of the boxes, obtained directly from Equations (3.4), is given in Table 1. In some boxes the flow direction depends on the choice of the maximum flux rate parameters, $a_i$ for $i = 1, \ldots, 4$, and/or the input level, $a_0$. Note that in states 200,210 and 220 there is no ambiguity in the direction of $x_1$ under our assumption that $a_0 < a_1$.

It is clear from Table 1 that in some cases the flow in two adjacent boxes can be directed towards the boundary between them from both sides, so these are black walls. For example, in $200$, $x_2$ is increasing and some trajectories in this box will hit the wall where $x_2 = \theta_{21}$, while if $a_1 < a_2$, then in $210$ $x_2$ is decreasing. Thus, if a trajectory enters the wall between these two boxes, it cannot leave the wall into either box and can only slide along the wall. If $a_1 > a_2$, however, this wall is not black but transparent and the flow passes through from 200 to 210. We will use singular perturbation theory to determine the flow in black walls, assuming that the true switching is a steep Hill function, and considering the limit of infinite steepness.

In Table 2, we give the directions of flow in each box in terms of the possible "successor" states, i.e., states that the flow from a given box may enter next. Flow is directed towards one box or another, depending on where in the given box one starts, and in some cases depending on relative parameter values. The flow may enter these boxes, or may be stopped by a black wall, which is then the successor state. All of the possible successor states in each case are given in the second column, including boxes, if the flow goes through a transparent wall, or a black wall if one exists. Black walls between boxes are labelled with $\frac{1}{2}$ or $\frac{3}{2}$ instead of an integer for the variable that is at its threshold value, the former when $x_i = \theta_{i1}$ and the latter when $x_i = \theta_{i2}$. Thus, for example, the state $2\frac{1}{2}0$ is the wall between $200$ and $210$.

To determine the flow within a black wall where $x_i = \theta_{ij}$, we transform the equation for the variable $x_i$ into one for $X_{ij}$ by means of Eq (3.3), taking

and considering the limit as $q\to 0$. This analysis is outlined above at the end of Section 3.1, and given more completely by Plahte and Kjøglum ^[19]. The equation of such a switching variable becomes

where ${\bf X}$ is a vector of values $X_{k\ell}$, and where the derivative is with respect to the fast time variable, $\tau = t/q$. As long as $X_{ij}$ converges to a fixed point in $(0, 1)$, Tikhonov's theorem applies, and we can use the equilibrium value of $X_{ij}$ to determine the flow of the slow variables, $x_k$ ($k\ne i$).

As an example, consider the wall $\frac{1}{2}21$, where $x_1 = \theta_{11}$, which is black in the case $a_0 < a_3-a_4$ (which is of course only possible if $a_3 > a_4$). Then,

so $X_{11}\to \frac{a_0+a_4}{a_3}\in(0, 1)$ asymptotically (in the fast $\tau$ time). Then

Thus, $x_2$ decreases while $x_3$ increases and trajectories must exit the black wall at $x_2 = \theta_{22}$. At this point, both $x_1$ and $x_2$ are at threshold values, and we label this state $\frac{1}{2}\frac{3}{2}1$. A singular perturbation analysis of such threshold intersection states is then needed to determine where the flow goes from there. The newly reached threshold may simply be transparent, in which case trajectories pass through to the wall on the other side (where the first variable is still at threshold), but it may not be transparent and the first variable may no longer be constrained to its wall, so there are many possibilities, in general. The flow in all possible black walls is given in Table 3, and the successor states (threshold transition states) are given in Table 4.

To illustrate the analysis of the flow from the intersection of two thresholds, consider state $\frac{1}{2}\frac{3}{2}1$ as above. We transform both the $x_1$ and $x_2$ equations in terms of $X_{11}$ and $X_{22}$ to get

Clearly, $X_{22}$ simply decreases here, no matter the value of $X_{11}X_{22}$, so $X_{22}\to 0$. It is not difficult to see, then, that eventually $X_{11}$ must increase, because $a_0+a_4-a_3X_{11}X_{22}\to a_0+a_4 > 0$ as $X_{22}\to 0$. Now, $X_{11} = 1$ is a fixed point of the first equation above, but it can only be approached asymptotically, and similarly for $X_{22}\to 0$, so the flow in the square $(X_{11}, X_{22})\in [0, 1]^2$ asymptotically approches the corner $(X_{11}, X_{22}) = (1, 0)$. Thus, the trajectory emerges in the box $111$ (since $x_1$ goes up from $\theta_{11}$ and $x_2$ goes down from $\theta_{22}$).

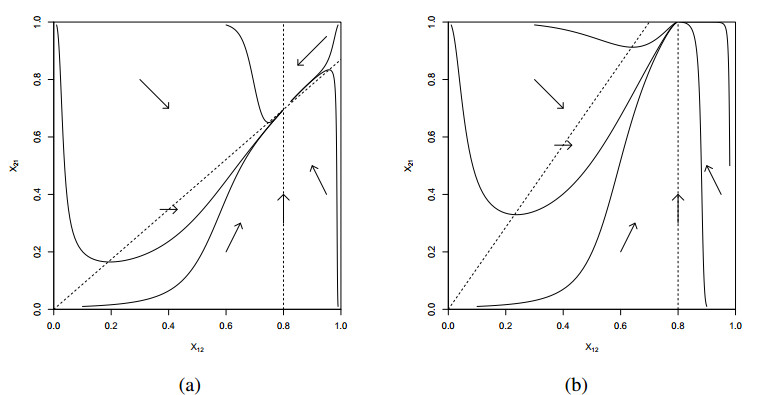
The situation is somewhat different in the state $\frac{3}{2}\frac{1}{2}1$. Tables 3 and 4 tell us that trajectories can only arrive at this threshold intersection from $\frac{3}{2}01$, which is only black when $a_0 < a_1-a_4$ (and so $a_1 > a_4$), from $\frac{3}{2}11$ when $a_0 < a_2-a_4$, and again this wall is only black when $a_0 < a_1-a_4$, or from $2\frac{1}{2}1$ when $a_0 < a_1-a_4$, and this wall is only black when $a_1 < a_2$. Thus, all three routes to this state require $a_0 < a_1-a_4$, and the third route also requires $a_1 < a_2$, while the second route also requires $a_0 < a_2-a_4$. The fast flow in this state is given by

Since $a_0 < a_1-a_4$, we have that $X_{12}\to \frac{a_0+a_4}{a_1}\in (0, 1)$. Then, $(X_{12}, X_{21}) = \left(\frac{a_0+a_4}{a_1}, \frac{a_0+a_4}{a_2}\right)$ is a fixed point in $(0, 1)^2$ if $a_0 < a_2-a_4$ as well, and the stability of this point can be found from the Jacobian matrix:

which clearly has negative eigenvalues, being lower triangular with negatives on the diagonal, so the fixed point is stable, locally, but also globally, as can be seen from the flow directions in the phase portrait. See Figure 5(a).

Thus, when $a_0 < a_2-a_4$, the flow becomes constrained to the threshold intersection region $x_1 = \theta_{12}, x_2 = \theta_{21}$ and $x_3$ evolves in slow time according to

so we arrive eventually in the state $\frac{3}{2}\frac{1}{2}\frac{1}{2}$ where $x_3 = \theta_3$ also. Here, it can be shown that this state is transparent, in that $X_3\to 0$, so the subsequent state is $\frac{3}{2}\frac{1}{2}0$. In fact, the fast flow in the triple threshold intersection is given by

so $X_3\to 0$, and then $X_{12}\to \frac{a_0}{a_1}$ and $X_{21}\to \frac{a_0}{a_2}$. Note that $a_0 < a_2-a_4 < a_2$, so $X_{21}$ as well as $X_{12}$ stay within the interval $(0, 1)$. In the region where $x_3 < \theta_3$, we will have $\dot{x}_3 = 0$, so the trajectory does not actually drop below $x_3 = \theta_3$, but this is an artifact of the infinite steepness of the switching. If the switching were perturbed by any amount into a steep sigmoidal form ($q > 0$), then $x_3$ would continue to drop below $\theta_3$. This is indicated by the fact that $X_3\to 0$, so we should consider the trajectory to enter the state $\frac{3}{2}\frac{1}{2}0$.

If, on the other hand, $a_0 > a_2-a_4$, then the flow in the domain $(X_{12}, X_{21})\in [0, 1]^2$ can be determined from the nullclines and flow directions between them. The $X_{12}$ nullcline is just the vertical line in the $(X_{12}, X_{21})$ plane, $X_{12} = \frac{a_0+a_4}{a_1}$, and the $X_{21}$ nullcline is the line $X_{21} = \frac{a_1}{a_2}X_{12}$, but it is important to realize that $X_{12} = 0$ or $1$ and $X_{21} = 0$ or $1$ are nullclines, too. When $a_0 > a_2-a_4$, the two interior nullclines do not intersect in $[0, 1]^2$, but would intersect above it (where $X_{21} > 1$). An analysis of the phase portrait shows that the flow must approach the point $(X_{12}, X_{21}) = \left(\frac{a_0+a_4}{a_1}, 1\right)$ asymptotically. See Figure 5(b). Thus, the trajectory exits into the state $\frac{3}{2}11$.

The possible successor states for all feasible double and triple threshold intersections are given in Table 5.

With complete information on the state transition diagram for any parameter values, we are now in a position to prove the following two results, giving first local and then global stability of a unique fixed point, a different point in the case $a_0 < a_2$ than in the case $a_0 > a_2$.

Proposition 2. Suppose $a_0 < \min\{ a_1, a_2+a_3, a_2+a_4\}$ in system (3.4). If $a_0 < a_2$, the state $\frac{3}{2}\frac{1}{2}0$ (i.e., $x_1 = \theta_{12}, x_2 = \theta_{21}, x_3 < \theta_3$) is locally stable. If $a_0 > a_2$, the state $\frac{3}{2}\frac{3}{2}\frac{1}{2}$ (i.e., $x_1 = \theta_{12}, x_2 = \theta_{22}, x_3 = \theta_3$) is locally stable.

Proof. The singular perturbation expansion for $x_1$ and $x_2$ in state $\frac{3}{2}\frac{1}{2}0$ is

Since $a_0 < a_1$, $X_{12}\to \frac{a_0}{a_1}\in (0, 1)$ and eventually, $X_{21}\to \frac{a_1}{a_2}X_{12} = \frac{a_0}{a_2}\in (0, 1)$, when $a_0 < a_2$. The Jacobian is again the one given in (3.6), and so the equilibrium is locally stable, and global stability within $(0, 1)^2$ is easy to ascertain from the phase portrait. Thus, once this threshold intersection is reached, it is stable in the $x_1$ and $x_2$ directions. Then $\dot{x}_3 = 0$ so there is no movement in the $x_3$ direction either. The fact that a trajectory from $\frac{3}{2}\frac{1}{2}0$ into any adjacent state would contradict the flow can be read in part from Table 4, where it is seen that from $\frac{3}{2}00$, $\frac{3}{2}10$, and $2\frac{1}{2}0$, the flow is into $\frac{3}{2}\frac{1}{2}0$. The state $1\frac{1}{2}0$ is a transparent wall:

so $X_{21}\to 0$, and there is no sliding flow along this wall (either into or out of $\frac{3}{2}\frac{1}{2}0$). A trajectory from $\frac{3}{2}\frac{1}{2}0$ into any of the adjacent boxes, $100$, $110$, $200$, and $210$, contradicts the flow direction in one or both variables, from Table 2. So, from either the macroscopic or microscopic perspective, $\frac{3}{2}\frac{1}{2}0$ is stable. It must be noted that although Tikhonov's theorem only guarantees convergence on finite time intervals, the flow here is into the $\frac{3}{2}\frac{1}{2}0$ state from all adjacent regions, and this is still true for the perturbed system with $q > 0$ sufficiently small, so no escape is possible for the perturbed system either^* and the point $x_1 = \theta_{12}, x_2 = \theta_{22}, x_3 = \theta_3$ is genuinely locally stable.

^*The finite time interval of convergence in Tikhonov's theorem becomes a problem if there is flow towards the boundary in some parts of the $|S|$-cube $[0, 1]^{|S|}$, the phase space of the fast variables, here $(X_{12}, X_{21})$. For example, there may be a saddle point as well as an asymptotically stable fixed point in the interior of this cube (or square if $|S| = 2$), as occurs in Example 4 of ^[9].

The singular perturbation expansion in state $\frac{3}{2}\frac{3}{2}\frac{1}{2}$ is

which has equilibrium $(X^*_{12}, X^*_{22}, X^*_3) = (\frac{a_0}{a_1}, \frac{a_0-a_2}{a_3}, \frac{a_0-a_2}{a_4})\in (0, 1)^3$ when $a_0 > a_2$ (note that $a_0 < a_2+a_3$, so $\frac{a_0-a_2}{a_3} < 1$, and $a_0 < a_2+a_4$, so $\frac{a_0-a_2}{a_4} < 1$). Letting $u_1 = \frac{X^*_{12}(1 - X^*_{12})}{\theta_{12}}$, $u_2 = \frac{X^*_{22}(1 - X^*_{22})}{\theta_{22}}$, and $u_3 = \frac{X^*_3(1 - X^*_3)}{\theta_3}$, the Jacobian evaluated at the equilibrium is

with characteristic equation

Rewriting the equation as $\lambda^3 + b_1\lambda^2 + b_2\lambda + b_3 = 0$, we have $b_1 > 0$ and $b_3 > 0$ because all $a_i > 0$ and $u_i > 0$. Furthermore, $b_1b_2 > b_3$ because $b_1b_2$ contains the term $a_1a_3a_4u_1u_2u_3 = b_3$ added to exclusively positive terms. Hence, by the Routh-Hurwitz Criterion, the fast-time system is stable at the equilibrium $(X^*_{12}, X^*_{22}, X^*_3)$. Again, Tikhonov's theorem only guarantees convergence on finite time intervals, but the flow is into state $\frac{3}{2}\frac{3}{2}\frac{1}{2}$ from all adjacent states, when $a_0 > a_2$, and this is still true for $q > 0$ sufficiently small, so no escape is possible and $x_1 = \theta_{12}, x_2 = \theta_{22}, x_3 = \theta_3$ is locally stable.

Note that if $a_0 < a_2$, then the flow in the interior of the $(X_1, X_2, X_3)$ cube above is towards the point $\left(\frac{a_0}{a_1}, 0, 0\right)$, so the trajectory from $\frac{3}{2}\frac{3}{2}\frac{1}{2}$ exits into the region $\frac{3}{2}10$.

Proposition 3. If $a_0 < \min\{ a_1, a_2+a_3, a_2+a_4\}$, then solutions to system (3.4) are bounded. If $a_0 < a_2$, the state $\frac{3}{2}\frac{1}{2}0$ (i.e., $x_1 = \theta_{12}, x_2 = \theta_{21}, x_3 < \theta_3$) is globally stable. If $a_0 > a_2$, the state $\frac{3}{2}\frac{3}{2}\frac{1}{2}$ (i.e., $x_1 = \theta_{12}, x_2 = \theta_{22}, x_3 = \theta_3$) is globally stable.

Proof. First we show that, eventually, all trajectories lead to the region where $x_1\ge\theta_{12}$ and cannot then escape. From Equations (3.4), it is clear that $\dot{x}_2\le 0$ when $x_1 < \theta_{12}$, and the former inequality is strict when $x_2 > \theta_{21}$. Also, $\dot{x}_1 > 0$ when $x_1 < \theta_{12}$, except possibly when $x_1\ge \theta_{11}$ and $x_2\ge \theta_{22}$. In fact, it can be deduced from Tables 4 and 5 that when $x_2 = \theta_{22}$ (i.e., when in a state $\cdot \frac{3}{2}\cdot$), there is no possibility of a transition from a state $2\frac{3}{2}\cdot$ or $\frac{3}{2}\frac{3}{2}\cdot$ to a state $1\cdot\cdot$, so that if $x_2$ is only equal to its second threshold and not above it, $x_1$ cannot decrease below $\theta_{12}$. Thus, if $x_1 < \theta_{12}$, and $x_2\le\theta_{22}$, then $x_2$ cannot increase above $\theta_{22}$ but $x_1$ must increase until it reaches $x_{12}$. If $x_1 < \theta_{12}$ and $x_2 > \theta_{22}$ then either $x_2$ decreases to $\theta_{22}$ first or $x_1$ increases to $\theta_{12}$ first. In either case, $x_1\ge\theta_{12}$ will be achieved in finite time, but we must show that it cannot repeatedly drop below $\theta_{12}$ again, so further analysis is needed.

We can partition the system states into four subsets:

We will show that although $S_1\cup S_2$ is not an invariant set, it is eventually invariant in the sense that trajectories that leave must return and cannot leave again. (In fact, there is a subset of $S_1\cup S_2$ that is strictly invariant, but it is easier to work with these sets.) The argument above shows that from $S_4$ we must go to $S_1$, but from $S_3$ we can go to $S_4$ or to $S_2$.

Now, we show that to get from $x_1 \ge \theta_{12}$ to $x_1 < \theta_{12}$ we must be in a state where $x_2 > \theta_{22}$. Equivalently, the only route from $S_1\cup S_2$ to $S_3\cup S_4$ is $S_2\to S_3$. This transition is only possible if $a_0 < a_3$ at least. The proof comes from inspection of Tables 2, 4 and 5, which show the only states in which $x_1$ can decrease again below $\theta_{12}$ (from a state $\frac{3}{2}\cdot\cdot$ or $2\cdot\cdot$ to a state $1\cdot\cdot$) is from $220$ to $120$ (if $a_0 < a_3$) or $221$ to $121$ (if $a_0 < a_3-a_4$). In both of these cases $x_2 > \theta_{22}$ both before and after the transition, and the weakest parameter condition is $a_0 < a_3$.

Next, we show that, possibly after a finite transient time, we can only get from $x_2 \le \theta_{22}$ to $x_2 > \theta_{22}$ in states where $x_1 > \theta_{12}$, or equivalently, the only way to get to $S_2\cup S_3$ from $S_1 \cup S_4$ is from $S_1$ to $S_2$ and only when $X_{12} = 1$. This transition is only possible if $a_1 > a_2+a_3$ at least. This can be deduced again from the Tables, but it is clear anyway from the $\dot{x}_2$ equation in (3.4) that $x_2$ can only increase when $X_{12} > 0$. It is possible to go from state $\frac{3}{2}\frac{3}{2}1$ in $S_1$ to either $221$ or $\frac{3}{2}21$ in $S_2$ in some parameter regimes, but these all require $a_3 < a_4$ (or else one of our basic conditions $a_0 < a_1$ or $a_0 < a_2+a_3$ must be violated). If $a_3 < a_4$ then whenever $X_3 = 1$, $x_3$ is decreasing, so after a finite time, $x_3\le \theta_3$, and $X_3 < 1$. So, after a transient, the transitions from $\frac{3}{2}\frac{3}{2}1$ to $\cdot 21$ are not accessible. Thus, eventually, the only route to $S_2$ from $S_1$ is from states $2\cdot\cdot$. All of these transitions require $a_1 > a_2+a_3$.

Going back one step further, we can only get to $x_2 > \theta_{12}$ from $x_2 \le \theta_{12}$ in $S_1$ in states where $x_3 > \theta_3$, and we must have $a_0 > a_1-a_4$ at least. To see this, note in the first equation in (3.4) that if $X_{22} = 0$, and $X_3 = 0$, then $x_1$ cannot be increasing when $x_1 > \theta_{12}$, since $a_0 < a_1$. However, to check threshold states, we refer again to the Tables, which show that the only transitions that lead to $2\cdot\cdot$ from a state with $x_1$ and $x_2$ lower than state $2$ are $101\to 201$, $111\to 211$, $\frac{3}{2}\frac{1}{2}1$ to $211$, and $\frac{3}{2}\frac{3}{2}1\to 221$ or $\frac{3}{2}21$, in all of which $X_3 = 1$. Note that the last two were shown to be feasible only during a transient, and the others all require at least $a_0 > a_1-a_4$.

Let us summarize the above arguments. The flow is always from $S_4$ to $S_1$. From $S_3$, the flow must also always take the system out of $S_3$, usually to $S_4$, though in some parameter ranges it is possible to go back to $S_2$ as well. There can be transients involving an initial state in $S_1$ with $x_1 > \theta_{12}$ going to $S_2$ or initially in $S_2$ and passing from there to $S_3$, or if $a_3 < a_4$ with $x_3 > \theta_3$ initially, involving the finite time it takes for $x_3$ to reach $\theta_3$, so that $X_3 = 1$ is no longer accessible. After these finite transients, the only way to transition from $S_2$ to $S_3$ is by means of a trajectory that passes through $S_1$ with $x_1$ going from $\theta_{12}$ or below to above $\theta_{12}$, then passing through $S_2$ and then to $S_3$. The minimum conditions for the three steps are $a_0 > a_1-a_4$, $a_1 > a_2+a_3$ and $a_0 < a_3$, respectively. In fact, the last transition requires $a_0 < a_3-a_4$ if it goes from $221\to 121$. But this last is inconsistent with the previous two conditions: $a_1 > a_2+a_3 \implies a_1 > a_3$ and then this and $a_0 > a_1-a_4 \implies a_0 > a_3-a_4$. Under the conditions required to arrive at $221$, the flow must go to $\frac{3}{2}21$, and thence down to $\frac{3}{2}\frac{3}{2}1$. So, the only accessible route from $S_2$ to $S_3$ is from $220\to 120$. Coming from states in $S_1$ where $x_3 > \theta_3$ means that when we reach $220$ we have $x_3 = \theta_3$ with $X_3 = 0$ (which we can think of as being infinitesimally below the threshold $x_3 = \theta_3$ and thus inside the $220$ box). This occurs because $x_3$ can never decrease below $\theta_3$ once it has ever reached or exceeded it, since $\dot{x}_3 \ge 0$ when $X_3 = 0$. Thus, if a trajectory subsequently reaches $220$, where in principle $x_3$ or $x_1$ can switch next, $x_3$ will always switch instantly, before $x_1$ has a chance. So the subsequent state must then be $221$, and the route $220\to 120$ to $S_3$ is closed.

Although it is possible to go from $S_2\to S_3\to S_2$, it is not possible to go from $S_3\to S_2 \to S_3$. Thus, no cycling through $S_2$ and $S_3$ is possible. This can be seen by examining state transitions within $S_2\cup S_3$ in all allowable cases of parameter values. See Figure 6. There are seven possible state transition diagrams, depending first on whether or not $a_3 < a_4$, and secondly on the magnitute of $a_0$ in relation to $a_3$ and $a_1+a_3-a_4$ when $a_3 < a_4$, and in relation to $a_3$ and $a_3-a_4$ when $a_3 > a_4$. Note that when $a_3 < a_4$, it is not possible to have $a_0 < a_3-a_4$, and when $a_3 > a_4$, it is not possible to have $a_0 > a_1+a_3-a_4$ (since $a_0 < a_1$).

This establishes that even if initially a trajectory goes from $S_2$ to $S_3$, it cannot do so again. Thus, $S_1 \cup S_2$ is eventually invariant.

Next, we show that within $S_1$, the set $S_0 = \{ x_1 = \theta_{12}, x_2 \le \theta_{22}, x_3 \le \theta_3 \} = \{ 0 < X_{12} < 1, X_{22} < 1, X_3 < 1 \}$ is invariant. When $X_{22} = 0$ and $X_3 = 0$ it is clear from the first equation in (3.4) that $x_1$ increases when $X_{12} = 0$ and decreases when $X_{12} = 1$, so the wall is black and it is not possible for $x_1$ to leave the threshold. For threshold states in $x_2$ and $x_3$, inspection of Tables 4 and 5 shows that possible successor states to any state in $S_0$, namely, $\frac{3}{2}00$, $\frac{3}{2}10$, $\frac{3}{2}\frac{1}{2}0$, $\frac{3}{2}\frac{3}{2}0$, or $\frac{3}{2}\frac{3}{2}\frac{1}{2}$, are all within $S_0$.

All other states in $S_1 \cup S_2$ lead to $S_0$. This can be seen from the Tables. If initially in $S_2$, the flow can go immediately to $S_1$ or to $S_3\to S_4\to S_1$ or to $S_3\to S_2\to S_1$. It is not possible to stay in $S_2$. If initially in $S_1$, then either one goes to $S_2$ and follows one of the flows previously outlined, all of which end up at $S_0$, or one goes directly to $S_0$.

The final step is to see that within $S_0$, if $a_0 < a_2$, all trajectories go to the stable state $\frac{3}{2}\frac{1}{2}0$ and if $a_0 > a_2$, all trajectories go to the stable state $\frac{3}{2}\frac{3}{2}\frac{1}{2}$.

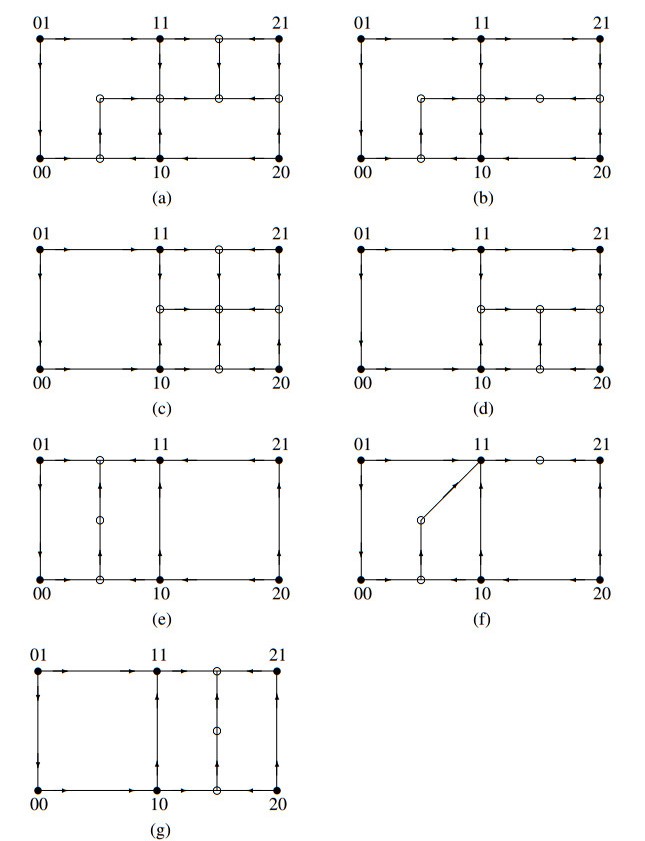
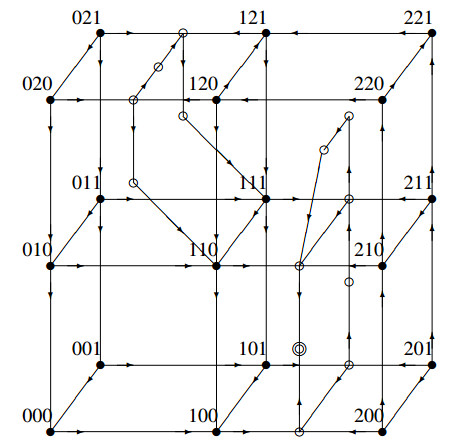
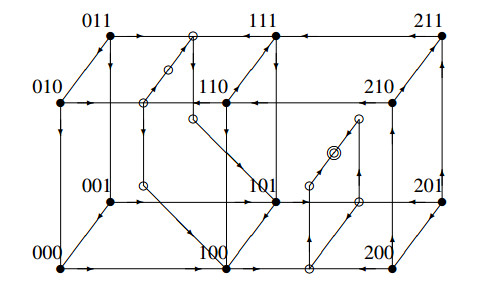
Examples of the full state transition diagrams for representative choices of parameter relationships are given in Figures 7 and 8. There are many other possible choices of parameter values, of course, and for each set of parameter inequalities there is a different state transition diagram. The propositions above hold for any set of parameters that satisfy Assumption 1.

Now we consider the system with the PSV but with equal thresholds for primary and secondary branches. We will see that prioritization of primary output at low input levels cannot be achieved when relying on the PSV alone.

3.6.   The PSV model without threshold separation

In Equations (3.4), we now have $X_{21} = X_{22}$, since $\theta_{21} = \theta_{22} = \theta_2$.

While Propostion 1 is, of course, still true, its converse is no longer true without including another condition.

Proposition 4. If Assumption 1 is satisfied, $\theta_{21} = \theta_{22} = \theta_2$ and $a_0 > \frac{a_4}{a_3}(a_2+a_3)$, then the flow in the state $x_1 = \theta_{12}, x_2 = \theta_2, x_3 > \theta_3$ (i.e., $\frac{3}{2}\frac{1}{2}1$) is unbounded.

Proof. The singular perturbation analysis of the fast time equations for the switching variables leads to

and the nullclines in $(0, 1)^2$ intersect at

when this point is in $(0, 1)^2$. That is the case when $a_0+a_4 < a_2+2a_3$ and $(a_0+a_4)(a_2+a_3) < a_1(a_2+2a_3)$, i.e., when

The state $\frac{3}{2}\frac{1}{2}1$ is stable if the switching variables are confined to remain at their thresholds, which is equivalent to the above condition for a stable fixed point of the fast variables in $(0, 1)^2$, and if $x_3$ remains above its threshold, i.e., if $\dot{x}_3\ge 0$. The flow is unbounded if $\dot{x}_3 > 0$. This last condition is $X_2 > \frac{a_4}{a_3}$, i.e., $\frac{a_0+a_4}{a_2+2a_3} > \frac{a_4}{a_3}$, or equivalently,

By Assumption 1, $a_0 < a_2+a_3$, so inequality (3.8) can only be achieved if $a_3 > a_4$. Inequalities (3.7) and (3.8) can be simultaneously satisfied by some values of $a_0$ if and only if $\frac{a_4}{a_3}(a_2+a_3) < a_2+2a_3-a_4$ and $\frac{a_4}{a_3}(a_2+a_3) < \frac{a_1(a_2+2a_3)}{a_2+a_3}-a_4$. The first of these is equivalent to $(2a_3+a_2)(a_3-a_4) > 0$, which is true exactly when $a_3 > a_4$, and the second is equivalent to $a_1 > \frac{a_4}{a_3}(a_2+a_3)$, which must be true under Assumption 1 (note that if $a_1 < \frac{a_4}{a_3}(a_2+a_3)$ but $a_0 > \frac{a_4}{a_3}(a_2+a_3)$, then $a_0 > a_1$, which violates Assumption 1).

Thus, if Assumption 1 is satisfied, and $a_0 > \frac{a_4}{a_3}(a_2+a_3)$, then state $\frac{3}{2}\frac{1}{2}1$ is stable and $x_3$ increases to infinity.

Thus, we now need an additional assumption to ensure bounded behaviour in the equal threshold case:

Assumption 2. $a_0 < \frac{a_4}{a_3}(a_2+a_3)$

The analysis of the state transition diagram for all parameter conditions satisfying Assumptions 1 and 2 can be done as in the case with Threshold Separation. The calculations are done in the same manner as for the separated threshold case, but keeping in mind that in equations (3.4), we now have $X_{21} = X_{22}$, since $\theta_{21} = \theta_{22} = \theta_2$, so the state label for $x_2$ can only be $0$ ($x_2 < \theta_2$), $\frac{1}{2}$ ($x_2 = \theta_2$) or $1$ ($x_2 > \theta_2$) (or more accurately, $X_2 = 0, X_2\in (0, 1), X_2 = 1$).

Tables 6 and 7 show the flow and successor states for each regular domain in the case of equal thresholds.

Table 8 shows the flow for each of the potentially black walls in the equal threshold case, and the conditions under which those walls are black.

Table 9 shows the possible successor states for each of the black walls above, under the condition that the wall is black, of course, in addition to any other conditions mentioned.

Finally, Table 10 shows the successor states to the double and triple threshold intersections that arise from the flow.

The result of the analysis represented by the above Tables is that the state $\frac{3}{2}\frac{1}{2}\frac{1}{2}$ is globally stable under Assumptions 1 and 2. First we confirm that this state is locally stable, and then we prove that it is also globally attracting.

Proposition 5. Suppose $a_0 < \min\{a_1, a_2+a_3, a_2+a_4, \frac{a_4}{a_3}(a_2+a_3)\}$ in system (3.4). Then the state $\frac{3}{2}\frac{1}{2}\frac{1}{2}$ (i.e., $x_1 = \theta_{12}, x_2 = \theta_2, x_3 = \theta_3$) is locally stable.

Proof. The singular perturbation expansion in state $\frac{3}{2}\frac{1}{2}\frac{1}{2}$ is

which has equilbrium $(X^*_{12}, X^*_2, X^*_3) = \left(\frac{a_0}{a_1}, \frac{a_0}{a_2+a_3}, \frac{a_0a_3}{a_4(a_2+a_3)}\right)$, which is in $(0, 1)^3$ under Assumptions 1 and 2. Letting $u_1 = \frac{X^*_{12}(1-X^*_{12})}{\theta_{12}}$, $u_2 = \frac{X^*_{2}(1-X^*_{2})}{\theta_{2}}$, and $u_3 = \frac{X^*_{3}(1-X^*_{3})}{\theta_{3}}$, the Jacobian evaluated at the equilibrium is

with characteristic equation

which is $\lambda^3+b_1\lambda^2+b_2\lambda+b_3 = 0$ with $b_1, b_3 > 0$ and $b_1b_2 > b_3$ since $b_1b_2$ contains the term $a_1(a_2+a_3)a_4u_1u_2u_3 = b_3$, plus other terms all positive. Thus, the Routh-Hurwitz Criterion implies that the fast-time system is stable at the equilibrium. The Tikhonov theorem allows us to conclude that solutions to the perturbed system ($q > 0$ sufficiently small) converge to this solution on finite time intervals, but the fact that the flow is inwards to this state from all adjacent states, even for the perturbed system, guarantees that the point $x_1 = \theta_{12}, x_2 = \theta_2, x_3 = \theta_3$ is locally stable.

Proposition 6. If $a_0 < \min\{a_1, a_2+a_3, a_2+a_4, \frac{a_4}{a_3}(a_2+a_3)\}$, then solutions to system (3.4) are bounded, and the state $\frac{3}{2}\frac{1}{2}\frac{1}{2}$ is globally stable.

Proof. The proof follows that of Proposition 3 very closely, except that $X_{22}$ and $\theta_{22}$ must be replaced everywhere with $X_2$ and $\theta_2$. We do not reproduce it all in detail again. Some parts of the proof are simpler, since there are fewer possibilities of successor states, and at the very end, it is clear that all states in $S_0 = \{x_1 = \theta_{12}, x_2 \le \theta_2, x_3 \le \theta_3\}$ go to state $\frac{3}{2}\frac{1}{2}\frac{1}{2}$, regardless of the input being low or high (but still satisfying Assumptions 1 and 2, of course).

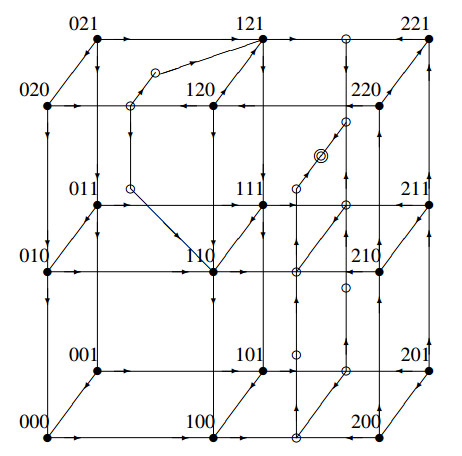
Figures 9 and 10 show representative state transition diagrams for the equal threshold PSV system, in the low input ($a_0 < a_2$) and high input ($a_0 > a_2$) conditions, respectively. Note that the globally attracting steady state is the same for high and low input.

4.   Discussion

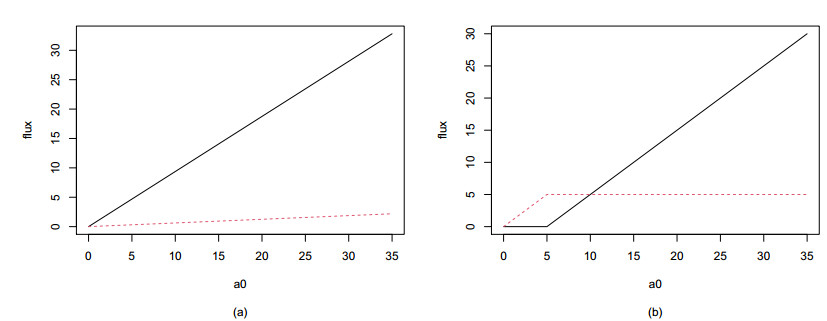
For the model in which thresholds for primary and secondary outputs are the same, the consequence of Propositions 5 and 6 is that for any feasible input level, $a_0$ (satisfying the boundedness assumptions), $X_2$ and $X_3$ both go to a positive level depending linearly on $a_0$: $X_2 = \frac{a_0}{a_2+a_3}$ and $X_3 = \frac{a_0a_3}{a_4(a_2+a_3)}$. The primary and secondary output fluxes are therefore:

and thus, there is no prioritization of primary output at low input levels. If $a_3$ is large in relation to $a_2$, to allow large secondary output at high input levels, then secondary output flux is also large relative to primary output flux at low input levels. Note that $V_2+V_4 = a_0$ as it must be to balance input and output fluxes.

This is in contrast to the case with Threshold Separation, from Propositions 2 and 3, in which case the outputs depend on whether input is low ($a_0 < a_2$) or high ($a_0 > a_2$). In the low input case, $X_{21}$ goes to $\frac{a_0}{a_2}$, and $X_3$ goes to $0$, so primary and secondary output fluxes are

while in the high input case, $X_{21}$ goes to $1$, and $X_3$ goes to $\frac{a_0-a_2}{a_4}$, so the primary and secondary output fluxes are

Again, note that $V_2+V_4 = a_0$ as necessary.

Figure 11 shows these primary and secondary fluxes in the two cases: without and with the Threshold Separation.

These fluxes can be compared to those of Glass and Edwards ^[10] for the sharply-switching system without the PSV. There, converting to our current notation, the fluxes were exactly as found here for the system with the PSV, both in the case of separated thresholds and equal thresholds. Thus, the flux plots in the absence of the PSV are essentially the same as in Figure 11. The final conclusion, therefore, is that for a sharply-switching system, the PSV does not help to prioritize primary output at low input levels, though the separation of thresholds for primary and secondary pathways is effective in achieving this. This is in contrast to the original Michaelis-Menten model, where the PSV was effective in prioritizing primary output at low input levels even when thresholds were equal, and improved the prioritization when thresholds were somewhat separated. In fact, here, in the sharply-switching model, the Threshold Separation mechanism can be seen to be completely effective, no matter how small the separation, since $V_4 = 0$ at low input levels in that case. Including the PSV cannot improve on that. When the fluxes switch on more gradually, then threshold separation by itself must be quite extreme to effectively prioritize primary output at low input. Thus, it is only with more gradually increasing flux terms that the PSV provides an enhancement to the prioritization effect, so that thresholds need not be separated by much or at all.

Thus, one expects not to find a PSV mechanism in sharply-switching systems where branch prioritization is needed at low input. Rather, threshold separation should be expected in such cases. In systems with gradually increasing production terms, however, we may expect to find a PSV used to effect branch prioritization at low input. This is the case for the phenylpropanoid network in plants, the system that motivated consideration of the PSV, but it is likely to be a motif that appears in other contexts, although the authors are not aware yet of any other examples.

Finally, the above analysis shows how sharply-switching open systems without degradation terms can be analyzed by means of state transition diagrams and singular perturbation analysis, similar to the theory developed for Glass networks. The same method of analysis could be applied to any such biochemical network, as long as the activation functions are sharply-switching. This analysis could, in principle, be automated, so that tables of successor states and state transition diagrams could be computed for specific parameter ranges, much like is done in software used to determine the behaviour of gene networks ^[5,15,16]. For more gradual activating functions, like that of Michaelis-Menten kinetics, a different set of behaviours can arise, one example being the PSV motif, but analysis is more difficult. In future work, we propose to study ramp approximations of Michaelis-Menten functions as a way to simplify the analysis.

Acknowledgments

The first author is supported by grant RGPIN-2017-04042 from the Natural Sciences and Engineering Research Council (NSERC) of Canada.

Conflict of interest

All authors declare no conflicts of interest in this paper.