Nomenclature
1.
Introduction
The description of non-Newtonian fluids has fascinated the interest of various authors due to their wide variety of practical uses in various fields. Walter's B liquid is subclass of non-Newtonian liquids with several manufacturing process applications in industry sectors such as chemical science, biosystems, biophysical techniques of thermal conduction in tissues, chemical manufacturing, and bioengineering. Walters [1] was a pioneer of the Walters'-B liquid relation. Nandepanavar et al. [2] discussed the impact of nanomaterials in Walters'-B liquid. The effect of nanoparticles in the Walters-B fluid was investigated by Nadeem et al. [3]. The effect of the radiative-Walters-B liquid flow and stretched wedge was investigated by Hayat et al. [4]. In addition, several scientists have applied the Walters-B relation, which shows the phenomenon of different polymer flows (see [5,6,7,8,9,10]).
A nanofluid is a fluid that consists of a base fluid with nanosized particles (1–100 nm) suspended in it. Thus, Choi and Eastman [11] discussed the fundamental idea of nanomaterials with enhanced thermophysical aspects. Buongiorno [12] explained seven-slipping procedures in the movement of nanomaterials, including thermophoresis and Brownian diffusion. Mixed convective nanoliquid transport with the impact of a magnetic field was observed by Hsiao [13]. Rashidi et al. [14] numerically premeditated the convection characteristics of a nanoliquid through a nonlinear isothermal stretching sheet. Sheikholeslami and Bhatti [15] identified the impact of nanomaterials on the transport of nanoliquids via forced-convection through gravitational-force. Turkyilmazoglu [16] analyzed nanomaterial transport by vertical surfaces. Ellahi et al. [17] noted Jeffrey MHD nanoliquid motion between two parallel-disks. Pantokratoras et al. [18] discussed mixed convective fluids with nanoparticles. Rashid et al. [19] deliberated the behavior of activation energy in the MHD flow of Maxwell nanoliquid. Tayebi et al. [20] explored the magnetic hydrodynamic heat-transport of nanoliquids when wave conduction rings occurred. Hayat et al. [21] discussed the third grade magnetohydrodynamic nanoliquid flow with activation-energy. Muhammad et al. [22] explored the 3D radiative Eyring-Powell nanoliquid transport in the presence of activation-energy by a Riga plate. The transport of second-order slip nanoliquids under the effect of the Stefan blow was examined by Alamri et al. [23]. Khan et al. [24] discussed the stratification and heat generation in mixed convective Prandtl liquid flow. Anwar et al. [25] observed the nonlinear radiative heat transport with MHD nanoliquid spray. Gailitis [26] developed a Riga electromagnetic surface, which comprised clearly constructed electrode and magnet sets. Ahmad et al. [27] investigated the impact of nanoliquid flow through Riga plate. The features of microorganisms in nanoliquids across Riga plate were analyzed by Iqbal et al. [28]. Recent works have experimentally explored nanofluids in [29,30,31,32,33,34,35].
Bioconvection resulting from the combined density gradient of the microorganism simulates macroscopic fluid convection movements. The presence of these self-contained motile microorganisms enhances the primary-density of the fluid through swimming. This important thought certainly escorts to a delicate low-density surface. There are various distinct and related properties of nanoparticles and motile microorganisms. Immunology-microsystems such as enzyme biomaterials usually include bioconvection technologies. Therefore, Kuznetsov [36] recommended that nano-organisms should be involved in the development of bio microsystems, where they played a significant role in the dispensation of mass transport. Li et al. [37] studied the bioconvective flow of second- grade nanoliquids because of Wu's slipping. Muhammad et al. [38] analyzed the influence of bioconvection in Carreau nanoliquid under slip formed by a wedge. Khan et al. [39] examined the 2-D couple stress nanoliquid transport with magnetic-field and gyrotactic motile microorganisms. The characteristics of activation energy in radiative nanoliquid flow with bioconvection features through shrinking/stretching disks were addressed by Zhang et al. [40]. Thermal radiative Oldroyd-B nanoliquid flow subject to motile microorganisms by rotating disk was examined by Waqas et al. [41]. Khan et al. [42] examined the bioconvective aspect between stretchable moving-disks subject to entropy generation and nanofluids. Mamatha et al. [43] discussed the movement of magneto-hydrodynamic liquid by a stretched surface. Ferdows et al. [44] observed the heat and mass transportation of viscous liquid via cylinder with motile microorganisms. Amirsom et al. [45] addressed the 3-D motion of bioconvection nanoliquids consisting of gyrotactic microorganisms. Kasaragadda et al. [46] illustrated the consequence of strong hydrophobic surfaces on the recognition of structures of nanoparticle-reinforced biomaterials. Ansari et al. [47] explored the significance of motile microorganisms and biomaterials on bioconvective Casson liquid flow by a nonlinear extended boundary. Recent work on bioconvection is given in investigations [48,49,50,51,52,53,54,55].
In this paper, we generalize the analysis of [56] in four directions. First, we model the flow-analysis in the presence of nanoparticles. Attention is mainly given to Brownian and thermophoretic diffusion. Second, we consider the swimming gyrotactic motile microorganisms. Third, we analyzed the concentration and temperature in the presence of variable thermal-conductivity and concentration-diffusion. Fourth, we develop the numerical solution using the MATLAB bvp4c solver, which follows the Lobatto-IIIa formula. The consequences of parameters of interest versus the flow field are presented through graphs and tabular data.
2.
Mathematical modeling
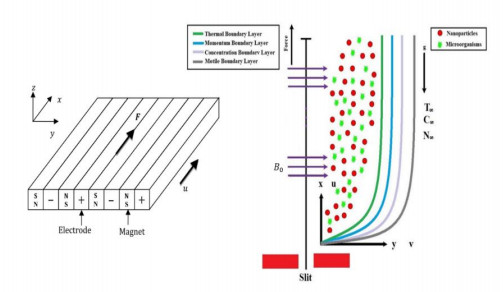
The two-dimensional magnetohydrodynamic flow of Walter's B nanoliquid containing gyrotactic motile microorganisms configured by a Riga plate in the occurrence of variable thermal conduction and concentration diffusion is considered. Features of heat generation/absorption and Arrhenius activation energy are also accounted for in the considered flow problems. The movement of fluid is caused by a stretchable surface. The features of thermal radiation are employed. The significance of Brownian and thermophoresis movements is considered. The physical flow configuration is depicted in Figure 1.
Based on these assumptions, the governing expressions and boundary constraints are given as [1,28,55]:
In expressions (3) and (4), the variable thermal conduction and concentration diffusion are [55]:
The boundary restrictions of the current flow are given by [28,50]:
The suitable transformations are [28,50]:
By implementing these transformations, governing partial differential equations are transformed into dimensionless ordinary differential equations i.e., [1,28,50,55]:
The dimensionless boundary restrictions are [28,50]:
The physical flow parameters in equations (9)-(13) are expressed by
The quantities of interest, e.g., skin coefficient Cf, Nusselt number Nux, Sherwood number Sux and microorganism number Snx are [27,28,56]:
where
Hence the dimensionless forms of the above physical quantities are:
Here Rex(=cx2v) is the local Reynolds number.
3.
Numerical approach
The coupled nonlinear dimensionless system (9)–(12) with boundary constraints (13) is solved using the Matlab bvp4c scheme for different variations of important physical prominent parameters [57,58,59,60,61]. The bvp4c-function is a finite-difference code that follows the three steps of Lobatto-IIIa formula. Until the process begins, problems with higher-order boundary value are converted into an initial value problem by adding several new variables. Considering
with
4.
Results and discussion
Significant contributions of the prominent numbers against the velocity of the Walter's B nanoliquid, thermal, concentration and micro-organism profiles are graphically demonstrated and discussed as follows:
4.1. Velocity profile
Figure 2a is constructed to display the outcomes of M and Nc against velocity f′. Velocity field f′ declines when M and Nc increase. The resistive forces are upgraded with the augmentation of M; hence, the velocity profile reduces. Basically, the magnetic number involves the Lorentz force. This resistive type of force is responsible for the decay in fluid velocity [39]. Figure 2b predicts the impacts of We and Nr against velocity profile f′. With increasing estimations of We, the velocity f′ diminishes. Similarly, velocity f′ shows a decreasing behavior for Nr. The modified Hartmann parameter Q and mixed convective number B∗ affect the velocity of Walter's B nanofluid f′ past a Riga plate, as clarified in Figure 2c. Both parameters have similar effects on velocity field f′. Figure 2d shows the impact of velocity ratio parameter S versus velocity field f′, where there is boundary layer for both S<0 and S>0. Velocity f′ increases for larger velocity ratio parameter S. A larger velocity ratio number increases the velocity of the fluid. When the velocity ratio is zero, the usual profile at the free stream is obtained far from the plate.
4.2. Thermal profile
Figure 3a anticipates the inspiration of the Biot number Bi and thermal conductivity parameter λ1 across the thermal field θ. Temperature θ increases for larger estimations of thermal Biot numberBi. Basically, a larger Biot number corresponds to more heat provided to the working fluid, which leads to a stronger temperature field [30]. Thermal function θ is enhanced to increase the thermal conductivity λ1. Figure 3b depicts the contributions of Pr and θf to the temperature of species θ. The thermal profile of species θ in Walter's B nanoliquid decreases with increasing estimations of Prandtl number Pr, while it increases for a larger temperature ratio parameter θf.
4.3. Nanoparticles concentration profile
Figure 4a characterizes the impact of E and λ2 against the nanoparticle concentration ϕ. The nanoparticle concentration ϕ increases when E increases. Furthermore, ϕ grows with larger concentration diffusivity λ2. Figure 4b reveals that Nt and Nb increase with the concentration of species ϕ. Here, the solutal profile of species ϕ decreases with increasing Brownian motion parameter Nb, while it increases with increasing thermophoresis parameterNt. The natures of Pr and Le against the concentration field of species ϕ are examined in Figure 4c. Here, ϕ decreases with increasing Pr and Le.
4.4. Microorganism profile
Figure 5 examines the outcome of bioconvection Lewis parameter Lb and Peclet parameter Pe versus the microorganism field χ. The microorganism field χ decreases with higher estimations of both parameters Lb and Pe.
4.5. Tabular data
Tables 1–4 are captured to check the behaviors of skin friction −f″(0), Nusselt −θ′(0), Sherwood −ϕ′(0) and microorganism −χ′(0) numbers versus various interesting parameters. Table 1 displays the contribution of −f″(0) versus B∗, Q, M, Nr and Nc. Here −f″(0) decays by augmenting estimations of B∗, Q and M. Table 2 compares f″(0) for varying B∗ with Ahmad et al. [27]. Here, we found agreement between the presented bvp4c solution and the shooting solution in Ahmad et al. [27] in the limiting case. Table 3 shows the contribution of −θ′(0) versus Pr, Nb, Nt, Le, M, Bi, B∗, Nr and Nc. We note that −θ′(0) increases as Nb and Prare increased. In Table 4, −ϕ′(0) decreases for Le and increases for larger Nt. Table 5 shows that −χ′(0) decreases for Pe and Lb.
5.
Conclusions
The current work discusses the bioconvection nonlinear flow of Walter's B nanoliquid over a Riga plate with variable thermal conduction and concentration diffusion features. The aspects of thermal radiation and activation energy are considered. First, the coupled partial differential equations are embedded into the dimensionless system of nonlinear ODEs through suitable transformations [62,63,64,65]. The achieved dimensionless system of ODEs is solved by using the MATLAB built-in bvp4c solver, which follows the Lobatto-IIIa formula. The main results of the considered problem are summarized below.
● Velocity has an enlarging effect for higher estimations of mixed convection and modified Hartmann numbers.
● The temperature of Walter's B nanoliquid increases via larger estimations of Biot number and thermal conductivity parameter.
● The nanoparticle concentration is improved for larger concentration diffusion and activation energy parameters.
● Microorganism fields have similar features for both Peclet and microorganism Lewis parameters.
● The current bioconvective nonlinear Walter's B nanoliquid model has a significant role in the power generation, medical sciences, energy manufacturing, metallurgical industry, thermal recovery of oil, heat storage devices, etc. [66,67,68,69,70].
Acknowledgment
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia for funding this work through Large Groups Project under grant number RGP.2/206/43.
Conflict of interest
The author declares no conflict of interest.









 DownLoad:
DownLoad: