Higher-order Randić index and isomorphism of double starlike trees

1.   Introduction

In mathematical chemistry, a topological index is a numeric quantity derived mathematically in a direct and unambiguous manner from the structural graph of a molecule, which is used to characterize some properties of a molecular graph. It is also a graph invariant since isomorphic graphs have the same value for a given topological index.

Many topological indices have been developed through the years and related successfully to physicochemical properties of organic molecules ^[1,2]. In order to define the concept of branching in molecular species ^[3,4], Randić ^[5] introduced in 1975 a topological index–the connectivity index (now called the Randić index), defined for a simple graph $G$ as

where $\pi$ extends over all paths of length 1 and $v_i(\pi)$ denotes the degree of the $i$-th vertex of the path $\pi$. Note that for a path with $(n+1)$ vertices and $n$ edges, both of the vertex and edge can appear exactly once. It has become one of the most widely used and most successful in applications to physical and chemical properties ^[6]. For a review of historical details and a further bibliography on the chemical applications of the Randić index see ^[7,8,9,10].

For an integer $h\geq 0$, the connectivity index of order $h$ (also called $h$-Randić index) ^[11] is defined as

where $\pi$ extends over all paths of length $h$ in $G$ and $v_i(\pi)$ denotes the degree of the $i$-th vertex of the path $\pi$.

Higher-order Randić indices are of great interest in the theory of molecular graph theory and some of its mathematical properties have been reported in ^[12]. Examples of non-isomorphic trees $T$ and $T'$ such that $R^{h}(T) = R^{h}(T')$ for all $h\geq 0$ exist ^[13]. However, it will not occur in starlike trees, i.e. trees that have a unique vertex of a degree greater than 2. In fact, Rada and Araujo ^[14] proved that starlike trees which have equal $h$-connectivity index for $h\geq 0$ are isomorphic.

Very recently, by a relation on trees with respect to edge division vectors, Song and Huang ^[15] found some sufficient conditions to determine whether some trees with the same topological index value are isomorphic or not. Further, several classes of trees, including balanced starlike trees and double star $S_{p, q}$, are uniquely determined by edge division vectors.

This leads naturally to determine $h$-Randić index of a double starlike tree, i.e., a tree that has only two vertices of a degree greater than $2$. In this paper, we will show that for every integer $h\geq 0$, the higher-order Randić $R^{h}(T)$ of a double starlike tree $T$ is completely determined by its branches of length $\leq h$. As a consequence, we show that almost all the double starlike trees that have equal $h$-Randić index for all $h\geq 0$ are isomorphic.

2.   Some conceptions for double starlike trees

Let $G$ be a graph. The maximum vertex degree and the number of $i$-vertices (an $i$-vertex is a vertex of degree $i$) will be denoted by $\Delta(G)$ and $k_i(G)$, respectively. For an integer $m\geq 2$, a starlike tree $T$ is a tree for which $k_1(T) = \Delta(T) = m$. The set of all starlike trees on $n$ vertices with the maximal degree $m$ is denoted by $\Omega_{n, m}$.

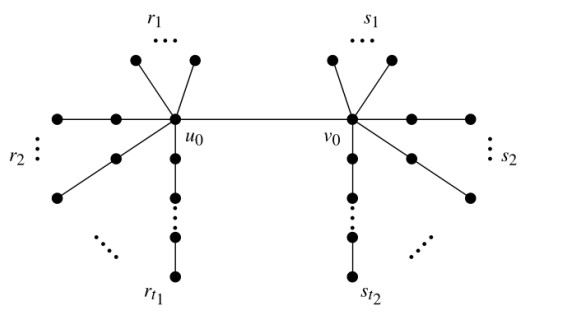
For two integers $m_1, m_2\geq 2$, a double starlike tree $T$ is a tree with an edge $u_0v_0$ such that the components of $T-\{u_0v_0\}$ are two starlike trees $T_{u_0}$ and $T_{v_0}$ with their maximal degrees $m_1-1$ and $m_2-1$, respectively, where $d_T(u_0) = m_1$ and $d_T(v_0) = m_2$. If $n_1 = |V(T_{u_0})|$ and $n_2 = |V(T_{v_0})|$, then $n_1+n_2 = n = |V(T)|$. A double starlike tree is displayed as in Figure 1. The set of all double starlike trees on $n$ vertices with two adjacent branching vertices of degrees $m_1$ and $m_2$ are denoted by $\Omega_{n, m_1, m_2}$. Specifically, if one of the values $m_1$ and $m_2$ is 2, then the double starlike tree is a starlike tree.

For any two vertices $u, w$ in $T$, we use $[u, w]$ to represent the shortest path connecting $u$ and $w$, and keep in mind that the number of edges in $[u, w]$ is called the distance. Let $T\in\Omega_{n, m_1, m_2}$. If $\{u_1, u_2, \cdots, u_{m_1-1}\}$ is the set of $1$-vertices in $T_{u_0}$, an $l$-branch of $T_{u_0}$ is a path $[u_0, u_i]$ of $T_{u_0}$ such that $d(u_0, u_i) = l$. There is a similar definition for $T_{v_0}$. We denote by $r_l(T)$ and $s_l(T)$ the numbers of $l$-branches in $T_{u_0}$ and $T_{v_0}$, respectively (see Figure 1).

Based on the notations introduced above, we clearly have the following relations:

where $t_1$ and $t_2$ represent the length of the longest branch in $T_{u_0}$ and $T_{v_0}$, respectively.

3.   Higher-order Randić index for double starlike trees

In this section, we will determine the higher-order Randić index of double starlike trees.

Theorem 3.1. Let $T\in \Omega_{n, m_1, m_2}$, where $m_1\neq m_2$. Then

As a consequence, if $T'\in \Omega_{n, m_1', m_2'}$, then $R^{0}(T) = R^{0}(T')$ if and only if $m_1 = m_1'$ and $m_2 = m_2'$.

Proof.It is not difficult to obtain that $k_1(T) = m_1+m_2-2$, $k_2(T) = n-m_1-m_2$ and $k_{m_1}(T) = k_{m_2}(T) = 1$. Hence,

Let $f(m_1, m_2) = (m_1+m_2)(1-\frac{1}{\sqrt{2}})+\frac{1}{\sqrt{m_1}}+\frac{1}{\sqrt{m_2}}$. Clearly, $m_1+m_2\in N^+$, and $\frac{1}{\sqrt{m_1}}+\frac{1}{\sqrt{m_2}}\notin N^+$. If $R^{0}(T) = R^{0}(T')$, then we have

In the following, we show that $m_1 = m_1'$ and $m_2 = m_2'$. Assume that $m_1\neq m_1'$ and $m_2\neq m_2'$, thus $m_1\neq m_1'\neq m_2\neq m_2'$. For convenience, let $a = \sqrt{m_1}$, $b = \sqrt{m_2}$, $c = \sqrt{m_1'}$ and $d = \sqrt{m_2'}$. Without loss of generality, assume $b < d < c < a$. From equations (3.1) and (3.2), it can be concluded that

Therefore,

On the other hand, according to $b < d < c < a$, we have $ac > bd$ and $a+c > b+d$, i.e.,

a contradiction. Therefore, the assumption is not valid and the proof is done. □

In the following, the set of all rational numbers is denoted by $Q$ and the set of all irrational numbers is $R-Q$.

Theorem 3.2. Let $T\in \Omega_{n, m_1, m_2}$, where $m_1\neq m_2$. Then

Consequently, for $T'\in \Omega_{n, m_1', m_2'}$, where $m_1' = m_1$ and $m_2' = m_2$, if $R^{1}(T) = R^{1}(T')$, then

(i) $r_1 = r_1'$ and $s_1 = s_1'$ when $m_1 = 2$ or $m_2 = 2$;

(ii) $r_1 = r_1'$ and $s_1 = s_1'$, except for the case $\sqrt{m_1}, \sqrt{m_2}\in R-Q$ and $\sqrt{2m_1}, \sqrt{2m_2}\in Q$, when $m_1, m_2\geq 3$.

Proof. Note that $\frac{1}{2}\sum_{i = r_1+1}^{m_1-1}d(u_0, u_i)+\frac{1}{2}\sum_{i = s_1+1}^{m_2-1}d(v_0, v_i) = \frac{1}{2}(n-r_1-s_1-2)$. Keeping the notation of $R^{1}(T)$, we have

where $\lambda (n, m_1, m_2) = \Big[\frac{m_1+m_2-2}{\sqrt{2}}+\frac{m_1-1}{\sqrt{2m_1}}+\frac{m_2-1}{\sqrt{2m_2}}+\frac{1}{\sqrt{m_1m_2}}-(m_1+m_2)+\frac{n}{2}+1\Big]$.

For convenience, let $a = (\frac{1}{\sqrt{m_1}}-\frac{1}{\sqrt{2m_1}}+\frac{1}{2}-\frac{1}{\sqrt{2}})$, and $b = (\frac{1}{\sqrt{m_2}}-\frac{1}{\sqrt{2m_2}}+\frac{1}{2}-\frac{1}{\sqrt{2}})$.

(i) If one of $m_1$ and $m_2$ is 2, assume that $m_1 = 2$. Then $R^{1}(T) = ar_1+bs_1+\lambda (n, m_1, m_2)$. We can immediately deduce $s_1 = s_1'$ from the condition $R^{1}(T) = R^{1}(T')$. In this case, we have $r_1 = r_1' = 1$ and $a = 0$.

(ii) If $m_1, m_2\geq 3$, from $R^{1}(T) = R^{1}(T')$, we obtain that $ar_1+bs_1 = ar_1'+bs_1'$. If $r_1 = r_1'$(or $s_1 = s_1'$), then we can obtain that $s_1 = s_1'$ (or $r_1 = r_1'$), the theorem is true. In the following, we will deduce a contradiction under the assumption of $r_1\neq r_1'$ and $s_1\neq s_1'$. Denote

Let's discuss in three cases according to whether $\sqrt{m_1}$ and $\sqrt{m_2}$ are rational numbers.

Case 1. $\sqrt{m_1} = c\in Q$ and $\sqrt{m_2} = d\in Q$.

From Equation (3.3), it can be concluded that

and we get $t = \frac{d(c+2)}{c(d+2)} = \frac{d(c+1)}{c(d+1)}$. Furthermore, we have $c = d$, i.e., $m_1 = m_2$, which contradicts with $m_1\neq m_2$.

Case 2. $\sqrt{m_1} = c\in Q$ and $\sqrt{m_2}\in R-Q$.

Subcase 2.1. $\sqrt{2m_2} = d\in Q$.

From Equation (3.3), it can be concluded that

Thus, we get $t = \frac{d(c+2)}{c(d-2)} = \frac{d(c+1)}{c(d-2)}$, i.e., $c+1 = c+2$, a contradiction.

Subcase 2.2. $\sqrt{2m_2}\in R-Q$.

By Equation (3.3), we obtain

and we have $t = \frac{c+2}{c} = \frac{-\sqrt{m_2}(c+1)}{(\sqrt{2}-\sqrt{m_2}-1)c}$, which implies $\sqrt{2}(2+c)-\sqrt{m_2}-(2+c) = 0$, i.e., $c = -2$ and $m_2 = 0$, a contradiction.

Case 3. $\sqrt{m_1}\in R-Q$, $\sqrt{m_2}\in R-Q$.

Subcase 3.1. $\sqrt{2m_1} = c\in Q$, $\sqrt{2m_2}\in R-Q$.

By Equation (3.3), we obtain

Then we have $t = \frac{c-2}{c} = \frac{\sqrt{2m_2}(\sqrt{2}-\sqrt{m_1})}{c(\sqrt{2}-\sqrt{m_2}-1)}$, i.e., $m_1 = 2$, which contradicts with $m_1\geq 3$.

Subcase 3.2. $\sqrt{2m_1}\in R-Q$, $\sqrt{2m_2}\in R-Q$.

By Equation (3.3), we obtain

Similarly, it can be concluded that $t = 1 = \frac{\frac{1}{\sqrt{m_1}}-\frac{1}{\sqrt{2m_1}}}{\frac{1}{\sqrt{m_2}}-\frac{1}{\sqrt{2m_2}}}$, i.e., $m_1 = m_2$, which contradicts with $m_1\neq m_2$.

Therefore, taking into account the above situations, we obtain that $r_1 = r_1'$ and $s_1 = s_1'$, except for the case $\sqrt{m_1}, \sqrt{m_2}\in R-Q$ and $\sqrt{2m_1}, \sqrt{2m_2}\in Q$. □

Next, We will extend this result to $R^{h}(T)$, where $h\geq 2$.

Let $u_0$ and $v_0$ be the $m_1$-vertex and $m_2$-vertex of $T$ (see Figure 1). Let $P_h$ represent the set of all paths of length $h$ in $T$, $N = \{0, 1, 2, \cdots\}$ as the set of natural numbers and the function $\Psi: P_h\longrightarrow N^{h+1}$ by $\Psi(\pi) = (v_1(\pi), \cdots, v_{h+1}(\pi))$, where $v_i(\pi)$ denotes the degree of the $i$-th vertex of the path $\pi$.

We first consider all paths in $P_h$ that contain $u_0$ or $v_0$ as an end-vertex, or do not contain $u_0$ and $v_0$. There are twelve possibilities for the images under $\Psi$ of these paths:

We then consider all paths in $P_h$ that contain only one of $u_0$ and $v_0$, but not as an end-vertex. In this case the image of $\Psi$ is as follows:

$Y_1(a) = (1, \underbrace{2, \cdots, 2}_{a}, m_1, \underbrace{2, \cdots, 2}_{h-1-a}), \; Y_1'(a) = (1, \underbrace{2, \cdots, 2}_{a}, m_2, \underbrace{2, \cdots, 2}_{h-1-a})$, where $0\leq a\leq h-2.$

$Y_2(a) = (1, \underbrace{2, \cdots, 2}_{a}, m_1, \underbrace{2, \cdots, 2}_{h-2-a}, 1), \; Y_2'(a) = (1, \underbrace{2, \cdots, 2}_{a}, m_2, \underbrace{2, \cdots, 2}_{h-2-a}, 1)$, where $0\leq a\leq \frac{h}{2}-1.$

$Y_3(a) = (\underbrace{2, \cdots, 2}_{a}, m_1, \underbrace{2, \cdots, 2}_{h-a}), \; \; Y_3'(a) = (\underbrace{2, \cdots, 2}_{a}, m_2, \underbrace{2, \cdots, 2}_{h-a})$, where $1\leq a\leq \frac{h}{2}.$

Finally, consider all paths in $P_h$ that contain both $v_0$ and $u_0$, but not one as an end-vertex. In this case the image of $\Psi$ is as follows:

$Z_1(a) = (1, \underbrace{2, \cdots, 2}_{a}, m_1, m_2, \underbrace{2, \cdots, 2}_{h-2-a}), \; Z_1'(a) = (1, \underbrace{2, \cdots, 2}_{a}, m_2, m_1, \underbrace{2, \cdots, 2}_{h-2-a})$, where $0\leq a\leq h-3.$

$Z_2(a) = (1, \underbrace{2, \cdots, 2}_{a}, m_1, m_2, \underbrace{2, \cdots, 2}_{h-3-a}, 1)$, where $0\leq a\leq h-3$.

$Z_3(a) = (\underbrace{2, \cdots, 2}_{a}, m_1, m_2, \underbrace{2, \cdots, 2}_{h-1-a})$, where $1\leq a\leq h-2.$

Now, let's prove our main result.

Theorem 3.3. Let $T\in \Omega_{n, m_1, m_2}$, where $m_1\neq m_2$. Then

where $\lambda (h, n, m_1, m_2, r_1, s_1, \cdots, r_{h-1}, s_{h-1})$ is a real number determined by the values of $h, n, m_1$, $m_2, \cdots, r_{h-1}, s_{h-1}$.

Proof. Clearly, $R^{h}(T)$ is determined by the numbers $|\Psi^{-1}(X_i)|$, $|\Psi^{-1}(X_i')|$, $|\Psi^{-1}(Y_i(a))|$, $|\Psi^{-1}(Y_i'(a))|$, $|\Psi^{-1}(Z_i(a))|$ and $|\Psi^{-1}(Z_i'(a))|$, where $|\Psi^{-1}(W)|$ represents the number of elements in the inverse image of $W$ under $\Psi$, i.e.,

We can express $|\Psi^{-1}(X_i)|$, $|\Psi^{-1}(X_i')|$, $|\Psi^{-1}(Y_i(a))|$, $|\Psi^{-1}(Y_i'(a))|$, $|\Psi^{-1}(Z_i(a))|$ and $|\Psi^{-1}(Z_i'(a))|$ in terms of $r_1, s_1, \cdots, r_{h}, s_{h}$ by a counting argument together with the reduction formulas as follows:

We can see that $|\Psi^{-1}(X_i)|$, $|\Psi^{-1}(X_i')|$, $|\Psi^{-1}(Y_j(a))|$, $|\Psi^{-1}(Y_j'(a))|$, $|\Psi^{-1}(Z_j(a))|$ and $|\Psi^{-1}(Z_j'(a))|$ depend on the numbers $h, m, r_1, s_1, \cdots, r_{h-1}, s_{h-1}$ for all $a$ and $i = 5, 6$ and$j = 1, 2, 3$; while for $i = 1, 2, 3, 4$, $|\Psi^{-1}(X_i)|$ and $|\Psi^{-1}(X_i')|$ depend on the numbers $h, m, r_1, s_1, \cdots, r_{h}, s_{h}$. Hence, by grouping in a convenient way we can get

where $\lambda (h, n, m_1, m_2, r_1, s_1, \cdots, r_{h-1}, s_{h-1})$ is a real number determined by the values of $h, n, m_1$, $m_2, r_1, s_1, \cdots, r_{h-1}, s_{h-1}$, and

Thus, the theorem holds. □

Example 3.4. Let $T\in \Omega_{18, 7, 4}$ with $r_1(T) = 3$, $r_2(T) = 2$, $r_3(T) = 1$, $s_1(T) = 2$ and $s_4(T) = 1$, where $m_1 = 7, m_2 = 4$. In order to calculate $R^{3}(T)$, we first determine the number of paths of each type:

Hence, we obtain from Theorem 3.3

□

Theorem 3.5. Let $T, T'\in \Omega_{n, m_1, m_2}$, where $m_1\neq m_2$. Then $T$ and $T'$ are isomorphic if and only if

(i) $R^{h}(T) = R^{h}(T')$ for all $h\geq 0$, where $min\{m_1, m_2\} = 2$; or

(ii) $R^{h}(T) = R^{h}(T')$ for all $h\geq 0$, where $m_1, m_2\geq 3$, except for the case $\sqrt{m_1}, \sqrt{m_2}\in R-Q$ and $\sqrt{2m_1}, \sqrt{2m_2}\in Q$.

Proof. The necessity is clear, we only need to prove sufficiency. Assume that $T, T'\in \Omega_{n, m_1, m_2}$. Since $R^{0}(T) = R^{0}(T')$, by Theorem 3.1, $m_1 = m_1'$ and $m_2 = m_2'$. Now, from $R^{1}(T) = R^{1}(T')$ and Theorem 3.2, we have $r_1 = r_1'$ and $s_1 = s_1'$, where $min\{m_1, m_2\} = 2$, or where $m_1, m_2\geq 3$, except for the case $\sqrt{m_1}, \sqrt{m_2}\in R-Q$ and $\sqrt{2m_1}, \sqrt{2m_2}\in Q$. Next, applying Theorem 3.3 for $h = 2$, we get

i.e.,

By a proof process similar to Theorem 3.2, we have $r_2 = r_2'$ and $s_2 = s_2'$. Continuing this process by repeated use of Theorem 3.3 and Theorem 3.2, we can conclude that $r_i = r_i'$ and $s_i = s_i'$ for all $i\in N$. Therefore, $T$ and $T'$ are isomorphic. □

Finally, let $T\in \Omega_{n, m_1, m_2}$. If $min\{m_1, m_2\} = 2$, then $T$ is a starlike tree, i.e., $T\in \Omega_{n, m}$, where $m = max\{m_1, m_2\}$. From Theorem 3.3 and Theorem 3.5, we have the following corollaries which are given in ^[14].

Corollary 3.6. ^[14] Let $T\in \Omega_{n, m}$. Then

where $\lambda (h, n, m, s_1, \cdots, s_{h-1})$ is a real number determined by the values of $h, n, m, s_1, \cdots, s_{h-1}$.

Corollary 3.7. ^[14] Let $T, T'\in \Omega_{n, m}$. Then $T$ and $T'$ are isomorphic if and only if $R^{h}(T) = R^{h}(T')$ for all $h\geq 0$.

4.   Conclusions

In this paper, we mainly investigated the $h$th order Randić index $R^{h}(T)$ of the double starlike tree $T$, which is a tree with two vertices of degrees $m_1, m_2 > 2$. First, the formula of the $h$th order Randić index $R^{h}(T)$ has been completely determined by its branches of length $\leq h$. Second, it was taken that $m_1 \neq m_2$, and we have shown that almost all the double starlike trees $T\in \Omega_{n, m_1, m_2}$ with equal $h$-Randić index for all $h\geq 0$ are isomorphic. In addition, some results of starlike trees have been obtained, which were given in ^[14].

These results lead to a natural question, which we pose as a problem.

Problem 3.8. Which index can determine isomorphism of double starlike trees $T\in \Omega_{n, m_1, m_2}$, where $m_1 = m_2$?

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the Department of Education of Hunan Province (22B0763), (22B0828), the National Natural Science Foundation of China (12201634), and the Natural Science Foundation of Hunan Province (2023JJ30070).

Conflict of interest

The authors declare that they have no conflicts of interest.