1.
Introduction
Let C be the complex field. The set Cm×n denotes the set of all m×n complex matrices over the complex field C. Let A∈Cm×n. The symbol A∗ denotes the conjugate transpose of A. Notations R(A)={y∈Cm:y=Ax,x∈Cn} and N(A)={x∈Cn:Ax=0} will be used in the sequel. The smallest positive integer is k, such that rank(Ak)=rank(Ak+1) is called the index of A∈Cn×n and denoted by ind(A).
Let A∈Cm×n. If a matrix X∈Cn×m satisfies AXA=A, XAX=X, (AX)∗=AX, (XA)∗=XA, then X is called the Moore-Penrose inverse of A [13,17] and denoted by X=A†. Let A,X∈Cn×n with ind(A)=k. Then, the algebraic definition of the Drazin inverse is as follows if
then X is called the Drazin inverse of A. If such X exists, then it is unique and denoted by AD [7]. Note that for a square complex matrix, the algebraic definition of the Drazin inverse is equivalent to the functional definition of the Drazin inverse. We have the following lemma by the canonical form representation for A and AD in Theorem 7.2.1 [5].
Lemma 1.1. Let A∈Cn×n with ind(A)=k>0, then the Drazin inverse exists.
The core inverse and the dual core inverse for a complex matrix was introduced by Baksalary and Trenkler [4]. Let A∈Cn×n. A matrix X∈Cn×n is called a core inverse of A if it satisfies AX=PA and R(X)⊆R(A), where R(A) denotes the column space of A and PA is the orthogonal projector onto R(A). If such a matrix exists, then it is unique (and denoted by 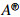 ). Baksalary and Trenkler gave several characterizations of the core inverse by using the decomposition of Hartwig and Spindelböck [10,11]. In [12], Mary introduced a new type of generalized inverse, namely the inverse along an element. This inverse is depended on Green's relations [9]. The inverse along an element contains some known generalized inverses, such as group inverse, Drazin inverse and Moore-Penrose inverse. Many existence criterion for the inverse along an element can be found in [12,16]. Manjunatha Prasad and Mohana[15] introduced the core-EP inverse of a matrix. Let A∈Cn×n. If there exists X∈Cn×n such that XAX=XandR(X)=R(X∗)=R(Ak), then X is called the core-EP inverse of A. If such inverse exists, then it is unique and denoted by
). Baksalary and Trenkler gave several characterizations of the core inverse by using the decomposition of Hartwig and Spindelböck [10,11]. In [12], Mary introduced a new type of generalized inverse, namely the inverse along an element. This inverse is depended on Green's relations [9]. The inverse along an element contains some known generalized inverses, such as group inverse, Drazin inverse and Moore-Penrose inverse. Many existence criterion for the inverse along an element can be found in [12,16]. Manjunatha Prasad and Mohana[15] introduced the core-EP inverse of a matrix. Let A∈Cn×n. If there exists X∈Cn×n such that XAX=XandR(X)=R(X∗)=R(Ak), then X is called the core-EP inverse of A. If such inverse exists, then it is unique and denoted by 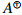 . The weak group inverse of a complex matrix was introduced by Wang and Chen [22], which is the unique matrix X such that AX2=X and
. The weak group inverse of a complex matrix was introduced by Wang and Chen [22], which is the unique matrix X such that AX2=X and 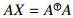 and denoted by X=AⓌ.
and denoted by X=AⓌ.
Let A∈Cn×n. The core-nilpotent decomposition [14, see Theorem 2.2.21] of A is the sum of two matrices A1 and A2, i.e., A=A1+A2, such that rank(A1)=rank(A21), A2 is nilpotent and A1A2=A2A1=0. It is well known that this decomposition is unique. Moreover, A1=AADA=ADA2=A2AD by [5, Definition 7.3.1], if ind(A)⩽1, and thus A coincides with A1. A1 is called the core part of A. Also, A2=A−AADA is the nilpotent part of A. In [21, Theorem 2.1], Wang introduced a new matrix decomposition, namely the core-EP decomposition of A∈Cn×n with ind(A)=k. Given a matrix A∈Cn×n, then A can be written as the sum of matrices ˆA1∈Cn×n and ˆA2∈Cn×n. That is A=ˆA1+ˆA2, where ˆA1 is an index one matrix, ˆAk2=0 and ˆA∗1ˆA2=ˆA2ˆA1=0. In [21, Theorems 2.3 and 2.4], Wang proved this matrix decomposition is unique and that there exists a unitary matrix U∈Cn×n such that
where T∈Cr×r is nonsingular, N∈C(n−r)×(n−r) is nilpotent and r is number of nonzero eigenvalues of A. In [21, Theorem 2.3], Wang proved that ˆA1 can be described by using the Moore-Penrose inverse of Ak. The explicit expressions of ˆA1 can be found in the following lemmas.
Lemma 1.2. Let A∈Cn×n with ind(A)=k. If A=ˆA1+ˆA2 is the core-EP decomposition of A, then ˆA1=Ak(Ak)†A and ˆA2=A−Ak(Ak)†A.
Let A∈Cn×n with ind(A)=k. The EP-nilpotent decomposition of A was introduced by Wang and Liu [23]. A can be written as A=˜A1+˜A2, where ˜A1 is an EP matrix, ˜Ak+12=0 and ˜A2˜A1=0. By the proof of [23, Theorem 2.2], one can get the following lemma.
Lemma 1.3. [23, Theorem 2.1] Let A∈Cn×n with ind(A)=k and A=˜A1+˜A2 be the EP-nilpotent decomposition of A. Then, there exists a unitary matrix U∈Cn×n such that
where T∈Cr×r is nonsingular, N∈C(n−r)×(n−r) is nilpotent and r is the number of nonzero eigenvalues of A.
The core part of the EP-nilpotent decomposition can be expressed by the Moore-Penrose inverse of Ak, where ind(A)=k.
Lemma 1.4. [23, Theorem 2.2] Let A∈Cn×n with ind(A)=k and A=˜A1+˜A2 be the EP-nilpotent decomposition of A as (1.2), then ˜A1=AAk(Ak)†.
Let A,B,C∈Cn×n. We say that Y∈Cn×n is a (B,C)-inverse of A if we have
If such Y exists, then it is unique (see [1, Definition 4.1] and [19, Definition 1.2]). We also call the (B,C)-inverse of A is the inverse of A along B and C. Note that the (B,C)-inverse was introduced in the setting of semigroups [8]. The (B,C)-inverse of A will be denoted by A‖(B,C). Note that Bapat et al. [2] investigated an outer inverse in Theorem 5 that is exactly the same as the (y,x)-inverse, where x and y are elements in a semigroup. In [20], Rao and Mitra showed that A‖(B,C)=B(CAB)−C, where (CAB)− stands for the arbitrary inner inverse of CAB, where CAB is the product of A,B,C∈Cn×n.
Lemma 1.5. [18, Lemma 2.2.6(g)] Let A,B,C∈Cn×n. If rank(CAB)=rank(B)=rank(C), then B(CAB)−C is invariant for any choice of (CAB)−.
The following lemma shows that the (B,C)-inverse of A is an outer inverse of A, and can be characterized by using the column space of B and the null space of C.
Theorem 1.6. [8, Theorem 2.1 (ii) and Proposition 6.1] Let A,B,C∈Cn×n. Then, Y∈Cn×n is the (B,C)-inverse of A if, and only if, YAY=Y, R(Y)=R(B) and N(Y)=N(C).
The following lemma can be found in [24, Lemma 3.11] for elements in rings, which also shows that the Drazin inverse is the inverse along Ak and Ak, where k is the index of A.
Lemma 1.7. [8, p1910] Let A∈Cn×n with ind(A)=k, then the Drazin inverse of A coincides with the (Ak,Ak)-inverse of A. In particular, the group inverse of A coincides with the (A,A)-inverse of A.
Lemmas 1.8 and 1.9 show that the core-EP inverse of A is a generalization of the core inverse of A. Moreover, the core inverse of Ak is the core-EP inverse of A, where k is the index of A.
Lemma 1.8. [8, p1910] Let A∈Cn×n with ind(A)=1, then the core inverse of A coincides with the (A,A∗)-inverse of A.
Lemma 1.9. [19, Theorem 1.10] Let A∈Cn×n with ind(A)=k, then the core-EP inverse of A coincides with the (Ak,(Ak)∗)-inverse of A.
Lemma 1.10. [3, Remark 2.2 (i)] Let A,B,C,U,V∈Cn×n. If R(B)=R(U) and N(C)=N(V), then A is (B,C)-invertible if and only if A is (U,V)-invertible. In this case, we have A‖(B,C)=A‖(U,V).
Based on the core parts of the core-nilpotent decomposition, core-EP decomposition and EP-nilpotent decomposition of A∈Cn×n, respectively, three generalized inverses along two matrices are investigated, namely, the Drazin inverse, the weak group inverse and the core-EP inverse. Let X1, X4 and X7 be the generalized inverses along A1, ˆA1 and ˜A1, respectively. The major contributions of the article can be highlighted as follows:
1) Three generalized inverses related the core part A1 of the core-nilpotent decomposition are investigated.
2) Three generalized inverses related the core part ˆA1 of the core-EP decomposition are investigated.
3) Three generalized inverses related the core part ˜A1 of the EP-nilpotent decomposition are investigated.
4) We show that the Drazin inverse, the weak group inverse and the core-EP inverse are different generalized inverses.
5) For a singular complex matrix, we can prove that the Drazin inverse coincides with the weak group inverse, which is different from the core-EP inverse. Moreover, we can show that the Drazin inverse, the weak group inverse and the core-EP inverse can be same for a certain singular complex matrix.
The paper is organized as follows. In section two, we prove that Xi is the same as Xj. Moreover, Xj coincides with the Drazin inverse of A, where i,j∈{1,2,3}. In section three, we can prove that Xi is the same as Xj and that Xj coincides with the weak group inverse of A, where i,j∈{4,5,6}. In section four, we can prove that Xi is the same as Xj and Xj coincides with the core-EP inverse of A, where i,j∈{7,8,9}. In section five, relationships between Xi and Xj for i,j∈{1,2,⋯,9} are investigated.
2.
Three generalized inverses related the core part A1 of the core-nilpotent decomposition
In this section, three generalized inverses along the core parts of matrix decompositions are introduced. In Table 1, one can see that we denoted the generalized inverse along the core parts of the core-nilpotent decomposition as X1 by using the symbol of the generalized inverse along two matrices. In a similar way, X2 denotes the generalized inverse along the core part of the core-EP decomposition and the core part of the core-nilpotent decomposition. X3 denotes the generalized inverse along the core part of the EP-nilpotent decomposition and the core part of the core-nilpotent decomposition. In addition, we prove that Xi is the same as Xj and that Xj coincides with the Drazin inverse of A, where i,j∈{1,2,3}.
Theorem 2.1. Let A∈Cn×n with ind(A)=k. The X1 coincides with the Drazin inverse of A. That is the Drazin inverse of A is the inverse along A1, where A1 is the core part of the core-nilpotent decomposition.
Proof. Let A1 be the core part of the core-nilpotent decomposition, then A1=ADA2 and we have
Thus, we have
For any x∈N(A1), then
For any y∈N(AD), then
So,
by the Eqs (2.3) and (2.4). For any u∈N(AD), then
For any v∈N(Ak), then
So,
by the Eqs (2.6) and (2.7). Thus, we have
by the Eqs (2.5) and (2.8). Therefore, X1 coincides with the Drazin inverse by Eqs (2.2) and (2.9) and Lemmas 1.7 and 1.10. □
Theorem 2.2. Let A∈Cn×n with ind(A)=k. The X2 coincides with the Drazin inverse of A. That is the Drazin inverse of A is the inverse along ˆA1 and A1, where ˆA1 is the core part of the core-EP decomposition and A1 is the core part of the core-nilpotent decomposition.
Proof. By the equalities ˆA1=Ak(Ak)†A=Ak[(Ak)†Ak]∗(Ak)†A=Ak(Ak)∗[(Ak)†]∗(Ak)†A and Ak(Ak)∗=Ak(Ak)†Ak(Ak)∗=Ak(Ak)†AAk−1(Ak)∗=ˆA1Ak−1(Ak)∗, we have
Thus, X2 coincides the inverse along Ak(Ak)∗ and (Ak)∗A. That is X2=A∥(Ak(Ak)∗,(Ak)∗A), which is equivalent to X2 as the (Ak(Ak)∗,(Ak)∗A)-inverse. By ˆA1=Ak(Ak)†A and Ak=Ak(Ak)†Ak=Ak(Ak)†AAk−1=A1Ak−1, we have R(ˆA1)=R(Ak). Thus, the condition (2.10) can be replaced by R(ˆA1)=R(Ak) and we have the following theorems.
Thus, X2 coincides with the Drazin inverse of A by Lemma 1.10, and the proof of Theorem 2.1. □
Theorem 2.3. Let A∈Cn×n with ind(A)=k. The X3 coincides with the Drazin inverse of A, that is the Drazin inverse of A is the inverse along ˜A1 and A1, where ˜A1 is the core part of the EP-nilpotent decomposition and A1 is the core part of the core-nilpotent decomposition.
Proof. Since
we have R(Ak+1)=R(˜A1), which implies
Thus, X2 coincides the inverse along Ak(Ak)∗ and (Ak)∗A. That is X2=A∥(Ak(Ak)∗,(Ak)∗A), which is equivalent to X2 as the (Ak(Ak)∗,(Ak)∗A)-inverse. By ˆA1=Ak(Ak)†A and Ak=Ak(Ak)†Ak=Ak(Ak)†AAk−1=A1Ak−1, we have R(ˆA1)=R(Ak). Thus, the condition (2.10) can be replaced by R(ˆA1)=R(Ak) and we have the following theorem. Thus, X3 coincides with the Drazin inverse of A by Lemma 1.10, and the proof of Theorem 2.1. □
Theorem 2.4. Let A∈Cn×n with ind(A)=k, then, Xi is the same as Xj. Moreover, Xj coincides with the Drazin inverse of A, where i,j∈{1,2,3}.
Proof. It is trivial by Theorems 2.1–2.3. □
3.
Three generalized inverses related the core part ˆA1 of the core-EP decomposition
In this section, three generalized inverses along the core parts of matrix decompositions are introduced. In Table 2, one can see that we denoted the generalized inverse along the core parts of the core-EP decomposition as X4 by using the symbol of the generalized inverse along two matrices. In a similar way, X5 denotes the generalized inverse along the core part of the core-nilpotent decomposition and the core part of the core-EP decomposition. X6 denotes the generalized inverse along the core part of the EP-nilpotent decomposition and the core part of the core-EP decomposition decomposition. In addition, we prove that Xi is the same as Xj and that Xj coincides with the weak group inverse of A, where i,j∈{4,5,6}.
Theorem 3.1. Let A∈Cn×n with ind(A)=k, then the generalized inverse X4 coincides with the (Ak(Ak)∗,(Ak)∗A)-inverse of A.
Proof. Let ˆA1 be the core part of the core-EP decomposition as (1.1), the ˆA1=Ak(Ak)†A by Lemma 1.2. For any x∈N((Ak)†A), we have
For any y∈N(ˆA1), we have
Thus, we have
by Eqs (3.1) and (3.2). Also, we have
by
and
Equations (3.3) and (3.4) imply
By ˆA1=Ak(Ak)†A=Ak(Ak)†Ak(Ak)†A=Ak[(Ak)†Ak]∗(Ak)†A=Ak(Ak)∗[(Ak)†]∗(Ak)†A and Ak(Ak)∗=Ak(Ak)†Ak(Ak)∗=Ak(Ak)†AAk−1(Ak)∗=ˆA1Ak−1(Ak)∗, we have
Thus, X4 coincides the inverse along Ak(Ak)∗ and (Ak)∗A. That is, X4=A∥(Ak(Ak)∗,(Ak)∗A), which is equivalent to X4 as the (Ak(Ak)∗,(Ak)∗A)-inverse. □
We have ˆA1=Ak(Ak)†A and Ak=Ak(Ak)†Ak=Ak(Ak)†AAk−1=A1Ak−1 by Lemma 1.2, so R(ˆA1)=R(Ak). Thus, condition (2.10) can be replaced by R(ˆA1)=R(Ak) and we have the following theorem.
Theorem 3.2. Let A∈Cn×n with ind(A)=k, then X4 coincides with the (Ak,(Ak)∗A)-inverse.
For the square matrix A1, an inner inverse of A1 with columns belonging to the linear manifold generated by the columns of A1 and rows belonging to the linear manifold generated by the rows of A1 will be called a generalized constrained inverse of A and denoted by A−gRC[6, Definition 3.1]. That is, if X∈Cn×n satisfies A1XA1=A1, R(X)⊆R(A1) and RS(X)⊆RS(A1), then X=A−gRC. In the following lemmas, one can see that the generalized constrained inverse of A coincides with the weak group inverse by Lemma 3.3. Moreover, the weak group inverse of A coincides with the group inverse of ˆA1 by Lemma 3.5, thus the generalized constrained inverse of A coincides with the group inverse of ˆA1. By Lemma 3.4 and Theorem 3.2, we have that X4 coincides with the generalized constrained inverse of A.
Lemma 3.3. [6, Theorem 3.4] Let A∈Cn×n. If X∈Cn×n is a generalized constrained inverse of A, then this generalized constrained inverse of A is unique. Moreover, the generalized constrained inverse of A coincides with the weak group inverse; that is, A−gRC=AⓌ.
Lemma 3.4. [6, Theorem 4.4] Let A∈Cn×n with ind(A)=k. The generalized constrained inverse of A coincides with the (Ak,(Ak)∗A)-inverse of A.
Lemma 3.5. [22, Theorem 3.7] Let A∈Cn×n with ind(A)=k and A=ˆA1+ˆA2 be the core-EP decomposition of A as given in (1.1). The weak group inverse of A coincides with the group inverse of ˆA1; that is, AⓌ=ˆA#1.
Lemma 3.6. Let A∈Cn×n with ind(A)=k and A=ˆA1+ˆA2 be the core-EP decomposition of A as given in (1.1). The weak group inverse of A coincides with the (ˆA1,ˆA1)-inverse of A.
Proof. It is trivial by Lemmas 3.5 and 1.7. □
Theorem 3.7. Let A∈Cn×n with ind(A)=k and A=ˆA1+ˆA2 be the core-EP decomposition of A as (1.1). Then, the inverse X4 coincides with the weak group inverse of A.
Proof. It is trivial by Lemma 3.6 and the definition of the inverse of X2. □
Theorem 3.8. Let A∈Cn×n with ind(A)=k, then the generalized inverse X5 coincides with the (Ak,(Ak)∗A)-inverse of A.
Proof. It is trivial by Theorems 2.1 and 3.1. □
Theorem 3.9. Let A∈Cn×n with ind(A)=k, then the generalized inverse X6 coincides with the (Ak,(Ak)∗A)-inverse of A.
Proof. It is trivial by Theorems 2.3 and 3.1. □
Theorem 3.10. Let A∈Cn×n with ind(A)=k, then Xi is the same as Xj. Moreover, Xj coincides with the weak group inverse of A, where i,j∈{4,5,6}.
Proof. It is obvious by Theorems 3.1, 3.8 and 3.9. □
4.
Three generalized inverses related the core part ˜A1 of the EP-nilpotent decomposition
In this section, three generalized inverses along the core parts of matrix decompositions are introduced. In Table 3, one can see that we denoted the generalized inverse along the core parts of the EP-nilpotent decomposition as X7 by using the symbol of the generalized inverse along two matrices. In a similar way, X8 denotes the generalized inverse along the core part of the core-nilpotent decomposition and the core part of the EP-nilpotent decomposition. X9 denotes the generalized inverse along the core part of the core-EP decomposition and the core part of the EP-nilpotent decomposition decomposition. In addition, we prove that Xi is the same as Xj and that Xj coincides with the core-EP inverse of A, where i,j∈{7,8,9}.
Theorem 4.1. Let A∈Cn×n with ind(A)=k. The X7 coincides with the inverse of A along Ak+1(Ak)∗ and (Ak)∗, that is X7 is the (Ak,(Ak)∗)-inverse. Moreover, the generalized inverse X7 is the core-EP inverse of A.
Proof. Let X3 be the (˜A1,˜A1)-inverse of A. That is the (Ak+1(Ak)†,Ak+1(Ak)†)-inverse of A by Lemma 1.4. Since
we have R(Ak+1)=R(˜A1), which implies
For any u∈N(˜A1),
by Lemma 1.1. For any v∈N((Ak)∗),
and we have
Thus, X7 coincides with the inverse of A along Ak+1(Ak)∗ and (Ak)∗ by (2.12), (4.5) and Lemma 1.10. Therefore, the generalized inverse X7 is the core-EP inverse of A by Lemma 1.8 and the condition X7 is the (Ak,(Ak)∗)-inverse. □
Theorem 4.2. Let A∈Cn×n with ind(A)=k, then X8 coincides with the inverse of A along Ak+1(Ak)∗ and (Ak)∗, that is X8 is the (Ak,(Ak)∗)-inverse. Moreover, the generalized inverse X8 is the core-EP inverse of A.
Proof. It is trivial by Theorems 2.1 and 4.1. □
Theorem 4.3. Let A∈Cn×n with ind(A)=k, then X9 coincides with the inverse of A along Ak+1(Ak)∗ and (Ak)∗, that is X9 is the (Ak,(Ak)∗)-inverse. Moreover, the generalized inverse X9 is the core-EP inverse of A.
Proof. It is trivial by Theorems 3.1 and 4.1. □
Theorem 4.4. Let A∈Cn×n with ind(A)=k, then Xi is the same as Xj. Moreover, Xj coincides with the core-EP inverse of A, where i,j∈{7,8,9}.
Proof. It is obvious by Theorems 4.1–4.3. □
Let X1, X4 and X7 be the generalized inverses along A1, ˆA1 and ˜A1, respectively. Note that X1 denotes the inverse along A1 and A1; X2 denotes the inverse along ˆA1 and A1; X3 denotes the inverse along ˜A1 and A1; X4 denotes the inverse along A1 and ˆA1; X5 denotes the inverse along ˆA1 and ˆA1; X6 denotes the inverse along ˜A1 and ˆA1; X7 denotes the inverse along A1 and ˜A1; X8 denotes the inverse along ˆA1 and ˜A1 and X9 denotes the inverse along ˜A1 and ˜A1. Table 4 shows that X1, X2 and X3 have the same column and nilpotent parts and R(Xi)=R(Ak) and N(Xi)=N(Ak) for i=1,2,3; X4, X5 and X6 have the same column and nilpotent parts and that R(Xj)=R(Ak) and N(Xj)=N((Ak)∗A) for j=4,5,6 and X7, X8 and X9 have the same column and nilpotent parts and R(Xk)=R(Ak) and that N(Xk)=N((Ak)∗) for k=7,8,9.
5.
Relationships between Xi and Xj for i,j∈{1,2,⋯,9}
Let A∈Cn×n with indA=k. In this section, we will show that the generalized inverses X1, X4 and X7 are different generalized inverses. For a singular complex matrix, we can prove that the Drazin inverse coincides with the weak group inverse, which is different from the core-EP inverse. Moreover, we show that the Drazin inverse, the weak group inverse and the core-EP inverse can be the same for a certain singular complex matrix.
Example 5.1. Let A=[1101111112]∈C3×3. Then, it is easy to check that ind(A)=2 and
However, X1≠X4, X1≠X7, X4≠X7.
It is trivial that the generalized inverses X1, X4 and X7 are different generalized inverses by Example 5.1. Thus, we have the following theorem.
Theorem 5.2. Let A∈Cn×n with indA=k, then generalized inverses X1, X4 and X7 are different generalized inverses.
Example 5.3. Let A=[10120112002400−1−2]∈C4×4. Then, it is easy to check that ind(A)=2, and
However, X1≠X7, X4≠X7.
For a singular complex matrix, Example 5.3 shows that the Drazin inverse coincides with the weak group inverse, which is different from the core-EP inverse.
Example 5.4. Let A=[10000100001525002545]∈C4×4. Then, it is easy to check that ind(A)=1, and
However, X1=X2=X3=X4=X5=X6=X7=X8=X9=[10000100001525002545].
Example 5.4 shows that the Drazin inverse, the weak group inverse and the core-EP inverse can be the same for a certain singular complex matrix.
Example 5.5. Let A=[101−1011−100010000]∈C4×4, B=[1−110000001000010]∈C4×4. Then, it is easy to check that ind(A)=2 and ind(B)=3, but
with X1≠X4, X1≠X7, X4≠X7, and
with Y1≠Y4, Y1≠Y7, Y4≠Y7.
Example 5.5 shows that the difference index of the complex matrices does not affect the relationships between the Drazin inverse, the weak group inverse and the core-EP inverse.
Theorem 5.2 and Example 5.1 show that the generalized inverses X1, X4 and X7 are different generalized inverses. Thus, we have the following Tables 5 and 6.
6.
Conclusions
New characterizations for generalized inverses along the core parts of three matrix decompositions were investigated in this paper. A number of characterizations and different representations of the Drazin inverse, the weak group inverse and the core-EP inverse were given by using the core parts A1, ˆA1 and ˜A1. Some useful examples were given, which showed that the generalized inverses X1, X4 and X7 are different generalized inverses. We believe that investigation related to the generalized inverses along the core parts of related matrix decompositions will attract attention, and we describe perspectives for further research:
1) Considering the matrix partial orders based on the generalized inverses can relate the core parts of matrix decompositions.
2) Extending the generalized inverses can relate the core parts of matrix decompositions to an element in rings.
3) The column space and the null space of a complex matrix can be described by the core parts of matrix decompositions.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The research article is supported by the National Natural Science Foundation of China (No. 12001223), the Qing Lan Project of Jiangsu Province, the Natural Science Foundation of Jiangsu Province of China (No. BK20220702), the Natural Science Foundation of Jiangsu Education Committee (No. 22KJB110010), "Five-Three-Three" Talents of Huaian City and College Students Innovation and Entrepreneurship Training Program (No. 202311049024Z).
Conflict of interest
The authors declare no conflict of interest.









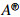 ). Baksalary and Trenkler gave several characterizations of the core inverse by using the decomposition of Hartwig and Spindelböck [
). Baksalary and Trenkler gave several characterizations of the core inverse by using the decomposition of Hartwig and Spindelböck [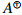 . The weak group inverse of a complex matrix was introduced by Wang and Chen [
. The weak group inverse of a complex matrix was introduced by Wang and Chen [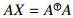 and denoted by
and denoted by  DownLoad:
DownLoad:



