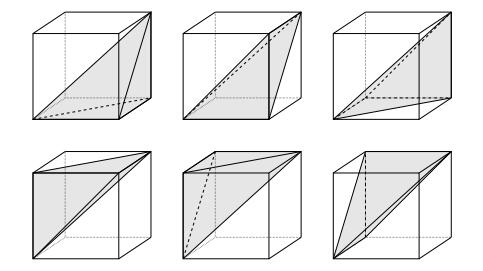
The six tetrahedra in the Kuhn decomposition of a three-dimensional cube
.In this paper, we introduce certain different characterizations and several new properties of the m-weak group inverse of a complex matrix. Also, the relationship between the m-weak group inverse and a nonsingular bordered matrix is established as well as the Cramer's rule for the solution of the restricted matrix equation that depends on the m-weak group inverse.
Citation: Wanlin Jiang, Kezheng Zuo. Further characterizations of the m-weak group inverse of a complex matrix[J]. AIMS Mathematics, 2022, 7(9): 17369-17392. doi: 10.3934/math.2022957
| [1] | Roberto Alicandro, Giuliano Lazzaroni, Mariapia Palombaro . Derivation of a rod theory from lattice systems with interactions beyond nearest neighbours. Networks and Heterogeneous Media, 2018, 13(1): 1-26. doi: 10.3934/nhm.2018001 |
| [2] | Roberto Alicandro, Andrea Braides, Marco Cicalese . Phase and anti-phase boundaries in binary discrete systems: a variational viewpoint. Networks and Heterogeneous Media, 2006, 1(1): 85-107. doi: 10.3934/nhm.2006.1.85 |
| [3] | Mathias Schäffner, Anja Schlömerkemper . On Lennard-Jones systems with finite range interactions and their asymptotic analysis. Networks and Heterogeneous Media, 2018, 13(1): 95-118. doi: 10.3934/nhm.2018005 |
| [4] | Thomas Hudson . Gamma-expansion for a 1D confined Lennard-Jones model with point defect. Networks and Heterogeneous Media, 2013, 8(2): 501-527. doi: 10.3934/nhm.2013.8.501 |
| [5] | Andrea Braides, Margherita Solci, Enrico Vitali . A derivation of linear elastic energies from pair-interaction atomistic systems. Networks and Heterogeneous Media, 2007, 2(3): 551-567. doi: 10.3934/nhm.2007.2.551 |
| [6] | Claudio Canuto, Anna Cattani . The derivation of continuum limits of neuronal networks with gap-junction couplings. Networks and Heterogeneous Media, 2014, 9(1): 111-133. doi: 10.3934/nhm.2014.9.111 |
| [7] | Bernd Schmidt . On the derivation of linear elasticity from atomistic models. Networks and Heterogeneous Media, 2009, 4(4): 789-812. doi: 10.3934/nhm.2009.4.789 |
| [8] | Michele Gianfelice, Marco Isopi . On the location of the 1-particle branch of the spectrum of the disordered stochastic Ising model. Networks and Heterogeneous Media, 2011, 6(1): 127-144. doi: 10.3934/nhm.2011.6.127 |
| [9] | Manuel Friedrich, Bernd Schmidt . On a discrete-to-continuum convergence result for a two dimensional brittle material in the small displacement regime. Networks and Heterogeneous Media, 2015, 10(2): 321-342. doi: 10.3934/nhm.2015.10.321 |
| [10] | Victor A. Eremeyev . Anti-plane interfacial waves in a square lattice. Networks and Heterogeneous Media, 2025, 20(1): 52-64. doi: 10.3934/nhm.2025004 |
In this paper, we introduce certain different characterizations and several new properties of the m-weak group inverse of a complex matrix. Also, the relationship between the m-weak group inverse and a nonsingular bordered matrix is established as well as the Cramer's rule for the solution of the restricted matrix equation that depends on the m-weak group inverse.
In this paper we study an atomistic model for (possibly heterogeneous) nanowires. We consider a scaling of the energy that corresponds to a reduction of the system from
Specifically, in the homogeneous case, we study the asymptotic behaviour of the energy defined by
| εε(u):=∑i,j∈ZN|i−j|≤R(|u(εi)−u(εj)|ε−|i−j|)p, | (0.1) |
where
This model was first studied in [14,15] under the assumption that the admissible deformations satisfy the non-interpenetration condition, namely, that the Jacobian determinant of a suitably defined piecewise affine interpolation of
For the scaling of (0.1), we obtain a complete description of the
The
The paper is organised as follows. In Section 1 we introduce the model. In Section 1 we introduce the minimal costs to bridge different equilibria and study their dependence on the thickness of the nanowire. In Sections 3-5, performing a discrete to continuum limit and a dimension reduction simultaneously, we characterise the
Notation. We recall some basic notions of geometric measure theory for which we refer to [3]. Given a bounded open set
For
Finally,
In the paper, the same letter
We study the dimension reduction of a discrete model for heterogeneous nanowires. Let
| Lε(k):=εZN∩¯Ωkε, | (1.1) |
where
The bonds between the atoms are defined by means of the so-called Kuhn decomposition, which is relevant for modelling some specific Bravais lattices. (See [2,Remark 2.6] for details on the treatment of some lattices in dimension two and three, such as the hexagonal or equilateral triangular, the face-centred cubic, and the body-centred cubic.) First we define a partition
| {{0,ei1,ei1+ei2,…,ei1+ei2+⋯+eiN}:(12⋯Ni1i2⋯iN)∈SN}, |
where
| B1:={ξ∈RN:x and x+ξ are contiguous}. | (1.2) |
If both simplices
| B2:={ξ∈RN:x and x+ξ are opposite vertices}, | (1.3) |
and remark that, by periodicity,
We assume that
| L−ε(k):={x∈Lε(k):x1<0},L+ε(k):={x∈Lε(k):x1≥0}, |
respectively, where
| ε1,λε(u,k):=∑x∈L−ε(k)ξ∈B1∪B2x+εξ∈Lε(k)c(ξ)||u(x+εξ)−u(x)|ε−|Hξ||p+∑x∈L+ε(k)ξ∈B1∪B2x+εξ∈Lε(k)c(ξ)||u(x+εξ)−u(x)|ε−λ|Hξ||p, | (1.4) |
where
To simplify the presentation, we restrict our attention to the case of
| ∑x∈L−ε(k)ξ∈B1∪B2x+εξ∈Lε(k)ϕ1(ξ,|u(x+εξ)−u(x)|e−|Hξ|)+∑x∈L+ε(k)ξ∈B1∪B2x+εξ∈Lε(k)ϕλ(ξ,|u(x+εξ)−u(x)|e−λ|Hξ|), |
where
| C1|z|p≤ϕμ(ξ,z)≤C2|z|pfor μ=λ,1, |
for some positive constants
In principle, all the results that we present in the sequel extend to the case when the two components of the nanowire have equilibria of the form
We study the limit behaviour of
The main novelty of the present paper is that we remove the non-interpenetration assumption made in [14,15], allowing for changes of orientations. Furthermore, in the study of the
In the sequel of the paper we will often consider the rescaled domain
| Ωk,∞:=R×(−k,k)N−1. |
We define the associated lattice and subsets
| L∞(k):=ZN∩¯Ωk,∞,L−∞(k):={x∈L∞(k):x1<0},L+∞(k):={x∈L∞(k):x1≥0}, |
where
| E1,λ∞(u,k):=∑x∈L−∞(k)ξ∈B1∪B2x+ξ∈L∞(k)c(ξ)||u(x+ξ)−u(x)|−|Hξ||p+∑x∈L+∞(k)ξ∈B1∪B2x+ξ∈L∞(k)c(ξ)||u(x+ξ)−u(x)|−λ|Hξ||p. | (1.5) |
We identify every deformation
| Aε(Ωkε):={u∈C0(¯Ωkε;RN):u piecewise affine, ∇u constant on Ωkε∩εT ∀T∈T}. |
Similarly, for (1.5) we define
| A∞(Ωk,∞):={u∈C0(¯Ωk,∞;RN):u piecewise affine, ∇u constant on Ωk,∞∩T ∀T∈T}. |
As customary in dimension reduction problems, we rescale the domain
| Aε:=diag(1,ε,…,ε); | (1.6) |
i.e.,
| I1,λε(˜u,k):=E1,λε(u,k)for ˜u∈˜Aε(Ωk), | (1.7) |
with
| ˜Aε(Ωk):={˜u∈C0(A−1ε(¯Ωkε);RN):˜u piecewise affine, ∇˜u constant on Ωk∩(A−1εεT) ∀T∈T}. |
For later use it will be convenient to set the following notation:
| Ω−k:=(−L,0)×(−k,k)N−1,Ω+k:=(0,L)×(−k,k)N−1. |
We recall that, throughout the paper,
We will study the
| γ(P1,P2;k):=inf{E1,λ∞(v,k):M>0, v∈A∞(Ωk,∞),∇v=P1H for x1∈(−∞,−M),∇v=P2H for x1∈(M,+∞)}; | (2.1a) |
for
| γ(P1,P2;k):=inf{E1,1∞(v,k):M>0, v∈A∞(Ωk,∞),∇v=P1H for x1∈(−∞,−M),∇v=P2H for x1∈(M,+∞)}, | (2.1b) |
where
| E1,1∞(v,k):=∑x∈L∞(k)ξ∈B1∪B2x+ξ∈L∞(k)c(ξ)||v(x+ξ)−v(x)|−|Hξ||p; |
for
| γ(P1,P2;k):=inf{Eλ,λ∞(v,k):M>0,v∈A∞(Ωk,∞),∇v=P1Hforx1∈(−∞,−M),∇v=P2Hforx1∈(M,+∞)}, | (2.1c) |
where
| Eλ,λ∞(v,k):=∑x∈L∞(k)ξ∈B1∪B2x+ξ∈L∞(k)c(ξ)||v(x+ξ)−v(x)|−λ|Hξ||p. |
The next proposition shows that the relevant quantities defined through (2.1) are in fact four: the minimal costs of the transition at the interface between the energy wells
Proposition 1. For each
| γ(R,R′;k)=γ(Q,Q′;k)=γ(λR,λR′;k)=γ(λQ,λQ′;k)=0, | (2.2a) |
| γ(R,λR′;k)=γ(Q,λQ′;k)=γ(I,λI;k), | (2.2b) |
| γ(R,λQ;k)=γ(Q,λR;k)=γ(I,λJ;k), | (2.2c) |
| γ(R,Q;k)=γ(Q,R;k)=γ(I,J;k),and | (2.2d) |
| γ(λR,λQ;k)=γ(λQ,λR;k)=γ(λI,λJ;k). | (2.2e) |
Moreover,
| γ(λP1,λP2;k)=λpγ(P1,P2;k)forevery P1,P2∈O(N). | (2.3) |
Proof. First one notices that
We now prove estimates on the asymptotic behaviour of
Theorem 2.1.[2,Theorem 3.1] Let
| εN−1∑ξ∈B1∪B2∑x,x+εξ∈εZN∩(0,1)N||uε(x+εξ)−uε(x)|ε−|Hξ||p<C. | (2.4) |
Then there are a subsequence (not relabelled) and a function
| ∇u∈SBV((0,1)N;O(N)H). | (2.5) |
Specifically,
| u(x)=∑i∈N(RiHx+bi)χEi(x), | (2.6) |
where
We now prove the main result of this section.
Theorem 2.2. Let
| γ(P1,P2;k)≤CkN. | (2.7) |
Moreover,
| limk→∞γ(P1,P2;k)kN−1=+∞. | (2.8) |
Proof. The upper bound (2.7) is proven by comparing test functions for
For the proof of the lower bound (2.8) we will use Theorem 2.1 in each of the subsets
| 1kN−1jE1,λ∞(uj,kj)<C, | (2.9) |
for some positive
| Lj:=1kjZN∩¯Ω1,∞,L+j:=Lj∩{x1>0},L−j:=Lj∩{x1<0}. |
Expressing
| E1,λ∞(uj,k)=∑x∈L−jξ/kj∈B1∪B2x+ξ/kj∈Ljc(ξ)||vj(x+ξkj)−vj(x)|1kj−|Hξ||p+∑x∈L+jξ/kj∈B1∪B2x+ξ/kj∈Ljc(ξ)||vj(x+ξkj)−vj(x)|1kj−λ|Hξ||p. | (2.10) |
The above term controls the (piecewise constant) gradient of
| v(x)=∑i∈N(RiHx+ai)χEi(x)+∑j∈N(λQjHx+bj)χE+j(x), |
where
Remark 1. An estimate similar to (2.8) was proven in [14,15] (for a hexagonal lattice in dimension two and a class of three-dimensional lattices) via a different argument, based on the non-interpenetration condition. In fact, in [14,15] a stronger result is proven, namely, that
The non-interpenetration assumption turns out to be necessary if the energy involves only nearest neighbour interactions; indeed, in such a case, one can exhibit deformations that violate the non-interpenetration condition and for which (2.8) does not hold, see [14,Section 4.2]. Such deformations, which consist of suitable foldings of the lattice, would be energetically expensive (and, in particular, would not provide a counterexample to (2.8)) in the present setting, exactly because of the effect of the interactions across neighbouring cells. It is the latter ones that prevent folding phenomena and allow one to prove (2.8), via Theorem 2.1.
Before characterising the
Essential tools for the compactness and the lower bound are provided by the following rigidity estimates.
Theorem 3.1. [12,Theorem 3.1] Let
| ‖∇u−R‖Lp(U;MN×N)≤C(U)‖dist(∇u,SO(N))‖Lp(U). | (3.1) |
The constant
It is convenient to define the energy of a single simplex
| Ecell(uF;T):=N∑i≤j=0||F(xi−xj)|−|H(xi−xj)||pfor every F∈MN×N, |
where
Lemma 3.2. [2,Lemma 2.2] There exists a constant
| distp(F,SO(N)H)≤CEcell(uF;T)∀F∈MN×N:detF≥0, | (3.2a) |
| distp(F,(O(N)∖SO(N))H)≤CEcell(uF;T)∀F∈MN×N:detF≤0. | (3.2b) |
The next lemma asserts that if in two neighbouring simplices the sign of
| Ecell(u;S∪T):=N∑i≤j=0||u(xi)−u(xj)|−|H(xi−xj)||p |
| +N∑j=1||u(y0)−u(xj)|−|H(y0−xj)||p+||u(y0)−u(x0)|−|H(y0−x0)||p. |
Lemma 3.3. [2,Lemma 2.3] There exists a positive constant
| det(∇u|S)det(∇u|T)≤0, |
then
Lemma 3.2 will allow us to apply Theorem 3.1. More precisely, in the part of the wire with
Due to the fact that a minimum energy has to be paid for each change of orientation, see Lemma 3.3, the parts with positive determinant do not mix with those with negative determinant. Hence, passing to the weak* limit we obtain functions taking values in
Remark 2. It is well known that
| co(SO(2))={(α−ββα):α2+β2≤1},co(O(2)∖SO(2))={(αββ−α):α2+β2≤1}. |
In particular,
| co(SO(N))∪co(O(N)∖SO(N))⊊co(O(N)) |
for
Henceforth, the symbol
Proposition 2. Let
| lim supε→0+I1,λε(˜uε,k)≤C. | (3.3) |
Then there exist functions
| (3.4) |
and
| (∂1˜u|d2|⋯|dN)∈{co(SO(N))Ha.e.in (−L,0)∩U,co(O(N)∖SO(N))Ha.e.in (−L,0)∖U,λco(SO(N))Ha.e.in (0,L)∩U,λco(O(N)∖SO(N))Ha.e.in (0,L)∖U, | (3.5) |
and
| lim infε→0+I1,λε(˜uε,k)≥ γ(I,J;k)H0(∂U∩(−L,0))+γ(λI,λJ;k)H0(∂U∩(0,L))+γ(I,λI;k)[1−χ∂U(0)]+γ(I,λJ;k)χ∂U(0). | (3.6) |
Remark 3. The right-hand side of (3.6) contains different contributions. The first term corresponds to the minimal energy needed to bridge a rotation with a rotoreflection, or viceversa, in the left part of the nanowire; the energy spent depends on the number of changes of orientation, i.e., on the cardinality of
Proof. (Compactness) The assumption (3.3) implies that
In order to show
Specifically, for each
| ∫(ai,ai+ε)×(kε,kε)N−1|∇uε−Pε(ai)|pdx≤C∫(ai,ai+ε)×(kε,kε)N−1distp(∇uε,O(N)H)dx, |
and for every
| ∫(ai,ai+ε)×(kε,kε)N−1|∇uε−Pε(ai)|pdx≤C∫(ai,ai+ε)×(kε,kε)N−1distp(∇uε,λO(N)H)dx. |
Moreover for
| ∫Ω−k|∇˜uεA−1ε−Pε(x1)|pdx≤C∫A−1ε(¯Ωkε)∩{x1<0}distp(∇˜uεA−1ε,O(N)H)dx≤Cε, | (3.7a) |
| ∫Ω+k|∇˜uεA−1ε−Pε(x1)|pdx≤C∫A−1ε(¯Ωkε)∩{x1>0}distp(∇˜uεA−1ε,λO(N)H)dx≤Cε, | (3.7b) |
where the last inequality of each line follows by applying Lemma 3.2 to each subdomain with
We now define the sets
| Kε:={aεi∈(−L,L):Pε(x1)∈SO(N)H∪λSO(N)H for x1∈[aεi,aεi+ε)},Uε:=⋃aεi∈Kε[aεi,aεi+ε), |
and remark that Lemma 3.2, Lemma 3.3, and assumption (3.3) imply that the cardinality of
| U=n⋃i=1(αi,βi),−L≤α1<β1<α2<β2<⋯<αn<βn≤L. | (3.8) |
Since we can write
| Pε(x1)=Rε(x1)(χUε∩(−L,0)H+χUε∩(0,L)λH)+JRε(x1)((1−χUε∩(−L,0))H+(1−χUε∩(0,L))λH), |
where
(Lower bound) Inequality (3.6) is proven by a standard argument which can be found, for example, in [14,16,17]. We will briefly sketch the main ideas and refer the reader to [14,16,17] for full details. First recall that
| (αεi−2σ,αεi−σ)⊂(−L,L)∖Uε,(αεi+σ,αεi+2σ)⊂Uε, | (3.9a) |
| (βεi−2σ,βεi−σ)⊂Uε,(βεi+σ,βεi+2σ)⊂(−L,L)∖Uε. | (3.9b) |
Moreover, if
| vε(x1,x2,…,xN):=1ε˜uε(εx1+αεi,x2,…,xN)=1εuε(εx1+αεi,εx2,…,εxN). |
Then,
| ∫(−2σε,−σε)×(−k,k)N−1distp(∇vε,λ(O(N)∖SO(N))H)dx+∫(σε,2σε)×(−k,k)N−1distp((∇vε,λSO(N)H)dx≤C. | (3.10) |
From (3.10), Theorem 3.1 and the Poincaré inequality, we deduce that there exists a unit interval contained in
| I1,λε(˜uε,k)|(αεi−2σ,αεi+2σ)×(−k,k)N−1≥Eλ,λ∞(ˆvε,k)−Cεσ, |
where
We prove that the bound (3.6) is in fact optimal.
Proposition 3. Let
| F∈{co(SO(N))Ha.e.in (−L,0)∩U,co(O(N)∖SO(N))Ha.e.in (−L,0)∖U,λco(SO(N))Ha.e.in (0,L)∩U,λco(O(N)∖SO(N))Ha.e.in (0,L)∖U. | (4.1) |
Then there exists a sequence
| ˜uεA−1ε∗⇀Fweakly∗in L∞(Ωk;MN×N), | (4.2) |
and
| lim supε→0+I1,λε(˜uε,k)≤ γ(I,J;k)H0(∂U∩(−L,0))+γ(λI,λJ;k)H0(∂U∩(0,L))+γ(I,λI;k)[1−χ∂U(0)]+γ(I,λJ;k)χ∂U(0) | (4.3) |
Proof. Using a standard approximation argument we may assume that
| F=−1∑i=mχ(ai,ai+1)RiH+n∑i=0χ(ai,ai+1)λRiH |
and
| U=int⋃{[ai,ai+1]:Ri∈SO(N), m≤i≤n−1}. |
The following construction is similar to that in [14,Proposition 3.2], so we will show the details only for what concerns the changes of orientation. We introduce a mesoscale
We now complete the definition of
If
| ∇v=Ri−1H for x1∈(−∞,−M),∇v=RiH for x1∈(M,+∞) |
and
| E1,1∞(v,k)≤γ(I,J;k)+η, |
where we used also Proposition 1. With this at hand, we define
| ˜uε(x):=εv(1εAεx)+b. |
The constant vector
The case
In the next theorem we characterise the
| A1,λ(k):={u∈W1,∞(Ωk;RN):∂2u=⋯=∂Nu=0 a.e. in Ωk,|∂1u|≤1 a.e. in Ω−k, |∂1u|≤λ a.e. in Ω+k}. | (5.1) |
We show that on such domain the
Theorem 5.1. The sequence of functionals
| I1,λ(u,k)={γ(k)if u∈A1,λ(k),+∞otherwise, | (5.2) |
with respect to the weak* convergence in
| γ(k):=min{γ(I,λI;k),γ(I,λJ;k)}. | (5.3) |
Proof. (Liminf inequality) Let
| I1,λ(u,k)≤lim infε→0+I1,λε(˜uε,k). |
We assume that
(Limsup inequality) Given a function
| lim supε→0+I1,λε(˜uε,k)≤I1,λ(u,k). | (5.4) |
We assume that
The construction of the recovery sequence depends on the precise value of the minimum in (5.3). Since we do not know such value, we explain how to proceed in the case when
| (∂1u|d2|⋯|dN)∈{co(SO(N))Ha.e. in Ω−k,λco(SO(N))Ha.e. in Ω+k. |
| (∂1u|d2|⋯|dN)∈{co(SO(N))Ha.e. in Ω−k,λco(O(N)∖SO(N))Ha.e. in Ω+k. |
Proposition 3 can be now applied to
Remark 4. As long as the
Below we show that, if a stronger topology is chosen, the value of the
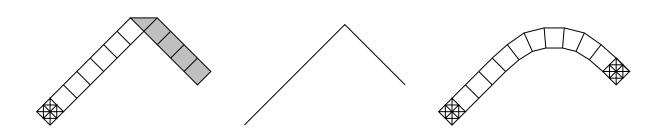
Two possible recovery sequences for the profile at the centre of the figure. Here we picture only a part of the wire containing just one species of atoms, therefore the transition at the interface is not represented. A kink in the profile may be reconstructed by folding the strip, i.e., mixing rotations and rotoreflections (left); or by a gradual transition involving only rotations or only rotoreflections (right). In the limit, the former recovery sequence gives a positive cost, while the latter gives no contribution. If the stronger topology is chosen, the appropriate recovery sequence will depend on the value of the internal variable, which defines the orientation of the wire
.We introduce the sequence of functionals defined for
| ˆI1,λε(˜u,D,k):={I1,λε(˜u,k)if˜u∈˜Aε(Ωk)andD=(∂1˜u|ε−1∂2˜u|⋯|ε−1∂N˜u),+∞otherwise. |
In the next theorem we study the
| ˆA1,λ(k):={(u,D):u∈A1,λ(k), D∈L∞(Ωk;MN×N), De1=∂1u, ∂2D=…=∂ND=0 a.e. in Ωk, D∈co(SO(N))H∪co(O(N)∖SO(N))H a.e. in Ω−k,D∈λco(SO(N))H∪λco(O(N)∖SO(N))H a.e. in Ω+k}, |
where
Definition 5.2. Given
| D∈{co(SO(N))Hfor a.e. x1∈(−L,0)∩U,co(O(N)∖SO(N))Hfor a.e. x1∈(−L,0)∖U,λco(SO(N))Hfor a.e. x1∈(0,L)∩U,λco(O(N)∖SO(N))Hfor a.e. x1∈(0,L)∖U. | (5.5) |
For
| J(U):= γ(I,J;k)H0(∂U∩(−L,0))+γ(λI,λJ;k)H0(∂U∩(0,L))+γ(I,λI;k)[1−χ∂U(0)]+γ(I,λJ;k)χ∂U(0) |
and
| Jmin(u,D):=minU∈U(u,D)J(U). | (5.6) |
The last definition will be used to apply Propositions 2 and 3 towards the characterisation of the
| {J(U):U∈U(u,D)}⊂{m1γ(I,J;k)+m2γ(I,λI;k)+m3γ(I,λJ;k)+m4γ(λI,λJ;k):mi∈N}. |
A minimiser needs not be unique as shown in the following example.
Example 5.3. Fix
Theorem 5.4. The sequence of functionals
| ˆI1,λ(u,D,k):={Jmin(u,D)if (u,D)∈ˆA1,λ(k),+∞otherwise, | (5.7) |
with respect to the weak* convergence in
Proof. The liminf inequality is obtained by applying Proposition 2 and arguing as in Theorem 5.1. Also the derivation of the limsup inequality is similar to the one performed in Theorem 5.1; let us simply point out that, while in the proof of Theorem 5.1 the matrix field
Remark 5. We underline that Theorem 5.4 provides a nontrivial
In the present section we discuss how the previous results extend to the case when the functional (1.4) is complemented by boundary conditions or external forces. Although our considerations apply to the case of general
Boundary conditions. Let
| {∇u(x)=B−x if −L<x1<−L+ε,∇u(x)=B+x if L−ε<x1<L. | (6.1) |
It is easy to see that while the compactness result of Proposition 2 remains valid, the
| γ(B−,P;k):=inf{E1,1M(v,k):M>0, v∈A∞(Ωk,∞),∇v=B− for x1∈(−∞,−M),∇v=P for x1∈(M,+∞)}, | (6.2) |
| γ(P,B+;k):=inf{E1,1M(v,k):M>0, v∈A∞(Ωk,∞),∇v=P for x1∈(−∞,−M),∇v=B+ for x1∈(M,+∞)}, | (6.3) |
where
Remark 6. By Proposition 2 and the properties of
| γ(I,B±;k)→0asdist(B±;SO(N))→0 |
and therefore, as long as
External forces. We study a class of tangential/radial forces acting along the rod. Let
| Fε(u,k):=∑(±Lε,x2,…,xN)∈Lε(k)F1⋅(u(Lε,x2,…,xN)−u(−Lε,x2,…,xN))+∑(x1,±εk,…,xN)∈Lε(k)F2(x1)⋅(u(x1,εk,x3,…,xN)−u(x1,−εk,x3,…,xN))+⋯…+∑(x1,…,xN−1,±εk)∈Lε(k)FN(x1)⋅(u(x1,…,xN−1,εk)−u(x1,…,xN−1,−εk)), | (6.4) |
where
| Fε(u,k)=Lε−ε∑x1=−Lε ∑(x1,…,xN)∈Lε(k)F1⋅(u(x1+ε,…,xN)−u(x1,…,xN))+ε(k−1)∑x2=−εk ∑(x1,…,xN)∈Lε(k)F2(x1)⋅(u(x1,x2+ε,…,xN)−u(x1,x2,…,xN))+⋯⋯+ε(k−1)∑xN=−εk ∑(x1,…,xN)∈Lε(k)FN(x1)⋅(u(x1,…,xN+ε)−u(x1,…,xN)), |
hence we have that
Introducing the new variables
| ˜Fε(˜u,k):=∑(±Lε,x2,…,xN)∈A−1εLε(k)F1⋅(˜u(Lε,x2,…,xN)−˜u(−Lε,x2,…,xN))+∑(x1,±k,…,xN)∈A−1εLε(k)F2(x1)⋅(˜u(x1,k,x3,…,xN)−˜u(x1,−k,x3,…,xN))+…⋯+∑(x1,…,xN−1,±k)∈A−1εLε(k)FN(x1)⋅(˜u(x1,…,xN−1,k)−˜u(x1,…,xN−1,−k))= Fε(u,k), |
so that
| Gε(˜u,D,k):=ˆI1,1ε(˜u,D,k)−˜Fε(˜u,k), ˜u∈˜Aε(Ωk),D∈L∞(Ωk;MN×N). | (6.5) |
Note that in this context we cannot use the weak* convergence in
| Cε∫Ωk(|∇˜uA−1ε|p−1)dx≤Cε∫Ωkdistp(∇˜uA−1ε,O(N))dx≤ˆI1,1ε(˜u,k) |
and
| ˜Fε(˜u,k)≤C(∫Ωk|F|p′dx+∫Ωk|∇˜uA−1ε|pdx). |
Let now
| lim supε→0+Gε(˜uε,Dε,k)≤C. |
The previous inequalities imply that
Theorem 6.1. The following results hold:
(Compactness) Let
| lim supε→0+Gε(˜uε,Dε,k)≤C. |
Then there exists
(
| G(u,D,k):=ˆI1,1(u,D,k)−˜F(D,k), | (6.6) |
with respect to the weak* convergence in
| ˜F(D,k):=(2k)N−1∫L−L(F1⋅d1+⋯+FN⋅dN)dx1 |
for
As a consequence of the previous theorem and the standard properties of
Corollary 1. We have that
| limε→0min{Gε(u,D):(u,D)∈˜Aε(Ωk)×L∞(Ωk;MN×N)}=min{G(u,D,k):(u,D)∈ˆA1,1(k)}. |
Moreover if
| limε→0Gε(uε,Dε)=limε→0min{Gε(u,D):(u,D)∈˜Aε(Ωk)×L∞(Ωk;MN×N)}, |
then any cluster point
We now come back to the question of the consistency of the model with the non-interpenetration condition. In this context we cannot expect that minimisers of (6.5) preserve orientation for the whole class of loads defined above. This is clarified in the following remark.
Remark 7. Minimisers of the functional defined by (6.6) may have transition points between the two wells
Define
| C:=min(u,D)∈ˆA1,10(k)−˜F(D,k)>−˜F(ˉD,k)=−(2k)N−1(N−1∑i=1∫L−Lfidx1+∫a−LfNdx1−∫LafNdx1). |
Therefore, if
| −˜F(¯D,k)+γ(I,J;k)<C, |
then it is energetically preferred to have a transition at
The lattice mismatch in heterostructured materials, corresponding to
Following the ideas of [14], in dimension
| Lε(ρ,k):=L−ε(1,k)∪L+ε(ρ,k), |
where
| L−ε(1,k):=ρεZ2∩¯Ωkε∩{x1<0},L+ε(ρ,k):=ρεZ2∩¯Ωkε∩{x1≥0}, |
and
In presence of dislocations, the choice of the interactions and of the equilibria strongly depends on the lattice that one intends to model. Therefore, in this section we focus on the simplest situation of hexagonal (or equilateral triangular) Bravais lattices in dimension two and we fix
| H:=(1−120√32). |
The lattice
The bonds between nearest and next-to-nearest neighbours are defined first in the lattice
Once the bonds in the lattice
| B1(x):={ξ∈RN:Hx, H(x+ξ)∈HLε(ρ,k) are nearest neighbours},B2(x):={ξ∈RN:Hx, H(x+ξ)∈HLε(ρ,k) are next-to-nearest neighbours}. |
We remark that if
| E1,λε(u,ρ,k):=∑x∈L−ε(ρ,k)ξ∈B1(x) c1||u(x+ξ)−u(x)|e−1|p+∑x∈L+ε(ρ,k)ξ∈B1(x)c1||u(x+ξ)−u(x)|e−λ|p+∑x∈L−ε(ρ,k)ξ∈B2(x) c2||u(x+ξ)−u(x)|e−√3|p+∑x∈L+ε(ρ,k)ξ∈B2(x)c2||u(x+ξ)−u(x)|e−√3λ|p. |
Notice that away from the interface all bonds in the reference configuration are in equilibrium if
The results shown in detail in this paper for the defect-free case (corresponding to
| L∞(ρ,k):=L−∞(1,k)∪L+∞(ρ,k),L−∞(1,k):=ρZ2∩¯Ωk,∞∩{x1<0},L+∞(ρ,k):=ρZ2∩¯Ωk,∞∩{x1≥0}, |
where the triangulation is chosen in analogy with the one for
| γ(P1,λP2;ρ,k):=inf{E1,λ∞(v,ρ,k):M>0, v∈A∞(Ωk,∞),∇v=P1H for x1∈(−∞,−M),∇v=λρP2H for x1∈(M,+∞)}, |
with
| E1,λ∞(u,ρ,k):=∑x∈L−∞(ρ,k)ξ∈B1(x) c1||u(x+ξ)−u(x)|−1|p+∑x∈L+∞(ρ,k)ξ∈B1(x)c1||u(x+ξ)−u(x)|−λ|p+∑x∈L−∞(ρ,k)ξ∈B2(x) c2||u(x+ξ)−u(x)|−√3|p+∑x∈L+∞(ρ,k)ξ∈B2(x)c2||u(x+ξ)−u(x)|−√3λ|p. |
Theorem 7.1. The sequence of functionals
| I1,λ(u,ρ,k)={γ(ρ,k)if u∈A1,λ(ρ,k),+∞otherwise, |
with respect to the weak* convergence in
| A1,λ(ρ,k):={u∈W1,∞(Ωk;RN):∂2u=0 a.e. in Ωk,|∂1u|≤1 a.e. in Ω−k, |∂1u|≤λρ a.e. in Ω+k} |
and
| \gamma(\rho, k): = \min\big\{ \gamma(I, \lambda I;\rho, k), \gamma(I, \lambda J;\rho, k) \big\} \, . |
The stronger topology introduced in Theorem 5.4 allows us to take into account the cost of "folding" the lattice using rotoreflections, giving deeper insight into deformations that bridge different equilibria. Indeed, it is possible to combine Theorems 5.4 and 7.1 giving the
Remark 8. It is easy to see that for
| C_1 k\le \gamma (\lambda, k)\le C_2 k |
for some constants
| \gamma (\rho, k)\le C_\rho \, k^2 \;\;\;\;\;\text{and} \;\;\;\;\;\lim\limits_{k\to\infty}\frac{\gamma (\rho, k)}{k} = +\infty \, . |
This gives a mathematical proof of the experimentally observed fact that dislocations are preferred in order to relieve the lattice mismatch when the thickness of the specimen is sufficiently large. We recall that a similar result was proven in [14,15] (under the non-interpenetration assumption), see also Remark 1.
The results sketched here for hexagonal lattices can be obtained also for other lattices by adapting the technique to each specific case. In particular, we refer to [15] for details on the rigidity of face-centred and body-centred cubic lattices in dimension three.
| [1] |
M. P. Drazin, Pseudo-inverses in associative rings and semigroups, Am. Math. Mon., 65 (1958), 506–514. https://doi.org/10.2307/2308576 doi: 10.2307/2308576

|
| [2] |
Y. Wei, G. Wang, The perturbation theory for the Drazin inverse and its applications, Linear Algebra Appl., 258 (1997), 179–186. https://doi.org/10.1016/s0024-3795(96)00159-0 doi: 10.1016/s0024-3795(96)00159-0

|
| [3] |
R. E. Hartwig, G. Wang, Y. Wei, Some additive results on Drazin inverse, Linear Algebra Appl., 322 (2001), 207–217. https://doi.org/10.1016/j.amc.2009.05.021 doi: 10.1016/j.amc.2009.05.021

|
| [4] | D. S. Cvetkovi\rm \acute{c}-Ili\rm\acute{c}, Xiaoji Liu, Y. Wei, Some additive results for the generalized Drazin inverse in a Banach algebra, Electronic J. Linear Algebra, 22 (2011), 1049–1058. |
| [5] |
D. S. Cvetkovi\rm \acute{c}-Ili\rm\acute{c}, New additive results on Drazin inverse and its applications, Appl. Math. Comp., 218 (2011), 3019–3024. https://doi.org/10.1016/j.amc.2011.08.083 doi: 10.1016/j.amc.2011.08.083

|
| [6] |
N. P. Karampetakis, S. Vologiannidis, DFT calculation of the generalized and Drazin inverse of a polynomial matrix, Appl. Math. Comput., 143 (2003), 501–521. https://doi.org/10.1016/S0096-3003(02)00377-6 doi: 10.1016/S0096-3003(02)00377-6

|
| [7] |
N. P. Karampetakis, P. S. Stanimirovi\rm \acute{c}, M. B. Tasi\rm \acute{c}, On the computation of the Drazin inverse of a polynomial matrix, Far East J. Math. Sci., 26 (2007), 1–24. https://doi.org/10.1016/s1474-6670(17)38994-2 doi: 10.1016/s1474-6670(17)38994-2

|
| [8] |
P. S. Stanimirovi\rm \acute{c}, V. N. Katsikis, H. Ma, Representations and properties of the W-Weighted Drazin inverse, Linear Multilinear A., 65 (2017), 1080–1096. https://doi.org/10.1080/03081087.2016.1228810 doi: 10.1080/03081087.2016.1228810

|
| [9] |
I. I. Kyrchei, Weighted quaternion core-EP, DMP, MPD, and CMP inverses and their determinantal representations, RACSAM Rev. R. Acad. A, 114 (2020), 198. https://doi.org/10.1007/s13398-020-00930-3 doi: 10.1007/s13398-020-00930-3

|
| [10] |
S. B. Malik, N. Thome, On a new generalized inverse for matrices of an arbitrary index, Appl. Math. Comput., 226 (2014), 575–580. https://doi.org/10.1016/j.amc.2013.10.060 doi: 10.1016/j.amc.2013.10.060

|
| [11] |
K. Zuo, D. S. Cvetkovi\rm \acute{c}-Ili\rm\acute{c}, Y. Cheng, Different characterizations of DMP-inverse of matrices, Linear Multilinear A., 70 (2022), 411–418. https://doi.org/10.1080/03081087.2020.1729084 doi: 10.1080/03081087.2020.1729084

|
| [12] |
L. Meng, The DMP inverse for rectangular matrices, Filomat, 31 (2017), 6015–6019. https://doi.org/10.2298/FIL1719015M doi: 10.2298/FIL1719015M

|
| [13] |
I. I. Kyrchei, D. Mosi\rm \acute{c}, P. S. Stanimirovi\rm \acute{c}, MPD-DMP-solutions to quaternion two-sided restricted matrix equations, Comput. Appl. Math., 40 (2021), 177. https://doi.org/10.1007/s40314-021-01566-8 doi: 10.1007/s40314-021-01566-8

|
| [14] | D. S. Cvetkovi\rm \acute{c}-Ili\rm\acute{c}, Y. Wei, Algebraic properties of generalized inverses, In: Developments on Mathematics, Springer, Singapore, 52 (2017). http://dx.doi.org/10.1007/978-981-10-6349-7 |
| [15] | H. Wang, J. Chen, Weak group inverse, Open Math., 16 (2018), 1218–1232. https://doi.org/10.1515/math-2018-0100 |
| [16] |
H. Wang, Core-EP decomposition and its applications, Linear Algebra Appl., 508 (2016), 289–300. https://doi.org/10.1016/j.laa.2016.08.008 doi: 10.1016/j.laa.2016.08.008

|
| [17] | H. Wang, X. Liu, The weak group matrix, Aequationes Math., 93 (2019), 1261–1273. https://doi.org/10.1007/s00010-019-00639-8 |
| [18] | M. Zhou, J. Chen, Y. Zhou, Weak group inverses in proper *-rings, J. Algebra Appl., 19 (2020). https://doi.org/10.1142/S0219498820502382 |
| [19] | Y. Zhou, J. Chen, M. Zhou, m-weak group inverses in a ring with involution, RACSAM Rev. R. Acad. A, 115 (2021). https://doi.org/10.1007/s13398-020-00932-1 |
| [20] | M. Zhou, J. Chen, Y. Zhou, N. Thome, Weak group inverses and partial isometries in proper *-rings, Linear Multilinear A., 2021. https://doi.org/10.1080/03081087.2021.1884639 |
| [21] |
D. E. Ferreyra, V. Orquera, N. Thome, A weak group inverse for rectangular matrices, RACSAM Rev. R. Acad. A, 113 (2019), 3727–3740. https://doi.org/10.1007/s13398-019-00674-9 doi: 10.1007/s13398-019-00674-9

|
| [22] | Y. Zhou, J. Chen, Weak core inverses and pseudo core inverses in a ring with involution, Linear Multilinear A., 2021. https://doi.org/10.1080/03081087.2021.1971151 |
| [23] |
R. Penrose, A generalized inverse for matrices, Math. Proc. Cambridge Philos. Soc., 51 (1955), 406–413. https://doi.org/10.1017/S0305004100030401 doi: 10.1017/S0305004100030401

|
| [24] | G. Wang, Y. Wei, S. Qiao, Generalized inverses: Theory and computations, In: Developments on Mathematics, Springer and Beijing, Science Press, 53 (2018). http://dx.doi.org/10.1007/978-981-13-0146-9 |
| [25] | O. M. Baksalary, G. Trenkler, Core inverse of matrices, Linear Multilinear A., 58 (2010), 681–697. http://dx.doi.org/10.1080/03081080902778222 |
| [26] |
H. Kurata, Some theorems on the core inverse of matrices and the core partial ordering, Appl. Math. Comput., 316 (2018), 43–51. http://dx.doi.org/10.1016/j.amc.2017.07.082 doi: 10.1016/j.amc.2017.07.082

|
| [27] | G. Luo, K. Zuo, L. Zhou, Revisitation of core inverse, Wuhan Univ. J. Nat. Sci., 20 (2015), 381–385. https: //doi.org/10.1007/s11859-015-1109-6 |
| [28] | K. Prasad, K. S Mohana, Core-EP inverse, Linear Multilinear A., 62 (2014), 792–802. http://dx.doi.org/10.1080/03081087.2013.791690 |
| [29] |
D. E. Ferreyra, F. E. Levis, N. Thome, Revisiting the core-EP inverse and its extension to rectangular matrices, Quaest. Math., 41 (2018), 1–17. http://dx.doi.org/10.2989/16073606.2017.1377779 doi: 10.2989/16073606.2017.1377779

|
| [30] |
K. Zuo, Y. Cheng, The new revisitation of core EP inverse of matrices, Filomat, 33 (2019), 3061–3072. https://doi.org/10.2298/FIL1910061Z doi: 10.2298/FIL1910061Z

|
| [31] | J. Benítez, E. Boasso, H. Jin, On one-sided (B, C)-inverse of arbitrary matrices, Electron. J. Linear Al., 32 (2017), 391–422. https://arXiv.org/pdf/1701.09054v1.pdf |
| [32] |
M. P. Drazin, A class of outer generalized inverses, Linear Algebra Appl., 436 (2012), 1909–1923. https://doi.org/10.1016/j.laa.2011.09.004 doi: 10.1016/j.laa.2011.09.004

|
| [33] |
X. Wang, C. Deng, Properties of m-EP operators, Linear Multilinear A., 65 (2017), 1349–1361. https://doi.org/10.1080/03081087.2016.1235131 doi: 10.1080/03081087.2016.1235131

|
| [34] |
C. Deng, H. Du, Representation of the Moore-Penrose inverse of 2\times2 block operator valued matrices, J. Korean Math. Soc., 46 (2009), 1139–1150. https://doi.org/10.4134/JKMS.2009.46.6.1139 doi: 10.4134/JKMS.2009.46.6.1139

|
| [35] |
D. E. Ferreyra, F. E. Levis, N. Thome, Maximal classes of matrices determining generalized inverses, Appl. Math. Comput., 333 (2018), 42–52. https://doi.org/10.1016/j.amc.2018.03.102 doi: 10.1016/j.amc.2018.03.102

|
| [36] |
D. E. Ferreyra, F. E. Levis, N. Thome, Characterizations of k-commutative equalities for some outer generalized inverses, Linear Multilinear A., 68 (2020), 177–192. https://doi.org/10.1080/03081087.2018.1500994 doi: 10.1080/03081087.2018.1500994

|
| [37] |
Y. Yuan, K. Zuo, Compute \lim_{\lambda \to 0}X(\lambda I_{p}+YAX)^{-1}Y be the product singular value decomposition, Linear Multilinear A., 64 (2016), 269–278. https://doi.org/10.1080/03081087.2015.1034641 doi: 10.1080/03081087.2015.1034641

|
| [38] | P. S. Stanimirovi\rm \acute{c}, M. \rm \acute{S}iri\rm\acute{c}, I. Stojanovi\rm \acute{c}, D. Gerontitis, Conditions for existence, representations, and computation of matrix generalized inverses, Complexity, 2017 (2017). https://doi.org/10.1155/2017/6429725 |
| [39] | Y. Wei, P. S. Stanimirovi\rm \acute{c}, M. D. Petkovi\rm \acute{c}, Numerical and symbolic computations of generalized inverses, World Scientific Publishing Co. Pte. Ltd., Hackensack, 2018. http://dx.doi.org/10.1142/10950 |
| [40] |
P. S. Stanimirovi\rm \acute{c}, M. D. Petkovi\rm \acute{c}, D. Mosi\rm\acute{c}, Exact solutions and convergence of gradient based dynamical systems for computing outer inverses, Appl. Math. Comput., 412 (2022), 126588. https://doi.org/10.1016/j.amc.2021.126588 doi: 10.1016/j.amc.2021.126588

|
| 1. | Silvio Fanzon, Marcello Ponsiglione, Riccardo Scala, Uniform distribution of dislocations in Peierls–Nabarro models for semi-coherent interfaces, 2020, 59, 0944-2669, 10.1007/s00526-020-01787-5 | |
| 2. | Prashant K. Jha, Timothy Breitzman, Kaushik Dayal, Discrete-to-Continuum Limits of Long-Range Electrical Interactions in Nanostructures, 2023, 247, 0003-9527, 10.1007/s00205-023-01869-6 |