The instability of periodic solutions for a population model with cross-diffusion

1.   Introduction

Since 1946, biologist Crombic proved the stability effect through experiments ^[1,2] and more and more scholars analyzed the refuge effect on the population model ^{[3,4,5,6,7,8,9]}, mainly focused on the self-diffusion effect on dynamic behavior of the population system. In addition to the effect of self-diffusion, cross-diffusion also plays an important role during the population pattern formation. About the predator-prey systems with diffusion terms, many scholars have studied the Turning instability and Hopf bifurcation of its constant equilibrium ^{[10,11,12,13,14,15,16,17]}. At present, for the reaction-diffusion predator-prey system, most literatures ^{[18,19,20,21,22,23,24,25]} focus on Turing instability of the constant equilibrium, but there are few research results on the stability of the periodic solutions. Therefore, it is significant to study the Turing pattern formation of Hopf bifurcating periodic solutions for the cross-diffusion population model with prey refuge and the Holling Ⅲ functional response.

In 2015, Yang et al. ^[9] studied a diffusive prey-predator system in Holling type Ⅲ with a prey refuge:

Here, $u, v$ indicates the quantity of prey and predator respectively; $\alpha, \beta, a, r, c, k$ are all positive; $a$ is the intrinsic growth rate of the prey; ${a}/{r}$ represents the maximum carrying capacity of the environment on the prey; $c$ is the mortality rate of the predator; $k$ represents the conversion rate after the predator eating the prey; $m\in \left[0, 1 \right)$ indicates the refuge coefficient, i.e., the proportion of the protected prey. Only $(1-m)u$ can be caught by the predator. In the real world, the mobility of each species is affected not only by itself but also by the density of other species. Therefore, on the basis of (1.1), we introduce the cross-diffusion terms and establish the population model as follows:

where $\Omega = (0, l\pi)$ is a bounded domain with smooth boundary $\partial \Omega$ in ${{\mathbb{R}}^{n}}$ and ${{D}_{11}}, {{D}_{22}}$ and ${{D}_{12}}, {{D}_{21}}$ are the self-diffusivity and cross-diffusivity of $u$ and $v$. We assume that the diffusion coefficients satisfy ${{D}_{11}}{{D}_{22}}-{{D}_{12}}{{D}_{21}} > 0$.

The organizational structure of the rest is as follows: In section two, we study the stability of Hopf bifurcating periodic solutions for the ordinary differential population model and derive the first derivative formula of the periodic function for the corresponding perturbed model. In section three, we give the conditions of Turing patterns occurring at Hopf bifurcating periodic solutions in the reaction-diffusion population system. In section four, we give a brief conclusion. Finally, the relevant conclusions are verified by numerical simulations.

2.   Dynamics of the zero-dimensional population model

In order to research conveniently, we nondimensionalize model (1.2). Let $\hat{u} = \frac{u}{\beta }, \hat{v} = \frac{v}{k\beta }, \hat{t} = at$, and we still replace $\hat{u}, \hat{v}, \hat{t}$ with $u, v, t$, then model (1.2) becomes

where, ${{d}_{11}} = \frac{{{D}_{11}}}{a}, {{d}_{12}} = \frac{{{D}_{12}}}{a}, {{d}_{21}} = \frac{{{D}_{21}}}{a}, {{d}_{22}} = \frac{{{D}_{22}}}{a}, \theta = \frac{c}{a}$ and $p = \frac{r\beta }{a}, s = \frac{k\alpha }{a}$.

2.1.   Stability of periodic solutions of the ordinary differential population model

The ordinary differential equations corresponding to the reaction-diffusion population model (2.1) are

By calculation, four equilibria of model (2.2) are ${{P}_{0}} = (0, 0), {{P}_{1}} = (1/p, 0), {{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right), {{P}_{-}} = \left({{u}_{-}}, {{v}_{-}} \right)$ with

Clearly, the equilibrium ${{P}_{-}} = \left({{u}_{-}}, {{v}_{-}} \right)$ has no biological significance, so we do not study its dynamic behavior. Let's make the following assumptions:

${\bf (A_1)}\; \; \; s > \theta, 0\le \kappa < \frac{1}{p}$;

${\bf (A_2)}\; \; \; s < 2\theta, \frac{2\theta -s}{2\theta p} < \kappa < \frac{1}{p}$;

${\bf (A_3)}\; \; \; s\ge 2\theta, \sqrt{\frac{\theta }{s-\theta }} < \kappa < \frac{1}{p}$;

${\bf (A_4)}\; \; \; \theta < s < 2\theta, \sqrt{\frac{\theta }{s-\theta }} < \kappa < \frac{2\theta -s}{2\theta p}$.

Theorem 2.1. Let ${{\kappa }_{0}} = \frac{2\theta -s}{2\theta p}$ and assume that ${\bf (A_1)}$ satisfies. The following results are true for model (2.2).

(1) If ${\bf (A_2)}$ $(or\; {\bf (A_3)})$ holds, then the positive equilibrium ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$ is locally asymptotically stable. If ${\bf (A_4)}$ holds, then the positive equilibrium ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$ is unstable.

(2) If ${\bf (A_3)}$ holds, the positive equilibrium ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$ is locally asymptotically stable for $\kappa \in \left({{\kappa }_{0}}, \frac{1}{p} \right)$, while unstable for $\kappa \in \left(\sqrt{\frac{\theta }{s-\theta }}, {{\kappa }_{0}} \right)$. When $\kappa = {{\kappa }_{0}}$, the model undergoes a supercritical Hopf bifurcation at ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$, a family of periodic solutions $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$ bifurcate from ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$ and the bifurcating periodic solutions are stable.

Proof. If ${\bf (A_1)}$ holds, then ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$ is a unique positive equilibrium of (2.2). Setting the Jacobi matrix of (2.2) at $\left(\kappa, {{v}_{\kappa }} \right)$ is

where, $a(\kappa) = \frac{2\theta }{s}\left(1-p\kappa \right)-1, b(\kappa) = -\theta$ and $c(\kappa) = \frac{2(s-\theta)}{s}\left(1-p\kappa \right)$. The characteristic equation of $J\left(\kappa \right)$ is

with

then the roots of Eq (2.3) are

If ${\bf (A_2)}\; (or\; {\bf (A_3)})$ satisfies, then all the eigenvalues of $J\left(\kappa\right)$ have strictly negative real parts according to the stability theory, and ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$ is locally asymptotically stable. If ${\bf (A_4)}$ is true, then all the eigenvalues of $J\left(\kappa\right)$ have positive real parts, hence, ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$ is unstable. For an arbitrary $\kappa \in \left(\sqrt{\frac{\theta }{s-\theta }}, {{\kappa }_{0}} \right)$, model (2.2) is unstable at ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$, and for an arbitrary $\kappa \in \left({{\kappa }_{0}}, \frac{1}{p} \right)$, ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$ (2.2) is locally asymptotically stable. When $\kappa = {{\kappa }_{0}}$, $J\left({{\kappa }_{0}} \right)$ has a pair of pure imaginary roots $\lambda = \pm i{{\omega }_{0}}$ with ${{\omega }_{0}} = {{\left(s-\theta \right)}^{\frac{1}{2}}}$. Let $\text{ }\lambda \left(\kappa \right) = \beta \left(\kappa \right)\pm i\omega \left(\kappa \right)$ be the roots of Eq (2.3) near $\kappa = {{\kappa }_{0}}$, then we have

According to the Poincaré-Andronov-Hopf bifurcation theorem, system (2.1) undergoes Hopf bifurcation at $\kappa = {{\kappa }_{0}}$. Let the eigenvectors of $J\left({{\kappa }_{0}} \right)$ and ${{J}^{*}}\left({{\kappa }_{0}} \right)$ corresponding to the eigenvalues $i{{\omega }_{0}}$ and $-i{{\omega }_{0}}$ be $q = {{\left(1, {{b}_{0}} \right)}^{T}}, {{q}^{*}} = {{\left(a_{0}^{*}, b_{0}^{*} \right)}^{T}}$, satisfying $< {{q}^{*}}, q > = 1$ and $< {{q}^{*}}, \bar{q} > = 0$, where ${{b}_{0}} = -\frac{{{\omega }_{0}}}{\theta }i, a_{0}^{*} = \frac{1}{2l\pi }$, $b_{0}^{*} = -\frac{\theta }{2l\pi {{\omega }_{0}}}$. Denote

by ^[26], and we give the expression of the cubic coefficient ${{c}_{1}}({{\kappa }_{0}})$ in normal form. Calculating ${{Q}_{qq}}$, ${{Q}_{q\bar{q}}}$ and ${{C}_{qq\bar{q}}}$,

with

as well as

Then, we can obtain

so

Its real and imaginary parts are

and

If $\operatorname{Re}\left({{c}_{1}}\left({{\kappa }_{0}} \right) \right) < 0\left(>0 \right)$, then the Hopf bifurcation is backward (forward) and the bifurcating periodic solutions $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$ are stable (unstable). □

2.2.   Dynamics of the perturbed population model

In this subsection, for the perturbed population model, we derive the first derivative formula of the periodic function about the perturbation coefficients. On the basis of model (2.1), we introduce the perturbation term $\tau$ and coefficients $\left(\begin{matrix} {{k}_{11}} & {{k}_{12}} \\ {{k}_{21}} & {{k}_{22}} \\ \end{matrix} \right)$. The corresponding perturbed population model is

where $\tau$ is sufficiently small such that $\left(\begin{matrix} 1+\tau {{k}_{11}} & \tau {{k}_{12}} \\ \tau {{k}_{21}} & 1+\tau {{k}_{22}} \\ \end{matrix} \right)$ is reversible, then (2.7) can be reduced to

where

At ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$, the Jacobian matrix of (2.8) is

where,

Let the characteristic equation corresponding to $J(\kappa, \tau)$ be

where

When $\kappa \to {{\kappa }_{\tau }}$, let $\bar{\beta }({{\kappa }_{\tau }})\pm i\bar{\omega }({{\kappa }_{\tau }})$ be the roots of the characteristic Eq (2.11), then

Lemma 2.1. (See ^[26]) When $\kappa \to {{\kappa }_{0}}$, the population model (2.2) has a stable periodic solution $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$ bifurcating from ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$ and $T$ is the minimum positive period of $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$. Then there is a positive number ${{\tau }_{1}}$ such that for any $\tau \in \left(-{{\tau }_{1}}, {{\tau }_{1}} \right)$, the perturbed population model (2.7) has a periodic solution $\left({{u}^{T}}(t, \tau), {{v}^{T}}(t, \tau) \right)$ depending on if $\tau$, $T\left(\tau \right)$ is the minimum positive periodic function. When $\tau \to 0$, $\left({{u}^{T}}(t, \tau), {{v}^{T}}(t, \tau) \right)\to \left({{u}^{T}}(t), {{v}^{T}}(t) \right)$ and $T\left(\tau \right)\to T$, then

$\operatorname{Re}\left({{c}_{1}}\left({{\kappa }_{\tau }} \right) \right)$ and $\operatorname{Im}\left({{c}_{1}}\left({{\kappa }_{\tau }} \right) \right)$ are the real and imaginary parts of ${{c}_{1}}\left({{\kappa }_{\tau }} \right)$, and $\bar{\beta }\left({{\kappa }_{\tau }} \right)$ and $\bar{\omega }\left({{\kappa }_{\tau }} \right)$ are defined by (2.13).

Theorem 2.2. When $\kappa \to {{\kappa }_{0}}$ for the perturbed population model (2.7), the first-order derivative formula of the periodic function, with respect to the perturbation coefficients, is

where $b({{\kappa }_{0}}) = -\theta, c({{\kappa }_{0}}) = \frac{s-\theta }{\theta }, D({{\kappa }_{0}}) = s-\theta$. $\operatorname{Re}\left({{c}_{1}}\left({{\kappa }_{0}} \right) \right)$ and $\operatorname{Im}\left({{c}_{1}}\left({{\kappa }_{0}} \right) \right)$ are defined in (2.5) and (2.6).

Proof. By Lemma 2.1, differentiating the periodic function $T\left(\tau \right)$, we have

If $\kappa \to {{\kappa }_{\tau }}$, then $O\left(\kappa -{{\kappa }_{\tau }} \right)\to 0$, and setting $\tau = 0$, then $\bar{\omega }\left({{\kappa }_{0}} \right) = \omega ({{\kappa }_{0}}) = \sqrt{D({{\kappa }_{0}})}$.

We first compute ${{\left. \frac{d{{\kappa }_{\tau }}}{d\tau } \right|}_{\tau = 0}}$. At $\kappa = {{\kappa }_{\tau }}$, by the expression of $H(\kappa, \tau)$ defined in (2.12), we can gain

Differentiating (2.14) with respect to $\tau$, we obtain

and setting $\tau = 0$, we have

with

Second, we calculate ${\bar{\omega }}'\left({{\kappa }_{0}} \right)$. When $\kappa \to {{\kappa }_{\tau }}$, we derive

thereby,

Since $H\left({{\kappa }_{\tau }}, \tau \right) = 0$ and ${{\partial }_{\kappa }}D\left({{\kappa }_{\tau }}, \tau \right) = \frac{1}{K(\tau)}{D}'\left({{\kappa }_{\tau }} \right)$, we have

At last, we calculate ${{\left. \frac{d}{d\tau }\left(\bar{\omega }\left({{\kappa }_{\tau }} \right) \right) \right|}_{\tau = 0}}$. By $\bar{\omega }\left({{\kappa }_{\tau }} \right) = \sqrt{D\left({{\kappa }_{\tau }}, \tau \right)}$, we can get

According to $D\left({{\kappa }_{\tau }}, \tau \right) = \frac{D\left({{\kappa }_{\tau }} \right)}{K(\tau)}$, we have

Setting $\tau = 0$, we can obtain

Therefore, from (2.16) and (2.20), we have

By (2.18) and (2.21), we obtain

Again, by (2.16), (2.17) and (2.22), we can derive

□

3.   Turing patterns of periodic solutions for the reaction-diffusion population model

With respect to the population model (1.2) and according to the theory expounded in ^[27], we study the mathematical mechanisms of Turing patterns occurring at the stable periodic solution $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$. By the first derivative formula of the periodic function of the perturbed population model (2.7), we give the following theorem.

Theorem 3.1. If hypothesis ${\bf (A_4)}$ and $\operatorname{Re}\left({{c}_{1}}\left({{\kappa }_{0}} \right) \right) < 0$ hold, when $\kappa \to {{\kappa }_{0}}$, the stable spatially homogeneous Hopf bifurcating periodic solution bifurcates $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$ from ${{P}_{+}} = \left(\kappa, {{v}_{\kappa }} \right)$. If the domain $\Omega$ is large enough and

then the following conclusions are true:

(1) The reaction-diffusion population model (1.2) produces Turing patterns at the periodic solution $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$;

(2) If $\operatorname{Im}\left({{c}_{1}}\left({{\kappa }_{0}} \right) \right) < 0\left(>0 \right)$, then when ${{k}_{12}} > {{M}_{1}}\left({{k}_{21}} > {{M}_{2}} \right)$, the reaction-diffusion population model (1.2) produces Turing patterns. That is, Turing patterns occuring at the periodic solution are determined by the cross-diffusion coefficients ${{k}_{12}}\left({{k}_{21}} \right)$, where

$\operatorname{Re}\left({{c}_{1}}\left({{\kappa }_{0}} \right) \right)$ and $\operatorname{Im}\left({{c}_{1}}\left({{\kappa }_{0}} \right) \right)$ from (2.5) and (2.6):

Proof. Let the linearized vector form of the population model (2.1) at $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$ be

where,

is the Jacobian matrix of model (2.1) at $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$. $D: = \left(\begin{array}{*{35}{l}} {{d}_{11}} & {{d}_{12}} \\ {{d}_{21}} & {{d}_{22}} \\ \end{array} \right)$, $\Delta$ is the Laplace operator. Let ${{\alpha }_{n}}$ and ${{\eta }_{n}}\left(x \right)$ be the eigenvalues and eigenfunctions of $-\Delta$ in region $\Omega$, respectively, and ${{(\phi, \varphi)}^{T}} = {{(h(t), g(t))}^{T}}\underset{n = 0}{\overset{\infty }{\mathop \sum }}\, {{k}_{n}}{{\eta }_{n}}\left(x \right)$. For the sake of convenience, we set $\varsigma : = {{\alpha }_{n}}\ge 0, n\in {{\mathbb{N}}_{0}}: = \left\{ 0 \right\}\bigcup \mathbb{N}$, then

If $D = \bf{0}$, then Eq (3.2) can be reduced to

Setting $\rho (t)$ as the fundamental solution matrix of Eq (3.3), it satisfies $\rho (0) = {{I}_{2}}$. Let ${{\lambda }_{i}}, i = 1, 2$ be the eigenvalues of $\rho (T)$, the corresponding eigenfunctions are ${{\left({{\xi }_{i}}, {{\eta }_{i}} \right)}^{T}}, i = 1, 2$, i.e.,

where ${{\lambda }_{1}}$ and ${{\lambda }_{2}}$ are Floquet multipliers. Define

clearly,

Differentiating with respect to $t$ in (2.2), we can obtain

then ${{\lambda }_{1}} = 1$ is the eigenvalue of $\rho (T)$ and the eigenvector is ${{\left({{\phi }_{1}}(t), {{\psi }_{1}}(t) \right)}^{T}} = {{\left({{\left. \frac{d{{u}^{T}}(t)}{dt} \right|}_{t = 0}}, {{\left. \frac{d{{v}^{T}}(t)}{dt} \right|}_{t = 0}} \right)}^{T}}$. Since $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$ is stable, $\left| {{\lambda }_{i}} \right| < 1$. Let $\rho (t, \varsigma)$ be the fundamental solution matrix of Eq (3.2), then we have

and $\rho (t, 0) = \rho (t)$. By the implicit function theorem, there is ${{\varsigma }_{1}} > 0$, $\varsigma \in \left(-{{\varsigma }_{1}}, {{\varsigma }_{1}} \right)$ and continuous differentiable functions ${{\delta }_{i}}(\varsigma), {{\xi }_{i}}(\varsigma), {{\eta }_{i}}(\varsigma)$, such that

where ${{\delta }_{1}}(\varsigma)$ and ${{\delta }_{2}}(\varsigma)$ are Floquet multipliers. Make the following definition

by $\rho (0, \varsigma) = I$, we have

From (3.4) and (3.6), we can gain

and especially

Taking $i = 1$, by (3.5), we know

Hence, we can derive

Differentiating the above equation with respect to $\varsigma$ and setting $\varsigma = 0$, we obtain

where, ${{\phi }_{1\varsigma }}: = {{\partial }_{\varsigma }}{{\phi }_{1}}, {{\psi }_{1\varsigma }}: = {{\partial }_{\varsigma }}{{\psi }_{1}}$. On the other hand, from (3.4) and (3.5), we can get

Differentiating with respect to $\varsigma$, we have

Let $\varsigma = 0$ by (3.6) and ${{\delta }_{1}}(0) = {{\lambda }_{1}} = 1$, and we can derive

According to Lemma 2.1, $\left({{u}^{T}}(t, \tau), {{v}^{T}}(t, \tau) \right)$ is the periodic solution of the perturbed population model (2.7), i.e.,

Differentiating with respect to $\tau$ and letting $\tau = 0$, we have

where ${{\partial }_{t}}{{u}^{T}}(t, 0) = {{\phi }_{1}}(t), {{\partial }_{t}}{{v}^{T}}(t, 0) = {{\psi }_{1}}(t)$. Since $T\left(\tau \right)$ is the minimum positive periodic solution of $\left({{u}^{T}}(t, \tau), {{v}^{T}}(t, \tau) \right)$, we have

Differentiating with respect to $\tau$ and letting $\tau = 0, t = 0$, we can gain

where ${{u}^{T}}(t, 0) = {{u}^{T}}(t), {{v}^{T}}(t, 0) = {{v}^{T}}(t), T(0) = T$. Define

and by (3.7)–(3.10), we get

Let $Z(t) = \mathfrak{A}(t){{\left({{Z}_{1}}, {{Z}_{2}} \right)}^{T}}$ be the general solution of (3.11), where any vector ${{\left({{Z}_{1}}, {{Z}_{2}} \right)}^{T}}\in {{\mathbb{R}}^{2}}$. Since ${{\left({{\phi }_{1}}(0), {{\psi }_{1}}(0) \right)}^{T}}$ and ${{\left({{\phi }_{2}}(0), {{\psi }_{2}}(0) \right)}^{T}}$ are linearly independent, there exits constants ${{p}_{1}}$ and ${{p}_{2}}$ such that

Substituting (3.13) into (3.12), we get ${{{\delta }'}_{1}}(0)+{T}'(0) = 0$. According to Theorem 2.2, if ${T}'(0) < 0$, then ${{{\delta }'}_{1}}(0) > 0$. Assuming that $\Omega$ is sufficiently large, then there is at least one eigenvalue ${{\alpha }_{n}}$ of $-\Delta$ so that ${{\delta }_{1}}(\varsigma) = {{\delta }_{1}}\left({{\alpha }_{n}} \right) > 1$. Therefore, the population model (1.2) appears to have Turing patterns at $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$. When ${T}'(0) < 0$ by Theorem 2.2, we have

Since ${\bf (A_3)}$ is true, we can obtain $b({{\kappa }_{0}}) = -\theta < 0, c({{\kappa }_{0}}) = \frac{s-\theta }{\theta } > 0$. If $\operatorname{Re}\left({{c}_{1}}\left({{\kappa }_{0}} \right) \right) < 0$, then when $\operatorname{Im}\left({{c}_{1}}({{\kappa }_{0}}) \right) < 0$,

From (3.14), we gain

When the cross-diffusion coefficient ${{d}_{12}} > {{M}_{1}}$, the cross-diffusion population model (1.2) generates Turing patterns at the periodic solution $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$. Similarly, if $\operatorname{Im}\left({{c}_{1}}({{\kappa }_{0}}) \right) > 0$, then

so

When the cross-diffusion coefficient ${{d}_{21}} > {{M}_{2}}$, the cross-diffusion population model (1.2) produces Turing patterns at the periodic solution $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$. □

4.   Numerical simulations

We shall conduct numerical simulations in three cases to verify the relevant conclusions: The diffusive population model forms Turing patterns at the periodic solutions. Fix the parameters in model (2.1):

then $\left(\kappa, {{v}_{\kappa }} \right) = \left(7.5, 46.3 \right)$ is a unique positive equilibrium. By calculation, ${{\kappa }_{0}} = 7.505$. According to Theorem 2.1, when $\kappa \to {{\kappa }_{0}}$, $b({{\kappa }_{0}}) = -0.09, c({{\kappa }_{0}}) = \frac{1}{9}, D({{\kappa }_{0}}) = 0.01$, $\operatorname{Re}{{c}_{1}}\left({{\kappa }_{0}} \right) = -3.1316\times {{10}^{-3}} < 0$ and $\operatorname{Im}{{c}_{1}}\left({{\kappa }_{0}} \right) = 4.3667\times {{10}^{-3}}$, simultaneously, hypothesis (A4) is true. Take the initial values as ${{u}_{0}} = 8+0.1\cos \left(x \right), {{v}_{0}} = 47+0.1\cos \left(x \right)$.

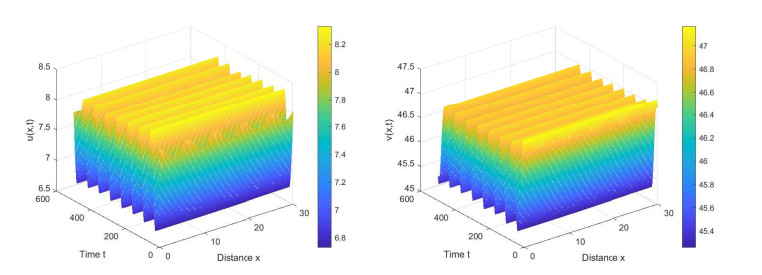
(1) If ${{d}_{11}} = 1, {{d}_{22}} = 1, {{d}_{12}} = {{d}_{21}} = 0$, then $\sqrt{D({{\kappa }_{0}})}{{d}_{11}}+\sqrt{D({{\kappa }_{0}})}{{d}_{22}} = 0.2 > 0$. By Theorem 3.1, in model (1.2), Turing patterns do not appear at $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$, namely, the same self-diffusion rates do not destroy the stability of the periodic solution(See ^[28]). If ${{d}_{11}}\ne {{d}_{22}}, {{d}_{11}} > 0, {{d}_{22}} > 0$ and ${{d}_{12}} = {{d}_{21}} = 0$, then $\sqrt{D({{\kappa }_{0}})}{{d}_{11}}+\sqrt{D({{\kappa }_{0}})}{{d}_{22}} > 0$ and the periodic solution of diffusion model (1.2) is stable (Figure 1).

(2) If ${{d}_{11}} = 0.2, {{d}_{22}} = 0.5, {{d}_{12}} = 0.05$, then ${{M}_{2}} = 0.6195$. Select ${{d}_{21}} = 0.7$ by calculating ${T}'(0) < 0$. According to Theorem 3.1, when ${{d}_{21}} > {{M}_{2}} = 0.6195$, cross-diffusion induces system (1.2) to produce Turing patterns at $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$ (Figure 2).

(3) If ${{d}_{11}} = 1, {{d}_{22}} = 1, {{d}_{12}} = 0.02$, then ${{M}_{2}} = 1.6184$. We choose ${{d}_{21}} = 1.7$, through computation and ${T}'(0) < 0$. According to Theorem 3.1, when ${{d}_{21}} > {{M}_{2}}$, cross-diffusion induces system (1.2) to produce Turing patterns at $\left({{u}^{T}}(t), {{v}^{T}}(t) \right)$ (Figure 3).

5.   Conclusions

In this paper, we established a cross-diffusion population model with prey refuge and Holling Ⅲ functional response, and studied the mathematical mechanisms of Turing patterns generated by the diffusion-driven instability of the periodic solutions. The results show that when $\operatorname{Im}\left({{c}_{1}}\left({{\kappa }_{0}} \right) \right) < 0\left(>0 \right)$, the symbol of the diffusivity expression ${T}'(0)$ is actually determined by the cross-diffusion coefficient ${{d}_{21}}\left({{d}_{12}} \right)$. That is, when ${{d}_{21}} > {{M}_{2}}\left({{d}_{12}} > {{M}_{1}} \right)$ and the region $\Omega$ is sufficiently large, ${T}'(0) < 0$ and model (1.2) generate Turing patterns at the periodic solutions. Our research more accurately determined the range of cross-diffusion coefficients of Turing patterns occurring at the periodic solutions. This provided a new idea for model (1.2) to generate Turing instability at the periodic solutions.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that they have no competing interests.