Pattern dynamics and Turing instability induced by self-super-cross-diffusive predator-prey model via amplitude equations

1.   Introduction

Pattern formation has captivated scholars in recent decades as a way to better understand natural processes, and Turing's key work on reaction-diffusion systems gave rise to the concept of using it with reaction-diffusion systems ^[36]. Turing instability causes a variety of spatial structures to arise, including spots, spirals, squares, hexagons, combinations of spots and stripes, and so on ^[2,3,14,28]. Non-Turing patterns, such as traveling wave, periodic traveling wave, spatiotemporal chaos, and so on, can be detected using diffusion concepts ^[9,25]. Many of these patterns in the spatio-temporal expansion of interactive population systems, which include competing species and predator-prey systems, were discovered using reaction-diffusion equations ^[2,3,25].

Cross-diffusion is vital in the emergence of patterns in the disciplines of chemistry, biology, and ecology. In ecology, the concentration gradient of one species influences the flow of another; this phenomena is known as cross-diffusion in the perspective of the reaction-diffusion model, as detailed in ^[30,37]. Positive cross-diffusion distributes the respective components, whilst negative cross-diffusion causes them to accumulate locally.The influence of cross-diffusion on excitatory chemical systems has already been discussed extensively for Chemical self-replication according to the Templetor model ^[7], the chlorite-iodide-malonic acid-starch autocatalytic reaction system ^[35], the Fitzhugh-Nagumo type reaction kinetics ^[40], and Stokes equations ^[5]. Vanag and Epstein ^[37] investigated the effects of cross-diffusion in cognitive and various chemical systems in particular. Cross-diffusion terms can be used to characterize prey's tendency to avoid predators and also the predator population's weakening in the presence of high-density prey regions ^[18,19,22]. The predator-prey pursuit-evasion technique is another cross-diffusion paradigm wherein waves propagate via taxis described by nonlinear cross-diffusion parameters.

Super-diffusion may be seen all over the place in nature. The limiting output of L$\acute{e}$vyflight is represented at the molecular level, with the jumping length dispersion containing infinite intervals during the relative motion of the individual particles. The particle conducts large hops at this moment. Surface diffusion, turbulence, animal and plasma motion, and other processes can all be affected by these phenomena. They might also have a big influence on pattern creation. The influence of the super diffusion implications on the several models, like the activator-inhibitor model ^[43], the Fitzhugh-Nagumo model ^[15], the Lengyel-Epstein model ^[23], and the complex fractional-order HIV diffusion model ^[16]] has lately been noted by many investigators. In a predator-prey model ^[24] and a three-species food chain model with harvesting ^[17], only a few outcomes have been reported around super-cross-diffusion. As stated in the introduction, we will investigate the Hopf bifurcation along with the Turing patterns described for the predator-prey system with in the self-super-cross diffusion in this research.

For decades, Turing instability ^[36] has piqued the curiosity of scientists as a frequent obstacle in the development of morphological patterns. In reaction-diffusion systems, mathematical analysis and numerical simulations have given a range of results on pattern formation. Song et al. ^[31] investigated the generation of Turing patterns via the Gierer-Meinhardt model in two spatial dimensions with a saturation term. They obtained the spotting, striping, cohabitation, and labyrinth patterns. The results showed the mechanism of morphogenetic processes in mesenchymal cells that have reached maturity. In both the supercritical and subcritical circumstances, the amplitude equations of the stationary pattern were found in the Turing domain.

Regarding the parameter values close to the Turing bifurcation curve ^[4,9,21], amplitude equation is critical in explaining the behavior of a reaction-diffusion system. The system's homogeneous steady state loses its stability due to tiny amplitude heterogeneous disturbances ^[25]. The system exhibits a critical slowdown at a bifurcation threshold, indicating that it takes a substantial amount of time to switch from a stable steady-state homogeneous condition to an inhomogeneous configuration ^[39].

As a result, multi-scale perturbation analysis may be used for deriving amplitude equations for the studying of the dynamics of active slow modes. The amplitude equations' stability analysis offers information on possible patterns that would occur near the boundary of Turing bifurcation when the amplitude equations are extracted out from the reaction-diffusion equations original system. This technique may also be used to learn about pattern selection and stability around the onset ^[41]. Zemskov et al. ^[40] investigated pattern formation in the Oregonator and Brusselator models involving cross-diffusion via WNA. Topaz and Catla ^[33] and Chen ^[6] employed this approach to explore patterns created around a Turing-Hopf bifurcation point, which occurs whenever the system seems unstable because both temporal and spatial disturbances are considered. The amplitude equations were established to analyze the production of spatial patterns utilizing WNA, such as rhomboid, squares and rolls, in an epithelial model theory for insect, mammal, and fish skin pattern generation. The approach was further modified for the spatial and temporal expansion of interactive population models, including the cross-diffusion augmented competitive model ^[12], the hyperbolic mortality model ^[42], Beddington-DeAngelis functional responsiveness in the predator-prey model ^[41], and also the herd behavior model ^[39].

Numerical simulations might be used to better understand the influence of diffusion, as a consequence of which represent intriguing phenomena like stationary, pulses, fronts, and periodic patterns, among others ^[7]. Cross-diffusion and self-diffusion are put into consideration in interactive population modeling including prey-predator models and competitive models ^[32], interesting spatiotemporal patterns emerge. Numerical simulations will be used to validate the analytical results.

The following is a breakdown of how this article is structured. The temporal and spatiotemporal predator-prey model will be introduced in the next section. We present the conditions that ensure that the Turing instability arises in Section 3 by examining the local equilibrium points' stability. In Section 4, we use WNA to find the amplitude equations, and in Section 5, we use numerical simulations to test the validity of the analytical findings. Finally, we present conclusions derived from our paper.

2.   The predator-prey model

Differential equations are used in predation theory when it can be assumed that generations overlap and populations fluctuate continuously over time. For this method to be fair, the time scale must be set in accordance with the species being investigated. For the majority of mammals, variation should be represented on an annual basis, but for many planktonic creatures, a daily scale is necessary. In situations when the dynamics of a population cannot be approximated by continuous functions, difference equations may be preferable. The Lotka-Volterra model, from which the idea of predation evolved, contains a number of generally acknowledged flaws. In spite of this, differential equations have remained an essential tool in the following development of the theory, and this method penetrates a significant portion of contemporary ecological thought.

The fundamental model for predator-prey interaction may be expressed using nonlinear coupled ordinary differential equations ^[1,25]. Corresponding to Gause ^[10] for predator–prey interaction subject to nonnegative initial conditions is defined as:

where $\mathbf{U}\equiv \mathbf{U}(t)$ and $\mathbf{V}\equiv \mathbf{V}(t)$ are the density of prey and predator at time $t$, respectively. $\mu$, supposed to be ^[1] constant, is the intrinsic mortality rate of predators and $\mathbf{B}\; (0 < \mathbf{B} < 1)$ is the food conversion efficiency of the predator. Additionally, $g(\mathbf{U})$ is the prey based functional response^[11] and $f(\mathbf{U})$ is the per capita rate to grow the prey (when the predation is absent). In this paper, we assume that $f(\mathbf{U})$ follows logistic growth law and takes the form

where $b$ is the environmental carrying capacity for the prey population and $\mathbf{A}$ is the intrinsic density–independent growth rate. The notion of employing the prey dependent functional response was suggested by Feng and Kang ^[11] and Tian et al. ^[32] that is

where "gamma($\mu$)" indicates the predator's attack rate and $H$ denotes the half-saturating constant. Combining $f(\mathbf{U})$ and $g(\mathbf{U})$, hence the system (2.1) takes the form

with regard to the initial conditions $\mathbf{U}(0), \; \mathbf{V}(0) > 0$ for $(\mathbf{U}, \mathbf{V})\neq(0, 0)$. When $(\mathbf{U}, \mathbf{V}) = (0, 0)$. The system described above has been simplified to $\frac{d\mathbf{U}}{dt} = \frac{d\mathbf{V}}{dt} = 0$.

$\tilde{t} = \mathbf{A} t, \tilde{\mathbf{V}} = \frac{\mu \mathbf{V}}{b\mathbf{A}}$ and $\; \tilde{\mathbf{U}} = \frac{\mathbf{U}}{b}$ is taken for the non–dimensional time, predator and prey population density, respectively. For the sake of simplicity, we drop the over–bars to get the following non–dimensional model

where $\mathbf{C} = \frac{\mathbf{B} \mu}{\mathbf{A}}$, $\mathbf{D} = \frac{\mu}{\mathbf{A}}$, and $h = \frac{H}{b}$ are all positive parameters. The nonnegative solutions of

are the steady state solutions of (2.3). Aside from the general solution $(0, 0)$ (complete extinction), (2.4) yields the predator-free steady state point $(1, 0)$ as well as the coexisting equilibrium point $\mathfrak{L}\bigg(\mathbf{U}^* = \frac{\mathbf{D}h}{\mathbf{C}-\mathbf{D}}, \; \mathbf{V}^* = (1-\mathbf{U}^*)(\mathbf{U}^*+h)\bigg)$ in the first quadrant's interior.

The temporal model (2.3) fits the spatiotemporal model having self-super-cross-diffusion terms. It is necessary to understand how the pattern formation phenomenon takes place in a diffusive model that is anomalous. The unsustainably diffusive operator ^[13,29,38] is expressed by (using the Fourier transform) $(-\Delta)^{\frac{\mu}{2}}$ with the following definition:

When $1 < \mu < 2$, the above operator is known as super-diffusion. The associated random walk's displacement moment develops slower (sub-diffusion) and faster (super-diffusion) than in regular diffusion. For $\mu = 2$, we have the Laplacian operator $\Delta$ as a special form of the above operator. Here, the predator-prey system is investigated on the basis of self-super-cross-diffusion in a bounded domain $\Omega\subset\mathbf{R}^2$, with a smooth boundary $\partial\Omega$, as follows:

$d_1$ is indeed the prey's diffusion coefficient, $d_2$ is a coefficient of the cross diffusion that anticipates the movement of prey species based on predator population ^[19,26,38], and $d_3$ is a coefficient of the cross diffusion in which the predator species movement is influenced by prey population. The unit normal vector along $\partial\Omega$ in outward direction is denoted by $n$. There is no flux via the boundary when the Neumann boundary conditions are homogeneous.

The alternative obtaining of the fractional operator $\nabla^{\mu}$ for $(1 < \mu < 2)$ can be done as follows:

where ${}_{{RL}}{D}_{-\infty, \mathbf{y}}^\mu$ and $\; {}_{{RL}}{D}_{\mathbf{y}, +\infty}^\mu$, , in respective order, as given below:

with $\Gamma (.)$ refers to the Gamma function.

3.   Diffusion driven instability

Turing instability takes place as a stable homogeneous steady-state turns out to be unstable in the presence of tiny amplitude heterogeneous disturbances surrounding it ^[25,36]. With the cross-diffusion term $d_3$, the equilibrium point in (2.5), which itself is stable like a solution of the problem (2.3) in the absence of the cross-diffusion term $d_3$, becomes unstable. Suppose $\mathbf{U}(x, y, t)$ and $\mathbf{V}(x, y, t)$ denote the homogeneous steady states that satisfy these equations for (2.5). Suppose that under temporal perturbation for Turing instability, asymptotically, the homogeneous steady state is stable. This means that the requirements $\mathfrak{j}_{11}\mathfrak{j}_{22}-\mathfrak{j}_{12}\mathfrak{j}_{21} > 0$ and $\mathfrak{j}_{11}+\mathfrak{j}_{22} < 0$ are met. Linear stability analysis for the spatiotemporal model (2.5) at $\mathfrak{L}(\mathbf{U}^*, \mathbf{V}^*)$ is used to identify the constraints of the Turing instability ^[25].

Theorem 3.1. System (2.3) has a single positive equilibrium $\mathfrak{L}(\mathbf{U}^*, \; \mathbf{V}^*)$ if $\mathbf{D}\neq \mathbf{C}$, and $\mathfrak{L}$ is asymptotically locally stable.

Proof. The Jacobian $\mathfrak{J}_0$ of the system (2.3) at the coexisting equilibrium point $\mathfrak{L}(\mathbf{U}^*, \; \mathbf{V}^*)$, is given by

Assume that $h$ is the model's Hopf bifurcation parameter (2.3). By solving

we obtain

The equilibrium point $\mathfrak{L}(\mathbf{U}^*, \; \mathbf{V}^*)$ that co-exists in relation with the parameter $h$ is loses stability by Hopf bifurcation at $h = h_H$ and locally asymptotically stable for $h > h_H$.

We perturb the system (2.3) around $\mathfrak{L}(\mathbf{U}^*, \; \mathbf{V}^*)$ as

The characteristic equation for the growth rate $\lambda$ is as follows, where $\lambda$ refers to the rate of perturbation growth. As a result of the replacement of (3.4) into (2.3), the growth rate's characteristic equation "($\lambda$)" is as follows:

Hence

Both $\mathfrak{j}_{12}\mathfrak{j}_{21}$ and $\mathfrak{j}_{11}$ may be easily verified as negative. As a result, the two roots $\lambda_{1, 2}$ have their own negative real components. The completion of the proof is done accordingly.

In the following, the stability of $\mathfrak{L}(\mathbf{U}^*, \; \mathbf{V}^*)$ is to be examined in system (2.5) with no cross–diffusion term $d_3$, having the following,

Theorem 3.2. Let's say the wave number vector is $\mathbf{ \pmb{\mathsf{ ν}}} = (\nu_1, \nu_2)$, and the wave number is $\nu = |\mathbf{ \pmb{\mathsf{ ν}}}|$. If $\mathbf{D}\neq \mathbf{C}$, then $\mathfrak{L}(\mathbf{U}^*, \; \mathbf{V}^*)$ of system (3.7) is asymptotically and locally stable without the cross-diffusion factor $d_3$.

Proof. The system (3.7) is perturbed about $\mathfrak{L}(\mathbf{U}^*, \; \mathbf{V}^*)$ as follows:

in which $\lambda$ refers to the perturbation growth rate. By the substitution of (3.8) into (3.7), we get

The formulae for $\mathfrak{j}_{11}, \; \mathfrak{j}_{12}, \; \mathfrak{j}_{21}$ and $\mathfrak{j}_{22}$ may be discovered in (3.1). As a result, the characteristic equation becomes

in which

Clearly, $h_\nu$ and $T_\nu$ are both positive. As a result, the two roots $\lambda_{1, 2}$ have their own negative real components. The completion of the proof is done accordingly.

The perturbation all around homogeneous steady state $\mathfrak{L}(\mathbf{U}^*, \; \mathbf{V}^*)$ for system (2.5) as

By the substitution of (3.11) into (2.5), we get

Hence, the characteristic equation is

in which

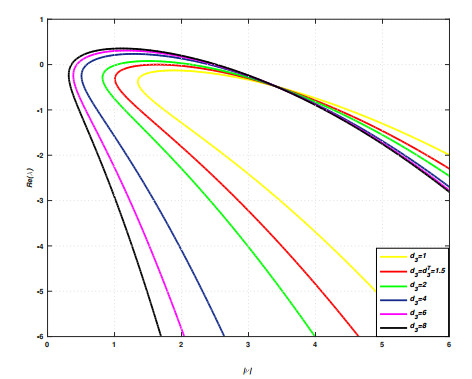
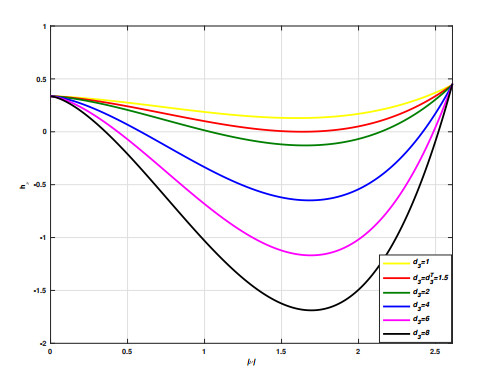
Checking that $T_\nu$ is positive is easy. Regarding $d_3$ as the bifurcation parameter, we investigate the Turing bifurcation threshold for $\nu\equiv \nu_T$ at $d_3 = d_3^T$ such that $h_\nu^T = 0$. The $h_\nu$-derivative is assessed in regard to $\nu^\mu$ at $\nu = \nu_T$, and using $\frac{dh_\nu}{d\nu^\mu}\big|_{\nu = \nu_T} = 0$, one can obtain $\nu_T = \sqrt{\frac{\mu}{2+\mu} \bigg(\frac{\mathfrak{j}_{11}d_3\mathbf{U}^*-\mathfrak{j}_{12}d_3\mathbf{V}^*-\mathfrak{j}_{21}d_2\mathbf{U}^*}{d_1d_3\mathbf{U}^*}\bigg)}$. Through the substitution of the value of $\nu_T$ in $h_\nu$ it is possible to find the value of $d_3$ such that $h_\nu < 0$ suggesting that the cross–diffusion term $d_3$ alters an equilibrium point's stability in the way presented in Figure 1.

When $\mathfrak{j}_{11}+\mathfrak{j}_{22} < 0$, $\mathfrak{j}_{11}\mathfrak{j}_{22}-\mathfrak{j}_{12}\mathfrak{j}_{21} > 0$ and $d_3 < d_3^T$, the homogeneous steady state $\mathfrak{L}(\mathbf{U}^*, \; \mathbf{V}^*)$ is stable in the presence of spatiotemporal or heterogeneous perturbation. When $\mathfrak{j}_{11}\mathfrak{j}_{22}-\mathfrak{j}_{12}\mathfrak{j}_{21} > 0$, $\mathfrak{j}_{11}+\mathfrak{j}_{22} < 0$ and $d_3 > d_3^T$, the homogeneous steady state $\mathfrak{L}$ becomes unstable.

For the model parameters $\mu = 1.5$, $h = 0.45$, $\mathbf{D} = 0.8$, $d_1 = 0.1$, $d_2 = 0.1$, $\mathbf{C} = 2$ and $d_3^T > d_3 = 1$ the real component of the eigenvalue "$\lambda$" becomes negative (Figure 2). For heterogeneous disturbances, this implies the stability of a homogeneous stable state. When $d_3^T < d_3$ is taken into account, the matching curves (black, pink, blue, green) in Figure 2 show that inside the interval of $|\mathbf{ \pmb{\mathsf{ ν}}}|$, where the system appears unstable to diversified perturbations and creates Turing patterns, the largest real fraction of the eigenvalue is positive. However, we have no way of knowing which Turing patterns were chosen. The stability of various forms of Turing patterns and also structural transformations among them will be interpreted using the amplitude equations of Turing patterns at inception $d_3 = d_3^T$.

4.   Weakly nonlinear analysis

The system's dynamics change very slowly near the Turing bifurcation threshold. The slow modes get implicated in this condition, and the amplitude equations ^[39,40,41] may be used to analyze pattern creation. We create amplitude equations and analyze the stability selection of various patterns by employing multiple-scale perturbation assessment such as labyrinthine, squares, spots, and mixes of stripes and spots. We take into consideration three pairs of active resonant modes $(\mathbf{ \pmb{\mathsf{ ν}}}_j, \; -\mathbf{ \pmb{\mathsf{ ν}}}_j)\; (j = 1, \; 2, \; 3)$ and making angles of $2\pi/3$ with $|\mathbf{ \pmb{\mathsf{ ν}}}_j| = \nu_T$ ^[39,41]. First, by putting the perturbations $\mathbf{a} = \mathbf{U}-\mathbf{U}^*$ and $\mathbf{b} = \mathbf{V}-\mathbf{V}^*$ about $\mathfrak{L}(\mathbf{U}^*, \; \mathbf{V}^*)$, we may construct the linearized version of model (2.5) as follow:

in which $\mathbf{L}$ is the linear operator that is give as

The results of (2.5) can be expanded as follows (at the initiation of Turing instability):

where $\mathbf{X}_j$, $-\mathbf{X}_j$ are the relative amplitudes of the modes $\mathbf{ \pmb{\mathsf{ ν}}}_j$, $-\mathbf{ \pmb{\mathsf{ ν}}}_j$.

We alter the bifurcation parameter $d_3$ with $\mathbf{a}, \; \mathbf{b}, \; t$ as close to the Turing bifurcation threshold as possible by writing

This yields

where

The amplitude, indicated by $\mathbf{X}_j\; (j = 1, 2, 3)$, is treated as a variable which shows slow change with respect to time $\frac{\partial \mathbf{X}_j}{\partial t} = 0$ ^[39,41]. Thus,

To derive the amplitude equations: Substituting (4.4) into (4.1) and collecting the like power coefficients of "$\epsilon$". The linear system at $\mathbf{O}(\epsilon)$ is obtained as follows:

Due to the fact that $(\mathbf{a}_1, \; \mathbf{b}_1)^t$ is the linear combination of the eigenvectors correlating to the eigenvalue $0$, and $\mathbf{L}^T$ is the system's linear operator at the Turing bifurcation threshold. After solving (4.8), one can get

where $\mathbf{N} = \frac{(d_3\nu_T^\mu \mathbf{U}_*)} {\mathfrak{j}_{21}-d_3\nu_T^\mu \mathbf{V}_*}$ and amplitude $\mathbf{Y}_j$ of mode $\exp^{i\nu_j\cdot r}$. At $\mathbf{O}(\epsilon^2)$, we obain

The Fredholm solvability criterion stipulates that to assure the nontrivial solution existence (4.10), on the right side of Eq (4.10), the vector function ought to be orthogonal to the eigenvectors of the zero eigenvalue of $\mathbf{L}^{T+}$ ($\mathbf{L}^{T+}$ stands for adjoint of $\mathbf{L}^T$). The eigenvectors of the operator $\mathbf{L}^{T+}$ are $\left(\begin{array}{c} 1 \\ \mathbf{M} \\ \end{array} \right)\exp^{i\nu_j\cdot r}+c.c.\; (j = 1, 2, 3),$ in which $\mathbf{M} = \frac{\mathfrak{j}_{11}-d_1\nu_T^2-d_2\nu_T^\mu \mathbf{V}^*}{d_3^T\nu_T^\mu -\mathfrak{j}_{12}}$. The condition of orthogonality is $(1, \mathbf{M})\left(\begin{array}{c} F_x^j \\ F_y^j \\ \end{array} \right) = 0,$ in which $F_x^j$ and $F_y^j$ denote the coefficients of $\exp^{i\nu_j\cdot r}$ term, in respective order. For example, by the substitution of (4.9) into (4.10) and equation of the coefficient of $\exp^{i\nu_1\cdot r}$, we get

where

We obtain the following result when we use the solvability criterion.

Taking the coefficients of $\exp^{i\nu_2\cdot r}$ and $\exp^{i\nu_3\cdot r}$, we obtain the following relationships.

Equation (4.10) has the following solution:

The substitution of Eq (4.15) into Eq (4.10) and collection of the coefficients of $\exp^{2i\nu_j\cdot r}$ gives

that provides

The coefficients of components of (4.15) involving $\exp^0$, $\exp^{i\nu_m\cdot r}$ and $\exp^{i(\nu_1-\nu_2)\cdot r}$ are calculated similarly and given as

The coefficients of the components of (4.15) corresponding to $\exp^{i(\nu_2-\nu_3)\cdot r}$ and $\exp^{i(\nu_3-\nu_1)\cdot r}$ are obtained by permuting the suffixes. At $\mathbf{O}(\epsilon^3)$, we obtain

in which

The coefficients for $\exp^{i\nu_1\cdot r}$ can be found by collecting them from (4.22).

In the case of $\mathbf{O}(\epsilon^2)$, the Fredholm solvability criterion is used, we have $(1, \mathbf{M})\left(\begin{array}{c} G_x^j \\ G_y^j \\ \end{array} \right) = 0$. In simplified form, it gives

in which

The permutation of $\mathbf{Y}$'s subscript can be used to determine the other two equations. $\mathbf{X}_m = \epsilon \mathbf{Y}_m+\epsilon^2 b_m+O(\epsilon^3)$ can be used to extend the amplitude $\mathbf{X}_m\; (m = 1, 2, 3)$.

We can correlate the amplitude equation to $\mathbf{X}_1$ by using $\mathbf{X}_m$ expression and (4.7).

in which

The other two equations may be obtained in a similar way by permuting the subscript of $\mathbf{X}$:

Stability analysis of amplitude equation

There are two parts to the amplitude Eq (4.25): a mode $\mathfrak{f}_m = |\mathbf{X}_m|$ and a phase $\Theta m$. By separating the imaginary and real components and putting $\mathbf{X}_m = \mathfrak{f}_m \exp^{i\Theta_m}$ into (4.25) the four real-valued differential equations that proceed are generated.

in which $\Theta_1+\Theta_2+\Theta_3 = \Theta$.

Properties

The solution of the dynamical system (4.28) is found as follows:

$(1)$ $\mathfrak{f}_1 = \mathfrak{f}_2 = \mathfrak{f}_3 = 0$ is the stationary state, which is stable for $\eta < \eta_2 = 0$. As a consequence, for $\eta > \eta_2$ we get a spatial pattern and for $\eta < \eta_2$ we get a stable homogeneous steady state.

$(2)$ The striped pattern produced by $\mathfrak{f}_1 = \sqrt{\frac{\eta}{\mathbf{G}_1}}\neq0$, $\mathfrak{f}_2 = \mathfrak{f}_3 = 0$ is stable for $\eta > \eta_3 = \mathbf{E}_2^2\frac{\mathbf{G}_1}{(\mathbf{G}_2-\mathbf{G}_1)^2}$ and instability occurs for $\eta < \eta_3$.

$(3)$ The mixed state is given by $\mathfrak{f}_1 = \frac{|\mathbf{E}_2|}{\mathbf{G}_1-\mathbf{G}_2}$, $\mathfrak{f}_2 = \mathfrak{f}_3 = \sqrt{\frac{\eta+\mathbf{G}_1\mathfrak{f}1^2}{(\mathbf{G}_1+\mathbf{G}_2)}}$, is always unstable.

$(4)$ Hexagon pattern represented by $\mathfrak{f}_1 = \mathfrak{f}_2 = \mathfrak{f}_3 = \frac{|\mathbf{E}_2|\pm\sqrt{\mathbf{E}_2^2+4(\mathbf{G}_1+2\mathbf{G}_2)\eta}}{2(\mathbf{G}_1+2\mathbf{G}_2)}$ exists when $\eta > \eta_1 = -\frac{\mathbf{E}_2^2}{4(\mathbf{G}_1+2\mathbf{G}_2)}$. The solution $\rho = \frac{|\mathbf{E}_2|+\sqrt{\mathbf{E}_2^2+4(\mathbf{G}_1+2\mathbf{G}_2)\eta}}{2(\mathbf{G}_1+2\mathbf{G}_2)}$ is stable for $\eta < \eta_4 = \mathbf{E}_2^2\frac{2\mathbf{G}_1+\mathbf{G}_2}{(\mathbf{G}_2-\mathbf{G}_1)^2}$, otherwise unstable.

Therefore, the amplitude equations show how distinct patterns emerge when different thresholds of $\eta$ are achieved. At this point, we will look at the numerical simulation results and make a comparison with the underlying theory in Section 4.

5.   Numerical simulation

For the purpose of demonstrating the theoretical analysis, a numerical simulation is presented. To verify our numerical approach with the space fractional reaction-diffusion model, we have used fractional exponential integrator methodology ^[8,20,27,34]. Furthermore, in our simulation, boundary constraints in the spatial domain are imposed to verify that Turing patterns are produced. All the simulations were run at $N = 60$. The numerical graphs were made using the Matlab software. The 2019b version of the Matlab was used for the numerical simulation.

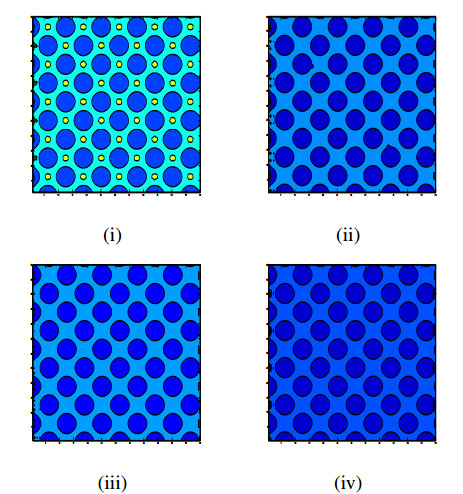
Existence of hexagonal patterns can be seen from (4) where $\mathbf{C} = 3$, $\mathbf{D} = 1$, $h = 0.45$, $\mu = 1.5$, $d_3 = 6$, $d_2 = 1$ and $d_1 = 1$ initially perturbed as $\mathbf{a} = 0.1+0.4\cos(y)\sin(x)$, $\mathbf{b} = 0.5+0.1\cos(y)\sin(x)$ with iterations (ⅰ) $\mathfrak{i}$ = 50, (ⅱ) $\mathfrak{i}$ = 60, (ⅲ) $\mathfrak{i}$ = 70 and (ⅳ) $\mathfrak{i}$ = 80 (see Figure 3).

Existence of big spots can be seen from (4) where $\mathbf{C} = 8$, $\mathbf{D} = 2$, $h = 0.45$, $\mu = 1.5$, $d_3 = 10$, $d_2 = 1$ and $d_1 = 1$ initially perturbed as $\mathbf{a} = 0.1+0.5\cos(y)\cos(x)$, $\mathbf{b} = 0.1+0.5\cos(\frac{y}{2})\sin(\frac{x}{2})$ with iterations (ⅰ) $\mathfrak{i}$ = 60, (ⅱ) $\mathfrak{i}$ = 100, (ⅲ) $\mathfrak{i}$ = 120 and (ⅳ) $\mathfrak{i}$ = 140 (refers to Figure 4).

Existence of small spots can be seen from (4) where $\mathbf{C} = 2$, $\mathbf{D} = 0.8$, $h = 0.45$, $\mu = 1.5$, $d_3 = 4$, $d_2 = 0.1$ and $d_1 = 0.1$ initially perturbed as $\mathbf{a} = 0.5+0.1\cos(y)\cos(x)$, $\mathbf{b} = 0.7+0.1\cos(y)\cos(x)$ with iterations (ⅰ) $\mathfrak{i}$ = 100, (ⅱ) $\mathfrak{i}$ = 110, (ⅲ) $\mathfrak{i}$ = 200 and (ⅳ) $\mathfrak{i}$ = 350 (refers to Figure 5).

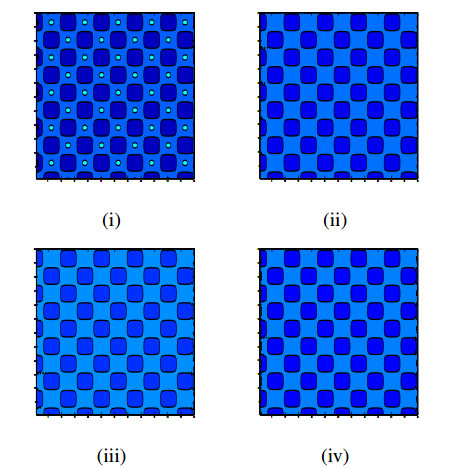
Existence of square patterns can be seen from (4) where $\mathbf{C} = 4$, $\mathbf{D} = 0.5$, $h = 0.45$, $\mu = 1.5$, $d_3 = 10$, $d_2 = 1$ and $d_1 = 1$ initially perturbed as $\mathbf{a} = 0.1+\cos(\frac{y}{2})\cos(\frac{x}{2})$, $\mathbf{b} = 0.1+\cos(\frac{y}{2})\cos(\frac{x}{2})$ with iterations (ⅰ) $\mathfrak{i}$ = 100, (ⅱ) $\mathfrak{i}$ = 110, (ⅲ) $\mathfrak{i}$ = 120 and (ⅳ) $\mathfrak{i}$ = 140 (refers to Figure 6).

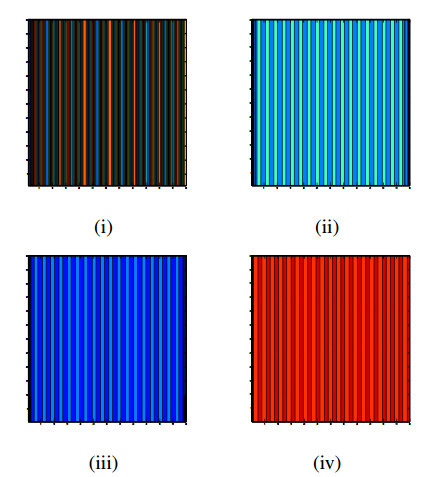
Existence of stripe patterns can be seen from (4) where $\mathbf{C} = 6$, $\mathbf{D} = 2$, $h = 0.45$, $\mu = 1.5$, $d_3 = 2$, $d_2 = 0.1$ and $d_1 = 0.1$ initially perturbed as $\mathbf{a} = 0.1+0.1\sin^2(x)$, $\mathbf{b} = 0.5+0.1\cos^2(x)$ with iterations (ⅰ) $\mathfrak{i}$ = 64, (ⅱ) $\mathfrak{i}$ = 128, (ⅲ) $\mathfrak{i}$ = 256 and (ⅳ) $\mathfrak{i}$ = 512 (refers to Figure 7).

Cross-diffusion plays a crucial role in determining and selecting patterns in the spatio-temporal extension of the model under consideration. In addition to random diffusion (known as self-diffusion) of both species, cross-diffusion components are introduced to account for the influence of the population density of one species on the movement of other species. Due to the effect of cross-diffusion factors, the homogeneous stable state of the self-diffusion model, which is stationary under heterogeneous perturbation, loses its stability and generates diverse patterns, such as big spot, mixture of spots and stripes, and labyrinthine. Cross-diffusion changes the big spot pattern created by the self-diffusion model into a homogeneous steady state or other patterns such as a mixture of big spot and stripes as well as labyrinthine. This clarifies both the stabilizing and destabilizing effects of the nonlinear cross-diffusion factors. In addition, when the self-diffusion coefficients are assumed to be equal, the homogeneous stable state of the self-diffusion model loses its stability and creates spatial patterns consisting of small spots, followed by a mixture of small spots and stripes, and finally labyrinthine. As a result of cross-diffusion, the prey and predator populations display an inverse connection, which is another significant finding in this instance.

6.   Conclusions

Using amplitude equations, the impacts of super-cross diffusion on a system containing a self-diffusive term have been explored through our study. Until linear or nonlinear super-cross-diffusion terms are utilized in the systems, the self-diffusion approach does not yield significant Turing pattern whenever the prey dependent functional responses are addressed. By using the stability analysis, several criteria have been specified to assure the system's Turing instability. Under such conditions, the system will accommodate the Turing instabilities while producing the related specified configurations. Multiple-scale perturbation analysis has also been done all around Turing bifurcation boundary to obtain the amplitude equations used to analyze the stability of several Turing patterns. These findings are mathematically verified and appear to be in good order. Hexagons, huge spots, tiny spots, squares, and stripes are all produced with the inclusion of self and super-cross-diffusion terms.

Acknowledgments

This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation, (grant number~B05F650018).

Conflict of interest

The authors declare that they have no conflicts of interest.