Distance measures of picture fuzzy sets and interval-valued picture fuzzy sets with their applications

Sijia Zhu; Zhe Liu; Sijia Zhu; Zhe Liu

doi:10.3934/math.20231525

AIMS Mathematics

2023, Volume 8, Issue 12: 29817-29848. doi: 10.3934/math.20231525

Previous Article Next Article

Research article

Distance measures of picture fuzzy sets and interval-valued picture fuzzy sets with their applications

Sijia Zhu ^{1
,
,},
Zhe Liu ^{2
,
,}

1.
Cw Chu College, Jiangsu Normal University, Xuzhou, 221116, China
2.
School of Computer Sciences, Universiti Sains Malaysia, Penang, 11800, Malaysia

Received: 28 September 2023 Revised: 28 October 2023 Accepted: 30 October 2023 Published: 02 November 2023
MSC : 03E72, 28E10, 90B50

Picture fuzzy sets (PFSs) are a versatile generalization of fuzzy sets and intuitionistic fuzzy sets (IFSs), providing a robust framework for modeling imprecise, uncertain, and inconsistent information across various fields. As an advanced extension of PFSs, interval-valued picture fuzzy sets (IvPFSs) offer superior capabilities for handling incomplete and indeterminate information in various practical applications. Distance measures have always been an important topic in fuzzy sets and their variants. Some existing distance measures for PFSs have shown limitations and may yield counterintuitive results under certain conditions. Furthermore, there are currently few studies on distance measures for IvPFSs. To solve these problems, in this paper we devised a series of novel distance measures between PFSs and IvPFSs inspired by the Hellinger distance. Specifically, all the distance measures were divided into two parts: One considered the positive membership degree, neutral membership degree and negative membership degree, and the other added the refusal membership degree. Moreover, the proposed distance measures met some important properties, including boundedness, non-degeneracy, symmetry, and consistency, but also showed superiority compared to the existing measures, as confirmed through numerical comparisons. Finally, the proposed distance measures were validated in pattern recognition and medical diagnosis applications, indicating that the proposed distance measures can deliver credible, reasonable results, particularly in similar cases.
- picture fuzzy sets,
- interval-valued picture fuzzy sets,
- Hellinger distance,
- pattern recognition,
- medical diagnosis
Citation: Sijia Zhu, Zhe Liu. Distance measures of picture fuzzy sets and interval-valued picture fuzzy sets with their applications[J]. AIMS Mathematics, 2023, 8(12): 29817-29848. doi: 10.3934/math.20231525

Related Papers:

Abstract

Picture fuzzy sets (PFSs) are a versatile generalization of fuzzy sets and intuitionistic fuzzy sets (IFSs), providing a robust framework for modeling imprecise, uncertain, and inconsistent information across various fields. As an advanced extension of PFSs, interval-valued picture fuzzy sets (IvPFSs) offer superior capabilities for handling incomplete and indeterminate information in various practical applications. Distance measures have always been an important topic in fuzzy sets and their variants. Some existing distance measures for PFSs have shown limitations and may yield counterintuitive results under certain conditions. Furthermore, there are currently few studies on distance measures for IvPFSs. To solve these problems, in this paper we devised a series of novel distance measures between PFSs and IvPFSs inspired by the Hellinger distance. Specifically, all the distance measures were divided into two parts: One considered the positive membership degree, neutral membership degree and negative membership degree, and the other added the refusal membership degree. Moreover, the proposed distance measures met some important properties, including boundedness, non-degeneracy, symmetry, and consistency, but also showed superiority compared to the existing measures, as confirmed through numerical comparisons. Finally, the proposed distance measures were validated in pattern recognition and medical diagnosis applications, indicating that the proposed distance measures can deliver credible, reasonable results, particularly in similar cases.

References

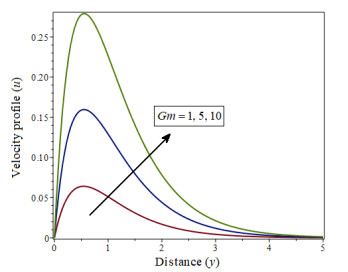
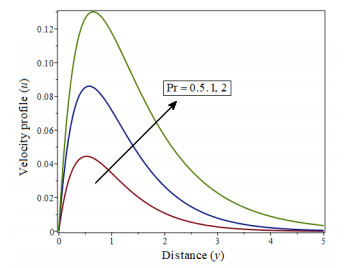
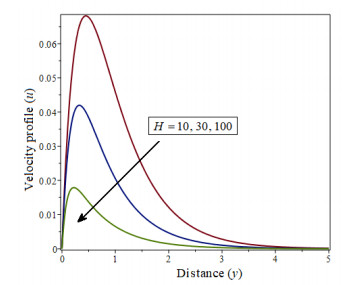
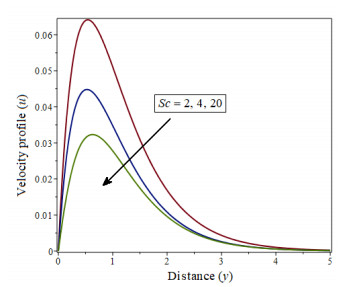
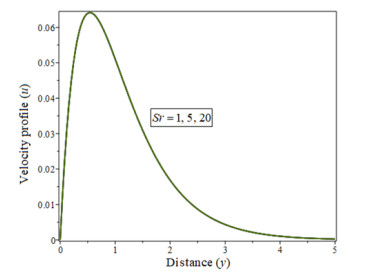
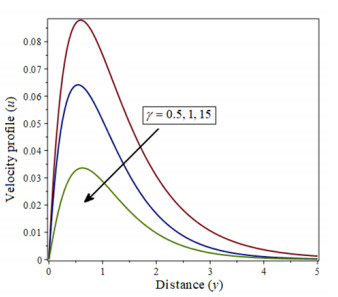
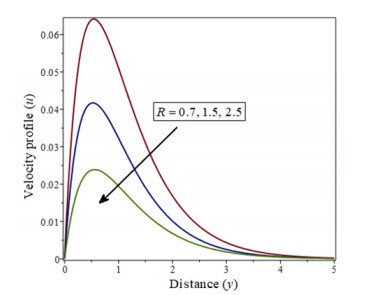
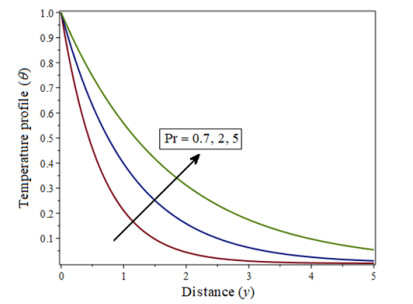
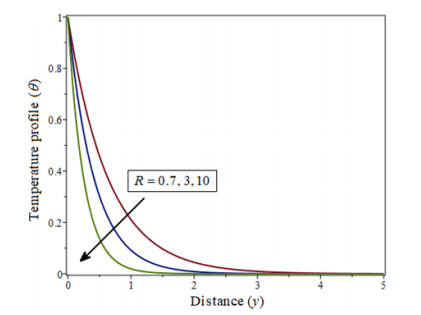
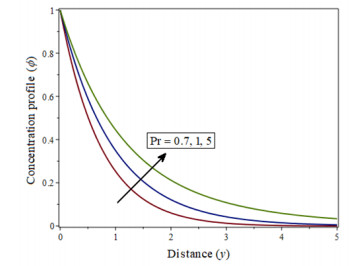
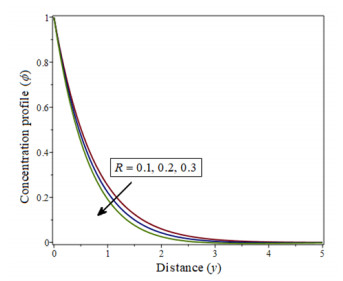
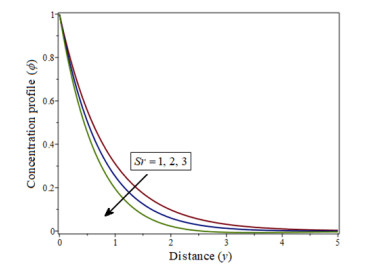
[1]	Z. Ali, T. Mahmood, M. S. Yang, Aczel-alsina power aggregation operators for complex picture fuzzy (cpf) sets with application in cpf multi-attribute decision making, Symmetry, 15 (2023), 651. https://doi.org/10.3390/sym15030651 doi: 10.3390/sym15030651
[2]	V. Arya, S. Kumar, A novel todim-vikor approach based on entropy and jensen-tsalli divergence measure for picture fuzzy sets in a decision-making problem, Int. J. Intell. Syst., 35 (2020), 2140–2180. https://doi.org/10.1002/int.22289 doi: 10.1002/int.22289
[3]	K. T. Atanassov, Operators over interval valued intuitionistic fuzzy sets, Fuzzy Set. Syst., 64 (1994), 159–174. https://doi.org/10.1016/0165-0114(94)90331-X doi: 10.1016/0165-0114(94)90331-X
[4]	K. T. Atanassov, S. Stoeva, Intuitionistic fuzzy sets, Fuzzy Set. Syst., 20 (1986), 87–96. https://doi.org/10.1007/978-3-7908-1870-3_1 doi: 10.1007/978-3-7908-1870-3_1
[5]	N. M. F. H. N. Badrul, K. M. N. K. Khalif, N. I. Jaini, Synergic ranking of fuzzy z-numbers based on vectorial distance and spread for application in decision-making, AIMS Math., 8 (2023), 11057–11083. https://doi.org/10.3934/math.2023560 doi: 10.3934/math.2023560
[6]	G. Cao, L. Shen, A novel parameter similarity measure between interval-valued picture fuzzy sets with its app-lication in pattern recognition, J. Intell. Fuzzy Syst., 44 (2023), 1–27. https://doi.org/10.3233/JIFS-224314 doi: 10.3233/JIFS-224314
[7]	T. Chen, Evolved distance measures for circular intuitionistic fuzzy sets and their exploitation in the technique for order preference by similarity to ideal solutions, Artif. Intell. Rev., 56 (2023), 7347–7401. https://doi.org/10.1007/s10462-022-10318-x doi: 10.1007/s10462-022-10318-x
[8]	Z. Chen, P. Liu, Intuitionistic fuzzy value similarity measures for intuitionistic fuzzy sets, Comput. Appl. Math., 41 (2022), 45. https://doi.org/10.1007/s40314-021-01737-7 doi: 10.1007/s40314-021-01737-7
[9]	B. Cuong, Picture fuzzy sets-first results, part 1, seminar neuro-fuzzy systems with applications, Institute of Mathematics, Hanoi, 2013.
[10]	B. C. Cuong, V. Kreinovich, Picture fuzzy sets, J. Comput. Sci. Technol., 30 (2014), 409–420.
[11]	P. Dutta, Medical diagnosis via distance measures on picture fuzzy sets, Adv. Model. Anal. A, 54 (2017), 657–672.
[12]	P. Dutta, Medical diagnosis based on distance measures between picture fuzzy sets, Int. J. Fuzzy Syst., 7 (2018), 15–36. https://doi.org/10.4018/IJFSA.2018100102 doi: 10.4018/IJFSA.2018100102
[13]	Rasyidah, R. Efendi, N. M. Nawi, M. M. Deris, S. A. Burney, Cleansing of inconsistent sample in linear regression model based on rough sets theory, Soft Comput., 5 (2023), 200046. https://doi.org/10.1016/j.sasc.2022.200046 doi: 10.1016/j.sasc.2022.200046
[14]	A. H. Ganie, S. Singh, P. K. Bhatia, Some new correlation coefficients of picture fuzzy sets with applications, Neural. Comput. Appl., 32 (2020), 12609–12625. https://doi.org/10.1007/s00521-020-04715-y doi: 10.1007/s00521-020-04715-y
[15]	A. Ganie, A picture fuzzy distance measure and its application to pattern recognition problems, Iran. J. Fuzzy Syst., 20 (2023), 71–85.
[16]	E. Haktanır, C. Kahraman, Intelligent replacement analysis using picture fuzzy sets: Defender-challenger comparison application, Eng. Appl. Artif. Intell., 121 (2023), 106018. https://doi.org/10.1016/j.engappai.2023.106018 doi: 10.1016/j.engappai.2023.106018
[17]	M. K. Hasan, M. Y. Ali, A. Sultana, N. K. Mitra, Extension principles for picture fuzzy sets, J. Intell. Fuzzy Syst., 44 (2023), 6265–6275. https://doi.org/10.3233/JIFS-220616 doi: 10.3233/JIFS-220616
[18]	A. G. Hatzimichailidis, G. A. Papakostas, V. G. Kaburlasos, A novel distance measure of intuitionistic fuzzy sets and its application to pattern recognition problems, Int. J. Intell. Syst., 27 (2012), 396–409. https://doi.org/10.1002/int.21529 doi: 10.1002/int.21529
[19]	E. Hellinger, Neue begründung der theorie quadratischer formen von unendlichvielen veränderlichen., J. Reine Angew. Math., 1909 (1909), 210–271. https://doi.org/10.1515/crll.1909.136.210 doi: 10.1515/crll.1909.136.210
[20]	I. M. Hezam, P. Rani, A. R. Mishra, A. Alshamrani, An intuitionistic fuzzy entropy-based gained and lost dominance score decision-making method to select and assess sustainable supplier selection, AIMS Math., 8 (2023), 12009–12039. https://doi.org/10.3934/math.2023606 doi: 10.3934/math.2023606
[21]	H. Huang, Z. Liu, X. Han, X. Yang, L. Liu, A belief logarithmic similarity measure based on dempster-shafer theory and its application in multi-source data fusion, J. Intell. Fuzzy Syst., 45 (2023), 4935–4947. https://doi.org/10.3233/JIFS-230207 doi: 10.3233/JIFS-230207
[22]	C. M. Hwang, M. S. Yang, W. L. Hung, New similarity measures of intuitionistic fuzzy sets based on the jaccard index with its application to clustering, Int. J. Intell. Syst., 33 (2018), 1672–1688. https://doi.org/10.1002/int.21990 doi: 10.1002/int.21990
[23]	R. Jaikumar, S. Raman, M. Pal, Perfect score function in picture fuzzy set and its applications in decision-making problems, J. Intell. Fuzzy Syst., 44 (2023), 3887–3900. https://doi.org/10.3233/JIFS-223234 doi: 10.3233/JIFS-223234
[24]	A. M. Khalil, S. G. Li, H. Garg, H. Li, S. Ma, New operations on interval-valued picture fuzzy set, interval-valued picture fuzzy soft set and their applications, IEEE Access, 7 (2019), 51236–51253.
[25]	X. Li, Z. Liu, X. Han, N. Liu, W. Yuan, An intuitionistic fuzzy version of hellinger distance measure and its application to decision-making process, Symmetry, 15 (2023), 500. https://doi.org/10.3390/sym15020500 doi: 10.3390/sym15020500
[26]	D. Y. F. Lin, Influence of weight function for similarity measures, AIMS Math., 7 (2022), 6915–6935. https://doi.org/10.3934/math.2022384 doi: 10.3934/math.2022384
[27]	M. Lin, C. Huang, Z. Xu, Multimoora based mcdm model for site selection of car sharing station under picture fuzzy environment, Sustain. Cities Soc., 53 (2020), 101873. https://doi.org/10.1016/j.scs.2019.101873 doi: 10.1016/j.scs.2019.101873
[28]	M. Lin, X. Li, R. Chen, H. Fujita, J. Lin, Picture fuzzy interactional partitioned heronian mean aggregation operators: An application to madm process, Artif. Intell. Rev., 55 (2022), 1171–1208. https://doi.org/10.1007/s10462-021-09953-7 doi: 10.1007/s10462-021-09953-7
[29]	M. Lin, J. Wei, Z. Xu, R. Chen, Multiattribute group decision-making based on linguistic pythagorean fuzzy interaction partitioned bonferroni mean aggregation operators, Complexity, 2018 (2018), 1–25. https://doi.org/10.1155/2018/9531064 doi: 10.1155/2018/9531064
[30]	D. Liu, X. Chen, D. Peng, Interval-valued intuitionistic fuzzy ordered weighted cosine similarity measure and its application in investment decision-making, Complexity, 2017 (2017), 1891923. https://doi.org/10.1155/2017/1891923 doi: 10.1155/2017/1891923
[31]	M. Liu, S. Zeng, T. Balezentis, D. Streimikiene, Picture fuzzy weighted distance measures and their application to investment selection, Amfiteatru Econ., 21 (2019), 682–695. https://doi.org/10.24818/EA/2019/52/682 doi: 10.24818/EA/2019/52/682
[32]	P. Liu, M. Munir, T. Mahmood, K. Ullah, Some similarity measures for interval-valued picture fuzzy sets and their applications in decision making, Information, 10 (2019), 369. https://doi.org/10.3390/info10120369 doi: 10.3390/info10120369
[33]	Z. Liu, Credal-based fuzzy number data clustering, Granul. Comput., 8 (2023), 1907–1924. https://doi.org/10.1007/s41066-023-00410-0 doi: 10.1007/s41066-023-00410-0
[34]	Z. Liu, An effective conflict management method based on belief similarity measure and entropy for multi-sensor data fusion, Artif. Intell. Rev., 56 (2023), 15495–15522. https://doi.org/10.1007/s10462-023-10533-0 doi: 10.1007/s10462-023-10533-0
[35]	Z. Liu, Y. Cao, X. Yang, L. Liu, A new uncertainty measure via belief rényi entropy in dempster-shafer theory and its application to decision making, Commun. Stat.-Theor. M., 2023, 1–20. https://doi.org/10.1080/03610926.2023.2253342 doi: 10.1080/03610926.2023.2253342
[36]	Z. Liu, H. Huang, Comment on "new cosine similarity and distance measures for fermatean fuzzy sets and topsis approach", Knowl. Inf. Syst., 65 (2023), 5151–5157. https://doi.org/10.1007/s10115-023-01926-2 doi: 10.1007/s10115-023-01926-2
[37]	Z. Liu, H. Huang, S. Letchmunan, Adaptive weighted multi-view evidential clustering, In Int. Conf. Artif. Neural Netw., Springer, 2023,265–277. https://doi.org/10.1007/978-3-031-44216-2_22
[38]	M. Luo, W. Li, Some new similarity measures on picture fuzzy sets and their applications, Soft Comput., 27 (2023), 6049–6067. https://doi.org/10.1007/s00500-023-07902-w doi: 10.1007/s00500-023-07902-w
[39]	M. Luo, Y. Zhang, A new similarity measure between picture fuzzy sets and its application, Eng. Appl. Artif. Intell., 96 (2020), 103956. https://doi.org/10.1016/j.engappai.2020.103956 doi: 10.1016/j.engappai.2020.103956
[40]	Z. Ma, Z. Liu, C. Luo, L. Song, Evidential classification of incomplete instance based on k-nearest centroid neighbor, J. Intell. Fuzzy Syst., 41 (2021), 7101–7115. https://doi.org/10.3233/JIFS-210991 doi: 10.3233/JIFS-210991
[41]	T. Mahmood, H. M. Waqas, Z. Ali, K. Ullah, D. Pamucar, Frank aggregation operators and analytic hierarchy process based on interval-valued picture fuzzy sets and their applications, Int. J. Intell. Syst., 36 (2021), 7925–7962. https://doi.org/10.1002/int.22614 doi: 10.1002/int.22614
[42]	A. Ohlan, Novel entropy and distance measures for interval-valued intuitionistic fuzzy sets with application in multi-criteria group decision-making, Int. J. Gen. Syst., 51 (2022), 413–440. https://doi.org/10.1080/03081079.2022.2036138 doi: 10.1080/03081079.2022.2036138
[43]	P. Perveen, S. J. John, H. Kamacı, T. Baiju, A novel similarity measure of picture fuzzy sets and its applications, J. Intell. Fuzzy Syst., 44 (2023), 4653–4665.
[44]	C. Qin, M. Liu, Z. Zhang, H. Yu, Y. Jin, H. Sun, et al., An adaptive operating parameters decision-making method for shield machine considering geological environment, Tunn. Undergr. Space Technol., 141 (2023), 105372. https://doi.org/10.1016/j.tust.2023.105372 doi: 10.1016/j.tust.2023.105372
[45]	A. U. Rahman, M. Saeed, H. Khalifa, W. A. Afif, Decision making algorithmic techniques based on aggregation operations and similarity measures of possibility intuitionistic fuzzy hypersoft sets, AIMS Math., 7 (2022), 3866–3895. https://doi.org/10.3934/math.2022214 doi: 10.3934/math.2022214
[46]	P. Rathnasabapathy, D. Palanisami, A theoretical development of improved cosine similarity measure for interval valued intuitionistic fuzzy sets and its applications, J. Ambient. Intell. Humaniz Comput., 2022, 1–13. https://doi.org/10.1007/s12652-022-04019-0 doi: 10.1007/s12652-022-04019-0
[47]	N. Rico, P. Huidobro, A. Bouchet, I. Díaz, Similarity measures for interval-valued fuzzy sets based on average embeddings and its application to hierarchical clustering, Inf. Sci., 615 (2022), 794–812. https://doi.org/10.1016/j.ins.2022.10.028 doi: 10.1016/j.ins.2022.10.028
[48]	J. Sanabria, K. Rojo, F. Abad, A new approach of soft rough sets and a medical application for the diagnosis of coronavirus disease, AIMS Math., 8 (2023), 2686–2707. https://doi.org/10.3934/math.2023141 doi: 10.3934/math.2023141
[49]	M. Saqlain, M. Riaz, R. Imran, F. Jarad, Distance and similarity measures of intuitionistic fuzzy hypersoft sets with application: Evaluation of air pollution in cities based on air quality index, AIMS Math., 8 (2023), 6880–6899. https://doi.org/10.3934/math.2023348 doi: 10.3934/math.2023348
[50]	H. Seiti, A. Hafezalkotob, L. Martínez, R-numbers, a new risk modeling associated with fuzzy numbers and its application to decision making, Inf. Sci., 483 (2019), 206–231. https://doi.org/10.1016/j.ins.2019.01.006 doi: 10.1016/j.ins.2019.01.006
[51]	J. A. Shah, D. Sukheja, P. Bhatnagar, A. Jain, A decision-making problem using dissimilarity measure in picture fuzzy sets, Mater. Today, 80 (2023), 3405–3410.
[52]	M. S. Sindhu, T. Rashid, A. Kashif, An approach to select the investment based on bipolar picture fuzzy sets, Int. J. Fuzzy Syst., 23 (2021), 2335–2347. https://doi.org/10.1007/s40815-021-01072-3 doi: 10.1007/s40815-021-01072-3
[53]	A. Singh, S. Kumar, Picture fuzzy set and quality function deployment approach based novel framework for multi-criteria group decision making method, Eng. Appl. Artif. Intell., 104 (2021), 104395. https://doi.org/10.1016/j.engappai.2021.104395 doi: 10.1016/j.engappai.2021.104395
[54]	P. Singh, N. K. Mishra, M. Kumar, S. Saxena, V. Singh, Risk analysis of flood disaster based on similarity measures in picture fuzzy environment, Afrika Mat., 29 (2018), 1019–1038. https://doi.org/10.1007/s13370-018-0597-x doi: 10.1007/s13370-018-0597-x
[55]	L. H. Son, Measuring analogousness in picture fuzzy sets: From picture distance measures to picture association measures, Fuzzy Optim. Decis. Mak., 16 (2017), 359–378. https://doi.org/10.1007/s10700-016-9249-5 doi: 10.1007/s10700-016-9249-5
[56]	A. Taouti, W. A. Khan, Fuzzy subnear-semirings and fuzzy soft subnear-semirings, AIMS Math., 6 (2021), 2268–2286. https://doi.org/10.3934/math.2021137 doi: 10.3934/math.2021137
[57]	N. X. Thao, S. Y. Chou, Novel similarity measures, entropy of intuitionistic fuzzy sets and their application in software quality evaluation, Soft Comput., 2022, 1–12. https://doi.org/10.1007/s00500-021-06373-1 doi: 10.1007/s00500-021-06373-1
[58]	N. V. Dinh, N. X. Thao, N. Xuan, Some measures of picture fuzzy sets and their application in multi-attribute decision making, Int. J. Math. Sci. Comput., 4 (2018), 23–41.
[59]	G. Wei, F. E. Alsaadi, T. Hayat, A. Alsaedi, Projection models for multiple attribute decision making with picture fuzzy information, Int. J. Mach. Learn. Cybern., 9 (2018), 713–719. https://doi.org/10.1007/s13042-016-0604-1 doi: 10.1007/s13042-016-0604-1
[60]	J. Wu, L. Li, W. Sun, Gödel semantics of fuzzy argumentation frameworks with consistency degrees, AIMS Math., 5 (2020), 4045–4064.
[61]	F. Xiao, Efmcdm: Evidential fuzzy multicriteria decision making based on belief entropy, IEEE T. Fuzzy Syst., 28 (2020), 1477–1491. https://doi.org/10.1109/TFUZZ.2019.2936368 doi: 10.1109/TFUZZ.2019.2936368
[62]	F. Xiao, W. Pedrycz, Negation of the quantum mass function for multisource quantum information fusion with its application to pattern classification, IEEE T. Pattern Anal., 45 (2023), 2054–2070. https://doi.org/10.1109/TPAMI.2022.3167045 doi: 10.1109/TPAMI.2022.3167045
[63]	D. Xie, F. Xiao, W. Pedrycz, Information quality for intuitionistic fuzzy values with its application in decision making, Eng. Appl. Artif. Intell., 109 (2022), 104568. https://doi.org/10.1016/j.engappai.2021.104568 doi: 10.1016/j.engappai.2021.104568
[64]	C. Xu, Y. Wen, New measure of circular intuitionistic fuzzy sets and its application in decision making, AIMS Math., 8 (2023), 24053–24074. https://doi.org/10.3934/math.20231226 doi: 10.3934/math.20231226
[65]	C. Yang, F. Xiao, An exponential negation of complex basic belief assignment in complex evidence theory, Inf. Sci., 622 (2023), 1228–1251. https://doi.org/10.1016/j.ins.2022.11.160 doi: 10.1016/j.ins.2022.11.160
[66]	J. Ye, Interval-valued intuitionistic fuzzy cosine similarity measures for multiple attribute decision-making, Int. J. Gen. Syst., 42 (2013), 883–891. https://doi.org/10.1080/03081079.2013.816696 doi: 10.1080/03081079.2013.816696
[67]	L. A. Zadeh, Fuzzy sets, Inf. Control, 8 (1965), 338–353. https://doi.org/10.1142/9789813238183_0001 doi: 10.1142/9789813238183_0001
[68]	S. Zhang, F. Xiao, A TFN-based uncertainty modeling method in complex evidence theory for decision making, Inf. Sci., 619 (2023), 193–207. https://doi.org/10.1016/j.ins.2022.11.014 doi: 10.1016/j.ins.2022.11.014
[69]	X. Zhang, Y. Ma, Y. Li, C. Zhang, C. Jia, Tension prediction for the scraper chain through multi-sensor information fusion based on improved dempster-shafer evidence theory, Alex. Eng. J., 64 (2023), 41–54. https://doi.org/10.1016/j.aej.2022.08.039 doi: 10.1016/j.aej.2022.08.039

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)