Solvability of a fluid-structure interaction problem with semigroup theory

1.   Introduction

The concept of strongly continuous semigroups has proven to be an elegant method for the derivation of the well-posedness of time-dependent PDE that can be interpreted as abstract Cauchy problems on Banach spaces. Utilizing the well-known generation theorems by Hille-Yosida ^[1,2] and Lumer-Phillips ^[3], the existence of mild, as well as classical solutions to linear and non-linear evolution equations can be efficiently verified. Thereby, in various pure and applied mathematical problems, the methodology is a valid alternative to existing proof strategies based on Galerkin approaches. In this paper, we present the application of a semigroup approach in the context of a fluid-structure interaction (FSI) problem.

We consider the setting of two domains occupied with fluid governed by the non-stationary Stokes equations, separated by a porous, thin linear elastic plate with a small in-plane period ${\varepsilon}$. The structure's displacement is governed by linear elasticity with regularized contact conditions. Linearized coupling conditions, namely the continuity of velocity and normal stresses are imposed at the fluid-structure interface. Comparable FSI problems typically arise in biological, as well as in filtration modeling, see e.g., ^[4,5,6,7]. The arising microscopic FSI system was recently analyzed in ^[8,9] in terms of its well-posedness and the scale-limit ${\varepsilon}\to 0$ in the context of two-scale convergence (see e.g., ^[10]).

The stationary form of the microscopic structure equations under consideration were first proposed in ^[11]. For the proof of existence and uniqueness of a solution to the non-stationary formulation, the sufficient conditions of the Lumer-Phillips theorem are verified, which ensure that the linear operator associated to the spatial bilinear form of the problem generates a contraction semigroup.

Afterwards, the homogenized and dimension reduced macroscopic FSI problem for the limit ${\varepsilon}\to 0$ from ^[8,9] is recalled. In the limit, the porous plate shrinks to a manifold, a 2D interface between the two fluid domains with a coupling condition between the jump of fluid stresses and the interface curvature. The governing equations of the macroscopic structure have been derived outside the FSI context in ^[12,13], utilizing the periodic unfolding method (see e.g., ^[14]).

Unintuitively, in the asymptotic limit, the interface is no-longer permeable. Since, for our modeling purpose, the mass transport through the interface is essential, we propose a novel, heuristic asymptotic model that extends the rigorously derived macroscopic FSI problem by a flow resistance term obeying Darcy's law. Well-posedness of the new model is first verified by a classical Galerkin approach. Under frequently met assumptions on the symmetry of the microscopic structure, a much simpler proof can be performed utilizing a semigroup approach, guaranteeing existence and uniqueness of mild and classical solutions to the new FSI model with the Lumer-Phillips theorem.

2.   Microscopic structure model

In this section, we introduce the governing equations for the displacement of the periodic microscopic structure. A linear elasticity model on domains in contacts is formulated. At contact surfaces, a linearized contact condition is prescribed. The model corresponds to the non-stationary case of the system considered in ^[11]. Existence and uniqueness of a solution to the structure model is verified utilizing a semigroup approach.

2.1.   Domain description

In this paper, we utilize the microscopic structure description as periodic, 2D-like filters consisting of slender yarns in contact established in ^[11]. For notation, in particular the description of spatial domains, we mainly adopt the notation of the FSI problem considered in ^[9].

For our modeling purposes, we deal with domains of the following type.

Definition 2.1. We say the tuple $(\Omega, S)$ with open set $\Omega\subset{{{\mathbb{R}}}}^3$ and $S\subset \partial \Omega$ is a chain of domains in contact if there exist finitely many bounded Lipschitz domains $\Omega_i\subset{{{\mathbb{R}}}}^3$ fulfilling

(1) $\Omega = \bigcup_i \Omega_i$,

(2) $\Omega_i\cap \Omega_j = \emptyset$ for $i\neq j$,

(3) ${\rm{int}}\; \bigcup_i \overline{ \Omega}_i = {\rm{int}}\; \overline{ \Omega}$ is a connected set and

(4) $S = \bigcup_{i, j} S_{ij}$, where $S_{ij}: = \overline{ \Omega}_i\cap \overline{ \Omega}_j$.

In general, we say a subset $\Omega$ of ${{{\mathbb{R}}}}^n$ is a domain if it is non-empty, open and connected. We call it a Lipschitz domain if additionally the boundary $\partial \Omega$ is locally the graph of a Lipschitz continuous function.

For domains in contact as described, we require the following functional space.

Definition 2.2. Let $(\Omega, S)$ be a chain of domains in contact. The broken Sobolev space $\hat{H}^1(\Omega)$ is given by

equipped with the inner product

and induced norms $\Vert \cdot\Vert_{\hat{H}^1(\Omega)}$, respectively. In notation, the hat is omitted, as it is clear from context.

For general open sets and union of open sets $\Omega$, we denote the standard inner product on $L^2(\Omega)$ by $(u, v)_ \Omega$.

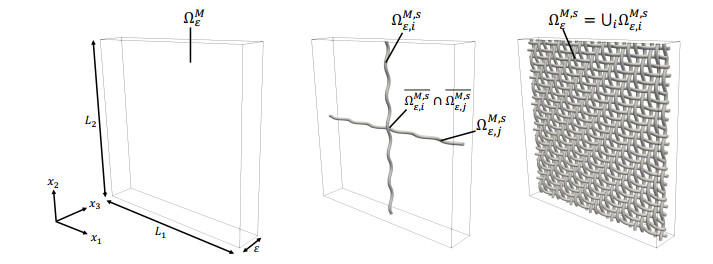
Next, we introduce the microscopic filter domain. Consider a thin, cuboidal domain

of thickness ${\varepsilon} \ll L_1, L_2$ being an enclosing box for a solid domain $\Omega_ {\varepsilon}^{M, s}$, which we also refer to as structure or filter. The solid domain is chosen as a chain of domains in contact $(\Omega_ {\varepsilon}^{M, s}, S_ {\varepsilon}^c)$ with

where the bounded Lipschitz domains $\Omega_{ {\varepsilon}, i}^{M, s}$ are representing individual yarns. The common interfaces of the closures of the yarn domains are denoted by $S_ {\varepsilon}^c$, i.e.,

which we refer to as contact surfaces. A visual reference of the introduced domains is given in Figure 1. The general description of the yarn domains $\Omega_{ {\varepsilon}, i}^{M, s}$ is arbitrary for what follows. However, the domains in mind in filtration application with textile-like filters are slender curved rods with constant cross-section.

We refer to $\Omega_ {\varepsilon}^M$ as membrane domain and define the complement $\Omega_ {\varepsilon}^{M, f}: = \Omega_ {\varepsilon}^M\setminus \overline{ \Omega_ {\varepsilon}^{M, s}}$, assumed to be connected, which is occupied with viscous fluid in the FSI model. The abbreviations s and f in the domains are for structure/solid and fluid, respectively.

The exposed part $\partial \Omega^{M, s} \setminus S_ {\varepsilon}^c$ of the boundary $\partial \Omega^{M, s}$ is assumed to be the disjoint union of a Dirichlet boundary $\partial^\text{fix} \Omega^{M, s}$ and a Neumann boundary $\partial^\text{fs} \Omega^{M, s}$. The abbreviation fs is for fluid-structure, which we motive as follows: For later modeling purposes, the Dirichlet boundary is chosen as

where we assume that this set is of non-zero measure and does not contain any part of the lateral surfaces $\{ x_3 = \pm {\varepsilon}/2\}$. The modeling intuition is the fixation of the outer edges of the filter. By this choice, $\partial^\text{fs} \Omega^{M, s}$ describes the entire interface between $\Omega^{M, s}$ and $\Omega^{M, f}$, which corresponds to the microscopic fluid-structure interface in the FSI model.

For an $x = (x_1, x_2, x_3)^T \in {{{\mathbb{R}}}}^3$, we write ${\bar{x}}: = (x_1, x_2)$ denoting the in-plane direction. We refer to $x_3$ as the normal or outer-plane direction. The structure is expected to be periodic in in-plane direction with a period ${\varepsilon}$.

Due to the above periodicity assumption, the structure can be efficiently characterized by its smallest periodic unit $Y^s_ {\varepsilon} = {\varepsilon} Y^s$ contained in a reference cell $Y_ {\varepsilon} = {\varepsilon} Y$, where $Y = (0, 1)^2\times(-1/2, 1/2)$ is referred to as unit cell. We follow the convention of denoting the spatial variable in the reference cell by $y$.

To avoid dealing with dissected cells near the boundary of $\Omega_ {\varepsilon}^M$, we make the technical assumption $L_{1, 2}/ {\varepsilon}\in \mathbb{N}$.

Furthermore, to ensure an overall connected domain, we assume that $Y_ {\varepsilon}^s$ intersects the in-plane boundaries $\{ y_1 = 0\}, \{ y_1 = {\varepsilon}\}$ as well as $\{y_2 = 0\}, \{y_2 = {\varepsilon}\}$ and is periodic in the sense that

We denote the contact interfaces in $Y_ {\varepsilon}$ with $S_{Y, {\varepsilon}}^c = {\varepsilon} S_{Y}^c$ and write $Y_ {\varepsilon}^f = {\varepsilon} Y^f = Y_ {\varepsilon}\setminus \overline{Y_ {\varepsilon}^s}$. We emphasize the important observation that by construction, the periodic units $(Y^s_ {\varepsilon}, S_{Y, {\varepsilon}}^c), (Y^s, S_{Y}^c)$ also describe chains of domains in contact.

One exemplary reference cell is illustrated in Figure 2 for visual reference. The membrane domain $\Omega^M_ {\varepsilon}$ can be imagined as periodic repetition of $Y_ {\varepsilon}$ in the in-plane direction.

2.2.   Governing equations

Let $T > 0$ denote some finite time. The microscopic displacement of the structure

is governed by linear elasticity with additional regularized contact conditions, see ^[11]. Let

denote the symmetric strain tensor and let

with ${\underline{\mathit{\boldsymbol{A}}}}\in L^\infty_\text{per}(Y^s)^{3\times 3\times 3\times 3}$ be the fourth-order microscopic stiffness tensor. According to Hooke's law, there exists a linear relation between the Cauchy stress tensor $\sigma_s^ {\varepsilon}({\mathit{\boldsymbol{u}}_{\varepsilon}})$ and the strain tensor reading

with which the governing equation of motion for the structure becomes

Here, $\rho_s > 0$ denotes a (constant) solid density and ${{\boldsymbol{g}}}_ {\varepsilon}$ is some body force density. For notational convenience, we assume $\rho_s = 1$.

Furthermore, we impose zero Dirichlet and zero Neumann conditions reading

with $\mathit{\boldsymbol{\eta}}$ denoting the unit outward normal. It is clear how to extend the subsequent results to in-homogeneous boundary conditions.

Since the contact surfaces $S_ {\varepsilon}^c$ are interior boundaries, we need to fix an orientation of their normal vector $\mathit{\boldsymbol{\eta}}$, respectively. The choice on each surface is arbitrary. With this preliminary step, we can prescribe regularized contact conditions given by the Robin-type condition

with a contact matrix ${{\boldsymbol{R}}}^ {\varepsilon}(x) = {{\boldsymbol{R}}}(x/ {\varepsilon})\in L^\infty_\text{per}(S_Y^c)^{3\times 3}$.

Here, and in the following, we utilize the notation $\left[\!\left[{} \right. \cdot \left. {} \right]\!\right]$ for the jump operator across a given interface with fixed orientation $\mathit{\boldsymbol{\eta}}$, i.e.,

for a given function $w$ defined on the left and right side of the interface. According to (2.3), normal stresses at the contact surfaces are continuous but the displacement is allowed to differ in-between two adjacent yarns, e.g., due to shearing.

The choice of scaling w.r.t. ${\varepsilon}$ in (2.3) is crucial for the asymptotic analysis. If one considers the scaling of ${\varepsilon}^0$ instead of ${\varepsilon}^{-1}$, the contacts are too weak and they will vanish in the asymptotic limit. The resulting structure will disassemble. On the other-hand, a scaling of ${\varepsilon}^{-2}$ or larger corresponds to too strong or glued contacts that would dominate the macroscopic displacement such that the resulting structure is rigid.

Summarizing all equations, the microscopic structure model reads

which we accompany with initial conditions ${\mathit{\boldsymbol{u}}_{\varepsilon}}(0) = {{\boldsymbol{u}}}_0, \partial_t {\mathit{\boldsymbol{u}}_{\varepsilon}}(0) = {{\boldsymbol{w}}}_0$. In the case of glued yarns, that is ${{\boldsymbol{R}}}^ {\varepsilon}\to\infty$, problem (2.4) coincides with a classical elasticity problem on a single connected domain.

Further assumptions on the arising model parameters have to be prescribed. The first of the following are standard in linear elasticity modeling (see e.g., Chapter 1 of ^[15]), while the assumptions on the Robin condition matrix are intuitive.

Assumption 2.3. The stiffness tensor ${\underline{\mathit{\boldsymbol{A}}}} = (a_{ijkl})_{i, j, k, l = 1}^3$ satisfies Hooke's law, meaning it is

● symmetric, i.e., for almost every $y \in Y^s$ we have $a_{ijkl}(y) = a_{jikl}(y) = a_{jkil}(y)$,

● coercive on the space of symmetric matrices, i.e., there exists a constant $\underline{c} > 0$, such that for all ${{\boldsymbol{P}}}\in{{{\mathbb{R}}}}^{3\times 3}$ with ${{\boldsymbol{P}}}^T = {{\boldsymbol{P}}}$ the bound $({\underline{\mathit{\boldsymbol{A}}}}(y) {{\boldsymbol{P}}}) : {{\boldsymbol{P}}} \geq \underline{c} \Vert {{\boldsymbol{P}}}\Vert_F$ holds for almost every $y \in Y^s$.

Furthermore, the Robin condition matrix ${{\boldsymbol{R}}}$ is

● symmetric, i.e., for almost every $y \in S^c_Y$ we have ${{\boldsymbol{R}}}(y) = \left({{\boldsymbol{R}}}(y)\right)^T$,

● coercive, i.e., there exists a constant $\underline{c} > 0$ such that for all ${{\boldsymbol{a}}}\in{{{\mathbb{R}}}}^3$ the bound ${{\boldsymbol{R}}}(y) {{\boldsymbol{a}}}\cdot {{\boldsymbol{a}}}\geq \underline{c} \vert {{\boldsymbol{a}}}\vert$ holds for almost every $y\in S^c_Y$.

Example 2.4. The above assumptions on ${\underline{\mathit{\boldsymbol{A}}}}$ are fulfilled e.g., for yarns made out of an isotropic, homogeneous material with Young's modulus $E > 0$ and Poisson's ratio $\nu\in (0, 1/2)$, respectively. The entries of the stiffness tensor for this choice are the constants

with the Dirac-delta $\delta_{ij}$, see e.g., Chapter 3 in ^[16].

As proposed in ^[11], one possible choice for ${{\boldsymbol{R}}}$ reads

for the $3\times 3$ unit matrix ${{\boldsymbol{I}}}$ and two parameters $R_n, R_t > 0$, penalizing normal and tangential deviations of displacements, respectively.

2.3.   Existence proof utilizing semigroup theory

The existence and uniqueness of solutions to (2.4) is derived utilizing continuous semigroup theory. This aproach is applicable to general linear Cauchy problems in Banach spaces ${{\mathcal{Y}}}$ of the form

where ${{\boldsymbol{y}}}\colon (0, T)\to {{\mathcal{Y}}}, {{\boldsymbol{F}}}\colon (0, T)\to {{\mathcal{Y}}}$ and ${\boldsymbol{\Phi}}\colon {{\mathcal{Y}}}\to {{\mathcal{Y}}}$ is a linear operator on ${{\mathcal{Y}}}$.

We recall the fundamental concepts and results from literature that are required for our considered systems.

Definition 2.5. (Strongly continuous semigroups) Let $G(t)$ be a family of continuous linear operators on a Banach space ${{\mathcal{Y}}}$ depending on a parameter $t\geq 0$. We call $G(t)$ a strongly continuous semigroup in ${{\mathcal{Y}}}$ if and only if

(1) $\Vert G(t)\Vert_ {{\mathcal{L}}} \leq M(t)$ for some $M(t) > 0$,

(2) $G(0) = {{\boldsymbol{I}}}$, where ${{\boldsymbol{I}}}$ is the identity operator on ${{\mathcal{Y}}}$,

(3) for all $t, s\geq 0$ the equality $G(t+s) = G(t)\circ G(s)$ holds, and

(4) for all ${{\boldsymbol{y}}}\in {{\mathcal{Y}}}$ we have $\Vert G(t) {{\boldsymbol{y}}} - {{\boldsymbol{y}}}\Vert_ {{\mathcal{Y}}} \to 0$ as $t\to 0$.

We follow the usual convention of writing $C_0$-semigroup for strongly continuous semigroups.

Definition 2.6. We call the potentially unbounded operator ${\boldsymbol{\Phi}}\colon {{\mathcal{Y}}}\to {{\mathcal{Y}}}$ defined by

generator of the $C_0$-semigroup $G(t)$. The domain $D({\boldsymbol{\Phi}})$ is the set of all ${{\boldsymbol{y}}}\in {{\mathcal{Y}}}$ for which the expression above is well-defined.

The fundamental existence result of solutions to problems of the form (2.5) can e.g., be found in Section 12.1.3 of ^[17]. It can be interpreted as the generalization of the classical variation of constants method for finite dimensional Cauchy problems.

Theorem 2.7. Let $G(t)$ be a $C_0$-semigroup in ${{\mathcal{Y}}}$ with generator ${\boldsymbol{\Phi}}$. Assume that ${{\boldsymbol{y}}}_0\in {{\mathcal{Y}}}$ and let ${{\boldsymbol{F}}} \in L^1((0, T), {{\mathcal{Y}}})$. Then

is the unique mild solution to (2.5).

If additionally ${{\boldsymbol{y}}}_0\in D({\boldsymbol{\Phi}})$ as well as ${{\boldsymbol{F}}}\in C^0([0, T], {{\mathcal{Y}}})$ and additionally either

then ${{\boldsymbol{y}}}\in C^0([0, T], D({\boldsymbol{\Phi}}))\cap C^1((0, T), {{\mathcal{Y}}})$ is the unique classical solution to (2.5).

For Hilbert spaces, one of the most versatile tools for the characterization of generators is the Lumer-Phillips theorem, see ^[3].

Theorem 2.8. (Lumer-Phillips) Consider a linear operator ${\boldsymbol{\Phi}}\colon D({\boldsymbol{\Phi}})\subset {{\mathcal{Y}}}\to {{\mathcal{Y}}}$ defined on a linear subspace $D({\boldsymbol{\Phi}})$ of a Hilbert space ${{\mathcal{Y}}}$. Then ${\boldsymbol{\Phi}}$ is generator of a contraction semigroup, that is a $C_0$-semigroup $G(t)$ with $\Vert G(t)\Vert_ {{\mathcal{L}}} \leq 1$ for all $t\geq 0$, if and only if

(1) $D({\boldsymbol{\Phi}})$ is dense in ${{\mathcal{Y}}}$,

(2) ${\boldsymbol{\Phi}}$ is dissipative, that is $\mathit{\text{Re}} ({\boldsymbol{\Phi}} {{\boldsymbol{y}}}, {{\boldsymbol{y}}}) \leq 0$ for all ${{\boldsymbol{y}}}\in D({\boldsymbol{\Phi}})$, and

(3) there exist $\lambda > 0$ such that $\lambda - {\boldsymbol{\Phi}}$ is surjective.

Our goal is to verify the sufficient conditions of the Lumer-Phillips theorem for (2.4). For this purpose, we start with a Korn inequality for chains of domains in contact.

Theorem 2.9. (Korn's inequality for domains in contact) Let $(\Omega, S)$ be a chain of domains in contact. Assume that ${{\mathcal{U}}}$ is a closed subspace of $H^1(\Omega)^3$ and assume that

fulfills $\tilde{ {{\mathcal{U}}}} \cap {{\mathcal{R}}}({\rm{int}}\; \overline{ \Omega}) = \{0\}$, where ${{\mathcal{R}}}({\rm{int}}\; \overline{ \Omega})$ denotes the space of rigid displacements, that is

Then there exists a Korn constant $\overline{c} = \overline{c}(\Omega) > 0$ such that

for all ${{\boldsymbol{u}}}\in {{\mathcal{U}}}$.

Proof. See ^[11], Theorem 1. The proof utilizes the same contradiction argument as that of Korn's second inequality, see e.g., Theorem 2.5 in ^[15], for a single Lipschitz domain. In fact, both statements coincide for the special case that $\Omega$ is a single Lipschitz domain. □

Note that the expression $\left[\!\left[{} \right. {{\boldsymbol{u}}} \left. {} \right]\!\right]$ on the surfaces $S$ in Theorem 2.9 is well-defined by the standard Trace theorem for $H^1(\Omega_i)^3$ for every sub-domain $\Omega_i$ of $(\Omega, S)$.

Example 2.10. We provide two examples of functional spaces for which the assumptions of Theorem 2.9 are fulfilled. They are required in upcoming proofs.

(1) Consider the spatial solution space

such that

by construction. Note that the space $\tilde{ {{\mathcal{U}}}}^ {\varepsilon}$ is the classical Sobolev space on the single connected domain ${\rm{int}}\; \overline{ \Omega^{M, s}_ {\varepsilon}}$.

Let ${{\boldsymbol{u}}}_ {\varepsilon} \in \tilde{ {{\mathcal{U}}}^ {\varepsilon}}\cap {{\mathcal{R}}}({\rm{int}}\; \overline{ \Omega_ {\varepsilon}^{M, s}})$ be arbitrarily chosen. According to Theorem 1.6-1 in ^[18], we can write ${{\boldsymbol{u}}}_ {\varepsilon}(x) = {{\boldsymbol{a}}} \times x + {{\boldsymbol{b}}}$ for some ${{\boldsymbol{a}}}, {{\boldsymbol{b}}}\in{{{\mathbb{R}}}}^3$, where $\times$ denotes the standard cross product. We will prove that ${{\boldsymbol{u}}}_ {\varepsilon} = {\bf{0}}$: By choice of the Dirichlet boundary and the periodicity of the structure domain, there exists a Dirichlet boundary point $x$ on the plane $(0, L_1) \times \{0\}\times (- {\varepsilon}/2, {\varepsilon}/2)$ such that

from which we directly deduce $a_1 = a_3 = 0$. Similarly, we can choose a Dirichlet boundary point from the plane $\{0\}\times (0, L_2) \times (- {\varepsilon}/2, {\varepsilon}/2)$ to derive $a_2 = 0$ and consequently also ${{\boldsymbol{b}}} = {\bf{0}}$.

(2) Consider the solid part $Y^s$ of the unit periodicity cell which is a chain of domains in contact by construction. Let ${{\mathcal{U}}} = H^1_{\text{per}, 0}(Y^s)^3$ such that $\tilde{ {{\mathcal{U}}}} = H^1_{\text{per}, 0}({\rm{int}}\; \overline{Y^s})^3$ and let ${{\boldsymbol{u}}}\in \tilde{ {{\mathcal{U}}}}\cap {{\mathcal{R}}}({\rm{int}}\; \overline{Y^s})$. Then again ${{\boldsymbol{u}}}(y) = {{\boldsymbol{a}}}\times y + {{\boldsymbol{b}}}$ for some ${{\boldsymbol{a}}}, {{\boldsymbol{b}}}\in{{{\mathbb{R}}}}^3$. Due to periodicity of ${{\boldsymbol{u}}}$ and construction of $Y^s$, we can derive ${{\boldsymbol{a}}} = {\bf{0}}$ as in the first example. Hence, ${{\boldsymbol{u}}}$ is a constant displacement field. Further, by vanishing mean value, we deduce ${{\boldsymbol{b}}} = {\bf{0}}$.

With the first example in mind, we can prove an auxiliary lemma covering symmetry, boundedness and coercivity of the spatial bilinear form associated with (2.4).

Lemma 2.11. The bilinear form $a_ {\varepsilon}\colon {{\mathcal{U}}}^ {\varepsilon}\times {{\mathcal{U}}}^ {\varepsilon}\to{{{\mathbb{R}}}}$ with

is symmetric, continuous and coercive. The norm $\Vert {{\boldsymbol{u}}}\Vert_{ {{\mathcal{U}}}^ {\varepsilon}}$ associated to the inner product $({{\boldsymbol{u}}}, {{\boldsymbol{U}}})_{ {{\mathcal{U}}}^ {\varepsilon}}: = a_ {\varepsilon}({{\boldsymbol{u}}}, {{\boldsymbol{U}}})$ is equivalent to the $H^1(\Omega^{M, s}_ {\varepsilon})$-norm.

Proof. The statement can be directly verified with the Trace theorem for continuity and the Korn inequality from Theorem 2.9 for coercivity in combination with the material properties in Assumption 2.3. □

We have gathered all necessary preliminary results to conclude this section with the well-posedness of (2.4).

Theorem 2.12. Let ${{\boldsymbol{g}}}_ {\varepsilon} \in L^1 \left((0, T), L^2(\Omega^{M, s}_ {\varepsilon})^3 \right)$ and $({{\boldsymbol{u}}}_0, {{\boldsymbol{w}}}_0)^T\in {{\mathcal{U}}}_ {\varepsilon} \times L^2(\Omega^{M, s}_ {\varepsilon})^3$. Then there exists a unique mild solution ${{\boldsymbol{u}}}_ {\varepsilon} \in C^0 \left([0, T], {{\mathcal{U}}}^ {\varepsilon} \right)$ to (2.4).

If additionally $({{\boldsymbol{u}}}_0, {{\boldsymbol{w}}}_0)^T\in \left(H^2(\Omega^{M, s}_ {\varepsilon})^3\cap {{\mathcal{U}}}^ {\varepsilon} \right) \times {{\mathcal{U}}}^ {\varepsilon}$ and ${{\boldsymbol{g}}}_ {\varepsilon} \in C^0 \left([0, T], L^2(\Omega^{M, s}_ {\varepsilon})^3 \right)$, as well as either

then there exists a unique classical solution

to (2.4).

Proof. To begin, we introduce the auxiliary structure velocity variable ${{\boldsymbol{w}}}_ {\varepsilon} = \partial_t {{\boldsymbol{u}}}_ {\varepsilon}$ and write ${{\boldsymbol{y}}}(t) : = ({{\boldsymbol{u}}}_ {\varepsilon}(t), {{\boldsymbol{w}}}_ {\varepsilon}(t))^T$. We consider the spatial solution space ${{\mathcal{Y}}} : = {{\mathcal{U}}}_ {\varepsilon} \times L^2(\Omega^{M, s}_ {\varepsilon})^3$, where ${{\mathcal{U}}}_ {\varepsilon}$ is equipped with the inner product $(\cdot, \cdot)_{ {{\mathcal{U}}}^ {\varepsilon}}$ from Lemma 2.11.

With the presupposition above, system (2.4) can be expressed in operator notation as

where

with ${{\boldsymbol{G}}}(t) = ({\bf{0}}, \mathit{\boldsymbol{g}}_ {\varepsilon}(t))^T$ and identity operator ${{\boldsymbol{I}}}$, as well as ${{\boldsymbol{A}}}$ being the operator associated to the bilinear form $a_ {\varepsilon}$ from Lemma 2.11. We have $D({\boldsymbol{\Phi}}) = (H^2(\Omega^{M, s}_ {\varepsilon})^3 \cap {{\mathcal{U}}}_ {\varepsilon}) \times {{\mathcal{U}}}_ {\varepsilon}$.

We verify the sufficient conditions of the Lumer-Phillips theorem to deduce that ${\boldsymbol{\Phi}}$ is generator of a contraction semigroup in ${{\mathcal{Y}}}$.

(1) Clearly, $D({\boldsymbol{\Phi}})$ is dense in ${{\mathcal{Y}}}$.

(2) The operator ${\boldsymbol{\Phi}}$ is dissipative: Let ${{\boldsymbol{y}}} = ({{\boldsymbol{u}}}, {{\boldsymbol{w}}})^T \in D({\boldsymbol{\Phi}})$. Then

(3) There exists $\lambda > 0$ such that $\lambda - {\boldsymbol{\Phi}}$ is surjective: We can choose any $\lambda > 0$. For a given $\mathit{\boldsymbol{f}} = (\mathit{\boldsymbol{f}}_1, \mathit{\boldsymbol{f}}_2)^T\in {{\mathcal{Y}}}$ consider the equation

which is equivalent to

With Lemma 2.11, we can verify that the left-hand side of (2.8) is associated to a continuous and coercive bilinear form on ${{\mathcal{U}}}_ {\varepsilon}$. Moreover, the right-hand side is associated to a linear and bounded functional on ${{\mathcal{U}}}_ {\varepsilon}$. Hence, we can apply the Lax-Milgram theorem to derive the existence and uniqueness of a solution ${{\boldsymbol{u}}}\in {{\mathcal{U}}}^ {\varepsilon}$. Standard elliptic regularity results further guarantee ${{\boldsymbol{u}}}\in D({{\boldsymbol{A}}}) = H^2(\Omega^{M, s}_ {\varepsilon})^3 \cap {{\mathcal{U}}}_ {\varepsilon}$. By plugging ${{\boldsymbol{u}}}$ into (2.7), we attain the desired existence of ${{\boldsymbol{w}}}\in {{\mathcal{U}}}_ {\varepsilon}$.

Hence, ${\boldsymbol{\Phi}}$ is generator of a contraction semigroup in ${{\mathcal{Y}}}$ and the statement follows with Theorem 2.7. □

3.   Macroscopic FSI model

In this section, a macroscopic FSI model for the flow-induced displacement of the filter structure from the previous section is presented and analyzed. For this purpose, the derived homogenized FSI model from ^[8,9] for Stokes flow through the flexural filter is recalled and afterwards extended by an interface flux term obeying Darcy's law. Existence and uniqueness of solutions to the new model problem are verified utilizing a semigroup approach.

3.1.   Homogenized FSI model

Utilizing the mathematical method of two-scale convergence, the authors in ^[8,9] rigorously derived a macroscopic FSI system for the underlying microscopic problem of incompressible Stokes flow in a cuboidal channel, that is separated in half by a thin, periodic filter structure. The considered scale limit ${\varepsilon}\to 0$ corresponds to the simultaneous homogenization and dimension reduction of the filter.

In the microscopic model of ^[8], the microscopic structure is a single connected plate, while the model of ^[9] describes the more general case with a globally connected fluid domain. The latter is directly applicable to our microscopic structure description in the case of glued yarns, that is ${{\boldsymbol{R}}}^ {\varepsilon}\to\infty$. Both models result in comparable limit systems.

In both models, fluid and structure equations are formulated on time-independent domains and coupled via linearized coupling conditions, namely the continuity of velocity and the continuity of normal stresses at the fluid-structure interface $\partial^\text{fs}\Omega_ {\varepsilon}^{M, s}$. Thereby, the models cover the fundamental case of small structure displacements. For further details, we refer to the cited articles.

A sketch of the considered microscopic model setup is given in Figure 3.

Recalling the derived macroscopic FSI system, we consider incompressible Stokes flow in two disjoint cuboidal domains

The entire model domain is denoted as

Its boundary is composed of three sets, namely

In the scale limit, the membrane domain $\Omega^M_ {\varepsilon}$ is reduced to the structure's mean-plane, denoted by

The orientation of the interior boundary $\Sigma$ is chosen as ${{\boldsymbol{e}}}_3$. The displacement of $\Sigma$ is governed by the clamped Kirchhoff-Love plate equations. As coupling conditions, the jump of fluid stresses across $\Sigma$ enters as a right-hand side of the plate equations, while the normal fluid and plate velocities coincide. The tangential fluid velocity vanishes.

Concretely, the homogenized and dimension reduced problem is to find the macroscopic fluid velocity and pressure

as well as the in-plane displacement and deflection of the structure's mean-plane

satisfying

for some given force densities $\mathit{\boldsymbol{f}}\colon (0, T)\times {\Omega_0^-\cup\Omega_0^+}\to {{{\mathbb{R}}}}^3, g_3\colon (0, T)\times \Sigma\to {{{\mathbb{R}}}}$ and initial condition ${{\boldsymbol{v}}}_0$. Here, and in the following, we write $D_ {\bar{x}}, \nabla^2_ {\bar{x}}$ for the symmetric strain tensor and the Hessian operator with respect to the in-plane variables, respectively. The parameters $\mu$ and $\rho_f$ are the fluid's dynamic viscosity and density, respectively.

The arising macroscopic model parameters are the fourth-order tensors ${\underline{\mathit{\boldsymbol{A}}}^\text{hom}}, {\underline{\mathit{\boldsymbol{B}}}^\text{hom}}$ and ${\underline{\mathit{\boldsymbol{C}}}^\text{hom}}\in{{{\mathbb{R}}}}^{2\times2\times2\times2}$. They denote the homogenized elasticity tensors of the structure that are attained from membrane and bending (elasticity) cell problems formulated on the unit cell $Y$.

Augmenting the standard elasticity cell problems by the Robin-type contact conditions of our structure model, the cell problems are to find $Y$-periodic cell solutions ${\mathit{\boldsymbol{\chi}}}_{ij}^{M, B}, i, j = 1, 2$ such that

and

where ${{\boldsymbol{M}}}^{ij} = \frac{1}{2}({{\boldsymbol{e}}}_i\otimes {{\boldsymbol{e}}}_j + {{\boldsymbol{e}}}_j\otimes {{\boldsymbol{e}}}_i) \in {{{\mathbb{R}}}}^{3\times 3}$ are the unit matrices in the space of symmetric matrices. Note that since ${{\boldsymbol{M}}}^{ij} = {{\boldsymbol{M}}}^{ji}$, we have ${\mathit{\boldsymbol{\chi}}}_{ij}^{M, B} = {\mathit{\boldsymbol{\chi}}}_{ji}^{M, B}$ and hence we attain a total of six independent cell problems.

The same cell problems have been derived with the periodic-unfolding method outside of the FSI context in ^[12,13] for the homogenization and dimension reduction of periodic, perforated structures. In the linear case, the corresponding macroscopic problems coincide with the plate Eqs (3.1) (9)-(10).

With the Korn inequality from Theorem 2.9 and the second case of Example 2.10, the proof of well-posedness of the cell problems can be easily performed.

Proposition 3.1. For each of the cell problems (3.2), (3.3), there exists a unique weak solution ${\mathit{\boldsymbol{\chi}}}_{ij}^{M, B}\in H^1_{\mathit{\text{per}}, 0}(Y^s)^3$. Here, $H^1_{\mathit{\text{per}}, 0}(Y^s)$ denotes the Sobolev space of $Y$-periodic functions with vanishing mean value on $Y^s$.

Having established the existence and uniqueness of cell solutions, we can conclude that the homogenized stiffness tensors ${\underline{\mathit{\boldsymbol{A}}}^\text{hom}}, {\underline{\mathit{\boldsymbol{B}}}^\text{hom}}$ and ${\underline{\mathit{\boldsymbol{C}}}^\text{hom}}$ with entries reading

are well defined.

In literature, a common terminology for these tensors in classical plate theory are extensional, coupling and bending stiffness tensor. Formally speaking, the entries of the tensor ${\underline{\mathit{\boldsymbol{A}}}^\text{hom}}$ determine the resistance to tensional and shearing loads, while the entries of ${\underline{\mathit{\boldsymbol{C}}}^\text{hom}}$ describe the flexural and torsional stiffness of the structure. The tensor ${\underline{\mathit{\boldsymbol{B}}}^\text{hom}}$ introduces an additional coupling between in-plane displacements and bending. In the case of glued yarns ${{\boldsymbol{R}}}^ {\varepsilon}\to\infty$, we attain the homogenized tensors denoted by $a^\star, b^\star, c^\star$ in ^[9].

Even though the FSI system (3.1) was rigorously derived in ^[8,9], its direct application for our modeling purposes is highly troublesome. This is due to the coupling condition (3.1) (11): Since the normal fluid velocity coincides with the plate's normal velocity $\partial_t u_3$ at the interface, we can deduce that there is no mass transport through the latter. For our application purposes with main flow direction being normal to the structure, the mass transport is vital, as one can easily verify that e.g., in the stationary case, system (3.1) does not posses a solution for standard inflow conditions.

Unfortunately, up to this day it is an open question if and how it is possible to derive an asymptotic model starting from the microscopic FSI problem in ^[9], which incorporates both structure displacement and mass transport (see also the conclusion of ^[9]). An extended asymptotic analysis to close this gap is in current process in ^[19]. For the time being, we fall back to a heuristic model formulation that we motivate in the following section.

3.2.   Extended homogenized FSI model

In order to perform meaningful FSI simulations in the macroscopic setting, we propose a novel heuristic model. It is an extension of system (3.1) by incorporating an additional porous interface condition obeying Darcy's law. The proposed modified FSI system requires to find

and

that satisfy

The modification of system (3.1) comes in form of the dissipative surface term (3.5) (10) with inverse permeability (i.e., resistivity) tensor ${{\boldsymbol{K}}}^{-1}$. The tensor ${{\boldsymbol{K}}}\in {{{\mathbb{R}}}}^{3\times 3}$ itself is assumed to be symmetric and positive definite. In particular, ${{\boldsymbol{K}}}^{-1}$ exists and is symmetric and positive definite as well. For notational convenience, we will write ${\hat{{{\boldsymbol{K}}}}} = \frac{1}{\mu} {{\boldsymbol{K}}}$.

It is important to note that the no-slip condition for the tangential velocity on $\Sigma$ from (3.1) is no-longer present. Furthermore, we remark that in the left-hand side of (3.5) (10), we consider the fluid velocity corrected by the normal velocity of the plate, compare e.g., with the Darcy interface condition in ^[20].

As a consequence, the dissipative term can be interpreted as a generalization of the term (3.1) (11): For the limit case ${\hat{{{\boldsymbol{K}}}}}\to {\bf{0}}$, i.e., a non-permeable interface, we recover the original coupling of fluid and plate normal velocity, as well as the no-slip condition for $v_{1, 2}$. On the other hand, if ${\hat{{{\boldsymbol{K}}}}} \to \infty$, i.e., no flow resistance at the interface, the jump of stresses $\left[\!\left[{} \right. 2\mu D({{\boldsymbol{v}}}) - p {{\boldsymbol{I}}} \left. {} \right]\!\right] {{\boldsymbol{e}}}_3$ vanishes and we attain regular Stokes flow in the entire domain $\Omega_0$.

In the stationary case, the fluid and structure equations are only one-way coupled. The resulting Stokes-Stokes problem is actually reminiscent of the system considered in ^[21] to model the blood flow through immersed (rigid) stents. The mentioned model is based on the asymptotic Stokes-Sieve results in ^[22,23].

3.3.   Preliminary results

For the derivation of well-posedness of problem (3.5), we recall some established results from literature regarding the macroscopic model parameters.

Lemma 3.1. The homogenized stiffness tensors ${\underline{\mathit{\boldsymbol{A}}}^\mathit{\text{hom}}}, {\underline{\mathit{\boldsymbol{C}}}^\mathit{\text{hom}}}$ posses the same symmetry properties as the microscopic stiffness tensor ${\underline{\mathit{\boldsymbol{A}}}}$. In general, ${\underline{\mathit{\boldsymbol{B}}}^\mathit{\text{hom}}}$ only satisfies

The next statement is a vital auxiliary Lemma required for derivation of coercivity bounds, whose proof can be found e.g., in Theorem 2 of ^[13] and references therein.

Lemma 3.2. There exists a positive constant $\underline{c} > 0$ such that for all symmetric matrices ${{\boldsymbol{P}}}^M, {{\boldsymbol{P}}}^B\in{{{\mathbb{R}}}}^{2\times 2}$ we have

We emphasize that with the choices of ${{\boldsymbol{P}}}^B = {\bf{0}}$ (respectively ${{\boldsymbol{P}}}^M = {\bf{0}}$) in Lemma 3.2, we can in particular directly verify that ${\underline{\mathit{\boldsymbol{A}}}^\text{hom}}$ and ${\underline{\mathit{\boldsymbol{C}}}^\text{hom}}$ are coercive on the space of symmetric matrices.

Definition 3.3. Let $\bar{ {{\mathcal{U}}}}: = H_0^1(\Sigma)^2, {{\mathcal{U}}}_3 : = H_0^2(\Sigma)$ and set ${{\mathcal{U}}}: = \bar{ {{\mathcal{U}}}} \times {{\mathcal{U}}}_3$ as the space of admissible macroscopic displacements equipped with the standard norm

We define the bilinear form ${a^\text{hom}}\colon {{\mathcal{U}}} \times {{\mathcal{U}}}\to{{{\mathbb{R}}}}$ induced by ${\underline{\mathit{\boldsymbol{A}}}^\text{hom}}, {\underline{\mathit{\boldsymbol{B}}}^\text{hom}}, {\underline{\mathit{\boldsymbol{C}}}^\text{hom}}$ as

The gathered knowledge about the homogenized stiffness tensors is sufficient to verify the following statement.

Lemma 3.4. The bilinear form ${a^\mathit{\text{hom}}}$ is bounded and coercive on ${{\mathcal{U}}}$. It is symmetric if and only if ${\underline{\mathit{\boldsymbol{B}}}^\mathit{\text{hom}}}$ satisfies ${b^\mathit{\text{hom}}}_{ijkl} = {b^\mathit{\text{hom}}}_{klij}$ for all $i, j, k, l = 1, 2$.

In particular, the bilinear form

defines an inner product on ${{\mathcal{U}}}$ and the induced norm

is equivalent to the norm $\Vert\cdot \Vert_ {{\mathcal{U}}}$.

3.4.   Existence proof utilizing Galerkin approach

We begin with a classical Galerkin approach, which can be applied to ensure existence of solutions for the most general form of (3.5). Uniqueness in general is only achievable under further restricting assumptions. For the overall strategy, we can adapt the provided framework for a similar FSI problem in ^[20]. The existence proof utilizes the main idea of Rothe's method or horizontal line method from numerical methods for parabolic PDE.

Recall the definition of solely space-dependent function spaces for the displacements

from the previous subsection. We let

We equip the space ${{\mathcal{Y}}}_\text{div}$ with the standard norm

Furthermore, we define the time-dependent solution spaces in the Galerkin setting as

The test space in the Galerkin setting is defined as

with $C^1_c$ denoting the space of continuously differentiable functions with compact support. We denote functions in the solution space as ${{\boldsymbol{y}}} = ({{\boldsymbol{v}}}, {\bar{\mathit{\boldsymbol{u}}}}, u_3)\in H_{ {{\mathcal{Y}}}_\text{div}}$ and use capital letters ${{\boldsymbol{Y}}} = ({{\boldsymbol{V}}}, {\bar{\mathit{\boldsymbol{U}}}}, U_3)\in H_{ {{\mathcal{Y}}}_\text{div}}^\text{test}$ for test functions.

For the rest of this subsection, we denote the inner product in $L^2((0, T), L^2(\Omega))$ for some domain $\Omega$ by $\langle \cdot, \cdot\rangle_ \Omega$. With this notation, we can derive the variational formulation by standard means.

Proposition 3.2. The variational formulation of (3.5) in the Galerkin setting is to find ${{\boldsymbol{y}}} \in H_{{ {{\mathcal{Y}}}}_\mathit{\text{div}}}$ such that for all ${{\boldsymbol{Y}}}\in H_{ {{\mathcal{Y}}}_\mathit{\text{div}}}^\mathit{\text{test}}$ the equation

is solved.

Proof. We briefly summarize the derivation of the fluid part to show how the interface term arises. By testing (3.5) (1) with ${{\boldsymbol{V}}}$ and performing partial integration in the time, as well as in the space variable, we attain

utilizing the vanishing divergence of ${{\boldsymbol{V}}}$, as well as ${{\boldsymbol{V}}}$ vanishing at time $T$. Furthermore, by plugging in the interface coupling condition (3.5) (10), we attain

By the choice of solution space, (3.5) (2) is fulfilled by default. □

For the rest of this subsection, we assume the following regularity of the right-hand side functions.

Assumption 3.5. We have that $\mathit{\boldsymbol{f}}\in L^2((0, T), L^2({\Omega_0^-\cup\Omega_0^+})^3)$ and $g_3 \in L^2((0, T), L^2(\Sigma))$.

In a next step, we derive a semi-discrete formulation of (3.5). Let $N > 1$ be a fixed number of discrete time steps and let ${[\Delta t^{}]} = T / N > 0$ denote a constant step size in time. We perform a semi-discretization of (3.5) using the backwards difference quotients

for approximation of time derivatives with $({{\boldsymbol{v}}}^n, {\bar{\mathit{\boldsymbol{u}}}}^n, u_3^n)\in {{\mathcal{Y}}}_\text{div}, n = 0, \dots, N$ being solely space dependent functions approximating $({{\boldsymbol{v}}}, {\bar{\mathit{\boldsymbol{u}}}}, u_3)$ at time $t^n = n{[\Delta t^{}]}$. For $n = 0$, this approximation is given by the initial conditions.

By plugging in the backwards approximation into (3.5), testing the system and performing partial integration solely w.r.t. the space variable, we can verify that for step $n+1$, the semi-discrete system reads as follows.

Proposition 3.3. For a time-step $n+1, n\in\{0, \dots, N-1\}$, the semi-discrete formulation of (3.5) is to find ${{\boldsymbol{y}}}^{n+1} = ({{\boldsymbol{v}}}^{n+1}, {\bar{\mathit{\boldsymbol{u}}}}^{n+1}, u_3^{n+1}) \in {{\mathcal{Y}}}_\mathit{\text{div}}$ such that

for all $({{\boldsymbol{V}}}, {\bar{\mathit{\boldsymbol{U}}}}, U_3)\in {{\mathcal{Y}}}_\mathit{\text{div}}$, where we choose

Lemma 3.6. For all $n = 0, \dots, N-1$, there exists a unique solution $({{\boldsymbol{v}}}^{n+1}, {\bar{\mathit{\boldsymbol{u}}}}^{n+1}, u_3^{n+1})\in {{\mathcal{Y}}}_\mathit{\text{div}}$ to the semi-discrete system (3.7).

Proof. For clearer notation, we can assume that all arising scalar constants, apart from ${[\Delta t^{}]}$, are equal to 1.

The statement follows by induction. For a given $n$, we start by rearranging (3.7) to

using the definition of the backwards difference quotients and by multiplying with ${[\Delta t^{}]}^2$ to remove all denominators. Our overall goal is to apply the Lax-Milgram theorem to ensure existence and uniqueness of solutions.

As the bilinear form associated to the left-hand side of (3.8) is not coercive due to improper scaling in ${[\Delta t^{}]}$, it is mandatory to consider the scaled test functions ${[\Delta t^{}]}^{-1} {\bar{\mathit{\boldsymbol{U}}}}, {[\Delta t^{}]}^{-1} U_3$, which results in the equivalent system

Note that the formulation with scaled test functions is in fact equivalent, as we require systems (3.8) and (3.9) to be fulfilled for all possible test functions in ${{\mathcal{Y}}}_\text{div}$.

To prove coercivity of the bilinear form $a^N\colon {{\mathcal{Y}}}_\text{div} \times {{\mathcal{Y}}}_\text{div} \to{{{\mathbb{R}}}}$, we estimate

for some constant $\underline{c} = \underline{c}({[\Delta t^{}]}) > 0$. Here, the first equality is due to the symmetry of ${\hat{{{\boldsymbol{K}}}}}^{-1}$. In the second equality we additionally utilized the positive definiteness of ${\hat{{{\boldsymbol{K}}}}}^{-1}$, guaranteeing the existence of the (unique) square root ${\hat{{{\boldsymbol{K}}}}}^{-\frac{1}{2}}$. The last estimate utilizes the standard Korn inequality for ${{\boldsymbol{v}}}^{n+1}$.

Moreover, the continuity of $a^N$ follows from application of the Trace theorem to the interface terms involving ${{\boldsymbol{v}}}^{n+1}, {{\boldsymbol{V}}}$.

With the same argument, one can verify that the right-hand side of (3.9) is a bounded linear functional when we treat solutions at the prior time step as given data. Here, we require that $\mathit{\boldsymbol{f}}^{n+1}\in L^2({\Omega_0^-\cup\Omega_0^+})^3, g_3^{n+1}\in L^2(\Sigma)$, which is guaranteed by Assumption 3.5.

By inductive application of the Lax-Milgram theorem, we can deduce that there exists a unique solution $({{\boldsymbol{v}}}^{n+1}, {\bar{\mathit{\boldsymbol{u}}}}^{n+1}, u_3^{n+1})\in {{\mathcal{Y}}}_\text{div}$ to (3.9) and hence also to (3.7) for all $n = 0, \dots, N-1$. □

As a next step, from the solutions of the semi-discrete systems for given $N$, we construct a sequence $\{ {{\boldsymbol{y}}}^{[N]} \}_{N\in \mathbb{N}}$ of piecewise constant functions in time defined by

Similarly, we approximate the right-hand side functions by

With the above constructions, we can verify the following statement.

Proposition 3.4. For given $N$, the function ${{\boldsymbol{y}}}^{[N]}$ is solution to the system

for all ${{\boldsymbol{Y}}} = ({{\boldsymbol{V}}}, {\bar{\mathit{\boldsymbol{U}}}}, U_3)\in H_{ {{\mathcal{Y}}}_\mathit{\text{div}}}^\mathit{\text{test}}$, where $\dot w^{[N]}, \ddot w^{[N]}$ denote the backwards difference quotients

for piecewise constant $w^{[N]}$.

Proof. For a given $n$, we have that ${{\boldsymbol{y}}}^{[N]}\vert_{(t^{n-1}, t^n]} = ({{\boldsymbol{v}}}^n, {\bar{\mathit{\boldsymbol{u}}}}^n, u_3^n)$ solves the semi-discrete system (3.7) for all test functions in ${{\mathcal{Y}}}_\text{div}$. By construction, we further have that ${{\boldsymbol{Y}}}(t)\in {{\mathcal{Y}}}_\text{div}$ for any given ${{\boldsymbol{Y}}}\in H_{ {{\mathcal{Y}}}_\text{div}}^\text{test}$. Hence, we can utilize ${{\boldsymbol{Y}}}(t)$ as a test function of (3.7) and integrate in time over $(t^{n-1}, t^n]$. The statement then follows by adding all attained equations for $n = 1, \dots, N$. □

Moreover, we have the following convergence result for the right-hand side functions from Assumption 3.5.

Lemma 3.7. There exists a subsequence of the sequence $\{(\mathit{\boldsymbol{f}}^{[N]}, g_3^{[N]})\}_{N\in \mathbb{N}}$, denoted with the same index, such that

Proof. One can directly compute that the respective norms of $\mathit{\boldsymbol{f}}^{[N]}, g_3^{[N]}$ are bounded by that of the original functions $\mathit{\boldsymbol{f}}, g_3$ and we can utilize weak compactness to extract a weakly converging subsequence, respectively. □

Our main goal is to extract a subsequence of $\{ {{\boldsymbol{y}}}^{[N]} \}_{N\in \mathbb{N}}$ that weakly converges to a solution of (3.6) in the limit $N\to\infty$. For this purpose, we first derive uniform bounds for ${{\boldsymbol{y}}}^{[N]}$ in the following lemma. In the statement, we write ${{\mathcal{U}}}_3^\star$ for the dual space of ${{\mathcal{U}}}_3$.

Lemma 3.8. There exists a uniform constant $\overline{c} > 0$ independent of $N$ such that

Proof. Similar to the previous proof, we will assume that all arising scalar constants, apart from ${[\Delta t^{}]}$, are equal to 1.

We consider a fixed $N$ and choose $n\leq N-1$. By testing the semi-discrete system (3.7) with the solution variables ${{\boldsymbol{V}}} = {{\boldsymbol{v}}}^{n+1}, {\bar{\mathit{\boldsymbol{U}}}} = \dot {\bar{\mathit{\boldsymbol{u}}}}^{n+1}, U_3 = \dot u_3^{n+1}$ and multiplying with ${[\Delta t^{}]}$, we attain

After application of Young's inequality to all mixed terms and absorbing all appearing constants apart from ${[\Delta t^{}]}$, we can derive the estimate

for some constant $\overline{c}_1 > 0$ independent of $N$.

Next, by summation of the inequalities (3.11) for $k = 0, \dots, n$, we attain

for all $n = 0, \dots, N-1$. With Lemma 3.7, the right-hand side of (3.12) is uniformly bounded with a constant solely dependent on initial data, applied forces and the constant $\overline{c}_1$.

From the definition of ${{\boldsymbol{y}}}^{[N]}$ as piecewise constant function in time and Lemma 3.4 we deduce that (3.12) implies

for some constant $\overline{c}_2 > 0$ independent of $N$.

Finally, by setting all test functions apart from $U_3$ in (3.7) to zero, we attain the equality

for all $n = 0, \dots, N-1$. Summation over all $n$ together with (3.13) directly delivers the uniform estimate

for a constant $\overline{c}_3 > 0$ independent of $N$ as desired. □

We have gathered all necessary tools to derive the existence of solutions.

Theorem 3.9. There exists at least one solution $({{\boldsymbol{v}}}, {\bar{\mathit{\boldsymbol{u}}}}, u_3)\in H_{{ {{\mathcal{Y}}}}_\mathit{\text{div}}}$ to (3.6).

Proof. The uniform bounds from Lemma 3.8 are sufficient to ensure the convergence

for a subsequence of $\{ {{\boldsymbol{y}}}^{[N]}\}_{N\in \mathbb{N}}$ in $H_{{ {{\mathcal{Y}}}}_\text{div}}$ denoted with the same index.

For a given $N$, we test equation (3.10) with an arbitrary test function ${{\boldsymbol{Y}}} \in H_{{ {{\mathcal{Y}}}}_\text{div}}^\text{test}$. Due to linearity and the above weak convergences of ${{\boldsymbol{y}}}^{[N]}$, we can go to the limit $N\to\infty$ to directly attain that ${{\boldsymbol{y}}} \in H_{{ {{\mathcal{Y}}}}_\text{div}}$ is solution to the variational formulation (3.6). □

In general, we are not be able to derive uniqueness of solutions without additional assumptions on the regularity of the displacements w.r.t. time.

Assumption 3.10. We assume that $\partial_t {\bar{\mathit{\boldsymbol{u}}}}, \partial_t u_3$ are admissible test functions in the sense that

Note that this assumption is for example fulfilled for classical solutions of (3.5).

Theorem 3.11. If the solutions to (3.6) fulfill Assumption 3.10, then there exists a unique solution.

Proof. The statement follows with a standard energy estimate. Consider the difference $({{\boldsymbol{v}}}, {\bar{\mathit{\boldsymbol{u}}}}, u_3)\in H_{ {{\mathcal{Y}}}_\text{div}}$ of two solutions to (3.6), which itself solves the system for zero right-hand side and initial conditions. Let $t\in (0, T)$ and test (3.5) with $({{\boldsymbol{v}}}, \partial_t {\bar{\mathit{\boldsymbol{u}}}}, \partial_t u_3)$. Together with the coercivity of ${a^\text{hom}}$ from Lemma 3.4 we attain

for some constant $\underline{c} > 0$.

Integrating with respect to time delivers

for all $t$ and Gronwall's inequality implies $({{\boldsymbol{v}}}, {\bar{\mathit{\boldsymbol{u}}}}, u_3) = {\bf{0}}$ which concludes the proof. □

3.5.   Existence proof utilizing semigroup theory

As seen, the existence proof utilizing a classical Galerkin approach is quite tedious. Hence, we provide a secondary proof utilizing semigroup theory. It is applicable for the case ${\underline{\mathit{\boldsymbol{B}}}^\text{hom}} = {\bf{0}}$, which is a frequently met case for symmetric microstructures such as woven filters, see e.g., Lemma 6.9 in ^[12].

For this subsection, we consider the space-dependent functional spaces

Theorem 3.12. Assume that ${\underline{\mathit{\boldsymbol{B}}}^\mathit{\text{hom}}} = {\bf{0}}$. Let ${{\boldsymbol{v}}}_0 \in L^2_\mathit{\text{div}}({\Omega_0^-\cup\Omega_0^+})$ and $\mathit{\boldsymbol{f}}\in L^1((0, T), L^2_\mathit{\text{div}}({\Omega_0^-\cup\Omega_0^+}))$, as well as $g_3\in L^1((0, T), L^2(\Sigma))$. Then (3.5) has a unique mild solution with ${\bar{\mathit{\boldsymbol{u}}}} = {\bf{0}}$ and $({{\boldsymbol{v}}}, u_3) \in C^0([0, T], L^2_\mathit{\text{div}}({\Omega_0^-\cup\Omega_0^+}) \times H_0^2(\Sigma))$.

If additionally ${{\boldsymbol{v}}}_0 \in {{\mathcal{V}}}$, as well as $\mathit{\boldsymbol{f}}\in C^0([0, T], L^2_\mathit{\text{div}}({\Omega_0^-\cup\Omega_0^+})), g_3 \in C^0([0, T], L^2(\Sigma))$ and either one of the conditions

and

is satisfied, respectively, then (3.5) has a unique classical solution with ${\bar{\mathit{\boldsymbol{u}}}} = {\bf{0}}$ and

Proof. Again, for notational convenience, we assume that the scalar coefficients are equal to 1. We introduce the auxiliary variable $w_3 = \partial_t u_3$ denoting the plate's normal velocity. The spatial solution space is chosen as

where we equip the space ${{\mathcal{U}}}_3$ with the inner product

and induced norm $\Vert \cdot\Vert_{ {{\mathcal{U}}}_3}$. Note that this choice is possible by symmetry and coercivity of ${\underline{\mathit{\boldsymbol{C}}}^\text{hom}}$ on the space of symmetric matrices.

Due to the vanishing coupling stiffness tensor ${\underline{\mathit{\boldsymbol{B}}}^\text{hom}}$, we can immediately deduce ${\bar{\mathit{\boldsymbol{u}}}} = {\bf{0}}$, such that system (3.5) can be expressed in operator form as

with $\mathit{\boldsymbol{F}}(t) = (\mathit{\boldsymbol{f}}(t), 0, g_3(t))^T$ and

where the arising operators are associated with the bilinear forms

and the identity operator ${{\boldsymbol{I}}}$. We have $D({\boldsymbol{\Phi}}) = {{\mathcal{V}}} \times \left(H^4(\Sigma) \cap {{\mathcal{U}}}_3 \right) \times {{\mathcal{U}}}_3$.

We show that ${\boldsymbol{\Phi}}$ is generator of a contraction semigroup in ${{\mathcal{Y}}}$ utilizing the sufficient conditions in the Lumer-Phillips theorem.

(1) Clearly, $D({\boldsymbol{\Phi}})$ is dense in ${{\mathcal{Y}}}$.

(2) The operator ${\boldsymbol{\Phi}}$ is dissipative: Let ${{\boldsymbol{y}}}\in D({\boldsymbol{\Phi}})$. We can directly compute

Here, ${\hat{{{\boldsymbol{K}}}}}^{-\frac{1}{2}}\in{{{\mathbb{R}}}}^{3\times 3}$ denotes the square root of ${\hat{{{\boldsymbol{K}}}}}^{-1}$ which is uniquely defined by symmetry and positive definiteness.

(3) There exists a $\lambda > 0$ such that $\lambda - {\boldsymbol{\Phi}}$ is surjective: Let $\lambda > 0$ and $\mathit{\boldsymbol{f}} = (\mathit{\boldsymbol{f}}_1, f_2, f_3)^T\in {{\mathcal{Y}}}$ be given. We want to prove the solvability of the system

which is equivalent to

Solely considering equations (3.14) and (3.16), we can verify that the left-hand side is associated to the bilinear form

which is continuous for all $\lambda$. Moreover, we can compute

Hence, for $\lambda = 1$ we attain

and thereby coerciveness. We can apply the Lax-Milgram theorem to deduce the existence of a unique $({{\boldsymbol{v}}}, u_3)^T\in {{\mathcal{V}}} \times {{\mathcal{U}}}_3$. Elliptic regularity further ensures $u_3\in H^4\cap {{\mathcal{U}}}_3$. From Eq (3.15), we finally deduce the existence of $w_3\in {{\mathcal{U}}}_3$.

Hence, ${\boldsymbol{\Phi}}$ is generator of a contraction semigroup in ${{\mathcal{Y}}}$ and the statement follows with Theorem 2.7. □

4.   Conclusions

A fluid-structure interaction problem of non-stationary Stokes flow through a thin, permeable structure was considered. A homogenized and dimension reduced model was presented and extended by an interface-flux term obeying Darcy's law. The existence and uniqueness of solutions to the non-stationary microscopic structure model was verified utilizing a semigroup approach. Furthermore, well-posedness of the new macroscopic FSI model was derived with a classical Galerkin approach, as well as with a semigroup approach under frequently met assumptions on the microscopic structure.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The research is funded by the DFG-Project OR 190/6-3 in the department of Flow and Material Simulation of the Fraunhofer ITWM, which covers dimension reduction approaches on the yarn level for the FSI simulation with deterministic filter media.

We thank Prof. Dr. Grigory Panasenko, University of Lyon / University of Saint-Etienne, for helpful discussions regarding dimension reduction for fluid-structure interaction problems with periodic media.

We thank Dr. Konrad Steiner, Fraunhofer ITWM, for suggestions regarding the extension of the homogenized FSI model by a Darcy interface term.

Conflict of interest

All authors declare no conflicts of interest in this paper.