Study on the symmetries and conserved quantities of flexible mechanical multibody dynamics

Mingliang Zheng; Mingliang Zheng

doi:10.3934/math.20231430

AIMS Mathematics

2023, Volume 8, Issue 11: 27969-27982. doi: 10.3934/math.20231430

Previous Article Next Article

Research article Special Issues

Study on the symmetries and conserved quantities of flexible mechanical multibody dynamics

Mingliang Zheng ^{1,2
,
,}

1.
Faculty of Mechanical Engineering, Taihu University of Wuxi, Qianrong Road 68, Wuxi 21400, China
2.
Jiangsu Key Laboratory of Green Process Equipment, Changzhou University, Changzhou 213000, China

Received: 22 July 2023 Revised: 17 September 2023 Accepted: 26 September 2023 Published: 11 October 2023
MSC : 34C14, 37M05

In this paper, in order to provides a powerful new tool for quantitative and qualitative analysis of dynamics properties in flexible mechanical multibody systems, the symmetry theory and numerical algorithms for preserving structure in modern analytical mechanics is introduced into flexible multibody dynamics. First, taking the hub-beam systems as an example, the original nonlinear partial differential-integral equations of the system dynamics model are discretized into the finite-dimensional Lagrange equations by using the assumed modal method. Second, the group analysis theory is introduced and the criterion equations and the corresponding conserved quantities of Noether symmetries are given according to the invariance principle, which provide an effective way for analytic integral theory of dynamic equations. Finally, a conserved quantity-preserving numerical algorithm is constructed by coordinates incremental discrete gradient, which makes full use of the invariance of conserved quantity to eliminate the error consumption for a long time. The simulation results show that the deeper mechanical laws and motion characteristics of flexible mechanical multibody systems dynamics can be obtained with the help of symmetries and conserved quantities, which can provide reference for more precise dynamic optimization design and advanced control of systems.

Keywords:

Citation: Mingliang Zheng. Study on the symmetries and conserved quantities of flexible mechanical multibody dynamics[J]. AIMS Mathematics, 2023, 8(11): 27969-27982. doi: 10.3934/math.20231430

Related Papers:

[1]	Lina Zhang, Xiaoting Rui, Jianshu Zhang, Guoping Wang, Junjie Gu, Xizhe Zhang . A framework for establishing constraint Jacobian matrices of planar rigid-flexible-multibody systems. AIMS Mathematics, 2023, 8(9): 21501-21530. doi: 10.3934/math.20231096
[2]	Tamara M. Garrido, Rafael de la Rosa, Elena Recio, Almudena P. Márquez . Conservation laws and symmetry analysis of a generalized Drinfeld-Sokolov system. AIMS Mathematics, 2023, 8(12): 28628-28645. doi: 10.3934/math.20231465
[3]	Chaudry Masood Khalique, Oke Davies Adeyemo, Kentse Maefo . Symmetry solutions and conservation laws of a new generalized 2D Bogoyavlensky-Konopelchenko equation of plasma physics. AIMS Mathematics, 2022, 7(6): 9767-9788. doi: 10.3934/math.2022544
[4]	Adil Jhangeer, Ali R Ansari, Mudassar Imran, Beenish, Muhammad Bilal Riaz . Lie symmetry analysis, and traveling wave patterns arising the model of transmission lines. AIMS Mathematics, 2024, 9(7): 18013-18033. doi: 10.3934/math.2024878
[5]	Miguel Vivas-Cortez, Yasir Masood, Absar Ul Haq, Imran Abbas Baloch, Abdul Hamid Kara, F. D. Zaman . Symmetry analysis and conservation laws of time fractional Airy type and other KdV type equations. AIMS Mathematics, 2023, 8(12): 29569-29576. doi: 10.3934/math.20231514
[6]	Huizhang Yang, Wei Liu, Yunmei Zhao . Lie symmetry reductions and exact solutions to a generalized two-component Hunter-Saxton system. AIMS Mathematics, 2021, 6(2): 1087-1100. doi: 10.3934/math.2021065
[7]	Miao Yang, Lizhen Wang . Lie symmetry group, exact solutions and conservation laws for multi-term time fractional differential equations. AIMS Mathematics, 2023, 8(12): 30038-30058. doi: 10.3934/math.20231536
[8]	Amjad Hussain, Muhammad Khubaib Zia, Kottakkaran Sooppy Nisar, Velusamy Vijayakumar, Ilyas Khan . Lie analysis, conserved vectors, nonlinear self-adjoint classification and exact solutions of generalized $\left(N+1\right)$ -dimensional nonlinear Boussinesq equation. AIMS Mathematics, 2022, 7(7): 13139-13168. doi: 10.3934/math.2022725
[9]	Ziying Qi, Lianzhong Li . Lie symmetry analysis, conservation laws and diverse solutions of a new extended (2+1)-dimensional Ito equation. AIMS Mathematics, 2023, 8(12): 29797-29816. doi: 10.3934/math.20231524
[10]	Gözde Özkan Tükel . Integrable dynamics and geometric conservation laws of hyperelastic strips. AIMS Mathematics, 2024, 9(9): 24372-24384. doi: 10.3934/math.20241186

Abstract

1. Introduction

With the development of modern science and technology, in practical engineering, especially in vehicle, spacecraft, mechanism and robot, there are many intelligent and lightweight materials, which are usually connected with rigid parts through joints and/or force elements such as spring and damping, forming an independent discipline branch called flexible multibody systems dynamics ^[1]. Its research focus is the accurate calculation of the spatial characteristics of actuator motion (such as vibration frequency) and the control (such as stability, flutter and obstacle avoidance) ^[2]. At present, the flexible multibody systems dynamics are applied to the torsional vibration of deployable slender flexible antenna and solar array ^[3,4], the movement deformation of service space robot on orbit ^{[5,6,7,8,9,10]}, the flexibility of high-speed vehicle carriage ^[11], the vibration of turbine elastic blade ^[12], the elastic vibration and control for mechanical arm of textile machine ^[13]. All of these studies show that there is a strong nonlinear coupling between the vibration deformation and the large-scale space motion of flexible body, which has a great effect on the dynamic behavior of the system, and has become an important factor in the system's analysis and control. Flexible body dynamics is a kind of strongly coupled, time-varying, distributed parameter and high-dimensional nonlinear process. The primary tasks on the dynamics of flexible mechanical multibody systems are: (a) to establish the general equation models for the system's kinematics and dynamics; (b) to design the efficient calculation method for the kinematics law and dynamics response.

The symmetry theory of dynamic systems is a higher-level rule in theoretical physics, engineering mathematics and modern mechanics. The research on the symmetries of system motion equations is helpful to reveal the internal characteristics and deep-seated laws of mechanical systems ^[14]. The symmetries of mechanical systems are closely related to conserved quantities. The conserved quantity not only has obvious physical significance, but also are the first integral, which can reduce the order of original equations and construct structure-preserving numerical algorithms. The main methods to find the system's conserved quantities by symmetries are Noether symmetry ^[15] and Lie symmetry ^[16]. However, at present, the research of flexible mechanical multibody systems dynamics mainly uses the classical numerical algorithm or the CAD/CAE software joint-simulation, which has not been carried out in-depth in the analytical integration and structure-preserving numerical theory. As we all know, the analytic solution of a differential equation can more directly reflect the quantitative display relationship between system's parameters and obtain the global properties of a nonlinear system in a large range. The conserved quantity can also be used as the design of difference schemes to improve the accuracy of numerical algorithms. Therefore, it is of great significance to study the symmetries and conserved quantities of flexible mechanical multibody systems dynamics in this paper.

The purposes to study the symmetries and conserved quantities of flexible multibody dynamics is to construct some mechanical structure-preserving numerical algorithms. The merits of the conserved quantity-preserving numerical algorithm based on symmetry theory. First, it does not contain artificial dissipation and is not a "white noise" error and can effectively maintain the symplectic structure of the Hamiltonian system, so that the evolutionary behavior of the overall structure over time can be more realistically preserved. Second, it can overcome the shortcomings of traditional numerical algorithms such as Euler or Runge Kutta in terms of integrity, stability, maintaining physical significance, and long-term tracking ability and more importantly, it can improve computational accuracy and verify the regularity of the system.

2. Dynamics model of flexible mechanical multibody systems

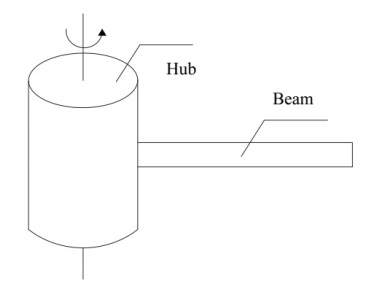
Flexible mechanical multibody systems can be divided into ideal unconstrained systems, holonomic constrained systems and nonholonomic constrained systems according to the constraint forms. From the topological structure of the model, the objects of flexible multibody systems dynamics are similar to multi-rigidbody systems, which have tree-type open-chain structures, closed chain structures and mixed structures, as shown in Figure 1. The most typical basic system configuration in flexible spacecraft and outer space robots is a hub-beam system, as shown in Figure 2. The rotating motion of the central rigid body is coupled with the vibration of the flexible beam.

Figure 1. Topological structure of flexible multibody systems.

DownLoad: Full-Size Img PowerPoint

Figure 2. Hub-beam system schematic.

DownLoad: Full-Size Img PowerPoint

At present, the methods for deriving the dynamics model of the flexible mechanical multibody systems are mainly divided into two categories ^[17]: those based on vector analysis, i.e., the Newton-Euler method and the developed Roberson-Wittenberg method, and those based on variational principle, the i.e., D'Alembert-Lagrange principle, the Lagrange equations, the Jourdan principle, the Gauss principle, the Kane method developed from D-L principle and the Hamilton method. Because analytical mechanics starts from the energy point of view and makes full use of constraints, the Euler-Lagrange equations obtained have the characteristics of universality and wide applicability. Without loss of generality, we will mainly use the method of analytical mechanics to study the dynamics theory of unconstrained (free floating) hub-beam.

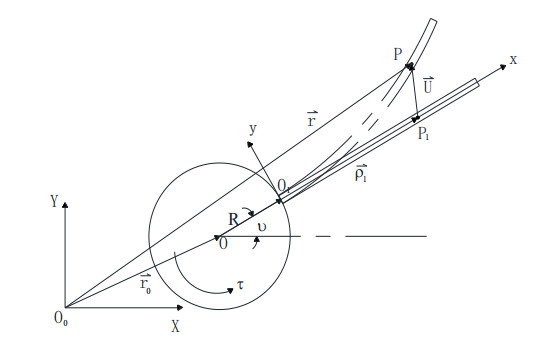
The flexible beam is isotropic and uniform section, the shear and torsional deformations. The gravity and damping forces are not considered. The angular velocity of the central rigid body is lower, and the beam is slightly deformed. Establish a plane coordinate system perpendicular to the rotation axis as shown in Figure 3.

Figure 3. Hub-beam dynamic model.

DownLoad: Full-Size Img PowerPoint

O₀-XY is the inertial frame ${{\bf{\vec e}}^0}$ , O₁-XY is the floating coordinate system ${{\bf{\vec e}}^1}$ consolidated on the beam, the rigid body rotation angle $\theta$ , the deformation u at any point P on the beam, the transformation matrix

$A = \left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$

from ${{\bf{\vec e}}^1}$ to ${{\bf{\vec e}}^0}$ . The other structural parameters include the moment of inertia J, mass m, radius R, length of the flexible beam l, cross-sectional area A, modulus of elasticity E, moment of inertia I of section to neutral axis, and linear density $\kappa.$

The Lagrange equations of motion in analytical mechanics are:

$\frac{d}{{dt}}\left[ {\frac{{\partial L}}{{\partial {{\dot q}_i}}}} \right] - \frac{{\partial L}}{{\partial {q_i}}} = {F_i}.$

(1)

Here, $L = T - V$ is the Lagrange function and ${F_i}$ is the nonpotential external force corresponds to the generalized coordinate ${q_i}.$

A very important proposition in flexible mechanical multibody dynamics and control is how to discretize the elastic continuum. For Euler-Bernoulli beams, flexible modes or finite elements can be used for discretization. The flexible mode method is

${\bf{U}}(x, t) = {\bf{\Phi }}(x){\bf{u}}(t).$

(2)

Here, ${\bf{\Phi }}$ is the modal shape matrix and ${\bf{u}}$ is the modal coordinate matrix.

The generalized coordinates of the system are ${\bf{q}} = {[\begin{array}{*{20}{c}} X & Y & \theta & {\bf{u}} \end{array}]^T}$ . The kinetic energy of the system is

$T(X, Y, \theta , {\bf{u}}) = \frac{1}{2}{\dot {\vec r}_0}m{\dot {\vec r}_0} + \frac{1}{2}J{\theta ^2} + \frac{1}{2}\kappa \int_0^l {{{\dot {\vec r}}^T}\dot {\vec r}dx} = \frac{1}{2}{{\bf{\dot q}}^T}{\bf{M\dot q}}.$

(3)

Here, ${\bf{M}}$ is the generalized mass matrix.

The potential energy of the system is:

$V({\bf{u}}) = \frac{1}{2}EI\int_0^l {(\frac{{\partial U}}{{\partial {x^2}}})} dx = \frac{1}{2}{{\bf{q}}^T}{\bf{Kq}}.$

(4)

Here, ${\bf{K}}$ is the stiffness matrix corresponding to the generalized coordinates q.

The equivalent generalized external forces of the system about the external control input torque ${\bf{ \pmb{\mathsf{ τ}} }}$ acting on the generalized coordinates ${\bf{q}}$ are

$Q = {[\begin{array}{*{20}{c}} {{Q_1}}&{{Q_2}}&{{Q_3}}&{{\bf{Q'}}} \end{array}]^T} .$

Substituting the Eqs (3) and (4) into the Eq (1), the dynamic equations of the hub-beam can be obtained as:

${\bf{M\ddot q}} + [\frac{{d{\bf{M}}}}{{dt}} - \frac{1}{2}(\frac{{\partial {\bf{M}}}}{{\partial {\bf{q}}}}{\bf{\dot q}})]{\bf{\dot q}} + {\bf{Kq}} = {\bf{Q}}.$

(5)

The dynamic equations of the above flexible mechanical multibody systems are of mixed coordinates forms. The joint coordinates are coupled with the deformation of the flexible beam. The mass matrix is highly nonlinear and the stiffness matrix is the same as that in structural vibration dynamics.

3. Noether symmetries and conserved quantities

The form of Hamilton action of hub-beam is

$S(\gamma ) = \int_{{t_1}}^{{t_2}} {L(t, {\bf{q}}, {\bf{\dot q}})} dt = \int_{{t_1}}^{{t_2}} {(T - V)} dt.$

(6)

Taking the infinitesimal transformation about time and coordinates

${t^*} = t + \Delta t = t + \varepsilon {\xi _0}(t, {\bf{q}}, {\bf{\dot q}}), q_s^* = {q_s}(t) + \Delta {q_s} = {q_s}(t) + \varepsilon {\xi _s}(t, {\bf{q}}, {\bf{\dot q}}).$

(7)

Here, ${\xi _0}, {\xi _s}$ are infinitesimal generator functions.

The generalized quasi Noether symmetry is that the total variation of action (6) under the transformation (7) satisfies

$\Delta S = - \int_{{t_1}}^{{t_2}} {\{ \frac{d}{{dt}}(\Delta G) + \sum\limits_{s = 1}^n {{Q_s}\delta {q_s}} } \} dt.$

(8)

Here, $\Delta G = \varepsilon {G_N}(t, {\bf{q}}, {\bf{\dot q}})$ , ${G_N}$ is a canonical function and ${Q_s}$ is nonpotential generalized force.

According to the relationship between the total variation and the isochronous variation

$\delta {q_s} = \Delta {q_s} - {\dot q_s}\Delta t = \varepsilon ({\xi _s} - {\dot q_s}{\xi _0}) .$

By expanding the Eq (8), we have:

$\frac{{\partial L}}{{\partial t}}{\xi _0} + \sum\limits_{s = 1}^n {\frac{{\partial L}}{{\partial {q_s}}}{\xi _s}} + \sum\limits_{s = 1}^n {\frac{{\partial L}}{{\partial {{\dot q}_s}}}({{\dot \xi }_s}} - {\dot q_s}{\dot \xi _0}) + L{\dot \xi _0} + \sum\limits_{s = 1}^n {{Q_s}({\xi _s} - {{\dot q}_s}{\xi _0}) + {{\dot G}_N}} = 0.$

(9)

For the convenience of spacecraft control design, the central rigid body only rotates and only the first mode and corresponding mode function $\Phi (x) = \sin \frac{\pi }{{2l}}x$ of flexible body are only selected, i.e., the Lagrange function of the system is

$L = \frac{1}{2}[J+\kappa ({u}^{2}\frac{l}{2}+\frac{{l}^{3}}{3}+R{l}^{2}+{R}^{2}l)]{\dot{\theta }}^{2}+\kappa \frac{l}{4}{\dot{u}}^{2}+(\kappa R\frac{2l}{\pi }+\kappa \frac{4{l}^{2}}{{\pi }^{2}})\dot{u}\dot{\theta }-\frac{{\pi }^{4}}{64{l}^{3}}EI{u}^{2}.$

(10)

Substituting the Eq (10) into the Eq (9) to obtain:

$\begin{array}{l}(\frac{1}{2}l{\dot{\theta }}^{2}u-\frac{{\pi }^{4}}{32{l}^{3}}EIu){\xi }_{2}+(-\frac{{\pi }^{4}}{32{l}^{3}}EI{u}^{2}-L)(\frac{\partial {\xi }_{0}}{\partial t}+\frac{\partial {\xi }_{0}}{\partial \theta }\dot{\theta }+\frac{\partial {\xi }_{0}}{\partial u}\dot{u})\\ +[(J+\kappa ({u}^{2}\frac{l}{2}+\frac{{l}^{3}}{3}+R{l}^{2}+{R}^{2}l))\dot{\theta }+(\kappa R\frac{2l}{\pi }+\kappa \frac{4{l}^{2}}{{\pi }^{2}})\dot{u}](\frac{\partial {\xi }_{1}}{\partial t}+\frac{\partial {\xi }_{1}}{\partial \theta }\dot{\theta }+\frac{\partial {\xi }_{1}}{\partial u}\dot{u})\\ +[\kappa \frac{L}{2}\dot{u}+(\kappa R\frac{2l}{\pi }+\kappa \frac{4{l}^{2}}{{\pi }^{2}})\dot{\theta }](\frac{\partial {\xi }_{2}}{\partial t}+\frac{\partial {\xi }_{2}}{\partial \theta }\dot{\theta }+\frac{\partial {\xi }_{2}}{\partial u}\dot{u})+{Q}_{1}({\xi }_{1}-\dot{\theta }{\xi }_{0})\\ = -\frac{\partial {G}_{N}}{\partial t}-\frac{\partial {G}_{N}}{\partial \theta }\dot{\theta }-\frac{\partial {G}_{N}}{\partial u}\dot{u};\\ (-\frac{{\pi }^{4}}{32{l}^{3}}EI{u}^{2}-L)\frac{\partial {\xi }_{0}}{\partial \dot{\theta }}+[(J+\kappa ({u}^{2}\frac{l}{2}+\frac{{l}^{3}}{3}+R{l}^{2}+{R}^{2}l))\dot{\theta }\\ +(\kappa R\frac{2l}{\pi }+\kappa \frac{4{l}^{2}}{{\pi }^{2}})\dot{u}]\frac{\partial {\xi }_{1}}{\partial \dot{\theta }}+[\kappa \frac{L}{2}\dot{u}+(\kappa R\frac{2l}{\pi }+\kappa \frac{4{l}^{2}}{{\pi }^{2}})\dot{\theta }]\frac{\partial {\xi }_{2}}{\partial \dot{\theta }}\\ = \frac{\partial {G}_{N}}{\partial \dot{\theta }};\\ (-\frac{{\pi }^{4}}{32{l}^{3}}EI{u}^{2}-L)\frac{\partial {\xi }_{0}}{\partial \dot{u}}+[(J+\kappa ({u}^{2}\frac{l}{2}+\frac{{l}^{3}}{3}+R{l}^{2}+{R}^{2}l))\dot{\theta }\\ +(\kappa R\frac{2l}{\pi }+\kappa \frac{4{l}^{2}}{{\pi }^{2}})\dot{u}]\frac{\partial {\xi }_{1}}{\partial \dot{u}}+[\kappa \frac{L}{2}\dot{u}+(\kappa R\frac{2l}{\pi }+\kappa \frac{4{l}^{2}}{{\pi }^{2}})\dot{\theta }]\frac{\partial {\xi }_{2}}{\partial \dot{u}}\\ = \frac{\partial {G}_{N}}{\partial \dot{u}}.\end{array}$

(11)

By solving the above generalized killing Eq (11), we get

${\xi _0} = 1, {\xi _1} = {\xi _2} = 0, {G_N} = \tau \theta .$

(12)

The symmetry of continuous transformation corresponds to a conserved quantity (the first integration), which can reduce the order of differential equation and play an important role in the integrability, linearization, motion constant and stability of dynamic equation. The Noether symmetry can directly lead to a class of Noether-type conserved quantity in ^[18]. Then, by combining with the initial conditions, it is easier to solve the exact response solution of the original dynamical system.

The form of Noether-type conserved quantity is

${I_N} = L{\xi _0} + \sum\limits_{s = 1}^n {\frac{{\partial L}}{{\partial {{\dot q}_s}}}} ({\xi _s} - {\dot q_s}{\xi _0}) + {G_N} = {\text{cons}}t.$

(13)

Substituting the Eq (12) into the Eq (13), we can get the conserved quantity of hub-beam:

${I}_{N} = \tau \theta -\frac{1}{2}[J+\kappa ({u}^{2}\frac{l}{2}+\frac{{l}^{3}}{3}+R{l}^{2}+{R}^{2}l)]{\dot{\theta }}^{2}-\kappa \frac{l}{4}{\dot{u}}^{2}-(\kappa R\frac{2l}{\pi }+\kappa \frac{4{l}^{2}}{{\pi }^{2}})\dot{u}\dot{\theta }-\frac{{\pi }^{4}}{64{l}^{3}}EI{u}^{2}.$

(14)

Obviously, the Eq (14) represents the energy conservation law of the mechanical system.

4. Numerical simulation by conserved quantity-preserving

When the rotation is slow and flexible beams have only transverse deflection, the dynamic Eq (5) of hub-beam can be written as

$\begin{array}{l}{\bf{M}}\left[\begin{array}{c}\ddot{\theta }\\ \ddot{u}\end{array}\right]+{\bf{G}}\left[\begin{array}{c}\dot{\theta }\\ \dot{u}\end{array}\right]+{\bf{K}}\left[\begin{array}{c}\theta \\ u\end{array}\right] = {\bf{F}}, \\ {\bf{M}} = \left[\begin{array}{cc}J+\kappa ({u}^{2}\frac{l}{2}+\frac{{l}^{3}}{3}+R{l}^{2}+Rl)& \kappa R\frac{2l}{\pi }+\kappa \frac{4{l}^{2}}{{\pi }^{2}}\\ \kappa R\frac{2l}{\pi }+\kappa \frac{4{l}^{2}}{{\pi }^{2}}& \kappa \frac{l}{2}\end{array}\right], \\ {\bf{G}} = \left[\begin{array}{cc}\kappa \frac{l}{2}u\dot{u}& \kappa \frac{l}{2}u\dot{\theta }\\ -\kappa \frac{l}{2}u\dot{\theta }& 0\end{array}\right], \\ {\bf{K}} = \left[\begin{array}{cc}0& 0\\ 0& \frac{{\pi }^{4}}{32{l}^{3}}EI\end{array}\right], {\bf{F}} = \left[\begin{array}{c}\tau \\ 0\end{array}\right].\end{array}$

(15)

For introducing the generalized momentum

${p_1} = \frac{{\partial L}}{{\partial \dot \theta }}, {p_2} = \frac{{\partial L}}{{\partial \dot u}},$

the Hamilton function of the system is

$H({\bf{q}}, {\bf{p}}) = {p_1}\dot \theta + {p_2}\dot u - L .$

So, the canonical equations form is:

$\frac{{d{\bf{z}}}}{{dt}} = \left[ {\begin{array}{*{20}{c}} {\dot \theta } \\ {\dot u} \\ {{{\dot p}_1}} \\ {{{\dot p}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\bf{M}}^{ - 1}}{\bf{p}} - \frac{1}{2}{{\bf{M}}^{ - 1}}{\bf{Gq}}} \\ { - \frac{1}{2}{\bf{G}}{{\bf{M}}^{ - 1}}{\bf{p}} + (\frac{1}{4}{\bf{G}}{{\bf{M}}^{ - 1}}{\bf{G}} - {\bf{K}}){\bf{q}} + {\bf{F}}} \end{array}} \right].$

(16)

For the Eq (16), in ^[19], we consider the numerical algorithm based on the coordinate increment discrete gradient, which is conserved quantity-preserving for the conserved quantity (13):

$\begin{array}{l} {{\bf{z}}_{n + 1}} = {{\bf{z}}_n} + h{J^{ - 1}}\bar \nabla {I_N}({{\bf{z}}_{n + 1}}, {{\bf{z}}_n}), \hfill \\ \bar \nabla {I_N}({{\bf{z}}_{n + 1}}, {{\bf{z}}_n}) = \left[ {\begin{array}{*{20}{c}} {\frac{{{I_N}({\theta _{n + 1}}, {u_n}, {p_{1(n)}}, {p_{2(n)}}) - {I_N}({\theta _n}, {u_n}, {p_{1(n)}}, {p_{2(n)}})}}{{{\theta _{n + 1}} - {\theta _n}}}} \\ {\frac{{{I_N}({\theta _{n + 1}}, {u_{n + 1}}, {p_{1(n)}}, {p_{2(n)}}) - {I_N}({\theta _{n + 1}}, {u_n}, {p_{1(n)}}, {p_{2(n)}})}}{{{u_{n + 1}} - {u_n}}}} \\ {\frac{{{I_N}({\theta _{n + 1}}, {u_{n + 1}}, {p_{1(n + 1)}}, {p_{2(n)}}) - {I_N}({\theta _{n + 1}}, {u_{n + 1}}, {p_{1(n)}}, {p_{2(n)}})}}{{{p_{1(n + 1)}} - {p_{1(n)}}}}} \\ {\frac{{{I_N}({\theta _{n + 1}}, {u_{n + 1}}, {p_{1(n + 1)}}, {p_{2(n + 1)}}) - {I_N}({\theta _{n + 1}}, {u_{n = 1}}, {p_{1(n + 1)}}, {p_{2(n)}})}}{{{p_{2(n + 1)}} - {p_{2(n)}}}}} \end{array}} \right]. \hfill \end{array}$

(17)

Here, h is a step size,

${J^{ - 1}} = - J = \left[ {\begin{array}{*{20}{c}} 0&{ - {e_{2 \times 2}}} \\ {{e_{2 \times 2}}}&0 \end{array}} \right] .$

The specific parameters of the simulation are as shown in Table 1:

Table 1. The level of parameter ^[20].

l(m)	k(kg/m)	E(Gpa)	I(m⁴)
2	0.216	70	2.67×10^-11
R(m)	J(kg·m²)	A(m²)	$\tau$ (N·m)
0.1	0.025	7.8×10^-5	0.1

| Show Table

DownLoad: CSV

The initial state vector of hub-beam is

${{\bf{z}}^{(0)}} = {[0.1, - 1, 0, 0]^T} .$

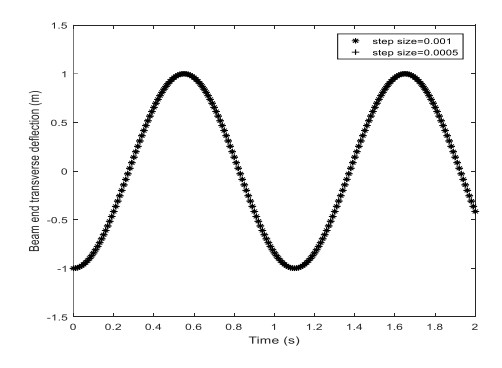
The steps h(s) are taken as 0.0005 and 0.001 respectively, and there were 4000 steps taken in total. According to the conserved quantity-preserving algorithm (17), the displacement-time curve of deflection response at the end of the flexible beam is shown in Figure 4.

Figure 4. Transverse deflection response of flexible beam end.

DownLoad: Full-Size Img PowerPoint

Figure 4 shows that the deformation response of the beam is consistent for different integration steps by using the conserved quantity-preserving algorithm to solve the dynamic equation of the hub-beam. So the conserved quantity-preserving algorithm has good stability.

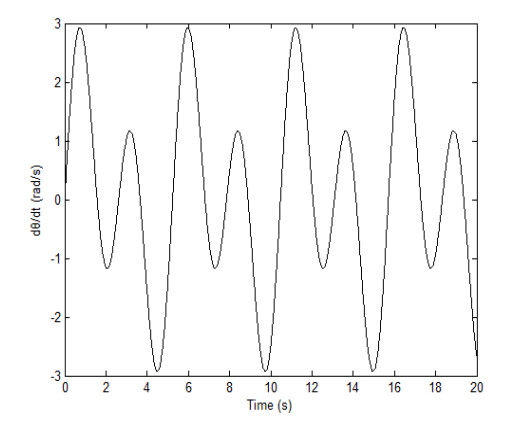
From the Figure 5, it can be seen that the variation in the rotational speed of the central rigid body is uneven. This is because when the central rigid body undergoes bending deformation, the flexible beam oscillates back and forth. When the direction of oscillation is the same as the rotational speed of the central rigid body, there is an acceleration effect. When the direction of oscillation is opposite to the rotational speed of the central rigid body, there is a deceleration effect.

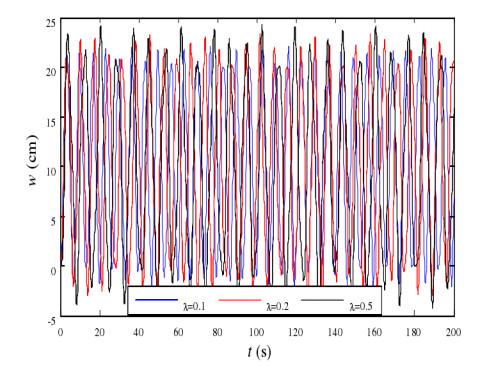
Figure 5. Rotational angular velocity response of the hub.

DownLoad: Full-Size Img PowerPoint

In order to verify the correctness of , ^[20] give the transverse response of the tip of the different quality flexible beam, where the ratio of the mass of a flexible beam to the mass of the central rigid body is $\lambda$ . The transverse response of the tip of the flexible beam, where $\lambda$ is 0.1, 0.2 and 0.5, respectively, is shown in Figure 6.

Figure 6. The transverse response of the tip of the different quality flexible beam ^[20].

DownLoad: Full-Size Img PowerPoint

Comparing Figures 4 and , we can see that the form of the response curve is completely consistent, all showing periodic fluctuations. Therefore, the model and numerical algorithm established in this article are effective. Meanwhile, from , we can see that as the ratio of the mass of the flexible beam to the central rigid body increases, the transverse vibration amplitude at the end of the flexible beam, and the transverse vibration period at the end of the flexible beam will also increase. When the entire system stabilizes, the bending deformation of the flexible beam will stabilize around 20–25 cm. It is consistent with the theoretical result obtained from the actual formula $f \approx \sqrt {k/m}$ , that is, the larger the mass of the structure, the lower the frequency of the system. Thus, and thus the period will increase.

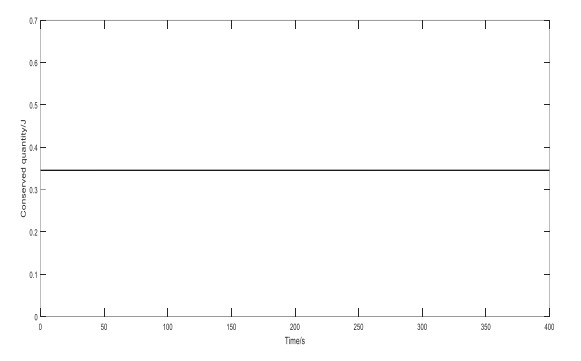
Considering the long-time behavior of the algorithm, when the time runs for 400 s, the function value of the system's conserved quantity ${I_N}({\bf{z}})$ is shown in Figure 7.

Figure 7. Function value

${I_N}$ under conserved quantity-preserving algorithm.

DownLoad: Full-Size Img PowerPoint

It can be seen from that the function value of the system's conserved quantity ${I_N}$ is constant near 0.3456. So, the conserved quantity-preserving numerical method constructed by discrete gradient will not introduce artificial dissipation with the growth of time and has better tracking ability.

Finally, to further demonstrate the effectiveness of the conserved quantity-preserving algorithm constructed by Noether symmetry, we use a numerical example to compare and illustrate.

There is an ordinary differential equation:

$\left[ {\begin{array}{*{20}{c}} {\frac{{d{z_1}}}{{dt}}} \\ {\frac{{d{z_2}}}{{dt}}} \\ {\frac{{d{z_3}}}{{dt}}} \\ {\frac{{d{z_4}}}{{dt}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&0&{ - 1}&0 \\ 0&0&0&{ - 1} \\ 1&0&0&0 \\ 0&1&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{z_1}} \\ {{z_2}} \\ {4z_3^3 + 8{z_3}z_4^2} \\ {4z_4^3 + 8z_3^2{z_4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 4z_3^3 - 8{z_3}z_4^2} \\ { - 4z_4^3 - 8z_3^2{z_4}} \\ {{z_1}} \\ {{z_2}} \end{array}} \right] = {\bf{f}}({\bf{z}}).$

(18)

We can obtain a conserved quantity of Eq (18):

${I_N} = \frac{1}{2}(z_1^2 + z_2^2) + z_3^4 + z_4^4 + 4z_3^2z_4^2.$

(19)

Now, we use the conserved quantity-preserving difference scheme (17) to numerically calculate the Eq (18), the step size is 0.125, the total steps are 3200, and the initial condition is

${[{z_{10}}, {z_{20}}, {z_{30}}, {z_{40}}]^T} = {[0, 1, 1, 0]^T}.$

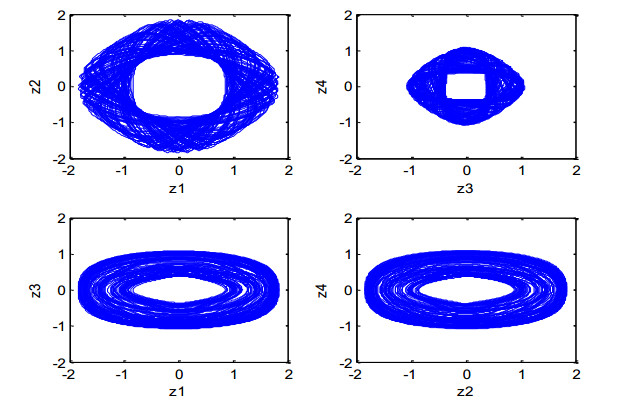
The long-term system trajectory is shown in Figure 8.

Figure 8. The long-term phase diagram of conserved quantity-preserving algorithm.

DownLoad: Full-Size Img PowerPoint

For comparing, we use the classic numerical algorithm (implicit Euler midpoint algorithm):

${{\bf{z}}_{n + 1}} - {{\bf{z}}_n} = h{\bf{f}}[\frac{{{{\bf{z}}_{n + 1}} + {{\bf{z}}_n}}}{2}].$

(20)

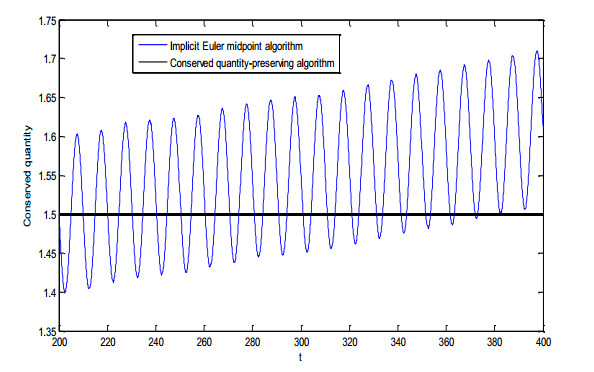
gives the function values of conserved quantity ${I_N}$ during long-time iteration processes. From Figure 8, it can be seen that the difference scheme (17) is a conserved quantity-preserving algorithm the implicit Euler midpoint algorithm cannot maintain the energy conservation and the error value of conserved quantity continues to spread. Thus, the implicit Euler midpoint algorithm cannot maintain the structural characteristics of the system.

Figure 9. The function values of conserved quantity under different numerical algorithms.

DownLoad: Full-Size Img PowerPoint

Comparing Figures 6 and 9, we can see that the form of the conserved quantity is completely consistent, which is an invariant over time. It is either an engineering or numerical case. Therefore, the difference scheme algorithm (17) is effective.

5. Conclusions

The symmetries theory of mechanical systems is rich and it has a broad application prospect in mathematical science and engineering technology. On the premise of computer technology, it is necessary to study the integral theory and the optimal numerical algorithm for flexible mechanical multibody dynamics. In this paper, the models and computing methods of flexible mechanical multibody systems are summarized. The dynamic equations of flexible beam with central rigid body, Noether symmetries and conserved quantities, and energy-preserving numerical algorithm are studied. We arrive at three main conclusions:

(1) When the rotation speed of the central rigid body is low and the flexible beam is slightly deformed, the second kind of Lagrange equations of discretization are zero-order approximate coupling, which is suitable for the design of the controller.

(2) The criterion equations of Noether symmetries have open solutions. The corresponding Noether type conserved quantities are the first integration of the dynamic response of multibody systems and also an extension of non-conservative mechanical energy conservation law.

(3) The numerical algorithm by preserving conserved quantity based on the discrete gradient, the numerical algorithm is stable for different steps, the energy deviation of the system is not diffused and the simulation process is not distorted for a long time.

It should be noted that the symmetry and conserved quantity method is easy to standardize. With the introduction of symbolic software technology, the solution of the upper process will be very efficient by computer programming, which can get the first integral of the system dynamic response and lay the foundation for parameter optimization. Furthermore, the research method in this paper can be extended to the flexible mechanical multibody dynamics with complex boundary constraints.

Use of AI tools declaration

The author declares he has not used Artificial Intelligence (AI) tool in the creation of this article.

Acknowledgments

This research received support from Jiangsu Key Laboratory of Green Process Equipment (GPE202203) and a sponsored by Qing Lan Project of Universities in Jiangsu Province (2022-29).

Conflict of interest

The author declares that there is no conflict of interest.

References

[1]	H. T. Wu, Y. L. Xiong, Multibody system dynamics problems in mechanical engineering, China Mech. Eng., 11 (2000), 608–610. https://doi.org/10.3321/j.issn:1004-132X.2000.06.002 doi: 10.3321/j.issn:1004-132X.2000.06.002
[2]	G. Q. Zhang, Modeling and control of flexible multibody systems, Ph. D. thesis, China University of Science and Technology, 2008.
[3]	J. C. Miao, Study on computational stretgy for flexible multi-body dynamics and analysis of large deployable antenna, Ph. D. thesis, Shanghai Jiao Tong University, 2008.
[4]	J. Y. Liu, J. Z. Hong, Contact-impact of satellite's panels, J. Astronaut., 21 (2000), 34–38. https://doi.org/10.3321/j.issn:1000-1328.2000.03.006 doi: 10.3321/j.issn:1000-1328.2000.03.006
[5]	K. F. Guo, Study on dynamic modeling and elastic vibration control of flexible manipulator, Ph. D. thesis, Zhengzhou University, 2017.
[6]	D. S. Meng, X. Q. Wang, W. F. Xu, B. Liang, Space robots with flexible appendages: dynamic modeling, coupling measurement, and vibration suppression, J. Sound Vib., 396 (2017), 30–50. https://doi.org/10.1016/j.jsv.2017.02.039 doi: 10.1016/j.jsv.2017.02.039
[7]	X. F. Liu, H. Q. Li, J. S. Wang, G. P. Cai, Dynamics analysis of flexible space robot with joint friction, Aerosp. Sci. Technol., 47 (2015), 164–176. https://doi.org/10.1016/j.ast.2015.09.030 doi: 10.1016/j.ast.2015.09.030
[8]	M. Benosman, G. L. Vey, Control of flexible manipulators: a survey, Robotica, 22 (2004), 533–545. https://doi.org/10.1017/S0263574703005642 doi: 10.1017/S0263574703005642
[9]	Z. Mohamed, J. M. Martins, M. O. Tokhi, J. S. da Costa, M. A. Botto, Vibration control of a very flexible manipulator system, Control Eng. Pract., 13 (2005), 267–277. https://doi.org/10.1016/j.conengprac.2003.11.014 doi: 10.1016/j.conengprac.2003.11.014
[10]	W. J. Hua, D. G. Zhang, Collision dynamics modeling of flexible robot system, J. Mech. Eng., 43 (2008), 222–228. https://doi.org/10.3321/j.issn:0577-6686.2007.12.040 doi: 10.3321/j.issn:0577-6686.2007.12.040
[11]	P. Y. Guo, Y. H. Hou, Q. X. Wang, Ride comfort analysis of mine narrow-type trackless vehicle based on rigid-flexible coupling, Coal Mine Mach., 40 (2019), 88–90. https://doi.org/10.13436/j.mkjx.201906027 doi: 10.13436/j.mkjx.201906027
[12]	Y. L. Cheng, Z. P. Xue, T. Jiang, W. Y. Wang, Y. K. Wang, Numerical simulation on dynamic response of flexible multi-body tower blade coupling in large wind turbine, Energy, 152 (2018), 601–612. https://doi.org/10.1016/j.energy.2018.03.137 doi: 10.1016/j.energy.2018.03.137
[13]	F. Huang, X. H. Zhang, J. Q. Gao, Vibration and trajectory motion control of textile machinery flexible manipulators based on Lagrange equation and modal theory, World Sci. Technol. Res. Dev., 38 (2016), 594–597. https://doi.org/10.16507/j.issn.1006-6055.2016.03.023 doi: 10.16507/j.issn.1006-6055.2016.03.023
[14]	R. Leone, T. Gourieux, Classical Noether theory with application to the linearly damped particle, Eur. J. Phys., 36 (2015), 065022. https://doi.org/10.1088/0143-0807/36/6/065022 doi: 10.1088/0143-0807/36/6/065022
[15]	P. Balseiro, Hamiltonization of solids of revolution through reduction, J. Nonlinear Sci., 27 (2017), 2001–2035. https://doi.org/10.1007/s00332-017-9394-1 doi: 10.1007/s00332-017-9394-1
[16]	K. Singla, R. K. Gupta, Conservation laws for certain time fractional nonlinear systems of partial differential equations, Commun. Nonlinear Sci. Numer. Simul., 53 (2017), 10–21. https://doi.org/10.1016/j.cnsns.2017.04.032 doi: 10.1016/j.cnsns.2017.04.032
[17]	Y. L. Zhao, Modeling, reduction of order and fine computation of flexible multibody systems dynamics, Ph. D. thesis, Northwestern Polytechnical University, 2000.
[18]	F. X. Mei, Analytical mechanics (Ⅱ), 2 Eds., Beijing Institute of Technology Press, 2013.
[19]	J. J. Wu, The research of energy-preserving numerical methods for Hamilton equations, Ph. D. thesis, Beijing Jiao Tong University, 2017.
[20]	Q. Gao, Fully coupled dynamic analysis of the flexible hub-beam system, Ph. D. thesis, Xi'an University of Technology, 2021.

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(1188) PDF downloads(56) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(9) / Tables(1)

AIMS Mathematics

Study on the symmetries and conserved quantities of flexible mechanical multibody dynamics

Related Papers:

Abstract

1. Introduction

2. Dynamics model of flexible mechanical multibody systems

3. Noether symmetries and conserved quantities

4. Numerical simulation by conserved quantity-preserving

5. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Study on the symmetries and conserved quantities of flexible mechanical multibody dynamics

Related Papers:

Abstract

1. Introduction

2. Dynamics model of flexible mechanical multibody systems

3. Noether symmetries and conserved quantities

4. Numerical simulation by conserved quantity-preserving

5. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog