1.
Introduction
The study on flow of fluids which are electrically conducting is known as magnetohydrodynamics (MHD). The magnetohydrodynamics have important applications in the polymer industry and engineering fields (Garnier [1]). Heat transfer caused by hydromagnetism was discussed by Chakrabarthi and Gupta [2]. Using an exponentially shrinking sheet, Nadeem et al. [3] investigated the MHD flow of a Casson fluid. Krishnendu Bhattacharyya [4] examined the effect of thermal radiation on MHD stagnation-point Flow over a Stretching Sheet.
Mixed convection magnetohydrodynamics flow is described by Ishak on a vertical and on a linearly stretching sheet [5,6,7]. Hayat et al. [10] examine a mixed convection flow within a stretched sheet of Casson nanofluid. Subhas Abel and Monayya Mareppa, examine magnetohydrodynamics flow on a vertical plate [11]. Shen et al. [12], examined a vertical stretching sheet which was non-linear. Ishikin Abu Bakar [13] investigates how boundary layer flow is affected by slip and convective boundary conditions over a stretching sheet. A vertical plate oscillates with the influence of slip on a free convection flow of a Casson fluid [14].
Nasir Uddin et al. [15] used a Runge-Kutta sixth-order integration method. Barik et al. [16] implicit finite distinction methodology of Crank Sir Harold George Nicolson sort Raman and Kumar [17] utilized an exact finite distinction theme of DuFort–Frankel. Mondal et al. [18] used a numerical theme over the whole vary of physical parameters. With the laplace transform method, we can determine the magnetohydrodynamic flow of a viscous fluid [19]. Thamizh Suganya et al. [20] obtained that the MHD for the free convective flow of fluid is based on coupled non-linear differential equations. In this study, the analytical approximation of concentration profiles in velocity, temperature and concentration using homotopy perturbation method (HPM).
2.
Mathematical construction of the problem
The governing differential equations in dimensionless form [19] as follows:
The dimensionless boundary conditions given by:
and
3.
Solutions of steady-state concentration profile using the Homotopy Perturbation Method
He [21,22] established the homotopy perturbation method, which waives the requirement of small parameters. Many researchers have used HPM to obtain approximate analytical solutions for many non-linear engineering dynamical systems [23,24]. The basic concept of the HPM as follows:
with initial and boundary conditions given by:
Homotopy for the above Eqs (3.1) to (3.4) can be constructed as follows:
The approximate solution of the Eqs (3.5) to (3.7) are
Substitution Eqs (3.5) to (3.7) in Eqs (3.8) to (3.10) respectively. We obtain the following equations
and
and
Equating the coefficient of p on both sides, we get the following equations
The boundary conditions are
and
Solving the Eqs (3.9)–(3.14), we obtain
Considering the iteration, we get,
4.
Approximate analytical solutions for the skiin friction, Nusselt and Sherwood numbers
From the Eqs (3.25)–(3.27), we obtain
5.
Results and discussion
The combined impacts of transient MHD free convective flows of an incompressible viscous fluid through a vertical plate moving with uniform motion and immersed in a porous media are examined using an exact approach. The approximate analytical expressions for the velocity u, temperature θ, and concentration profile ϕ are solved by using the homotopy perturbation method for fixed values of parameters is graphically presented.
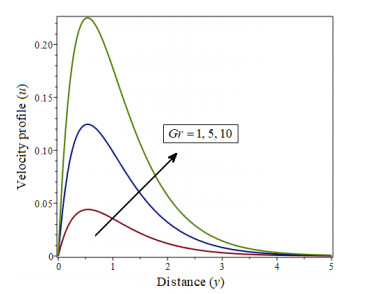
Velocity takes time at first, and for high values of y, it takes longer, and the velocity approaches zero as time increases. The velocity of fluid rises with Gr increasing, as exposed in Figure 1.
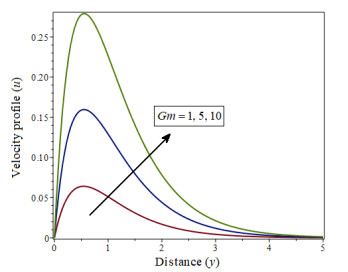
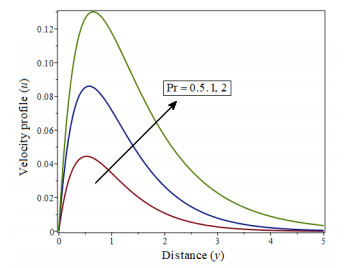
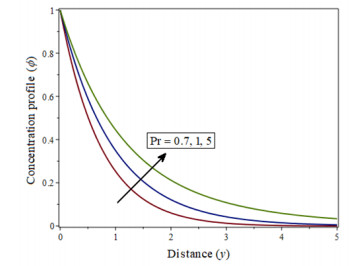
The variations of parameter Gm are depicted in Figure 2. It has been established that as the value of increases, neither does the concentration. Gm. This is because increasing the number of 'Gm' diminishes the slog energy, allow the fluid to transfer very rapidly.The dimensionless Prandtl number is a number which combines the viscosity of a fluid with its thermal conductivity. For example, Figure 3 shows how a decrease in 'Pr'increases the concentration of velocity profile.
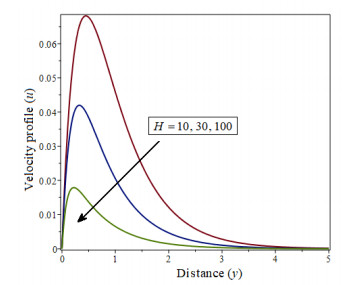
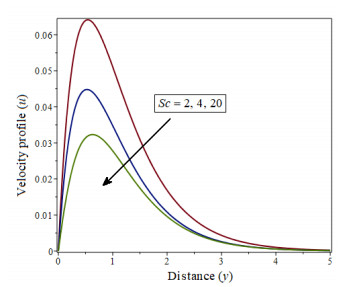
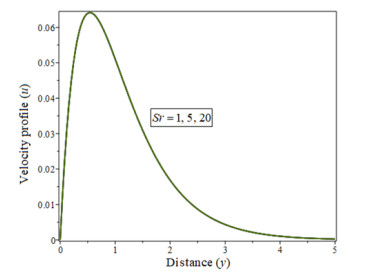
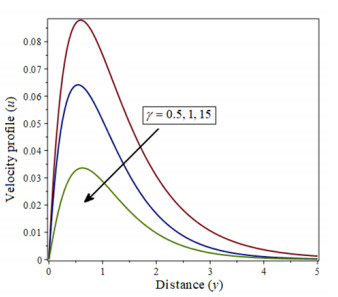
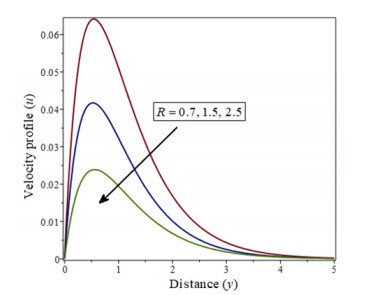
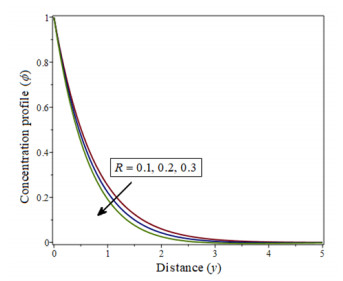
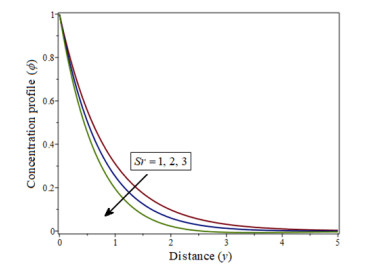
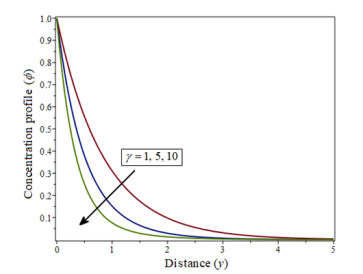
The Figure 4 shows how a decrease in concentration occurs when the value of H increases.As shown in Figure 5, when the Schmidt number Sc increases, the concentration of velocity profiles decreases, while the opposite is true for the Soret number Sr, as shown in Figures 6, 7 and 8, represented the radiation parameter R, chemical reaction parameter γ is increasing when it implies a decrease in concentration.
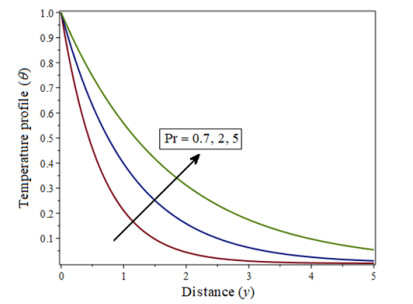
Based on Figure 9, it is evident that the thickness of the momentum boundary layer increases for fluids with Pr<1. When Pr<0.015, the heat diffuses rapidly in comparison to the velocity.
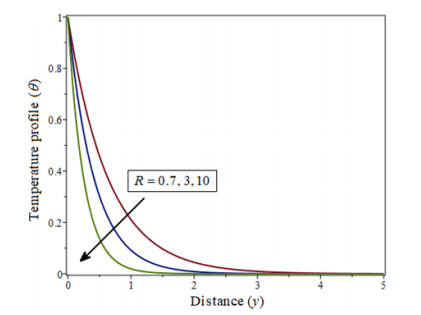
Figure 10 depicts the impact of the radiation parameter R on temperature profiles. The temperature profiles θ, which are a decreasing function of R, are found to decrease the flow and lower fluid velocity. As the radiation parameter R is increased, the fluid thickens, temperatures and thermal boundary layer thickness to decrease.
This statement is justified because the thermal conductivity of a fluid declines by the growing Prandtl number Pr and hence the thickness of thermal boundary layers and temperature profiles decrease as well. Based on Figure 9, we see an increase in fluid concentration with large Prandtl numbers Pr. Radiation parameter R and temperature profiles are illustrated in Figure 10. The temperature profiles θ, which are a decreasing function of R, are initiate to reduction the flow and decline the fluid velocity. Radiation parameter R increases as fluid thickness increases, temperature increases, and thickness of thermal boundary layer decreases.
The influence of Pr, R, γ, Sc, and Sr on the concentration profiles ϕ is shown in Figures 11–15. The fluid concentration rises on highest values of Pr, as shown in Figure 11. The profile of temperature is affected by the radiation parameter R which is shown in Figure 12. As a function of R, the concentration profiles reduce the flow and decrease fluid velocity.
The growing values of γ and Sc lead to falling in the concentration profiles, is described from Figures 13 and 15. The concentration profiles increase as the number of sorts (Sr) increases, as shown in Figure 14.
6.
Conclusions
A free convection magnetohydrodynamic (MHD) flow past a vertical plate embedded in a porous medium was offered in this paper. Homotopy perturbation method is used to find approximate analytical solutions for the concentration of species. The effects of system parameters on temperature and velocity profiles were investigated using these analytical expressions. The graphic representation of the impact of several physical parameters attempting to control the velocity, temperature, and concentration profiles and a brief discussion. Analytical expressions were also developed for the Skin-friction and Nusselt and Sherwood numbers.
Conflict of interest
The authors declare that they have no conflict of interest.
Acknowledgement
The authors are thankful to the reviewers for their valuable comments and suggestions to improve the quality of the paper. The work of H. Alotaibi is supported by Taif University Researchers Supporting Project Number (TURSP-2020/304), Taif University, Taif, Saudi Arabia.









 DownLoad:
DownLoad: