On the logarithmic coefficients for some classes defined by subordination

1.   Introduction and preliminaries

Let $\mathcal{A}$ be the class of analytic functions in the open unit disk $\mathbb{D}: = \{z\in\mathbb{C}:\left\vert z\right\vert < 1\}$ of the form

and let $\mathcal{S}$ be the class of functions $f\in\mathcal{A}$ which are univalent in $\mathbb{D}$.

Using the principle of subordination Ma and Minda ^[16] introduced the class $\mathcal{S}^{\ast}(\varphi)$ (so called Ma-Minda-type functions)

where in our paper we suppose that $\varphi$ is univalent in the unit disk $\mathbb{D}$, it has positive real in $\mathbb{D}$, and satisfies the condition $\varphi(0) = 1$, while the symbol "$\prec$" stands for the usual subordination. It is well-known that $\mathcal{S}^{\ast}(\varphi)\subset\mathcal{S}$, and we emphasize that some special subclasses of the class $\mathcal{S}^{\ast}(\varphi)$ play a significant role in Geometric Function Theory because of many interesting geometric aspects.

For example, taking $\varphi(z): = (1+Az)/(1+Bz)$, where $A\in\mathbb{C}$, $-1\le B\le 0$ and $A\neq B$, we get the class $\mathcal{S}^{\ast}[A, B]$. This class with the restriction $-1\le B < A\le 1$ reduces to the popular class of Janowski starlike functions.

Remark 1. (ⅰ) By considering $\varphi(z): = \wp(z) = 1+z\mathrm{e}^z$ in ^[15], the researchers introduced and studied another Ma-Minda-type function class $\mathscr{S}^{\ast}(\wp)$ of starlike functions, where $\wp$ maps the unit disk onto a cardioid domain.

(ⅱ) We emphasize that the class $\mathcal{S}^{\ast}_{ \text{C}}$ of functions $f\in\mathcal{A}$ with $\varphi(z): = \phi_ \text{C}(z) = 1+\dfrac{4z}{3}+\dfrac{2z^{2}}{3}$ such that

that maps the open unit disk into the cardioid domain

was extensively investigated by Sharma et al. ^[28].

(ⅲ) In ^[12], by using the polynomial function $\varphi(z): = \phi_{ \text{car}}(z) = 1+z+\dfrac{z^{2}}{2}$ the corresponding class $\mathcal{S}^{\ast}_ \text{car}$ of functions was investigated by different authors (see also, for example ^[13,22,26]), while the function $\phi_{ \text{car}}$ maps the open unit disk into the cardioid domain

The logarithmic coefficients $\gamma_n$ of the function $f\in\mathcal{S}$ are defined with the aid of the following power series expansion

These coefficients play an important role for different estimates in the theory of univalent functions, and note that we use $\gamma_n$ instead of $\gamma_n(f)$; in this regard see [17, Chapter 2] and ^[18,19]. In ^[6], authors determined bounds on the difference of the moduli of successive coefficients for some classes defined by subordination using the logarithmic coefficients.

The logarithmic coefficients $\gamma_n$ of an arbitrary function $f\in\mathcal{S}$ (see [10, Theorem 4]) satisfy the inequality

and the equality is obtained for the Koebe function. For $f\in\mathcal{S}^{\ast}$, the inequality $\left|\gamma_n\right|\le1/n$ holds but it is not true for the whole class $\mathcal{S}$ (see [9, Theorem 8.4]). However, the problem of the best upper bounds for the logarithmic coefficients of univalent functions for $n\ge 3$ is presumably still a concern.

Recently, Ponnusamy et al. ^[24] studied the logarithmic coefficients problems in families related to starlike and convex functions and obtained the sharp upper bound for $|\gamma_n|$ when $n = 1, 2, 3$ and $f$ belongs to the families. Some first logarithmic coefficients $\gamma_n$ were obtained for certain subclasses of close-to-convex functions by Ali and Vasudevarao ^[5] and Pranav Kumar and Vasudevarao ^[25]. In ^[14], Kowalczyk and Lecko obtained related bounds with these coefficients for strongly starlike and strongly convex functions.

Due to the major importance of the study of the logarithmic coefficients, in recent years several authors have investigated the issues regarding the logarithmic coefficients and the related problems for some subclasses of analytic functions (for example, see ^{[2,3,4,7,8,11,21,23,25,30,31,32]}.

In ^[1] the authors obtained the bounds for the logarithmic coefficients $\gamma_n$ $\left(n\in\mathbb{N}\right)$ of the general class $\mathcal{S}^{\ast}(\varphi)$, while the given bounds would generalize many previous results.

Theorem A. [1, Theorem 1(ⅰ)] Let the function $f\in\mathcal{S}^{\ast}(\varphi)$. If $\varphi$ is convex (univalent), then the logarithmic coefficients of $f$ satisfy the inequalities:

and

All inequalities in (1.4) and (1.5) are sharp for the function $f_n$ given by ${zf_n^{\prime}(z)}/{f_n(z)} = \varphi(z^n)$ for any $n\in\mathbb{N}$ and the function $f$ given by ${zf^{\prime}(z)}/{f(z)} = \varphi(z)$, respectively.

We correct that the next inequality (and some other results in ^[1]) is sharp only for $n = 1$ as it is shown in the following result:

Theorem B. [1, Theorem 1(ⅱ)] Let the function $f\in\mathcal{S}^{\ast}(\varphi)$. If $\varphi$ is starlike (univalent) with respect to $1$, then the logarithmic coefficients of $f$ satisfy the inequality

The above inequality is sharp for $n = 1$ for the function $f$ given by ${zf^{\prime}(z)}/{f(z)} = \varphi(z)$.

If we do direct calculations to get the upper bound of $\left|\gamma_1\right|$ we will also get the same sharp bound $\left|\gamma_1\right|\le \dfrac{|B_1|}{2}$. Therefore, this shows this theorem is sharp for n = 1. But there are some examples like the mentioned classes in Remark 1(ⅱ) and Remark 1(ⅲ) and using Theorem 3 and Theorem 2, respectively, that show Theorem B is not sharp for $n > 1$.

A possible sharper version of Theorem B could be conjectured as follows:

Conjecture. Let the function $f\in\mathcal{S}^{\ast}(\varphi)$ for some $\varphi$. If $\varphi$ is starlike (univalent) with respect to $1$, then the logarithmic coefficients of $f$ satisfy the inequality

The above inequality is sharp for each $n$.

Lemma 1. ^[9,27] (Theorem 6.3, p. 192; Rogosinski's Theorem Ⅱ (ⅰ)) Let $f(z) = \sum\limits_{n = 1}^{\infty}{a_nz^n}$ and $g(z) = \sum\limits_{n = 1}^{\infty}{b_nz^n}$ be analytic in $\mathbb{D}$, and suppose that $f(z)\prec g(z)$ where $g$ is univalent in $\mathbb{D}$. Then,

Using Theorem 3.1d of ^[20] (see also ^[29]), we have the following result.

Lemma 2. Let $h$ be starlike in $\mathbb{D}$, with $h(0) = 0$. If $F$ is analytic in $\mathbb{D}$, with $F(0) = 0$, and satisfies

then

Moreover, the function $q$ is convex and is the best dominant.

The main purpose of this paper is to get the sharp bounds for some relations associated with the logarithmic coefficients of the functions belonging to the class $\mathcal{S}^{\ast}(\varphi)$ of Ma-Minda type functions and of other subclasses. Some applications of our results are given here as special cases.

2.   Main results

First, we give a similar result to the inequality (1.5) of Theorem A for the case that $\varphi$ is starlike with respect to $1$ and univalent in $\mathbb{D}$, that is under weaker assumption than those of Theorem A.

Theorem 1. Let the function $f\in\mathcal{S}^{\ast}(\varphi)$, with $\varphi(z) = 1+\sum\limits_{n = 1}^{\infty}B_{n}z^{n}$ be a starlike function with respect to $1$, univalent in $\mathbb{D}$, and $\operatorname{Re}\varphi(z) > 0$ for all $z\in\mathbb{D}$. Then, the logarithmic coefficients of $f$ satisfy the following inequalities:

and

Both inequalities are sharp since there are attained for the function $f_{\ast}\in\mathcal{S}^{\ast}(\varphi)$ given by $zf_{\ast}^{\prime}(z)/f_{\ast}(z) = \varphi(z)$, that is

Proof. Supposing that $f\in\mathcal{S}^{\ast}(\varphi)$, let us define the function $H(z): = \dfrac{f(z)}{z}$, which is an analytic function in $\mathbb{D}$, $H(0) = 1$. From the relation (1.2) it satisfies

where $\phi$ is starlike univalent in $\mathbb{D}$.

Now, let's take in Lemma 2 the functions

Then, since $\phi$ is starlike in $\mathbb{D}$ with $\phi(0) = 0$, and $F(0) = 0$ (because $H(0) = 1$), we should only to prove that $F$ is analytic in $\mathbb{D}$. Since the function $f\in\mathcal{S}^{\ast}(\varphi)$, with $\operatorname{Re}\varphi(z) > 0$ for all $z\in\mathbb{D}$, $f\in\mathcal{S}^{\ast}(\varphi)\subset\mathcal{S}^{\ast}\subset\mathcal{S}$, where $\mathcal{S}^{\ast}$ represents the class of starlike functions in $\mathbb{D}$. Thus, $f(z)\neq0$ for $z\in\mathbb{D}\setminus\{0\}$ and $z_0 = 0$ is a simple zero for $f$. Hence, $H(z) = \dfrac{f(z)}{z}\neq0$ for all $z\in\mathbb{D}$, and therefore $F$ is analytic in $\mathbb{D}$. Since all conditions of Lemma 2 are satisfied, from (1.6) and (2.5) it follows that

and the relation (2.6) results in

where (2.7) is equal to

In addition, we know that if $\phi$ is starlike in $\mathbb{D}$, then $\int_{0}^{z}\dfrac{\phi(t)}{t}\, \mathrm{d}t$ is convex (univalent) in $\mathbb{D}$, and conversely. Denoting with $\gamma_n$ the logarithmic coefficients of $f$ given by (1.3), the subordination (2.8) is equivalent to

Since the function $\int_{0}^{z}\dfrac{\phi(t)}{t}\, \mathrm{d}t$ is univalent in $\mathbb{D}$, by using Lemma 1 the subordination (2.9) implies

and taking $k\to\infty$ in (2.10) we conclude that

Now, the relation (2.11) shows that the inequality (2.1) is proved.

To prove the second inequality of our theorem, let $f\in\mathcal{S}^{\ast}(\varphi)$. Then, using the power series expansion formula (1.3) we get

Now, according to Lemma 1 the subordination (2.12) leads to

and letting $k\to\infty$ in (2.13), the assertion (2.2) is proved.

For proving the sharpness of these bounds it is sufficient to use the equality

The relation (2.14) shows that the upper bound of the inequalities (2.1) and (2.2) is the best possible and it is attained for the function $f_{\ast}$ given by $\dfrac{zf_{\ast}^{\prime}(z)}{f_{\ast}(z)} = \varphi(z)$. □

The following results represent two special cases of the above theorem connected with the logarithmic coefficients $\gamma_n$ for the subclasses $\mathcal{S}^{\ast}(z+\sqrt{1+z^{2}})$ and $\mathcal{S}^{\ast}(1+\sin z)$ defined in ^[26] and ^[8], respectively.

Corollary 1. If the function $f\in\mathcal{S}^{\ast}(z+\sqrt{1+z^{2}})$, then the logarithmic coefficients of $f$ satisfy the inequalities

and

These results are sharp for the function $f\in\mathcal{S}^{\ast}(z+\sqrt{1+z^{2}})$ given by ${zf^{\prime}(z)}/{f(z)} = z+\sqrt{1+z^{2}}$.

Proof. Taking

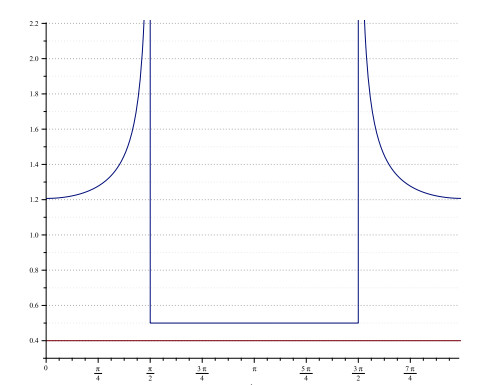
and using Theorem 2.1 of ^[26] it follows that $\operatorname{Re}\varphi(z) > 0$ for all $z\in\mathbb{D}$, and considering the main branch of the square root function we have $\varphi(0) = 1$. According to the Figure 1 made with MAPLE™ software we get that the function $\Phi$ defined by

is positive in $\mathbb{D}$, and hence $\varphi(z) = z+\sqrt{1+z^{2}}$ is a starlike function in $\mathbb{D}$ with respect to $1$. Since, in addition $\varphi^{\prime}(0) = 1\ne0$, the function $\varphi$ is univalent in $\mathbb{D}$. Thus our result follows immediately from Theorem 1.

□

Corollary 2. If the function $f\in\mathcal{S}^{\ast}(1+\sin z)$, then the logarithmic coefficients of $f$ satisfy the inequalities

and

These results are sharp for the function $f\in\mathcal{S}^{\ast}(1+\sin z)$ given by ${zf^{\prime}(z)}/{f(z)} = 1+\sin z$.

Proof. Considering

and using the Figure 2 (a) made with MAPLE™ software it follows that $\operatorname{Re}\varphi(z) > 0$ for all $z\in\mathbb{D}$. Also, from the Figure 2 (b) made with the same computer software, we get that the function $\Phi$ defined by

is positive in $\mathbb{D}$, and hence $\varphi(z) = 1+\sin z$ is starlike with respect to $1$. From here, since $\varphi^{\prime}(0) = 1\ne0$, the function $\varphi$ is univalent in $\mathbb{D}$. Therefore using Theorem 1 we get our result.

□

Remark 2. Corollary 2 is an improvement, without the convexity condition in $\mathbb{D}$ for the function $\varphi(z) = 1+\sin\left(r_{0}z\right)$ if $r_0\simeq0.345$, of the result given by [1, Corollary 3].

Corollary 3. If the function $f\in\mathscr{S}^{\ast}(\wp)$ where $\mathscr{S}^{\ast}(\wp)$ was defined in the Remark 1 (i), then the logarithmic coefficients of $f$ satisfy the inequalities

and

These results are sharp for the function $f\in\mathscr{S}^{\ast}(\wp)$ given by

Proof. For $\varphi(z): = \wp(z) = 1+z\mathrm{e}^z$ it is easy to check that

and this implies that the function $\varphi$ is starlike with respect to $1$ and univalent in $\mathbb{D}$ because $\varphi^\prime(0) = 1\neq0$. Also, from Lemma 2.1 (ⅰ) of ^[15] we obtain that $\operatorname{Re}\varphi(z)\ge0.136038\dots$ for all $z\in\overline{\mathbb{D}}$, hence $\varphi$ has real positive part in $\mathbb{D}$. Then, according to Theorem 1 we obtain the desired result. □

Corollary 4. If the function $f\in\mathcal{S}^{\ast}_{ \mathit{\text{C}}}$ where $\mathcal{S}^{\ast}_{ \mathit{\text{C}}}$ was defined in the Remark 1 (ii), then the logarithmic coefficients of $f$ satisfy the inequalities

and

These results are sharp for the function $f$ given by

Proof. For the function $\varphi(z): = \phi_ \text{C}(z) = 1+\dfrac{4z}{3}+\dfrac{2z^{2}}{3}$ we have

and $\varphi^{\prime}(0) = 4/3\ne0$. These show that the function $\varphi$ is starlike with respect to $1$ and univalent in $\mathbb{D}$. Also, from the right hand side of the relation (3.5) in ^[28] we obtain that $\varphi$ has real positive part in $\mathbb{D}$, and using Theorem 1 we get our result. □

Corollary 5. If the function $f\in\mathcal{S}^{\ast}_ \mathit{\text{car}}$ where $\mathcal{S}^{\ast}_ \mathit{\text{car}}$ was defined in the Remark 1 (iii), then the logarithmic coefficients of $f$ satisfy the inequalities

and

These results are sharp for the function $f$ given by $\dfrac{zf^{\prime}(z)}{f(z)} = 1+z+\dfrac{z^{2}}{2}$.

Proof. By using simple computations it is easy to check that the function $\varphi(z): = \phi_{ \text{car}}(z) = 1+z+\dfrac{z^{2}}{2}$ has positive real part, and it is starlike with respect to $1$ in $\mathbb{D}$ [12, p. 1148]. Since $\varphi^{\prime}(0) = 1\ne0$, it follows that $\varphi$ is univalent in $\mathbb{D}$. Hence, the result follows from Theorem 1. □

The following two results give the best upper bounds of the logarithmic coefficients $\gamma_n$ for two subclasses $\mathcal{S}^{\ast}_ \text{car}$ and $\mathcal{S}^{\ast}_{ \text{C}}$.

Theorem 2. If $f\in\mathcal{S}^{\ast}_ \mathit{\text{car}}$ (see the Remark 1 (iii)), then

This inequality is sharp for each $n\in\mathbb{N}$.

Proof. If $f\in\mathcal{S}^{\ast}_ \text{car}$, then by the definition of $\mathcal{S}^{\ast}_ \text{car}$ we obtain

Using the definition of the logarithmic coefficients $\gamma_n$ of the function $f$ given by (1.3) and the relation (2.15) we get

Setting in [27, Theorem Ⅵ (ⅰ)] the sequence $A_1 = 1$, $A_2 = \dfrac{1}{2}$, $A_n = 0$ for all $n\ge 3$, and $B_k = 0$ for all $k\ge n+1$, the function $F_1$ given by [27, (1.10.1) p. 62] becomes

The function $F_1$ is analytic in $\mathbb{D}$ and satisfy $\operatorname{Re}F_1(z) > 0$, $z\in\mathbb{D}$, hence all assumptions of [27, Theorem Ⅵ (ⅰ)] are satisfied. Therefore, from (2.16) we get

that represents our result.

For a fixed $n_0\in\mathbb{N}$, suppose that $f_{n_0}\in\mathcal{S}^{\ast}_ \text{car}$ satisfies the relation

Then, according to (2.17) the function $f_{n_0}$ is of the form

hence from (2.18) we get

The relation (2.19) concludes that the bound given by our theorem is sharp for the fixed value $n_0\in\mathbb{N}$ if $f = f_{n_0}$, that is $\left\vert\gamma_{n_0}\right\vert = \dfrac{1}{2n_0}$ for $f = f_{n_0}$, and this completes the proof. □

Theorem 3. If $f\in\mathcal{S}^{\ast}_{ \mathit{\text{C}}}$ (see the Remark 1 (ii)), then

This inequality is sharp for each $n\in\mathbb{N}$.

Proof. If $f\in\mathcal{S}^{\ast}_{ \text{C}}$, then by the definition of $\mathcal{S}^{\ast}_{ \text{C}}$ we have

and using the logarithmic coefficients $\gamma_n$ of the function $f$ given by (1.3) and (2.20) we get

Setting now in [27, Theorem Ⅵ (ⅰ)] the sequence $A_1 = \dfrac{4}{3}$, $A_2 = \dfrac{2}{3}$, $A_n = 0$ for all $n\ge 3$, and $B_k = 0$ for all $k\ge n+1$, the function $F_1$ given by [27, (1.10.1) p. 62] becomes

The function $F_1$ is analytic in $\mathbb{D}$ and satisfy $\operatorname{Re}F_1(z) > 0$, $z\in\mathbb{D}$, hence all assumptions of [27, Theorem Ⅵ (ⅰ)] are satisfied, therefore (2.21) results in

For a fixed $n_0\in\mathbb{N}$, suppose that $f_{n_0}\in\mathcal{S}^{\ast}_ \text{car}$ such that

According to (2.22) the function $f_{n_0}$ has the form

thus (2.23) implies

Regrading (2.24) the bound given in our result is sharp for the fixed $n_0\in\mathbb{N}$ if $f = f_{n_0}$, that is $\left\vert\gamma_{n_0}\right\vert = \dfrac{2}{3n_0}$ for $f = f_{n_0}$, which completes the proof. □

3.   Conclusions

In the current paper we obtained the upper bounds for some expressions associated with the logarithmic coefficients $\gamma_n$ $(n\in\mathbb{N})$ of functions that belong to the well-known class $\mathcal{S}^{\ast}(\varphi)$. Furthermore, we took some other particular functions $\varphi$ in main theorem to obtain the corresponding special cases. Moreover, we gave the best upper bounds of the logarithmic coefficients $\gamma_n$ for two subclasses $\mathcal{S}^{\ast}_ \text{car}$ and $\mathcal{S}^{\ast}_{ \text{C}}$.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of Interest

Prof. Dr. Nak Eun Cho is the Guest Editor of special issue "Geometric Function Theory and Special Functions" for AIMS Mathematics. Prof. Dr. Nak Eun Cho was not involved in the editorial review and the decision to publish this article.

The authors declare that they have no conflicts of interest.