1.
Introduction
In recent years, fractional differential equations have gained prominence due to their proven usefulness in several unrelated scientific and engineering fields. For example, the nonlinear oscillations of an earthquake can be characterized by a fractional derivative, and the fractional derivative of the traffic fluid dynamics model can solve the insufficiency resulting from the assumption of continuous traffic flows [1,3]. Numerous chemical processes, mathematical biology, engineering, and scientific problems [4,5,6,7] are also modeled with fractional differential equations. Nonlinear partial differential equations (NPDEs) characterize various physical, biological, and chemical phenomena. Current research is focused on developing precise traveling wave solutions for such equations. Exact and explicit solutions help scientists understand the complicated physical phenomena and dynamic processes portrayed by NPDEs [8,9,10]. In the past four decades, numerous essential methodologies for attaining accurate solutions to NPDEs have been proposed [11,12].
The Helmholtz equation (HE) derives from the elliptic and wave equations. In a multi-dimensional nonhomogeneous isotropic standard with velocity c, the wave result is υ(ξ,ψ), which corresponds to a source of harmonic (ξ,ψ) vibrating at a given frequency and satisfying the Helmholtz equation in the area R. The classical order HE is
Here, υ is a suitable boundary differentiable term of R, is a known function, and the wave number with wavelength 2/ξ=0 renders Eq (1.1) homogeneous. If (1.1) is expressed as
Then it explains mass transfer with density biochemical processes of the 1st order. Equation (1.1) is investigated using the decomposition method [13], the finite element approach [14], the differential transform method [15], the Trefftz method [16], and the spectral collocation method [17], among others [3,4,5].
The Helmholtz equation is a partial differential equation that describes wave phenomena in various fields of physics, such as electromagnetism, acoustics, and fluid mechanics. Traditionally, the Helmholtz equation has been formulated using integer-order derivatives. However, in recent years, there has been a growing interest in the use of fractional-order derivatives to describe complex phenomena more accurately. In particular, fractional-order space Helmholtz equations are derived directly from mathematical formulas that involve fractional derivatives, rather than being generalized from integer-order space derivative Helmholtz equations. These equations can provide a more accurate description of wave propagation in complex media, such as porous materials, biological tissues, and fractal structures. Fractional-order space Helmholtz equations have attracted significant attention due to their potential applications in a wide range of fields, including medical imaging, geophysics, and telecommunications. They offer a promising avenue for understanding the behavior of waves in complex media and developing new technologies for wave-based sensing and imaging [6,7,8].
It is advantageous to utilize fractional differential equations in physical problems due to their nonlocal features. Non-locality characterizes fractional-order derivatives, whereas locality characterizes integer-order derivatives [24,25,26,27]. It demonstrates that the future state of the physical system depends on all of its previous states in addition to its current state. Consequently, fractional models are more accurate. In fractional differential equations, the response expression has a parameter that specifies the fractional derivative of the variable order, which may vary to achieve many responses [9,10,11].
Standard HEs can be generalized to fractional-order Helmholtz equations by extending the Caputo fractional-order space derivative to the integer-order space derivative. The fractional Helmholtz equation in space is
with υ(0,ψ)=g(ψ) as the initial condition (IC). Gupta et al. [31] solved the multi-dimensional fractional Helmholtz equation using the homotopy perturbation approach. In contrast, Abuasad et al. [14] recently solved a fractional model of the Helmholtz problem using the reduced differential transform method.
2.
Preliminary concepts
This section describes the properties of the fractional derivatives and a few essential details concerning the Yang transform.
Definition 2.1. The fractional derivative in terms of Caputo is as follows
Definition 2.2. The YT is represented as follows
having inverse YT as follows
Definition 2.3. The nth derivative YT is stated as follows
Definition 2.4. The YT of derivative having fractional-order is stated as follows
3.
General implementation of the method
Consider the general fractional partial differential equations,
Using Yang transform of Eq (3.1), we get
Now, applying inverse Yang transform, we have
where
The parameter p is perturbation technique and p∈[0,1] defined as
The nonlinear function is expressed as
where Hn are He's polynomials in term of υ0,υ1,υ2,⋯,υn, and can be calculated as
where Dıp=∂ı∂pı.
Putting Eqs (3.6) and (3.7) in Eq (3.3), we achieved as
Comparison both sides of coefficient p, we get
Finally, present the obtained solution and check it with any available analytical or numerical solutions for the given PDE. The υı(ξ,ψ) components can be calculated easily which quickily converges to series form. We can get p→1,
4.
Applications
Problem 4.1. Consider the space fractional Helmholtz equation
with the ICs
Using the Yang transform of Eq (4.1), we obtained as
Taking inverse Yang Transformation, we have
Implemented HPM in Eq (4.5), we can achieve as
On both sides comparing coefficients of p, we get
The series type result of the first problem example is
The exact solution is
Similarly y-space can be calculated as:
with the IC
Thus, the solution of the above Eq (4.9) is obtain as
in the case when ϱ=2, then the solution through HPTM is
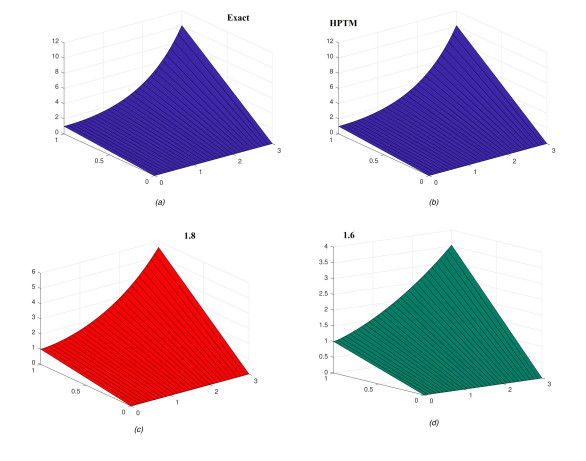
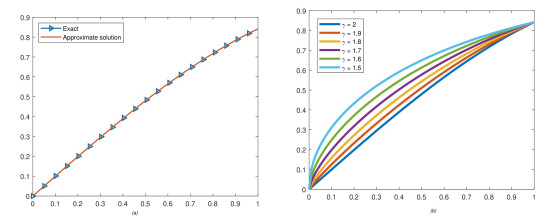
Figure 1 illustrates the exact and HPTM solutions in two-dimensional plots for various values of ϱ ranging from 2 to 1.5, with ξ values ranging from 0 to 1 and ψ set to 1. The solutions are presented in Figure 1a and b for the exact and HPTM methods, respectively. Figure 2 displays the 3-dimensional plots of the exact and HPTM solutions for ϱ=2 and analyzes the point of intersection between the two solutions. Figure 2c and d depict the HPTM solutions at ϱ=1.8 and 1.6 respectively for Problem 4.1. The fractional results were also evaluated for their convergence towards an integer-order result for each problem. Similarly, the figures for the ψ-space can also be generated using the same approach.
Problem 4.2. Consider the space-fractional HE
with the ICs
Using the Yang transform of Eq (4.12), we obtain as
Applying the inverse Yang Transform, we get
Using the HPM in Eq (4.16), we obtained as
On both sides comparing coefficients of p, we get
The series type result of second problem as
The exact solution is
Now similarly, the result of y-space can be calculated with the help of homotopy perturbation
with the IC
The solution of the Eq (4.20) is expressed as
The exact solution is
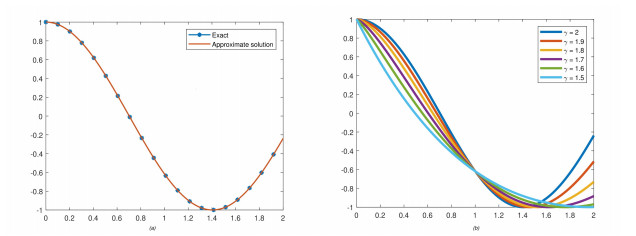
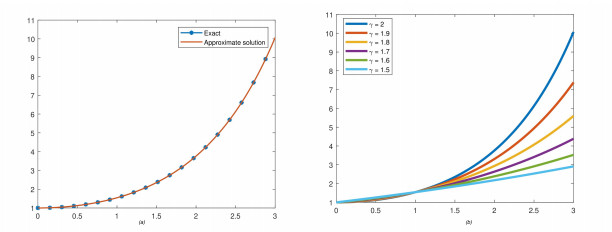
Figure 3 illustrates the solutions of exact and HPTM in two-dimensional plots, as shown in Figure 3a and b for different values of ϱ, ranging from 2 to 1.5, respectively. The interval considered for ξ is [0, 1], while ψ is constant at 1. The results obtained from the fractional-order model converge to the integer-order solution of the problem. In Figure 4, the 3-dimensional plots of exact and HPTM solutions are presented in Figures (a) and (b), respectively, for ϱ=2. The closed contact of the two solutions is analyzed. Additionally, Figure 4c and d depict the HPTM solutions at ϱ=1.8 and 1.6, respectively, for Problem 4.2. Similarly, graphs for ψ-space can also be generated.
Problem 4.3. Consider the space-fractional HE
with the ICs
Applying the Yang transform of Eq (4.23), we achieve
Implementing inverse Yang transform, we get
Applying Homotopy perturbation method in Eq (4.27), we achieved as
Both sides on comparison coefficients of p, we obtain
The series type result of the third problem is
The exact solution is
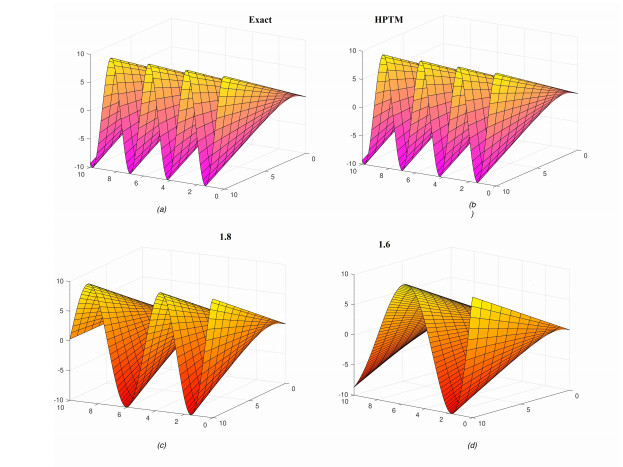
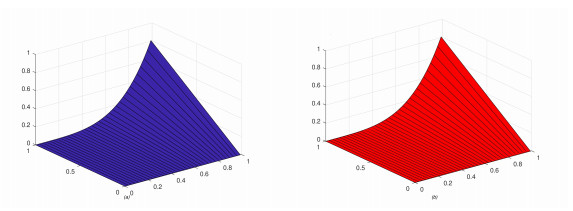
Figure 5a and b display the exact and HPTM solutions, respectively, in a 3-dimensional plot at ϱ=2. The closed contact between the exact and HPTM solutions is examined. Figure 6 depicts the exact and HPTM solutions in two-dimensional plot for various values of ϱ=2,1.9,1.8,1.7,1.6,1.5 for ξ∈[0,1] and ψ=1. The fractional results are observed to approach an integer-order solution of the problem. Similarly, the graphs for ψ-space fractional-order derivative can also be plotted.
5.
Conclusions
In this study, fractional-order Helmholtz equations were solved using the Homotopy Perturbation Yang transform method. Due to the great agreement between the generated approximative solution and the precise solution, the homotopy perturbation Yang transform method was demonstrated to be a successful method for solving partial differential equations with Caputo operators. The computation size of the approach was compared to those required by other numerical methods to demonstrate how tiny it is. Additionally, the procedure's quick convergence demonstrates its dependability and marks a notable advancement in the way linear and non-linear fractional-order partial differential equations are solved.
Acknowledgements
This research has been funded by Deputy for Research & Innovation, Ministry of Education through Initiative of Institutional Funding at University of Ha'il–Saudi Arabia through project number IFP-22 064.
Conflict of interest
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: