1.
Introduction
Let D be the unit disk in the complex plane C centered at the origin and denote T=∂D. The symbol Cn(Ω) stands for the class of all complex-valued n-times continuously differentiable functions from the domain Ω into C. In particular, we let C(Ω)=C0(Ω). A real-valued function u∈C2(Ω) is called real harmonic if it satisfies the following Laplace's equation:
A complex-valued function ω=u+iv is harmonic if both u and v are real harmonic. We refer the readers to [12] for an excellent discussion on harmonic mappings in the plane.
Suppose that g∈C(D). Then, it is well known that the solution of the Poisson's equation Δω=g in D satisfying the boundary condition ω|T=f∈L1(T) is given by
where
and m denotes the Lebesgue measure in the plane.
The hyperbolic metric on D, the Gaussian curvature of which is equal to -4, is given by |dz|/(1−|z|2). Then, the hyperbolic distance between two points z1,z2∈D is defined by
where the infimum is taken over all the rectifiable curves γ which connect z1 and z2 with γ∈D. It is well known that
Also, we can consider the quasihyperbolic metric |dz|/(1−|z|) on D. Then, it gives rise to the quasihyperbolic distance between two points z1,z2∈D, which is defined by
where the infimum is taken over all rectifiable curves γ which connect z1 and z2 with γ∈D. Actually, we can consider the general q-metric |dz|/(1−|z|q) on D,q∈[1,2], which leads to the following q-pseudo distance
where the infimum is taken over all rectifiable curves γ which connect z1 and z2 with γ∈D. For completeness, we will prove that this q-pseudo distance is a distance in Lemma 7.
A self-mapping f of D is said to be Lipschitz continuous with respect to the q-distance if there exists a constant L>0, such that the inequality
holds for any z1,z2∈D.
The classic Schwarz-Pick lemma plays an important role in complex analysis. It is stated as follows: If f is a holomorphic self-mapping of D, then we have
or
The Schwarz-Pick lemmas (1.6) or (1.7) have many generalizations. See the references [1,6,13,30,31,32,34,35,39,46] on this topic. The first work of this paper is to extend (1.7) to the case for the q-distance. It is presented as follows:
Theorem 1. Suppose that q∈[1,2]. If f is a holomorphic self-mapping of D satisfying f(0)=0, then the inequality
holds for any z1,z2∈D.
Suppose that f satisfies the following the Poisson differential inequality:
where |Df|=|fz|+|f¯z|. This kind of mapping contains many classical mappings. For example, it includes a holomorphic mapping, a harmonic mapping, the mapping satisfying Poisson's equation Δf=g (where g is continuous on ¯D), the harmonic mapping between Riemannian surfaces satisfying some inequalities and so on. In addition, those mappings that satisfy (1.9) are also closely related to the following partial differential equations
where Q=(Q1,Q2,…,Qm), Qj are quadratic polynomial on ∂ui/∂xk, i=1,…,m,k=1,2. This equation has a deep connection with the average curvature problem of surfaces in differential geometry, the conjugate isothermal coordinates of surfaces, and the Monge-Ampère equation and so on. Based on this backgrounds, the study of mappings that satisfy the Poisson differential inequality (1.9) has attracted much attention from researchers. See the articles [4,18,20,42,45] and the references therein. Recently, Kalaj [21] extended the results of Bernstein [4] and Heinz [18] to the case for spaces and applied the relevant results to the theory of harmonic quasiconformal mappings. The study of mappings satisfying the Poisson differential inequality that are also quasiconformal or quasiregular have also attracted many authors' interest, see [3,10,22].
Let f be a quasiconformal self-mapping of the unit disk satisfying the following Poisson differential equation
In [23], Kalaj obtained the following result.
Lemma 1. [23] Suppose that f is a K-quasiconformal self-mapping of D satisfying the Poisson differential equation (1.11), and that f(0)=0. Then there exists a constant C(B,K), which depends only on B and K, such that
The inequality (1.12) can be seen as a kind of Schwarz-Pick type inequality for the K-quasiconformal self-mapping of D satisfying the Poisson differential inequality (1.11). Generally, the condition for quasiconformality in Lemma 1 can not be removed. Recently, Zhong et al. [47] showed the following result.
Theorem 2. [47, Theorem 1.4] For a given q∈{1}∪[2,+∞). Suppose that f:¯D→¯D is continuous on ¯D, f|D∈C2,f|T∈C2 and f(0)=0, and that it satisfies the following Poisson differential inequality
as well as satisfying that |∂2f(eiφ)∂φ2|≤K, where 0<a<1/2,0<b,K<∞. If
then, we have
In the next result of this paper, we will improve Theorem 2 by giving the explicit constant L(a,b,K) and showing that the result is still valid when we consider all of the cases for q>0. Our result is presented as follows.
Theorem 3. For given q>0, suppose that f:¯D→¯D is continuous in ¯D, f|D∈C2,f|T∈C2 and f(0)=0, and that it satisfies the Poisson differential inequality |Δf(z)|≤a⋅|Df(z)|2+b and |∂2f(eiφ)∂φ2|≤K, where 0<a<1/2,0<b,K<∞. If, in addition, 48ab+640a<9 and max{a,b}⋅(L2(a,b,K)+1)<2/π, then we have
where
As an application of Theorem 3, we provide the following more general form of [47, Corollary 1.5].
Corollary 1. For a given q>0, suppose that f:¯D→¯D is continuous in ¯D, f|D∈C2,f|T∈C2 and f(0)=0, and that it satisfies the Poisson differential inequality |Δf(z)|≤a⋅|Df(z)|2+b and |∂2f(eiφ)∂φ2|≤K, where 0<a<1/2,0<b,K<∞. If, in addition, 48ab+640a<9 and max{a,b}⋅(L2(a,b,K)+1)<2/π, then we have
Proof. According to Lemma 9, we see that there exists a constant L(a,b,K) such that the inequality
holds for any z∈D. Combining this with Theorem 3, we get
By the definition of q-distance, we derive that inequality (1.15) is valid. □
The classic boundary Schwarz lemma for the holomorphic mapping states the following:
Lemma 2. ([14]) Let f be a holomorphic self-mapping of D satisfying that f(0)=0. If f is differentiable at the point z=1 and satisfies that f(1)=1, then we have the follwoing:
(i) f′(1)≥1;
(ii) f′(1)=1 if and only if f(z)=z.
The boundary Schwarz lemma is a basic and important result in complex analysis. Its generalizations and applications have received widespread attention; see [5,7,9,15,16,17,25,26,27,28,29,40,43,44]. In [25], Lemma 2 was generalized to the following form:
Lemma 3. ([25]) Let f be a holomorphic self-mapping of D satisfying that f(0)=0. If f is differentiable at the point z=α∈T and satisfies that f(α)=β∈T. Then we have the following
(i′) ¯βf′(α)α≥1;
(ii′) ¯βf′(α)α=1 if and only if f(z)=eiθz, where eiθ=βα−1 and θ∈R.
Recently, the extension of the boundary Schwarz lemma to harmonic mappings has also attracted scholars' attention. In [50], Zhu and Wang established the following harmonic version of the boundary Schwarz lemma.
Lemma 4. ([50, Theorem 1.2]) Suppose that g∈C(¯D). If f∈C2(D)⋂C(T) is a self-mapping of D satisfying the Poisson equation Δf=g and f(0)=0, and if f is differentiable at the point z=1 and satisfies that f(1)=1, then we have
where ||g||∞:=supz∈D|g(z)|.
This result was extended by Mohapatra et al. [37] and Mohapatra [38]. See the high dimensional version of the boundary Schwarz lemma for harmonic mappings in [24,33,36,49]. As a generalization of planar harmonic maps, those self-mappings that satisfy the Poisson differential inequality (1.11) can be naturally considered as analogous to the boundary Schwarz lemma. Unfortunately, those types of mappings generally are not associated with the boundary Schwarz lemma of types (1.16). This is because we have established the following results:
Theorem 4. There exists a self-mapping f of D, which is differentiable at z=1 and satisfies that f(0)=0 and f(1)=1, in addition to the Poisson differential inequality |Δf(z)|≤a⋅|Df(z)|2. But it satisfies the equation Re(fx(1))=0.
According to Lemma 4, we see that there exists a self-mapping of D that satisfies the Poisson differential inequality (1.9), which is associated with a boundary Schwarz lemma of type (1.16). Therefore, we naturally ask the following question: which subset of the family
has boundary Schwarz lemma of type (1.16)? Next, we establish a result in this regard.
Theorem 5. Suppose that f:¯D→¯D is continuous in ¯D, f|D∈C2,f|T∈C2 and f(0)=0, and that it satisfies the Poisson differential inequality |Δf(z)|≤a⋅|Df(z)|2+b and |∂2f(eiφ)∂φ2|≤K, where 0<a<1/2,0<b,K<∞. If, in addition, 48ab+640a<9 and max{a,b}⋅(L2(a,b,K)+1)<8/(3π), then we have
where
2.
Some preparations
L' Hospital's rule for monotonicity is important to derive some inequalities and it will be used to prove some results.
Lemma 5. ([2, Theorem 2]) Let −∞<a<b<+∞ and let f,g:[a,b]→R be continuous functions that are differentiable on (a,b) with f(a)=g(a)=0 or f(b)=g(b)=0. Suppose that g′(x)≠0 for each x∈(a,b). If f′/g′ is increasing (decreasing) on (a,b), then so is f/g.
The following lemma can be obtained in [48] by letting x=t2.
Lemma 6. For any q>0, the inequalities
hold for any x∈[0,1).
Remark 1. In the rest of this paper, we will always use the constant cq, which is defined by
In Section 1, we defined the following general q-pseudo distance in D:
where the infimum is taken over all rectifiable curves γ in D connected z1 and z2. Next, we will prove that it is a distance.
Lemma 7. The function dq(⋅,⋅) defined by (2.3) is a distance.
Proof. Obviously, for any z1,z2∈D, we have that dq(z1,z2)≥0 and dq(z1,z2)=dq(z2,z1). Hence, we only prove that if dq(z1,z2)=0, then z1=z2. This is because, by taking x=|z|2 in Lemma 6, we get
Hence, by the definitions of hyperbolic distance and q-pseudo distance, we have
Therefore, it must be that dhD(z1,z2)=0 if dq(z1,z2)=0. Since dhD(⋅,⋅) is a distance, we get that z1=z2. This shows that the q-pseudo distance dq(⋅,⋅) defined in D is a distance. □
We also need the following general Schwarz lemma for harmonic self-mappings of the unit disk, which was obtained by Hethcote [19].
Lemma 8. ([19, Theorem 1]) Suppose that f is a harmonic self-mapping of D. Then we have
In [18], Heinz obtained a gradient estimate for self-mappings of D satisfying the Poisson differential inequality. The upper bound he obtained was abstract. In what follows, we give an explicitly upper bound based on the proof in [18]. The disadvantage is that the range of a,b becomes smaller.
Lemma 9. Suppose that f:¯D→¯D is continuous in ¯D, f|D∈C2,f|T∈C2 and f(0)=0, and that it satisfies the Poisson differential inequality |Δf(z)|≤a⋅|Df(z)|2+b and |∂2f(eiφ)∂φ2|≤K, where 0<a<1/2,0<b,K<∞. If 48ab+640a<9, then the inequality
holds for any z∈D, where
Proof. First, we calculate c′10(a,b,K) in [18, P. 239]. According to [18, Lemma 11] and given
in [18, P. 239] and [18, (2.2.45), P. 238], we get
Hence, by [18, (2.2.47), P. 239], we can take
Next, we will estimate the constant c5(a,b) in [18]. According to the proof of [18, Theorem 2], we can take α=2,β=2(1−a) and γ=2b in [18, (2.1.27)]. Therefore, the formula given by [18, (2.1.27)] can be rewritten as
where λ and θ are constants satisfying that 0<λ<θ<1. Now, we take θ=2λ and assume that 0<λ<1/4. Since ln1θ≥1−θ and a21−a≤a (as a<1/2), we have
As the functions φ1(λ)=8a+4abλ+a(b+16)1−2λ,φ2(λ)=−(λ−1)2 are monotonically increasing on (0,1/4), we see that the inequality
holds for any 0<λ<1/4 when 48ab+640a<9. Especially, inequality (2.10) holds for any 0<λ≤1/8. Now, we take λ0=1/8 and θ0=1/4. Then by [18, (2.1.31), P. 227], we have
Hence, by the inequality given by[18, (2.1.31)], we get
Combining [18, P. 239] with (2.7) and (2.11), we have
This completes the proof. □
The proof of following estimate can be found in [8].
Lemma 10. ([8]) Suppose that g∈C(D). Then, |G[g](z)|≤(1−|z|2)⋅||g||∞4, where ||g||∞:=supz∈D|g(z)|.
Lemma 11. For any t∈[0,1), we have
Proof. Let φ1(t)=1−4π⋅arctant and φ2(t)=1−t,t∈[0,1). Then, φ1(1)=φ2(1)=0 and the function
is monotonically decreasing on t∈[0,1). By L' Hospital's rule for monotonicity [2], we see that the function φ1/φ2 is monotonically decreasing on t∈[0,1). Hence, by L'Hospital's rule, we get
This finishes the proof. □
The following result was proved by Ruscheweyh [41].
Lemma 12. ([41]) Suppose that f is a holomorphic self-mapping of D. Then,
In what follows, we generalize Lemma 12 to the following form.
Proposition 1. For any q∈[1,2], suppose that f is a holomorphic self-mapping from the unit disk D into itself; then, we have
where n∈{1,2,⋅⋅⋅}.
Proof. Let
Since (1−t2)′(1−tq)′=2q⋅t2−q is monotonically increasing on [0,1), the function φ is also monotonically increasing on [0,1). By Lindelöf's inequality, we have that |f(z)|≤|z|+|f(0)|1+|z|⋅|f(0)|,z∈D. Therefore,
Combining this with Lemma 12, we get
This has finished the proof. □
Remark 2. If q=2, then Proposition 1 becomes Lemma 12.
3.
Proof of Theorem 1
Proof. By using Proposition 1 for n=1 and f(0)=0, we get
Namely,
According to the definition of q-distance, we have that dq(f(z1),f(z2))≤dq(z1,z2). This finishes the proof. □
Remark 3. Considering the case for n=1 and f(0)=0 in Proposition 1, we get the following Schwarz-Pick lemma: Suppose that f is a holomorphic self-mapping from unit disk D into itself with f(0)=0; then, we have
From the proof of Proposition 1, we see that the inequality (3.2) is sharp. The equation holds if and only if |f(z)|=|z|, which is subject to the condition if and only if f(z)=eiθ⋅z,θ∈R is true.
4.
Proof of Theorem 3
Proof. According to Lemma 9, we see that there exists a constant L(a,b,K), such that the inequality
holds for any z∈D, where
Now, let
where h(z)=l(z)(|Df(z)|2+1) and ||l||∞≤max{a,b}. For example, we can define l as follows:
Since f∈C2(D), we see that h∈C(D). Hence, by Lemma 9, we get
By virtue of the solution of Poisson's equation, we have
where f|T:=k. Since P[k] is a harmonic self-mapping of D, we get the following by Lemma 8
Combining Lemmas 6, 8, 10 and 11, we get
This completes the proof. □
5.
Proof of Theorem 4
Proof. Consider the function
then, |f(z)|<1,f(eiθ)=eiθ,fz(z)=3−2|z|22,f¯z(z)=−z22,Δf(z)=4fz¯z(z)=−4z and |fz(z)|+|f¯z(z)|=3−|z|22. Therefore, f is a self-mapping of D satisfying that |Δf(z)|≤4(Df(z))2 and f(0)=0. But Re(fx(1))=Re(fz(1)+f¯z(1))=0. □
6.
Proof of Theorem 5
Proof. Set Δf(z)=h(z),z∈D, where h(z)=l(z)(|Df(z)|2+1) and ||l||∞≤max{a,b}. Since h∈C(D), we get, by Lemma 9 that ||h||∞≤max{a,b}⋅(L2(a,b,K)+1). Then,
where f|T:=k. Next, the method is similar to the one given in [50]. But, here, we do not demand that h∈C(¯D), as we only need h∈C(D). By virtue of (6.1) and Lemmas 8 and 10, we have
Since f is differential at z=1 and satisfies that f(1)=1, we get
Since |f(z)|2≤M2(z),
By letting z=r∈(0,1) and r→1−, we obtain
This finishes the proof. □
7.
Conclusions
By establishing the general Schwarz-Pick lemma, which is a generalization of the result of Ruscheweyh [41] and sharp when n=1 and f(0)=0, we have obtained a Schwarz-Pick-type lemma for the holomorphic self-mapping of the unit disk with respect to the q-distance. We also have established the general Schwarz-Pick lemma for self-mappings of the unit disk satisfying the Poisson differential inequality. This obtained result improved the one in [47] by giving the explicit constant L(a,b,K), and it showed that the result is still valid when we consider all of the cases for q>0. As an application, it has been proven that this mapping is Lipschitz continuous with respect to the q-distance under certain conditions; Moreover, the corresponding explicit Lipschitz constant has been given. Next, we investigated the boundary Schwarz lemma for self-mappings of the unit disk satisfying the Poisson differential inequality. We found that those types of mappings are generally not associated with the boundary Schwarz lemma. With some additional conditions, we have established a boundary Schwarz lemma for self-mappings of the unit disk satisfying the Poisson differential inequality.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors would like to express their sincere thanks to the referees for their great efforts to improve this paper. This work was supported by the Guangdong Basic and Applied Basic Research Foundation (No. 2022A1515110967; No. 2023A1515011809) and Research Foundation of Shenzhen Polytechnic University (No. 6023312032K).
Conflict of interest
The authors declare that they have no competing interests.











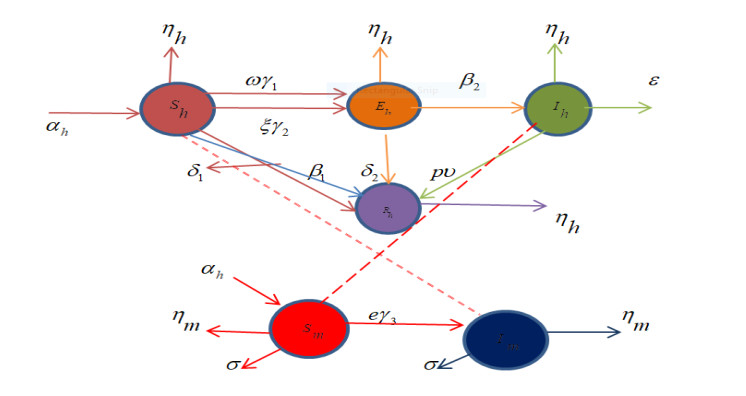


 DownLoad:
DownLoad: