1.
Introduction
This paper considers the weighted Linear Complementarity Problem (wLCP) introduced by Potra [14] which consists in finding vectors x∈Rn,s∈Rn,y∈Rm such that
Here P∈R(n+m)×n,Q∈R(n+m)×n,R∈R(n+m)×m are given matrices, d∈Rn+m is a given vector, w≥0 is a given weight vector (the data of the problem) and xs is the componentwise product of the vectors x and s. The matrix R is assumed to have full column rank. If the weight vector w is chosen to be the zero vector, then the wLCP reduces to the general LCP studied in [21]. The wLCP is called monotone, if
The wLCP can be used for modeling a larger class of problems from science and engineering. For example, Fisher's competitive market equilibrium model can be formulated as a wLCP that can be efficiently solved by interior-point methods [14]. Moreover, the Quadratic Programming and Weighted Centering problem, which generalizes the notion of a Linear Programming and Weighted Centering problem proposed by Anstreicher [1], can be formulated as a monotone wLCP [14]. Lately, Chi et al. [3] and Gowda [10] studied wLCP on Euclidean Jordan algebras.
Since Potra introduced the notion of wLCP [14], many numerical algorithms have been proposed for solving this problem. One class of effective algorithms is interior-point methods. For example, Potra [14] proposed two interior-point methods for solving general monotone wLCPs. In [15], Potra proposed a corrector-predictor interior-point method for solving the sufficient wLCP. Asadi et al. [2] introduced a full-Newton step interior-point method for solving the monotone wLCP. Chi et al. [4] proposed a full-modified-Newton infeasible interior-point method for solving a special wLCP. It is worth pointing out that, to establish the computational complexity of interior-point methods, one usually requires that the wLCP is monotone (e.g., [2,14]). Another class of effective algorithms for solving the wLCP is smoothing Newton-type algorithms. This class of algorithms is to use a smoothing function to reformulate the wLCP as a system of smooth nonlinear equations and then solve it by Newton method. For example, Zhang [22] presented a smoothing Newton algorithm for solving the wLCP. Tang [16] proposed a variant nonmonotone smoothing algorithm for solving the wLCP with improved numerical results. Tang and Zhang [17] proposed a nonmonotone smoothing Newton algorithm for solving general wCPs. Notice that, to ensure Newton step be feasible, smoothing Newton-type algorithms in [16,17,22] also require that the wLCP is monotone. Moreover, to obtain local fast convergence rate, smoothing Newton-type algorithms in [16,22] need the nonsingularity condition.
Lately, based on a nonsmooth weighted complementarity function, Tang and Zhou [19] reformulated the wLCP as a nonsmooth nonlinear equation and proposed a damped Gauss-Newton method to solve it. Their method can be used to solve nonmonotone wLCPs and has local quadratic convergence under the local error bound condition which is weaker than the nonsingularity condition. Motivated by their work, in this paper we introduce a weighted complementarity function which is smooth everywhere. By using this function, we reformulate the wLCP as a smooth nonlinear equation and propose a Levenberg-Marquardt method to solve it. Different from current Levenberg-Marquardt type methods (e.g., [7,8,9]), the proposed method is designed based on a simple derivative-free line search technique. Compared with smoothing Newton-type algorithms in [16,17,22], the proposed method has two advantages. (i) It is well-defined and is globally convergent without any additional condition. Hence it can be used to solve nonmonotone wLCPs. (ii) It has local sub-quadratic convergence rate under the local error bound condition. It is worth pointing out that, to obtain the local fast convergence rate, classical Levenberg-Marquardt methods (e.g., [7,8,9]) also need the condition that the Jacobian is Lipschitz continuous. In this paper we show that this condition holds for our method (see, Lemma 4.1 below). We also report some numerical results which indicate that our method is more effective for solving monotone and nonmonotone wLCPs than the damped Gauss-Newton method studied in [19].
This paper is organized as follows. In Section 2, we reformulate the wLCP as a smooth nonlinear equation and propose a Levenberg-Marquardt method to solve it. In Section 3, we give its global convergence. In Section 4, we analyze its local sub-quadratic convergence under the local error bound condition. Numerical results are reported in Section 5. Some conclusions are given in Section 6.
Throughout this paper, Rn denotes the set of all n dimensional real vectors. All vectors are column vectors and for simplicity, the column vector (uT1,…,uTn)T is written as (u1,…,un) where ui∈Rni. ‖⋅‖ denotes the 2-norm. For any vector x∈Rn, we denote x by vec(xi) and the diagonal matrix whose ith diagonal element is xi by diag(xi). For a given set S⊂Rn and for any u∈Rn, dist(u,S)=infv∈S{‖u−v‖}. For any α,β>0, α=O(β) (respectively, α=o(β)) means that limsupβ→0αβ<∞ (respectively, limsupβ→0αβ=0).
2.
A smooth Levenberg-Marquardt method
2.1. The reformulation of wLCP
The weighted complementarity function serves an important role in designing Newton-type methods for solving the wLCP. For a fixed c≥0, a function ϕc(a,b):R2→R is called a weighted complementarity function if it satisfies
One popular weighted complementarity function is
When c=0, ϕc(a,b) is the well-known Fischer-Burmeister function for nonlinear complementarity problems. Obviously, ϕc(a,b) is not continuously differentiable (smooth) everywhere. By using ϕc(a,b), Tang and Zhou [19] reformulated the wLCP as the following nonsmooth nonlinear equation:
where w=(w1,...,wn)T≥0 is the weight vector given in the wLCP. Tang and Zhou [19] presented a damped Gauss-Newton method to solve Φ(x,s,y)=0 and established its local quadratic convergence under the local error bound condition.
In this paper, for a fixed c≥0, we consider the following nonnegative function:
The following lemma shows that ψc is a weighted complementarity function and it is smooth everywhere.
Lemma 2.1. Let ψc be defined by (2.1).Then the following results hold.
(i) ψc is a weighted complementarity function, i.e.,
(ii) ψc is continuously differentiable at any (a,b)∈R2 and
where ∇aψc(0,0)=∇bψc(0,0)=−√2c and for any (a,b)≠(0,0),
(iii) For any (a,b)∈R2, one has
(iv) For any (a,b)∈R2, one has
Proof. The result (i) obviously holds. By a direct computation, we can obtain the result (ii). Moreover, for any (a,b)∈R2, by the result (ii), we have ∇aψc(0,0)∇bψc(0,0)=2c≥0, and if (a,b)≠(0,0), then we also have
where the inequality holds because
Now we prove the result (iv). First, we prove the implication
Since “⟹” obviously holds, we only need to prove “⟸”. By the result (ii), ∇aψc(0,0)=0 gives c=0 and so ψc(0,0)=0. For (a,b)≠(0,0), ∇aψc(a,b)=0 gives ϕc(a,b)=0 or 1−a√a2+b2+2c=0. If ϕc(a,b)=0, then ψc(a,b)=0 and we are done. If 1−a√a2+b2+2c=0, then a=√a2+b2+2c which yields b=c=0 and a=|a|. These implies that ϕc(a,b)=0 and so ψc(a,b)=0. By the same way, we can also prove ψc(a,b)=0⟺∇bψc(a,b)=0. The proof is completed.$
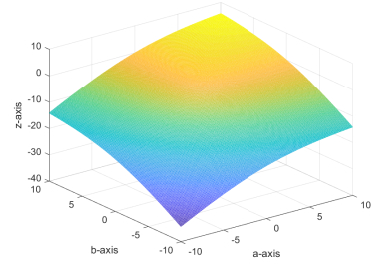
Figures 1 and 2 illustrate the geometrical interpretations of ϕc and ψc with c=1 which show that they are very different.
By using the weighted complementarity function ψc given in (2.1), we now reformulate the wLCP as the following smooth nonlinear equation:
By Lemma 2.1, we have the following result.
Lemma 2.2. (i) H(x,s,y)=0 if and only if (x,s,y) is a solution of the wLCP.
(ii) H(x,s,y) is continuously differentiable at any (x,s,y)∈R2n+m withthe Jacobian
in which ∇xiψwi(⋅,⋅) and ∇siψwi(⋅,⋅) are given in Lemma 2.1 (ii).
2.2. The algorithm
Let z:=(x,s,y) and H(z) be given in (2.2). We define the merit function Ψ:R2n+m→R as
Then, by Lemma 2.2, we have the following result.
Lemma 2.3. (i) Ψ(z)=0 if and only if z=(x,s,y) is a solution of the wLCP.
(ii) Ψ(z) is continuously differentiable at any z∈R2n+m with its gradient ∇Ψ(z)=H′(z)TH(z).
Now we describe our method as follows.
Algorithm 2.1. (A smooth Levenberg-Marquardt method)
Step 0: Choose parameters θ,ρ,γ∈(0,1) and an initial point z0:=(x0,s0,y0).Set k:=0.
Step 1: If ∇Ψ(zk)=0, then stop.
Step 2: Set μk:=θ‖H(zk)‖δ where δ∈[1,2] is a constant. Compute the search direction dk∈R2n+m by solving
Step 3: Find a step-size αk:=ρmk, where mk is the smallest nonnegative integer m satisfying
Step 4: Set zk+1:=zk+αkdk. Set k:=k+1 and go to Step 1.
The algorithmic framework of Algorithm 2.1 is much simpler than many Levenberg-Marquardt type methods (e.g, [7,8,9,13,18,23]). The main feature of Algorithm 2.1 is that it adopts a simple derivative-free line search in Step 3 which avoids computing the gradient ∇Ψ(zk).
Theorem 2.1. Algorithm 2.1 is well-defined.
Proof. For some k, if ∇Ψ(zk)≠0, then H(zk)≠0 and hence μk=θ‖H(zk)‖δ>0. So, H′(zk)TH′(zk)+μkI is positive definite and the search direction dk in Step 2 is well-defined. Since ∇Ψ(zk)≠0, by (2.5) we have dk≠0 and
This implies that dk is a descent direction of the merit function Ψ(z) at zk. Next, we show that there exists at least a nonnegative integer m satisfying (2.6). On the contrary, we suppose that for any nonnegative integer m,
Multiplying both sides of the above inequality by 12[‖H(zk+ρmdk)‖+‖H(zk)‖], we have
Since Ψ is continuously differentiable at zk, by letting m→∞ in (2.8), we have ∇Ψ(zk)Tdk≥0 which contradicts (2.7). So, we can find a step-size αk in Step 3 and get the (k+1)-th iteration zk+1=zk+αkdk in Step 4. Hence, Algorithm 2.1 is well-defined.
3.
Global convergence
In the following, we assume ∇Ψ(zk)≠0 for all k≥0, so that Algorithm 2.1 generates an infinite sequence {zk}. To establish the global convergence, we need the following lemma.
Lemma 3.1. Let {zk} be the sequence generated by Algorithm 2.1.Then one has:
(i) ‖dk‖≤12√θ‖H(zk)‖1−δ2 for all k≥0;
(ii) limk→∞‖αkdk‖=0.
Proof. For any k≥0, we suppose that the singular value decomposition of H′(zk) is
where Uk and Vk are orthogonal matrices and Σk=diag(σk1,...,σkr,0,...,0) with σk1≥⋯≥σkr>0. Then, by (2.5) we have for any k≥0,
where the inequality holds because σki(σki)2+μk≤12√μk for all i=1,...,r. This together with μk=θ‖H(zk)‖δ gives the result (i). Moreover, by (2.6) we have
Since {‖H(zk)‖} is a monotonically decreasing sequence by (2.6), there exists a constant H∗≥0 such that limk→∞‖H(zk)‖=H∗. This together with (3.1) proves the result (ii).
Theorem 3.1. Let z∗be any accumulation point of the sequence {zk} generated by Algorithm 2.1. Thenz∗ is a stationary point of the merit function Ψ(z), i.e., ∇Ψ(z∗)=0.Moreover, if H′(z∗) is nonsingular, then H(z∗)=0 and so z∗=(x∗,s∗,y∗) is a solution of the rmwLCP.
Proof. Without loss of generality, we may assume that z∗ is the limit of the subsequence {zk}k∈K where K⊂{0,1,...}, i.e, lim(K∋)k→∞zk=z∗. Then, by the continuity of H and H′,
and consequently
Obviously, ∇Ψ(z∗)=0 when H(z∗)=0. Now we assume ‖H(z∗)‖>0 and will derive a contradiction. Since {‖H(zk)‖} is a monotonically decreasing sequence, by Lemma 3.1 (i), we have for all k∈K,
Thus, {dk}k∈K has a convergent subsequence and we may assume lim(K1∋)k→∞dk=d∗ where K1⊂K. In the following, we show that d∗=0. In fact, if d∗≠0, then by Lemma 3.1 (ii), we have lim(K1∋)k→∞αk=0. Moreover, from Step 3 we have for all k∈K1,
Multiplying both sides of this inequality by 12[‖H(zk+ρ−1αkdk)‖+‖H(zk)‖], we have for all k∈K1,
Since Ψ is continuously differentiable at z∗, by letting k→∞ with k∈K1 in (3.2), we have
On the other hand, by (2.7) we have
So, from (3.3) and (3.4) we have ∇Ψ(z∗)Td∗=0, which together with (2.5) gives
Since ‖H(z∗)‖>0, the matrix H′(z∗)TH′(z∗)+θ‖H(z∗)‖δI is positive definite. Hence, we have d∗=0. A contradiction is derived. Therefore, we have d∗=0. Then, by letting k→∞ with k∈K1 in (2.5), we have
This proves the first result. The second result follows from ∇Ψ(z∗)=H′(z∗)TH(z∗)=0. We complete the proof.
Theorem 3.2. Let {zk} be the sequence generated by Algorithm 2.1. If {zk} has an isolated accumulation pointz∗, then the whole sequence {zk} converges to z∗.
Proof. By Lemma 3.1 (ii), we have limk→∞‖zk+1−zk‖=0. This together with [6,Proposition 8.3.10] proves the theorem.
At the end of this section, we consider a special wLCP which consists in finding vectors x∈Rn,s∈Rn such that
where q∈Rn and M∈Rn×n is a P0 matrix, that is, for any ξ∈Rn with ξ≠0, there exists an index i0∈{1,...,n} such that ξi0≠0 and ξi0(Mξ)i0≥0.
When w is chosen to be the zero vector, the P0 wLCP (3.5) reduces to the following standard P0 LCP:
which has many applications in economics and engineering and has been extensively studied in literatures (e.g., [11,12,24,25,26]). By using the weighted complementarity function ψc(a,b) defined by (2.1), we can reformulate the P0 wLCP as the smooth nonlinear equation
and apply Algorithm 2.1 to solve it. For the P0 wLCP, we have the following global convergence result.
Theorem 3.3. Let {(xk,sk)} be the sequence generated by Algorithm 2.1 for solving the nonlinear equation (3.6).Then any accumulation point (x∗,s∗) of {(xk,sk)} is a solution of the P0 wLCP.
Proof. Since the P0 wLCP is a special case of the wLCP, Theorem 3.1 still holds. So, we have ∇Ψ(x∗,s∗)=H′(x∗,s∗)TH(x∗,s∗)=0. By (3.6), we have
in which ∇xiψwi(⋅,⋅) and ∇siψwi(⋅,⋅) are given in Lemma 2.1 (ii). Then, it follows from H′(x∗,s∗)TH(x∗,s∗)=0 that
Now we assume Mx∗+q−s∗≠0. Since M is a P0 matrix and so is MT, there exists an index i0∈{1,...,n} such that (Mx∗+q−s∗)i0≠0 and
By (3.8) and (3.9), we have
which together with (3.10) gives
On the other hand, by Lemma 2.1 (iii), we have
From (3.13) and (3.14) it holds that
This together with Lemma 2.1 (iv) gives ψwi0(x∗i0,s∗i0)=0. Then, by (3.12) we have (Mx∗+q−s∗)i0=0 which contradicts the choice of the index i0 such that (Mx∗+q−s∗)i0≠0. Hence, Mx∗+q−s∗=0. Furthermore, by (3.8) we have ∇xiψwi(x∗i,s∗i)ψwi(x∗i,s∗i)=0 which together with Lemma 2.1 (iv) yields ψwi(x∗i,s∗i)=0 for all i=1,...,n. Therefore, H(x∗,s∗)=0 and (x∗,s∗) is a solution of the P0 wLCP.
4.
Local sub-quadratic convergence
Let H(z) be given in (2.2). Denote
In this section, we assume that the whole sequence {zk} generated by Algorithm 2.1 converges to some point z∗∈Z∗. Then limk→∞H(zk)=H(z∗)=0. Now we make the following assumption.
Assumption 4.1. H(z) provides a local error bound on some neighbourhood of z∗, i.e., thereexist constants ξ>0 and ϵ>0 such that
As it is well-known, Assumption 4.1 is the local error bound condition which is weaker than the nonsingularity condition. It is worth pointing out that, to obtain the local quadratic convergence, classical Levenberg-Marquardt methods (e.g., [7,8,9]) also need to assume that the Jacobian is Lipschitz continuous on the set N(z∗,ϵ). In the following, we show that this assumption holds for our method.
Lemma 4.1. The Jacobian H′(z) given in (2.3) is Lipschitz continuous on R2n+m, i.e., there exists a constant M>0 such that
Proof. Obviously, we only need to prove that the gradient ∇ψc(a,b) given in Lemma 2.1 (ii) is Lipschitz continuous on R2. First, by [5,Lemma 3.1], ∇ψc(a,b) is Lipschitz continuous on R2 when c=0. Now we consider c>0. Then ψc(a,b) is twice continuously differentiable at any (a,b)∈R2 with
where
Since
also notice that
we have
Moreover, it is clear that
Thus, we have
This implies that there exists a constant C>0 independent of (a,b) such that
Then, by the Mean-Value Theorem, we have
holds for all (a,b),(˜a,˜b)∈R2. The proof is completed.
By Lemma 4.1, we can directly have
and there exists a constant L>0 such that
In the following, we denote ˉzk as the vector in Z∗ that satisfies
Lemma 4.2. Let {zk} be the sequence generated by Algorithm 2.1.If Assumption 4.1 holds, then for all sufficiently large k,
Proof. Notice that for all sufficiently large k,
which implies that ˉzk sufficiently close to z∗. So, by (4.5), for all sufficiently large k,
For any k≥0, we consider the following optimization problem:
Then, the search direction dk generated by (2.5) is the solution of (4.9) because φk(d) is a strictly convex quadratic function and dk is a stationary point of φk(d). Hence, for all sufficiently large k, by (4.4) and (4.8) we have
This together with (4.9) yields
Moreover, for all sufficiently large k, by Assumption 4.1, we have
which together with (4.9) and (4.10) gives
The proof is completed.
Theorem 4.1. Let {zk} be the sequence generated by Algorithm 2.1.If Assumption 4.1 holds, then for all sufficiently large k, we have
Proof. By (4.7), for all sufficiently large k,
where c1:=1+√M2+θLδθξδ. This implies that zk+dk sufficiently close to z∗. Hence, by (4.4), for all sufficiently large k,
which together with (4.6) and (4.7) gives
where c2:=√M2+θLδ+M(M2+θLδ)θξδ. Thus, by (4.1) and (4.15), for all sufficiently large k,
Let ˜zk be the vector in Z∗ that satisfies ‖zk+dk−˜zk‖=dist(zk+dk,Z∗). Then, by (4.13) and (4.16), for all sufficiently large k,
which yields ˜zk sufficiently close to z∗. So, by (4.1), (4.5) and (4.16), also notice that H(˜zk)=0 as ˜zk∈Z∗, for all sufficiently large k,
Moreover, by (4.1) and (4.7), for all sufficiently large k,
Hence, by (4.17) and (4.18) we have
which implies that for all sufficiently large k,
This shows that the step-size αk=1 is accepted in Step 3 for all sufficiently large k. Consequently, for all sufficiently large k, we have zk+1=zk+dk which together with (4.16) prove the theorem.
By Theorem 4.1, similarly as the proof of [19,Theorem 5.2], we can obtain the following sub-quadratic convergence property.
Theorem 4.2. Let {zk} be the sequence generated by Algorithm 2.1.If Assumption 4.1 holds, then one has
5.
Numerical results
In this section, we report some numerical results of Algorithm 2.1. All experiments are carried on a PC with CPU of Inter(R) Core(TM)i7-7700 CPU @ 3.60 GHz and RAM of 8.00GB. The codes are written in MATLAB and run in MATLAB R2018a environment. The parameters used in Algorithm 2.1 are chosen as θ=10−4,ρ=0.8,γ=10−4,δ=1.
We apply Algorithm 2.1 to solve the wLCP (1.1) in which
where A∈Rm×n is a full row rank matrix with m<n, M∈Rn×n, b∈Rm and f∈Rn. This example comes from [14]. For the purposes of comparison, we also apply the the damped Gauss-Newton method studied by Tang and Zhou [19] to solve this test problem. In our experiments, we test the following two class of wLCPs.
(The monotone wLCP) We choose A=randn(m,n) with the rank of A being m and M=BBT/‖BBT‖ with B=rand(n,n). Then we choose ˆx=rand(n,1), f=rand(n,1) and set b:=Aˆx, ˆs:=Mˆx+f and w:=ˆxˆs. This wLCP is monotone. For each problem with sizes n(=2m), we generate ten instances and solve them by using the following three starting points:
(i) x0=s0=(1,...,1)T, y0=(0,...,0)T;
(ii) x0=s0=(1,0,...,0)T, y0=(0,...,0)T; (iii) x0=rand(n,1),s0=rand(n,1),y0=rand(m,1).
We use ‖H(zk)‖≤10−5 as the stopping criterion. Numerical results are listed in Table 1 where SLMM denotes the smooth Levenberg-Marquardt method studied in this paper, DGNM denotes the damped Gauss-Newton method studied in [19], SP denotes the starting point, AIT and ACPU denote the average number of iterations and the average CPU time in seconds respectively. From Table 1, we can see that SLMM has the advantage over DGNM, especially for large scale test problems.
(The nonmonotone wLCP) We choose M=B1/‖B1‖−B2/‖B2‖ with B1=rand(n,n) and B2=rand(n,n). The matrix A and vectors b,f,w are generated by the same way as before. Since the matrix M is not symmetric positive semidefinite, this class of wLCP may be nonmonotone. For each problem with sizes n(=2m), we also generate ten instances and solve them by using three starting points as before. Moreover, we use ‖H(zk)‖≤10−5 and iter<50 as the stopping criterion where iter denotes the number of iterations. Numerical results are listed in Table 2, where ∗ stands for that the method fails to solve some instances as the iteration number is grater than 50 and the average is based on the successful instances through our numerical reports. From Table 2, we can see that, although both SLMM and DGNM can be applied to solve nonmonotone wLCPs, the former has better numerical performance than the latter.
6.
Conclusions
Based on a smooth weighted complementarity function, we reformulated the wLCP as a smooth nonlinear equation and proposed a Levenberg-Marquardt method to solve it. The proposed method is well-defined and it is globally convergent without any additional condition. Moreover, we proved that the proposed method has local sub-quadratic convergence rate under the local error bound condition which is weaker than the nonsingularity condition. Numerical results show that our method is very effective for solving monotone and nonmonotone wLCPs. In Algorithm 2.1, the Eq (2.5) is solved exactly in each iteration which maybe expensive for large-scale wLCPs. As a future research issue, it is worth investigating smooth inexact Levenberg-Marquardt method for solving wLCPs. Moreover, Wang and Fan [20] lately established the local convergence rate of Levenberg-Marquardt method under the Hölderian local error bound condition which is more general than Assumption 4.1 in this paper. Thus, another interesting issue is whether Algorithm 2.1 in this paper has local fast convergence rate under the Hölderian local error bound condition.
Acknowledgments
This paper is partly supported by Natural Science Foundation of Henan Province (222300420520) and Key scientific research projects of Higher Education of Henan Province (22A110020).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad:




