Cauchy problem for non-autonomous fractional evolution equations with nonlocal conditions of order $(1, 2)$

1.   Introduction

Unemployment is a serious problem for many nations since the problem is related to economic and social factors such as inflation, increase/decrease in GDP, and economic depression. Moreover, prolonged unemployment can lead to an erosion of skill, a negative effect on mental health, and worsen the physical health of unemployed people. For these reasons, the government of each country has been attempting to reduce the number of unemployed persons. A goal of many governments is full employment. There are various policies used to solve the problem such as monetary policy and fiscal policy. The government intervention helps to speed up the matching process between unemployed persons and entrepreneurs through the support of vacancies creation. Mathematical models for unemployment are one of the tools that are being used to introduce methods that can be used to manage the unemployment problem.

To understand the dynamic system of unemployment, we have followed up on the following work. In ^[21], Nikolopoulos and Tzanetis introduced and analyzed a mathematical model for a housing allocation of homeless families because of a natural disaster. Based on some concept of ^[21], Misra and Singh ^[15,16] introduced and analyzed mathematical models for the unemployment problem and focused on the stability analysis of models. In ^[15], the authors proposed a nonlinear differential equation of the unemployment model. For this study, three variables have been considered, namely, the numbers of unemployed, temporarily employed, and regularly employed persons. They assumed that the number of unemployed persons is continuously increasing due to graduation and it decreases because unemployed persons migrate and get a job. Moreover, the total numbers of each available vacancies are assumed to be constants. Furthermore, they assumed that employed persons become unemployed persons because of layoff, and the number of employed person decreases due to retirement. In ^[16], based on their previous work, the authors proposed a nonlinear dynamical system with time delay. In their study, a mathematical model with three variables has been proposed, namely, the numbers of unemployed persons, employed persons, and newly created vacancies. Besides, they assumed that firms may reduce vacancies because of a lack of financial resources. Moreover, they assumed that the government helps to support vacancies creation and the new vacancies are determined by considering previously collected data of unemployment, namely, a time delay is incorporated in creating new vacancies. Therefore, the model is presented by delay differential equations. In ^[19], Munoli and Gani proposed a dynamic unemployment model based on concept of ^[15,16]. They assumed that the new vacancies are determined by considering the number of unemployed persons. They also assumed that vacancies are incurred due to layoffs and retirement. The model without time delay is considered by three states, namely, the number of employed persons, unemployed persons, and vacancies. The optimal control analysis of the model was derived. In ^{[8,9,17,20,23,25]}, the authors have constructed and analyzed the models of unemployment based on the above-mentioned works. In ^{[13,18,22,24,28,31,32]}, the authors have studied and analyzed some viral infection models with intracellular delays. Some authors have focused on the local asymptotic stability and Hopf-bifurcation by taking delay as a bifurcating parameter, such as ^[22,24,28]. On the other hand, some authors have focused on the global asymptotic stability by using the Lyapunov functional technique and LaSalle theorem, such as ^{[13,18,31,32]}.

Based on the concepts of ^[15,16,19], we have developed an unemployment model, taking into consideration the role of government for the support of vacancies creation. In this study, we modify the unemployment model of Munoli and Gani with new assumptions. The model is considered by three variables, namely, the number of unemployed persons, employed persons, and vacancies. Under some additional assumptions, we assume that workers are dismissed and they may become unemployed persons, migrate to other countries, or change to a business owner. We also assume that vacancies are incurred due to retirement and some job positions are maintained and job positions are not terminated. Moreover, we assume that the new vacancies are incurred by the government policy and the government uses previously collected data of unemployment to determine the new vacancies. In this paper, the unemployment model is presented by delay differential equations. We have analyzed the local and global stability of the system. Numerical results are given to illustrate the effectiveness of theoretical results. Furthermore, we have observed behavior of solutions of the system when some parameters are varied.

2.   The mathematical model

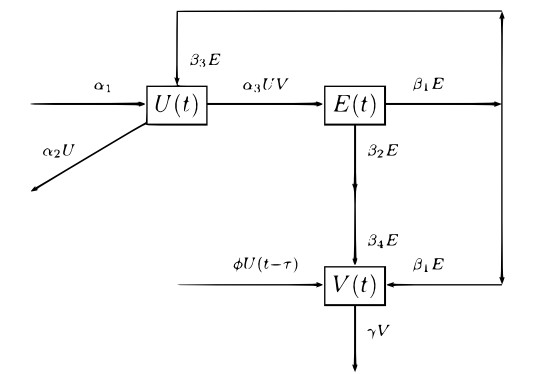
Let $U(t)$, $E(t)$, and $V(t)$ be the number of unemployed persons, employed persons, and vacancies at time $t$, respectively. In this study, we assume the following:

(ⅰ) all entrants to unemployment class are fully qualified for doing any job;

(ⅱ) the unemployed persons are continuously increasing in number with a constant rate;

(ⅲ) the unemployed persons migrate from their local place to other places and the migration rate of unemployed persons is assumed to be proportional to their number;

(ⅳ) the rate of movement from the unemployment class to the employed class is jointly proportional to the numbers of unemployed persons and available vacancies;

(ⅴ) the employed persons may leave their jobs because of layoff and join the unemployed class;

(ⅵ) layoff of employed persons is regarded as for vacancies. They were dismissed to become unemployed persons but some persons do not become unemployed persons because they may migrate to other countries or become a business owner;

(ⅶ) the employed persons may leave their jobs because of retirement and vacancies are incurred after they are retired but some job positions may be terminated;

(ⅷ) firms may reduce vacancies because of lack of financial resources and the reduction rate of vacancies is assumed to be proportional to their numbers;

(ⅸ) the new vacancies are created at a rate proportional to the number of unemployed persons and time delay is incorporated in creating new vacancies.

The flow schematic diagram and parameters of the model considered in this study are given in Figure 1 and Table 1, respectively. In view of the above consideration, the mathematical model may be written as follows:

where $\beta_1 > \beta_3$ and $\beta_2 > \beta_4$.

The initial conditions and history functions for system (2.1) are assumed to be of the forms:

where $(\Phi_1(\zeta), \Phi_3(\zeta), \Phi_3(\zeta)) \in C([-\tau, 0), \mathcal{R}^{3}_{+})$.

3.   Analysis of the model

In this section, we analyze the system (2.1) using the stability theory of differential equations ^[6,10,14] and delay differential equations ^[5,7,11,27]. The following Lemmas show that we can find the region of attraction and the positive equilibrium points of the system (2.1), respectively.

Lemma 3.1. The set $\Omega = \{ (U, E, V):0 \leq U+E \leq \frac{\alpha_1}{\delta_1}, 0 \leq V(t) \leq \frac{\delta_2 \alpha_1}{\delta_1 \gamma} \},$ where $\delta_1 = min\{\alpha_2, \beta_1+\beta_2-\beta_3\}$ and $\delta_2 = max\{\beta_1+\beta_4, \phi\}$ is a region of attraction for the system (2.1) and attracts all solution initiating in the interior of positive octant.

Proof. From the system (2.1), we have

Let $\delta_1 = min\{\alpha_2, \beta_1+\beta_2-\beta_3\}$, we obtain

This implies

Consider the third equation of system (2.1) and let $\delta_2 = max\{\beta_1+\beta_4, \phi\}$, we get

Therefore,

Lemma 3.2. Suppose $A = \alpha_2\alpha_3(\beta_1+\beta_4)-\alpha_3(\beta_1+\beta_2-\beta_3)\phi$, $B = \alpha_1\alpha_3(\beta_1+\beta_4)+\alpha_2\gamma(\beta_1+\beta_2)$, $C = \alpha_1\gamma(\beta_1+\beta_2)$, $\bar{D} = (\beta_1+\beta_2)\gamma-(\beta_1+\beta_4)\alpha_3\bar{U}$ and $\check{D} = (\beta_1+\beta_2)\gamma-(\beta_1+\beta_4)\alpha_3\check{U}$. Then we have the following:

(i) If $A = 0$ holds, then positive equilibrium point $E_1(\hat{U}, \hat{E}, \hat{V})$ exists, where

(ii) If $A > 0$ and $\bar{D} > 0$ hold, then positive equilibrium point $E_2(\bar{U}, \bar{E}, \bar{V})$ exists, where

(iii) If $A < 0$ and $\check{D} > 0$ hold, then positive equilibrium point $E_3(\check{U}, \check{E}, \check{V})$ exists, where

Proof. To obtain all positive equilibrium points of the system (2.1), we set the right-hand side of (2.1) equal to zero. The equations for the equilibrium points are as follows:

From (3.2), we get

Substituting (3.4) into (3.3), we obtain

This gives,

Substituting (3.4) and (3.5) into (3.1), we get the following equations in $U$:

As a result, we have the quadratic equation

For $A = 0$, the equilibrium point $E_1(\hat{U}, \hat{E}, \hat{V})$ exists.

For $A \neq 0$, we solve the quadratic equation and obtain

Since $B^2-4AC > 0$, the values of $U$ are real numbers. If $A < 0$, then one root of $U$ is positive and the other is negative. If $A > 0$, then both roots of $U$ are positive. However, we require positive equilibrium points. Therefore, two feasible equilibrium points exist, namely, $E_2(\bar{U}, \bar{E}, \bar{V})$ for $A > 0$ and $\bar{D} > 0$ or $E_3(\check{U}, \check{E}, \check{V})$ for $A < 0$ and $\check{D} > 0$.

We now examine the local asymptotic stability of the positive equilibrium points we have found in Lemma (3.2) and determine the conditions for the nonexistence of delay induced instability by analyzing characteristic equations. For this purpose, we assume that an equilibrium point $E(\tilde{U}, \tilde{E}, \tilde{V})$ exists and then linearize the system (2.1) by using the following transformation

where $u, e$ and $v$ are small perturbations around the equilibrium point $E(\tilde{U}, \tilde{E}, \tilde{V})$.

The linearized system of (2.1) may be written in the matrix form as

where

Let us take the solution of model (3.8) as $u(t) = k_1e^{\lambda t}, e(t) = k_2e^{\lambda t}$, and $v(t) = k_3e^{\lambda t}$, where $k_1, k_2$ and $k_3$ are arbitrary constants. Thus, we have

By setting $\det (\lambda I-L_1-L_2e^{-\lambda \tau}) = 0$, this leads to the following characteristic equation:

where

Next, we analyze (3.9) by substituting $\lambda = i\omega$ in (3.9) and then rearranging it as follows,

Then, by separating real and imaginary parts, we obtain

Squaring both sides of (3.11) and (3.12), we get

Next, after adding (3.13) and (3.14) and rearranging, we have

Therefore, we get

where $c_{1} = p_1^2-2p_2, c_{2} = p_2^2-2p_1 p_3-q_1^2$ and $c_{3} = p_3^2-q_2^2$.

By letting $\sigma = \omega^2$, (3.15) becomes a cubic equation given by

We now define

Thus, we have shown that the Eq (3.9) has no purely imaginary roots if and only if (3.16) has no positive real roots. Next, we analyze Eq (3.16) using the methods for third-degree exponential polynomials given by Ruan and Wei ^[26]. According to the work in ^[26], for a polynomial in the form of (3.16), the following lemma is obtained.

Lemma 3.3. Suppose $\sigma_0 = \frac{1}{3}(-c_1+\sqrt{c_1^2-3c_2})$ and equilibrium point $E(\tilde{U}, \tilde{E}, \tilde{V})$ exists. If one of the following holds:

(i) $c_{3} \geq 0$ and $c_1^2 < 3c_2$,

(ii) $c_{3} \geq 0$ and $\sigma_0 \leq 0$,

(iii) $c_{3} \geq 0$, $\sigma_0 > 0$ and $F(\sigma_0) > 0$,

then Eq (3.16) has no positive roots.

From the lemma above, if the conditions of Lemma 3.3 are satisfied, then the system cannot have purely imaginary eigenvalues and therefore a Hopf-bifurcation cannot exist. Then, we apply Lemma 3.3 to the following propositions.

Proposition 3.4. Suppose $A = 0$ and $\hat{\sigma} = \frac{1}{3}(-\hat{c_1}+\sqrt{\hat{c_1}^2-3\hat{c_2}})$ where

If one of the following holds:

(i) $\hat{c_1}^2 < 3\hat{c_2}$,

(ii) $\hat{c_2} \geq 0$,

(iii) $\hat{c_2} < 0$ and $F(\hat{\sigma}) > 0$,

then the equation

has no positive roots.

Proposition 3.5. Suppose $A > 0$, $\bar{D} > 0$ and $\bar{\sigma} = \frac{1}{3}(-\bar{c_1}+\sqrt{\bar{c_1}^2-3\bar{c_2}})$ where

If one of the following holds:

(i) $\bar{c_1}^2 < 3\bar{c_2}$,

(ii) $\bar{c_2} \geq 0$,

(iii) $\bar{c_2} < 0$ and $F(\bar{\sigma}) > 0$,

then the equation

has no positive roots.

Proposition 3.6. Suppose $A < 0$, $\check{D} > 0$ and $\check{\sigma} = \frac{1}{3}(-\check{c_1}+\sqrt{\check{c_1}^2-3\check{c_2}})$ where

If one of the following holds:

(i) $\check{c_1}^2 < 3\check{c_2}$,

(ii) $\check{c_2} \geq 0$,

(iii) $\check{c_2} < 0$ and $F(\check{\sigma}) > 0$,

then the equation

has no positive roots.

Note that, it is easy to show that $\hat{c_3} > 0$, $\bar{c_3} > 0$ and $\check{c_3} > 0$. Next, by using the above propositions and analyzing characteristic equations, we obtain the following theorems.

Theorem 3.7. Suppose $A = 0$. If one of the conditions in Proposition 3.4 holds, then $E_1(\hat{U}, \hat{E}, \hat{V})$ is locally asymptotically stable for all $\tau \geq 0$.

Proof. Since $A = 0$, $E_1(\hat{U}, \hat{E}, \hat{V})$ exists. The characteristic equation of the linearized the system (2.1) is

When $\tau = 0$, the characteristic Eq (3.21) becomes

Clearly, $\hat{p_1}$, $\hat{p_2}$, $\hat{p_3}$, $\hat{q_1}$ and $\hat{q_2}$ are positive and $\hat{p_1}(\hat{p_2}+\hat{q_1}) > \hat{p_3}+\hat{q_2}$. By using the Routh-Hurwitz criterion ^[3], all the roots of (3.22) have negative real parts. For $\tau > 0$, if one of the conditions in Proposition 3.4 holds then (3.18) has no positive real roots, namely, all solutions of (3.18) should be negative or zero. But zero roots cannot occur since $\hat{c_3} > 0$. Hence, we obtain only negative roots for (3.18). This implies that (3.21) has negative real parts for all $\tau \geq 0$. Consequently, $E_1(\hat{U}, \hat{E}, \hat{V})$ is locally asymptotically stable for all $\tau \geq 0$.

Theorem 3.8. Suppose $A > 0$ and $\bar{D} > 0$. If one of the conditions in Proposition 3.5 holds, then $E_2(\bar{U}, \bar{E}, \bar{V})$ is locally asymptotically stable for all $\tau \geq 0$.

Proof. Since $A > 0$ and $\bar{D} > 0$, $E_2(\bar{U}, \bar{E}, \bar{V})$ exists. The characteristic equation of the linearized the system (2.1) is

Similar to the proof of Theorem 3.7, we may show that $E_2(\bar{U}, \bar{E}, \bar{V})$ is locally asymptotically stable for all $\tau \geq 0$.

Theorem 3.9. Suppose $A < 0$ and $\check{D} > 0$. If one of the conditions in Proposition 3.6 holds, then $E_3(\check{U}, \check{E}, \check{V})$ is locally asymptotically stable for all $\tau \geq 0$.

Proof. Since $A < 0$ and $\check{D} > 0$, $E_3(\check{U}, \check{E}, \check{V})$ exists. The characteristic equation of the linearized the system (2.1) is

Similar to the proof of Theorem 3.7, we may show that $E_3(\check{U}, \check{E}, \check{V})$ is locally asymptotically stable for all $\tau \geq 0$. Next, we study the global stability of the system (2.1). For convenience, we define a function $g:R^+ \to R^+$ as $g(x) = x-1-\ln x$. Here, $g(x) \geq 0$ for all $x > 0$ and $g(1) = 0$. We have the following theorems.

Theorem 3.10. Suppose $A > 0$ and $\bar{D} > 0$. If $\alpha_2 \geq \phi$, $\beta_2 - \beta_4 \geq \beta_3$, $\frac{\gamma}{\alpha_3} \geq \bar{U}$, and one of the conditions in Proposition 3.5 holds, then $E_2(\bar{U}, \bar{E}, \bar{V})$ is globally asymptotically stable for all $\tau \geq 0$.

Proof. Since $A > 0$ and $\bar{D} > 0$, $E_2(\bar{U}, \bar{E}, \bar{V})$ exists. Now, we define a Lyapunov functional as follows:

Note that, $W_1 \geq 0$ for all positive $U$, $E$, $V$ and $\zeta \in [0, \tau]$. Moreover, the global minimum $W_1 = 0$ occurs at $E_2(\bar{U}, \bar{E}, \bar{V})$. Then, by differentiating $W_1$ along the solution of system (2.1) with respect to $t$, we obtain

Using the equalities $\alpha_1 = \alpha_2 \bar{U}+\alpha_3 \bar{U} \bar{V}-\beta_3 \bar{E}$, $\alpha_3 \bar{U} \bar{V} = (\beta_1+\beta_2) \bar{E}$, and $\gamma \bar{V} = \phi \bar{U}+(\beta_1+\beta_4) \bar{E}$ into the above equation, we get

By rearrangement, we have

From assumptions that $\alpha_2 \geq \phi$, $\beta_2 - \beta_4 \geq \beta_3$, and $\frac{\gamma}{\alpha_3} \geq \bar{U}$, i.e., $\alpha_2-\phi \geq 0$, $\beta_2-\beta_3-\beta_4 \geq 0$ and $\gamma - \alpha_3 \bar{U} \geq 0$, we have $\frac{dW_1}{dt} \leq0$. As a result, $W_1$ is bounded and non-increasing and thus $\lim_{t \to +\infty} W_1(t)$ exists. Moreover, $\frac{dW_1}{dt} = 0$ if and only if $U(t) = U(t-\tau) = \bar{U}$, $E(t) = \bar{E}$ and $V(t) = \bar{V}$ for all $t \geq 0$. It follows that the largest invariant set in $\{(U, E, V) | \frac{dW_1}{dt} = 0 \}$ is $E_2(\bar{U}, \bar{E}, \bar{V})$. Thus, by LaSalle invariant principle ^[12], we conclude that the solution of the system (2.1) tends to the largest invariant set. Consequently, $E_2(\bar{U}, \bar{E}, \bar{V})$ is globally asymptotically stable for all $\tau \geq 0$.

Theorem 3.11. Suppose $A < 0$ and $\check{D} > 0$. If $\alpha_2 \geq \phi$, $\beta_2 - \beta_4 \geq \beta_3$, $\frac{\gamma}{\alpha_3} \geq \check{U}$, and one of the conditions in Proposition 3.6 holds, then $E_3(\check{U}, \check{E}, \check{V})$ is globally asymptotically stable for all $\tau \geq 0$.

Proof. Since $A < 0$ and $\check{D} > 0$, $E_3(\check{U}, \check{E}, \check{V})$ exists. Then, we define

Similar to the proof of Theorem 3.10, we may show that $E_3(\check{U}, \check{E}, \check{V})$ is globally asymptotically stable for all $\tau \geq 0$.

Theorem 3.12. Suppose $A = 0$. If $\alpha_2 \geq \phi$, $\beta_2 - \beta_4 \geq \beta_3$, $\frac{\gamma}{\alpha_3} \geq \hat{U}$, and one of the conditions in Proposition 3.4 holds, then $E_1(\hat{U}, \hat{E}, \hat{V})$ is globally asymptotically stable for all $\tau \geq 0$.

Proof. Since $A = 0$, $E_1(\hat{U}, \hat{E}, \hat{V})$ exists. Then, we define

Similar to the proof of Theorem 3.10, we may show that $E_1(\hat{U}, \hat{E}, \hat{V})$ is globally asymptotically stable for all $\tau \geq 0$.

Remark 3.13. In the case of the unemployment model without time-delay, namely for the case $\tau = 0$, it is assumed that the new vacancies are determined by using unemployment data in the current time.

Remark 3.14. The conditions $\alpha_2 \geq \phi$, $\beta_2 - \beta_4 \geq \beta_3$, and $\frac{\gamma}{\alpha_3} \geq U_l$ for $l = 1, 2, 3$ mean that the rate of creating new vacancies should not exceed the migration rate of unemployed persons, the layoff rate should not exceed the rate of vacancies lost because of retirement, and an equilibrium point value of unemployed persons should not exceed the ratio of the reduction rate of vacancies and employment rate. These conditions are assumed to analyze the global asymptotic stability of the system. If we could find a more suitable Lyapunov functional, then this may lead to improved sufficient conditions for global asymptotic stability.

4.   Numerical results

In this section, we provide a practical application and a numerical example to illustrate the effectiveness of theoretical results.

Example 4.1 We first consider a practical example of an unemployment situation in Thailand. According to the latest education statistics of Thailand from the academic year of 2016-2017 ^[4] provided by the Ministry of Education of Thailand, we may estimate the average number of new graduates as $\alpha_1 = 288081$. According to the labor statistics yearbook, 2019 of Thailand ^[29] and social security statistics 2019 of Thailand ^[30] provided by the Ministry of Labour of Thailand, we may estimate the rate of overseas labor migration as $\alpha_2 = 0.071$, the rate at which the unemployed persons become employed persons as $\alpha_3 = 0.0000055$, the layoff rate as $\beta_1 = 0.0081$, and the retirement rate as $\beta_2 = 0.028$, respectively. Moreover, from the labor statistics yearbook, 2019 of Thailand ^[29], the numbers of unemployed persons ($U$), employed persons ($E$), and newly created vacancies ($V$) are 145000, 8196600, and 168396, respectively. As a result, we may obtain the initial values as $U(0) = 145000$, $E(0) = 8196600$, and $V(0) = 168396$, respectively. However, due to the lack of some population statistical information, we are unable to estimate the unemployment rate due to layoff ($\beta_3$), the rate of vacancies due to retirement ($\beta_4$), the reduction rate of vacancies because of lack of financial resources ($\gamma$), and the rate of creating new vacancies from the government policy ($\phi$). As a result, to study the unemployment model in Thailand, we need to estimate $\beta_3$, $\beta_4$, $\gamma$, and $\phi$ as follows. First, we assume that the unemployment rate due to layoff is 90 percent of the layoff rate, namely, $\beta_3 = 0.9\beta_1 = 0.00729$. Next, we assume that the rate of vacancies because of retirement is 5 percent of retirement, namely, $\beta_4 = 0.05\beta_2 = 0.0014$. Then, we assume that the reduction rate of vacancies because of lack of financial resources is $\gamma = 0.05$. Finally, we assume that the rate of creating new vacancies from the government policy is $\phi = 0.01$.

Now, we provide numerical simulations of the unemployment model in Thailand for the system (2.1) without time delay by using the parameters and initial values from statistical data of Thailand as mentioned above. It is straight forward to verify that these parameter values satisfy the condition (ii) of Lemma 3.2, Proposition 3.5, and Theorem 3.8. Therefore, the equilibrium point of the system exists which can be found from the condition (ii) of Lemma 3.2 as $(34400, 9914500, 1890600)$. Furthermore, it follows from Theorem 3.8 that the equilibrium point is locally asymptotically stable. In Figure 2, we illustrate the change of numbers of unemployed persons, employed persons, and vacancies as time evolves. The simulation indicates that, as time evolved, the number of vacancies increases due to layoff, retirement, and the creation of new vacancies from the government policy. Moreover, the number of unemployed persons is increasing at the beginning and eventually it is decreasing as unemployed persons are getting jobs, as time evolves. On the other hand, the number of employed persons is decreasing for early-stage but eventually, it is increasing because unemployed persons have become employed persons. Furthermore, the number of vacancies is greater than the number of unemployed persons, namely, there are enough vacancies for unemployed persons. In general, in crises such as COVID-19 pandemic, economic recession, government as well as private sectors are not creating job vacancies, but rather providing other policies such as emergency funds for unemployment, food bank, tax-exempts, respectively.

Next, we illustrate the change in the number of unemployed persons as the rate of creating new vacancies from the government policy is being varied, as time evolves. To this end, we provide numerical simulations of the unemployment model in Thailand for the system (2.1) without time delay when the parameters and initial values are the same as those used in Figure 2 but the values of $\phi$ is being varied, namely, $\phi = 0.01$, $0.11$, and $0.21$, respectively. From Figure 3, the numbers of unemployed persons are given, as time evolved, when the rate of creating new vacancies is being varied as $\phi = 0.01$, $0.11$, and $0.21$, respectively. The simulation indicates that the number of unemployed persons is increasing at the beginning and eventually it is decreasing as time evolves. Moreover, it can be seen that the number of unemployed persons decreases as the rate of creating new vacancies increases. Note that all three sets of parameters used in Figure 3 satisfy theoretical results for locally asymptotically stable.

Then, we compare the numbers of unemployed persons as time evolved when the rate at which the unemployed persons become employed persons is being varied. We provide numerical simulations of the unemployment model in Thailand for the system (2.1) without time delay when the parameters and initial values are the same as those used to obtain the Figure 2 but the value of $\alpha_3$ is being varied, namely, $\alpha_3 = 0.0000055, 0.000055$, and $0.00055$, respectively. From figure 4, it is shown that the numbers of unemployed persons as time evolved when the rate at which the unemployed persons become employed persons is being varied as $\alpha_3 = 0.0000055, 0.000055$, and $0.00055$, respectively. It can be seen that the number of unemployed persons decreases as the rate at which the unemployed persons become employed person increases. Moreover, the number of unemployed persons is quite small when the rate at which the unemployed persons become employed persons is set as $\alpha_3 = 0.00055$. A plausible reason is that at this rate of the unemployed persons become employed persons, the matching between vacancies to unemployed persons takes place quickly. Finally, we note that all three sets of parameters used in Figure 4 satisfy theoretical results for equilibrium states to be locally asymptotically stable.

Example 4.2 In this example, we give numerical results to support the theoretical results for system (2.1). The numerical results based on the Runge-Kutta methods for differential equations ^[2] and delay differential equations ^[1]. The sets of parameters used in this numerical example are shown in Table 2.

The parameter value set 1 satisfies condition (i) of Lemma 3.2, Proposition 3.4, Theorem 3.7, and Theorem 3.12. Therefore, $E_{1}(5000000, 20000000, 8000000)$ exists and it is locally and globally asymptotically stable. Next, if we use the parameter value set 2 which satisfies (ii) of Lemma 3.2, Proposition 3.5, Theorem 3.8, and Theorem 3.10. Therefore, $E_{2}(5969000, 18708000, 6269000)$ exists and it is locally and globally asymptotically stable. Then, we consider the parameter value set 3. The parameter value set 3 corresponds to conditions (iii) of Lemma 3.2, Proposition 3.6, Theorem 3.9, and Theorem 3.11. Therefore, $E_{3}(6667000,$ $13333000, 6667000)$ exists and it is locally and globally asymptotically stable. Figure 5, Figure 6, and Figure 7 show numerical simulations of the system (2.1) by using the parameter value sets 1, 2, and 3, respectively, with the initial values $(1000000, 15000000, 1000000)$ for $\tau = 0$ and the initial functions $(1000000e^{-0.063\zeta}, 15000000, 1000000)$ for $\tau = 10$, $\zeta \in [-\tau, 0)$. From Figure 5, Figure 6, and Figure 7, we see that trajectories of solutions converge to $E_{1}$, $E_{3}$, and $E_{3}$, respectively which are in agreement with theoretical results.

Next, we consider the parameter value set 4 given in Table 2. This set satisfies condition (ⅰ) of Lemma 3.2, Proposition 3.4, and Theorem 3.7, but not Theorem 3.12. It follows that $\bar{E_1}(645000, 25806000, 8000000)$ exists and this point is locally asymptotically stable. However, the conditions in Theorem 3.12 is sufficient conditions for global asymptotic stability. Now, we give the initial conditions far from the equilibrium point $\bar{E_1}$ and simulate the numerical results of the system (2.1) by using the parameter value set 4 with the initial values $(5000000, 10000000,$ $400000)$ for $\tau = 0$ and the initial functions $(5000000e^{-0.063\zeta}, 10000000, 400000)$ for $\tau = 10$, $\zeta \in [-\tau, 0)$. These two situations are shown in Figures 8. In this case, although we give initial conditions far from the equilibrium point, the solutions converge to $\bar{E_1}$.

5.   Conclusions

In this paper, the unemployment model with time delay is proposed. It has been shown that the model has three feasible positive equilibrium points in Lemma 3.2. Next, we have analyzed the local and global stability of all positive equilibrium points. The conditions for the nonexistence of delay induced instability are determined in Proposition 3.4 to Proposition 3.6. The analysis has indicated that the phenomena of a Hopf-bifurcation cannot exist under conditions given in these propositions. Moreover, the conditions for locally and globally asymptotically stable are obtained in Theorem 3.7 to Theorem 3.11. Numerical results confirmed the theoretical analysis as well. Furthermore, we observe that if the rate of creating new vacancies or the employment rate increase, then the number of unemployed persons decreases. This observation has indicated that the strategy of a government to create new vacancies and speed up the matching process between unemployed persons and entrepreneurs has an effect to reduce the number of unemployed persons.

Acknowledgments

This work is supported by Chiang Mai University. The authors would like to thank reviewers and editors for their valuable comments and suggestions for improving the quality of the manuscript. The first author is supported by the Development and Promotion of Science and Technology Talents Project (DPST).

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.