Approximation properties of the new type generalized Bernstein-Kantorovich operators

1.   Introduction

Approximation theory has an important place in application areas such as analysis and CAGD. In particular, Bernstein polynomials play an important role in approximation theory. Hence, due to the increasing interest in Bernstein polynomials, the question arises of how to construct its modifications that give better convergence results. That's why the books of Lorentz ^[4] and Lupaş ^[5] are of great importance.

For $\psi \in C(I = [0, 1])$, the classical Bernstein-Kantorovich operators are defined by

where $p_{\rho, \vartheta }(\zeta) = \binom{\rho }{\vartheta }\zeta ^{\vartheta }(1-\zeta)^{\rho -\vartheta }$ is the Bernstein basis function. For Kantorovich-type modifications of Bernstein operators, we refer to the articles ^{[6,7,8,9,10,11,12,13,14,15]}. Recently, Chen et al. ^[1] introduced a generalization of the $\alpha$-Bernstein operators as follows:

where $\underset{\rho \geq 2}{p_{\rho, \vartheta }^{\left(\alpha \right) }} (\zeta) = \left[ \binom{\rho -2}{\vartheta }\left(1-\alpha \right) \zeta + \binom{\rho -2}{\vartheta -2}\left(1-\alpha \right) \left(1-\zeta \right) + \binom{\rho }{\vartheta }\alpha \zeta \left(1-\zeta \right) \right] \zeta ^{i-1}\left(1-\zeta \right) ^{\rho -\vartheta -1}, \; \zeta \in \left[ 0, 1 \right].$The authors of ^[1] have studied many approximation properties of $\alpha$-Bernstein operators (1.2) such as rate of convergence and shape of preserving properties. After that, Mohiuddine et al. ^[16] introduced the Kantorovich variant of $\alpha$-Bernstein operators (1.2) and examined the approximation properties. In ^[20], authors presented a Kantorovich variant of the operators proposed by ^[1] based on non-negative parameters and studied the estimate of the rate of approximation by using the modulus of smoothnes and Lipschitz type function for these operators. Very recently, Deo et al.^[17] studied the direct local approximation theorem, Voronovskaya type asymtotic estimate formula and bounded variation for $\alpha$-Bernstein-Kantorovich operators ^[16].

Mohiuddine and Özger ^[18] introduced Stancu variant of $\alpha$ -Bernstein-Kantorovich operators and studied approximation properties for these operators. Very recently, Q. B. Cai et al. ^[19] introduced the bivariate $\alpha$-Bernstein-Kantorovich operators based $q$-integer and studied degree of approximation for these bivariate operators in terms of the partial moduli of continuity and Peetre's K-functional. We present the following new type generalized Kantorovich-Bernstein operators.

2.   The new type generalized Bernstein-Kantorovich operators

In ^[2] Kantorovich variant of $T_{\rho, \alpha }\left(\psi; \zeta \right)$ (1.2) defined as follows:

In this paper, we introduce the new type generalized Kantorovich variant of $T_{\rho }^{\alpha }\left(\psi, \zeta \right)$ as follows:

where $\psi \in \left[ 0, 1\right]$, $l\in \mathbb{Z} ^{+}$ and $\alpha \in \left[ 0, 1\right].$

In particular, if $l = 1$ and $\alpha = 1$, then the operator

i.e., it reduces to classical Bernstein - Kantorovich operators. In this work, $C\left[ 0, 1\right]$ denote the space of all bounded real valued continuous function on $\left[ 0, 1\right]$. This space is equipped with the following norm:

Moments of positive operators have an important place in the approximation theory. Therefore, from the definition of $K_{\rho, \alpha }^{l}(\psi; \zeta)$ and next two lemmas$,$ we can derive the formula for moments of $K_{\rho, \alpha }^{l}(t^{m}; \zeta).$

Lemma 1. The following formulas hold

and

Lemma 2. ^[1] Let $\alpha \in \left[ 0, 1\right].$ Then moments of theoperators $T_{\rho }^{\alpha }(\zeta)$ (1.2) are asfollows:

Lemma 3. For $\alpha \in \left[ 0, 1\right], \; l\in \mathbb{Z} ^{+}$ and $\rho \in \mathbb{N}$, we have

where

Proof. It follows from (2.1) that

Using formula (2.2), we can calculate $K_{\rho, \alpha }^{l}(t^{j}; \zeta)$ for $j = 0, 1, 2.$

Lemma 4. Let $\alpha \in \left[ 0, 1\right], \; l\in \mathbb{Z} ^{+}$ and $\rho \in \mathbb{N}$, We have

Proof. We give the proof for only $K_{\rho, \alpha }^{l}(t^{2};\zeta)$. Using (2.2), we get

The linearity property of $K_{\rho, \alpha }^{l}(\psi; \zeta)$ allows us to obtain the next lemma.

Lemma 5. Let $\alpha \in \left[ 0, 1\right]$, $\rho \in \mathbb{N}$ and $l\in \mathbb{Z} ^{+}$. For every $\zeta \in \left[ 0, 1\right]$ there holds

Proof. Using the linearity property of $K_{\rho, \alpha }^{l}(t; \zeta)$ and Lemma 4, we can prove all the above equalites with the same method. Thus, we give proof for only $K_{\rho, \alpha }^{l}((t-\zeta)^{2};\zeta)$.

Lemma 6. Let $\alpha \in \left[ 0, 1\right], \rho \in \mathbb{N}$ and $l\in \mathbb{Z} ^{+}$. For every $\zeta \in \left[ 0, 1\right]$ there hold

Proof. By Lemma 5, we have

and

In the next theorem, we examined Korovkin type approximation theorem for $K_{\rho, \alpha }^{l}(\psi; \zeta).$

Theorem 7. Let $\alpha \in \left[ 0, 1\right], \rho \in \mathbb{N}$ and $l\in \mathbb{Z} ^{+}.$ For each $\psi \in C\left[ 0, 1\right]$, we have $\ K_{\rho, \alpha}^{l}(\psi; \zeta) \; \rightrightarrows \psi$ on $[0, 1]$, where the symbol $\rightrightarrows$ denotes the uniform convergence.

Proof. By the Korovkin's Theorem it is sufficient to show that

By Lemma 4 (i), (ii) and (iii), it is clear that

and

which yields

Similarly

which concludes

Thus the proof is completed.

3.   Local approximation

For $\psi \in C\left[ 0, 1\right]$ and $\delta > 0,$first and second order modulus of smoothness for $\psi$ defined as

and

Recall that the Peetre's $K$-functional is defined by

where $C^{2}\left[ 0, 1\right] : = \left\{ g\in C\left[ 0, 1\right] :g^{^{\prime }}, g^{^{\prime \prime }}\in C\left[ 0, 1\right] \right\}$.

Then, we know that (Theorem 2.4 in ^[21]),

where $L$ absolute constant.

Lemma 8. Let $\psi \in C\left[ 0, 1\right].$ Consider the operators

Then, for all $g\in C^{2}\left[ 0, 1\right],$ we have

Proof. From (3.2) we have

Let $\zeta \in \left[ 0, 1\right]$ and $g\in C^{2}\left[ 0, 1\right].$ Using the Taylor's formula,

Applying $^{\ast }K_{\rho, \alpha }^{l}$ to both sides of the (3.5) and using (3.4), we have

On the other hand, since

and

we conclude that

Using Lemma 5, we get

Theorem 9. Let $\rho \in \mathbb{N}, \; \alpha \in \left[ 0, 1\right]$ and $l\in \mathbb{Z} ^{+}.$ Then, for every $\psi \in C\left[ 0, 1\right],$ there exists aconstant $M > 0$ such that

where

and

Proof. It follows from Lemma 8, that

Now, considering the boundedness of $\ $the $^{\ast }K_{\rho, \alpha }^{l}$ and inequality (3.3), we get

Now, taking infimum on the right side over all $g\in C^{2}\left[ 0, 1\right]$ and using (3.1), we get the following result

Let us consider the Lipschitz-type with two parameters ^[22]. For $\beta _{1}\geq 0, \beta _{2} > 0$, we define

where $0 < \eta \leq 1.$

Theorem 10. Let $\psi \in$ Lip$_{M}^{\beta _{1}, \beta _{2}}\left(\eta \right)$. Thenfor all $\zeta \in \left(0, 1\right]$, we have

Proof. Let we prove theorem for the case $0 < \eta \leq 1$, applying Holder's inequality with $p = \frac{2}{\eta }, q = \frac{2}{2-\eta },$

Theorem 11. Let $\psi \; \in C\left[ 0, 1\right]$, $\alpha \in \left[ 0, 1\right]$ and $l\in \mathbb{Z} ^{+}$. Then the inequality

takes place, where $\delta _{\rho, \alpha }^{l}(\zeta) = \sqrt{K_{\rho, \alpha }^{l}(t-\zeta)^{2}}.$

Proof. It is known that

So, we have

Choosing $\delta = \delta _{\rho }(\zeta) = \sqrt{K_{\rho, \alpha }^{l}(t-\zeta)^{2}}$, we have

Let $C^{k}\left[ I\right]$ denote space of $k$-times continuously differentiable function on $I$.

Theorem 12. For any $\psi \in C^{1}\left[ 0, 1\right]$ and $\zeta \in \left[ 0, 1\right]$, we have

Proof. Let $\psi \in C^{1}\left[ 0, 1\right].$ For any $t\in \left[ 0, 1\right], \zeta \in \left[ 0, 1\right]$, we have

Using $K_{\rho, \alpha }^{l}\left(.; \zeta \right)$ on both sides of the above equation, we have

Using the property of modulus of continuity $\left\vert \psi (t)-\psi (\zeta)\right\vert \leq w(\psi, \delta)\left(\frac{\left\vert t-\zeta \right\vert }{\delta }+1\right), \delta > 0,$ we obtain

it follows that

From Cauchy-Schwarz inequality, we have

Now, taking $\delta = \sqrt{K_{\rho, \alpha }^{l}((t-\zeta)^{2};\zeta)}$, we obtain (3.6).

In the next section, we state the direct global approximation theorem for operators $K_{\rho, \alpha }^{l}(\psi; \zeta).$

4.   Global approximation

Let $AC\left[ 0, 1\right]$ denote the absolutely continuous on $\left[ 0, 1 \right].$ For $\psi \in C\left[ 0, 1\right]$, the first and second order Ditzian-Totik moduli of smoothness are defined by

and

respectively.

Moreover, the second-order modified $K$-functional for $\psi \in C\left[ 0, 1 \right]$ is defined by

where $\delta > 0, \phi (x) = \sqrt{x(1-x)} \; \left(x\in \left[ 0, 1\right] \right)$and

It is well-known ^[23] that, for any $\delta > 0$,

holds for some absolute constant $D > 0.$

Theorem 13. Let $\rho \in \mathbb{N}, \; \alpha \in \left[ 0, 1\right]$ and $l\in \mathbb{Z} ^{+}$. Then, for every $\psi \in C\left[ 0, 1\right]$ and $\zeta \in \left[0, 1\right]$, there exist an absolute $C > 0$ such that

where $\theta _{l} = l\left(1+2x\right).$

Proof. If we use the operators $^{\ast }K_{\rho, \alpha }^{l}$ given by (3.2), then for a given $g\in \; W^{2}\left(\phi \right)$, we obtain that

Let $\lambda _{\rho }(\zeta) = \zeta (1-\zeta)+\frac{l}{(\rho +l)}.$ Taking $u = \beta \zeta +\left(1-\beta \right) t$, $\beta \in \left[ 0, 1\right],$and also using concavity $\lambda _{\rho }$, we have

Using the last inequality, we observe that

Then we get from (4.3) that

On the other hand, since the operators $^{\ast }K_{\rho, \alpha }^{l}(g; \zeta)$ are uniformly bounded, we get

Taking infimum on the right hand side of the above inequality over all $g\in W^{2}\left(\phi \right)$, we obtain

Now, using the function $\theta _{_{l}}(\zeta) = l+2xl$, we can also get

where $I_{l}(\zeta) = \left\{ t\in \left[ 0, 1\right] :t+\theta _{_{l}}(t) \frac{\frac{l}{2}-xl}{(\rho +l)}\in \left[ 0, 1\right] \right\}$. Finally, using (4.1), we get desired result.

5.   Voronovskaya type results

Here, we Voronovskaya type result for the $K_{\rho, \alpha }^{l}(\psi; \zeta)$ operators.

Theorem 14. Let $\psi \in C\left[ 0, 1\right]$. If $\psi ^{^{\prime \prime }}$ exist ata point $\zeta \in \; \left[ 0, 1\right]$, then we have

where $p\in \mathbb{N}, l\in \mathbb{Z} ^{+}$ and $\alpha \in \left[ 0, 1\right]$.

Proof. For $\zeta \in \left[ 0, 1\right]$, the Taylor's formula $\psi$ is given by

Here $r(t, \zeta)$ is Peano form of remainder and $r(., \zeta)\in C\left[ 0, 1 \right]$ and $\underset{t\rightarrow \zeta }{\lim }r(t, \zeta) = 0.$ Applying the operator $K_{\rho, \alpha }^{l}$ to $\left(\text{5.1}\right)$, we get

Using Cauchy-Schwarz inequality in the last term, we have

Observe that $r^{2}(t, \zeta) = 0$ and $r^{2}(., \zeta)\in C\left[ 0, 1\right].$

Hence from Theorem 7,

uniformly for $\zeta \in \left[ 0, 1\right].$

Therefore

From Lemma 6,

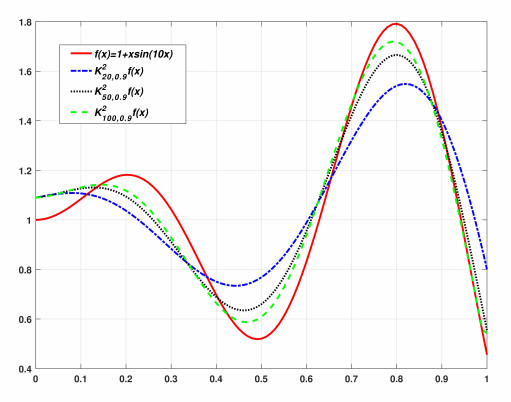
Now, we show graphical analysis for the convergence of operators $K_{\rho, \alpha }^{l}(\psi; \zeta)$ to the function $\psi (\zeta) = 1+\zeta \sin (10\zeta)$.

In Figure 1, we show the approximation to this function $\psi$ by the operators $K_{\rho, 0.9}^{2}(\psi; \zeta)$ for $\rho = 20, 50,100$ respectively.

Morever, in Table 1, we compute the error of $\ $approximation $K_{\rho, 0.9}^{2}(\psi; \zeta)$ of our $\psi (\zeta) = 1+\zeta \sin (10\zeta)$ for $\rho = 20, 50,100.$

6.   Bivariate $\alpha$- Bernstein-Kantorovich operators

In this section, we introduce the bivariate extension of the operators (2.1). The bivariate extension of the $K_{\rho, \alpha }^{l}(\psi; \zeta)$ (2.1) can be defined by

where $\left(\zeta.\gamma \right) \in I^{2} = \left[ 0, 1\right] \times \left[ 0, 1\right]$, $\alpha _{1}, \alpha _{2}\in \left[ 0, 1\right]$ and $l_{1}, l_{2}\in \mathbb{Z} ^{+}$.

The bivariate $\alpha$-Bernstein-Kantorovich operators can be rewritten as

Lemma 15. Let $e_{ij}\left(\zeta, \gamma \right) = \zeta^{i}\gamma ^{j}$, $0\leq i+j\leq 2.$ For $\left(\zeta.\gamma \right) \in I^{2} = \left[ 0, 1\right] \times \left[ 0, 1\right], l_{1}, l_{2}\in \mathbb{Z} ^{+}$ and $\alpha _{1}, \alpha _{2}\in \left[ 0, 1\right]$, we have

Remark 16. According to above Lemma 15, we get

In the next theorem, we obtain the uniform convergence of the bivariate $\alpha$-Bernstein-Kantorovich operators to the bivariate functions defined on $I^{2} = \left[ 0, 1\right] \times \left[ 0, 1\right]$.

Theorem 17. Let $C(I^{2})$ be the space of continuous bivariate function on $I^{2} = \left[0, 1\right] \times \left[ 0, 1\right]$. Then for any $\psi \in C(I^{2})$, wehave

Proof. Using Lemma 16, we get

Hence, by Volkov's theorem ^[3], we deduce

We shall use the following modulus of continuity for bivariate real functions:

Theorem 18. Let $\psi \in C(I^{2})$. Then for all $\left(\zeta, \gamma \right) \in I^{2}$, the inequality

holds, where $\delta _{\rho _{1, }\alpha _{1}}(\zeta), \delta _{\rho_{2, }\alpha _{2}}(\gamma)$ are as in Remark 16.

Proof. By the linearity and positivity properties of the $K_{\rho _{1}, \rho _{2}, \alpha _{1}, \alpha _{2}}^{l_{1}, l_{2}}$, we can write

Applying Cauchy-Schwarz inequality, we obtain

Choosing $\delta _{1} = \delta _{\rho _{1, }\alpha _{1}}(\zeta)$ and $\delta _{2} = \delta _{\rho _{2, }\alpha _{2}}(\gamma)$, we have desired result.

Finally, in Figures 2 and 3, we show graphical analysis for the convergence of operators $K_{\rho _{1}, \rho _{2}, \alpha _{1}, \alpha _{2}}^{l_{1}, l_{2}}\left(\psi; \zeta, \gamma \right)$ to the function $\psi (\zeta) = \cos (2\pi \zeta)+\sin (3\pi \gamma)$.

7.   Conclusions

In this paper, we introduced new type of generalized Kantorovich variant of $\alpha$-Bernstein operators. We obtained estimates of rate of convergence involving first and second order modulus of continuity. Furthermore, we established Voronovskaya type theorem for these operators. Also, some graphical illustrations and numerical results are provided.

Conflict of interest

The author declares no conflict of interest.