Some approximation results for the new modification of Bernstein-Beta operators

1.   Introduction

Approximation theory, an old area of mathematical research, has an extensive potential for applications to a wide variety of areas. Bernstein operators are one of the most widely-investigated linear and positive operators in the theory of approximation. Bernstein operators are defined by ^[2] as

for function $k\in C[0, 1]$ and $x\in[0, 1]$. After that, numereous variations of linear positive operators are studied by researchers such as ^{[3,4,5,6,7,8,11,12,13,14,15,16,17]}.

In 2020, Usta ^[18] introduced a new modification of Bernstein operators. For $k\in C(0, 1)$, $m\in \mathbb{N}$ and $x\in(0, 1)$

In this modification, the constructed operators preserve constant test function and Korovkin's other test functions $t^i$, $i = 1, 2$ in limit case. Usta ^[18] gave $B^{*}_{m}(e_0;x) = 1$, $B^{*}_{m}(e_1;x) = \frac{m-2}{m}x+\frac{1}{m}$, $B^{*}_{m}(e_2;x) = \frac{m^2-7m+6}{m^2}x^2+\frac{5m-6}{m^2}x+\frac{1}{m^2}$ and the approximation results of the $B^{*}_{m}(k; x)$ operators. Motivated by this work, we develop a Beta-type modification of Bernstein operators. The newly constructed Bernstein-Beta operators are presented for $k\in C[0, 1]$ as follows:

where $x\in (0, 1)$, $m\in \mathbb{N}$ and $\beta(p+1, m-p+1)$ denotes the Beta function. For $r, s > 0$ Beta function is defined by

We can easily see that for $a, b\in \mathbb{R}$ and $k, f\in C[0, 1]$

Also, for $k\geq0$, $\widetilde{B_{m}}(k; x)\geq 0$. Thus, $\widetilde{B_{m}}(k; x)$ operators are linear and positive.

2.   Approximation properties of $\widetilde{B_{m}}$

Lemma 2.1. For each $x\in (0, 1)$, we obtain

where $e_i = t^i$ for $i = 0, 1, 2, 3, 4.$

Proof. By using the definition of Beta function (1.4), it is clear that

For $i = 1$, $k(t) = t$,

For $i = 2$, $k(t) = t^2$,

The proofs of $\widetilde{B_{m}}(e_3;x)$ and $\widetilde{B_{m}}(e_4;x)$ can be obtained in the same manner.

Lemma 2.2. For each $x\in (0, 1)$, we write

Proof. By using following equalities

we finish the proof of the lemma.

Remark 1. We have the following results

3.   Main results

Let the Banach space of all continuous functions $k$ on $[0, 1]$ is denoted by $C[0, 1]$ endowed with the norm

Theorem 3.1. For every $k\in C[0, 1]$

uniformly as $m\rightarrow \infty$.

Proof. It can be seen easily from Lemma 2.1 that

Then we apply Korovkin's theorem ^[19], which concludes the proof.

4.   Rate of convergence

For $k\in C[0, 1]$, the modulus of continuity is given by

Additionally, modulus of continuity of the function $k$ has the following property ^[1]:

Theorem 4.1. For each $x\in(0, 1)$ and $k\in C[0, 1]$, we have

where

Proof. By using the linearity of the $\widetilde{B_{m}}$ operators and Eq (4.1), we obtain

If we choose

then we arrive at

which is the required result.

Right now, we show the rate of convergence of $\widetilde{B_{m}}(k; x)$ by using the function $k$, which belongs to Lipschitz class. A function $k$ is said to be in the Lipschitz class $k\in Lip_{K}\left(c\right)$ if the inequality

holds. Hölder inequality ^[10] is defined as for $p > 1$ and $\frac{1}{p}+\frac{1}{q} = 1$

Theorem 4.2. Let $k\in Lip_{K}\left(c \right)$ and $0 < c \leq 1$ then we write

where $\delta_m(x)$ is the same as (4.3).

Proof. Let $k$ belongs to Lipschitz class $Lip_{K}\left(c \right)$ and $0 < c \leq 1$. From $\left(\text{4.4}\right)$ and by using the linearity and monotonicity of the operators $\widetilde{B_{m}}$, we get

By choosing $p = \frac{2}{c }$, $q = \frac{2}{2-c}$ in the Hölder inequality, we get

Here, $\delta_m(x)$ is as given in (4.3). Thus, we write

Now, the rate of convergence of the newly constructed operators $\widetilde{B_{m}}(k; x)$ is investigated by using the Peetre-$\mathcal{K}$ functionals.

Lemma 4.3. For $x\in(0, 1)$ and $k\in C[0, 1]$, we obtain

Proof. From the definition of $\widetilde{B_{m}}(k; x)$ operators, we have

Let $C^2 [0, 1]$ be the space of the functions $k$, for which $k, k'$ and $k''$ are continuous on $[0, 1]$. We write the norm of function $k$ in this space as follows:

The classical Peetre-$\mathcal{K}$ functional is defined as

and second modulus of smoothness of the function is given by

where $\delta > 0$. By DeVore and Lorentz ^[9], it is known that for $M > 0$

Theorem 4.4. Let $x\in(0, 1)$ and $k\in C[0, 1]$. Then for each $m \in \mathbb{N}$, there exists a positive constant $M$ such that

Here

and

Proof. We introduce the proof by defining an auxiliary operator $B_{m}^{**}:C[0, 1]\rightarrow C[0, 1]$ by

From Lemma 2.1, we have

For $s \in C^2[0, 1]$, we write by using the Taylor expansion that

Applying $B_{m}^{**}$ operator to both sides of the equation (4.10), we obtain

So,

By using (4.9) and (4.8), we achieve

Furthermore

and

When we rewrite (4.12) and (4.13) in the absolute value of (4.11). Then we get

where

Right now, we will try to find a bound for the auxiliary operator $B_{m}^{**}(s; x)$. In the light of the Lemma 4.3 and using Cauchy-Schwarz inequality we obtain

Consequently,

where

So, for all $k\in C^2[0, 1]$ by taking the infimum of the Eq (4.14), we get

As a result, using Eq (4.7), we obtain

Thusly, the proof is finished.

5.   Voronovskaya type theorem

In 1932, Voronovskaya ^[20] obtained the convergence rate of the Bernstein operators (1.1) to the function $k$. In this part, we derive a Voronovskaya-type asymptotic formula for $\widetilde{B_{m}}(k; x)$ operators.

Theorem 5.1. Let $k$ be integrable on the interval $(0, 1)$, also $k'$ and $k''$ exist at a fixed point $x\in(0, 1)$. Then we have

Proof. By using the well-known Taylor's formula, we write

Here, $\mathcal{R}(t, x): = \frac{k''(\xi)-k''(x)}{2}$ is the remainder term. $\xi$ is situated between $x$ and $t$. Also, $\lim\limits_{t \rightarrow x}\mathcal{R}(t, x) = 0$. When we apply $\widetilde{B_{m}}$ operators to (5.2), we obtain

By multiplying (5.3) by $m$ and take the limit as $m$ goes to infinity, we achieve

By taking into consideration Eqs (2.2) and (2.3), we obtain

and

Thus we have

By using the Cauchy-Schwarz inequality for the remainder term, we write

We already know the term $\widetilde{B_{m}}((t-x)^4;x)$ from Eq (2.1). Since $\mathcal{R}^2(., x)$ is continuous at $t\in (0, 1)$ and $\lim\limits_{t \rightarrow x}\mathcal{R}(t, x) = 0$, we observe that

Hence, by using (2.1), (5.5), (5.6) and positivity of the linear operators $\widetilde{B_{m}}$, we have

Finally, by substituting (5.7) in (5.4), we achieve

which is the desired result.

6.   Numerical experiments

In last section, we give the convergence behaviour of the newly constructed operators $\widetilde{B_{m}}$ with function $k$.

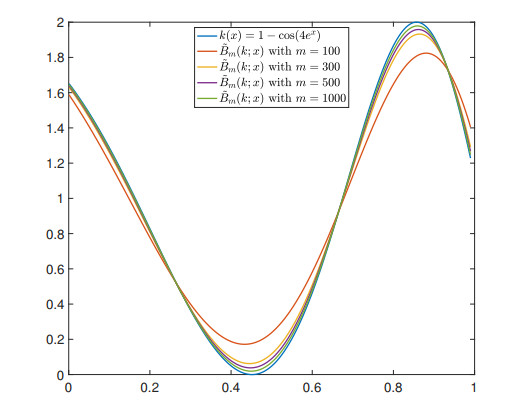
Example 1. Let the function $k$ be

The convergence behaviour of the operators $\widetilde{B_{m}}(k; x)$ is illustrated in Figure 1, where $k(x) = 1-\cos(4e^x)$, $x\in(0, 1)$ and $m\in \{100,300,500, 1000\}$.

The error estimation for operators $\widetilde{B_{m}}(k; x)$ to the function $k(x) = 1-\cos(4e^x)$ is presented in Table 1 for different values of $m$.

Example 2. Let the function $k$ be chosen as

We have shown the convergence behaviour of the $\widetilde{B_{m}}(k; x)$ Bernstein-Beta operators to the function $k$ in Figure 2 for $m\in\{20, 50,100,200\}$.

The error results of the operators $\widetilde{B_{m}}(k; x)$ to the function $k(x) = \left(x-\frac{1}{4} \right)\left(x-\frac{1}{2} \right)\left(x-\frac{3}{4} \right)$ are given in Table 2 for different values of $m$.

When we investigate these two examples, we understand that for the increasing values of $m$, the graph of the operators $\widetilde{B_{m}}(k; x)$ goes to the graph of the function $k$.

Acknowledgements

This work is supported by the Natural Science Foundation of Fujian Province of China (Grant No. 2020J01783), the Project for High-level Talent. Innovation and Entrepreneurship of Quanzhou (Grant No. 2018C087R) and the Program for New Century Excellent Talents in Fujian Province University. We also thank Fujian Provincial Big Data Research Institute of Intelligent Manufacturing of China.

Conflict of interest

The authors declared there is no conflict of interest associated with this work.