Rate of convergence of Euler approximation of time-dependent mixed SDEs driven by Brownian motions and fractional Brownian motions

1.   Introduction

Recently, boundary control for uncertain systems described by wave equations with dynamic boundary has been extensively investigated (see e.g., ^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} and references therein). However, most of the uncertainties considered in these works come from external disturbances ^{[3,5,6,7,8,9,10,11]} and constant parametric uncertainties ^{[1,2,4,12,13]}, few uncertainties are about unknown spatially varying or time-varying parameters, which are inevitable in practice. It is worth pointing out that ^{[14,15,16,17]} studied the cases with unknown spatially varying parameters in the hyperbolic PDEs therein, but the control schemes are developed for first-order hyperbolic PDEs with static boundary conditions and are not applicable to the second-order hyperbolic PDEs with dynamic boundary conditions. Moreover, in ^[1,4,12,13], adaptive technique was utilized to compensate system uncertainties, but the control objectives achieved are relatively conservative. Specifically, the control objectives are reduced that the distributed states in the closed-loop system are ultimately uniformly bounded in the sense of certain norm in ^[1], and the closed-loop systems are stable in the sense of certain norms in ^[4,12,13] (in these works, the performance of the states of the systems cannot be derived from these norms). Therefore, when a parameter involved in the wave equation is spatially varying and unknown, how to compensate the serious parametric uncertainties and design a desired boundary controller to achieve delicate objective with prescribed performance are challenging problems and worthy of thorough investigation.

In this paper, we consider the boundary control for the following wave equation with dynamic boundary condition and multiple parametric uncertainties:

where $w:\, [0, \, L]\times{{{\bf R}}}_+\to{{{\bf R}}}$ is the system state; $u:{{{\bf R}}}_+ \to{{{\bf R}}}$ is the control input of the system; $w(x, 0) = w_0(x)$ and $w_t(x, 0) = w_1(x)$ are the initial values of the system; $a(x)$ is an increasing function satisfying $a(0)\geq L^2$; $L$ is a positive constant denoting the length of the wave equation domain; $M$ is a positive constant; $b:[0, \, L]\to{{{\bf R}}}_+$ is an unknown spatially varying parameter, called in-domain damping coefficient; $\eta$ is an unknown positive constant, called boundary damping coefficient; $q$ and $\lambda$ are unknown positive constants.

The objective of this paper is to design an adaptive boundary controller for system (1.1) with dynamic boundary and rather essential uncertainties, to guarantee that all states of the resulting closed-loop system are bounded, and the original system state ultimately converges to an arbitrary prescribed small neighborhood of the origin, that is, $|w(x, t)| \; \leq\; \varepsilon$, $\forall t\geq T\, \, \mbox{for some} \, \, T > 0$, where $\varepsilon$ is a positive constant representing the prescribed accuracy. To achieve the objective, the following assumption is imposed on the unknown parameters $b(x)$, $q$, $\lambda$ and $\eta$:

Assumption 1. There exist known constants $\underline{b}$, $\overline{b}$, $\underline{q}$, $\overline{q}$, $\underline{\lambda}$, $\overline{\lambda}$, $\underline{\eta}$ and $\overline{\eta}$ such that

Boundary control has received considerable attention for system (1.1) and its variants in recent decades, since this class of systems has wide application background in engineering, such as crane systems ^[18,19], oilwell drillstring systems ^[1,20,21], sea cable problems ^[22,23] and cable elevators ^[24,25]. It is worth stressing that compared with the systems concerned in the above related literature, system (1.1) has two distinctive features: $\mathit{\boldsymbol{(i)}}$ Unknown in-domain damping coefficient and unknown boundary damping coefficient are allowed, and particularly, the in-domain damping coefficient is spatially varying. In fact, ^[1,18,19,24] rule out any dampings in the systems; ^{[20,21,23,25]} require that both the in-domain and boundary damping coefficients are known constants; ^[22] only allows that the boundary damping coefficient is unknown and constant. Remarkably, ^[26,27] investigated the more general cases where the in-domain damping coefficients are spatially varying, but the coefficients are required to be known. $\mathit{\boldsymbol{(ii)}}$ Dynamic boundary condition is considered in the present paper. This makes that the control schemes proposed by infinite-dimensional backstepping method in ^{[14,15,16,17]} (where unknown spatially varying parameters are allowed in the systems therein) cannot be applied to solve the control problem in the paper, since the explicit expression for the key kernel function in the infinite-dimensional backstepping method is rather difficult to construct in the presence of dynamic boundary condition ^[28,29]. Thus, one of the main contributions of the paper is that the system under discussion allows serious unknowns and is more practical than those in the existing related works.

This paper is devoted to developing an adaptive prescribed performance control scheme for system (1.1) with dynamic boundary condition, unknown in-domain spatially varying damping coefficient and unknown boundary constant damping coefficient. One key point in the control design is to construct the ingenious updating laws which not only can effectively counteract the serious unknowns but also are easily integrated with the control design for dynamic boundary condition. Specifically, adaptive technique based projection operator and backstepping method developed for ODEs (see e.g., ^[30,31,32]) are applied to compensate the multiple parametric uncertainties and simultaneously to design the desired controller, since the dynamic boundary condition at the control end can be written as a two-dimensional ODE system by letting $X_1(t) = w(L, t)$ and $X_2(t) = \dot{X}_1(t)$. Based on this, an adaptive controller is successfully designed in two steps, which guarantees that all states of the resulting closed-loop system are bounded, and furthermore the original system state ultimately converges to an arbitrarily prescribed small neighborhood of the origin. Therefore, the other main contributions of the paper is that a new adaptive control strategy, which is essentially different from those in ^[1,4,12,13], is proposed to achieve delicate control objective with prescribed convergence rate for uncertain systems described by wave equations with dynamic boundary condition.

The remainder of the paper proceeds as follows. In Section 2, the desired adaptive controller and dynamic compensators are designed. Section 3 summarizes the main results of the paper. Section 4 gives a simulation example, and Section 5 addresses some concluding remarks. The paper ends with a supplementary which gives several useful inequalities.

{Notations. Throughout the paper, ${{{\bf R}}}$ denotes the set of all real numbers; ${{{\bf R}}}_+$ denotes the set of all nonnegative real numbers; ${\bf L}^2(0, \, L)$ denotes the space of all measurable functions on $[0, \, L]$ with the property that $\int_0^L|f(x)|^2 {\mbox{d}} x < +\infty$; ${\bf H}^i(0, \, L)$ denotes the usual Sobolev space of functions in ${\bf L}^2(0, \, L)$ with derivatives up to $i$th order also in ${\bf L}^2(0, \, L)$.

2.   Adaptive controller design

This section is devoted to designing an appropriate adaptive controller for system (1.1). Particularly, ingenious updating laws and delicate Lyapunov function are constructed not only to deal with multiple parametric uncertainties but also to guarantee the stabilization with prescribed performance. Based on this, an adaptive controller is designed for system (1.1) by the idea of backstepping method for ODEs, since the boundary condition that the control $u(t)$ involved in can be rewritten as a two-dimensional ODE system.

Letting $X_1(t) = w(L, t)$ and $X_2(t) = \dot{X}_1(t)$. Then, system (1.1) can be rewritten as follows:

We now design the adaptive controller by two steps using the backstepping method for ODEs.

Step 1. Consider the control design for the following subsystem peeled from (2.1):

where $X^*_2(t)$ is the control input of system (2.2).

Let

Then, for system (2.2), we introduce the following energy function:

By the first equation in (2.2) and integration by parts, it can be easily verified that

Noting that $w(L, t) = X_1(t)$, $w_x(0, t) = q w_t(0, t)$ and $\dot{X}_1(t) = X_2(t)-X^*_2(t)+X^*_2(t)$ from (2.2), there holds

We choose

where $k_1$ is a positive design parameter to be determined later. Then, substituting (2.6) into (2.5), and using Assumption 1, we arrive at

Step 2. To design an appropriate controller $u(t)$ in this step, we define

by which, (2.3), Young's inequality and noting $a(x)\geq L^2$, we have

Then, for the following entire system:

its energy function is constructed as

where $\breve{X}_2(t) = X_2(t)-X^*_2(t)$; $\tilde{\lambda}(t) = \lambda-\hat\lambda(t)$ and $\tilde{\eta}(t) = \eta-\hat\eta(t)$ are the parameter estimate errors with $\hat\lambda(t)$ and $\hat\eta(t)$ being the estimates of unknown parameters $\lambda$ and $\eta$, respectively; $\gamma_1$, $\gamma_2$ and $\delta < 1$ are positive constants to be determined later.

Following similar arguments to the proof of (2.7), and by (2.6) and (2.9), we obtain

Then, by Young's inequality, there holds

where $c_0$ is a positive constant to be determined later. Substituting (2.12) into (2.11) yields

For the last term on the right-hand side of (2.13), by Assumption 1, integration by parts, Young's inequality and the increasing property of $a(x)$, it can be derived similar to the proof of the equality above (A3) in Lemma 2.1 in ^[10] that

where $0 < c_1 < \frac{1}{\overline{b}}$.

Substituting (2.14) into (2.13) results in

By choosing

there holds

To ensure the desired stability of the resulting closed-loop system, the adaptive controller and the updating laws of $\hat{\lambda}(t)$ and $\hat{\eta}(t)$ are designed as follows:

and

where $k_2$ is a design parameter satisfying $k_2 > \frac{1}{2c_0}$; $\gamma_i$ ($i = 1, 2$) are positive constants to be determined later, called adaptation gains; ${\bf Proj}_{[\cdot, \, \cdot]}\big\{\cdot, \, \cdot\big\}$ is a projection operator defined as

It is worth pointing out that the projection operator defined by (2.19) possesses some nice properties presenting in the following Lemma, which will play an important role in the stability analysis in Section 3, especially in guaranteeing the convergence of the system state.

Lemma 1. ^[15,30] For projection operator defined by (2.19), there hold

$(i)$ For $\hat{\theta}(0)\in[\underline{\theta}, \overline{\theta}]$, the solution of $\dot{\hat{\theta}} = {\bf Proj}_{[\underline{\theta}, \overline{\theta}]}\{\tau, \hat{\theta}\}$ remains in $[\underline{\theta}, \overline{\theta}]$;

$(ii)$ If $\underline{\theta}\leq\hat{\theta}\leq\overline{\theta}$ and $\underline{\theta}\leq \theta\leq\overline{\theta}$, then $-\tilde{\theta} {\bf Proj}_{[\underline{\theta}, \overline{\theta}]}\{\tau, \hat{\theta}\}\leq -\tilde{\theta}\tau$.

Substituting (2.17) and (2.18) into (2.16), and then using claims $(i)$ and $(ii)$ in Lemma 1, it follows that

This completes the design procedure of the desired adaptive controller.

3.   Main results

In this section, we aim to analyze the stability of the closed-loop system resulting from (1.1), (2.17) and (2.18), which is summarized in the following theorem.

Theorem 1. Consider system (1.1) under Assumption 1. If the positive design parameters $k_i$'s and $\gamma_j$'s are chosen to satisfy $k_1\; \geq\; c_0$, $k_2 > \frac{1}{2c_0}$ and $\frac{1}{\gamma_1}(\underline{\lambda}-\overline{\lambda})^2+\frac{1}{\gamma_2}(\underline{\eta}-\overline{\eta})^2 \leq \frac{\varepsilon^2}{4(1+2L)}$ with $c_0$ being a certain positive constant and $\varepsilon$ being an arbitrary pre-specified positive constant. Then, the adaptive controller described by (2.17) and (2.18) guarantees that for any initial values $w_0(x)\in{\bf H}^1(0, \, L)$, $w_1(x)\in{\bf L}^2(0, \, L)$, $\hat{\lambda}(0)\in[\underline{\lambda}, \, \overline{\lambda}]$ and $\hat{\eta}(0)\in[\underline{\eta}, \, \overline{\eta}]$, the resulting closed-loop system state $w(x, t)$ is bounded on $[0, \, L]\times[0, \, +\infty)$ while $\hat{\lambda}(t)$ and $\hat\eta(t)$ are bounded on $[0, \, +\infty)$, and furthermore,

Proof. By Assumption 1, claim $(i)$ of Lemma 1, $\hat{\lambda}(0)\in[\underline{\lambda}, \, \overline{\lambda}]$ and $\hat{\eta}(0)\in[\underline{\eta}, \, \overline{\eta}]$, we can see that $\hat{\lambda}(t)\in[\underline{\lambda}, \, \overline{\lambda}], \, \, \hat{\eta}(t)\in[\underline{\eta}, \, \overline{\eta}]$ on $[0, \, +\infty)$, and hence the boundedness of $\hat{\lambda}(t)$ and $\hat\eta(t)$ on $[0, \, +\infty)$ as well as the last relation in (3.1) are proved.

We next prove that for $x\in[0, L]$ and an arbitrary pre-specified positive constant $\varepsilon$, the system state $w(x, t)$ satisfies $\lim_{t\rightarrow \infty}\sup_{x\in[0, L]}|w(x, t)| \; \leq\; \varepsilon$. By (2.20) and denoting $l = \min\Big\{2\underline{b}+\delta\big(1-\frac{\overline{b}}{c_1}\big), \, \delta(1-c_1\overline{b})\Big\}$, there holds

From (2.8), we have $E_1(t)+\delta E_2(t)\leq(1+\delta)E_1(t)$. This, together with (2.10), results in

where $\varrho = \min\big\{\frac{l}{1+\delta}, \, 2k_1, \, 2k_2-\frac{1}{c_0}\big\}$. From this, it can be deduced that

By (2.10), (3.2) and $w(L, t) = X_1(t)$, we have

Noting that there exists a sufficiently large $T$, such that for $t\in[T, +\infty)$, there holds

which, together with

implies

On the other hand, by (2.8), there holds $(1-\delta)E_1(t)\leq E_1(t)+\delta E_2(t)$, which together with (3.2) yields

Thus, by (3.3) and (3.4), we can prove that

Then, by Agmon's inequality (see Lemma A.1 in Supplementary), we get

which, together with Poincaré's inequality (see Lemma A.2 in Supplementary), Young's inequality and $a(x)\geq L^2$, results in

Substituting (3.5) and (3.6) into (3.7), we can deduce that

Then, noting from (2.15), there holds

from which, it follows that

Thus, we achieve the first relation in (3.1). This completes the proof of the theorem.

Remark 1. From (3.2), we can see the necessity of introducing the term $-2k_1X_1(t)$ in (2.6). Actually, if $-2k_1X_1(t)$ is replaced by $-k_1X_1(t)$, the term $-k_1X_1(t)a(L)w_x(L, t)-k_1X_1^2(t)$ is no longer appears in (2.11). Then, by (2.20), inequality (3.2) becomes $V_2(t)\leq V_2(0)$. By which, (2.10), Poincaré's inequality and Agmon's inequality, we can see that only the boundedness of $w(x, t)$, $\hat{\lambda}(t)$ and $\hat\eta(t)$ can be derived. Thus, when $-2k_1X_1(t)$ is changed into $-k_1X_1(t)$, the key result $\lim_{t\rightarrow \infty}\sup_{x\in[0, L]}|w(x, t)| \; \leq\; \varepsilon$ of the paper, that is, the original system state ultimately converges to an arbitrary prescribed small neighborhood of the origin can not be established.

Remark 2. It is worth pointing out that for unknown parameters $b(x)$ and $q$, their updating laws can be explicitly constructed, although it is enough to guarantee the main results of the paper stated in Theorem 1 only by using their upper and lower bounds. In fact, when (2.4) is replaced by the following one:

where $\tilde{b}(x, t) = b(x)-\hat b(x, t)$ and $\tilde{q}(t) = q-\hat q(t)$ with $\hat b(x, t)$ and $\hat q(t)$ being the estimates of unknown parameters $b(x)$ and $q$, respectively, $\vartheta_1$ and $\vartheta_2$ are two positive constants to be determined later, then by choosing

and using claims $(i)$, $(ii)$ in Lemma 1, it follows that

Thus, by Assumption 1 and claim $(i)$ in Lemma 1, we can see that (2.7) still holds, by which and a similar argument as in deriving $\lim_{t\rightarrow \infty}\sup_{x\in[0, L]}|w(x, t)| \; \leq\; \varepsilon$, it follows that the main results as stated in Theorem 1 also can be established by choosing $\frac{1}{\vartheta_1}(\underline{b}-\overline{b})^2+\frac{1}{\vartheta_2}(\underline{q}-\overline{q})^2 +\frac{1}{\gamma_1}(\underline{\lambda}-\overline{\lambda})^2+\frac{1}{\gamma_2}(\underline{\eta}-\overline{\eta})^2 \leq \frac{\varepsilon^2}{4(1+2L)}$.

4.   Simulation results

This section is devoted to validate the effectiveness of the theoretical results for system (1.1). From references ^[18,19], it can be seen that system (1.1) models a motorized platform moving along an horizontal bench with a flexible cable attaching to the platform and holding a load mass, the state/solution $w(x, t)$ is the horizontal displacement at time $t$ of the point whose curvilinear abscissa is $x$ denoting the arc length along the cable, and control $u(t)$ is the force applied by the motor to the platform, seeing ^[18,19] for more detailed explanations.

To design the desired adaptive controller, the parameters of the system are given as follows: $L = 50\mbox{m}$, $M = 20\mbox{kg}$, $a(x) = \mathrm{g}x+\frac{\mathrm{g}m}{\rho}$ with $m = 1500\mbox{kg}$, $\rho = 5\mbox{kg/m}$ and $\mathrm{g} = 9.8\mbox{m/s}^2$. Obviously, $a(x) = 9.8x+2940$ is an increasing function satisfying $a(0) = 2940\geq L^2 = 2500$. The initial conditions $w_0(x)$ and $w_1(x)$ are respectively chosen as

and

The unknown parameters $b(x), q, \lambda$ and $\eta$ are supposed to be $b(x) = \frac{x}{15}+2.15$, $q = 0.01$, $\lambda = 0.25$ and $\eta = 7.5$, respectively. Then, we assume that $\underline{b} = 0.1$, $\overline{b} = 6$, $\underline{q} = 0.001$, $\overline{q} = 2$, $\underline{\lambda} = 0.01$, $\overline{\lambda} = 0.6$, $\underline{\eta} = 5$ and $\overline{\eta} = 9$. Clearly, system (1.1) satisfies Assumption 1.

Choose the design parameters $k_1 = 0.25$, $k_2 = 52$, $\gamma_1 = 5.75\times10^4$ and $\gamma_2 = 2.0\times10^6$. Obviously, $k_1\geq c_0 > 0$ and $k_2 > \frac{1}{2c_0}$ by letting $c_0 = 0.2$. Moreover, set $\varepsilon = 0.1$, it can be verified that $\frac{1}{\gamma_1}(\underline{\lambda}-\overline{\lambda})^2+\frac{1}{\gamma_2}(\underline{\eta}-\overline{\eta})^2 = 0.1405\times10^{-4} < \frac{\varepsilon^2}{4(1+2L)} = 0.25\times10^{-4}$. Then, by (2.17), (2.18) and choosing the initial conditions $\hat{\lambda}(0) = 0.3\in[0.01, 0.6]$ and $\hat{\eta}(0) = 5.75\in [5, 9]$, the following adaptive controller is designed for system (1.1):

with $\hat{\lambda}(t)$ and $\hat{\eta}(t)$ being given by

$\breve{X}_2(t) = w_t(L, t)+0.25\big(3430w_x(L, t)+2w(L, t)\big)$.

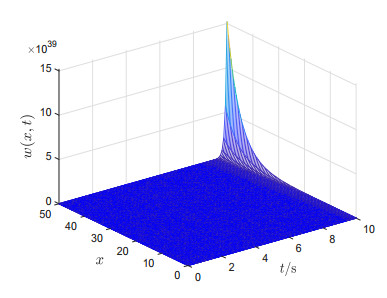
By using the implicit backward Euler method and explicit central difference method (see e.g., Pages 407 and 415 of ^[34], respectively) with the grid sizes are taken as $N_x = 100$ and $N_t = 50000$ in MATLAB software, four figures are obtained for the resulting closed-loop system signals. Specifically, Figure 1 shows the trajectory of the original system state $w(x, t)$ with $u(t) = 0$, from which we can see that the value of w(x, t) becomes very large as time increases; Figure 2 shows the trajectory of the original system state $w(x, t)$, from which we can see that $w(x, t)$ ultimately converges to an arbitrarily small neighborhood of the origin. Figures 3 and 4 show the trajectories of the estimates of unknown parameters $\lambda$ and $\eta$, respectively, from which we can see that $\hat \lambda(t)\in[0.01, 0.6]$ and $\hat \eta(t)\in [5, 9]$.

5.   Conclusions

In this paper, an adaptive prescribed performance control scheme has been developed for wave equations with dynamic boundary condition and multiple parametric uncertainties. To deal with these uncertainties, adaptive technique based projection operator is applied to construct the corresponding compensation mechanisms, which are integrated with the control design for dynamic boundary. Compared with the related literature, our design scheme can achieve the desired control objective, while dealing with rather serious parametric uncertainties. Remark that in this paper, the lower and upper bounds of the unknown parameters $b(x)$, $q$, $\lambda$ and $\eta$ are required to be known, and time varying parametric uncertainties are excluded in the considered system, hence, one of the future work is to consider the case with more essential uncertainties, such as $b(x)$, $q$, $\lambda$ and $\eta$ with unknown bounds or being unknown time varying parameters. Moreover, only one-dimensional wave equation is considered and $b(x)$ is required to be positive for $x\in[0, \, L]$ in the system in question, another future work is to study the case for PDE system described by multi-dimensional wave equation with $b(x)$ being negative for $x\in[0, \, L]$ (i.e., anti-damping case). Besides these, we shall explore how to achieve a further result that the original system state converges to zero for wave equations with serious uncertainties and how to generalize the proposed control scheme for wave equation to other PDEs, such as KdV and DMBBM equations presented in ^[35,36].

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundations of China (Grant Nos. 62003197 and 61773332).

Conflict of interest

The authors declare that they have no conflict of interest.

Supplementary

Useful inequalities

The following two lemmas provide several useful inequalities. The proofs of these two lemmas are similar to those of Lemmas B.1 and B.2 in ^[33] and hence are omitted here.

Lemma A.1. $($Agmon's Inequality$)$ For any $w\in{\bf H}^1(0, \, L)$, the following inequalities hold:

Lemma A.2. $($Poincaré's Inequality$)$ For any $w\in{\bf H}^1(0, \, L)$, the following inequalities hold: