Synchronizability of multilayer star-ring networks with variable coupling strength

1.   Introduction

Complex networks are extensively explored in the field of nonlinear dynamics ^[1,2,3]. Most of the previous studies of networks have focused on single-layer networks, while many real-world networks cannot be described specifically by single-layer networks alone. With advancements in theory and practice, it has gradually been found that networks do not isolate entities but rather interact with other networks in structure and function. For example, transportation networks ^[4] are composed of aviation networks, shipping networks and railway networks. The biological networks ^[5] consist of gene regulatory networks, metabolic networks and protein interaction networks. Therefore, it is imperative to study the multilayer networks formed by the interaction between each single-layer network in depth. It can be abstracted into a multilayer network model with intralayer and interlayer coupling to better interpret the association between sub-networks in the complex relationship. Recent research on multilayer networks has attracted some attention. Zhang et al. ^[6] studied the adaptive explosive synchronization of multilayer networks without considering the specific correlation between the oscillators and the natural frequency. Wang et al. ^[7] considered the nodes with Lur'e-type dynamics and investigated how to achieve synchronization from node to whole network in a directional topology. A series of studies have also been carried out in the field of topology identification for multilayer networks. Liu et al. ^[8] realized topology identification of the networks based on adaptive observers of chaotic external signals without complex linear independence assumptions. Different from previous research strategies, Mei et al. ^[9] studied the structure identification problem based on the compressed sensing method. In addition, in the study of multilayer network dynamics, Wang et al. ^[10] investigated the unique superdiffusion phenomenon caused by the directionality of connections. Turalska et al. ^[11] proved that the correlation existing in the networks would affect the dynamic cascade process and could prevent the spread of failures between layers. Therefore, it is imperative to undertake further exploration of multilayer networks.

Synchronization is a typical topic for the numerous dynamic behaviors observed in complex networks. It plays a significant role in various domains such as multi-agent cooperation, biological oscillators, signal transmission and numerous other applications ^{[12,13,14,15]}. In 1990, Pecora and Carroll ^[16] first proposed synchronization control for two coupled chaotic oscillators. Subsequently, the synchronization problems of single-layer complex networks are studied one after another. Wu et al. ^[17] investigated the phenomenon of projective synchronization in drive-response networks involving complex-variable chaotic systems. Hong et al. ^[18] researched the phenomenon of collective synchronization in a system of coupled oscillators that were organized on small-world networks. Li et al. ^[19] employed linear matrix inequalities to examine the synchronization issue in complex dynamical networks with time-varying delays. Due to the complexity of multilayer networks, some methods of synchronization in single-layer networks are no longer applicable. Currently, some advances have been achieved in the field of synchronization research in multilayer networks. Zhao et al. ^[20] focused on the synchronization of multiplex delayed networks with stochastic perturbations via pinning control, which significantly improved the synchronization efficiency. Fan et al. ^[21] delved into the study of adaptive event-triggered prescribed performance learning synchronization for complex dynamical networks. The above studies focused on the synchronization of chaotic systems and networks with given topological parameters and coupling strengths. However, the relationship between topological parameters, the size of parameters and coupling strengths changing with time to synchronizability analysis is not clear, which is a challenging task in multilayer networks that deserves further research.

In large-scale complex systems, individual behavior tends to be consistent, which is an external manifestation of synchronizability, and it is very important to understand its influence from the perspective of topology. A supra-Laplacian matrix based on the diffusion dynamics equation of multilayer networks is proposed to analyze its eigenvalue spectrum for studying complex network synchronizability ^[22,23,24]. So far, there have been some initial findings in the study of synchronizability in multilayer complex networks. Aguirre et al. ^[25] investigated the impact of node degree on the synchronization ability of two interconnected networks. They demonstrated that linking high-degree nodes in each network is the most effective approach for achieving synchronization. The two-layer star networks were derived strictly from the eigenvalue spectrum and analyzed for synchronizability by Xu et al. ^[26]. Li ^[27] proposed a two-layer dumbbell network model to analyze the synchronizability and verified the synchronization through a simple numerical simulation. Deng et al. ^[28] researched the synchronizability of multilayer chain networks. However, in real-world complex networks, whether they are single-layer or multilayer, studying the synchronizability of networks with weighted, directed and variable coupling strength is more meaningful. Variable coupling strength plays an important role in information transmission and complex system control. Adjusting its size can effectively optimize traffic flow regulation and signal coordination in the intelligent transportation system ^[29]. In the Internet of Things, its regulation can optimize the transmission and processing of information, enabling intelligent detection and control ^[30]. Given its extensive application in engineering, it cannot be ignored in synchronization analysis. Therefore, apart from considering the influence of topological parameters, we also focus on analyzing the influence of variable coupling strengths on the synchronizability of the network. The common control methods in complex networks include adaptive control, sliding mode control, impulsive control and so on ^[31,32]. Compared with other methods, the adaptive control strategy selected in this paper has the advantages of adjusting changes independently with network uncertainties, improving the efficiency of synchronization control, and having stronger robustness ^[33]. Shi et al. ^[34] realized finite/fixed-time synchronization of complex networks with uncertain internal coupling based on the quantitative adaptive control method. Qin et al. ^[35] used an adaptive control strategy to study the robust H_∞ synchronization problem of complex networks with multiple delays.

Inspired by the previous literature, we will examine two types of directed multilayer variable coupling strength star-ring networks: divergent coupling and aggregated coupling. In the case of divergent coupling, the hub node establishes connections directed toward the leaf nodes, thus forming a unidirectional communication flow, which plays an important role in improving the reliability and resource coordination of the sensor system ^[36]. Conversely, aggregated coupling involves the leaf nodes directing connections toward the hub nodes, with advantages such as multi-source data aggregation and resource optimization ^[37,38]. The major contributions of this paper can be summarized as follows:

(i) The eigenvalue spectrum of the multilayer networks with divergent and aggregated coupling is strictly derived.

(ii) The correlation between topological parameters and synchronizability is analyzed with bounded and unbounded synchronous regions.

(iii) The variable coupling strength in divergent and aggregated coupling star-ring networks has been investigated, which is only related to the synchronizability of the aggregated coupling mode.

The remaining sections of the paper are organized as follows. In Section 2, several preliminaries are provided to establish a foundation for the subsequent discussions. The synchronizability of multilayer divergent and aggregated directionally coupled star-ring networks under varying coupling is illustrated in detail in Sections 3 and 4, respectively. To validate the accuracy of our synchronizability analysis, synchronization controls are provided in Section 5. Finally, in Section 6, we summarize our conclusions and provide a brief discussion of future work.

2.   Preliminaries

Consider a complex multilayer network with M layers and N interconnected nodes in each layer. The evolution of a full network dynamical equation is described as follows ^[39]:

where x_i^K∈$\mathcal{R}^{N}$ denotes the state of the ith node in the Kth subnetwork, and f(x_i^K): $\mathcal{R}^{N}$→$\mathcal{R}^{N}$ governs a nonlinear function of the nodes, 1 ≤ i ≤ N, 1 ≤ K, Z ≤ M (K ≠ Z). c^K > 0 is the intralayer coupling strength, and H(x_j^K): $\mathcal{R}^{N}$ → $\mathcal{R}^{N}$ is the inner coupling continuous function of the intralayer. p > 0 is the interlayer coupling strength, and Γ(x_i^Z): $\mathcal{R}^{N}$ → $\mathcal{R}^{N}$ is the inner continuous coupling function of the interlayer. W^K = (w_ij^K)∈$\mathcal{R}$^N×N represents the coupling weight configuration matrix of the Kth layer, where w_ij^K is defined as follows: if there exists a connection between node i and j(i ≠ j) within the Kth layer, then w_ij^K = w_ji^K = 1; otherwise, w_ij^K = w_ji^K = 0. In addition, the diagonal elements of W^K satisfy the following condition:

Therefore, L^K = -c^K W^K is a Laplacian matrix of the Kth layer. Similarly, the interlayer weight d_i^KZ = d_i^ZK = 1 if node i in the Kth layer is connected to node j in the Zth layer. Otherwise, d_i^KZ = d_i^ZK = 0. Likewise,

Then, D = (d_i^KZ)∈$\mathcal{R}$^M×M is the negative Laplacian matrix of the interlayer. Let ${\boldsymbol{ \mathcal{L}}}$^L be the supra-Laplacian matrix that represents the interlayer topology and ${\boldsymbol{ \mathcal{L}}}$^I be the supra-Laplacian matrix that represents the intralayer topology. Then, the supra-Laplacian matrix of the above system is described as ^[40]:

Let L^I denote the Laplacian matrix of the interlayer networks. Specifically, the interlayer supra-Laplacian matrix is

where ⊗ is the Kronecker product and I_N represents the N × N identity matrix. The intralayer supra-Laplacian matrix of a multiplex network is defined as:

where K = 1, 2, …, M, and L^K is the Laplacian matrix of the Kth layer.

In accordance with the master stability function framework ^[41], we can analyze whether the eigenvalues of the multilayer network fall in the corresponding synchronous regions to judge the synchronizability of the network. Both bounded and unbounded regions are usually the two main categories for discussion. If the network has an unbounded synchronous region, the minimum nonzero eigenvalue λ₂ of ${\boldsymbol{ \mathcal{L}}}$ is key to research the synchronizability. Moreover, synchronizability is positively correlated with λ₂. On the other hand, if the network has a bounded synchronous region, the synchronizability depends on the ratio R = λ_max /λ₂, which is the maximum eigenvalue λ_max to the minimum nonzero eigenvalue λ₂ of ${\boldsymbol{ \mathcal{L}}}$. At this time, synchronizability is negatively correlated with R.

For the necessity of subsequent theoretical deduction, a lemma and two hypotheses are presented here:

Lemma 2.1. ^[42] A and B are N × N matrices, M is the number of layers, then

Hypothesis 2.1. ^[43] Suppose that there exists α > 0, i = 1, 2, …, N, K = 1, 2, …, M, such that

where, e_i^K(t) and s(t) represent the synchronization errors and target system of the network, respectively.

Hypothesis 2.2. ^[44] For any p, q∈${ \mathcal{R}}$ⁿ, there exists a positive definite matrix Q∈${ \mathcal{R}}$^n×n, and the following always holds:

3.   Synchronizability of multilayer network with divergent coupling

Based on the theory of Section 2, a multilayer star-ring network with divergent coupling is constructed, and its characteristic spectrum is strictly derived. Furthermore, when the synchronous region is unbounded or bounded, the influence of different topological parameters on synchronizability is studied in this section.

3.1.   The structure of the multilayer network with divergent coupling

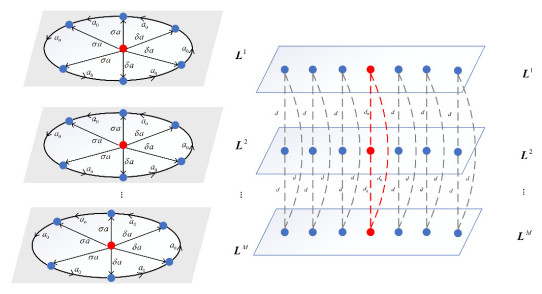
In this section, the synchronizability analysis of the divergent directionally coupled star-ring network is considered, and its topology is shown in Figure 1. The left panel describes the intralayer connection of each subnetwork in the multilayer network, and the right panel shows the one-to-one connection of the subnetwork nodes of each layer. L⁽¹⁾, L⁽²⁾, …, L^(M) represent each layer. Assume that the topologies of each subnetwork are the same. There are N nodes in each subnetwork, and M represents the number of layers. The blue nodes and the red nodes represent the leaf nodes and the hub nodes, respectively. The nodes at each layer are connected one to one. It is assumed that the connections between nodes within a layer exhibit directionality, while the interlayer connections of each subnetwork are undirected. The red nodes all point one way to the blue nodes and the blue node points to the next blue node. In the aggregated coupling network, d₀ represents the corresponding coupling strength between each leaf node in each subnetwork. The remaining d represents the coupling strength between each leaf node. The intralayer coupling strength of blue nodes is given by a₀. Suppose that the intralayer coupling strength of the red node points to the blue nodes is denoted as a and the total intralayer coupling strength is (N-1) a at the initial time. At some time, γ (γ is even) of coupling strength becomes σa, then the coupling strength of the remaining (N-γ-1) nodes becomes (N-σγ-1) a/(N-γ-1). We have denoted (N-σγ-1) a/(N-γ-1) as δa for convenience.

3.2.   The eigenvalue spectrum and synchronizability

The supra-Laplacian matrix of the network can be written as:

In detail, ${\bf{\Xi}} = diag{\left({ - {d_0}, - d, - d, \cdots, - d} \right)_{N \times N}}$, and

According to Lemma 2.1, the corresponding characteristic polynomial of ${\boldsymbol{\mathcal{L} }}$ is expressed as follows:

From the characteristic polynomial above, whether the topological parameter N is odd or even affects the eigenvalues, which will be discussed below.

1) N is odd, the eigenvalues ${\boldsymbol{\mathcal{L} }}$ are:

Where, 0 and 2a₀ are (N-1)/2 multiple roots, Md and Md+2a₀ are ((N-1)/2) (M-1) multiple roots, and Md₀+(N-1) a are M-1 multiple roots, respectively. Due to the fact that Md > > 2a₀, thus λ₂ = 2a₀, λ_max = Md₀+(N-1) a, R = λ_max /λ₂ = (Md₀+(N-1) a)/2a₀.

2) N is even, the eigenvalues ${\boldsymbol{\mathcal{L} }}$ are:

Both 0, Md, and Md₀+(N-1) a are multiple roots. As above, λ₂ = Md, λ_max = Md₀+(N-1) a, and R = λ_max/λ₂ = (Md₀+(N-1) a)/Md. It is obvious that σa doesn't affect the synchronizability based on the above eigenvalues.

The relationships between λ₂, R, and the topological parameters are depicted in Table 1. Similarly, Table 2 presents the correlations between the network's synchronizability and its topological parameters.

3.3.   Comparisons and discussions

Numerical experiments between topological parameters and λ₂, R of multilayer networks will be investigated. That is, including N, a, a₀, d, d_0, and M to discuss the synchronizability.

1) Influence of the number of subnetwork nodes N

Take a₀ = 0.6, d = 1, M = 15, d₀ = 0.1, and a = 1 to examine the synchronizability with N (N varies from 9 to 399 if N is odd; N varies from 10 to 400 if N is even). Figure 2(a) shows that λ₂ doesn't change with N in the subnetwork, that is, the synchronizability is not affected. The relationship between R and N is shown in Figure 2(b), which indicates that synchronizability is negatively correlated with N.

2) Influence of the intralayer coupling strength a

Take a₀ = 0.6, M = 15, d = 1, d₀ = 0.1, N (odd) = 399, and N (even) = 400 to examine the synchronizability with a. As is shown in Figure 3(a), λ₂ is unchanged with a, that is, the synchronizability is also unchanged with a. Then Figure 3(b) displays the relationships between R and a, which means that synchronizability is negatively correlated with a.

3) Influence of the intralayer coupling strength a₀

Take a = 1, M = 15, d = 1, d₀ = 0.1, N (odd) = 399, and N (odd) = 400 to explore the synchronizability with a₀. Notice from Figure 4(a) that when N is even, λ₂ unchanged with a₀, that is, the synchronizability is not affected. However, when N is odd, λ₂ exhibits a positive correlation with a₀, indicating that a higher value of a₀ is associated with increased synchronizability. Notice from Figure 4(b) that when N is even, R remains unchanged, so the synchronizability is not affected. However, R decreases with a₀, so the synchronizability strengthens.

4) Influence of the intralayer coupling strength a₀

Take a = 1, a₀ = 1, M = 15 (N = odd), M = 15, 16, 17 (N = even), d₀ = 0.1, N (odd) = 399, and N(even) = 400) to explore the synchronizability with d. From Figure 5(a), λ₂ is unchanged with d when N is odd, which means that synchronizability is unchanged. Additionally, λ₂ increases with d by selecting three group data when N is even, and the synchronizability becomes stronger. From Figure 5(b), R is unchanged with d when N is odd, which means that synchronizability is unchanged. And R decreases with d by selecting three group data when N is even, the synchronizability becomes stronger.

5) Influence of the interlayer coupling strength d₀

Take a = 1, a₀ = 1, M = 15, d = 1, N (odd) = 399, and N (even) = 400 to study the synchronizability with d₀. Figure 6(a) clearly indicates that λ₂ is not affected by the change of d₀, that is, the synchronizability is stable. As is shown in Figure 6(b), R increases with d₀. It is revealed that the greater the coupling strength d₀, the less favorable the synchronizability.

6) Influence of the number of layers M

Take a = 1, a₀ = 1, d = 1 (N = odd), d = 1, 1.3, 1.6 (N = even), N (odd) = 399, and N (even) = 400 to analyze the synchronizability with M. Figure 7(a) shows that λ₂ is unchanged with M when N is odd, which means the synchronizability is unchanged. Additionally, λ₂ increases with the M by selecting three group data, when N is even, the synchronizability becomes stronger with the M. Figure 7(b) shows that R increases slowly with M when N is odd, and then the synchronizability decreases. And R decreases with M when N is even; the synchronizability strengthens with M.

4.   Synchronizability of multilayer network with aggregated coupling

In contrast to the divergent coupling, a multilayer star-ring network with aggregated coupling is built. In addition, the characteristic spectrum of the network is rigorously derived. Through theoretical deduction, we find that variable coupling strength has a significant influence on synchronizability, except for topological parameters. Furthermore, the influence of variable coupling strength on synchronizability under different function variation rules is discussed in this section.

4.1.   The structure of the multilayer network with aggregated coupling

We consider an aggregated directionally coupled star-ring network as shown in Figure 8. Only, unlike the topology of Figure 1, the blue nodes all point to the red nodes within each layer.

4.2.   The eigenvalue spectrum and synchronizability

The supra-Laplacian matrix of the network can be written as:

In detail, ${\bf{\Xi}} = diag{\left({ - {d_0}, - d, - d, \cdots, - d} \right)_{N \times N}}$, and

According to Lemma 2.1, the corresponding characteristic polynomial ${\boldsymbol{\mathcal{L} }}$ is expressed as follows:

From the characteristic polynomial above, whether the topological parameter N is odd or even affects the eigenvalues, which will be discussed below.

1) N is odd, the eigenvalues of ${\boldsymbol{\mathcal{L} }}$ are:

Where, Md₀ is M-1 multiple roots, σa, σa+2a₀, Md+σa and Md+σa+2a₀ are (γ/2) (M-1) multiple roots, δa, δa+2a₀, Md+δa and Md+δa+2a₀ are ((N-γ-1)/2) (M-1) multiple roots. In view of Md₀ > > {σa, δa}, thus λ_max = max {Md+σa+2a₀, Md+δa+2a₀}, λ₂ = min {σa, δa}, R = λ_max/λ₂ = max {Md+σa+2a₀, Md+δa+2a₀}/min {σa, δa}.

2) N is even, the eigenvalues of ${\boldsymbol{\mathcal{L} }}$ are:

Where, Md₀ is M-1 multiple roots, σa and Md+σa are γ (M-1) multiple roots, δa and Md+δa are (N-γ-1) (M-1) multiple roots. In view of Md₀ > > {σa, δa}, thus λ_max = max {Md+σa, Md+δa}, λ₂ = min {σa, δa}, R = λ_max/λ₂ = max {Md+σa, Md+δa}/min {σa, δa}.

It is obvious that the variable coupling strengths σa and δa will affect the synchronizability from the above eigenvalues. Different from Section 3, the impact of varying coupling strengths σa and δa on synchronizability will be investigated in this section.

Remark 1. Compared with the unidirectional connection between the hub node and the leaf nodes in ^[45], we discuss the influence of topological parameters and variable coupling strength on synchronizability through divergent and aggregated coupling. Moreover, the characteristic spectrum of multilayer divergent and aggregated coupling networks is also accurately obtained. And it is concluded that the topological parameters influencing the synchronizability of the network are different when the directionality of the node connections is changed.

4.3.   Comparisons and discussions

According to the above theoretical derivation, the number of nodes in the subnetwork has no effect on synchronizability. Moreover, λ₂ and R in the two cases are basically similar, so N is selected as odd for further study. To investigate the network synchronizability under variable coupling strengths σa and δa, the partial coupling strength is varied. Let the variable coupling strength follow the principles of the proportional function, the inverse proportional function, the exponential function, the logarithmic function, and the trigonometric function, respectively. The principles of variable coupling strength are as follows: σ₁ = t, σ₂ = 1/t, σ₃ = 0.9^t, σ₄ = lg(t), σ₅ = sint+1.5.

1) Variable coupling strength follows the proportional function

We take σ₁ = t (then δ₁ = (N-tγ-1) /(N-γ-1)) for the numerical simulation. Then, λ₂ = min {σ₁a, δ₁a}, R = λ_max/λ₂ = max {Md+σ₁a+2a₀, Md+δ₁a+2a₀}/ min {σ₁a, δ₁a}. Figure 9(a) shows the coupling strength a versus the proportional function, and the color depth corresponds to the value of λ₂. If t is fixed, λ₂ increases with a, and synchronizability is improved. If a is fixed, λ₂ first increases and then decreases with t. Obviously, when t = 1 and a = 5, λ₂ reaches its maximum and the synchronizability is the strongest. Figure 9(b) shows the coupling strength a versus the proportional function, and the color depth corresponds to the value of R. If t is fixed, R decreases with a, and synchronizability is improved. Additionally, if a is fixed, R first decreases and then increases as t increases. Obviously, when t = 1 and a = 5, R reaches its minimum, and the synchronizability is the strongest.

2) Variable coupling strength follows the inverse proportional function

We take σ₂ = 1/t (then δ₂ = (N-(1/t) γ-1) /(N-γ-1)) for the numerical simulation. Then, λ₂ = min {σ₂a, δ₂a}, R = λ_max/λ₂ = max {Md+σ₂a+2a₀, Md+δ₂a+2a₀}/ min {σ₂a, δ₂a}. Figure 10(a) shows the coupling strength a versus the inverse proportional function, and the color depth corresponds to the value of λ₂. If t is fixed, λ₂ increases with a, and synchronizability is improved. Additionally, if a is fixed, λ₂ first increases and then decreases with t. Obviously, when t = 1 and a = 5, λ₂ reaches its maximum, and the synchronizability is the strongest. Figure 10(b) shows the coupling strength a versus the inverse proportional function, and the color depth corresponds to the value of R. If t is fixed, R decreases with a, and synchronizability is improved. Additionally, if a is fixed, R first decreases and then increases as t increases. Obviously, when t = 1 and a = 5, R reaches its minimum, and the synchronizability is the strongest.

3) Variable coupling strength follows the exponential function

We take σ₃ = 0.9^t (then δ₃ = (N-(0.9^t) γ-1) / (N-γ-1)) for the numerical simulation. Then λ₂ = min {σ₄a, δ₄a}, R = λ_max/λ₂ = max {Md+σ₄a+2a₀, Md+δ₄a+2a₀}/ min {σ₄a, δ₄a}. Then λ₂ = min {σ₄a, δ₄a}, R = λ_max/λ₂ = max {Md+σ₄a+2a₀, Md+δ₄a+2a₀}/ min {σ₄a, δ₄a}. Figure 11(a), (b) indicates the λ₂ and R for varying coupling strength a. Whatever the value of a is, λ₂ decreases and R increases gradually as time goes on. That is, the synchronizability weakens with time.

4) Variable coupling strength follows the logarithmic function

We take σ₄ = lg(t) (then δ₄ = (N-(lg(t)) γ-1) /(N-γ-1)) for the numerical simulation. Then λ₂ = min {σ₄a, δ₄a}, R = λ_max/λ₂ = max {Md+σ₄a+2a₀, Md+δ₄a+2a₀}/ min {σ₄a, δ₄a}. Figure 12(a), (b) indicates the λ₂ and R for varying coupling strength a. λ₂ gradually increases, then decreases as time goes on. R gradually decreases, then increases slowly. That is, the synchronizability strengthens first and weakens with time.

5) Variable coupling strength follows the trigonometric function

We take σ₅ = sint+1.5 (then δ₄ = (N-(sint+1.5) γ-1)/(N-γ-1)) for the numerical simulation. Then λ₂ = min{σ₅a, δ₅a}, R = λ_max/λ₂ = max{Md+σ₅a+2a₀, Md+δ₅a+2a₀}/min{σ₅a, δ₅a}. Figure 13(a), (b) indicates the λ₂ and R for varying coupling strength a. We could find λ₂ and R vary periodically.

By comparing and analyzing Sections 3 and 4, the variable coupling strengths σa and δa only have an impact on the divergent coupling star-ring network. Furthermore, the topological parameters of the network affect both coupling modes, whether the synchronous regions are bounded or unbounded.

5.   Synchronization control

A detailed and rigorous theoretical derivation is presented for the eigenvalue spectrum and synchronizability of the star-ring network under different coupling cases in Sections 3 and 4. Based on the theoretical analysis, simulations are conducted to investigate the effect of different topological parameters on synchronizability. In this section, synchronization control experiments on multilayer star-ring networks will be performed to verify the above analytical results. For simplicity, consider a multilayer network with M layers, each containing N nodes, which is described by

the relevant descriptions for Eq (8) are similar to Eq (1), uK i(t) is an adaptive controller particularly.

Assume the Hindmarsh-Rose ^[46,47] system is selected as the dynamic system described by:

where, x, y, and z are defined as the membrane potential of the neuron, the recovery variable, and the slow-varying adaptive current of the neuron in the system, respectively. a = 1, b = 3, c = 1, d = 5, r = 0.006, S = 4, x₀ = -1.56, I_ext = 3. Its chaotic system and time history are shown in Figure 14.

The target system s(t) of the network is defined as follows:

then synchronization errors of the networks are defined as:

Subsequently, the error systems can be derived as follows:

If lim_t→∞ ||e_i^K(t)|| = 0 is satisfied, it can be inferred that the multilayer complex networks and the target system have achieved synchronization. Designing an adaptive controller as follows:

where h_i^K > 0 and d_i^K(t) is the adaptive feedback control gains.

Theorem 5.1. Based on Hypothesises 2.1 and 2.2, the error system is asymptotically synchronization under the controller, if there exists d^* > 0 satisfying

where,

Proof. Consider the following Lyapunov-krasovskii ^[48] candidate as:

one gains

Where, β = ((e⁽¹⁾(t)) ^T, (e⁽²⁾(t)) ^T, …, (e^(M)(t)) ^T)^T. The error systems (16) are shown to achieve asymptotic synchronization by Theorem 5.1. Therefore, the proof is now completed.

Remark 2. In addition to the theoretical derivation of synchronizability in ^[49], the synchronization control of the constructed multilayer star-ring network model is added. Precise synchronization control can be achieved by changing the size of the topological parameters correlated to synchronizability.

In accordance with the master stability function theory, if the inner coupling continuous matrix Γ is an identity matrix, the synchronous region is unbounded. Therefore, the synchronizability of the network is determined by the λ2 of its Laplacian matrix ^[50]. We select a divergent directionally coupled star-ring network for simulation, and N is even. From Table 1, λ2 = Md. The following topological parameters of the multilayer star-ring network are selected for numerical simulation: N = 50, d0 = 1, a = 1, a0 = 1, d = 1 (when considering the variation of M), and M = 3 (when considering the variation of d). Figure 15 shows the synchronization errors ||e|| versus time. Figure 15 reveals that the synchronization speed increases with M, indicating greater synchronizability at higher M. From Figure 15(b), the speed of synchronization exhibits a gradual increase with d. Therefore, the synchronizability becomes stronger as d increases. Figure 16 shows the evolution of the error in each dimension of the node over time for different numbers of layers M. As the number of layers M increases, it can clearly be seen that synchronizability improves. Figure 17 shows the variation of the error of each dimension node over time with d, and the results show that a larger d leads to faster synchronization.

Conclusive evidence is provided by the synchronization control experiments in this section, confirming the validity of the synchronizability analysis results. As the network structure becomes larger, leading to an increase in synchronizability. Additionally, the strength of interlayer coupling also enhances synchronizability. Consequently, it is possible to effectively implement control by determining the key topology parameters that have a correlation with synchronizability.

6.   Conclusions and discussion

The eigenvalue spectrum of the supra-Laplacian matrix of multilayer star-ring networks is rigorously derived in this paper, considering divergent and aggregated coupling within the subnetwork. Compared with Sections 3 and 4, when the synchronized regions are bounded and unbounded, the variable coupled strengths σa and δa are closely connected to the synchronizability of the aggregated coupling but have no correlation with the divergent coupling. Synchronizability is firmly related to the topological parameters, including the number of nodes N, intralayer coupling strengths a and a₀, interlayer coupling strengths d and d₀, and the number of layers M in the divergent coupling model. In the case of an unbounded synchronous region, when N is odd, it is primarily influenced by the topological parameter a₀. A bounded synchronous region depends on several factors, including N, a, a₀, d₀, and M. In addition, when N is even, M and d are relevant to the synchronizability with the unbounded synchronous region. When N is even, it is determined by N, a, d₀, d, and M with the bounded synchronous region. Particularly, the synchronizability is significantly related to the intralayer variable coupling strengths σa and δa with aggregated coupling. When σ changes with different functions, the tendency toward synchronizability is found. Finally, a numerical simulation of a star-ring network composed of the Hindmarsh-Rose systems is given to verify the validity of the synchronizability analysis.

Based on the research on multilayer star-ring networks in this paper, coupling mode, coupling strength and topological parameters play an important role in the analysis of synchronizability. Through the analysis of synchronizability and the synchronization process, it has some theoretical reference value for understanding and exploring practical problems in engineering. In particular, adjusting traffic network signals, optimizing control in the Internet of Things and improving communication network transmission efficiency can give a certain theoretical perspective. So far, there are still many unsolved problems related to multilayer networks. There is a requirement for further research, as there are various theoretical and practical issues that need to be addressed and overcome.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Nos. 11602146, 11872304), the Science Foundation of Shanghai (No. 18ZR1438200), and the Chen Guang Project supported by the Shanghai Municipal Education Commission and Shanghai Education Development Foundation (No. 16CG65). Xia Tan is supported by National Natural Science Foundation of China (No. 12102266).

Conflict of interest

The authors declare there is no conflict of interest.