Electromagnetic radiation and electrical stimulation controls of absence seizures in a coupled reduced corticothalamic model

1.   Introduction

Absence seizure, a neurological disease of the brain, often occurs in the childhood ^[1,2], which is characterized by a temporary loss of consciousness and bidirectional synchronous spike wave discharges (SWDs) with a frequency of 2–4 Hz recorded in an electroencephalogram (EEG) ^[3]. These abnormal discharges can cause learning and cognitive problems ^[4,5,6]. Numerous studies have shown that the production of these abnormal discharges is related to the interaction between the cerebral cortex and thalamus ^[7,8,9]. Specially, the basal ganglia has already been confirmed to involve in the corticothalamic system to control epilepsy ^[10,11]. However, the control mechanism of the basal ganglia for epilepsy is unclear due to the complexity of the brain.

According to recent studies, thalamic reticular nucleus (TRN) is a structure of the thalamus and plays an important role in controlling electrical signals from the thalamus to the cerebral cortex ^[12,13]. Apart from this, TRN acts like a pacemaker to control epilepsy ^[14]. Some researchers have found that GABAergic (aminobutyric acid) signals released by TRN contribute to the inhibitory effect of thalamus on cerebral cortex. If these signals are disrupted, the patients will develop epilepsy in the brain ^[15,16]. Avanzini et al. pointed out that the oscillating activity of Ca2+ has an important effect on the generation of epilepsy ^[17]. Nanobashvili et al. shown that electrical discharge from TRN can cause limbic motor seizure ^[18]. Pantoja-Jiménez et al. demonstrated that high frequency discharge stimulation of TRN can inhibit the generation of SWDs in the corticothalamic system ^[19]. Clemente-Perez et al. proposed that TRN controls brain wide rhythms and seizures through electrical signs ^[20]. Chang et al. found that optical stimulation of TRN in mice can inhibit epilepsy ^[21]. However, there is still not enough theoretical basis for the control of epilepsy by TRN.

According to statistics, about one third of epileptic patients are difficult to control epilepsy through drug treatment in the world ^[22]. In some patients, surgical resection of the epileptic site may be a good treatment ^[23]. But 30–40% of adults with epilepsy are still difficult to treat ^[24]. Now we need an effective treatment for epilepsy patients. DBS has been applied to clinical treatment, animal brain research and theoretical models. Lehtimäki et al. reported that an epileptic patient was cured by stimulating the thalamus with DBS ^[25]. On the basis of the mean field model, Wang et al. demonstrated that the application of DBS in TRN can effectively inhibit epilepsy ^[14]. In the recent, CRS has been used to treat epilepsy as a new method of desynchronizing the firing of some abnormal neurons ^[26]. Fan et al. used CRS to stimulate different parts of the basal ganglia ^[27]. After that, the epileptic region of the whole model was reduced. However, how to select DBS and CRS to achieve the best therapeutic effect is still unclear.

In addition to the stimulation of external electrical signals can affect the activity of neurons, the change of the intracellular and extracellular ion concentration causing electromagnetic induction can also affect the activity of neurons. According to some studies, the electromagnetic induction caused by ion exchange and membrane current transmission can be described by magnetic flux ^[28,29,30]. Therefore, the external electromagnetic radiation is treated as a change in the magnetic flux in the cell, which can be simulated by a memristor ^[31]. Some studies have shown that memristors can be used to treat neurological diseases ^[32,33,34].

To understand the pathogenesis of epilepsy, the researchers have established the thalamocortical models. Fan et al. reduced the basal ganglia to a 2I:3O modulator ^[27]. The 2I:3O modulator receives two excitatory stimulation from the cerebral cortex and specific relay nuclei of thalamus (SRN) and outputs three inhibitory stimulation to the cerebral cortex, SRN and TRN. However, the above model only study a single thalamocortical model or two thalamocortical models without considering the influence of the basal ganglia. Therefore, our goal is to develop a model in which the two corticothalamic systems are connected by the basal ganglia. There are two main contributions in the paper. On the one hand, the basal ganglia is reduced to a simple and efficient connector, which receives two excitatory stimulations from the first cortical thalamic system and then outputs three inhibitory stimulations to the second cortical thalamic system. Particularly, to explore the internal mechanism of absence epilepsy, we found that epilepsy can be suppressed without adding stimulations only by adjusting the coupling strength of TRN₁-SRN₁ and TRN₂-SRN₂ pathways or the coupling strength of the connector and the second cortical thalamic system. On the other hand, to explore the suppression of absence epilepsy by different schemes and targets, we applied DBS, 1:0 CRS, 3:2 CRS and electromagnetic radiation stimulation to the TRN₁ and cerebral cortex, respectively.

2.   The coupled reduced corticothalamic model and numerical analysis

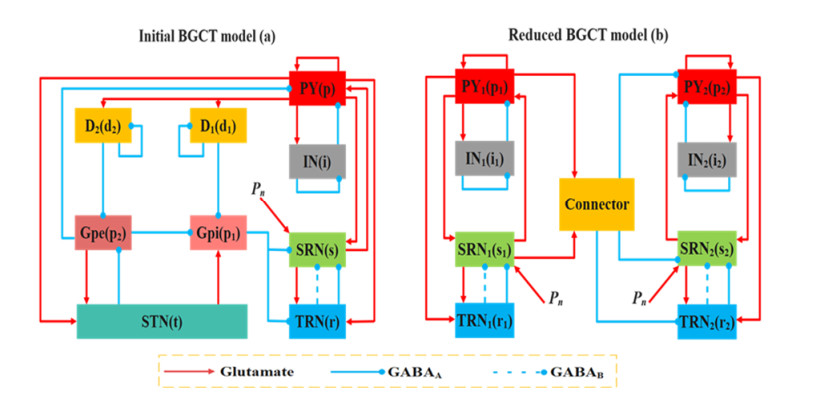
Chen et al. established a BGCT model as shown in Figure 1(a), which is composed of the cortical thalamic system and basal ganglia ^[35,36]. In this model, the cortical thalamic system is composed of two parts, cortical excitatory pyramidal neurons and inhibitory interneurons in the cortical thalamic system, thalamic relay nuclei and reticular nucleus in the thalamic system. The basal ganglia is made up of three parts: subthalamic nucleus, striatal D₁ and D₂, globus pallidus internal and external segments. In Figure 1(a), the excitatory stimulus is represented by the red arrow and is transmitted through the medium of glutamate. The soild and dashed blue lines indicate inhibitory stimulus mediators transmitted by GABA_A and GABA_B, respectively. P_n is a nonspecific subthalamic input. Fan et al. developed a simplified BGCT model ^[27]. The basal ganglia is simplified as a 2I:3O modulator which receives excitatory stimulation from the PY and SNR and then outputs inhibitory stimulation to PY, SNR and TRN. To further study the mechanism of epilepsy, we developed a model of two cortical thalamic systems connected by a connector, as shown in Figure 1(b). The connector receives excitatory stimulation from the PY₁ and SRN₁ and outputs inhibitory stimulation to PY₂, SRN₂ and TRN₂.

To describe the dynamic of neuron population, some researchers have introduced a mean field model ^[37,38]. The mean firing rate of each neuron population can be described as a sigmoid function that contains the maximum deviation of the mean firing rate and the mean membrane potential at a given location r and time t. The function is shown below:

where $a\in {\Lambda }_{1} = \left\{p, i, {d}_{2}, {d}_{1}, {p}_{2}, {p}_{1}, t, s, r\right\}$ represent different population of neurons, ${Q}_{a}^{max}$ represents the mean firing rate, ${\theta }_{a}$ and $\sigma$ are the threshold variability of firing rate and standard deviation of the mean firing threshold, respectively. When the mean membrane potential ${V}_{a}$ receives synaptic voltages from other neuron populations, the change in the mean membrane voltage can be modeled by the following formulas ^[39]:

where ${D}_{\alpha \beta }$ is the synaptic and dendritic filtering of the input signal represented by the differential operator. $\alpha$ and $\beta$ represent the response of the cell body to the delay and rise time of the input signal. Cab denotes the coupling strength of the neuron population b to a. ${\phi }_{b}\left(r, t\right)$ is the input pulse rate form neuron population b to a. The delay parameter $\tau$ simulates the synaptic dynamics of GABAB. Due to the influence of GABAB, the mathematical expression of the network model is changed into a delay differential equation ^[40]. In the network model, the pulse generated by each neuron population a propagates to the next neuron population with an average conduction velocity ${\upsilon }_{a}$ and produced a field ${\phi }_{a}$. This type of propagation can be described by a decaying wave equation ^[41,42]:

here ${\nabla }^{2}$ is the Laplace operator, ${r}_{a}$ is the characteristic range of axons in neuron population a, ${\gamma }_{a} = {v}_{a}/{r}_{a}$ represents the time decay rate of the control pulse. In this model, it is generally believed that only the axons of the cortical pyramidal neuron population are long enough to produce a significant propagation effect. In other neuron population, their axons are too short to achieve the similar effect, therefore, ${\phi }_{f} = F\left[{V}_{f}\right]\left(f\in \left\{p, {d}_{1}, {d}_{2}, {p}_{1}, {p}_{2}, s, r, t\right\}\right).$ In addition, absence seizures are typically generalized seizures with dynamic activity throughout the brain. When considering the whole brain as a continuum and assuming that the spatial activity in this mean field model is uniformly distributed, its spatial derivative can be ignored and set ${\nabla }^{2} = 0.$ Therefore, the excitatory axon field in the cortex is ultimately defined as ^[38]:

where ${\gamma }_{p} = \frac{{v}_{p}}{{r}_{p}}$. At the same time, the mean membrane voltage and mean firing rate of the cortical inhibitory interneuron population $i$ satisfy ${V}_{i} = {V}_{p}$ and ${Q}_{i} = {Q}_{p}$, respectively. This simplifies the mean field model and makes it more tractable for numerical simulation.

In the model of this paper, since the basal ganglia is simplified as a connector, the neuron population is represented as $a\in {\varLambda }_{2} = \left\{{p}_{1}, {s}_{1}, {r}_{1}, c, {p}_{2}, {s}_{2}, {r}_{2}\right\}.$ Based on the mathematical model established above, Figure 1(b) can be described by the following formulas:

Most of the parameters of formulas (6)–(14) are referenced from ^[35,36]. These parameters have been shown to apply to previous studies ^[43,44,45]. The parameters of this paper are shown in Tables A1 and A2.

DBS and CRS are a commonly used in the treatment of epilepsy. We applied DBS, 1:0 CRS and 3:2 CRS to TRN₁ to the model of this paper. The stimulus patterns of DBS, 1:0 CRS and 3:2 CRS are shown in Figure 2(a)–(c), respectively. Here we use a periodic step function to simulate DBS and CRS ^[14]:

when $P < 0$, we set $P = 0$, so the expression for 1:0 CRS is

if $M < 0$, we set $M = 0$, the expression of 3:2 CRS is

where $\rho$ is the amplitude of oscillation. $T$ and $\delta$ represent the period and pulse width of the function, we set $\rho = 6$ mV, $\frac{1}{T} = 500\text{Hz}$ and $\delta = 1\text{ms}$ in this paper. H is Heaviside function in MATLAB.

In addition to the external electrical signals can affect epilepsy, changes in ion concentration inside and outside the cell will produce electromagnetic induction, which can also affect the generation of epilepsy. Under the influence of the electromagnetic induction, we can introduce a memristor to represent the relationship between membrane potential and magnetic flux. The charge flux of the memristor varies as follow ^[46,47,48]:

where $c\left(\varphi \right)$ is the flux of charge on the memristor. $\varphi$ represents the magnetic flux.

A memristor is added to the model in this paper as shown below ^[32,33,34]:

$w$ is the gain factor association with media, ${w}_{1}{\phi }_{{p}_{1}}$ shows the effect of the electromagnetic induction and ${w}_{1}$ has different effects on epilepsy for different mediators. ${w}_{2}\varphi$ represents the self inductance effect and also explain the saturation of magnetic flux in the cell. The relevant parameters of the memristor also came from ^[32]. In this paper, the simulation environment is MATLAB R2019b and we use the forth-order Runge-Kutta method to solve the delay different equation. The total time of the numerical calculation is 15 s and the time step is 0.5 ms.

3.   Numerical results

3.1.   Generation of epilepsy in the thalamocortical system

Many studies have shown that GABA_B synapses in the thalamus play an important role in suppressing epilepsy in the TRN-SRN pathway, and GABA_B is related to the production of slow waves in the brain. Therefore, adjusting the coupling strength between TRN and SRN may lead to epilepsy ^[49,50,51]. In order to verify the validity of the above pathological factors in the model presented in this paper, we applied two related parameters: the inhibitory coupling strength ${C}_{{s}_{1}{r}_{1}}$ and the delay$\tau$of the GABA_B. Figure 3(a) and (b) respectively show the dynamic state analysis and frequency analysis in the parameter space $({C}_{{s}_{1}{r}_{1}}, \tau ).$ The first dynamic state is called the saturation state, where ${C}_{{s}_{1}{r}_{1}}$ is very small. Under this condition, inhibition of TRN₁ and SRN₁ pathways didn't successfully inhibit the over excitation of the cortical thalamic system. At this moment, the firing state of the neuron will quickly evolve from low to maximum, as shown in Figure 3(c). When the values of ${C}_{{s}_{1}{r}_{1}}$ and $\tau$ are appropriate, the SWD oscillating state with double peaks is shown in Figure 3(d). More importantly, we find that most SWD oscillations were in the frequency range of 2–4 Hz and the SWDs in these regions were very similar to the EEG signals of patients ^[3,23]. As the value of ${C}_{{s}_{1}{r}_{1}}$ continues to increase, there will be simple oscillatory state, the simple oscillatory state is shown in Figure 3(e). When the value ${C}_{{s}_{1}{r}_{1}}$ is relatively large, the low discharge state shown in Figure 3(f) will appear. In the paper, we denote saturation, simple oscillation, SWD, and low firing state by I, II, III, and IV, respectively.

The above findings confirm that the model in this paper can reproduce four different dynamic states in the human brain. More importantly, our model can successfully reproduce SWDs with the frequency of 2–4 Hz after introducing the above epileptic pathogenesis. In the next, we will try different coupling interaction and different stimulus methods to explore the pathogenesis of epilepsy.

3.2.   Effects of the TRN₁-SRN₁ pathway on epilepsy control after electrical stimulation and electromagnetic radiation stimulation

Based on Figure 3(a) and (b), electrical stimulation and electromagnetic radiation stimulation are applied to TRN₁ and PY₁ in the model respectively and then we observe the changes in the epileptic region. Electrical stimulation includes DBS, 1:0 CRS and 3:2 CRS, respectively. In addition, we use memristor to simulate the electromagnetic induction changes in the cell body.

As shown in Figure 4(a) and (b), the epileptic area changes from 16.02% in Figure 3(a) to 3.12% after adding DBS. The area of epilepsy is reduced to 8.16% after adding 1:0 CRS shown in Figure 4(c) and (d), 12.82% after adding 3:2 CRS shown in Figure 4(e) and (f), 6.78% after adding electromagnetic radiation shown in Figure 4(g) and (h). These studies have shown that both electrical stimulation and electromagnetic radiation stimulation have inhibitory effects on the production of epilepsy, among which DBS has a better inhibitory effect than 1:0 CRS and 3:2 CRS.

3.3.   Effects of the TRN₁-SRN₁ and TRN₂-SRN₂ pathways interaction on epilepsy after electrical stimulation and electromagnetic radiation stimulation

In addition to exploring the effect of a single pathway and corticothalamic system on epilepsy. Here, we will explore the effect of two pathways belonging to two different corticothalamic systems on epilepsy. We remain applying DBS, 1:0 CRS and 3:2 CRS to TRN₁ and electromagnetic radiation stimulation to PY₁. Figure 5(a) and (b) shows the dynamic states and dominant frequency analysis of the neurons without any external stimulus, in which the percentage of epileptic area is 25.91%. When we applied DBS to the model, the epileptic area accounts for 10.93% shown in Figure 5(c) and (d). The suppression effect is shown in Figure 5(e)–(h), the epileptic area accounts for 14.05% after adding 1:0 CRS and 21.85% after adding 3:2 CRS, respectively. In addition, the effect of memristor on the dynamic states and dominant frequency of neurons are shown in Figure 5(i) and (j), the epileptic area is significantly reduced compared with Figure 5(a) and (b).

To further explore how to reduce the area of epilepsy, we change the coupling strength between the connector and SRN₂. We set K₄ = 0 mV s. On this basis, then we apply electric stimulation and electromagnetic radiation stimulation to the model. In this case, no external stimulation is added as shown in Figure 6(a) and (b), where the epileptic area accounts for 20.92%. When DBS is applied to TRN₁, the proportion of epileptic area is 6.76% in Figure 6(c), its dominant frequency analysis is shown in Figure 6(d). We also added 1:0 CRS and 3:2 CRS to the model. As shown in Figure 6(e) and (g), the ratios of epileptic area are 13.22 and 17.59%, respectively. In the dominant frequency analysis diagrams of Figure 6(f) and (h), there are two SWD regions which become smaller than that shown in Figure 6(b). Figure 6(i) and (j) shows the inhibitory effect of the memristor on the cerebral cortex, and the proportion of epileptic area reduced to 11.97%.

In addition to the above examples, we can also change the coupling strength between the connector and TRN₂ to compare the inhibitory effect of various stimulation methods on epilepsy. In the absence of electrical stimulation and memristor, the dynamic states of neuron and dominant frequency analysis are shown in Figure 7(a) and (b) at K₅ = 0 mV s, the SWD oscillation state accounts for 15.50% of the total state. Figure 7(c) and (d) represents the effect of DBS on TRN₁ and the area of epilepsy accounts for 4.68%. The dynamic states and dominant frequency analysis of 1:0 CRS are shown in Figure 7(e) and (f), the percentage of epileptic area is 9.98%. The effect of 3:2 CRS on TRN₁ is shown in Figure 7(g) and (h), and its SWD area occupies 13.84%. When memristor stimulation is applied to PY₁, its inhibitive effect is shown in Figure 7(i) and (j), where the proportion of epileptic area is 0.00%.

In the case of TRN₁-SRN₁ and TRN₂-SRN₂ pathways interaction on epilepsy, comparing the inhibitory effects without external stimulus in Figure 8, we found that epileptic seizure is effectively suppressed by changing the coupling strengths K₄ and K₅, artificially. The K₅ = 0 produces a better suppression result than the other approach K₄ = 0. With external stimulus, the result shows that numbers of epileptic seizure take on degression after adding DBS, 1:0 CRS, 3:2 CRS and memristor shown in Figure 8. In particular, for optimal effectiveness, the control should be add memristor and set K₅ = 0.

4.   Conclusions

In the paper, we proposed a novelty model that is composed of two corticothalamic systems and a basal ganglia simplified as a connector. Based on the coupled reduced corticothalamic model, the dynamic state of epileptic seizures was reproduced, and three electrical stimulations and electromagnetic radiation stimulation were added to the model such as DBS, 1:0 CRS and 3:2 CRS. The main findings of the paper are as follows: the complexity of interneuronal iterations can be lessened by simplifying the basal ganglia as a connector. Without external stimulation, the epileptic area can be reduced by changing the coupling strength between the connector and second corticothalamic system. With external stimulation, the results show that DBS has a better effect inhibitory on epilepsy than 1:0 CRS and 3:2 CRS, and 1:0 CRS is better than 3:2 CRS. In addition, the electromagnetic induction from memristor is utilized to suppress epilepsy, and the results show that this method also has a great effect on the suppress epilepsy. This optimal control for electromagnetic induction is confirmed when K₅ = 0. These findings have significant implications for the understanding of how to do the theoretical experiment of mean field model for a more simple and convenient method, and how to select external stimulation for suppressing epilepsy. We hope that the numerical simulation results of this paper can provide some insights into the treatment of epileptic patients in clinical therapeutics. In the future work, we will design a closed-loop control method to inhibit epileptic seizure.

Acknowledgments

This research was supported by the National Natural Science Foundation of China (No. 11502139).

Conflict of interest

The authors declare there is no conflicts of interest.

Appendix

The following parameters are used to numerical simulations ^[35,36].