1.
Introduction
The models of the differential and integral equations have been appeared in different applications (see [1,2,3,4,6,7,9,12,13,14,15,16,17,18,19,20]).
Boundary value problems involving fractional differential equations arise in physical sciences and applied mathematics. In some of these problems, subsidiary conditions are imposed locally. In some other cases, nonlocal conditions are imposed. It is sometimes better to impose nonlocal conditions since the measurements needed by a nonlocal condition may be more precise than the measurement given by a local condition. Consequently, a variety of excellent results on fractional boundary value problems (abbreviated BVPs) with resonant conditions have been achieved. For instance, Bai [4] studied a type of fractional differential equations with m-points boundary conditions. The existence of nontrivial solutions was established by using coincidence degree theory. Applying the same method, Kosmatov [17] investigated the fractional order three points BVP with resonant case.
Although the study of fractional BVPs at resonance has acquired fruitful achievements, it should be noted that such problems with Riemann-Stieltjes integrals are very scarce, so it is worthy of further explorations. Riemann-Stieltjes integral has been considered as both multipoint and integral in a single framework, which is more common, see the relevant works due to Ahmad et al. [1].
The boundary value problems with nonlocal, integral and infinite points boundary conditions have been studied by some authors (see, for example [8,10,11,12]).
Here, we discuss the boundary value problem of the nonlinear differential inclusions of arbitrary (fractional) orders
with the nonlocal boundary condition
the integral condition
and the infinite point boundary condition
We study the existence of solutions x∈C[0,1] of the problems (1.1) and (1.2), and deduce the existence of solutions of the problem of (1.1) with the conditions (1.3) and (1.4). Then the existence of the maximal and minimal solutions will be proved. The sufficient condition for the uniqueness and continuous dependence of the solution will be studied.
This paper is organised as: In Section 2, we prove the existence of continuous solutions of the problems (1.1) and (1.2), and deduce the existence of solutions of the problem of (1.1) with the conditions (1.3) and (1.4). In Section 3, the existence of the maximal and minimal solutions is proved. In Section 4, the sufficient condition for the uniqueness and continuous dependence of the solution are studied. Next, in Section 5, we extend our results to the nonlocal problems (1.3) and (2.1). Finally, some existence results is proved for the nonlocal problems (1.4) and (2.1) in Section 6.
2.
Main results
Consider the following assumptions:
(I) (i) The set F1(t,x,y) is nonempty, closed and convex for all (t,x,y)∈[0,1]×R×R.
(ii) F1(t,x,y) is measurable in t∈[0,1] for every x,y∈R.
(iii) F1(t,x,y) is upper semicontinuous in x and y for every t∈[0,1].
(iv) There exist a bounded measurable function a1:[0,1]⟶R and a positive constant K1, such that
Remark 2.1. From the assumptions (i)–(iv) we can deduce that (see [3,6,7,13]) there exists f1∈F1(t,x,y), such that
(v) f1:[0,1]×R×R⟶R is measurable in t for every x,y∈R and continuous in x,y for t∈[0,1], and there exist a bounded measurable function a1:[0,1]→R and a positive constant K1>0 such that
and the functional f1 satisfies the differential equation
(II) f2:[0,1]×R⟶R is measurable in t for any x∈R and continuous in x for t∈[0,1], and there exist a bounded measurable function a2:[0,1]→R and a positive constant K2>0 such that
and
(III) 2K1γ+K1K2α<αγΓ(2−α),α,γ∈(0,1].
Remark 2.2. From (I) and (v) we can deduce that every solution of (1.1) is a solution of (2.1). Now, we shall prove the following lemma.
Lemma 2.1. If the solution of the problems (1.2)–(2.1) exists then it can be expressed by the integral equation
Proof. Consider the boundary value problems (1.2)–(2.1) be satisfied. Operating by I1−α on both sides of (2.1) we can obtain
Taking
then we obtain
Putting t=τ and multiplying (2.5) by Σmk=1ak, then we get
and
Then
Substituting (2.8) and (2.9) in (2.5), which completes the proof.
Theorem 2.1. Let assumptions (I)–(III) be satisfied. Then the integral equation (2.2) has at least one continuous solution.
Proof. Define a set Qr as
and the operator F by
For y∈Qr, then
Thus, the class of functions {Fy} is uniformly bounded on Qr and F:Qr→Qr. Let y∈Qr and t1,t2∈[0,1] such that |t2−t1|<δ, then
Thus, the class of functions {Fy} is equicontinuous on Qr and {Fy} is compact operator by the Arzela-Ascoli Theorem [5].
Now we prove that F is continuous operator. Let yn⊂Qr be convergent sequence such that yn→y, then
Using Lebesgue dominated convergence Theorem [5] and assumptions (iv)–(II) we have
Then F:Qr→Qr is continuous, and by Schauder Fixed Point Theorem[5] there exists at least one solution y∈C[0,1] of (2.2). Now
Putting t=τ and using (2.9), we obtain
then
This proves the equivalence between the problems (1.2)–(2.1) and the integral equation (2.2). Then there exists at least one solution y∈C[0,1] of the problems (1.2)–(2.1).
3.
Maximal and minimal solutions
Here, we shall study the maximal and minimal solutions for the problems (1.2) and (2.1). Let y(t) be any solution of (2.2), let u(t) be a solution of (2.2), then u(t) is said to be a maximal solution of (2.2) if it satisfies the inequality
A minimal solution can be defined by similar way by reversing the above inequality.
Lemma 3.1. Let the assumptions of Theorem 2.1 be satisfied. Assume that x(t) and y(t) are two continuous functions on [0,1] satisfying
where one of them is strict.
Let functions f1 and f2 be monotonic nondecreasing in y, then
Proof. Let the conclusion (3.1) be not true, then there exists t1 with
Since f1 and f2 are monotonic functions in y, then we have
This contradicts the fact that y(t1)=x(t1), then y(t)<x(t). This completes the proof.
For the existence of the continuous maximal and minimal solutions for (2.1), we have the following theorem.
Theorem 3.1. Let the assumptions of Theorem 2.1 be hold. Moreover, if f1 and f2 are monotonic nondecreasing functions in y for each t∈[0,1], then Eq (2.1) has maximal and minimal solutions.
Proof. First, we should demonstrate the existence of the maximal solution of (2.1). Let ϵ>0 be given. Now consider the integral equation
where
For ϵ2>ϵ1, we have
Also
Applying Lemma 3.1, we obtain
As shown before, the family of function yϵ(t) is equi-continuous and uniformly bounded, then by Arzela Theorem, there exist decreasing sequence ϵn, such that ϵn→0 as n→∞, and u(t)=limn→∞yϵn(t) exists uniformly in [0,1] and denote this limit by u(t). From the continuity of the functions, f2,ϵn(t,yϵn(t)), we get f2,ϵn(t,yϵn(t))⟶f2(t,y(t)) as n→∞ and
Now we prove that u(t) is the maximal solution of (2.1). To do this, let y(t) be any solution of (2.1), then
and
Applying Lemma 3.1, we obtain
From the uniqueness of the maximal solution it clear that yϵ(t) tends to u(t) uniformly in [0,1] as ϵ→0.
By a similar way as done above, we can prove the existence of the minimal solution.
4.
Uniqueness of the solution
Here, we study the sufficient condition for the uniqueness of the solution y∈C[0,1] of problems (1.2) and (2.1). Consider the following assumptions:
(I∗) (i) The set F1(t,x,y) is nonempty, closed and convex for all (t,x,y)∈[0,1]×R×R.
(ii) F1(t,x,y) is measurable in t∈[0,1] for every x,y∈R.
(iii) F1 satisfies the Lipschitz condition with a positive constant K1 such that
where H(A,B) is the Hausdorff metric between the two subsets A,B∈[0,1]×E.
Remark 4.1. From this assumptions we can deduce that there exists a function f1∈F1(t,x,y), such that
(iv) f1:[0,1]×R×R→R is measurable in t∈[0,1] for every x,y∈R and satisfies Lipschitz condition with a positive constant K1 such that (see [3,7])
(II∗)f2:[0,1]×R⟶R is measurable in t∈[0,T] and satisfies Lipschitz condition with positive constant K2, such that
From the assumption (I∗), we have
Then
where |a1(t)|=supt∈I|f1(t,0,0)|.
From the assumption (II∗), we have
Then
where |a2(t)|=supt∈I|f1(t,0)|.
Theorem 4.1. Let the assumptions (I∗) and (II∗) be satisfied. Then the solution of the problems (1.2) and (2.1) is unique.
Proof. Let y1(t) and y2(t) be solutions of the problems (1.2) and (2.1), then
Then
Since (αγΓ(2−α)−(2K1α+K1K2γ))<1, then y1(t)=y2(t) and the solution of (1.2) and (2.1) is unique.
4.1. Continuous dependence of the solution
Definition 4.1. The unique solution of the problems (1.2) and (2.1) depends continuously on initial data x0, if ϵ>0, ∃δ>0, such that
where y∗ is the unique solution of the integral equation
Theorem 4.2. Let the assumptions (I∗) and (II∗) be satisfied, then the unique solution of (1.2) and (2.1) depends continuously on x0.
Proof. Let y(t) and y∗(t) be the solutions of problems (1.2) and (2.1), then
then we obtain
and
Definition 4.2. The unique solution of the problems (1.2) and (2.1) depends continuously on initial data ak, if ϵ>0, ∃δ>0, such that
where y∗ is the unique solution of the integral equation
Theorem 4.3. Let the assumptions (I∗) and (II∗) be satisfied, then the unique solution of problems (1.2) and (2.1) depends continuously on ak.
Proof. Let y(t) and y∗(t) be the solutions of problems (1.2) and (2.1) and (∑mk=1a∗k)−1=A∗,
then we obtain
and
5.
Riemann-Stieltjes integral condition
Let y∈C[0,1] be the solution of the nonlocal boundary value problems (1.2) and (2.1). Let ak=(g(tk)−g(tk−1), g is increasing function, τk∈(tk−1−tk), 0=t0<t1<t2,...<tm=1, then, as m⟶∞ the nonlocal condition (1.2) will be
As the limit m⟶∞, we obtain
Theorem 5.1. Let the assumptions (I)–(III) be satisfied. If ∑mk=1ak be convergent, then the nonlocal boundary value problems of (1.3) and (2.1) have at least one solution given by
Proof. As m→∞, the solution of the nonlocal boundary value problem (2.1) will be
6.
Infinite-point boundary condition
Theorem 6.1. Let the assumptions (I)–(III) be satisfied, then the nonlocal boundary value problems of (1.4) and (2.1) have at least one solution given by
Proof. Let the assumptions of Theorem 2.1 be satisfied. Let ∑mk=1ak be convergent, then take the limit to (1.4), we have
Now
and by the comparison test (∑mk=1ak∫τk0(τk−θ)α−1Γ(α)y(θ)dθ) is convergent,
Furthermore, from (2.9) we have
Example 6.1. Consider the following nonlinear integro-differential equation
with boundary condition
Let
then
and also
It is clear that the assumptions (I) and (II) of Theorem 2.1 are satisfied with a1(t)=t4e−t∈L1[0,1], a2(t)=43Iγ|(cos(5t+1)|∈L1[0,1], and let α=13, γ=23, then 2K1γ+K1K2α=12<αγΓ(2−α)=12Γ(2−α). Therefore, by applying Theorem 2.1, the nonlocal problems (6.1) and (6.2) has a continuous solution.
7.
Conclusions
In this paper, we have studied a boundary value problem of fractional order differential inclusion with nonlocal, integral and infinite points boundary conditions. We have prove some existence results for that a single nonlocal boundary value problem, in of proving some existence results for a boundary value problem of fractional order differential inclusion with nonlocal, integral and infinite points boundary conditions. Next, we have proved the existence of maximal and minimal solutions. Then we have established the sufficient conditions for the uniqueness of solutions and continuous dependence of solution on some initial data and on the coefficients ak are studied. Finally, we have proved the existence of a nonlocal boundary value problem with Riemann-Stieltjes integral condition and with infinite-point boundary condition. An example is given to illustrate our results.
Conflict of interest
The authors declare no conflict of interest.










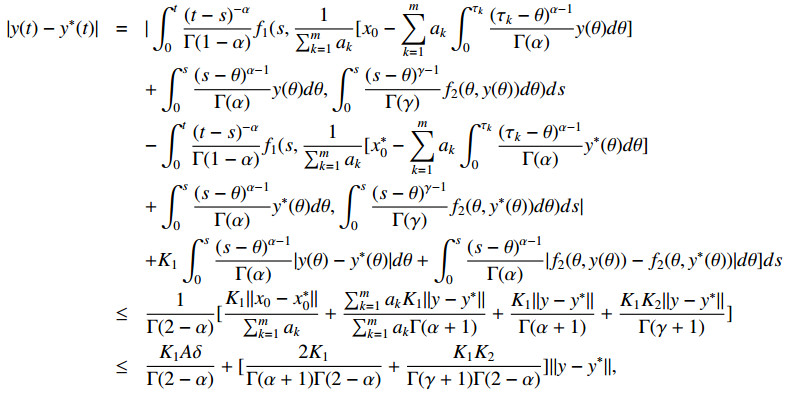













 DownLoad:
DownLoad: