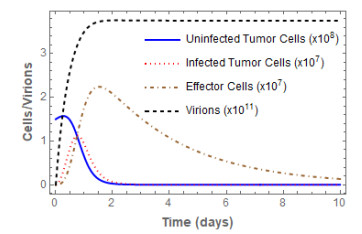
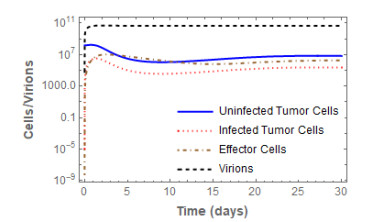
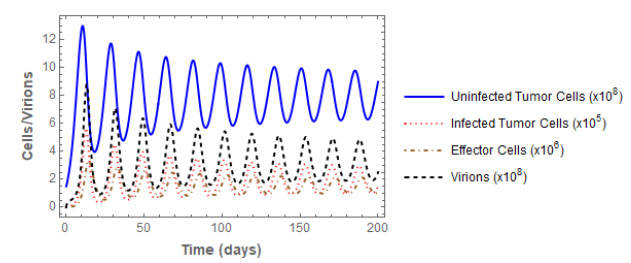
We present a system of four nonlinear differential equations to model the use of virotherapy as a treatment for cancer. This model describes interactions among infected tumor cells, uninfected tumor cells, effector T-cells, and virions. We establish a necessary and sufficient treatment condition to ensure a globally stable cure state, and we additionally show the existence of a cancer persistence state when this condition is violated. We provide numerical evidence of a Hopf bifurcation under estimated parameter values from the literature, and we conclude with a discussion on the biological implications of our results.
1.
Introduction
Motivated by the well-known fifth of 23 problems formulated by David Hilbert [1,2], the present paper establishes a digital topological version of a typical topological group. Since the present paper is based on some essential notions such as a digital image, a k-path, a digital space, and so on, we first will remind some concepts. In relation to the study of digital images X⊂Zn, Rosenfeld [3,4] initially introduced the digital k-connectivity for low dimensional digital images in Zn,n∈{1,2,3}. Let us consider a set X⊂Zn,n∈{1,2,3}, as a digital image with a certain digital k-connectivity, denoted by (X,k), as follows: For X⊂Z, we have (X,2). For X⊂Z2, we assume (X,k),k∈{4,8}. Besides, for X⊂Z3, we consider (X,k) with k∈{6,18,26}.
Hereinafter, for our purposes, for {a,b}⊂Z with a⪇b, the set [a,b]Z is assumed to be the set {s∈Z|a≤s≤b}.
Motivated by the above Rosenfeld's approach, a generalization of these adjacencies for low dimensional digital images was proposed to study a high dimensional digital image, as follows [5]: For a natural number t with 1≤t≤n, we say that the distinct points in Zn
are k(t,n)-adjacent if at most t of their coordinates differ by ±1 and the others coincide. Based on this statement, the k(t,n)-adjacency relations of Zn,n∈N, were formulated in [5,6], as follows:
where the notation ":=" is used to introduce a new terminology.
For instance,
For a set X⊂Zn,n∈N, with one of the k-adjacency of (1.1), we call (X,k) a digital image. For a digital image (X,k), assume two points x,y∈X. Then we say that a finite sequence (x0,x1,⋯,xm)⊂X⊂Zn,n∈N, is a k-path if xi is k-adjacent to xj, where j=i+1,i∈[0,m−1]Z.
Let us recall the notion of a digital space [7], as follows: A digital space is a kind of a relation set (X,π), where X is a nonempty set and π is a binary symmetric relation on X such that X is π-connected, where we say that X is π-connected if for any two elements x and y of X, there is a finite sequence (xi)i∈[0,l]Z of elements in X such that x=x0, y=xl and (xj,xj+1)∈π for j∈[0,l−1]Z.
Assume a digital image (X,k) with a certain group structure on X, say (X,∗), where X⊂Zn. Then a digital topological version of a topological group, called a digitally topological k-group (DT-k-group for brevity) and denoted by (X,k,∗), is logically defined as the combination of a group and a digital k-adjacency structure. Then, we strongly need to establish the most suitable adjacency of a digital product X×X, say Gk∗, derived from the given k-adjacency of (X,k) to support both Gk∗-connectedness of X×X and (Gk∗,k)-continuity of the multiplication α:(X×X,Gk∗)→(X,k). Indeed this is essential for formulating a DT-k-group structure of (X,k,∗). To achieve this initiative, we can consider some adjacencies of a digital product X×X that need not be typical k-adjacencies of Z2n in (1.1). In detail, given a digital image (X,k),X⊂Zn, the most important thing is that we need to establish a certain adjacency of the Cartesian product X×X that is suitable for formulating a DT-k-group structure based on both a group (X,∗) and a digital image (X,k).
Given a digital image (X,k), after introducing two kinds of adjacencies such as a Ck∗- and Gk∗-adjacency relation in X×X (see Definitions 3.2 and 4.4 in the present paper), the present paper further develops the notions of (Ck∗,k)- and (Gk∗,k)-continuity related to the multiplication (X×X,Gk∗)→(X,k). Note that the new adjacency relation Gk∗ in X×X⊂Z2n need not belong to the set {k:=k(t,n)|t∈[1,2n]Z} that is the set of typical k-adjacencies of Z2n (see (1.1)). Based on this approach, we can propose a digital version of a typical topological group derived from a certain group (X,∗) and a digital image (X,k). Indeed, both the LC-property in [8] and the C-compatible k-adjacency of a digital product in [9] can contribute to the establishment of a DT-k-group. Given two digital images (Xi,ki),i∈{1,2}, a C-compatible k-adjacency of a Cartesian product in [9] and a Ck∗-adjacency in the present paper play important roles in studying product properties of some digital topological invariants relating to the research of digital covering spaces and digital homotopy theory [8,10]. It was motivated by the Cartesian product adjacency of a graph product in typical graph theory [11]. However, it is clear that these two versions have their own features that need not be equivalent to each other (see Remark 3.2). Moreover, given two digital images (Xi,ki) in Zni,i∈{1,2}, it was proved that not every X1×X2⊂Zn1+n2 has a Ck∗-adjacency (see Example 3.1 and Remarks 3.4 and 3.6). Hence, the present paper proposes a new adjacency relation in X1×X2 and it develops two types of continuities for multiplications that are strongly used to formulate DT-k-groups. In relation to this work, we may raise some issues and queries, as follows:
● Is there a digital image (X,k) with a certain group structure on X?
● Given a digital image (X,k) with a certain group structure, what relation among elements in the Cartesian product X×X is the most suitable for establishing a DT-k-group structure on (X,k)?
Then we are strongly required to have a certain relation making the Cartesian product X×X connected with respect to the newly-established relation in X×X.
● With a newly-developed adjacency of X×X, how can we establish a DT-k-group structure on X derived from the given digital image (X,k)?
In case this relation is successfully formulated, it can support to get the earlier works in the literature corrected and vivid from the viewpoints of digital topology and digital geometry.
Next, given two digital images (Xi,ki),Xi⊂Zni,i∈{1,2}, suppose a digital product X1×X2 with a typical k′- or a Gk∗-adjacency addressing the above queries, say (X1×X2,k′) referred to in (1.1) or (X1×X2,Gk∗), derived from the given digital images (Xi,ki),Xi⊂Zni,i∈{1,2}. Then, we naturally pose the following queries.
● How to introduce the notion of (Gk∗,ki)-continuity of a map from (X1×X2,Gk∗) to (Xi,ki)?
● What differences are there among the typical (k′,ki)-continuity, the (Ck∗,ki)-continuity, and the (Gk∗,ki)-continuity?
● Let SCn,lk be a simple closed k-curve with l elements in Zn. Then, how to establish a group structure on SCn,lk?
Furthermore, given SCn,lk, we further have the following question.
● How can we formulate a DT-k-group of SCn,lk?
After developing several new notions, we will address the above mentioned topics.
This paper is organized as follows. Section 2 provides some basic notions that will be used in the paper. In Section 3, given a digital image (X,k),X⊂Zn, after establishing a Ck∗-adjacency of the digital product X×X, we define the notion of (Ck∗,k)-continuity of a map from (X×X,Ck∗) to (X,k). Then, we intensively investigate some properties of (Ck∗,k)-continuity of a map from (X×X,Ck∗) to (X,k). In Section 4, given a digital image (X,k), after establishing a new Gk∗-adjacency of the digital product X×X, we define the notion of (Gk∗,k)-continuity of a map from (X×X,Gk∗) to (X,k). Also, we compare among the typical (k′,k)-continuity, the (Ck∗,k)-continuity, and the (Gk∗,k)-continuity, where k′ is a adjacency of X×X⊂Z2n referred to in (1.1). Section 5 introduces the notion of a DT-k-group and proves that a simple closed k-curve, denoted by SCn,lk, has a group structure with a certain group operation, denoted by ∗, and finally proves that the combined set (SCn,lk,∗):=(SCn,lk,k,∗) consisting of both the group structure and the digital k-connectivity is a DT-k-group. In particular, given a DT-k-group (SCn,lk,∗), we can make each element x∈SCn,lk as an identity element depending on our needs after relabeling elements of SCn,lk (in detail, see Remark 5.4(1)). Also, we prove that (Zn,2n,+) is a DT-2n-group. Section 6 corrects some errors in the literature. Section 7 refers to some remarks and a further work. In the paper we will start with only a nonempty and k-connected digital image (X,k). In case a digital image (X,k) is not k-connected, it can invoke some trivial cases when studying k-continuous mappings [12]. Besides, given a set X, we usually use the notation X♯ to denote the cardinality of the given set X. In addition, since the paper has many notations, for the convenience of readers, using a certain beginning part of each section, we will give a block summarizing some notations which will used in each section.
2.
Preliminaries
To develop the notion of a DT-k-group, the adjacencies of Zn,n∈N, referred to in (1.1), are strongly required (see Sections 3–6).
In this section, we will use the following notations with several times.
(1) SCn,lk: A simple closed k-curve with l elements in Zn,n∈N∖{1}.
(2) dk: A function from (X,k) to N∪{0} inducing a metric on (X,k) (see (2.2) and (2.3)).
(3) Nk(p,1): A digital k-neighborhood of the given point p in (X,k).
(4) N0: The set of even natural numbers (see (2.1) and Example 5.1).
Let us now recall some terminology to develop two adjacencies of a digital product. For a digital image (X,k), two points x,y∈X are k-connected (or k-path connected) if there is a finite k-path from x to y in X⊂Zn [13]. We say that a digital image (X,k) is k-connected (or k-path connected) if any two points x,y∈X is k-connected (or k-path connected). In a digital image (X,k), it is clear that the two notions of k-connectedness and k-path connectedness are equivalent. Also, a digital image (X,k) with a singleton is assumed to be k-connected for any k-adjacency. Given a k-adjacency relation of (1.1), a simple k-path from x to y on X⊂Zn is assumed to be the sequence (xi)i∈[0,l]Z⊂X⊂Zn such that xi and xj are k-adjacent if and only if either j=i+1 or i=j+1 [13] and x0=x and xl=y. The length of this simple k-path, denoted by lk(x,y), is the number l. More precisely, lk(x0,x) is the length of a shortest simple k-path from x0 to x. In case there is no k-path between given distinct points x,y in (X,k), we say that lk(x,y)=∞. Besides, a simple closed k-curve with l elements in Zn, denoted by SCn,lk,4≤l∈N [5,10,13,14], is a sequence (xi)i∈[0,l−1]Z in Zn, where xi and xj are k-adjacent if and only if |i−j|=±1(modl) [13]. Indeed, the number l of SCn,lk depends on the situation [10] in (2.1) below. In Zn, we obtain
For instance, we have SC3,526, SC2,78, and so on.
As a matter of fact, the length lk(x,y) induces a metric function dk on a k-connected digital image (X,k) [5,14]. To be specific, assume a function on a k-connected digital image (X,k), as follows:
such that
Owing to (2.2) and (2.3), the map dk is obviously a function [5,14] satisfying dk(x,x′)≥1 whenever x≠x′. Hence it is clear that for a k-connected digital image (X,k), the map dk of (2.2) is a metric function on (X,k) [10,14]. Thus, we can represent a digital k-neighborhood of the point x0 with radius 1 [5,8] in the following way [14]
This k-neighborhood will be strongly used to develop the notions of a Ck∗- and a Gk∗-adjacency of a digital product in Sections 3 and 4 and comparing several adjacencies of digital products in Sections 3–6. To map every k0-connected subset of (X,k0) into a k1-connected subset of (Y,k1), the paper [4] established the notion of digital continuity. The digital continuity can be represented by using a digital k-neighborhood in (2.4), as follows:
Proposition 2.1. [5,14] Let (X,k0) and (Y,k1) be digital images on Zn0 and Zn1, respectively. A function f:X→Y is (k0,k1)-continuous if and only if for every x∈X, f(Nk0(x,1))⊂Nk1(f(x),1).
In Proposition 2.1, in case n0=n1 and k0=k1, we say that it is k0-continuous.
3.
Ck∗-adjacencies of digital products and an establishment of the (Ck∗,k′)-continuity
This section studies the notion of a Ck∗-adjacency of a digital product that will be strongly used to develop a digitally topological k-group (or DT-k-group in this paper) in Section 5. Next, we initially establish the notion of (Ck∗,ki)-continuity of a map from (X1×X2,Ck∗) to (Xi,ki),i∈{1,2}. More precisely, given two digital images (Xi,ki),i∈{1,2}, first we develop the so-called Ck∗-adjacency relation in the digital product X1×X2 derived from the given (Xi,ki),i∈{1,2}, so that we obtain a relation set (X1×X2,Ck∗) (see Proposition 3.7).
In this section, we will often use the following notations.
(1) C-compatible k-adjacency (see Definition 3.1).
(2) Ck∗-adjacency relation (see Definition 3.2) in a digital space (X1×X2,Ck∗).
(3) NCk∗(p): The set of the elements of Ck∗-neighbors of the given point p in a digital space (X1×X2,Ck∗) (see (3.5) and (3.6)).
(4) NCk∗(p,1): A Ck∗-neighborhood of the given point p in a digital space (X1×X2,Ck∗) (see (3.5).
(5) X♯: The cardinal number of the given set X. Indeed, to avoid some confusion with the absolute value used in Sections 2 and 5 (in particular, see the proof of Theorem 5.8), we will use the notation X♯.
Since this work is associated with both the C-compatible k-adjacency in [9] and the LC-property in [8] of a digital product, let us recall them as follows: Motivated by the Cartesian product of graphs in [11], various properties of digital products were used in studying digital homotopic properties and digital covering spaces [8,9]. Using the digital k-neighborhood of (2.4), we define the following:
Definition 3.1. [9] For two digital images (Xi,ki) on Zni,ki:=k(ti,ni),i∈{1,2}, consider the Cartesian product X1×X2⊂Zn1+n2. We say that a k-adjacency of X1×X2 is strongly Cartesian compatible (C-compatible, for brevity) with the given ki-adjacency, i∈{1,2}, if every point (x1,x2) in X1×X2 satisfies the following property:
where the k-adjacency is one of the typical k-adjacency of Zn1+n2 stated in (1.1).
As for the C-compatible k-adjacency of Definition 3.1, we can take some k-adjacency of X1×X2 depending on the situation, where k:=k(t,n1+n2) for some t∈[max{t1,t2},n1+n2]Z [9]. At the moment, note that
(1) not every X1×X2 always has a compatible k-adjacency (see Example 3.1) and further,
(2) not every number t∈[max{t1,t2},n1+n2]Z is used to formulate a compatible k-adjacency of X1×X2 (see Example 3.1).
(3) However, in case there is a C-compatible k-adjacency of X1×X2, at least the number t=max{t1,t2} supports the establishment of the C-compatible k(t,n1+n2)-adjacency of X1×X2.
For instance, consider the Cartesian product SC2,l4×SC2,l4⊂Z4 has the only one C-compatible k-adjacency, where k=k(1,4)=8 instead the other adjacencies of Z4.
Motivated by this feature, based on Definition 3.1, we now define the following adjacency which is stronger than the adjacency of Definition 3.1.
Definition 3.2. For two digital images (Xi,ki) in Zni,ki:=k(ti,ni),i∈{1,2}, assume the Cartesian product X1×X2⊂Zn1+n2 with a C-compatible k-adjacency. After that, we consider only the case
Equivalently, distinct points p:=(x1,x2) and q:=(x′1,x′2) in X1×X2⊂Zn1+n2, p is k-adjacent to q if and only if
After that, we take only the case of k∗:=k such that k:=k(t,n1+n2),t=max{t1,t2}.
Then we say that this k-adjacency is a Ck∗-adjacency of X1×X2⊂Zn1+n2 derived from the given two digital images (Xi,ki),i∈{1,2}.
As for the Ck∗-adjacency of X1×X2 of Definition 3.2, we can concretely say that a compatible k(t,n1+n2)-adjacency of X1×X2 satisfying the property of (3.2) is equal to the Ck∗-adjacency of X1×X2 such that k∗=k(t,n1+n2) and t=max{t1,t2}. We now use the notation (X1×X2,Ck∗) as a relation set to denote the digital product X1×X2 with a Ck∗-adjacency. From Definition 3.2, we obtain the relation set (X1×X2,Ck∗) derived from the given two digital images (Xi,ki) in Zni,ki:=k(ti,ni),i∈{1,2}, depending on the situation.
To represent a Cartesian product of the two digital images SCni,liki,i∈{1,2}, as a matrix, we use the notation (see (2.1))
Then, take the Cartesian product SCn1,l1k1×SCn2,l2k2⊂Zn1+n2 that can be represented as the following matrix:
where ci,j:=(ai,bj).
Remark 3.3. Assume (Xi,ki) on Zni,ki:=k(ti,ni),i∈{1,2}. Then we observe the following:
(1) In case there is a compatible k-adjacency of X1×X2, there is always a Ck∗-adjacency of X1×X2 such that
(2) As an example, consider SC2,48×SC2,48. While there are three types of C-compatible k-adjacencies, k∈{32,64,80}, there is the only C32-adjacency on SC2,48×SC2,48 because the only number 32=k(2,4) satisfies Definition 3.2.
Let us compare the typical Cartesian product adjacency in [11] and the current Ck∗-adjacency.
Remark 3.4. Each of the compatible k-adjacency and a Ck∗-adjacency is a little bit different from the Cartesian product adjacency in graph theory in [11]. More precisely, given any two graphs G1,G2, we always have a Cartesian product adjacency of a graph product G1×G2 [11]. However, as stated in Definitions 3.1 and 3.2, for two digital images (Xi,ki),i∈{1,2}, not every X1×X2 has a Ck∗-adjacency or a compatible k-adjacency of the given digital product (see also Example 3.1(4) below).
Definition 3.5. For two digital images (Xi,ki) in Zni,i∈{1,2}, assume the Cartesian product X1×X2⊂Zn1+n2 with a certain Ck∗-adjacency. Given a point p:=(x1,x2)∈X1×X2, we define the following sets around the point p∈(X1×X2,Ck∗), as follows:
In Definition 3.5, we call the set NCk∗(p,1) a Ck∗-neighborhood of the point p∈X1×X2. Using (3.5), we can represent a Ck∗-adjacency relation between distinct points p and q, as follows: Given an X1×X2 with a Ck∗-adjacency, for distinct points p and q in X1×X2, we observe that
In view of Definition 3.2, we observe that not every digital product has a Ck∗-adjacency, as follows:
Example 3.1. (1) ([a,b]Z×[c,d]Z,C4),
(2) (SC2,l4×[a,b]Z,C6),
(3) (SC2,l4×SC2,l4,C8), (SC2,68×SC3,426,C130), and (SC2,48×SC2,l8,C32), and
(4) none of SC2,l4×SC2,68⊂Z4 and SC2,68×SC2,68⊂Z4 has a Ck∗-adjacency.
In detail, consider the digital product SC2,44×SC2,68⊂Z4 in Example 3.1(4), where
Then any k-adjacency of Z4 of (1.2) is not eligible to be a Ck∗-adjacency for SC2,44×SC2,68⊂Z4. In detail, take the point c1,2:=(a1,b2)∈SC2,44×SC2,68. Then we obtain
whose cardinality is 8, i.e., (N32(c1,2,1))♯=8.
However, we have
whose cardinality is 5.
Hence N32(c1,2,1) is not equal to (N4(a1,1)×{b2})∪({a1}×N8(b2,1)). Owing to the point c1,2∈SC2,44×SC2,68, the digital product SC2,44×SC2,68 does not have a C32-adjacency. As a matter of fact, any typical digital adjacency of Z4 in (1.2) need not be a Ck∗-adjacency of SC2,44×SC2,68, k∗∈{8,32,64,80} (see (1.2)) because any k∗-adjacency of Z4 cannot support the property (3.1) for SC2,44×SC2,68.
By Definition 3.5, Remark 3.3, and Example 3.1, we obviously obtain the following:
Remark 3.6. (1) Not every point p∈X1×X2 has an NCk∗(p,1). For instance, SC2,44×SC2,68 has several elements p such that NC32(p,1) does not exist (see (3.8) and (3.9)). Besides, the other numbers k∗∈{8,64,80} does not satisfy the property (3.1) either.
(2) Given two digital images (Xi,ki),i∈{1,2}, only in case that a digital product X1×X2 has a Ck∗-adjacency, for a point p:=(x1,x2)∈X1×X2, using the properties of (3.1) and (3.5), we obtain
(2) Consider two digital images (Xi,ki) in Zni, i∈{1,2}, where ki:=k(ti,ni) (see (1.1)). Assume ki=2ni, i.e., ti=1,i∈{1,2}. Then the digital product X1×X2⊂Zn1+n2 always has a Ck∗-adjacency where k∗:=k(1,n1+n2)=2(n1+n2) [9]. For instance, see the case (SC2,84×SC2,84,C8). Besides, only the C2n-adjacency of Zn exists in terms of the two (Zn1,2n1) and (Zn2,2n2), where n=n1+n2, ni∈N,i∈{1,2}.
(3) The adjacency relation Ck∗ of the relation set (X1×X2,Ck∗) is symmetric.
Based on the product adjacency relation in X1×X2⊂Zn1+n2 stated in Definition 3.2, the papers [8,9] studied various properties of digital products with Ck∗-adjacencies. Indeed, a digital product with a Ck∗-adjacency (X1×X2,Ck∗) is a kind of relation set that is symmetric in X1×X2. Thus we examine if (X1×X2,Ck∗) is a kind of digital space. To do this work, we introduce some terminology, as follows:
Based on the Ck∗-adjacency of a digital product, motivated by the classical notions in a typical digital image in [13] (see the previous part in Section 2), we now have the following: Given two digital images (Xi,ki),Xi⊂Zni,i∈{1,2}, assume a digital product X1×X2⊂Zn1+n2 with a certain Ck∗-adjacency, i.e., (X1×X2,Ck∗). We say that two points z,w∈X1×X2 are Ck∗-connected (or Ck∗-path connected) if there is a finite Ck∗-path (z0,z1,⋯,zm)⊂X1×X2 from z to w on X1×X2 such that z0=z and zm=w, where we say that a Ck∗-path from z to w in X1×X2 means a finite sequence (z0,z1,⋯,zm)⊂X1×X2 such that zi is Ck∗-adjacent to zj if j=i+1,i∈[0,m−1]Z or i=j+1,j∈[0,m−1]Z. A singleton with Ck∗-adjacency is assumed to be Ck∗-connected. Given a Ck∗-adjacency relation in X1×X2, a simple Ck∗-path from z to w in X1×X2 is assumed to be the Ck∗-path (zi)i∈[0,l]Z⊂X1×X2⊂Zn1+n2 such that zi and zj are Ck∗-adjacent if and only if either j=i+1,i∈[0,l−1]Z or i=j+1,j∈[0,l−1]Z and z0=x and zl=y. Also, a simple closed Ck∗-curve with l elements in X1×X2, denoted by SCn,lCk∗, is a sequence (zi)i∈[0,l−1]Z in X1×X2, where zi and zj are Ck∗-adjacent if and only if |i−j|=±1(modl).
Proposition 3.7. Given ki-connected digital images (Xi,ki),Xi⊂Zni,i∈{1,2}, (X1×X2,Ck∗) is a digital space.
Proof: By Remark 3.6(3), since the Ck∗-adjacency relation in X1×X2 is obviously symmetric, we only examine if (X1×X2,Ck∗) is Ck∗-connected. Take any distinct points p:=(x1,x2) and q:=(x′1,x′2) in X1×X2. Then, without loss of generality, we may assume the case x1⪇x′1 and x2≤x′2 or the case x1≤x′1 and x2⪇x′2. For our purposes, we now take the first case, i.e., x1⪇x′1 and x2≤x′2. Then consider the differences |x1−x′1|⪈0 and |x2−x′2|≥0. According to these finite differences, we can take a finite set
such that pi is Ck∗-adjacent to pi+1 in X1×X2,i∈[1,n−1]Z and
Owing to (3.11) and (3.12), we can conclude that (X1×X2,Ck∗) is Ck∗-connected.
In case there is a Ck∗-adjacency of X1×X2 derived from (Xi,ki),Xi⊂Zni,i∈{1,2}, let us now introduce the notion of (Ck∗,k′)-continuity of a map f:(X1×X2,Ck∗)→(Y,k′).
Definition 3.8. Given two digital images (Xi,ki),Xi⊂Zni,i∈{1,2}, assume a digital product (X1×X2,Ck∗) and a digital image (Y,k′). A function f:(X1×X2,Ck∗)→(Y,k′) is (Ck∗,k′)-continuous at a point p:=(x1,x2) if for any point q∈X1×X2 such that q∈NCk∗(p) (denoted by p↔Ck∗q), we obtain f(q)∈Nk′(f(p),1) (denoted by f(p)⇔k′f(q)). In case the map f is (Ck∗,k′)-continuous at each point p∈X1×X2, we say that the map f is (Ck∗,k′)-continuous.
This continuity will play a crucial role in establishing a DT-k-group in Section 5.
Proposition 3.9. Assume a Cartesian product X1×X2⊂Zn1+n2 with a Ck∗-adjacency and a typical digital image (Y,k′). A map f:(X1×X2,Ck∗)→(Y,k′) is (Ck∗,k′)-continuous at a point p∈X1×X2 if and only if
Proof: By Definition 3.8, the proof is completed.
Example 3.2. Let (X,2n) be a 2n-connected subset of (Zn,2n). Then each of the typical projection maps Pi:(X×X,C4n)→(X,2n) is a (C4n,2n)-continuous map, i∈{1,2}.
Remark 3.10. Consider digital images (Xi,ki) in Zni, i∈{1,2}, and (Y,k′) in Zm. Given a map from X1×X2 to Y, the (Ck∗,k′)-continuity of a map not always exist because the existence of NCk∗(p,1)⊂X1×X2 depends on the situation. However, given the (Ck∗,k′)-continuity of a map, the (Ck∗,k′)-continuity is equal to the (k∗,k′)-continuity of the given map.
According to Remark 3.10, since the existence of a Ck∗-adjacency for a digital product depends on the situation, we now propose the following result that is the Ck∗-adjacency version of the C-compatible k-adjacency studied in [9] (see Theorem 3.8 of [9]) and Remark 3.3(1), as follows:
Theorem 3.11. Given SCni,liki,i∈{1,2},ki:=k(ti,ni) from (1.1), assume ki≠2ni,i∈{1,2} and t1≤t2. Then we obtain the following cases supporting a Ck∗-adjacency for SCn1,l1k1×SCn2,l2k2.
(Case 1) Consider the case t1=t2 and t1≠n1, i.e., k1≠3n1−1. For each element yj∈SCn2,l2k2:=(yj)j∈[0,l2−1]Z, assume the number of different coordinates of every pair of the consecutive points yj and yj+1(modl2) in SCn2,l2k2 is constant as the number t2 instead of "at most t2". Then the product SCn1,l1k1×SCn2,l2k2 has a Ck∗-adjacency such that k∗:=k(t1,n1+n2).
(Case 2) In case t1=n1, i.e., k1=3n1−1, assume that for each element yj∈SCn2,l2k2:=(yj)j∈[0,l2−1]Z, the number of different coordinates of every pair of the consecutive points yj and yj+1(modl2) is constant as the number t2 instead of "at most t2". Then the product SCn1,l1k1×SCn2,l2k2 has a Ck∗-adjacency such that k∗:=k(t2,n1+n2).
(Case 3) In case ti=ni,i∈{1,2}, i.e., ki=3ni−1 (or ti∉[0,ni−1]Z), then we can consider two cases:
(Case 3-1) Assume that for each element yj∈SCn2,l2k2:=(yj)j∈[0,l2−1]Z, the number of different coordinates of every pair of the consecutive points yj and yj+1(modl2) is constant as the number t2 instead of "at most t2". Then the product SCn1,l1k1×SCn2,l2k2 has a Ck∗-adjacency such that k∗:=k(t2,n1+n2).
(Case 3-2) Assume that for each element xi∈SCn1,l1k1:=(xi)i∈[0,l1−1]Z, the number of different coordinates of every consecutive points xi and xi+1(modl1) in SCn1,l1k1 is constant as the number n1 instead of "at most n1" and for each element yj∈SCn2,l2k2:=(yj)j∈[0,l2−1]Z, the number of different coordinates of every pair of the consecutive points yj and yj+1(modl2) is constant as the number t2 instead of "at most t2".
Then the product SCn1,l1k1×SCn2,l2k2 has a Ck∗-adjacency such that k∗:=k(t2,n1+n2) (see Definition 3.2).
Proof: After comparing with the assertion of Theorem 3.8 of [9], based on Definitions 3.1 and 3.2, we need to only prove the (Case 3-2). Owing to Remark 3.3(1), since the C-compatible k∗:=k(t2,n1+n2)-adjacency implies a Ck∗-adjacency, this assertion holds.
By Remark 3.6(2), we obtain the following:
Corollary 3.12. In Theorem 3.11, in case ki=2ni,i∈{1,2}, there is only a C2n1+2n2-adjacency of SCn1,l1k1×SCn2,l2k2.
4.
Developments of a Gk∗-adjacency relation in a digital product X1×X2 derived from two digital images (Xi,ki),i∈{1,2}, and the (Gk∗,k′)-continuity
This section initially develops a Gk∗-adjacency relation in a digital product and establishes the notion of (Gk∗,ki)-continuity of a map from a digital product (X1×X2,Gk∗) to (Xi,ki),i∈{1,2}. These notions will be strongly used to develop a DT-k-group in Section 5.
In this section, we will use the following notations with several times.
(1) Gk∗-adjacency (see Definition 4.1).
(2) MSC18: The minimal simple 18-curve with 6 elements in Z3 with 26-contractibility (see (4.2)).
(3) NGk∗(p): The set of the elements of Gk∗-neighbors of the given point p in a digital space (X1×X2,Gk∗) (see (4.3)).
(4) NGk∗(p,1): A Gk∗-neighborhood of the given point p in a digital space (X1×X2,Gk∗) (see (4.4)).
Given two digital images (Xi,ki) in Zni,i∈{1,2}, using the Gk∗-adjacency relation in a digital product X1×X2 (see Definition 4.1 below) derived from the given (Xi,ki),i∈{1,2}, we obtain the relation set (X1×X2,Gk∗). Then, we first establish the notion of (Gk∗,ki)-continuity of a map from (X1×X2,Gk∗) to (Xi,ki),i∈{1,2}. This approach is a generalization of the (Ck∗,ki)-continuity of a map from (X1×X2,Ck∗) to (Xi,ki),i∈{1,2}, studied in Section 3. Let us establish the new Gk∗-adjacency relation of a digital product that will be strongly used for formulating a DT-k-group in Section 5. Using the condition (3.2), we can define the following:
Definition 4.1. Assume two digital images (Xi,ki:=ki(ti,ni)),Xi⊂Zni,i∈{1,2}. For distinct points p,q∈X1×X2, we say that the point p:=(x1,x2)∈X1×X2⊂Zn1+n2 is related to q:=(x′1,x′2)∈X1×X2 if
After that, considering this relation under the k∗:=k-adjacency of Zn1+n2, where k:=k(t,n1+n2),t=max{t1,t2}, we say that these two related points p and q are Gk∗-adjacent in X1×X2 derived from the given (Xi,ki:=ki(ti,ni)),Xi⊂Zni,i∈{1,2}. Besides this adjacency is called a Gk∗-adjacency of X1×X2⊂Zn1+n2 derived from the given two digital images (Xi,ki),i∈{1,2}. In addition, we use the notation (X1×X2,Gk∗) to denote this digital product X1×X2 with the Gk∗-adjacency (or a digital space (X1×X2,Gk∗)).
Remark 4.2. (1) In Definition 4.1, in case the given two points p and q are Gk∗-adjacent in X1×X2, they should be k∗:=k(t,n1+n2)-adjacent such that they satisfy only the condition of (4.1) of Definition 4.1, i.e., t=max{t1,t2} and the adjacency k∗ is one of the digital connectivity of Zn1+n2 stated in (1.1). This implies that a Gk∗-adjacency relation may not be equal to a k∗-adjacency one between two points in X1×X2. Namely, the Gk∗-adjacency relation in X1×X2 is a new one in X1×X2 that need not be equal to a certain k-adjacency relation in Zn1+n2 of (1.1).
(2) Comparing the Gk∗-adjacency relation in X1×X2 and the adjacency relation of a product graph in [11], we obviously make a distinction from each other.
We use the pair (X1×X2,Gk∗) to denote this digital product X1×X2 with a Gk∗-adjacency. Owing to Definition 4.1, the Gk∗-adjacency is always determined by (or derived from) the given ki-adjacency of (Xi,ki:=ki(ti,ni)),Xi⊂Zni,i∈{1,2}. After comparing among the adjacency relations of Definitions 3.2 and 4.1, and the typical k-adjacency of X1×X2⊂Zn1+n2, we can make a distinction among them, as follows:
Remark 4.3. (1) The Gk∗-adjacency relation of Definition 4.1 is broader than the Ck∗-adjacency of Definition 3.2. More precisely, as stated in Definition 3.2, given two digital images (Xi,ki:=k(ti,ni)) on Zni,i∈{1,2} (see Definition 3.2), not every X1×X2 has a Ck∗-adjacency. However, according to Definition 4.1, we always have a Gk∗-adjacency relation in the digital product X1×X2⊂Zn1+n2.
(2) Two k∗-adjacent points in X1×X2⊂Zn1+n2 need not be Gk∗-adjacent. However, the converse holds. By Definition 4.1, two Gk∗-adjacent points in X1×X2⊂Zn1+n2 are k∗-adjacent.
(3) We strongly stress on the number k∗:=k(t,n1+n2) of a Gk∗-adjacency relation. Note that the number t is equal to max{t1,t2} to determine the number k∗:=k(t,n1+n2) for the Gk∗-adjacency of X1×X2, where ki:=ki(ti,ni)),i∈{1,2}. Namely, the number k∗ of a Gk∗-adjacency absolutely depends on the given (Xi,ki:=ki(ti,ni)),i∈{1,2} and the number t=max{t1,t2}. For instance, consider SC2,48×SC2,68. Then we have only the G32-adjacency relation in the digital product SC2,48×SC2,68.
As a special case of Definition 4.1, we define the following:
Definition 4.4. Given a digital image (X,k:=k(t,n)),X⊂Zn, the number k∗:=k(t,2n) for a Gk∗-adjacency of X×X is determined by the number t of (X,k:=k(t,n)) such that any two Gk∗-adjacent points in X×X should only satisfy the condition (4.1) of Definition 4.1.
This Gk∗-adjacency of X×X with the condition of k∗:=k(t,n) plays a crucial role in establishing a DT-k-group in Section 5 (see Definition 5.5).
Remark 4.5. (1) In Definition 4.4, the number k∗ of Gk∗ is assumed in X×X⊂Z2n that is different from the number k of the k-adjacency of the given digital image (X,k:=k(t,n)),X⊂Zn.
(2) Given two digital images (Xi,ki),i∈{1,2}, according to the situation, i.e., either (X1,k1)≠(X2,k2) (see Definition 4.1) or (X1,k1)=(X2,k2) (see Definition 4.4), we will follow Definitions 4.1 or 4.4 when taking a choice of Gk∗.
(3) In view of Definition 4.4, given (X,k:=k(t,n)), there is at least k∗:=k(t,2n) establishing a Gk∗-adjacency of X×X (see Remark 4.3(1)). For instance, assume SC2,68:=(bj)j∈[0,5]Z in (3.7) (see also Figure 3(a)). Let ci,j:=(bi,bj)∈SC2,68×SC2,68. Then consider the point c2,2 in SC2,68×SC2,68. While the point c1,1:=(b1,b1) is typically 32-adjacent to c2,2, it is not G32-adjacent to c2,2. However, any G32-adjacent elements in SC2,68×SC2,68⊂Z4 are 32-adjacent.
In the case of SCn,lk×SCn,lk, we have some features of a Gk∗-adjacency compared to a Ck∗-one. To be specific, while SC2,68×SC2,68 has at least a G32-adjacency, it does not have any Ck∗-adjacency, k∗∈{32,64,80}.
Example 4.1. (1) Given (Z,2), (Z2,G4) exists.
(2) (SCn,lk×[a,b]Z,Gk∗) exists, where k∗=k(t,n+1) is determined by the number t of k:=k(t,n). For instance, we obtain (SC2,84×[0,1]Z) with G6-adjacency (see Figure 1(a)) and (SC2,68×[0,1]Z) with G18-adjacency (see Figure 1(b)).
Lemma 4.6. Given two SCni,liki,i∈{1,2}, there is always a Gk∗-adjacency of the digital product SCn1,l1k1×SCn2,l2k2, where k∗:=k(t,n1+n2),t=max{t1,t2} and ki:=ki(ti,ni),i∈{1,2}. However, this Gk∗-adjacency need not be equal to a Ck∗-adjacency.
Proof: By Definition 4.1, with the hypothesis, we always have a Gk∗-adjacency of SCn1,l1k1×SCn2,l2k2 (see also Remark 4.3). To be specific, the Gk∗-adjacency of SCn1,l1k1×SCn2,l2k2 is determined by the number t=max{t1,t2}, where k∗:=k(t,n1+n2).
However, as mentioned in Remark 4.3, since not every SCn1,l1k1×SCn2,l2k2 has a Ck∗-adjacency, the Gk∗-adjacency of SCn1,l1k1×SCn2,l2k2 need not imply the Ck∗-adjacency of it. For instance, as mentioned in Remark 4.5(3), while we have a G32-adjacency for SC2,68×SC2,68, any k∗-adjacency, k∗∈{32,60,80}, cannot be a Ck∗-adjacency of it.
In view of Definitions 3.2, 4.1, and 4.4, and Remark 4.3, after comparing the Gk∗-adjacency with the Ck∗-adjacency relation, we observe that a Gk∗-adjacency relation is relatively weaker and softer than a Ck∗-one. As a generalization of Lemma 4.6, we obtain the following:
Corollary 4.7. In case there is a Ck∗-adjacency of X1×X2 derived from (Xi,ki) on Zni,i∈{1,2}, a Ck∗-adjacency of X1×X2 implies a Gk∗-adjacency of X1×X2 of Definition 4.1. However, in general, a Gk∗-adjacency in X1×X2 of Definition 4.1 need not imply a Ck∗-adjacency in X1×X2.
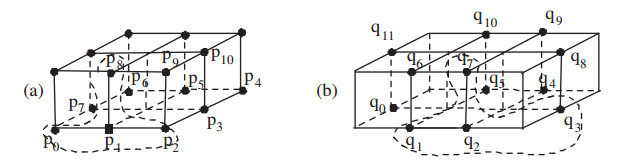
As a special case of SC3,618, let us recall the digital image MSC18⊂Z3 that is 26-contractible [8,9] (see Figure 2). For instance, we may take the set with an 18-adjacency as follows:
Then, MSC18 is 26-contractible [8,9]. Owing to this feature, the set MSC18 has been often called a minimal simple closed 18-curve in Z3 [8]. In Example 4.2 below, we will take a Gk∗-adjacency relation in MSC18×MSC18. Motivated by Theorem 3.11 and Lemma 4.6, and Definitions 3.2 and 4.1, we obtain the following:
Corollary 4.8. Given two SCni,liki,i∈{1,2}, assume that there is a Ck∗-adjacency of the digital product SCn1,l1k1×SCn2,l2k2 derived from the given SCni,liki,i∈{1,2}, where k∗:=k(t,n1+n2),t=max{t1,t2} and ki:=ki(ti,ni),i∈{1,2}. Then the Ck∗-adjacency in the digital product SCn1,l1k1×SCn2,l2k2 is equivalent to the Gk∗-adjacency in SCn1,l1k1×SCn2,l2k2.
Example 4.2. (1) SC2,48×SC2,68⊂Z4 has both a C32-adjacency and a G32-adjacency.
(2) MSC18×MSC18⊂Z6 does not have any Ck∗-adjacency such that k∗∈{72,232,472,664,728} (see Figure 2 and (1.2)).
(3) MSC18×MSC18⊂Z6 has a G72-adjacency (see Figure 2 and (1.2)).
Let us further characterize the Gk∗-adjacency relation using a certain neighborhood of a point of X1×X2. Based on the Gk∗-adjacency of Definition 4.1, we now establish the following Gk∗-neighborhood of a given point of X1×X2.
Definition 4.9. Given two digital images (Xi,ki:=k(ti,ni)),Xi⊂Zni,i∈{1,2}, assume the Cartesian product X1×X2⊂Zn1+n2 with a Gk∗-adjacency. For a point p∈X1×X2, we define
and
Then we call NGk∗(p,1) a Gk∗-neighborhood of p.
Corollary 4.10. In view of (4.4), for a digital product with a Gk∗-adjacency (X1×X2,Gk∗) and a point p:=(x1,x2)∈X1×X2, we have the following:
Based on Definition 4.4, we have the following:
Example 4.3. (1) Given a finite digital line ([0,l]Z,2), assume the set X:=[0,l]Z×[0,l]Z⊂Z2. Then we can take the Gk∗-adjacency on X⊂Z2 derived from ([0,l]Z,2) such that k∗:=k(1,2), i.e., k∗=4. Besides, each of these NGk∗(p,1)⊂X is equal to the N4(p,1)⊂X.
(2) In SC2,68×SC2,68 (see the elements of SC2,68 in (3.7) and Definition 4.4), we obtain
because
(3) No NC32(c2,2,1) exists because SC2,68×SC2,68 does not have C32-adjacency (see the points c1,1 and c2,2 of SC2,68×SC2,68).
Based on Remark 4.3 and the property of (4.4), we obtain the following:
Remark 4.11. Owing to the structure of (4.3), with the hypothesis stated in Definition 4.9, we obtain the following:
(1) NGk∗(p,1) always exists in X1×X2, where the number t of k:=k(t,n1+n2) is equal to the number "max{t1,t2}".
(2) NGk∗(p) need not be equal to N∗k∗(p), where N∗k∗(p):={q∈X1×X2|qisk∗−adjacenttop}, where the number k∗ is the digital connectivity of X1×X2 stated in (1.1).
(3) Not every Nk∗(p,1) is always equal to NGk∗(p,1),p∈X1×X2.
Let us characterize NGk∗(p) with some examples.
Example 4.4. Let us consider the digital images X1:=SC2,68:=(bj)j∈[0,5]Z in (3.7) (see also Figure 3(a)) and (X2:=[0,1]Z,2). Then, for a point p1:=(b1,0)∈X1×X2 (see Figure 3(b)), we can consider an NG18(p1,1) (see Figure 3(c)) in the digital product (X1×X2,G18) (see Figure 3(b)). Then, for the point p1:=(b1,0)=(1,−1,0), we obtain the following (see Figure 3(c)):
where p0:=(b0,0),p2:=(b2,0) (see Figure 3(b)). Then, we obviously observe that while the point p7:=(b2,1) is 18-adjacent to p1, it is not G18-adjacent to p1 (compare the objects in Figure 3(c) and (d)).
Remark 4.12. Given two digital images (Xi,ki:=k(ti,ni)),i∈{1,2}, assume a Gk∗-adjacency at a point p:=(x1,x2)∈X1×X2. Then, we have the following identity
Owing to the symmetric relation of a Gk∗-adjacency, we can obtain the following: Given two digital images (Xi,ki) in Zni,i∈{1,2}, assume the Cartesian product X1×X2⊂Zn1+n2 with a certain Gk∗-adjacency. We say that two points z,w∈X1×X2 are Gk∗-connected (or Gk∗-path connected) if there is a finite Gk∗-path (z0,z1,⋯,zm)⊂X1×X2 from z to w on X1×X2 such that z0=z and zm=w, where we say that a Gk∗-path from z to w in X1×X2 means a finite sequence (z0,z1,⋯,zm)⊂X1×X2 such that zi is Gk∗-adjacent to zj if j=i+1,i∈[0,m−1]Z or i=j+1,j∈[0,m−1]Z. We say that a digital product (X1×X2,Gk∗) is Gk∗-connected (or Gk∗-path connected) if any two points z,w∈X1×X2 are Gk∗-connected (or Gk∗-path connected). A singleton with Gk∗-adjacency, it is assumed to be Gk∗-connected. Given a Gk∗-adjacency relation in X1×X2, a simple Gk∗-path from z to w in X1×X2 is assumed to be the Gk∗-path (zi)i∈[0,l]Z⊂X1×X2 such that zi and zj are Gk∗-adjacent if and only if either j=i+1,i∈[0,l−1]Z or i=j+1,j∈[0,l−1]Z and z0=x and zl=y. Also, a simple closed Gk∗-curve with l elements in X1×X2⊂Zn1+n2, denoted by SCn,lGk∗,4≤l∈N, is a sequence (zi)i∈[0,l−1]Z in X1×X2, where zi and zj are Gk∗-adjacent if and only if |i−j|=±1(modl).
In view of these notions, we can take the following:
Remark 4.13. Given an (X1×X2,Gk∗) derived from (Xi,ki),i∈{1,2}, we have the following:
(1) While a Gk∗-path implies a k∗-path, the converse does not hold, where the k∗-adjacency is one of the typical adjacency of (1.1).
(2) SCn,lGk∗ need not be equal to SCn,lk∗. For instance, based on the digital products (SC2,88×[0,1]Z,G18) and (SC2,88×[0,1]Z,18), let us consider two digital images with a G18- and an 18-adjacency such as SC3,8G18 and SC3,818, respectively. As shown in Figure 4, assume a digital product SC2,88×[0,1]Z with a G18-adjacency (see Figure 4(a) and Figure 3(a)). It is clear that the set SC3,8G18:=(x0,x1,⋯,x7) in Figure 4(b) is an SC3,818, where x0:=p0,x1:=p1,x2:=p2,x3:=p3,x4:=p8,x5:=p9,x6:=p10,x7:=p11. However, SC3,818 in (c) is not an SC3,8G18 (see the objects in Figure 4 (a) and (c)).
Given a Gk∗-adjacency relation in a Cartesian product, we also have a certain digital space [7] associated with a Gk∗-adjacency relation, as follows:
Proposition 4.14. Given ki-connected digital images (Xi,ki),Xi⊂Zni,i∈{1,2}, the relation set (X1×X2,Gk∗) is a digital space.
Proof: Since the relation Gk∗-adjacency in X1×X2 is symmetric, we examine if (X1×X2,Gk∗) is Gk∗-connected. Take any distinct points p:=(x1,x2) and q:=(x′1,x′2) in X1×X2. Then, without loss of generality, we may assume the case x1⪇x′1 and x2≤x′2 or the case x1≤x′1 and x2⪇x′2. For the purpose of this study, we may take the first case, i.e., x1⪇x′1 and x2≤x′2. Then consider the differences |x1−x′1|⪈0 and |x2−x′2|≥0. According to the size of these finite differences, we can take a finite set
such that pi is Gk∗-adjacent to pi+1 in X1×X2,i∈[1,n−1]Z and
Owing to (4.7) and (4.8), we can conclude that (X1×X2,Gk∗) is Gk∗-connected.
Based on the relation set (X1×X2,Gk∗), we obtain the following:
Lemma 4.15. Assume the digital space (X1×X2,Gk∗) derived from two digital images (Xi,ki),Xi⊂Zni,i∈{1,2}. Then, for a point p∈X1×X2, we always obtain NGk∗(p,1)⊂Nk∗(p,1). However, NGk∗(p,1) need not be equal to Nk∗(p,1), i.e., (NGk∗(p,1))♯≤(Nk∗(p,1))♯.
Proof: For any point q∈NGk∗(p,1), according to the property (2.4) and Remark 4.3 and 4.11, we obtain q∈Nk∗(p,1). However, in view of Example 4.4 as a counterexample, we can disprove Nk∗(p,1)⊂NGk∗(p,1). Naively, consider the digital product (SC2,88×X2,G18) in Example 4.4. Then we can confirm NG18(p,1)⊊N18(p,1) (see Figure 3(c) and (d)).
Based on Definition 4.1, we obtain the following:
Proposition 4.16. Given two digital images (Xi,ki), Xi⊂Zni,i∈{1,2}, assume a Cartesian product X1×X2 with a Ck∗-adjacency. Then, for a point p∈X1×X2, while q∈NCk∗(p,1) implies q∈NGk∗(p,1), the converse does not hold.
Proof: With the hypothesis, it is clear that q∈NCk∗(p,1) implies q∈NGk∗(p,1). However, the converse does not hold with the following counterexample. Consider the digital product SC2,44×SC2,68:=(ci,j), where ci,j:=(ai,bj) and SC2,44:=(ai)i∈[0,3]Z and SC2,68:=(bj)j∈[0,5]Z in (3.7). Then, for the point c2,2, we obviously have NG32(c2,2,1) (see Definition 4.1) that consists of five elements. However, no NC32(c2,2,1) exists because the element c2,2 does not have any C32-adjacent to a point in the product SC2,44×SC2,68⊂Z4.
Corollary 4.17. Based on Definition 4.1, assume two digital images (Xi,ki), Xi⊂Zni,i∈{1,2}, and the Cartesian product X1×X2⊂Zn1+n2. Not every point p∈X1×X2 always has an NCk∗(p,1). However, in case there is a Ck∗-adjacency on X1×X2, we obtain
Namely, each of the Ck∗- and the Gk∗-adjacency is equal to the typical k∗-adjacency of (1.1).
Proof: By Definitions 3.5 and 4.1 and the properties (3.5) and (4.4), the proof is completed.
Based on the Gk∗-adjacency of a digital product, let us introduce the concept of (Gk∗,k′)-continuity of a map f:(X1×X2,Gk∗)→(Y,k′).
Definition 4.18. Given two digital images (Xi,ki), Xi⊂Zni,i∈{1,2}, consider the digital space (X1×X2,Gk∗) and a digital image (Y,k′). A function f:(X1×X2,Gk∗)→(Y,k′) is (Gk∗,k′)-continuous at a point p:=(x1,x2) if for any point q∈X1×X2 such that q∈NGk∗(p) (denoted by p↔Gk∗q), we obtain f(q)∈Nk′(f(p),1) (denoted by f(p)⇔k′f(q)). In case the map f is (Gk∗,k′)-continuous at each point p∈X1×X2, we say that the map f is (Gk∗,k′)-continuous.
The (Gk∗,k′)-continuity of Definition 4.18 can be represented by using both a Gk∗-neighborhood and a digital k′-neighborhood, as follows:
Proposition 4.19. Consider a Cartesian product X1×X2⊂Zn1+n2 with a Gk∗-adjacency and a typical digital image (Y,k′). A map f:(X1×X2,Gk∗)→(Y,k′) is (Gk∗,k)-continuous at the point p∈X1×X2 if and only if
A map f:(X1×X2,Gk∗)→(Y,k′) is (Gk∗,k)-continuous if and only if for every point p∈X1×X2 we have
As a special case of Proposition 4.19, based on Definition 4.4, we can consider the following:
Corollary 4.20. Given a digital image (X,k),X⊂Zn. Consider a Cartesian product X×X⊂Zn1+n2 with a Gk∗-adjacency. Consider a map f:(X×X,Gk∗)→(X,k). For a point p:=(x1,x2)∈X×X, the map f is (Gk∗,k)-continuous at the point p if and only if
A map f:(X×X,Gk∗)→(X,k) is (Gk∗,k)-continuous at every point p∈X×X, then the map f is (Gk∗,k)-continuous.
Example 4.5. (1) Assume a digital product (SC2,68×[0,1]Z):={pi|i∈[0,11]Z} with a G18-adjacency. Consider the map
defined by (see Figure 5(1))
Then the map g is a (G18,2)-continuous map.
(2) Assume a digital product (SC2,68×[0,1]Z) with a G18-adjacency and a subset X:={xi|i∈[0,7]Z} (see Figure 5(2)(a)) and Y:={yi|i∈[0,7]Z} (see Figure 5(2)(b)) with an 18-adjacency which is different from (X,G18). Consider the map f:(X,G18)→(Y,18) defined by f(xi)=yi,i∈[0,7]Z. Then the map f is a (G18,18)-continuous map because f(NG18(xi,1))⊂N18(f(xi),1).
Corollary 4.21. Let (X,2n) be a 2n-connected subset of (Zn,2n). Then each of the typical projection maps Pi:(X×X,G4n)→(X,2n) is a (G4n,2n)-continuous map, i∈{1,2}, such that the G4n-adjacency is equal to the typical 4n-adjacency.
With some hypothesis of the Gk∗-adjacency of X×X, the (Gk∗,k)-continuity of Corollary 4.20 will play a crucial role in establishing a certain continuity of a multiplication for formulating a DT-k-group (see Definition 5.5). Let us compare the (Gk∗,k′)-continuity and the typical (k,k′)-continuity.
Theorem 4.22. While the (Gk∗,k′)-continuity implies the typical (k∗,k′)-continuity, the converse does not hold.
Proof: By Definition 4.18 and Lemma 4.15, the proof is completed.
Corollary 4.23. While the (Ck∗,k′)-continuity implies the (Gk∗,k′)-continuity, the converse does not hold.
Proof: By Propositions 3.9, 4.16, and 4.19, and Corollary 4.20 the proof is completed.
Corollary 4.24. In case there is a Ck∗-adjacency of X1×X2, the (Ck∗,k′)-, the (Gk∗,k′)-, and the (k∗,k′)-continuity are equivalent to the other.
Proof: By Corollary 4.17, the proof is completed.
In view of Definitions 3.2 and 4.1, we obtain the following:
Remark 4.25 (Advantages of the Gk∗-adjacency of a digital product). Given two digital images (X,k1) and (Y,k2), there is always a Gk∗-adjacency derived from the two given digital images. However, an existence of Ck∗-adjacency of a digital product X×Y depends on the situation. Thus the Gk∗-adjacency of a digital product will be used in establishing a digital topological version of a typical topological group in Section 5. Furthermore, since the Gk∗-adjacency is a generalization of the Ck∗-adjacency of a digital product, some strong utilities of the Gk∗-adjacency can be considered in establishing DT-k-group structures (see Definition 5.5).
5.
A development of a DT-k-group with the most suitable adjacency for a digital product X×X from (X,k)
This section introduces the notion of a DT-k-group derived from a digital image (X,k) with a certain group structure (X,∗). Before proceeding with this work, given a digital image (X,k), we now recall some differences between the Ck∗-adjacency and the Gk∗-adjacency of a digital product X×X mentioned in Remarks 4.3 and 4.3. Naively, a Gk∗-adjacency of a digital product X×X is a generalization of a Ck∗-adjacency of it (see Remark 4.25). As mentioned in Remark 4.5(3), given a digital image (X,k:=k(t,n)),X⊂Zn, we always have at least a certain Gk∗-adjacency of a digital product X×X, where k∗:=k(t,2n) is determined by the number t of (X,k:=k(t,n)). Hence, in relation to the establishment of a DT-k-group, we will follow only this Gk∗-adjacency of a digital product X×X unless stated otherwise.
In this section, we will use the following notations with several times.
(1) (SCn,lk,∗): A digitally k-group with the given binary operation ∗ on SCn,lk (see Proposition 5.3).
(2) (Zn,2n,+): A digitally 2n-group with the given binary operation + on Zn (see Theorem 5.8)).
(3) N1: The set of odd natural numbers (see Example 5.1).
Remark 5.1. When studying DT-k-groups (X,k,∗), for a digital image (X,k:=k(t,n)),X⊂Zn, we will recall the following notions from Definitions 3.8 and 4.18 that will be essentially used in this section, e.g., the Gk∗- and Ck∗-adjacency of a digital product X×X⊂Z2n and the related continuities.
(1) We will take only the Gk∗-adjacency of a digital product X×X such that k∗:=k(t,2n) is determined by the number t of (X,k:=k(t,n)), so that this Gk∗-adjacency always exists. Furthermore, for each point p∈X×X, NGk∗(p,1) is uniquely determined (see Definitions 3.5 and 4.9 and the properties of (3.1) and (4.5), Example 4.2(3), and Remark 4.11(1)). Hence this Gk∗-adjacency, k∗:=k(t,2n), is enough to establish the notion of a DT-k-group derived from a digital image (X,k) with a certain group structure (X,∗).
(2) In relation to a digital space (X×X,Ck∗) derived from (X,k:=k(t,n)),X⊂Zn (see Proposition 3.7), we also take only k∗:=k(t,2n), where the number t of k∗:=k(t,2n) is exactly equal to the number t of (X,k:=k(t,n)).
(3) Based on this approach, we will take a Gk∗ (resp. Ck∗)-neighborhood of a given point in a digital space (X×X,Gk∗) (resp. (X×X,Ck∗)). Hence, the (Gk∗,k) (resp., (Ck∗,k))-continuity of Definition 4.18 (resp. Definition 3.8) is considered (see also Definition 4.4) for formulating a DT-k-group using only the k∗:=k(t,2n)-adjacency, where k∗:=k(t,2n) is induced by the number t of (X,k:=k(t,n)).
Lemma 5.2. The set Z2n,n∈N, has a G4n-adjacency derived from (Zn,2n) such that this G4n-adjacency is equal to the C4n-one derived from (Zn,2n), i.e., G4n=4n=C4n.
Proof: By Definitions 3.2 and 4.1, and Corollary 4.17, the proof is completed. To be specific, take a point p:=(p1,p2)∈Zn×Zn=Z2n. Since
and this NG4n(p,1) is equal to NC4n(p,1), the proof is completed.
Let us establish a group structure on the digital image SCn,lk.
Proposition 5.3. Given an SCn,lk:=(xi)i∈[0,l−1]Z for any k-adjacency of Zn, we have a group structure on SCn,lk with the following operation ∗.
given by
Then we denote by (SCn,lk,∗) the above group.
Proof: First, the operation "∗" is well-defined on SCn,lk as a binary operation for establishing a group structure on SCn,lk. Second, based on the property (5.1), the operation "∗" is associative. Third, the element x0 is the identity element and for two elements xi,xj∈SCn,lk
Hence, each element xi(≠x0) uniquely has xl−i as the inverse element and the element x0 has the inverse itself.
Example 5.1. (1) Given SCn,lk:=(xi)i∈[0,l−1]Z with l∈N0, there are only two elements such as x0 and xl2 in SCn,lk such that (x0)−1=x0 and (xl2)−1=xl2, where x−1 means the inverse element of x (see the two elements x0,x3 of SC2,68).
(2) Given SCn,lk:=(xi)i∈[0,l−1]Z with l∈N1, there is only one element such as x0 in SCn,lk whose inverse is itself (see the element x0 of SC3,526).
Remark 5.4. (1) Given an SCn,lk:=(xi)i∈[0,l−1]Z, according to our needs, we can relabel the elements of SCn,lk to obtain a new type of SCn,lk:=(yi)i∈[0,l−1]Z. Then the element y0 is the identity element of the group (SCn,lk:=(yi)i∈[0,l−1]Z,∗).
(2) The group (SCn,lk,∗) in Proposition 5.3 is abelian.
Based on the Gk∗-adjacency of X×X and the (Gk∗,k)- as well as the (Ck∗,k)-continuity stated in Remark 5.1(1) and (3), we now define the following.
Definition 5.5. A digitally topological k-group, denoted by (X,k,∗) and called a DT-k-group for brevity, is a digital image (X,k:=k(t,n)) combined with a group structure on X⊂Zn using a certain binary operation ∗ such that for (x,y)∈X2 the multiplication
and the inverse map
where the number k∗:=k(t,2n) of the Gk∗-adjacency of (5.3) is determined by only the number t of the k:=k(t,n)-adjacency of the given digital image (X,k:=k(t,n)).
In Definition 5.5, as for the Gk∗-adjacency of X×X, we strongly recall the requirement in Remark 5.1(1) and (3).
Remark 5.6. In view of Definition 5.5, a DT-k-group, (X,k,∗) has the two structures such as the digital image (X,k) and the certain group structure (X,∗) satisfying the properties of (5.3) and (5.4).
By Corollary 4.17, we have the following:
Corollary 5.7. In case there is a Ck∗-adjacency of X×X, i.e., a digital space ∃(X×X,Ck∗), the condition "(Gk∗,k)-continuous" of (5.3) of Definition 9 can be replaced by "(Ck∗,k)-continuous" because a Ck∗-adjacency of X×X implies a Gk∗-adjacency of it (see Corollaries 4.6 and 4.25). For instance, for the case SC2,48, SC2,48×SC2,48 can be assumed to be a digital space (SC2,48×SC2,48,C32). Thus we have a digital space (SC2,48×SC2,48,G32) (see Remark 4.3(1)). Hence the condition "(G32,8)-continuous" of (5.3) of Definition 5.5 may be replaced by "(C32,8)-continuous" or "(32,8)-continuous" because G32=32=C32.
Theorem 5.8. (Zn,2n,+) is a DT-2n-group.
Proof: First, (Zn,+) is a group with the following operation [15]. For two elements p:=(p1,⋯,pn),q:=(q1,⋯,qn)∈Zn, we define
Then, the operation "+" is a binary operation on Zn supporting the group (Zn,+) because it is associative, and it has the identity element 0n:=(0,⋯,0) with n-tuples and the inverse element of an element p, denoted by p−1, is equal to −p [15].
Using Example 3.2, Definitions 3.8 and 4.18, and Propositions 3.9 and 4.19 and Corollary 4.20, let us propose the DT-2n-group structure of (Zn,2n,+). To be specific, by Lemma 5.2, we have both a G4n- and a C4n-adjacency of Zn×Zn induced by the given (Zn,2n) such that G2n=C2n=2n. Hence, by Corollary 4.17, we may take G4n=4n to support the (G4n,2n)-continuity of the multiplication (see (3.13) and (4.9))
given by α(p,q):=p+q defined in (5.5).
To be precise, take any distinct points P:=(p,q),Q:=(p′,q′)inZn×Zn such that
More precisely, assume the two points P,Q such that
Then we may consider the two cases: The following four points that are components of the given two points P,Q∈Zn,
satisfy one of the following two cases.
(1) For the points p and p′ in Zn, owing to (5.7), there is only one i0∈[1,n]Z such that
(2) For the points q and q′ in Zn, there is only one j0∈[1,n]Z such that
Let us investigate these two cases more precisely.
(Case 1) Based on the above case (1), consider the mapping of the two points P and Q by the above map α, i.e.,
Owing to the properties of (5.8) and (5.9), the property (5.10) implies that
implying that the map α is (G4n,2n)-continuous at the point P∈Zn×Zn (see Definition 4.18 and Corollary 4.20).
(Case 2) With the above case (2), after considering the mapping of the two points P and Q by the above map α in (5.10), using a method similar to the approach of (Case 1), we obtain
implying that the map α is (G4n,2n)-continuous at the point P∈Zn×Zn (see Definitionv4.18 and Corollary 4.20).
For instance, let us show the DT-4-group structure of (Z2,4,+), as follows: Assume the two points
such that
where p:=(xi)i∈[1,2]Z, q:=(yj)j∈[1,2]Z, p′:=(x′i)i∈[1,2]Z, and q′:=(y′j)j∈[1,2]Z. Then, we consider the following two cases as mentioned above.
As for the (Case 1) above, in case there is only one i0∈[1,2]Z such that xi0≠x′i0 with |xi0−x′i0|=1 and for i∈[1,2]Z∖{i0}, we have xi=x′i, and yj=y′j,j∈{1,2} (see (5.8) and (5.9)). Then consider the mapping of the two points P and Q by the above map α such that
Then we obtain
Hence the map α is (G8,4)-continuous at the point P∈Z2×Z2 (see Corollary 4.20).
As for the (Case 2) above, in case there is only one j0∈[1,2]Z such that yj0≠y′j0 with |yj0−y′j0|=1 and for j∈[1,2]Z∖{j0}, we have yj=y′j, and xi=x′i,i∈{1,2} (see (5.8) and (5.9)). Then, after considering the mapping of the two points P and Q by the above map α using a method similar to the approach above, we obtain
implying that the map α is (G8,4)-continuous at the point P∈Z2×Z2 (see Corollary 4.20).
By Lemma 5.2, this (G8,4)-continuity of α is exactly equal to (8,4)-continuity of it.
Besides, there is also the 2n-continuity of the inverse map
given by
Naively, for any point p∈Zn, by Proposition 2.1, we obtain
implying that (Zn,2n,+) is a DT-2n-group.
Regarding the continuity of (5.6), note that the points (x,x) and (y,y) are not G2n-adjacent in Zn×Zn, where x:=(0,0,⋯,0) and y:=(1,0,⋯,0) in Zn (see Definition 4.1).
Remark 5.9. In Theorem 5.8, by Lemma 5.2, the (G4n,2n)-continuity of the map α of (5.6) is exactly equal to (4n,2n)-continuity of α (see the (Case 1) and (Case 2) in the proof of Theorem 5.8). For instance, consider a multiplication from (Z2,G4)→(Z,2) (see Figure 6). Then it is clear that it is (G4,2)-continuous (see Figure 6), which supports a DT-2-group of (Z,2,+). To be specific, for convenience, for each i∈Z, let Xi:={(x,y)|y=−x+i,x,y∈Z}⊂Z2. Then the G4-adjacency is equal to the C4-adjacency so we obtain each of G4- and C4-adjacency is equal to the 4-adjacency of Z2. For instance, consider the multiplication α:(Z2,G4)→(Z,2) is defined as α(Xi)=i. Then the map α is clearly (G4,2)-continuous.
Based on Definition 4.4 and (3.13) and (4.9), Remark 4.25, and Corollary 4.20, let us establish a DT-k-group structure of (SCn,lk,∗) derived from a Gk∗-adjacency of the digital product (SCn,lk×SCn,lk,Gk∗).
Proposition 5.10. (SCn,lk,∗) is a DT-k-group for any k-adjacency of Zn.
Proof: By Proposition 5.3, (SCn,lk,∗) is a group, where k:=k(t,n). Let us assume a Gk∗-adjacency on the Cartesian product SCn,lk×SCn,lk such that k∗:=k(t,2n).
Naively, we obtain the relation set (see Proposition 4.14)
where the number k∗:=k(t,2n) of the Gk∗-adjacency is determined by the number t of k:=k(t,n) from SCn,lk. For the purpose of this study, given SCn,lk:=(xi)i∈[0,l−1]Z, assume the set SCn,lk×SCn,lk as an (l×l)-matrix as follows:
Based on the structure of (5.11), let us further assume the map
Consider each point
Then, owing to the existence of a Gk∗-adjacency on the Cartesian product SCn,lk×SCn,lk, for any p=(xi,xj)∈SCn,lk×SCn,lk (see Remark 5.1(1)), we obviously have the set NGk∗(p,1) (see (5.13)) such that
implying the (Gk∗,k)-continuity of the map α (see Corollary 4.20).
Next, let us assume the map
Then we now prove that the map β is also k-continuous. To be precise, for any element xi∈SCn,lk, take the set Nk(xi,1). Then, owing to the map β, by Proposition 2.1, we have
implying that the map β is k-continuous.
Regarding the continuity of (5.12), note that the points (x0,x0) and (x1,x1) are not Gk∗-adjacent in SCn,lk×SCn,lk (see Definition 4.1). By Corollaries 4.17, 4.20, and 5.7, we obtain the following:
Corollary 5.11. In case the digital product SCn,lk×SCn,lk has a Ck∗-adjacency (see Theorem 3.11), i.e., ∃(SCn,lk×SCn,lk,Ck∗), (SCn,lk,∗) is a DT-k-group using the Ck∗-adjacency. Then, the multiplication of α related to this DT-k-group of (SCn,lk,∗) is (k∗,k)-continuous.
Proof: By Corollaries 4.18 and 5.7, and Proposition 5.10, the proof is completed.
In a DT-k-group (X,k,∗), in case the group (X,∗) is abelian, we say that the DT-k-group (X,k,∗) is abelian.
Remark 5.12. (1) There are various types of SCn,lk, e.g., SC3,618 that is not 26-contractible and MSC18, that lead to DT-k-groups of them.
(2) The DT-k-group (SCn,lk,∗) in Proposition 5.10 is abelian
Example 5.2. (1) (SC2,44,∗) is an abelian DT-4-group.
(2) (SC2,68,∗) is an abelian DT-8-group.
(3) (SC3,526,∗) is an abelian DT-26-group.
(4) (MSC18,∗) is an abelian DT-18-group.
Remark 5.13. A finite digital plane (X,k),X⊂Zn, need not be a DT-k-group.
6.
Remarks on the earlier approach to a digital topological version of a topological group in the literature of [16]
Motivated by the typical topological group [12,17], the paper [16] tried to formulate a digital version of a topological group called a "topological k-group". Then, the paper [16] used the notion of a minimal k-adjacency derived from the conditions of (6.1) below for supporting a kind of continuity of a multiplication associated with a topological k-group. This approach is quite different from the current one in the present paper. Furthermore, in case we follow the approach in [16], we will come across some fatal errors or the obtained results are trivial cases. Besides, the paper [16] referred to several examples and some properties related to a topological k-group. However, since the paper [16] started with a very insufficient, incorrect, and rough adjacency for a digital product, the obtained results related to the study of a topological k-group (see Section 4 of [16]) are mainly incorrect. More precisely, the paper [16] used the so-called the minimal adjacency of a digital product [16] that is incorrect or trivial, as follows:
Given two digital images (Xi,ki:=k(ti,ni)) in Zni,i∈{1,2}, the paper [16] defined the so-called "minimal adjacency", k∗, for a Cartesian product X1×X2, and denote by (X×X,k∗). Then the k∗-adjacency was derived from the following approach.
Given the Cartesian product X1×X2⊂Zn1+n2, the paper [16] says that two points (x1,x2), (x′1,x′2) in X1×X2 are "minimal k∗-adjacent" to each other if they satisfy "one of the following conditions"
In particular, first of all, we recall the conditions (2)–(4) are exactly equal to the conditions for establishing a normal k-adjacency of a digital product in [5]. Hence we need to cite it appropriately. Besides, based on the conditions of (6.1) formulating a minimal k∗-adjacency in [16] to establish a topological k-group, the paper [16] requires "one of the four conditions" to establish the so-called "minimal k∗-adjacency" of a digital product. Unfortunately, the approach using one the conditions of (6.1) leads to either trivial or incorrect results with the following reason. Based on the adjacency determined by the conditions of (6.1) suggested in [16], for our purposes, let us assume t1≤t2 in (Xi,ki:=k(ti,ni)) in Zni,i∈{1,2}. Then, let us examine if the requirement of "one of the four conditions" of (6.1) is meaningful as a condition for establishing a topological k-group.
Remark 6.1. (1) Let us assume only the first condition (1) of (6.1). Then we have a reflexive relation in the digital product, implying that the adjacency invokes a discrete case up to k-adjacency of a digital product. Namely, every point has only the reflexive self-adjacency that invokes a discrete relation in X1×X2 from the viewpoint of digital k-connectivity. Indeed, a discrete relation in a digital image is useless because every self-map of the digital product with any k-adjacency of (1.1) is continuous.
(2) In case we follow only the second condition (2) of (6.1), it might not satisfy the continuity of a multiplication of α:X×X→X (see the case of MSC18). For instance, in the case of MSC18, even though the notion of a "minimal adjacency of a digital product" in [16], according to [16], we may take a 72-adjacency of the digital product MSC18×MSC18⊂Z6 for the (72,18)-continuity of the multiplication MSC18×MSC18→MSC18. Then we obviously see that this multiplication MSC18×MSC18→MSC18 cannot be (72,18)-continuous (see Proposition 2.1).
(3) In case we take only one of the conditions (3)–(4) of (6.1), it also might not satisfy the continuity of a multiplication of α:X×X→X (see the case of MSC18 with the method used in (2) above).
Thus the approach using the condition of (6.1) cannot be suitable for establish a topological k-group.
Unlike the approach in [16], by Proposition 5.10, using the G72-adjacency of MSC18×MSC18⊂Z6, the pair (MSC18,∗) is an abelian 18-connected topological 18-group. However, it is not related to the conditions stated in (6.1). In view of Definition 4.4, the set of elements that are G72-adjacent in MSC18×MSC18 is a proper subset of elements that are 72-adjacent in MSC18×MSC18.
Example 6.1. The DT-18-group (MSC18,∗) using (5.12) guarantees the assertion of Remark 6.1.
7.
Some remarks and a further work
After developing several notions such as a Ck∗- and a Gk∗-adjacency of a digital product X×X derived from a given digital image (X,k) and a Ck∗- and a Gk∗-neighborhood of a point in (X×X,Ck∗) and (X×X,Gk∗) respectively, we established two types of continuities of a multiplication (X×X,Ck∗)→(X,k) or (X×X,Gk∗)→(X,k). Based on this approach, we finally formulated a DT-k-group. Besides, the paper gave various examples of DT-k-groups with some special kinds of binary operations.
As a further work, we can classify DT-k-groups in terms of a certain isomorphism from the viewpoint of DT-k-group theory.
Acknowledgements
The author was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education, Science and Technology(2019R1I1A3A03059103). Besides, this work was supported under the framework of international cooperation program managed by the National Research Foundation of Korea(2021K2A9A2A06039864).
Conflicts of interest
The author declares no conflict of interest.









 DownLoad:
DownLoad: